Adaptive Latin Hypercube Sampling for a Surrogate-Based Optimization with Artificial Neural Network
Abstract
:1. Introduction
2. Sampling Technique and Surrogate Modeling
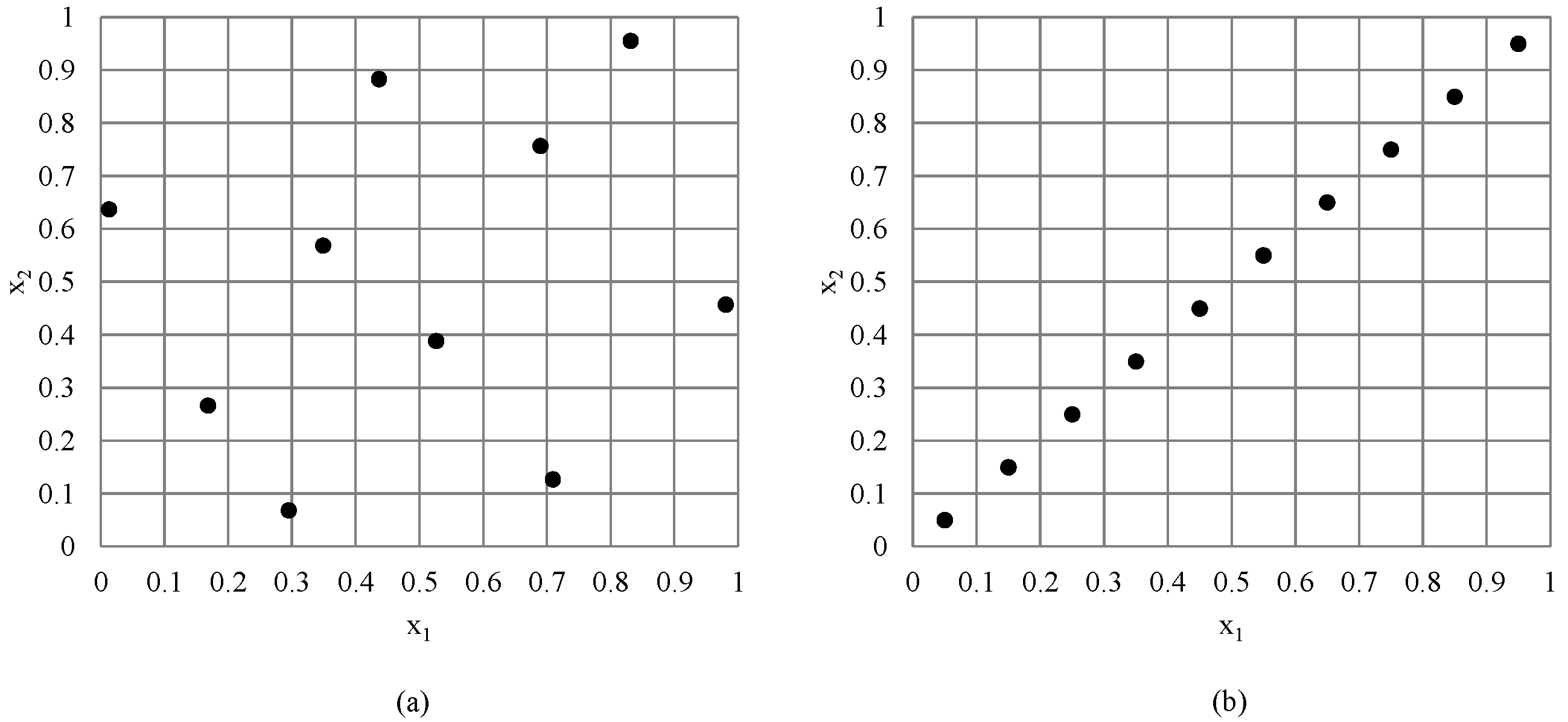
2.1. Latin Hypercube Sampling
2.2. Random Sampling
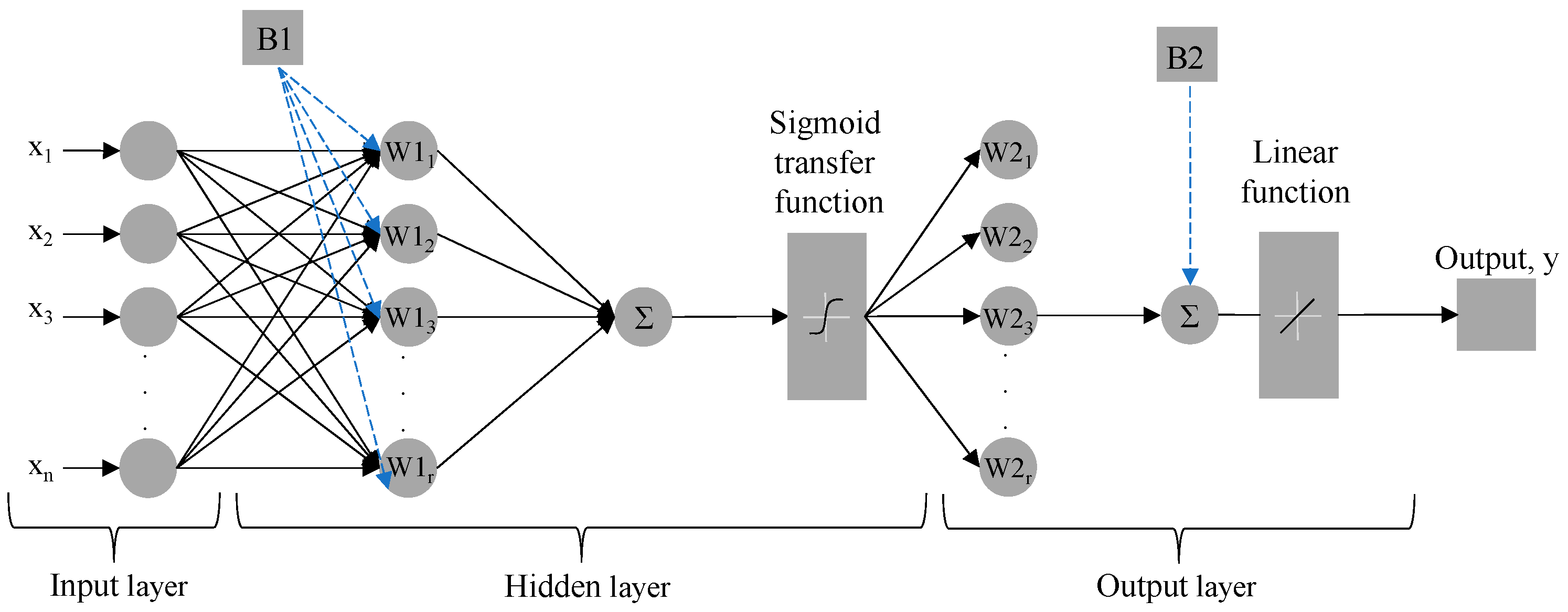
2.3. Artificial Neural Networks (ANNs)
3. Methodology
3.1. Proposed Adaptive LHS for Surrogate-Based Optimization Algorithm
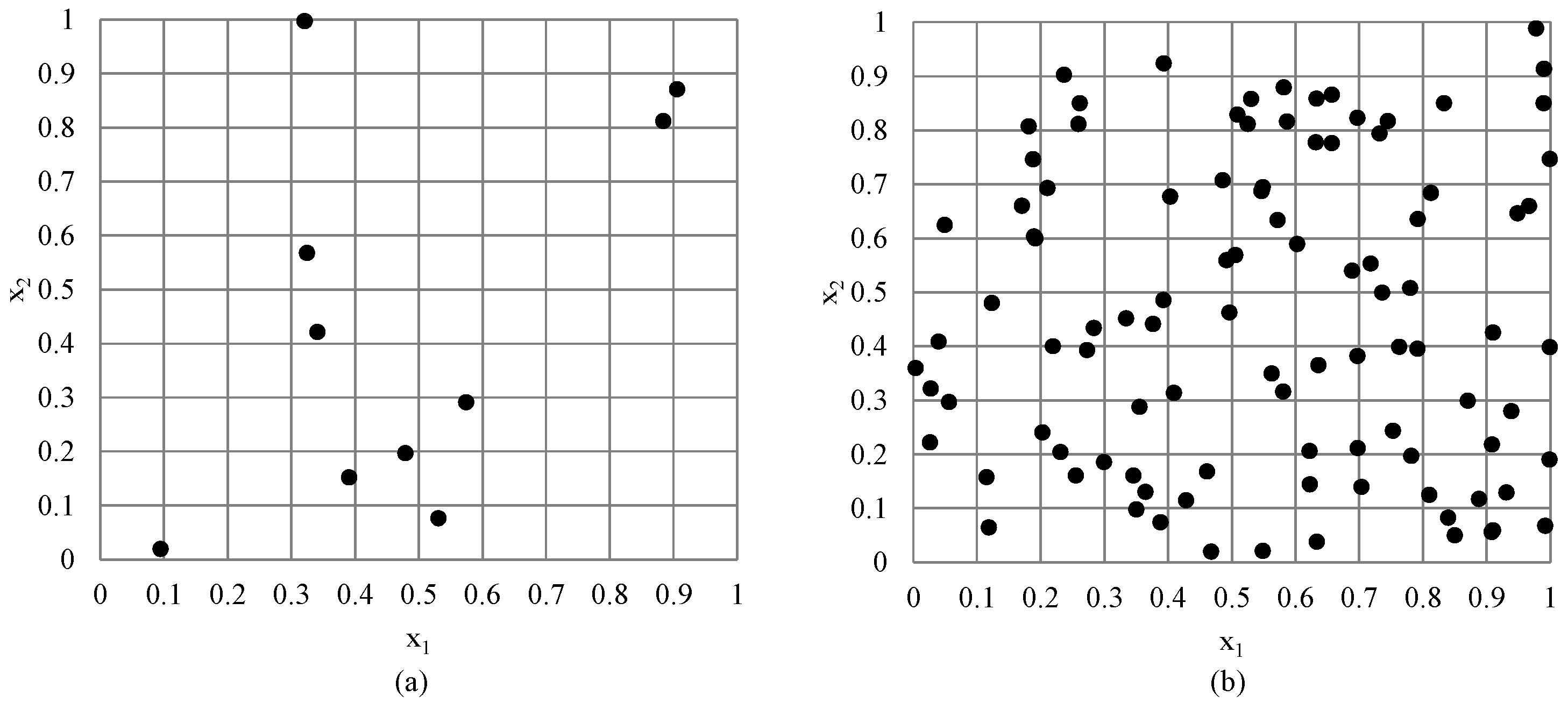
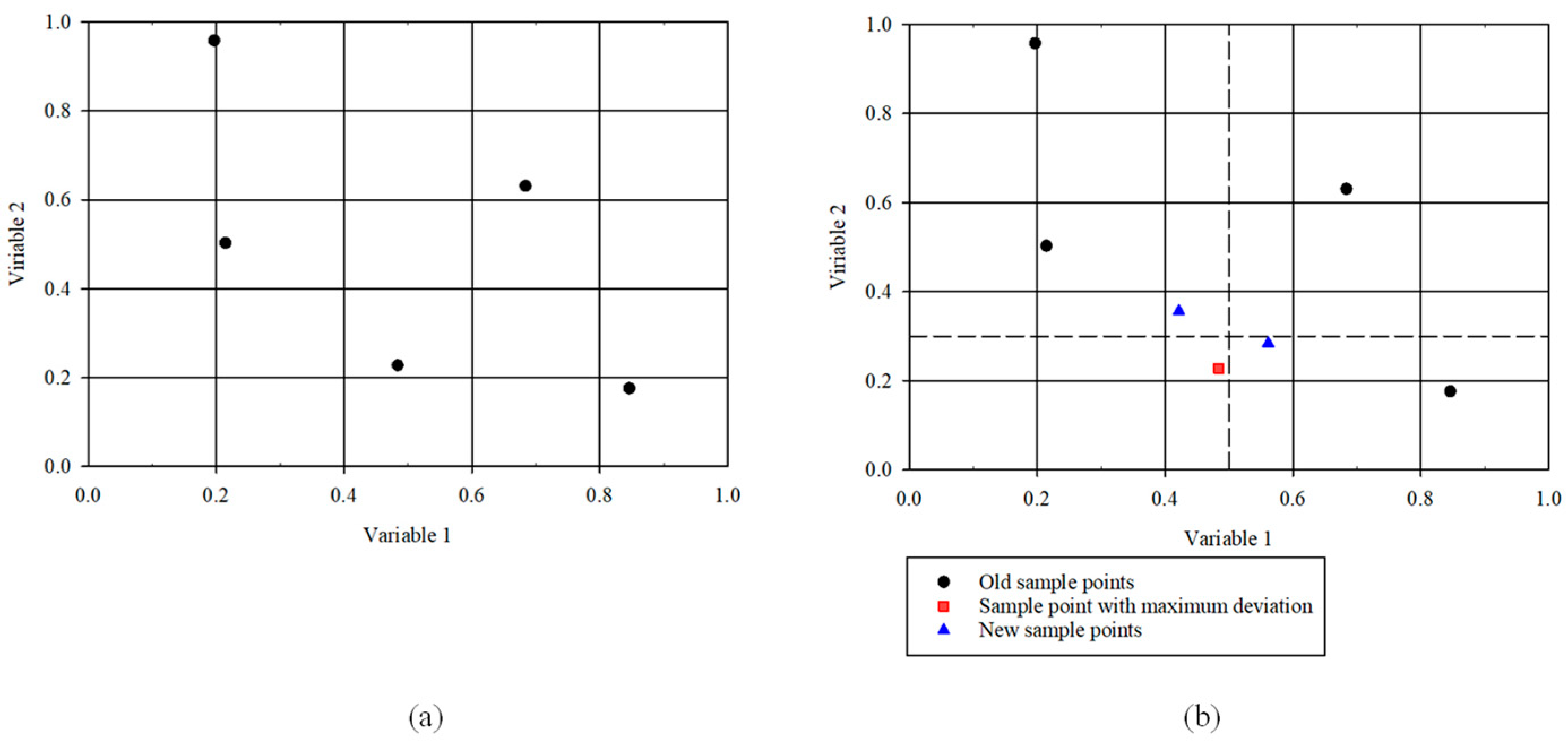
3.2. Adaptive Latin Hypercube Sampling: Addition of Sample Points
3.3. Verification of the Optimal Solution Using Random Sampling Technique
4. Case Study
4.1. Process Simulation and Economic Evaluation
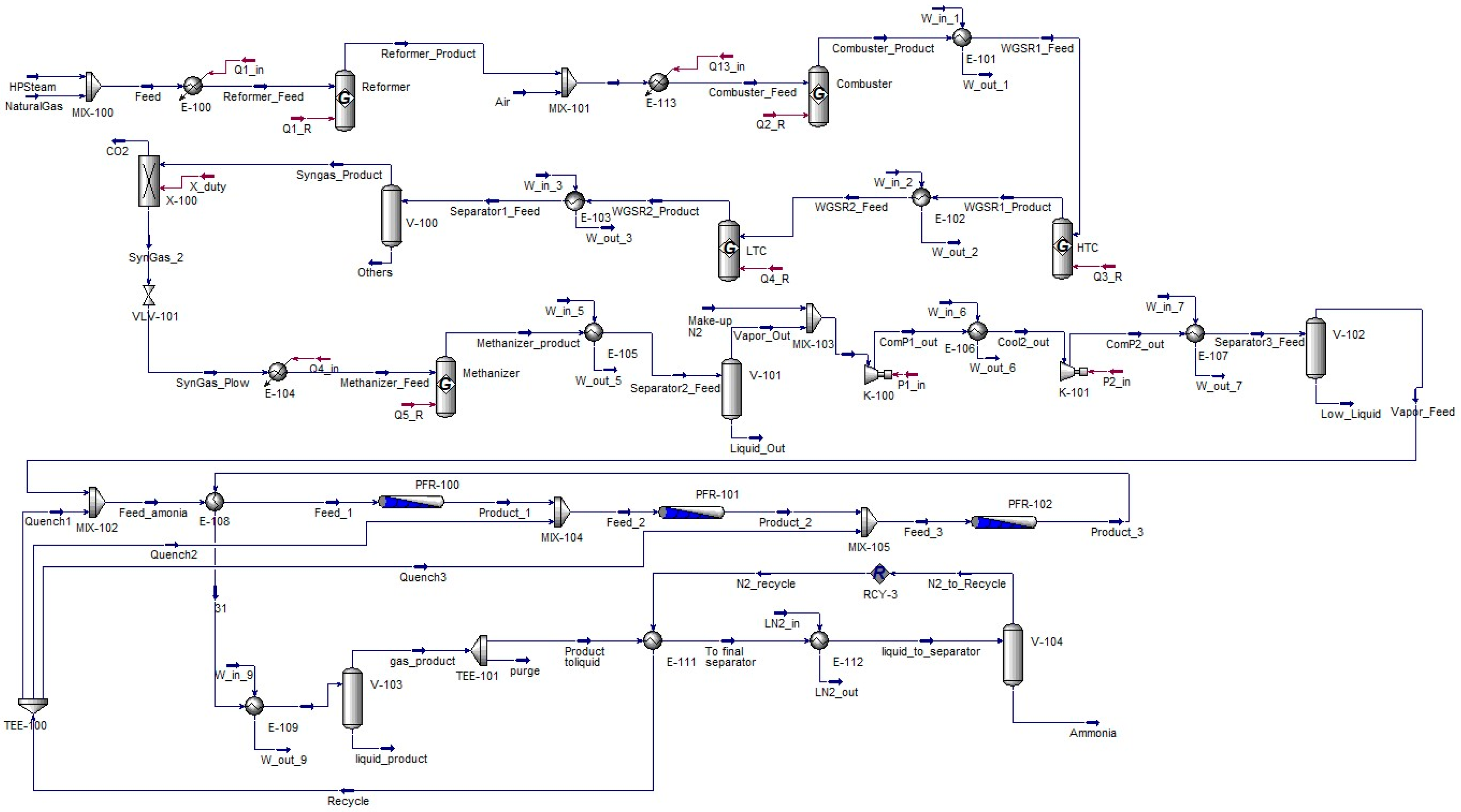
4.1.1. Case Study 1: Ammonia Production from Syngas
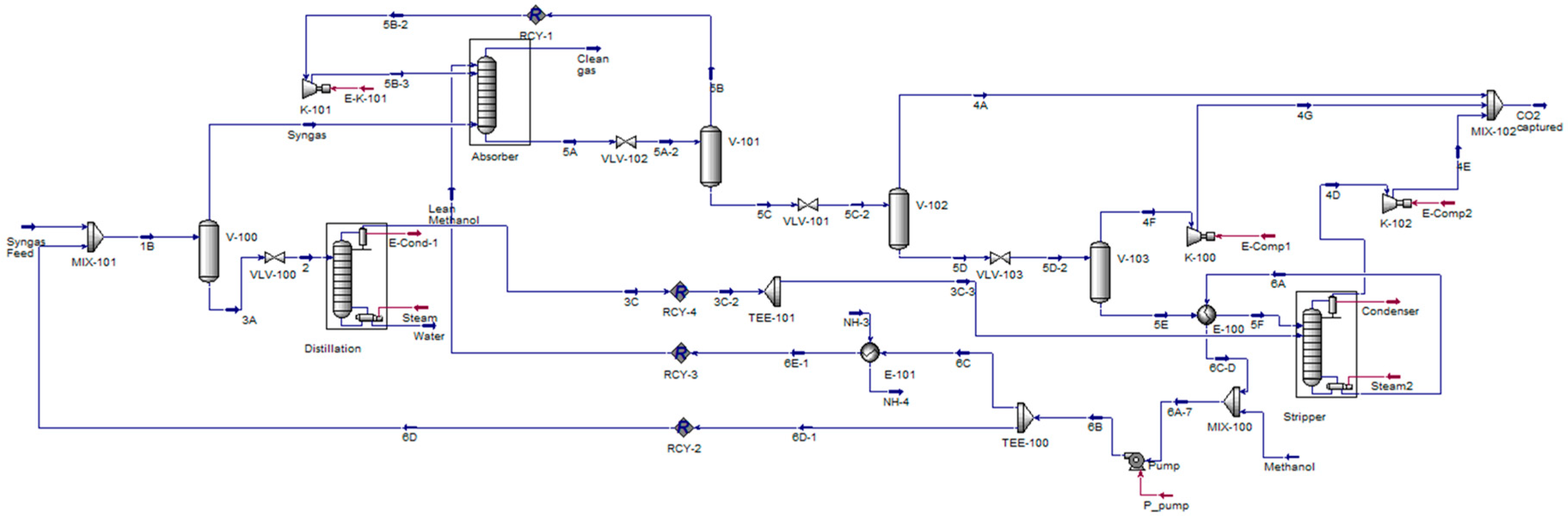
4.1.2. Case Study 2: Methanol Production via Carbon Dioxide Hydrogenation
4.1.3. Case Study 2: Methanol Production via Carbon Dioxide Hydrogenation
5. Results and Discussion
5.1. The Results of Monte Carlo or Random Sampling
5.2. The Convergence of the Proposed Adaptive LSH Optimization Algorithm
5.3. Comparison of Optimal Solutions between Proposed Sampling and Random Sampling
5.4. Recommendation for Future Work
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Crombecq, K.; Laermans, E.; Dhaene, T. Efficient space-filling and non-collapsing sequential design strategies for simulation-based modeling. Eur. J. Oper. Res. 2011, 214, 683–696. [Google Scholar] [CrossRef]
- Ahmadi, S.; Mesbah, M.; Igwegbe, C.A.; Ezeliora, C.D.; Osagie, C.; Khan, N.A.; Dotto, G.L.; Salari, M.; Dehghani, M.H. Sono electro-chemical synthesis of LaFeO3 nanoparticles for the removal of fluoride: Optimization and modeling using RSM, ANN and GA tools. J. Environ. Chem. Eng. 2021, 9, 105320. [Google Scholar] [CrossRef]
- Bashir, M.J.; Amr, S.A.; Aziz, S.Q.; Ng, C.A.; Sethupathi, S. Wastewater treatment processes optimization using response surface methodology (RSM) compared with conventional methods: Review and comparative study. Middle-East J. Sci. Res. 2015, 23, 244–252. [Google Scholar]
- Bezerra, M.A.; Santelli, R.E.; Oliveira, E.P.; Villar, L.S.; Escaleira, L.A. Response surface methodology (RSM) as a tool for optimization in analytical chemistry. Talanta 2008, 76, 965–977. [Google Scholar] [CrossRef]
- Hoseiny, S.; Zare, Z.; Mirvakili, A.; Setoodeh, P.; Rahimpour, M. Simulation–based optimization of operating parameters for methanol synthesis process: Application of response surface methodology for statistical analysis. J. Nat. Gas Sci. Eng. 2016, 34, 439–448. [Google Scholar] [CrossRef]
- Leonzio, G. Optimization through Response Surface Methodology of a Reactor Producing Methanol by the Hydrogenation of Carbon Dioxide. Processes 2017, 5, 62. [Google Scholar] [CrossRef]
- Mohammad, N.K.; Ghaemi, A.; Tahvildari, K. Hydroxide modified activated alumina as an adsorbent for CO2 adsorption: Experimental and modeling. Int. J. Greenh. Gas Control 2019, 88, 24–37. [Google Scholar] [CrossRef]
- Veljković, V.B.; Velickovic, A.V.; Avramović, J.M.; Stamenković, O.S. Modeling of biodiesel production: Performance comparison of Box–Behnken, face central composite and full factorial design. Chin. J. Chem. Eng. 2018, 27, 1690–1698. [Google Scholar] [CrossRef]
- Simpson, T.W.; Poplinski, J.D.; Koch, P.N.; Allen, J.K. Metamodels for Computer-Based Engineering Design: Survey and Recommendations. Eng. Comput. 2001, 17, 129–150. [Google Scholar] [CrossRef]
- Beers, W.C.M.v.; Kleijnen, J.P.C. Kriging interpolation in simulation: A survey. In Proceedings of the 2004 Winter Simulation Conference 2004, Washington, DC, USA, 5–8 December 2004. [Google Scholar]
- Eason, J.; Cremaschi, S. Adaptive sequential sampling for surrogate model generation with artificial neural networks. Comput. Chem. Eng. 2014, 68, 220–232. [Google Scholar] [CrossRef]
- Bliek, L. A Survey on Sustainable Surrogate-Based Optimisation. Sustainability 2022, 14, 3867. [Google Scholar] [CrossRef]
- Panerati, J.; Schnellmann, M.A.; Patience, C.; Beltrame, G.; Patience, G.S. Experimental methods in chemical engineering: Artificial neural networks–ANNs. Can. J. Chem. Eng. 2019, 97, 2372–2382. [Google Scholar] [CrossRef]
- Jin, Y.; Li, J.; Du, W.; Qian, F. Adaptive Sampling for Surrogate Modelling with Artificial Neural Network and Its Application in an Industrial Cracking Furnace. Can. J. Chem. Eng. 2016, 94, 262–272. [Google Scholar] [CrossRef]
- Vaklieva-Bancheva, N.G.; Vladova, R.K.; Kirilova, E.G. Simulation of heat-integrated autothermal thermophilic aerobic digestion system operating under uncertainties through artificial neural network. Chem. Eng. Trans. 2019, 76, 325–330. [Google Scholar]
- Hoseinian, F.S.; Rezai, B.; Kowsari, E.; Safari, M. A hybrid neural network/genetic algorithm to predict Zn(II) removal by ion flotation. Sep. Sci. Technol. 2020, 55, 1197–1206. [Google Scholar] [CrossRef]
- Bahrami, S.; Ardejani, F.D.; Baafi, E. Application of artificial neural network coupled with genetic algorithm and simulated annealing to solve groundwater inflow problem to an advancing open pit mine. J. Hydrol. 2016, 536, 471–484. [Google Scholar] [CrossRef]
- Mousavi, S.M.; Mostafavi, E.S.; Jiao, P. Next generation prediction model for daily solar radiation on horizontal surface using a hybrid neural network and simulated annealing method. Energy Convers. Manag. 2017, 153, 671–682. [Google Scholar] [CrossRef]
- Zendehboudi, S.; Rezaei, N.; Lohi, A. Applications of hybrid models in chemical, petroleum, and energy systems: A systematic review. Appl. Energy 2018, 228, 2539–2566. [Google Scholar] [CrossRef]
- Eslamimanesh, A.; Gharagheizi, F.; Mohammadi, A.H.; Richon, D. Artificial neural network modeling of solubility of supercritical carbon dioxide in 24 commonly used ionic liquids. Chem. Eng. Sci. 2011, 66, 3039–3044. [Google Scholar] [CrossRef]
- Mohammadpoor, M.; Torabi, F. A new soft computing-based approach to predict oil production rate for vapour extraction (VAPEX) process in heavy oil reservoirs. Can. J. Chem. Eng. 2018, 96, 1273–1283. [Google Scholar] [CrossRef]
- Bhutani, N.; Rangaiah, G.; Ray, A. First-principles, data-based, and hybrid modeling and optimization of an industrial hydrocracking unit. Ind. Eng. Chem. Res. 2006, 45, 7807–7816. [Google Scholar] [CrossRef]
- Zorzetto, L.F.M.; Filho, R.M.; Wolf-Maciel, M. Processing modelling development through artificial neural networks and hybrid models. Comput. Chem. Eng. 2000, 24, 1355–1360. [Google Scholar] [CrossRef]
- Tahkola, M.; Keranen, J.; Sedov, D.; Far, M.F.; Kortelainen, J. Surrogate Modeling of Electrical Machine Torque Using Artificial Neural Networks. IEEE Access 2020, 8, 220027–220045. [Google Scholar] [CrossRef]
- Adeli, H. Neural Networks in Civil Engineering: 1989–2000. Comput.-Aided Civ. Infrastruct. Eng. 2001, 16, 126–142. [Google Scholar] [CrossRef]
- Arora, S.; Shen, W.; Kapoor, A. Neural network based computational model for estimation of heat generation in LiFePO4 pouch cells of different nominal capacities. Comput. Chem. Eng. 2017, 101, 81–94. [Google Scholar] [CrossRef]
- Himmelblau, D.M. Applications of artificial neural networks in chemical engineering. Korean J. Chem. Eng. 2000, 17, 373–392. [Google Scholar] [CrossRef]
- Shahin, M.A.; Jaksa, M.B.; Maier, H.R. State of the art of artificial neural networks in geotechnical engineering. Electron. J. Geotech. Eng. 2008, 8, 1–26. [Google Scholar]
- Nayak, R.; Jain, L.C.; Ting, B.K.H. Artificial Neural Networks in Biomedical Engineering: A Review. In Computational Mechanics–New Frontiers for the New Millennium; Valliappan, S., Khalili, N., Eds.; Elsevier: Oxford, UK, 2001; pp. 887–892. [Google Scholar]
- Wang, C.; Luo, Z. A Review of the Optimal Design of Neural Networks Based on FPGA. Appl. Sci. 2022, 12, 771. [Google Scholar] [CrossRef]
- Garud, S.S.; Karimi, I.A.; Kraft, M. Design of computer experiments: A review. Comput. Chem. Eng. 2017, 106, 71–95. [Google Scholar] [CrossRef]
- Morshed, M.N.; Pervez, N.; Behary, N.; Bouazizi, N.; Guan, J.; Nierstrasz, V.A. Statistical Modeling and Optimization of Heterogeneous Fenton-like Removal of Organic Pollutant Using Fibrous Catalysts: A Full Factorial Design. Sci. Rep. 2020, 10, 16133. [Google Scholar] [CrossRef]
- Villa Montoya, A.C.; Mazareli, R.C.d.S.; Delforno, T.P.; Centurion, V.B.; de Oliveira, V.M.; Silva, E.L.; Varesche, M.B.A. Optimization of key factors affecting hydrogen production from coffee waste using factorial design and metagenomic analysis of the microbial community. Int. J. Hydrogen Energy 2020, 45, 4205–4222. [Google Scholar] [CrossRef]
- McKay, M.D.; Beckman, R.J.; Conover, W.J. A Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output from a Computer Code. Technometrics 1979, 21, 239–245. [Google Scholar]
- Sheikholeslami, R.; Razavi, S. Progressive Latin Hypercube Sampling: An Efficient Approach for Robust Sampling-Based Analysis of Environmental Models. Environ. Model. Softw. 2017, 93, 109–126. [Google Scholar] [CrossRef]
- Grosso, A.; Jamali, A.R.M.J.U.; Locatelli, M. Finding Maximin Latin Hypercube Designs by Iterated Local Search heuristics. Eur. J. Oper. Res. 2009, 197, 541–547. [Google Scholar] [CrossRef]
- Morris, M.D.; Mitchell, T.J. Exploratory designs for computational experiments. J. Stat. Plan. Inference 1995, 43, 381–402. [Google Scholar] [CrossRef]
- Pholdee, N.; Bureerat, S. An efficient optimum Latin hypercube sampling technique based on sequencing optimisation using simulated annealing. Int. J. Syst. Sci. 2015, 46, 1780–1789. [Google Scholar] [CrossRef]
- Park, J.-S. Optimal Latin-hypercube designs for computer experiments. J. Stat. Plan. Inference 1994, 39, 95–111. [Google Scholar] [CrossRef]
- Ye, K.Q.; Li, W.; Sudjianto, A. Algorithmic construction of optimal symmetric Latin hypercube designs. J. Stat. Plan. Inference 2000, 90, 145–159. [Google Scholar] [CrossRef]
- Fang, K.-T. Theory, Method and Applications of the Uniform Design. Int. J. Reliab. Qual. Saf. Eng. 2002, 9, 305–315. [Google Scholar] [CrossRef]
- Bates, S.; Sienz, J.; Toropov, V. Formulation of the Optimal Latin Hypercube Design of Experiments Using a Permutation Genetic Algorithm. In Proceedings of the 45th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics & Materials Conference, Palm Springs, CA, USA, 19–22 April 2004; American Institute of Aeronautics and Astronautics: Reston VA, USA, 2004. [Google Scholar]
- Jin, R.; Chen, W.; Sudjianto, A. An efficient algorithm for constructing optimal design of computer experiments. J. Stat. Plan. Inference 2005, 134, 268–287. [Google Scholar] [CrossRef]
- Van Dam, E.R.; Husslage, B.; Hertog, D.D.; Melissen, H. Maximin Latin Hypercube Designs in Two Dimensions. Oper. Res. 2007, 55, 158–169. [Google Scholar] [CrossRef]
- Viana, F.A.C.; Venter, G.; Balabanov, V. An algorithm for fast optimal Latin hypercube design of experiments. Int. J. Numer. Methods Eng. 2010, 82, 135–156. [Google Scholar] [CrossRef]
- Aziz, M.; Tayarani-N, M.-H. An adaptive memetic Particle Swarm Optimization algorithm for finding large-scale Latin hypercube designs. Eng. Appl. Artif. Intell. 2014, 36, 222–237. [Google Scholar] [CrossRef]
- Chen, R.-B.; Hsieh, D.-N.; Hung, Y.; Wang, W. Optimizing Latin hypercube designs by particle swarm. Stat. Comput. 2013, 23, 663–676. [Google Scholar] [CrossRef]
- Pan, G.; Ye, P.; Wang, P. A Novel Latin hypercube algorithm via translational propagation. Sci. World J. 2014, 2014, 163949. [Google Scholar] [CrossRef] [PubMed]
- Husslage, B.G.M.; Rennen, G.; van Dam, E.R.; Hertog, D.D. Space-filling Latin hypercube designs for computer experiments. Optim. Eng. 2011, 12, 611–630. [Google Scholar] [CrossRef]
- Wang, G.G. Adaptive Response Surface Method Using Inherited Latin Hypercube Design Points. J. Mech. Des. 2003, 125, 210–220. [Google Scholar] [CrossRef]
- Chang, Y.; Sun, Z.; Sun, W.; Song, Y. A New Adaptive Response Surface Model for Reliability Analysis of 2.5D C/SiC Composite Turbine Blade. Appl. Compos. Mater. 2018, 25, 1075–1091. [Google Scholar] [CrossRef]
- Roussouly, N.; Petitjean, F.; Salaun, M. A new adaptive response surface method for reliability analysis. Probabilistic Eng. Mech. 2013, 32, 103–115. [Google Scholar] [CrossRef]
- Liu, Z.-z.; Li, W.; Yang, M. Two General Extension Algorithms of Latin Hypercube Sampling. Math. Probl. Eng. 2015, 2015, 450492. [Google Scholar] [CrossRef]
- Liu, Z.; Yang, M.; Li, W. A Sequential Latin Hypercube Sampling Method for Metamodeling. In Theory, Methodology, Tools and Applications for Modeling and Simulation of Complex Systems; Springer: Singapore, 2016. [Google Scholar]
- Metropolis, N.; Ulam, S. The Monte Carlo Method. J. Am. Stat. Assoc. 1949, 44, 335–341. [Google Scholar] [CrossRef] [PubMed]
- Anawkar, S.; Panchwadkar, A. Comparison between Levenberg Marquart, Bayesian and scaled conjugate algorithm for prediction of cutting forces in face milling operation. AIP Conf. Proc. 2022, 2653, 030006. [Google Scholar]
- Borisut, P.; Nuchitprasittichai, A. Process Configuration Studies of Methanol Production via Carbon Dioxide Hydrogenation: Process Simulation-Based Optimization Using Artificial Neural Networks. Energies 2020, 13, 6608. [Google Scholar] [CrossRef]
- Janosovský, J.; Danko, M.; Labovský, J.; Jelemenský, L. Software approach to simulation-based hazard identification of complex industrial processes. Comput. Chem. Eng. 2019, 122, 66–79. [Google Scholar] [CrossRef]
- Adams, T.A.; Salkuyeh, Y.K.; Nease, J. Chapter 6—Processes and simulations for solvent-based CO2 capture and syngas cleanup. In Reactor and Process Design in Sustainable Energy Technology; Shi, F., Ed.; Elsevier: Amsterdam, The Netherlands, 2014; pp. 163–231. [Google Scholar]
- Nuchitprasittichai, A.; Cremaschi, S. An algorithm to determine sample sizes for optimization with artificial neural networks. AIChE J. 2013, 59, 805–812. [Google Scholar] [CrossRef]




| Algorithm | Criteria | Pros. | Cons. |
|---|---|---|---|
| Simulated annealing [36,37,38] | Maximize the inter-point distance | Effective for small-size problems | Converge very slowly |
| Exchange type and Newton type [39] | Maximize entropy | Fast to find optimal design for large-size problems | |
| Columnwise–pairwise [40] | Maximize the inter-point distance and Maximize entropy | Retain some orthogonality and high efficiency for small designs | Does not significantly reduce the searching time |
| Threshold accepting [41] | Minimize L2 discrepancy | Can be applied to both factorial and computer experiment | Cannot give a good design for small dimension |
| Genetic algorithm [42] | Maximize the inter-point distance | Requires a small amount of computational time | |
| Enhanced stochastic evolutionary algorithm [43] | Maximize the inter-point distance, maximize entropy and minimize L2 discrepancy | Needs a small number of exchanges; effective for large-size problems | |
| Branch-and-bound [44] | Maximize the inter-point distance | Can be used for non-collapsing designs | Obtain the optimum design for N < 70 |
| Translational propagation [45] | Maximize the inter-point distance | Obtain near-optimum LHDs up to medium dimensions | High computational cost for large number of sample points |
| Particle swarm optimization [46,47] | Maximize the inter-point distance | Fast accessibility to reach solutions | Local search algorithms become trapped in local optima |
| Translational propagation [48] | Maximize the inter-point distance and minimize L2 discrepancy | Effective in terms of the computation time and space-filling and projective properties | Not good in terms of performance of sampling points |
| Enhanced stochastic evolutionary algorithm [49] | Maximize the inter-point distance | Effective for large-size problems |
| Decision Variables | Range |
|---|---|
| Reformer temperature (°C) | 900 to 1200 |
| Combuster temperature (°C) | 1400 to 1700 |
| Low-temperature conversion reactor temperature (°C) | 160 to 290 |
| Decision Variables | Range |
|---|---|
| Pressure of the equilibrium reactor (bar) | 50 to 70 |
| Temperature of the equilibrium reactor (°C) | 190 to 210 |
| Temperature of the steam entering a separator (°C) | 60 to 80 |
| Recycle ratio | 0 to 1 |
| Decision Variables | Range |
|---|---|
| Lean methanol temperature (°C) | −55 to −20 |
| The 3rd stage separator pressure (bar) | 1.2 to 2 |
| Stripper reflux ration | 5 to 20 |
| Stripper inlet temperature (°C) | 10 to 40 |
| Distillation reflux ratio | 1 to 10 |
| Case Studies | Case Study I | Case Study II | Case Study III | |||||
|---|---|---|---|---|---|---|---|---|
| Sample points | 50 | 100 | 50 | 100 | 50 | 100 | 200 | 400 |
| R-squared | 0.9998 | 0.9999 | 1.0000 | 1.0000 | 0.9951 | 0.9999 | 0.9912 | 0.9998 |
| Minimum cost | 495.87 | 495.87 | 942.45 | 942.45 | 49.70 | 43.66 | 43.20 | 43.40 |
| Predicted cost | 505.89 | 496.73 | 926.29 | 948.23 | 39.37 | 42.83 | 45.88 | 43.66 |
| Error | 2.02% | 0.17% | 1.71% | 0.61% | 20.80% | 1.91% | 6.21% | 0.59% |
| Case Study I: Ammonia Production from Syngas | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Sampling Techniques | Total number of sample points | R2 | x1 (°C) | x2 (°C) | x3 (°C) | x4 | x5 | ypredicted () (USD per ton) | yactual (y) (USD per ton) | % error |
| Random Sampling | 100 | 0.9999 | 900 | 1400 | 160 | N/A | N/A | 496.73 | 495.87 | 0.17 |
| Proposed algorithm | ||||||||||
| Replication 1 | 38 | 0.9928 | 900 | 1400 | 160 | N/A | N/A | 498.40 | 495.87 | 0.51 |
| Replication 2 | 30 | 0.9995 | 900 | 1400 | 160 | N/A | N/A | 495.22 | 495.87 | 0.13 |
| Replication 3 | 30 | 0.9987 | 900 | 1400 | 160 | N/A | N/A | 492.14 | 495.83 | 0.74 |
| Case Study II: Methanol Production via Carbon Dioxide Hydrogenation | ||||||||||
| Sampling Techniques | Total number of sample points | R2 | x1 (bar) | x2 (°C) | x3 (°C) | x4 (-) | x5 | ypredicted () (USD per ton) | yactual (y) (USD per ton) | % error |
| Random Sampling | 100 | 1.0000 | 70 | 190 | 80 | 1 | N/A | 942.80 | 942.45 | 0.61 |
| Proposed algorithm | ||||||||||
| Replication 1 | 46 | 1.0000 | 70 | 190 | 80 | 1 | N/A | 942.37 | 942.45 | 0.01 |
| Replication 2 | 46 | 0.9993 | 70 | 190 | 80 | 1 | N/A | 943.85 | 942.45 | 0.15 |
| Replication 3 | 40 | 0.9991 | 70 | 190 | 76 | 1 | N/A | 944.31 | 945.94 | 0.17 |
| Case Study III: Carbon Dioxide Absorption by Methanol via Rectisol Process | ||||||||||
| Sampling Techniques | Total number of sample points | R2 | x1 (°C) | x2 (bar) | x3 (-) | x4 (°C) | x5 (-) | ypredicted () (USD per ton) | yactual (y) (USD per ton) | % error |
| Random Sampling | 400 | 0.9998 | −29.0 | 1.20 | 5 | 40 | 1 | 43.66 | 43.40 | 0.59 |
| Proposed algorithm | ||||||||||
| Replication 1 | 53 | 0.9958 | −20.0 | 1.20 | 5 | 40 | 1 | 45.74 | 45.47 | 0.60 |
| Replication 2 | 50 | 0.9987 | −20.0 | 1.27 | 5 | 40 | 1 | 45.91 | 45.67 | 0.51 |
| Replication 3 | 53 | 0.9980 | −26.7 | 1.28 | 5 | 40 | 1 | 43.25 | 43.19 | 0.14 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Borisut, P.; Nuchitprasittichai, A. Adaptive Latin Hypercube Sampling for a Surrogate-Based Optimization with Artificial Neural Network. Processes 2023, 11, 3232. https://doi.org/10.3390/pr11113232
Borisut P, Nuchitprasittichai A. Adaptive Latin Hypercube Sampling for a Surrogate-Based Optimization with Artificial Neural Network. Processes. 2023; 11(11):3232. https://doi.org/10.3390/pr11113232
Chicago/Turabian StyleBorisut, Prapatsorn, and Aroonsri Nuchitprasittichai. 2023. "Adaptive Latin Hypercube Sampling for a Surrogate-Based Optimization with Artificial Neural Network" Processes 11, no. 11: 3232. https://doi.org/10.3390/pr11113232
APA StyleBorisut, P., & Nuchitprasittichai, A. (2023). Adaptive Latin Hypercube Sampling for a Surrogate-Based Optimization with Artificial Neural Network. Processes, 11(11), 3232. https://doi.org/10.3390/pr11113232








