Abstract
The Physical Internet (PI) provides a solution for coping with the continuous rise in urban logistical demands by exploring same-level and cross-level paths. This research suggests a PI-based urban logistical distribution model based on PI distribution that minimizes transportation costs. It also intends to maintain the integrity of the logistical transportation process. This proposed model enhances the flexibility of goods operation and reduces the global cost of logistics’ distribution using an interconnected and open PI logistics distribution mode. This model also explores the functional aspects of the operational problems of city logistical systems and relates to optimization problems. These functionalities are realized by the hierarchical functional structure and are characterized by different cost specifications. The proposed framework provides better integration and cooperation between city logistics warehouses and higher utilization level of logistical infrastructure. The experimental results show that the distribution cost of the PI logistics model is significantly better than that of a traditional logistics model. The elastic and cost advantages grow relatively as the infrastructure for distribution scales up and interruptions from emergencies occur.
1. Introduction
Urban logistics are essential to the functioning of modern urban economies. Cities are places of consumption relying on frequent deliveries including retail goods, express deliveries to businesses, and a fast growing home-delivery market. For people, urban logistics ensures the supply of goods in stores and for firms it forms a vital link with suppliers and customers [1]. On the background of global economic integration, the rapid development of the logistics industry provides new business opportunities for urban construction. Urban logistics distribution, as an important part of overall logistics, has received increasing attention in recent years [2,3]. The research content is mainly focused on determining the rational allocation of urban logistics distribution and exploring its sharing and cooperation mode. In terms of optimization and transformation of urban logistics, Szymczyk [4] made it clear that urban logistics should be transformed into green and intelligent logistics and analyzed new schemes to improve the efficiency of transportation and distribution by taking the European Union (EU) logistics’ operation mode as an example. Because of the low-carbon requirements of an advanced logistics mode, Wang [5] proposed a low-emission closed-loop logistics distribution network model, which verified the feasibility and practicality of urban green logistics distribution. Skultety et al. [6] used the two-step clustering method to evaluate the development and implementation of logistical measures in each city and explored the effective distribution of urban logistics and the path to reduce environmental pressure and urban congestion. Considering the role of logistics in high-quality urban development and economic transformation, Fatnassi et al. [7] verified the necessity of expanding the comprehensive logistical distribution system and improving the efficiency of urban logistics under the normalization of epidemic prevention and control. In terms of sharing and cooperation in urban logistical distribution, Cleophas et al. [8] envisioned an urban multimodal transportation-sharing network integrating the subway, taxis, and trucks, and evaluated the network performance from the perspectives of the number of operating hubs and the willingness of drivers. Using a heuristic algorithm to select the most appropriate combination of distribution centers and hubs, Thompson [9] pointed out those node mergers between suppliers and distribution centers must be accompanied by resource sharing of global logistic participants. Because of the negative impact brought through the development of urban logistics, Yao et al. [10] explored the actual impact of information-sharing mechanisms on the cooperation of various logistical entities and demonstrated that collaborative logistics is an effective way to reduce distribution costs and improve the environmental condition. From the perspective of collaborative transportation and collaborative distribution, Gonzalez et al. [11] combined the demand generation model with the path optimization algorithm, and constructed a scenario corresponding to the urban logistical distribution pre-evaluation framework.
In recent years, complexity and requirements in city logistics have steadily increased. Factors such as timed delivery and transportation distribution costs present serious challenges to the logistical companies [12,13]. The expense of urban logistics is another significant issue that is improperly handled. The optimization concept of city logistics is not yet very developed [14]. Because logistics evolves with time, traditional logistical systems are able to adapt to these changes. As a result, we must implement a brand-new method of logistics known as a physical internet logistics system.
2. Literature Review
The Physical Internet logistical system may be viewed as a smart logistics system aiming to be socially responsible and environmental friendly by modularizing container transit [15]. The PI vision is based on the analogy of the digital Internet and was first proposed as a solution to major problems of economic, environmental, and social instability in the global logistics network [16]. The Physical Internet logistics model is introduced to replace the traditional logistics model for the following two reasons: (1) to reduce the cost of urban logistical distribution reasonably on the premise of ensuring the stable operation of the logistical distribution system; (2) to reduce the risk and uncertainty of logistical activities with a safe facility layout. Further, it uses the idea of Internet technology to construct a new logistical network and creates a unified container of public and open transportation modes and intelligent standards so that all kinds of goods are loaded through a unified container and they have the ability of free transmission in the logistical network. Considering the advantages of the sharing and collaboration mode of urban logistical distribution and the public and open characteristics of PI, Crainic [17] introduced the potential connection between PI and urban logistics and explored the possibility of changing logistical paths and improving economic, environmental, and social efficiency from the perspective of theoretical analysis. Venkatadri [18] analyzed the impact of PI logistical integration on distribution and inventory costs, established a cost minimization model, and studied the advantages of the PI system over the traditional logistical networks. Based on previous studies, Yang [19] also evaluated the ability of PI to deal with the interruption between distribution nodes, proposed an optimization model, and proved that PI has greater flexibility and elasticity. Treiblmaier et al. [20] summarized and analyzed a large quantity of PI literature related to logistics and supply chain management. The PI is anticipated to keep defying conventional supply chain and logistical models going forward while continuing to satisfy environmental and economic development standards [21]. The research on the PI spreads over various topics such as container standardization, delivery scheduling optimization, and vehicle routing optimization. Meyer at al. [22] proposed a block-chain-based conceptual framework to offer a solution for fundamental barriers of the Physical Internet concerning the exchange of value and physical assets in logistical networks and decentralized leadership structures. Ben Mohamed et al. [23] researched an interconnected city logistical network with PI containers as transportation methods within cities. Considering the complexity of city logistics, various features including the multi-period setting and multi-echelon distribution structure were incorporated into the model. The model was designed to minimize transportation cost for vehicles, interconnecting a large number of open and shared hubs. Hu et al. [24] dealt with an integrated production and inventor distribution problem for a PI-based three echelon supply chain network which consisted of set of a manufacturing plants, PI hubs, and retail outlets. In the study of Qiao et al. [25], a less-than-truckload request pricing and selection problem was addressed with the incorporation of future demand forecasting based on historical data of transport flows. They coupled the dynamic programming and integer programming approaches to optimize the carrier’s revenue in the PI context. A PI-enabled delivery optimization problem was addressed by Luo et al. [26] for customized furniture in urban areas. All customized furniture was stored and transported within standard PI-containers of different sizes. Funke and Kopfer [27] modeled the inland container transportation problem as a full truckload pickup and delivery problem or a full truckload pickup and delivery problem with time windows in the context of PI. Pan et al. [28] studied the digital interoperability through a bibliometric analysis based on 208 papers published between 2010 and 2020. The results revealed that the present state-of-the-art solutions of digital interoperability are not fully aligned with PI requirements and show new challenges, research gaps, and opportunities that need further discussion.
The published literature on the PI is very limited to date, though interest in this paradigm has recently been piqued. The behavior of the PI system compared with that of traditional logistics is still not well-presented. In this paper, we aim to address this gap by looking at the PI from the perspective of the urban logistical model. By doing this, we formulate the transportation optimization model to optimize the transportation distribution costs. Key ideas for merging urban logistics with PI are cooperation, consolidation, and a separation of the business transactions creating the demand and the manner in which the actual transit and storage of the freight loads are carried out. Urban logistics provide the last and final links in the PI-enabled hyper-connected logistical and transportation networks, therefore urban logistics and PI are no longer complimentary. We examine the essential connections and mutual benefits of these cutting-edge logistical and freight transportation systems. Further, we introduce the notion of a hyper-connected city logistical system to increase distribution efficiency and reduce distribution costs.
3. Methodology
3.1. PI Based Urban Logistical Distribution Model
Urban logistics and PI are two significant concepts related to warehousing, distribution centers, and transportation. Urban logistics aim to reduce the negative impact of urban transportation movements within the urban region and decrease the environmental impact in terms of congestion without lowering the level of social and economic activities. The principal idea of the PI methodology is a change in the way urban transportation movements occur within logistical network. The two ideas work well together to illustrate hyper-connected urban logistics. The establishment of the urban logistical distribution model based on PI must be based on the traditional logistical distribution model. In the process of traditional logistical distribution, the limited transportation efficiency and high distribution costs lead to the continuous high costs of urban logistical distribution. However, in the city logistical distribution model based on PI mode, all facilities within the system (including the warehouses, distribution centers, transportation) will be present to each main body (including logistical service providers and consumers) open and sharing, so as to realize a point-to-point scenario. Crainic and Montreuil [17] further improved the efficiency of distribution to reduce the distribution costs received face-to-face across the interconnected system. To break the barrier between the distribution node system and the private or relatively fixed logistical distribution line, enterprises achieve sustainable and accurate distribution to complete the effective control of distribution costs.
3.2. Main Factors (PI Distribution)
In the traditional logistical distribution network, the distribution mode of goods has been preset prior to entering the logistical network. The source and destination of any transport have experienced advanced planning, and the goods are passed layer by layer from the delivery point (DP), warehouse (WH), distribution center (DC), and terminal node to the consumers. However, with the aid of PI, data-driven, connective, extensively collaborative and efficient features can form a highly efficient logistical distribution model as shown in Figure 1. Each peer distribution between nodes is closely interconnected, and establishes a logistical network environment that is widely shared between each other, and thus has many path selections, a real-time dynamic adjustment of the new key characteristics, and increases the distribution of various possibilities. It helps to explore more flexible distribution solutions to further reduce the waiting time and inventory cost of goods at each node. To explore the best logistical distribution method based on PI, the following three core factors, namely PI infrastructure, distribution route, and transshipment standard, are analyzed to effectively depict the urban logistical distribution model of PI. (See Figure 2).
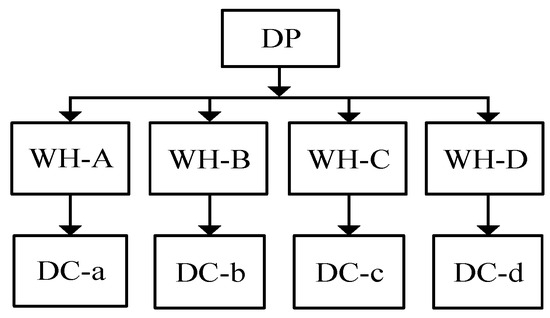
Figure 1.
Traditional logistical network.
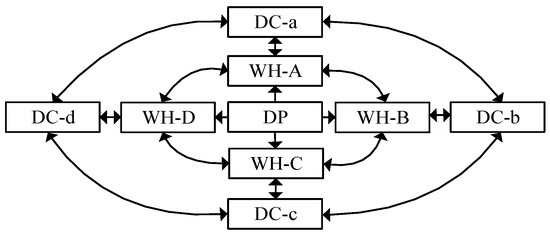
Figure 2.
Logistical network based on PI.
- (1)
- Infrastructure: The classical logistical network layout gives rise to the layout mode known as the PI infrastructure layout. The introduction of PI does not change the geographical location of the original node facilities. The PI is a revolutionary logistical system that seeks to level the playing field for the logistical network’s traditional centralized hierarchical structure through hierarchy-based development. The biggest differences in PI with a traditional layout are that all nodes are in the network facilities, transportation facilities, and service personnel. The global infrastructure of PI is based on the principles of maximum efficiency within reasonable use. To overcome the initial industrial hurdles, increase distribution efficiency, and reduce distribution costs, PI is incorporated into city logistics.
- (2)
- Distribution route: When Montreuil [29] initially proposed the concept of PI, it was obvious that the complete path in the PI network could be transformed from private network to open network. Due to delivery lead times and transportation cost restrictions, the shortest route is typically considered to be the best distribution route in a traditional logistical network of distribution. However, if distance is the only criterion used to choose the order of goods in the logistical network, which is predetermined at the starting location, then there is a significant loss of flexibility in the logistical system. However, transportation and distribution in the PI environment are more dynamic, and the flexible communication between warehouses and distribution centers at all levels gives a higher degree of freedom in route selection. PI considers the distribution distance and the use of network facilities with equal weightage, which helps to realize the uniform distribution of network traffic and improves the general satisfaction of customers.
- (3)
- Transshipment standard: All goods in the PI network are uniformly packaged in standard intelligent green modular containers. Considering the negative impact of long-distance transportation on society and the environment, the ordered goods often need to go through multi-stage combined transportation in PI. In the process of transit at each transport node for the comparative test and research results of Pan et al. [28] and Yang [19] et al., it can be seen that the best effect is achieved by direct transfer with the source substitution method, which is based on an intuitive and simple standard. Instead of dividing delivery orders or recombining existing containers, PI selects vehicles that meet the transport capacity and are close enough to the transfer node for transferring the goods.
3.3. Symbol Definition (PI Distribution)
The urban logistical distribution scheme based on PI should be directly related to the construction layout and logistical level of the city in which it is located. The gap between the layout and logistical capacity of different cities affects the focus of urban logistical distribution decision-making, but regardless of where they are in the PI network. The city logistical distribution follows a set of standards, making it possible to view the city logistical distribution model as a whole at each shipping port, industrial center, and distribution center based on its PI essence. For a reasonable response to all varieties of cargo and container transport distribution problems, the need to use the symbol definition (Table 1) is elucidated as follows:

Table 1.
Notations used in the optimization expression.
3.4. Model Construction (PI Distribution)
The research scope of the urban logistical distribution model based on PI is as follows: after arrival of the goods in a city, the whole level of process is covered from the point of delivery to the logistics warehouse and then to the basic distribution center. The fundamental goal is to minimize the total cost of logistical distribution as much as possible under the premise that accurate goods arrive on time. The proposed model needs to use the traditional logistical distribution model of facilities distribution and operation rules as the template to form its interconnectivity and offer a unique logistical distribution model. Since the composition of urban logistical distribution costs is complex and easily changeable with the characteristics of the city, fixed construction costs, inventory holding costs, transportation and distributions cost, and lastly penalty costs can be given priority according to the importance of degree. These costs are required to express the dependency on the distance of the warehouse from the city center. The model uses these costs to exhibit economies of scales. One would expect that with the increased sensitivity of cities to heavy goods traffic, the development of e-commerce, the expected substantial increase in these costs in the long term, the warehouse would locate closer to city centers, or at least not too much far away [30]. The fixed construction cost , inventory holding cost , transportation, distribution cost and last penalty cost that can be given priority according to the importance of degree. The fixed construction costs given in (1) represents the construction costs of site selection, decoration, acquisition of fixed assets for all warehouses, and distribution centers in PI city logistical distribution.
The inventory holding cost given in (2) is used to represent the costs of daily storage and guarantees the containers to be transferred from each transport node to the other transport node in PI.
Due to the influence of batch economy law, the unit inventory costs of the warehouse and distribution center should be different. The unit inventory costs of the warehouse are slightly lower than that of the distribution center. The transportation and distribution cost given in (3) is composed of the upstream transportation costs from the delivery point to the warehouse and the downstream transportation cost from the warehouse to the distribution center.
According to the actual logistics and distribution situation, the upstream and downstream transportation costs should also differ. By adding and , we obtain notation , which is called a penalty cost. The penalty cost also includes the compensation loss cost given in (4), caused by consumer complaints if ordered goods do not arrive on time that leads to the loss of invisible potential customers and damage to the company’s image.
Based on these settings, we present the following proposed PI-based city logistical model:
The goal of objective function (5) is to reduce the logistical distribution costs in PI city, taking into account the fixed construction cost of the logistics warehouse and distribution center, the inventory holding cost of the logistics warehouse and distribution center, the full transportation and distribution costs, and the possible penalty costs associated with failing to satisfy customer demands. The transportation needs of warehouses and distribution centers, as well as any transferred orders that cannot be separated before reaching their destination, are the limitations (6)–(8). For a specific day, we designate a warehouse to accept a container that the receiving source sends. It is 1 if the warehouse is usable as usual. In the event of an emergency or warehouse explosion, it is zero. For that specific day, we designate distribution facilities to accept containers that are shipped by the warehouse. The use of the normal operation node as the transport destination helps to ensure that the logistical distribution model accurately reflects the current situation while also making it simple to avoid the logistics warehouse after incuring a lost function in the system failure model. The constraint (9) indicates that the upper limit of the storage capacity of the logistics warehouse at a single time should not exceed and is as follows:
The above difference condition (11) is between the accumulated inflow and outflow of containers in any warehouse to prevent the warehouse from exploding or the nearby path from blocking and interrupting due to overload of material flow during operation. The constraint (10) indicates that the number of containers to be distributed in the PI system must be an integer to meet the PI operation standard. The urban logistical distribution problem based on PI is a nonlinear optimization problem. It is difficult to determine an optimal solution directly. Therefore, this paper considers the branch and bound algorithm to obtain satisfactory solutions for decision variables and objective functions.
4. Simulation and Result Analysis
We compare the city logistical distribution model based on PI with the traditional logistical model. To make the comparison more effective, this paper takes Xi’an city as an example and sets the cover points as warehouse. The distribution center’s logistical distribution network, compared with the traditional logistical model, involves the introduction of the PI-based method of maintaining the internal node location, for the network to benefit from the open features of the Internet. The GIS module in the simulation software version-1 is used to determine the names and geographical locations of the above nodes as shown in Table 2. To accurately explore the performance discrepancies between PI and the traditional logistical model in the comparative test process using the traditional logistical model as the reference group, the number of goods delivered daily by PI and the traditional logistical model are consistent with the target locations of all goods. Each cargo has been defined as the target distribution center when the delivery point is generated, and container is responsible for integrating the goods with the same destination and waiting for the corresponding truck to transport them. In a traditional logistical network, the circulation of goods or containers needs to follow the route of man-made rules, as shown in Figure 3. However, in the PI logistical model, all fixed routes will be broken and smart labels are on the containers for the freedom of choice. The ability to dynamically adjust the goods will be shipped in a single container for adjacent nodes without interrupting all paths to choose and form the best distribution route by free combination. We have generated data through the computer code which changes over time. So, it is not required to fix the data.

Table 2.
Location of logistical network nodes.
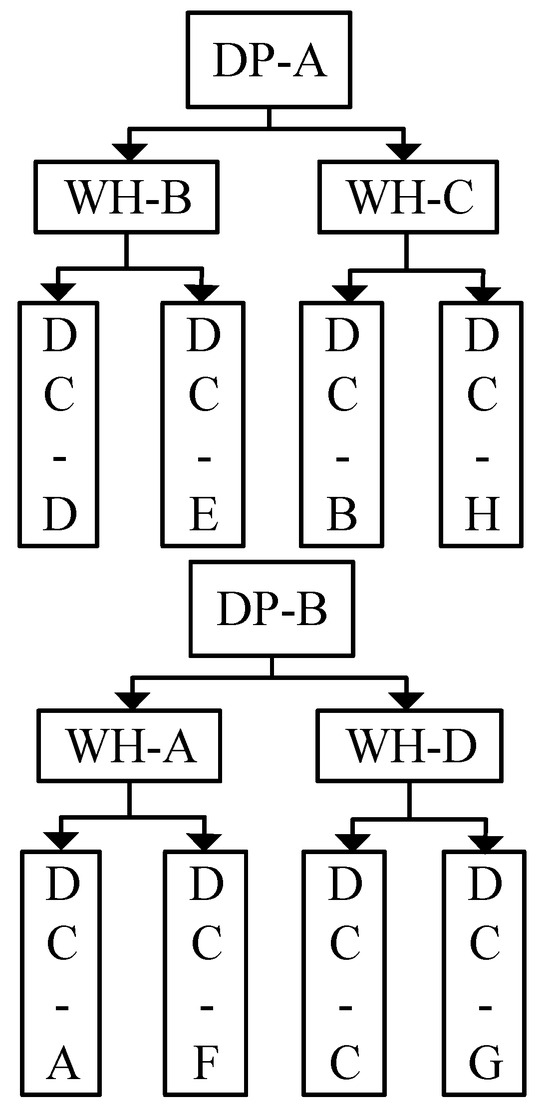
Figure 3.
Distribution roadmap of traditional logistical network.
According to the findings about Xi’an region logistics, the PI distribution system infrastructure construction fixed cost is CNY 199,142.96, and container logistical warehouse inventory cost is CNY 16.95 per day. At the distribution center level, inventory transportation lost focus size of dividends, so the container inventory costs rise accordingly to the upstream of 1.5 times above CNY 25.89 per day. At the same time, the upstream (transportation between the delivery point and the warehouse) cost is CNY 11.13 per km with a full load, and the downstream (transportation between the warehouse and the distribution center) cost is CNY 15.93 per km with a full load. In addition, assume that the maximum total simulated time is T = 100 days, the daily containerized quantity to be delivered at the delivery points A and B are each 100 pieces, the upper limit of the single transport quantity of the distribution vehicles is 20 pieces, and the random probability interval of daily abnormal use of each warehouse is [0.08, 0.10]. As shown in Figure 4, model operation and simulation are carried out on the hardware environment with Intel(R) Core(TM) I5-10210U CPU, 16 GB memory, and any logic software. By taking the mean value of 10 simulation results and eliminating the interference of random factors, the total cost changes of the traditional logistical model and PI distribution model under different distribution rules are obtained.
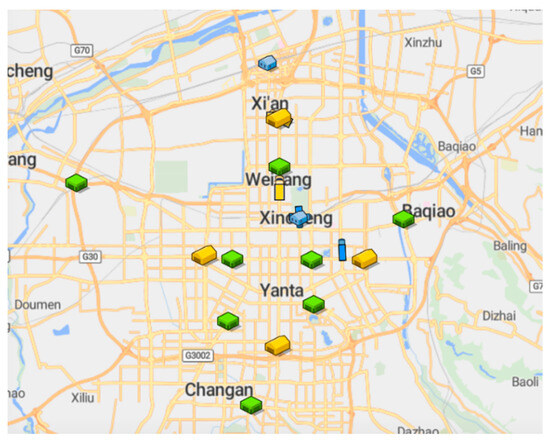
Figure 4.
Schematic diagram of Xi’an logistical distribution based on PI.
Discussion of Results
- (1)
- Comparative Analysis of Distribution models: With the given computation, we receive the traditional logistical model and PI logistical model under the condition of the same infrastructure. The total cost of logistical distribution changes over time. From Figure 5 and Table 3, it is obvious that the PI logistical model continues to provide the cost advantages over the traditional logistical model in the simulation process, despite the fact that the PI logistical model’s simulation period is less than 20 days. The traditional logistical model and the PI logistical model have similar distribution costs; however, as time goes on, the cumulative logistical cost saved by the PI logistical model keeps growing, and the PI logistical model’s cost advantage progressively becomes apparent. The PI logistical model’s greatest saving value, which is CNY 22,892.49 on day 100, has an average daily saving rate of 3.96%. This demonstrates that when compared to traditional logistical networks, the PI logistical distribution network is open and interconnection performance can efficiently provide more distribution paths. Additionally, when the scale of local logistical service consumers reaches medium or above and is stable, the cost of the PI logistical distribution network is significantly lower than the cost of traditional logistics. In particular, the trend line of the logistical distribution model based on the PI is not steep, and the growth rate is comparatively stable. It is also difficult for an increase in freight volume to cause a rise in distribution costs. For every 200 containers deployed inside the system, the overall logistical cost rises by CNY 3591.55 on average. Additionally, because the internal infrastructure of PI serves all demanders in the form of public rental, common third-party logistical companies, and e-commerce activities are exempted from the cost of building basic logistical facilities, further lowering logistical distribution costs and raising customer satisfaction.
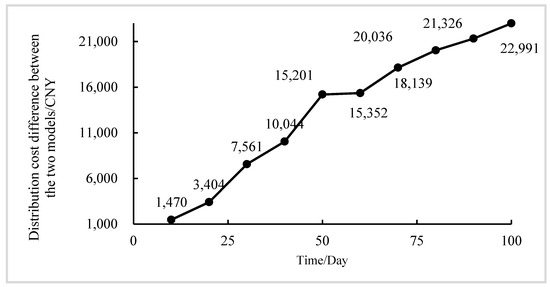 Figure 5. Comparison of distribution cost between traditional logistical mode and PI logistics.
Figure 5. Comparison of distribution cost between traditional logistical mode and PI logistics. Table 3. Distribution costs of the two models with different time lengths.
Table 3. Distribution costs of the two models with different time lengths.
- (2)
- The Core Factors Analysis: A surge in demand for logistical service providers and consumers has resulted from the gradual replacement of offline retail with online shopping. However, serious challenges have been brought about by “Shopping Day” blowing up and new epidemic outbreaks, which could cause transportation disruption on the elasticity of the logistical network. Experiments are carried out by gradually increasing the number of distribution centers from eight to twelve with a step size of 1, while keeping the same parameters in Table 1 and Figure 3, in order to further investigate the impact of the scale of logistical infrastructure and emergency interruption events on the cost advantage of the logistical distribution model in PI city. For simulation, the random outage chance for each warehouse was incrementally raised from 0.1 to 0.25, with a 0.125 step size. From Figure 6, it can be seen that the size of the logistical infrastructure for distribution has a positive promoting effect, lowering the total cost of the distribution center to give up the number of PI is higher at the end of the logistical distribution model of flexible selectivity, so the PI total cost of logistics and distribution center is roughly inversely proportional to the size number. Therefore, with each increase in a distribution center, the cost of distribution costs an average of about CNY 720.90. With the largest decrease in total cost of CNY 14,758.52, the cost optimization rate was 2.55%, only 48% of the PI logistical model improvement, and the visible PI cost optimization model was significantly higher than that of the traditional logistical model, so the expansion of the scale of the distribution center also brought some distribution advantages for the traditional logistical model. It can be seen from Figure 7 (taking the mean value after 10 simulations) that when the random interruption probability of each warehouse increases, the logistical network risk, and uncertainty increase, and the total cost of PI logistical distribution shows an increasing trend. When the interruption probability increases from 0.10 to 0.25, the total cost increases from CNY 555,116.96 to CNY 560,277.74, but the PI logistical model does not affect the optimization ability of the total cost. This is mainly reflected in the fact that the cost difference value and cost difference rate of the PI logistical model and traditional logistical model continues to rise, especially in the interval of interruption probability [0.10, 0.15] optimization increases significantly. Compared with the traditional logistical model, the total distribution cost savings of the PI logistical model are increased by CNY 6940.11, and the savings rate is increased by 1.23%. Moreover, the savings rate is consistently higher than 5.00% when the outage probability is greater than 0.15, which shows that PI has good robustness to sudden logistical outage events, while the traditional logistical distribution model has to start an emergency response when interruption occurs and to recover the distribution supply through manual allocation, which lacks good fault-tolerance. While comparing with the traditional logistical distribution model, Figure 6 and Figure 7 comprehensively show that the distribution of scale expansion and interruption probability increases when the PI cost savings rate has a high level of the model, the maximum of 6.87% and 5.55%, respectively. This further shows that the advantages of the PI logistical model in the escalating scale of logistical infrastructure and emergencies that frequently occur are still preserved. The cost and elasticity advantages are magnified under large-scale and highly intrusive external conditions.
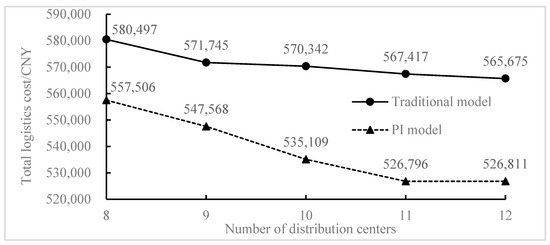 Figure 6. Influence of the number of distribution centers on the total cost of logistical distribution.
Figure 6. Influence of the number of distribution centers on the total cost of logistical distribution.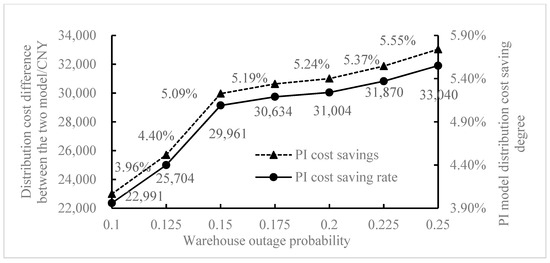 Figure 7. Influence of warehouse random outage probability on total logistical distribution cost.
Figure 7. Influence of warehouse random outage probability on total logistical distribution cost.
Overall, the obtained results are in favor of interconnectivity because the transportation plan improves when the number of warehouses increases with an impact on the economic and environmental facets. In addition, the results show a good tradeoff between the use of high capacity containers and low capacity vehicles in accordance to the density of the zone and the criticality of its congestion level. Furthermore, the numerical results are encouraging with regards to the service improvement obtained by optimization of the path designs across periods to reduce the number of postponed demands along the horizon [31]. Finally, our results highlight the efficiency of the pickup and delivery of PI containers without altering the economic performance of the transportation problem and by keeping the mean time per route and the mean load rate under reasonable levels. Under the proposed PI logistical model, in which the PI logistical size was increased, we observed that the multiplicity of warehouses and their interconnectivity enhance the global profit and reduce the transportation cost.
5. Conclusions, Limitations and Future Prospects
The traditional logistical model lacks the flexibility, sharing, and interconnection capabilities that PI possesses, making it possible to increase the effectiveness of logistical distribution while lowering the cost of logistical distribution. This research is based on analyses of the primary PI distribution parameters and makes sure that the logistical process integrity is a requirement in order to explore the PI network of the city logistical distribution system. Based on the city logistical distribution cost minimization model of PI, the model can be a PI delivery point in the international warehouses and distribution centers to form an open system of a distribution network. It improves the flexibility of goods operation and lowers the international cost of logistical distribution.
Modern concepts for freight transportation and logistical system improvement are very promising and provide challenging ideas for the future suitability and efficiency of supply chains. Next, to the rapid progress of digital technology such as automated identification, Internet of Things, machine learning, artificial intelligence, and intelligent transportation systems, we should address the improvement of freight movements in logistical networks at the global level. The essential ideas of the PI are limited to integration, environmental, and economic premises. However, this concept will be implemented in real logistical system and Big Data will be generated through physical flows. Without the intelligent and high performance of data analysis and optimization techniques, the potential results and benefits could be less than possible to obtain.
The framework that has been presented is merely an exploratory first step, and the concerns it raises should be explored in great detail. The following stage should involve developing the layers’ functions, thoroughly explaining the integration approaches, and investigating the best optimization strategies for specific decision-making scenarios. Extra research on the suitable selection of optimization methods and tools is necessary due to the specificity and characteristics of the decision issues in the provided idea, such as multi-criteria, NP-Hard large-size problems with many local minima, and uncertain parameters. Even in the event of an impact on the logistical model with PI from numerous unpredictable sources, the future model must discover the best solution in the allotted amount of time and with an acceptable level of accuracy. Resuming the Physical Internet concept’s integrated multi-layer decision-making framework for city logistics may be advantageous in terms of sustainability and efficiency. Numerous avenues for research and innovation become available with the introduction of the Physical Internet decision-making framework applied in urban environments.
Author Contributions
Conceptualization, H.F., J.L., K.K.L. and B.R.; methodology, H.F., J.L., K.K.L. and B.R.; software, H.F., J.L., K.K.L. and B.R.; validation, H.F., J.L., K.K.L. and B.R.; writing—original draft preparation, H.F., J.L., K.K.L. and B.R.; supervision, K.K.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Social Science Fund of China, grant number 21BGL200.
Data Availability Statement
Data are unavailable due to ethical restrictions.
Acknowledgments
We are very gratefully to the anonymous reviewers who provided constructive comments to enhance the manuscript. The fourth author acknowledges the support from the Centre of Digital Transformation, Indian Institute of Management Ahmedabad.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Crainic, T.G.; Ricciardi, N.; Storchi, G. Advanced freight transportation systems for congested urban areas. Transp. Res. Part C Emerg. 2004, 12, 119–137. [Google Scholar] [CrossRef]
- Behrends, S. Recent developments in urban logistics research–a review of the proceedings of the international conference on city logistics 2009–2013. Transp. Res. Procedia 2016, 12, 278–287. [Google Scholar] [CrossRef]
- Buldeo, R.H.; Dablanc, L. Hunting for treasure: A systematic literature review on urban logistics and e-commerce data. Transp. Rev. 2023, 43, 204–233. [Google Scholar] [CrossRef]
- Szymczyk, K.; Kadłubek, M. Challenges in general cargo distribution strategy in urban logistics–comparative analysis of the biggest logistics operators in EU. Transp. Res. Procedia 2019, 39, 525–533. [Google Scholar] [CrossRef]
- Wang, J.; Lim, M.K.; Tseng, M.L.; Yang, Y. Promoting low carbon agenda in the urban logistics network distribution system. J. Clean. Prod. 2019, 211, 146–160. [Google Scholar] [CrossRef]
- Škultéty, F.; Beňová, D.; Gnap, J. City logistics as an imperative smart city mechanism: Scrutiny of clustered eu27 capitals. Sustainability 2021, 7, 3641. [Google Scholar]
- Fatnassi, E.; Chaouachi, J.; Klibi, W. Planning and operating a shared goods and passengers on-demand rapid transit system for sustainable city-logistics. Transp. Res. B-Meth. 2015, 81, 440–460. [Google Scholar] [CrossRef]
- Cleophas, C.; Cottrill, C.; Ehmke, J.F.; Tierney, K. Collaborative urban transportation: Recent advances in theory and practice. Eur. J. Oper. Res. 2019, 273, 801–816. [Google Scholar]
- Thompson, R.G.; Hassall, K.P. A collaborative urban distribution network. Procedia Soc. Behav. Sci. 2012, 39, 230–240. [Google Scholar] [CrossRef]
- Yao, X.; Cheng, Y.; Song, M. Assessment of collaboration in city logistics: From the aspects of profit and CO2 emissions. Int. J. Logist. Res. 2019, 22, 576–591. [Google Scholar] [CrossRef]
- Gonzalez-Feliu, J. Sustainable Urban Logistics: Planning and Evaluation; John Wiley & Sons: Hoboken, NJ, USA, 2018. [Google Scholar]
- Montoya-Torres, J.R.; Muñoz-Villamizar, A.; Vega-Mejía, C.A. On the impact of collaborative strategies for goods delivery in city logistics. Prod. Plan. Control 2016, 27, 443–455. [Google Scholar]
- Taniguchi, E.; Thompson, R.G.; Yamada, T. New opportunities and challenges for city logistics. Transp. Res. Procedia 2016, 12, 5–13. [Google Scholar]
- Crainic, T.G. City logistics. In State-of-the-Art Decision-Making Tools in the Information-Intensive Age; INFORMS: Hanover, MD, USA, 2008; pp. 181–212. [Google Scholar]
- Fahim, P.B.; Rezaei, J.; Montreuil, B.; Tavasszy, L. Port performance evaluation and selection in the Physical Internet. Transp. Policy. 2022, 124, 83–94. [Google Scholar]
- Ambra, T.; Caris, A.; Macharis, C. Towards freight transport system unification: Reviewing and combining the advancements in the physical internet and synchromodal transport research. Int. J. Prod. Res. 2019, 57, 1606–1623. [Google Scholar]
- Crainic, T.G.; Montreuil, B. Physical internet enabled hyperconnected city logistics. Transp. Res. Procedia 2016, 12, 383–398. [Google Scholar]
- Venkatadri, U.; Krishna, K.S.; Ülkü, M.A. On Physical Internet logistics: Modeling the impact of consolidation on transportation and inventory costs. IEEE Trans. Autom. Sci. 2016, 13, 1517–1527. [Google Scholar]
- Yang, Y.; Pan, S.; Ballot, E. Mitigating supply chain disruptions through interconnected logistics services in the Physical Internet. Int. J. Prod. Res. 2017, 55, 3970–3983. [Google Scholar]
- Treiblmaier, H.; Mirkovski, K.; Lowry, P.B.; Zacharia, Z.G. The physical internet as a new supply chain paradigm: A systematic literature review and a comprehensive framework. Int. J. Logist. Manag. 2020, 31, 239–287. [Google Scholar]
- Montreuil, B. Toward a Physical Internet: Meeting the global logistics sustainability grand challenge. Logist. Res. 2011, 3, 71–87. [Google Scholar]
- Meyer, T.; Kuhn, M.; Hartmann, E. Blockchain technology enabling the Physical Internet: A synergetic application framework. Comput. Ind. Eng. 2019, 136, 5–17. [Google Scholar]
- Ben Mohamed, I.; Klibi, W.; Labarthe, O.; Deschamps, J.C.; Babai, M.Z. Modelling and solution approaches for the interconnected city logistics. Int. J. Prod. Res. 2017, 55, 2664–2684. [Google Scholar] [CrossRef]
- Hu, Z.; Askin, R.G.; Hu, G. Hub relay network design for daily driver routes. Int. J. Prod. Res. 2019, 57, 6130–6145. [Google Scholar] [CrossRef]
- Qiao, B.; Pan, S.; Ballot, E. Revenue optimization for less-than-truckload carriers in the Physical Internet: Dynamic pricing and request selection. Comput. Ind. Eng. 2020, 139, 105563. [Google Scholar] [CrossRef]
- Luo, H.; Tian, S.; Kong, X.T. Physical Internet-enabled customised furniture delivery in the metropolitan areas: Digitalisation, optimisation and case study. Int. J. Prod. Res. 2021, 59, 2193–2217. [Google Scholar] [CrossRef]
- Funke, J.; Kopfer, H. A model for a multi-size inland container transportation problem. Transp. Res. E Logist. Transp. Rev. 2016, 89, 70–85. [Google Scholar]
- Pan, S.; Trentesaux, D.; McFarlane, D.; Montreuil, B.; Ballot, E.; Huang, G.Q. Digital interoperability in logistics and supply chain management: State-of-the-art and research avenues towards Physical Internet. Comput. Ind. 2021, 128, 103435. [Google Scholar] [CrossRef]
- Pan, S.; Nigrelli, M.; Ballot, E.; Sarraj, R.; Yang, Y. Perspectives of inventory control models in the Physical Internet: A simulation study. Comput. Ind. Eng. 2015, 84, 122–132. [Google Scholar]
- Gorcun, O.F. Reduction of energy costs and traffic flow rate in urban logistics process. Energy Procedia 2017, 113, 82–89. [Google Scholar] [CrossRef]
- Yee, H.; Gijsbrechts, J.; Boute, R. Synchromodal transportation planning using travel time information. Comput. Ind. 2021, 125, 103367. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).