Effects of Topological Properties with Local Variable Apertures on Solute Transport through Three-Dimensional Discrete Fracture Networks
Abstract
:1. Introduction
2. Methodology
2.1. Generation of 3D DFNs
2.2. Fluid Flow
2.3. Solute Transport
2.4. Inverse Parameters from BTCs
3. Results
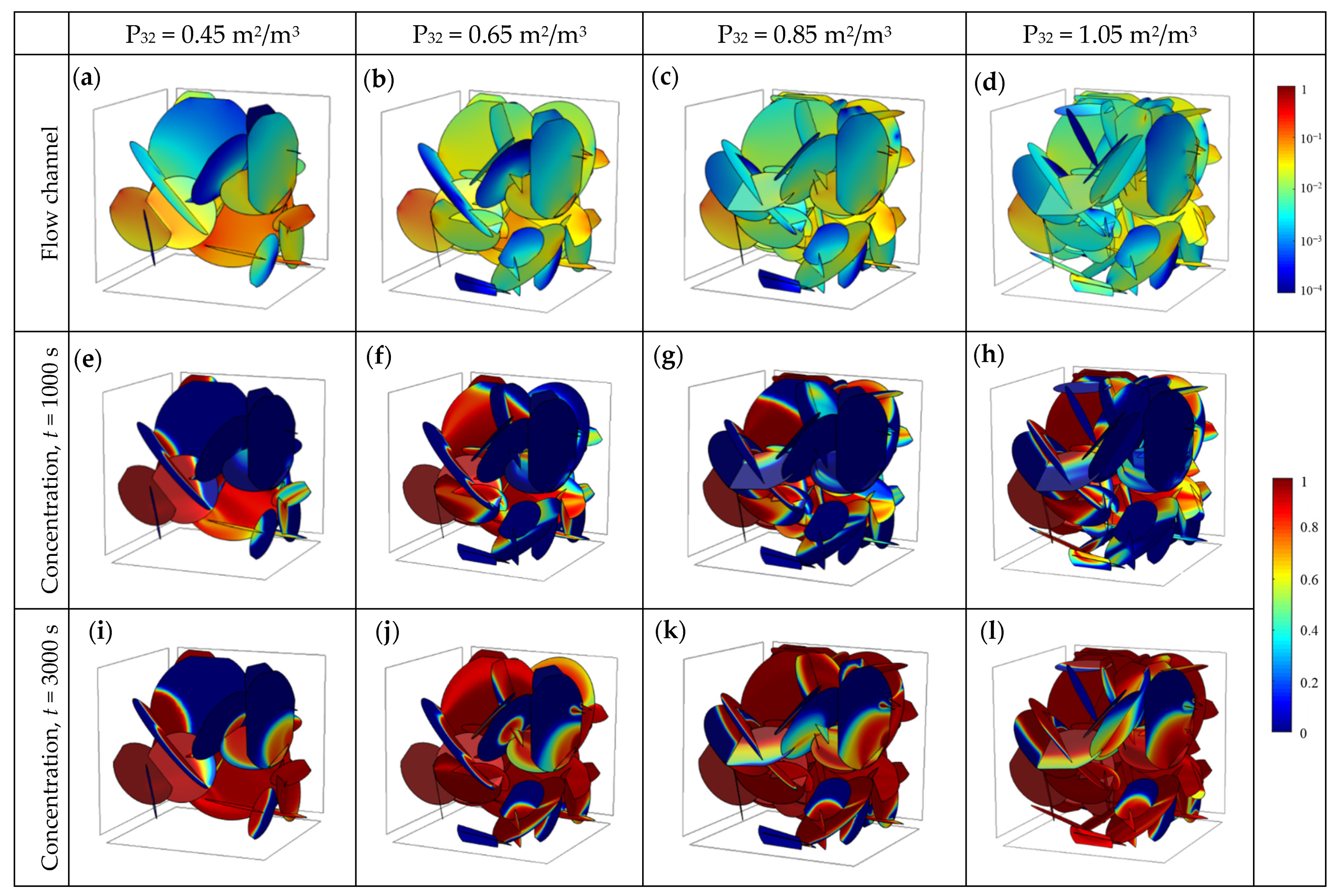
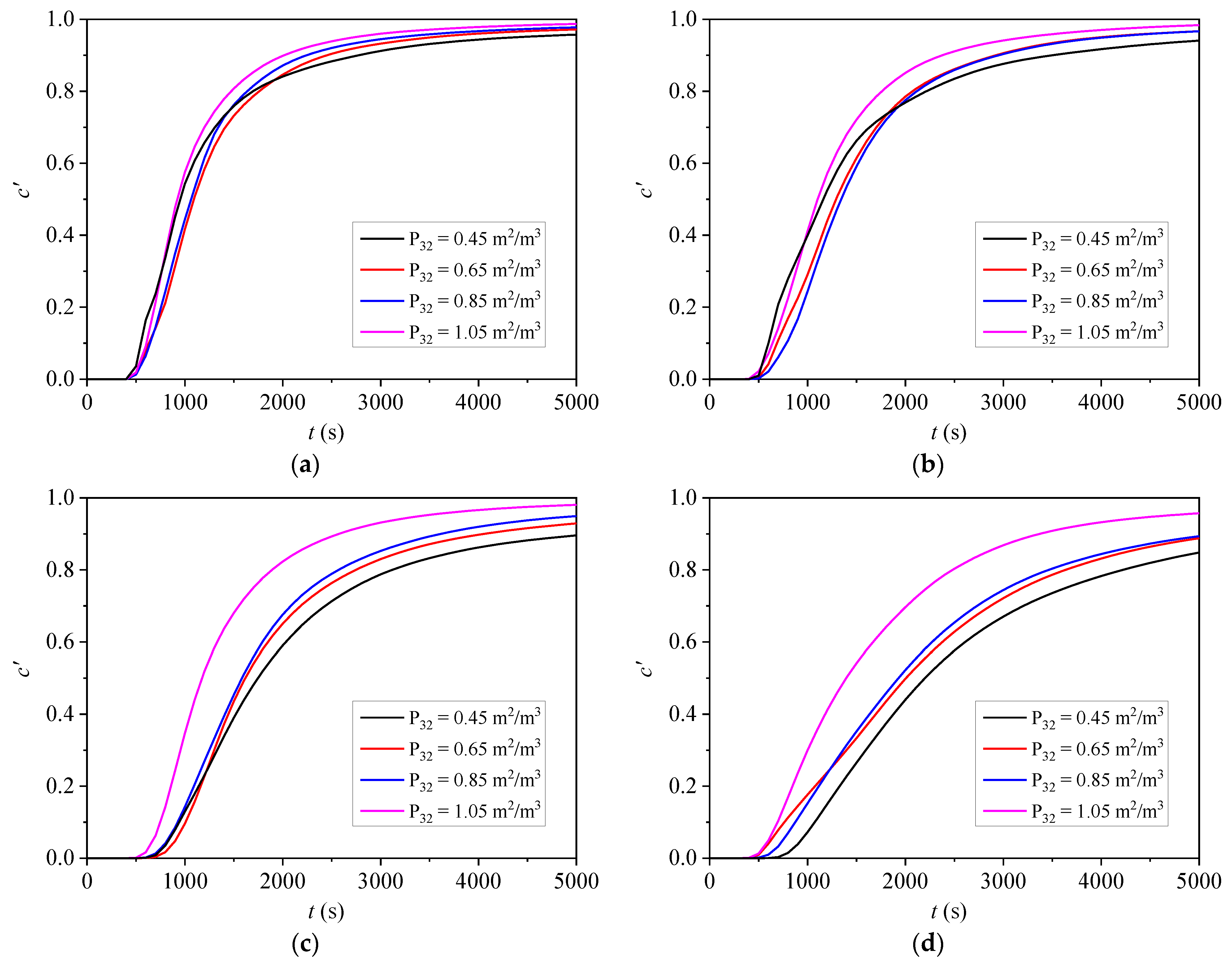
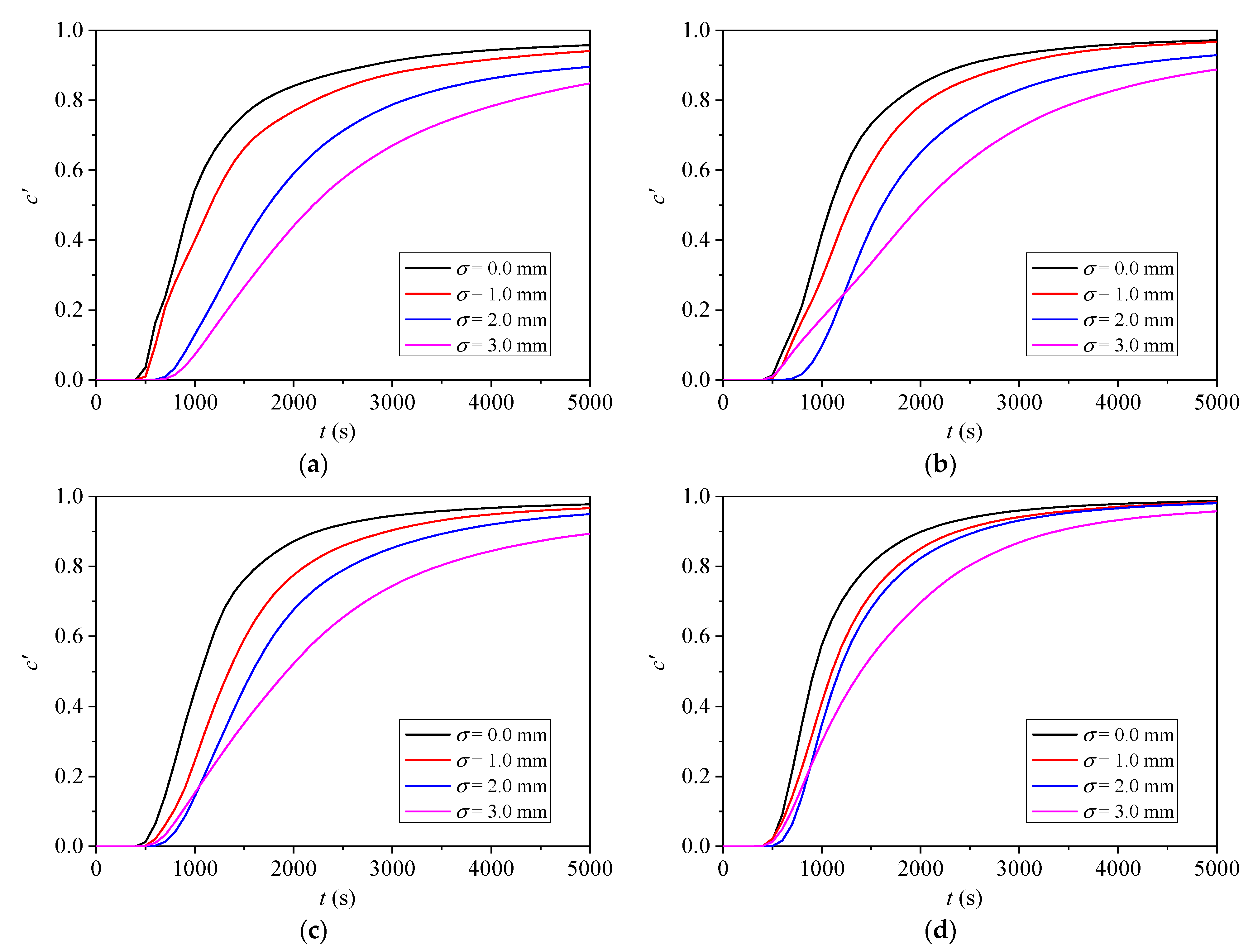
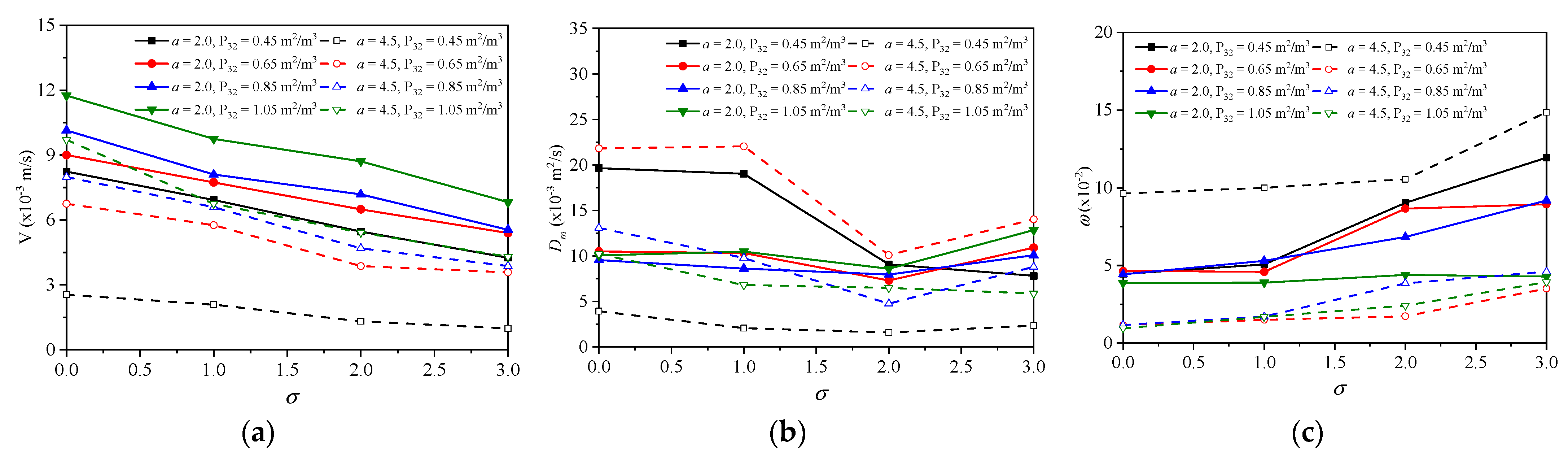
3.1. Effects of Network Topology
3.2. Effects of Aperture Heterogeneity
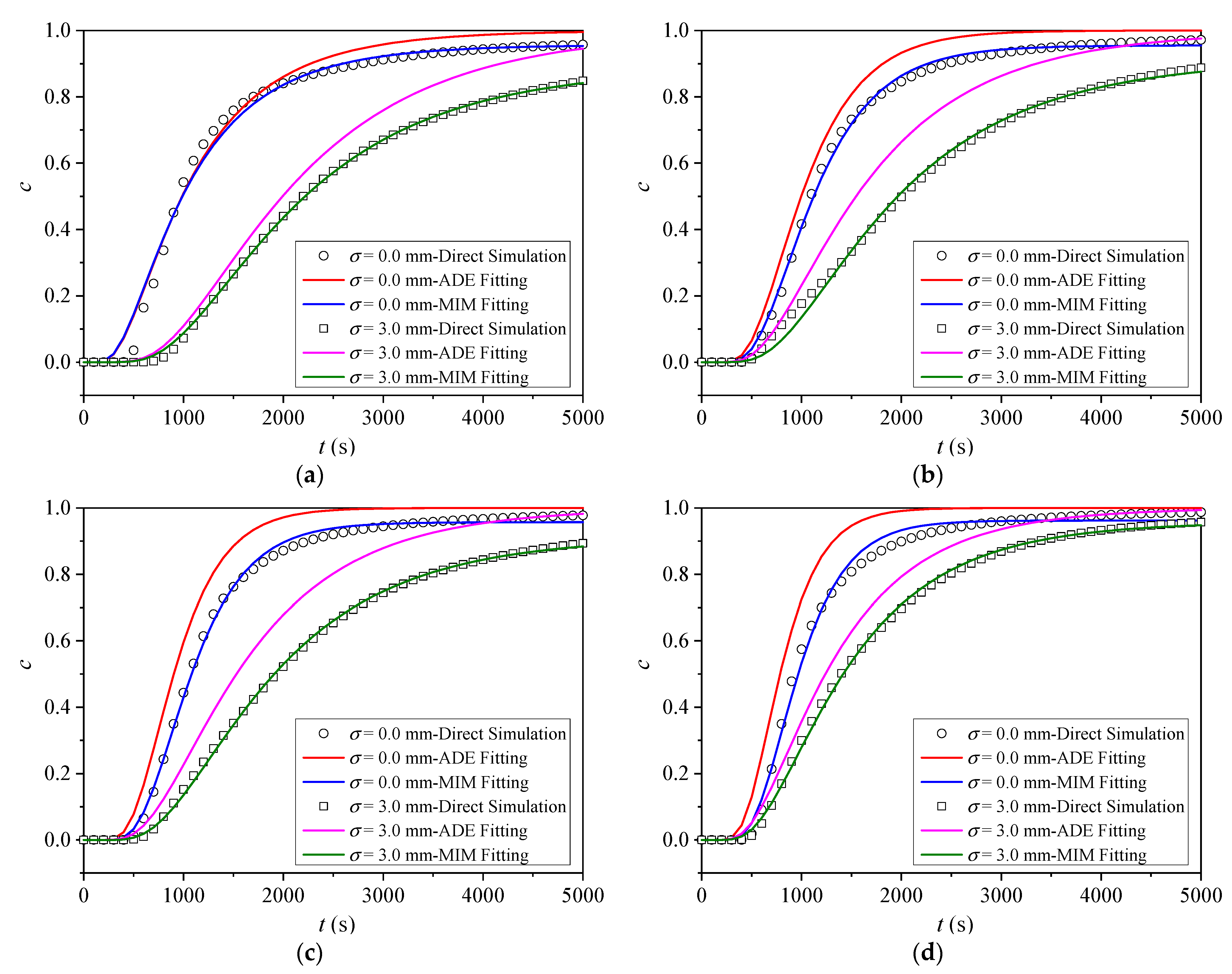
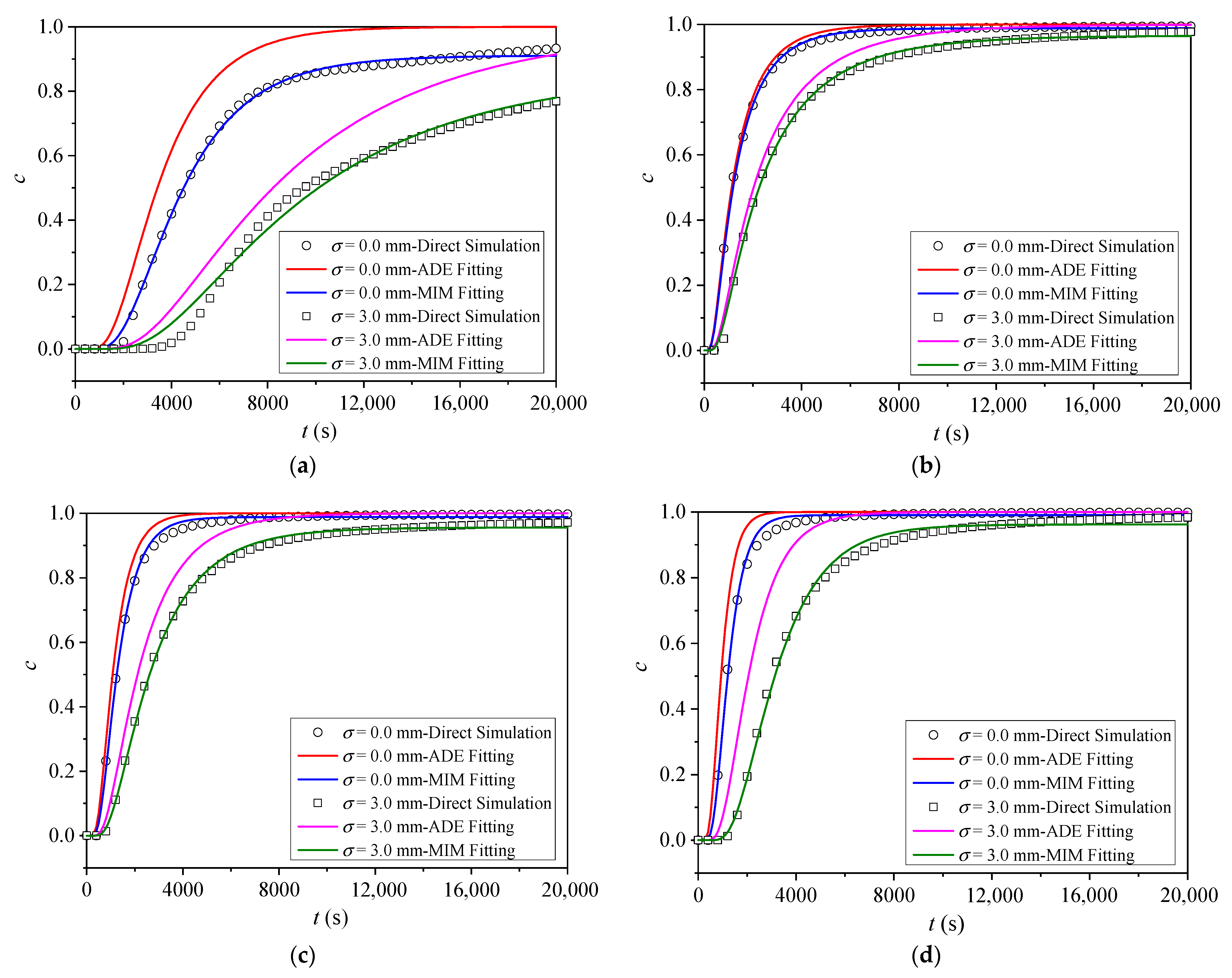
3.3. Inverse Model for BTCs
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Blum, P.; Mackay, R.; Riley, M.S.; Knight, J.L. Performance assessment of a nuclear waste repository: Upscaling coupled hydro-mechanical properties for far-field transport analysis. Int. J. Rock Mech. Min. Sci. 2005, 42, 781–792. [Google Scholar] [CrossRef]
- Hadgu, T.; Karra, S.; Kalinina, E.; Makedonska, N.; Hyman, J.D.; Klise, K.; Wang, Y. A comparative study of discrete fracture network and equivalent continuum models for simulating flow and transport in the far field of a hypothetical nuclear waste repository in crystalline host rock. J. Hydrol. 2017, 553, 59–70. [Google Scholar] [CrossRef]
- Lee, I.H.; Ni, C.F. Fracture-based modeling of complex flow and CO2 migration in three-dimensional fractured rocks. Comput. Geosci. 2015, 81, 64–77. [Google Scholar] [CrossRef]
- Carroll, S.; Carey, J.W.; Dzombak, D.; Huerta, N.J.; Li, L.; Richard, T.; Um, W.; Walsh, S.D.C.; Zhang, L. Role of chemistry, mechanics, and transport on well integrity in CO2 storage environments. Int. J. Greenh. Gas Control 2016, 49, 149–160. [Google Scholar] [CrossRef]
- Gao, Q.; Ghassemi, A. Three-dimensional thermo-poroelastic modeling and analysis of flow, heat transport and deformation in fractured rock with applications to a lab-scale geothermal system. Rock Mech. Rock Eng. 2020, 53, 1565–1586. [Google Scholar] [CrossRef]
- Huang, Y.; Pang, Z.; Kong, Y.; Watanabe, N. Assessment of the high-temperature aquifer thermal energy storage (HT-ATES) potential in naturally fractured geothermal reservoirs with a stochastic discrete fracture network model. J. Hydrol. 2021, 603, 127188. [Google Scholar] [CrossRef]
- Nemoto, K.; Watanabe, N.; Hirano, N.; Tsuchiya, N. Direct measurement of contact area and stress dependence of anisotropic flow through rock fracture with heterogeneous aperture distribution. Earth Planet. Sci. Lett. 2009, 281, 81–87. [Google Scholar] [CrossRef]
- Liu, R.; Li, B.; Jiang, Y. Critical hydraulic gradient for nonlinear flow through rock fracture networks: The roles of aperture, surface roughness, and number of intersections. Adv. Water Resour. 2016, 88, 53–65. [Google Scholar] [CrossRef]
- Huang, N.; Zhang, Y.; Yin, Q.; Jiang, Y.; Liu, R. Combined Effect of Contact Area, Aperture Variation, and Fracture Connectivity on Fluid Flow through Three-Dimensional Rock Fracture Networks. Lithosphere 2022, 2022, 2097990. [Google Scholar] [CrossRef]
- Kobayashi, A.; Chijimatsu, M. Continuous modeling of transport phenomena through fractured rocks. Soils Found. 1998, 38, 41–53. [Google Scholar] [CrossRef] [PubMed]
- Svensson, U. A continuum representation of fracture networks. Part I: Method and basic test cases. J. Hydrol. 2001, 250, 170–186. [Google Scholar]
- Marina, S.; Derek, I.; Mohamed, P.; Yong, S.; Imo-Imo, E.K. Simulation of the hydraulic fracturing process of fractured rocks by the discrete element method. Environ. Earth Sci. 2015, 73, 8451–8469. [Google Scholar] [CrossRef]
- Xia, L.; Zheng, Y.; Yu, Q. Estimation of the REV size for blockiness of fractured rock masses. Comput. Geotech. 2016, 76, 83–92. [Google Scholar] [CrossRef]
- Rutqvist, J.; Figueiredo, B.; Hu, M.; Tsang, C.F. Continuum modeling of hydraulic fracturing in complex fractured rock masses. In Hydraulic Fracture Modeling; Gulf Professional Publishing: Houston, TX, USA, 2018; pp. 195–217. [Google Scholar]
- Berkowitz, B.; Scher, H. Theory of anomalous chemical transport in random fracture networks. Phys. Rev. E 1998, 57, 5858. [Google Scholar] [CrossRef]
- Jing, L. Block system construction for three-dimensional discrete element models of fractured rocks. Int. J. Rock Mech. Min. Sci. 2000, 37, 645–659. [Google Scholar] [CrossRef]
- Lei, Q.; Latham, J.P.; Xiang, J.; Tsang, C.F.; Lang, P.; Guo, L. Effects of geomechanical changes on the validity of a discrete fracture network representation of a realistic two-dimensional fractured rock. Int. J. Rock Mech. Min. Sci. 2014, 70, 507–523. [Google Scholar] [CrossRef]
- Lang, P.S.; Paluszny, A.; Zimmerman, R.W. Permeability tensor of three-dimensional fractured porous rock and a comparison to trace map predictions. J. Geophys. Res. Solid Earth 2014, 119, 6288–6307. [Google Scholar] [CrossRef]
- Ren, F.; Ma, G.; Fan, L.; Wang, Y.; Zhu, H. Equivalent discrete fracture networks for modelling fluid flow in highly fractured rock mass. Eng. Geol. 2017, 229, 21–30. [Google Scholar] [CrossRef]
- Lee, I.H.; Ni, C.F.; Lin, F.P.; Lin, C.P.; Ke, C.C. Stochastic modeling of flow and conservative transport in three-dimensional discrete fracture networks. Hydrol. Earth Syst. Sci. 2019, 23, 19–34. [Google Scholar] [CrossRef]
- Huang, N.; Jiang, Y.; Liu, R.; Li, B.; Sugimoto, S. A novel three-dimensional discrete fracture network model for investigating the role of aperture heterogeneity on fluid flow through fractured rock masses. Int. J. Rock Mech. Min. Sci. 2019, 116, 25–37. [Google Scholar] [CrossRef]
- Akara, M.E.M.; Reeves, D.M.; Parashar, R. Impact of horizontal spatial clustering in two-dimensional fracture networks on solute transport. J. Hydrol. 2021, 603, 127055. [Google Scholar] [CrossRef]
- Khafagy, M.; El-Dakhakhni, W.; Dickson-Anderson, S. Analytical model for solute transport in discrete fracture networks: 2D spatiotemporal solution with matrix diffusion. Comput. Geosci. 2022, 159, 104983. [Google Scholar] [CrossRef]
- Maillot, J.; Davy, P.; Le Goc, R.; Darcel, C.; De Dreuzy, J.R. Connectivity, permeability, and channeling in randomly distributed and kinematically defined discrete fracture network models. Water Resour. Res. 2016, 52, 8526–8545. [Google Scholar] [CrossRef]
- Frampton, A.; Hyman, J.D.; Zou, L. Advective transport in discrete fracture networks with connected and disconnected textures representing internal aperture variability. Water Resour. Res. 2019, 55, 5487–5501. [Google Scholar] [CrossRef]
- Kang, P.K.; Hyman, J.D.; Han, W.S.; Dentz, M. Anomalous transport in three-dimensional discrete fracture networks: Interplay between aperture heterogeneity and injection modes. Water Resour. Res. 2020, 56, e2020WR027378. [Google Scholar] [CrossRef]
- Makedonska, N.; Painter, S.L.; Bui, Q.M.; Gable, C.W.; Karra, S. Particle tracking approach for transport in three-dimensional discrete fracture networks: Particle tracking in 3-D DFNs. Comput. Geosci. 2015, 19, 1123–1137. [Google Scholar] [CrossRef]
- Ngo, T.D.; Fourno, A.; Noetinger, B. Modeling of transport processes through large-scale discrete fracture networks using conforming meshes and open-source software. J. Hydrol. 2017, 554, 66–79. [Google Scholar] [CrossRef]
- Zhao, Z.; Li, B.; Jiang, Y. Effects of fracture surface roughness on macroscopic fluid flow and solute transport in fracture networks. Rock Mech. Rock Eng. 2014, 47, 2279–2286. [Google Scholar] [CrossRef]
- Dronfield, D.G.; Silliman, S.E. Velocity dependence of dispersion for transport through a single fracture of variable roughness. Water Resour. Res. 1993, 29, 3477–3483. [Google Scholar] [CrossRef]
- Johnson, J.; Brown, S. Experimental mixing variability in intersecting natural fractures. Geophys. Res. Lett. 2001, 28, 4303–4306. [Google Scholar] [CrossRef]
- Roux, S.; Plouraboué, F.; Hulin, J.P. Tracer dispersion in rough open cracks. Transp. Porous Media 1998, 32, 97–116. [Google Scholar] [CrossRef]
- Larsson, M.; Odén, M.; Niemi, A.; Neretnieks, I.; Tsang, C.F. A new approach to account for fracture aperture variability when modeling solute transport in fracture networks. Water Resour. Res. 2013, 49, 2241–2252. [Google Scholar] [CrossRef]
- Zou, L.; Cvetkovic, V. Impact of normal stress-induced closure on laboratory-scale solute transport in a natural rock fracture. J. Rock Mech. Geotech. Eng. 2020, 12, 732–741. [Google Scholar] [CrossRef]
- Zhou, J.Q.; Li, C.; Wang, L.; Tang, H.; Zhang, M. Effect of slippery boundary on solute transport in rough-walled rock fractures under different flow regimes. J. Hydrol. 2021, 598, 126456. [Google Scholar] [CrossRef]
- Qian, J.Z.; Chen, Z.; Zhan, H.B.; Luo, S.H. Solute transport in a filled single fracture under non-Darcian flow. Int. J. Rock Mech. Min. Sci. 2011, 48, 132–140. [Google Scholar] [CrossRef]
- Geiger, S.; Cortis, A.; Birkholzer, J.T. Upscaling solute transport in naturally fractured porous media with the continuous time random walk method. Water Resour. Res. 2010, 46, W12530. [Google Scholar] [CrossRef]
- Nowamooz, A.; Radilla, G.; Fourar, M.; Berkowitz, B. Non-Fickian transport in transparent replicas of rough-walled rock fractures. Transp. Porous Media 2013, 98, 651–682. [Google Scholar] [CrossRef]
- Bauget, F.; Fourar, M. Non-Fickian dispersion in a single fracture. J. Contam. Hydrol. 2008, 100, 137–148. [Google Scholar] [CrossRef] [PubMed]
- Dou, Z.; Sleep, B.; Zhan, H.; Zhou, Z.; Wang, J. Multiscale roughness influence on conservative solute transport in self-affine fractures. Int. J. Heat Mass Transf. 2019, 133, 606–618. [Google Scholar] [CrossRef]
- Hu, Y.; Xu, W.; Zhan, L.; Zou, L.; Chen, Y. Modeling of solute transport in a fracture-matrix system with a three-dimensional discrete fracture network. J. Hydrol. 2022, 605, 127333. [Google Scholar] [CrossRef]
- Cherubini, C.; Giasi, C.I.; Pastore, N. On the reliability of analytical models to predict solute transport in a fracture network. Hydrol. Earth Syst. Sci. 2014, 18, 2359–2374. [Google Scholar] [CrossRef]
- Lei, Q.; Latham, J.P.; Tsang, C.F.; Xiang, J.; Lang, P. A new approach to upscaling fracture network models while preserving geostatistical and geomechanical characteristics. J. Geophys. Res. Solid Earth 2015, 120, 4784–4807. [Google Scholar] [CrossRef]
- Darcel, C.; Bour, O.; Davy, P. Stereological analysis of fractal fracture networks. J. Geophys. Res. Solid Earth 2003, 108, 2451. [Google Scholar] [CrossRef]
- De Dreuzy, J.R.; Méheust, Y.; Pichot, G. Influence of fracture scale heterogeneity on the flow properties of three-dimensional discrete fracture networks (DFN). J. Geophys. Res. Solid Earth 2012, 117, B11207. [Google Scholar] [CrossRef]
- Detwiler, R.L.; Pringle, S.E.; Glass, R.J. Measurement of fracture aperture fields using transmitted light: An evaluation of measurement errors and their influence on simulations of flow and transport through a single fracture. Water Resour. Res. 1999, 35, 2605–2617. [Google Scholar] [CrossRef]
- Isakov, E.; Ogilvie, S.R.; Taylor, C.W.; Glover, P.W. Fluid flow through rough fractures in rocks I: High resolution aperture determinations. Earth Planet. Sci. Lett. 2001, 191, 267–282. [Google Scholar] [CrossRef]
- Lapcevic, P.A.; Novakowski, K.S.; Sudicky, E.A. The interpretation of a tracer experiment conducted in a single fracture under conditions of natural groundwater flow. Water Resour. Res. 1999, 35, 2301–2312. [Google Scholar] [CrossRef]
- Brown, S.R.; Kranz, R.L.; Bonner, B.P. Correlation between the surfaces of natural rock joints. Geophys. Res. Lett. 1986, 13(13), 1430–1433. [Google Scholar] [CrossRef]
- Masciopinto, C. Pumping-well data for conditioning the realization of the fracture aperture field in groundwater flow models. J. Hydrol. 2005, 309, 210–228. [Google Scholar] [CrossRef]
- Bonnet, E.; Bour, O.; Odling, N.E.; Davy, P.; Main, I.; Cowie, P.; Berkowitz, B. Scaling of fracture systems in geological media. Rev. Geophys. 2001, 39, 347–383. [Google Scholar] [CrossRef]
- Li, B.; Wang, J.; Liu, R.; Jiang, Y. Nonlinear fluid flow through three-dimensional rough fracture networks: Insights from 3D-printing, CT-scanning, and high-resolution numerical simulations. J. Rock Mech. Geotech. Eng. 2021, 13, 1020–1032. [Google Scholar] [CrossRef]
- Foias, C.; Manley, O.; Rosa, R.; Temam, R. Navier-Stokes Equations and Turbulence; Cambridge University Press: Cambridge, UK, 2001; Volume 83. [Google Scholar]
- Witherspoon, P.A.; Wang, J.S.; Iwai, K.; Gale, J.E. Validity of cubic law for fluid flow in a deformable rock fracture. Water Resour. Res. 1980, 16, 1016–1024. [Google Scholar] [CrossRef]
- Bear, J. Dynamics of Fluids in Porous Media; Courier Corporation: Chelmsford, MA, USA, 2013. [Google Scholar]
- De Marsily, G. Quantitative Hydrogeology; Paris School of Mines: Fontainebleau, France, 1986. [Google Scholar]
- Cherubini, C.; Giasi, C.I.; Pastore, N. Evidence of non-Darcy flow and non-Fickian transport in fractured media at laboratory scale. Hydrol. Earth Syst. Sci. 2013, 17, 2599–2611. [Google Scholar] [CrossRef]
- Parker, J.C.; Van Genuchten, M.T. Flux-averaged and volume-averaged concentrations in continuum approaches to solute transport. Water Resour. Res. 1984, 20, 866–872. [Google Scholar] [CrossRef]
- Thompson, M.E. Numerical simulation of solute transport in rough fractures. J. Geophys. Res. Solid Earth 1991, 96, 4157–4166. [Google Scholar] [CrossRef]
- Dou, Z.; Chen, Z.; Zhou, Z.; Wang, J.; Huang, Y. Influence of eddies on conservative solute transport through a 2D single self-affine fracture. Int. J. Heat Mass Transf. 2018, 121, 597–606. [Google Scholar] [CrossRef]
- Tang, G.; Mayes, M.A.; Parker, J.C.; Jardine, P.M. CXTFIT/Excel–A modular adaptable code for parameter estimation, sensitivity analysis and uncertainty analysis for laboratory or field tracer experiments. Comput. Geosci. 2010, 36, 1200–1209. [Google Scholar] [CrossRef]

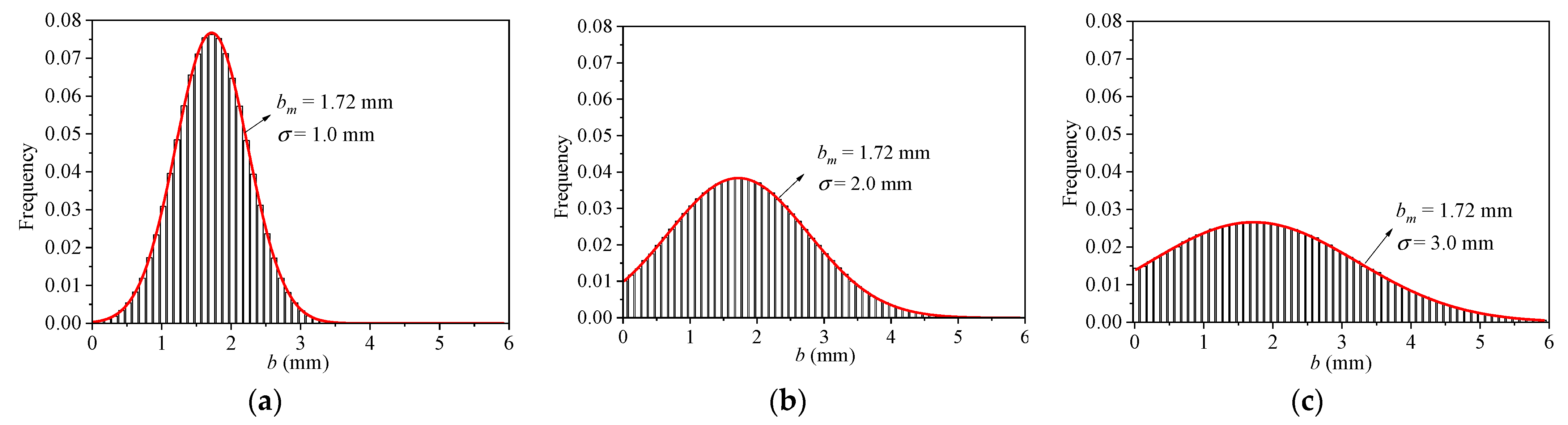



| P32 (m2/m3) | σ | a = 2.0 | a = 4.5 | ||
|---|---|---|---|---|---|
| EADE | EMIM | EADE | EMIM | ||
| 0.45 | 0 | 0.0529 | 0.0323 | 0.0478 | 0.0345 |
| 0.45 | 1 | 0.0345 | 0.0188 | 0.0292 | 0.0108 |
| 0.45 | 2 | 0.0779 | 0.0268 | 0.0277 | 0.0145 |
| 0.45 | 3 | 0.0342 | 0.0191 | 0.0524 | 0.0345 |
| 0.65 | 0 | 0.0517 | 0.0403 | 0.0213 | 0.015 |
| 0.65 | 1 | 0.0324 | 0.0249 | 0.0251 | 0.0174 |
| 0.65 | 2 | 0.0512 | 0.0382 | 0.0266 | 0.0186 |
| 0.65 | 3 | 0.0309 | 0.0236 | 0.028 | 0.0136 |
| 0.85 | 0 | 0.043 | 0.0323 | 0.0226 | 0.0142 |
| 0.85 | 1 | 0.0394 | 0.0304 | 0.0268 | 0.0166 |
| 0.85 | 2 | 0.0446 | 0.0346 | 0.0133 | 0.0085 |
| 0.85 | 3 | 0.0311 | 0.0234 | 0.0290 | 0.0196 |
| 1.05 | 0 | 0.0497 | 0.0360 | 0.0441 | 0.0256 |
| 1.05 | 1 | 0.0321 | 0.0218 | 0.0358 | 0.0269 |
| 1.05 | 2 | 0.0434 | 0.0337 | 0.0436 | 0.0298 |
| 1.05 | 3 | 0.0318 | 0.0233 | 0.0426 | 0.0328 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, N.; Zhang, Y.; Han, S. Effects of Topological Properties with Local Variable Apertures on Solute Transport through Three-Dimensional Discrete Fracture Networks. Processes 2023, 11, 3157. https://doi.org/10.3390/pr11113157
Huang N, Zhang Y, Han S. Effects of Topological Properties with Local Variable Apertures on Solute Transport through Three-Dimensional Discrete Fracture Networks. Processes. 2023; 11(11):3157. https://doi.org/10.3390/pr11113157
Chicago/Turabian StyleHuang, Na, Yubao Zhang, and Shengqun Han. 2023. "Effects of Topological Properties with Local Variable Apertures on Solute Transport through Three-Dimensional Discrete Fracture Networks" Processes 11, no. 11: 3157. https://doi.org/10.3390/pr11113157
APA StyleHuang, N., Zhang, Y., & Han, S. (2023). Effects of Topological Properties with Local Variable Apertures on Solute Transport through Three-Dimensional Discrete Fracture Networks. Processes, 11(11), 3157. https://doi.org/10.3390/pr11113157








