Performance Optimization of a Spoon Precision Seed Metering Device Based on a Maize Seed Assembly Model and Discrete Element Method
Abstract
:1. Introduction
2. Materials and Methods
2.1. Maize Seed Assembly Model
2.2. The Spoon Precision Seed Metering Device
2.3. The Parameter Selection in the DEM Simulation
2.4. Performance Research of the Seed Meter
2.4.1. Verification Simulation of the Maize Seed Assembly Model
2.4.2. Optimization Simulation of the Seed Metering Device
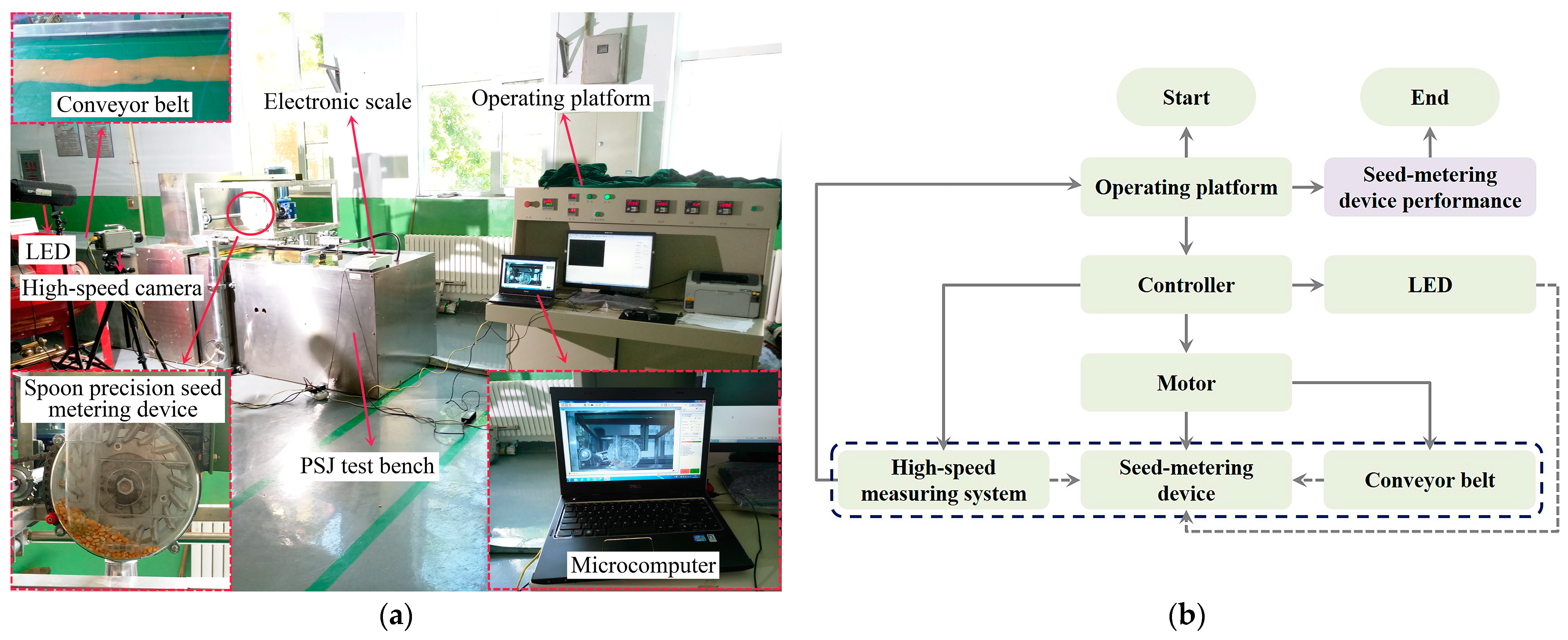
3. Experiment Verification
4. Results and Discussion
4.1. Validation Analysis of the Maize Seed Assembly Model
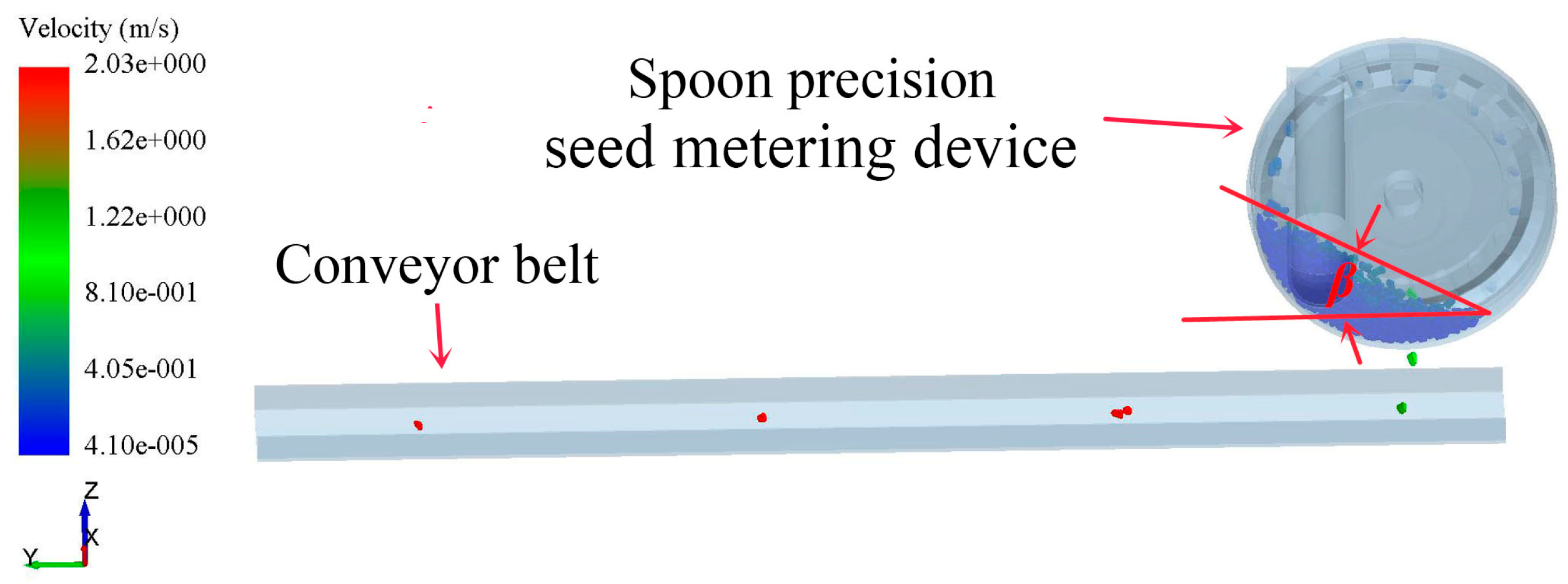
4.1.1. Maize Seed Particle Behavior
4.1.2. Seed Surface Inclination Angle
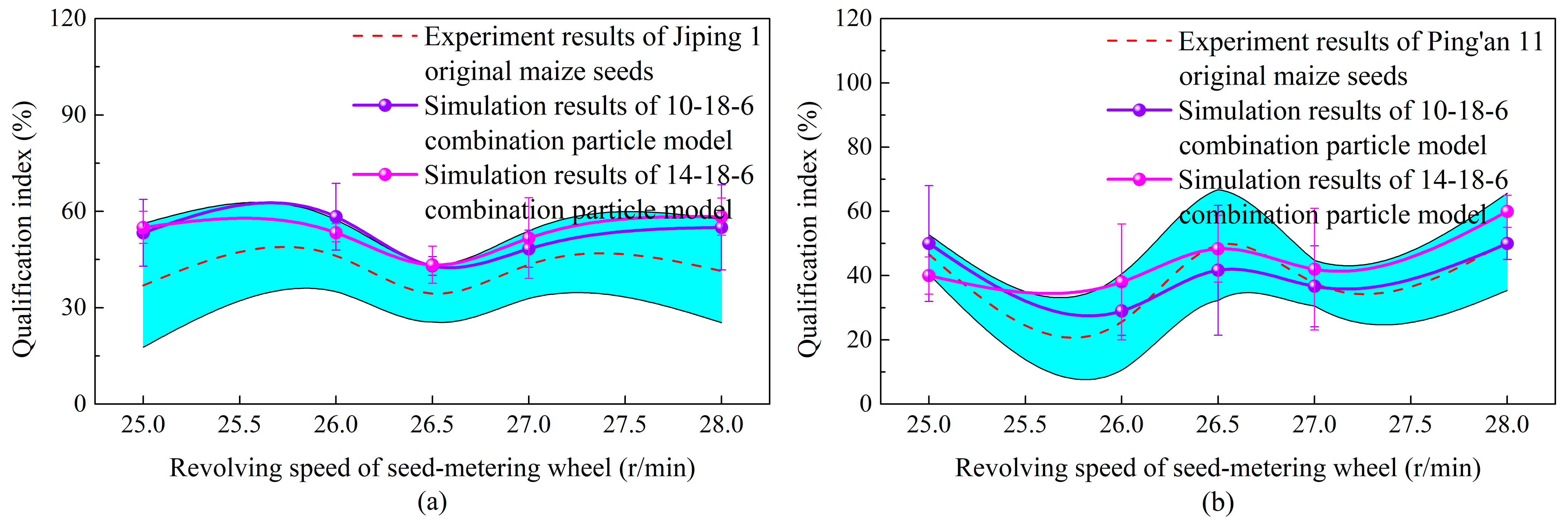
4.1.3. Qualification Index
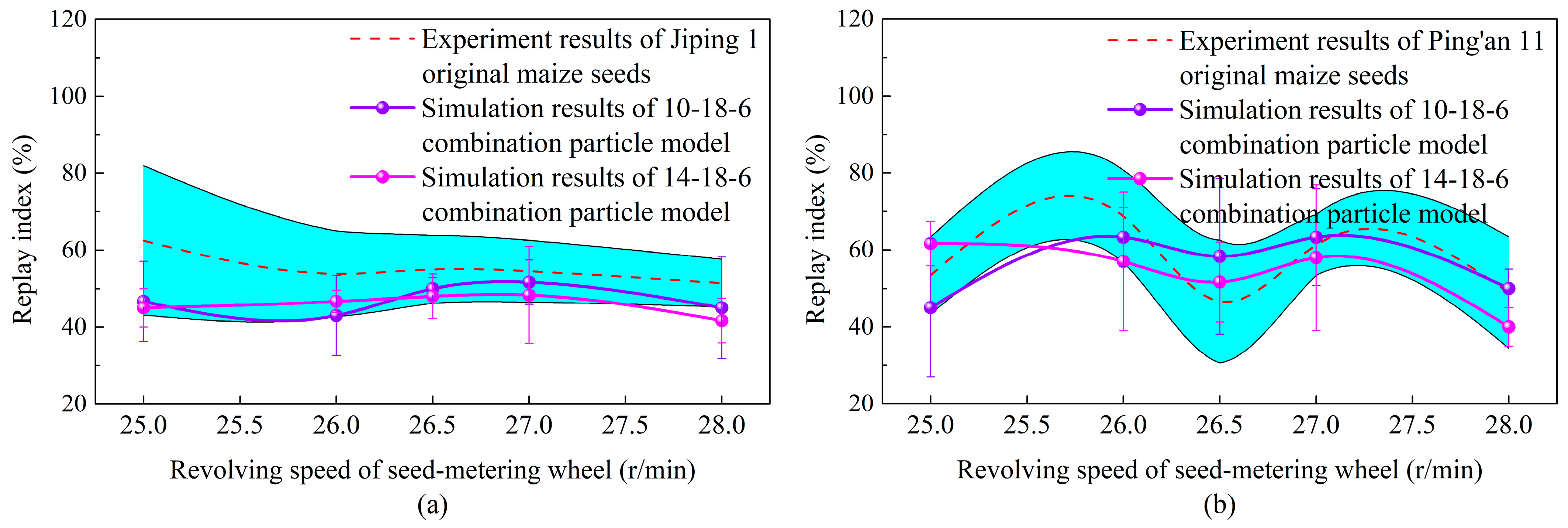
4.1.4. Replay Index
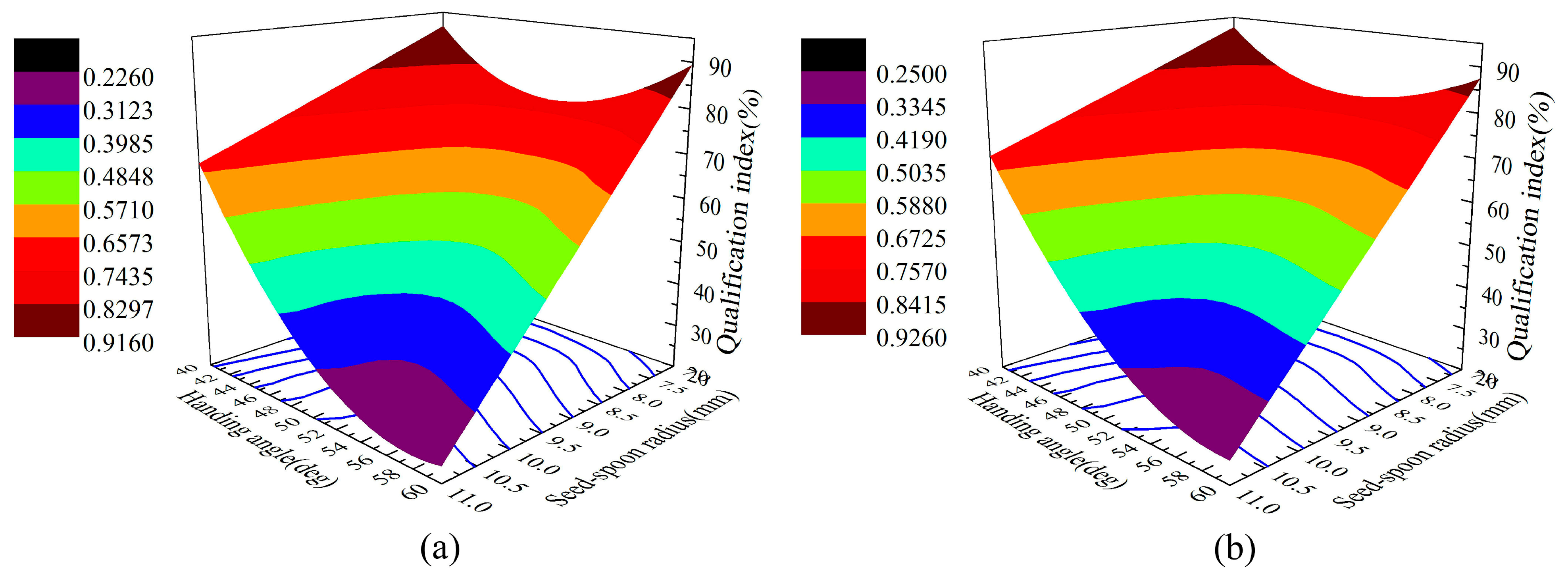
4.2. Optimization Analysis of Seed Metering Device Performance
4.2.1. Simulation Optimization
4.2.2. Verification Analysis
5. Conclusions
- (1)
- The validity of the maize seed assembly model is verified based on the sowing process, and the seed surface inclination angle increases first and then decreases with the increase in the revolving speed of the seed metering wheel;
- (2)
- The optimized Zone E has a larger radial length, which facilitates the process of seed guiding and seed delivery during the sowing process, and the replay index and the coefficient of variation both meet the corresponding technical requirements, which shows that the seed spacing is relatively stable;
- (3)
- With the increase in the revolving speed of the seed metering wheel, the perturbation of maize seeds by seed spoons became obvious, and the pressure on the head of the seed spoon in Zone E is higher;
- (4)
- In terms of the seed metering device performance, the seed spoon radius and the SR·HA interaction have a significant influence, and the SR·HA interaction shows an antagonistic effect.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cundall, P.A.; Strack, O.D. A discrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Boac, J.M.; Ambrose, R.P.K.; Casada, M.E.; Maghirang, R.G.; Maier, D.E. Applications of discrete element method in modeling of grain postharvest operations. Food Eng. Rev. 2014, 6, 128–149. [Google Scholar] [CrossRef]
- Ketterhagen, W.R. Modeling the motion and orientation of various pharmaceutical tablet shapes in a film coating pan using DEM. Int. J. Pharm. 2011, 409, 137–149. [Google Scholar] [CrossRef]
- Anand, A.; Curtis, J.S.; Wassgren, C.R.; Hancock, B.C.; Ketterhagen, W.R. Predicting discharge dynamics from a rectangular hopper using the discrete element method (DEM). Chem. Eng. Sci. 2008, 63, 5821–5830. [Google Scholar] [CrossRef]
- Whittles, D.N.; Kingman, S.; Lowndes, I.S.; Griffiths, R. An investigation into the parameters affecting mass flow rate of ore material through a microwave continuous feed system. Adv. Powder Technol. 2005, 16, 585–609. [Google Scholar] [CrossRef]
- Fu, H.; Wang, C.R.; Jin, C.; Yu, J.Q. Development of digital design software platform AgriDEM for agricultural machinery parts. Trans. Chin. Soc. Agric. Eng. 2017, 33, 1–9. [Google Scholar]
- Yu, J.Q.; Fu, H.; Li, H.; Shen, Y.F. Application of discrete element method to research and design of working parts of agricultural machines. Trans. Chin. Soc. Agric. Eng. 2005, 21, 1–6. [Google Scholar]
- He, Y.M.; Wu, M.L.; Xiang, W.; Yan, B.; Wang, J.Y.; Bao, P.F. Application progress of discrete element method in agricultural engineering. Chin. Agric. Sci. Bull. 2017, 33, 133–137. [Google Scholar]
- Wang, X.; Zhang, S.; Pan, H.; Zheng, Z.; Huang, Y.; Zhu, R. Effect of soil particle size on soil-subsoiler interactions using the discrete element method simulations. Biosyst. Eng. 2019, 182, 138–150. [Google Scholar] [CrossRef]
- Li, X.; Du, Y.; Liu, L.; Zhang, Y.; Guo, D. Parameter calibration of corncob based on DEM. Adv. Powder Technol. 2022, 33, 103699. [Google Scholar] [CrossRef]
- Yasunaga, T.; Yoshida, M.; Shimosaka, A.; Shirakawa, Y.; Andoh, T.; Ichikawa, H.; Ogawa, N.; Yamamoto, H. Mathematical modeling of coating time in dry particulate coating using mild vibration field with bead media described by DEM simulation. Adv. Powder Technol. 2022, 33, 103779. [Google Scholar] [CrossRef]
- Chen, Z.; Xue, D.; Guan, W.; Liu, Z.; Guo, J.; Wang, G.; Wang, S. Research on the disturbance behaviour of the track chassis to the sand-gravel pavement during the steering process of the electric shovel based on DEM. Adv. Powder Technol. 2022, 33, 103731. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, G.; Xue, D.; Cui, D. Simulation and optimization of crushing chamber of gyratory crusher based on the DEM and GA. Powder Technol. 2021, 384, 36–50. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, G.; Guan, W.; Guo, J.; Sun, G.; Chen, Z. Research on performance of a laboratory-scale SAG mill based on DEM-EMBD. Powder Technol. 2022, 406, 117581. [Google Scholar] [CrossRef]
- Shi, L.; Zhao, W.; Yang, X. Effects of typical corn kernel shapes on the forming of repose angle by DEM simulation. Int. J. Agric. Biol. Eng. 2022, 15, 248–255. [Google Scholar] [CrossRef]
- Yan, D.; Yu, J.; Wang, Y.; Zhou, L.; Sun, K.; Tian, Y. A review of the application of discrete element method in agricultural engineering: A case study of soybean. Processes 2022, 10, 1305. [Google Scholar] [CrossRef]
- Zhou, L.; Yu, J.; Liang, L.; Yu, Y.; Yan, D.; Sun, K.; Wang, Y. Study on key issues in the modelling of maize seeds based on the multi-sphere method. Powder Technol. 2021, 394, 791–812. [Google Scholar] [CrossRef]
- Wang, S.; Yu, Z.; Zhang, W. Aorigele, Study on the modeling method of sunflower seed particles based on the discrete element method. Comput. Electron. Agric. 2022, 198, 107012. [Google Scholar] [CrossRef]
- Chen, Z.; Yu, J.; Xue, D.; Wang, Y.; Zhang, Q.; Ren, L. An approach to and validation of maize-seed-assembly modelling based on the discrete element method. Powder Technol. 2018, 328, 167–183. [Google Scholar] [CrossRef]
- Rocha-Villarreal, V.; Hoffmann, J.F.; Vanier, N.L.; Serna-Saldivar, S.O.; Garcia-Lara, S. Hydrothermal treatment of maize: Changes in physical, chemical, and functional properties. Food Chem. 2018, 263, 225–231. [Google Scholar] [CrossRef] [PubMed]
- James, A.; Zikankuba, V.L. Mycotoxins contamination in maize alarms food safety in sub-Sahara Africa. Food Control 2018, 90, 372–381. [Google Scholar] [CrossRef]
- Yang, G.; Wang, Q.; Liu, C.; Wang, X.B.; Fan, S.X.; Huang, W.Q. Rapid and visual detection of the main chemical compositions in maize seeds based on Raman hyperspectral imaging. Spectrochim. Acta A Mol. Biomol. Spectrosc. 2018, 200, 186–194. [Google Scholar] [CrossRef] [PubMed]
- Tenaillon, M.I.; Charcosset, A. A European perspective on maize history L’histoire du maïs cultivé vue sous un angle européen. C. R. Biol. 2011, 334, 221–228. [Google Scholar] [CrossRef] [PubMed]
- Shi, S. Design and Experimental Research of the Pneumatic Maize Precision Seedmetering Device with Combined Holes; China Agricultural University: Beijing, China, 2015. [Google Scholar]
- Zhang, C.L.; Chen, L.Q.; Wu, R. Simulation analysis of seeding performance of spoon-wheel seed metering device based on the discrete element method. J. AnHui Agric. Univ. 2016, 43, 848–852. [Google Scholar]
- Yang, M.F. Study on Digital Design Method of Corn Seed-Metering Device Based on DEM; Jilin University: Changchun, China, 2009. [Google Scholar]
- Zhang, Y.; Li, C.H.; Ji, Y.J.; Sun, Y.J. Simulation analysis of seeding process for corn seed metering device based on discrete element method. J. Shenyang Ligong Univ. 2015, 34, 1–4. [Google Scholar]
- Zhao, S.H.; Chen, J.Z.; Wang, J.Y.; Chen, J.Q.; Yang, C.; Yang, Y.Q. Design and experiment on V-groove dialing round type guiding-seed device. Trans. Chin. Soc. Agric. Mach. 2018, 49, 146–158. [Google Scholar]
- Sun, S.C. Simulation Analysis of Working Process of Air Suction Corn Precision Seed-Metering Device Based on DEM-CFD Coupling Method; Jilin University: Changchun, China, 2016. [Google Scholar]
- Wang, Y.X.; Liang, Z.J. Calibration method of contact characteristic parameters for corn seeds based on EDEM. Trans. Chin. Soc. Agric. Eng. 2016, 32, 36–42. [Google Scholar]
- Wang, J.W.; Tang, H.; Wang, Q.; Zhou, W.Q.; Yang, W.P.; Shen, H.G. Numerical simulation and experiment on seeding performance of pickup finger precision seed-metering device based on EDEM. Trans. Chin. Soc. Agric. Eng. 2015, 31, 43–50. [Google Scholar]
- Wang, J.; Tang, H.; Wang, J.; Li, X.; Huang, H. Optimization design and experiment on ripple surface type pickup finger of precision maize seed metering device. Int. J. Agric. Biol. Eng. 2017, 10, 61–71. [Google Scholar]
- Zhang, K.; Yi, S.J. Simulation and experimental optimization on filling seeds performance of seed metering device with roller of air-suction. Trans. Chin. Soc. Agric. Mach. 2018, 7, 78–86. [Google Scholar]
- Han, D.D.; Zhang, D.X.; Yang, L.; Li, K.H.; Zhang, T.L.; Wang, Y.X.; Cui, T. EDEM-CFD simulation and experiment of working performance of inside-filling air-blowing seed metering device in maize. Trans. Chin. Soc. Agric. Eng. 2017, 33, 23–31. [Google Scholar]
- Zhou, L.; Yu, J.Q.; Wang, Y.; Yan, D.X.; Yu, Y.J. A study on the modelling method of maize-seed particles based on the discrete element method. Powder Technol. 2020, 374, 353–376. [Google Scholar] [CrossRef]
- Kudo, Y.; Yasuda, M.; Matsusaka, S. Effect of particle size distribution on flowability of granulated lactose. Adv. Powder Technol. 2020, 31, 121–127. [Google Scholar] [CrossRef]
- Pasha, M.; Hare, C.; Ghadiri, M.; Gunadi, A.; Piccione, P.M. Effect of particle shape on flow in discrete element method simulation of a rotary batch seed coater. Powder Technol. 2016, 296, 29–36. [Google Scholar] [CrossRef]
- Wang, X.Y.; Wang, J.W.; Tang, H.; Jiang, D.X.; Li, C.; Gao, J.W. Improve design and experiment on spoon of spoon precision seed metering device. J. Northeast Agric. Univ. 2015, 46, 79–85. [Google Scholar]
- Zhao, S.H.; Zhou, Y.; Liu, H.J.; Tan, H.W.; Zhang, X.M.; Yang, Y.Q. Design of reseed shift speed system of scoop-type metering device of corn. Trans. Chin. Soc. Agric. Mach. 2016, 47, 38–44. [Google Scholar]
- Yang, L.; Yan, B.X.; Zhang, D.X.; Zhang, T.L.; Wang, Y.X.; Cui, T. Research progress on precision planting technology of maize. Trans. Chin. Soc. Agric. Mach. 2016, 47, 38–48. [Google Scholar]
- ASAE Standards 2002: Standards Engineering Practices 49; Compression Test of Food Materials of Convex Shape. American Society of Agricultural Engineers: St. Joseph, MI, USA, 2002; pp. 592–599.
- Horabik, J.; Molenda, M. Parameters and contact models for DEM simulations of agricultural granular materials: A review. Biosyst. Eng. 2016, 147, 206–225. [Google Scholar] [CrossRef]
- Liu, Y.F.; Lin, J.; Li, B.F.; Ma, T.; Song, J.P.; Tian, Y. Design and experiment of horizontal disc seed metering device for maize seeder. Trans. Chin. Soc. Agric. Eng. 2017, 33, 37–46. [Google Scholar]
- Tang, H.; Xu, C.; Guo, F.; Yao, Z.; Jiang, Y.; Guan, R.; Sun, X.; Wang, J. Analysis and experiment on the seed metering mechanism of multi-grain cluster air suction type rice (Oryza sativa L.) hill direct seed metering device. Agriculture 2022, 12, 1094. [Google Scholar] [CrossRef]
- Ji, Y.J.; Xue, H.D.; Li, C.H. Simulation analysis of seed metering procedure in scoop metering device based on discrete element method. Appl. Mech. Mater. 2012, 157–158, 550–557. [Google Scholar] [CrossRef]
- Kim, T.K. Understanding one-way ANOVA using conceptual figures. Korean J. Anesthesiol. 2017, 70, 22–26. [Google Scholar] [CrossRef] [PubMed]





| Variety | Seed Shape | Primary Size Distribution (mm) | Percentage of Quantity (%) | ||
|---|---|---|---|---|---|
| Mean | Standard Deviation | Original | Normalization | ||
| Jiping 1 | horse tooth | 5.50 | 0.79 | 86.14 | 88.97 |
| spherical cone | 5.10 | 0.81 | 5.81 | 6.00 | |
| spheroid | 7.81 | 0.89 | 4.87 | 5.03 | |
| Ping’an 11 | horse tooth | 5.25 | 0.80 | 76.57 | 80.77 |
| spherical cone | 5.03 | 0.76 | 9.80 | 10.21 | |
| spheroid | 7.82 | 0.86 | 8.43 | 9.02 | |
| Parameters | Symbol | Jiping 1 | Ping’an 11 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Maize | Organic Glass | Aluminum Alloy | Rubber | Maize | Organic Glass | Aluminum Alloy | Rubber | ||
| Density (kg/m3) | ρ | 1276 | 1800 | 2700 | 9100 | 1306 | 1800 | 2700 | 9100 |
| Poisson’s ratio | v | 0.4 | 0.35 | 0.34 | 0.45 | 0.4 | 0.35 | 0.34 | 0.45 |
| Shear modulus (Pa) | G | 1.37 × 108 | 1.30 × 109 | 2.5 × 1010 | 1 × 106 | 1.37 × 108 | 1.30 × 109 | 2.5 × 1010 | 1 × 106 |
| Restitution coefficient | e | 0.7826 | 0.6983 | 0.774 | 0.0001 | 0.6526 | 0.7373 | 0.818 | 0.0001 |
| Static friction coefficient | μ | 0.12 | 0.333 | 0.307 | 1 | 0.12 | 0.3368 | 0.284 | 1 |
| Rolling friction coefficient | μr | 0.02 | 0.06 | 0.051 | 2 | 0.02 | 0.06 | 0.051 | 2 |
| Parameters | Jiping 1 | Ping’an 11 | ||||
|---|---|---|---|---|---|---|
| Horse Tooth | Spherical Cone | Spheroid | Horse Tooth | Spherical Cone | Spheroid | |
| Mean of volumes (V, mm3) | 339.21 | 346.93 | 351.59 | 328.46 | 348.99 | 353.19 |
| Standard deviation of volumes (σ, mm3) | 0.13 | 0.17 | 0.20 | 0.16 | 0.15 | 0.17 |
| Level | Experimental Factors | ||
|---|---|---|---|
| Seed Spoon Radius (z1, mm) | Handing Angle (z2, deg) | Revolving Speed of Seed Metering Wheel (z3, r/min) | |
| −1 | 7 | 40 | 25.0 |
| 0 | 9 | 50 | 26.5 |
| 1 | 11 | 60 | 28.0 |
| No. | Experimental Factor | Qualification Index | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| x0 | x1(z1) | x2(z2) | x3(z3) | x1·x2 | x1·x3 | x2·x3 | y1i | y2i | ||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0.20 | 0.19 | |
| 2 | 1 | 1 | 1 | −1 | 1 | −1 | −1 | 0.27 | 0.31 | |
| 3 | 1 | 1 | −1 | 1 | −1 | 1 | −1 | 0.60 | 0.62 | |
| 4 | 1 | 1 | −1 | −1 | −1 | −1 | 1 | 0.75 | 0.78 | |
| 5 | 1 | −1 | 1 | 1 | −1 | −1 | 1 | 0.82 | 0.80 | |
| 6 | 1 | −1 | 1 | −1 | −1 | 1 | −1 | 0.97 | 0.95 | |
| 7 | 1 | −1 | −1 | 1 | 1 | −1 | −1 | 0.95 | 0.99 | |
| 8 | 1 | −1 | −1 | −1 | 1 | 1 | 1 | 0.88 | 0.86 | |
| 9 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0.45 | 0.51 | |
| 10 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0.50 | 0.57 | |
| 11 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0.40 | 0.45 | |
| Analysis of variance | ||||||||||
| Dj | 11 | 8 | 8 | 8 | 8 | 8 | 8 | S = 0.7468 f = 10 | S = 0.6819 f = 10 | |
| Bj | Jiping 1 | 6.79 | −1.8 | −0.92 | −0.30 | −0.84 | −0.14 | −0.14 | Se-Jiping 1 = 0.0050 fe = 2 | Se-Ping’an 11 = 0.0072 fe = 2 |
| Ping’an 11 | 7.03 | −1.7 | −1 | 0.3 | −0.8 | 0.26 | −0.24 | |||
| bj | Jiping 1 | 0.62 | −0.23 | −0.12 | −0.04 | −0.11 | −0.02 | −0.02 | ||
| Ping’an 11 | 0.64 | −0.21 | −0.13 | −0.04 | −0.10 | −0.03 | −0.03 | |||
| Sj | Jiping 1 | 4.20 | 0.41 | 0.11 | 0.01 | 0.09 | 0.002 | 0.002 | fhui = 6 | fhui = 6 |
| Ping’an 11 | 4.493 | 0.361 | 0.125 | 0.011 | 0.08 | 0.008 | 0.007 | |||
| Fj | Jiping 1 | 1677 | 162 | 42.32 | 4.50 | 35.28 | 0.98 | 0.98 | ||
| Ping’an 11 | 1248 | 100.3 | 34.72 | 3.125 | 22.22 | 2.347 | 2 | |||
| αj | Jiping 1 | 0.01 | 0.05 | 0.25 | 0.05 | >0.25 | >0.25 | |||
| Ping’an 11 | 0.01 | 0.05 | 0.25 | 0.05 | >0.25 | 0.25 | ||||
| Varieties | Qualification Index (%) | Relative Error (%) | Replay Index (%) | Coefficient of Variation (%) | |
|---|---|---|---|---|---|
| Experiment Results | Predicted Results | ||||
| Jiping 1 | 91.55 | 90.00 | 1.69 | 7.86 | 14.46 |
| 92.40 | 90.00 | 2.60 | 7.50 | 13.35 | |
| 89.45 | 90.00 | 0.61 | 8.34 | 19.02 | |
| Ping’an 11 | 88.05 | 92.30 | 4.60 | 9.85 | 20.59 |
| 93.53 | 92.30 | 1.33 | 7.23 | 13.63 | |
| 90.56 | 92.30 | 1.89 | 8.46 | 15.21 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Xue, D.; Guan, W.; Guo, J.; Liu, Z. Performance Optimization of a Spoon Precision Seed Metering Device Based on a Maize Seed Assembly Model and Discrete Element Method. Processes 2023, 11, 3076. https://doi.org/10.3390/pr11113076
Chen Z, Xue D, Guan W, Guo J, Liu Z. Performance Optimization of a Spoon Precision Seed Metering Device Based on a Maize Seed Assembly Model and Discrete Element Method. Processes. 2023; 11(11):3076. https://doi.org/10.3390/pr11113076
Chicago/Turabian StyleChen, Zeren, Duomei Xue, Wei Guan, Jianbo Guo, and Zhengbin Liu. 2023. "Performance Optimization of a Spoon Precision Seed Metering Device Based on a Maize Seed Assembly Model and Discrete Element Method" Processes 11, no. 11: 3076. https://doi.org/10.3390/pr11113076
APA StyleChen, Z., Xue, D., Guan, W., Guo, J., & Liu, Z. (2023). Performance Optimization of a Spoon Precision Seed Metering Device Based on a Maize Seed Assembly Model and Discrete Element Method. Processes, 11(11), 3076. https://doi.org/10.3390/pr11113076






