Abstract
After the fourth industrial evolution, precision and automatic manufacturing have become increasingly widely accepted in production. With highly variable productivity and flexibility, flexible manufacturing systems (FMS) lower production costs and increase efficiency. Due to its resource shareability, unexpected system deadlock may occur in some specific situations. Many existing works use deadlock prevention as the primary control methodology in research on system deadlock control, while this type of control policy would constrain the transportation resources and reduce the system’s liveness. This paper adopts a new transition-based deadlock recovery policy as the direct control strategy, which uses generating and comparing aiding matrix (GCAM) to determine the optimal control transition. We also improve the existing GCAM-based method by reducing the computational redundancy. This kind of control strategy and its benefit could be demonstrated through two typical systems of simple sequential processes with resource (S3PR) nets and their Petri nets model.
1. Introduction
The flexible manufacturing system (FMS) [1,2,3,4,5,6,7,8] is an important and advantageous concept in industrial areas that adapts to various productive requirements. However, its high resource share ability can result in system deadlock occurring due to competition for resources between different pre-designed processing sequences. Petri net (PN) [9,10,11,12,13,14,15,16,17,18] is a modeling language theory, also a kind of discrete event dynamic system (DEDS), which is a powerful tool for addressing the deadlock problem of FMS. Additionally, PN is applied to various systems, such as automated manufacturing systems (AMS) [19,20,21,22,23,24], flexible assembly systems (FAS) [25], reconfigurable manufacturing systems (RMS) [26], and resource allocation systems (RAS) [27]. In contrast to the most adopted deadlock prevention strategy [28,29,30,31,32,33], some existing work uses deadlock recovery as the significant control policy [34,35,36,37,38,39,40,41,42,43], because of its higher system liveness.
There are two primary analyzing methodologies for system deadlock of FMS: structural analysis [44,45,46,47,48,49,50,51,52] and reachability graph (RG) analysis [28,29,53]. Structural analysis is based on some structural items (or subnet) for deadlock prevention policy, including siphons and place invariants (PI). This type of control policy is usually implemented by the set of control places and relevant arcs. However, this way obtains merely the suboptimal solution and cannot achieve maximal liveness.
In most of the research, RG analysis is regarded as the most outstanding method for dealing with the system deadlock of FMS. This kind of analyzing method first explores all possible markings, which can be reached by initial marking. The set of all reachable markings is called RG and can be further classified as legal, quasi-deadlock, deadlock markings, etc. In RG, all markings are presented as individual nodes and connected by directed arrows, representing transitions’ firing events. This way, it can clarify the relationship of each marking in RG and help design solutions for the deadlock problem. In most works, RG analysis seems to obtain the optimal solution to attain deadlock-free and maximal system liveness. Even so, this method may suffer from marking explosion problems when considering the system model with a more complex structure. The system deadlock problem of the PN model of FMS is known as an NP-hard problem, and it is not easy to find the optimal solution. Liu [54] further proved that the deadlock problem of such bounded PN of resource allocation (PNRA) is PSPACE-complete.
When considering the PN model with a larger scale and higher complexity, it is necessary to use assistant computer tools to explore the whole RG. In this paper, we use INA [55] and PNTools [56] to help illustrate the PN model’s RG. These tools can also recognize the property of each kind of system marking.
Chen [29] et al. proposed an optimal deadlock control policy based on the RG analyzing technique. They define the entry markings from the live zone to the dead zone of RG, which are called first-met bad markings (FBMs). The control policy is applied to the original PN model by the place invariant (PI) method, which designs a subnet controller consisting of control places and related arcs. This method can forbid all markings in dead zones and keep all legal markings reachable. However, the forbidding of such markings causes a reduction in the liveness of the system.
In past research on dealing with the deadlock problem of FMS, the deadlock prevention approach aims to apply well-designed constraints to the system to prevent it from reaching deadlock states. However, this kind of deadlock control approach decreases the reachable states and reduces system liveness. In order to remove system deadlock and keep system liveness simultaneously, deadlock recovery was introduced. The existing literature used various approaches to obtain highly effective controllers for achieving deadlock recovery strategy, such as graph techniques [34,43], structural analysis [37], RG analysis [35,38,39,41], integer linear programming problem (ILPP) [33], generating and comparing aid matrix (GCAM) [40,42], etc. Here, we give a summary of these works.
Huang et al. [34] first developed the control transition (CT) concept to deal with the deadlock problem in FMS. CT is a subnet of the PN model, which is constructed by transition rather than control places. A PN model uses a transition to reallocate tokens of all places and transform the system into another marking. Via this method, CTs are appropriately designed to lead the deadlock markings to legal ones. However, each CT is designed to recover only one deadlock marking in their work. When considering a more complicated model, there are possibly hundreds of deadlock markings, implying that the same number of CTs must be generated to solve them.
Based on RG analysis, Zhang and Uzam [35] developed a covering approach to further reduce the amount of CTs for deadlock recovery. In their study, the minimal set of CTs is obtained and added to the original PN model. However, this recovery method still does not achieve maximal liveness.
Chen et al. [36] developed two iterative methods using an integer linear programming problem (ILPP) to determine the optimal recovery transition. At every iteration, ILPP is formulated to maximize the number of solved deadlock markings until all deadlocks are entirely recovered.
Dong et al. [39] developed an iterative method for designing the optimal deadlock recovery policy. In each iteration, they first design recovery transitions for each deadlock marking. Then, a vector intersection approach is introduced to compute a recovery transition, which can recover multiple deadlocks.
Pan [40] first introduced the concept of GCAM, which is used to enumerate all possible CTs with recovering ability. Then all CTs in GCAM will be compared with others to find out the CT that can recover the most deadlock markings. Tseng et al. [42] proposed a computational concept to reduce the much higher computational cost of the GCAM-based method due to the explosion problem of RG analysis when considering the more complex system.
In our study, we further improve the existing GCAM-based method by reducing the computational redundancy. Solving the system deadlock problem of the PN model of bounded PNRA is a PSPACE-complete problem, so the computation consumption on time and space grows exponentially when considering a more extensive system. Therefore, decreasing the computational cost as much as possible is crucial.
The main contributions of this paper are summarized as follows:
- Improve FMS’s existing GCAM-based deadlock recovery strategy by reducing computational time and redundant steps. The system deadlock problem of FMS is an unexpected situation known as a PSPACE-complete problem; thus, the consumption of time and space (memory) may grow substantially. This study proposed approaches to lower computational costs and achieve higher efficiency than existing methods.
- This paper uses a deadlock recovery control policy to address the system deadlock problem based on control transition and GCAM. Though we adjust the existing algorithm for higher computational efficiency, the proposed method still maintains the same experimental results. As stated above, our method has the identical effect and lower computational cost.
- In computational complexity theory, the complexity of an algorithm is usually denoted by Big-O notation, which is a function of the size of the input problem . When considering the deadlock problem of the PN model, the parameter is the size of the model or its incidence matrix. However, while using RG analysis and GCAM-based recovery method, the parameter of estimating complexity may vary, such as the scale of RG, legal zone, or the set of deadlock markings. In this paper, we propose an efficiency evaluation approach for analyzing and estimating the improvement of the proposed method.
This paper has been organized in the following way. Section 2 gives an overview of PN theory. Section 3 concerns the central methodology and control strategy used for this study. Section 4 develops an algorithm for obtaining optimal control transition and a function for computational efficiency evaluation. Section 5 introduces two classic PN models of FMS to demonstrate the proposed method and compare it with existing works. The final section gives a summary and conclusion.
2. Preliminaries
2.1. Petri Net
A Petri net is a 5-tuple net [57,58], where and represent the set of places and transitions, respectively. Both of them are finite sets and , . is the set of arcs (flow relation) between places and transitions, where . The set represents the weighted value of each arc belonging to net , which is a multiset of positive integers. A system marking (or marking) means the token allocation in the PN model and denotes the initial marking. Note that a marking of the PN model is usually denoted as a multiset or an integer vector, representing the number of tokens stored in every place. For straightforward reading, a marking is usually presented as .
Given a node of PN model , the pre-set and the post-set are defined as and , respectively. A transition is enabled for firing at marking iff , which can also be denoted as . On the contrary, is disabled for firing if , which can also be denoted as .
A PN model can also present as an incidence matrix [14,57,58,59,60,61], which is a integer matrix and indexed by and . The incidence matrix can precisely describe a PN model in mathematical formation. An incidence matrix of a PN model must hold:
An incidence matrix could be divided into two parts: input matrix and output matrix , where . Each negative element in (or each non-zero element in ) represents one directed arc leading from place to transition, and so on. For easier understanding, here is an example of the PN model of FMS shown in Figure 1. The incidence matrix of the PN model in Figure 1 is shown in Equation (2).
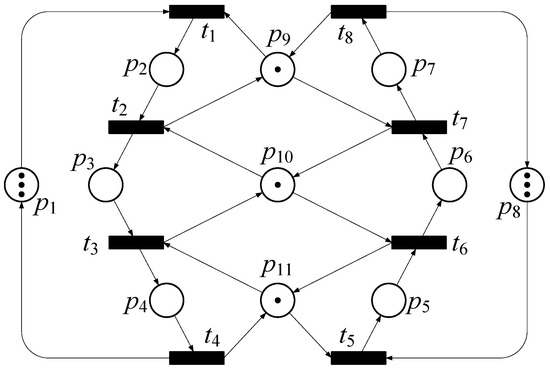
Figure 1.
A control transition of PN model, which is generated via two markings.
The PN model of Figure 1 has 11 places and 8 transitions in total, which are illustrated as hollow circles and black bars in Figure 1. Each pair of place and transition has a directed arc, and its corresponding value in the incidence matrix would not be zero. For example, given an arc lead from place to transition , then would be . Considering another arc leading from transition to place , would be , and so on. An incidence matrix of the PN model can describe its flow relation in detail.
2.2. Reachability Graph Analysis
With many advantages mentioned above, reachability graph (RG) analysis is adopted as the main analyzing technique for designing an optimal deadlock recovery policy. In RG analysis, all reachable markings of a PN model, which means the marking can be reached from the initial one, are enumerated for further analysis. In RG, these markings can be presented as nodes and connected by directed arrows labeled with a transition of the PN model, whose firing causes reaching from one marking to another.
By illustrating the RG of a PN model, all reachable states (markings) in the system and their relation will be explored. These markings’ properties would be used in advanced computation to design an optimal CT for solving deadlock problems. The reachable marking and RG could be defined as follows:
Definition 1.
(Reachable marking) Given a PN model , and each reachable marking must satisfy that , which denotes a fireable transition sequence.
Definition 2.
(Reachability graph) Given a PN model , and the relevant reachability graph satisfying that s.t. .
All reachable markings of a PN model could be grouped into three types: legal, quasi-deadlock, and deadlock markings, which are denoted as , and , respectively. The characteristics of these various types of markings could be well-described as the following definitions.
Definition 3.
(Deadlock marking) Given a reachability graph , the set of all reachable deadlock markings could be defined as follows:
Definition 4.
(Legal marking) Given a reachability graph , the set of all reachable legal marking could be defined as follows:
According to Definitions 3 and 4, the deadlock range and legal markings are clearly separated from RG. However, there are still some other markings in RG that do not belong to or , which are so-called quasi-deadlock markings. The set of quasi-deadlock markings is indicated as , where it means the markings belong to illegal zone but the system still not in a deadlock situation yet, i.e., there is at least one transition enabled in . According to Equation (4), it is believed that every quasi-deadlock marking must reach a deadlock marking in the end. The set of quasi-deadlock markings could be defined as follows:
Definition 5.
(Quasi-deadlock marking) Given a reachability graph , the set of all reachable quasi-deadlock markings satisfying that .
For easier understanding, we take the PN model in Figure 1 as an example. After traversal from the root node via simulation tools, such as INA [55] or PNTools [56], a total of 20 markings of RG are obtained. The contents of all markings are listed as Table 1.

Table 1.
All markings PN model in Figure 1 and their contents.
And its RG is illustrated in Figure 2, with each marking as a node and transition as a directed path. According to Definitions 3 to 5, , and the rest belong to .
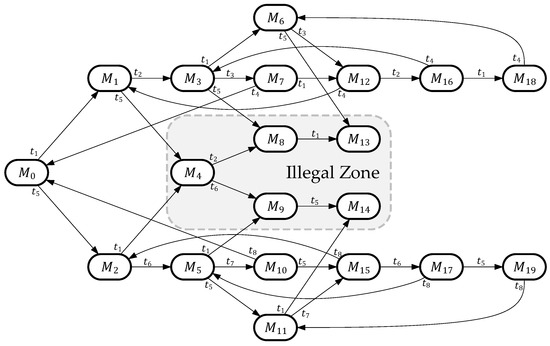
Figure 2.
RG of the PN model is shown in Figure 1.
2.3. Control Transition
Instead of using control place, this paper uses control transition (CT) as the main technique for dealing with the system deadlock problem of FMS. As mentioned above, system deadlock of FMS usually occurs because its high resource shareability could lead to resource competition between more than one scheduled sequence. According to elementary PN theory, places used to contain one or more tokens representing different meanings. When any transition fires (if enabled), tokens in part of places will be reallocated and transformed into new markings. Therefore, every transition could be illustrated as a directed arrow connecting a pair of markings in RG.
As stated above, system deadlock is unexpected in the operational sequence because no transition is enabled in the deadlock situation. In this study, we adopt the deadlock recovery technique as the main control strategy based on CT. CT is a set of well-designed transitions, denoted as and . CT is usually designed for recovering system liveness under deadlock marking, i.e., CT can form new paths of deadlock marking in RG.
According to elementary PN theory in Section 2, a transition fires in a marking would be denoted as , where is a newly generated marking after firing. Then, the value of marking could be calculated by . A new transition can also be calculated this way when two endpoint markings are already chosen. Supposing there are two markings , and a generated CT between them will be . And could be further defined as follows:
where and represent any two nodes (markings) in RG . According to the example in the last paragraph, and . Note that a system marking also can be denoted as a multiset or a 1-dimensional array. In this case, markings are presented as an array for quickly calculating, and also can be presented as an array of the same length. The RG of , , and is shown in Figure 3.

Figure 3.
A control transition of PN model, which is generated via two markings and a mapping from one to another.
3. Control Policy Based on Deadlock Recovery
3.1. Generating and Comparing Aiding Matrix (GCAM)
This paper aims to obtain the optimal transition-based controller to recover all system deadlocks and provide maximal liveness. Building the generating and comparing aiding matrix (GCAM) is necessary to develop the proposed deadlock recovery policy. Each PN model has its corresponding GCAM, which could find out all possible CT for dealing with deadlock markings. As mentioned in Section 2.3, a CT in RG is used to form new paths leading from one marking to another. To solve system deadlock, the predecessor of CT must be a deadlock marking, and the successor must be a legal one.
A GCAM is a 3-dimensional integer matrix indexed by , and . For easy understanding, all markings and CT could be regarded as independent nodes, then GCAM could be simplified as a 2-dimensional matrix . Each element belongs to means that the generated CT with ability to lead from to . To perform the entire property of GCAM and each CT, the complete GCAM is presented as a 3-dimensional integer matrix, while each CT is written as a -length array.
To build the whole GCAM, the characteristics of each RG marking must be verified first, such as legal, quasi-deadlock, and deadlock marking. With such proper definition above, the composition of RG and its scale could be well-defined. Here, we introduce two 1-dimension vectors, the deadlock zone vector, and the legal zone vector, to help illustrate the GCAM, which are defined as follows:
Definition 6.
(Deadlock zone vector) Given a reachability graph and a set of all deadlock marking , and its deadlock zone vector holds .
Definition 7.
(Legal zone vector) Given a reachability graph and set of all legal marking , and its legal zone vector holds .
These two vectors are used to list out all elements in and in array formation. Then the whole GCAM can be built as follows:
where .
Considering each CT as a -length array, the GCAM can be re-written as follows:
where and .
3.2. Comparing Computation
As mentioned above, a GCAM of the PN model is used to find the optimal CT to address the deadlock problem. In GCAM, all possible recovering paths in RG are enumerated, and each CT can solve at least one deadlock marking. According to definitions of transition and CT, its ability to reallocate tokens can form the paths from one marking to another in RG. Please note that not only one marking in RG satisfies the requirement of firing a certain transition. A transition, especially a CT, is possibly fired in more than one marking, i.e., a CT may recover more than one deadlock marking concurrently. In order to find the CT with maximal recovery ability, it is necessary to process comparing computations. When a CT appears more than one time in GCAM, then it is known that this CT can solve more than one deadlock marking. For example, supposing there is a CT in GCAM, which can solve deadlock marking and lead it to legal marking . Then there is another CT such that . Then, it is clear that can solve two deadlock markings, and .
Therefore, it is essential to compare all CTs to find the optimal one that can solve the most deadlocks. In the proposed method, we first pick up one CT from GCAM, then it will be compared to all others to find out its coverability in GCAM and recovery ability. After comparing the computation between all CTs and the rest of them, we check the recovery ability of every CT and choose the optimal one as the leading solution in this iteration.
3.3. Redundancy Reduction Approach
Solving the deadlock problem of FMS is known as a PSPACE-complete problem. The computational cost of solving such a problem may cause an exponential increase when considering a more complex system. This paper aims to improve the existing method for higher efficiency and keep the same experimental results. Some techniques are introduced in the following section to reduce computational consumption and enhance efficiency.
Theorem 1.
Given a GCAM , then each CT in the same row, which has the identical predecessor , has different values.
Proof of Theorem 1.
According to Equation (5), a can be obtained via , where . Considering a CT in GCAM, the predecessor of must be a deadlock marking, and the successor must be a legal marking. Every CT in the same row must have an identical predecessor , and each of them can lead to different legal markings . According to Equation (5), suppose that every of in the same row equals the the same , and represents each legal marking . Each belonging to the same row must be different from each other. □
Theorem 1 is introduced in the following methodology to reduce the computational redundancy. In the comparing computation, each CT in GCAM must be compared with others. Once the same CT is found, the rest of this row will be skipped, and the next comparison will start from the next row (deadlock marking). This way, it can reduce the computational cost a lot.
We also introduce another technique for redundancy reduction, which can help decrease the computational cost by comparing two CTs. It is known that CT is a -length vector. The comparison between two CTs usually starts from the first element of them until the comparison of all elements is completed. Then the similarity of both CTs would be identified. If the characteristic differences of each pair of CTs can be accurately recognized, then the same results can be obtained even without full-length comparisons. In Theorem 2, it is assumed that two CTs are different if any element of them is unequal.
Theorem 2.
Given two CTs for comparing computation. Once any element in and are different, such that , then it is clear that .
Proof of Theorem 2.
When it is said that , all elements in must be equal to another one in the corresponding position of , i.e., . On the contrary, if any element in is not equal to another one in , i.e., , it is clarified that . □
3.4. Recovering Coverage Function
In the proposed GCAM-based deadlock recovery policy, each CT is designed to form a new path in RG to lead the system from deadlock to legal situation. Note that at least one deadlock marking satisfies any CT’s firing constraints. It implies that a CT can recover one or more deadlock markings. To evaluate the recovery ability of all CTs, we introduce the recovery function to evaluate their recovery ability.
Definition 8.
(Recovery function) Given a CT and a deadlock marking . Suppose that denotes whether is able to recover and satisfies:
4. Algorithm
In this section, we develop a GCAM-based algorithm for designing the optimal recovery solution with maximal system liveness. The deadlock problem of FMS is known as a PSPACE-complete problem, implying that it is also an NP-hard problem. Solving such a problem means costing plenty of computational space and time. This GCAM-based method can find the optimal CT and recover all deadlock markings, which Pan first proposed [40]. In this paper, we further define it more precisely and improve its computational cost. We also designed an efficiency evaluation function to evaluate the improved method’s advantages.
Here, we summarize the main steps of the proposed method:
- Given a PN model of FMS, its RG must first be illustrated.
- Confirm the property of all markings, e.g., legal, quasi-deadlock, and deadlock markings.
- Build the corresponding GCAM.
- Run the comparing computation to find out the optimal CT.
- Add the CT to the PN model and back to step 1.
In this paper, we use GCAM and CT as the main solution techniques. Therefore, the GCAM would be built in each iteration after the RG was obtained. Note that a CT may be able to solve one or more deadlock markings, i.e., a CT may appear one or more times in GCAM. In order to find out the optimal CT, which can provide maximal liveness, it is necessary to compare each CT in GCAM to evaluate their frequency.
However, the number of possible CTs depends on the magnitude of RG. The size of GCAM becomes much larger when considering the PN model with more complexity. Therefore, in Section 3, we introduce some techniques to improve the original approach [40], which can provide higher efficiency in obtaining the optimal CT. An overview of the procedure of comparing computation is presented in Figure 4.
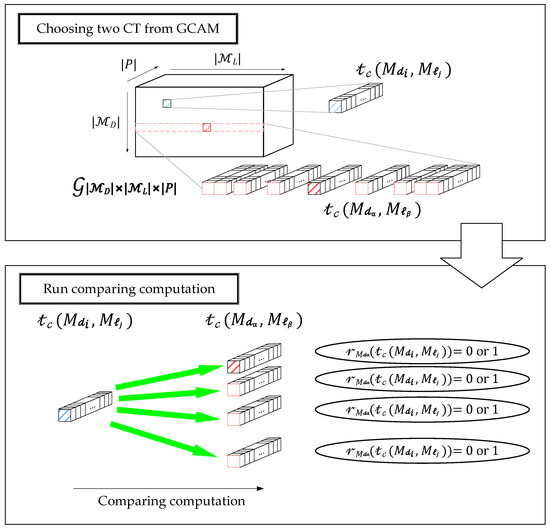
Figure 4.
Overview of generating and comparing aiding matrix (GCAM) and comparing computation.
In Figure 4, the GCAM is firstly illustrated as a box to represent a 3-dimensional matrix . After building the GCAM, we implement the comparing computation to obtain the optimal CT. First, a CT was chosen as the former one within comparison, presented as a blue bar. Then another CT was chosen as the latter one, which is presented as a bar in red color. According to Theorem 1, please note that there is at most one CT in row , which is illustrated as a pink bar, equaling to . Once a CT belongs to row is recognized as having the same value with , i.e., , the comparing computation for the row would be skipped, and the next comparison will start with the first CT in row as the latter one.
After comparing computation, the optimal CT, or the CT with maximal in other words, is obtained and able to solve the maximal system deadlocks. Then would be added to the original PN model and forming a new RG. If in the next iteration, GCAM would be built via newly generated RG.
Here, we develop the proposed Algorithm 1 as follows.
| Algorithm 1: Improved GCAM-based Recovery with High Comparing Efficiency |
| with system deadlocks. |
| Output: An optimal controlled FMS with CT. |
| 1. with all reachable markings. |
| 2. . |
| 3. . |
| 4. Run comparing computation. |
| while) do |
| for) do |
| for) do |
| for) do |
| if) then |
| else |
| end if |
| end for |
| end for |
| end for |
| Add to the PN model. |
| Back to Step 1. |
| end while |
| 5. , where . |
Note that not all deadlock problems can be solved entirely just by adding one CT. Therefore, we adopt an iterating method to obtain the set of the optimal CT . In each iteration, it is always to choose the CT with the maximal recovery ability, which has maximal . The chosen CT would be added to the original PN model when the iteration ends. Then, a new RG is generated to identify the set of legal and deadlock markings in the new iteration. This recovery policy keeps running until .
In Section 3.3, we propose two approaches to reduce computational redundancy, which are also used to improve the original algorithm. Known as a PSPACE-complete problem, solving the undesirable deadlock problem of FMS always costs a lot during the computation procedure. Through experiments in our study, these approaches are demonstrated to enhance efficiency and reduce operational costs significantly. To further estimate its improvement, we introduce an efficiency evaluation method to qualify the computational cost for judging the performance of the proposed control policy.
This paper adopts the GCAM-based deadlock recovery policy as the main analyzing methodology. The effectiveness of comparing computation greatly depends on the size of RG and GCAM, i.e., the size of and . According to computational complexity theory, the computational complexity of one algorithm can be expressed by using big O notation with input size . However, these different variables, including , , , and , could lead to difficulty in the measurement of computational complexity. In addition, please note that not all CTs in GCAM would be used during the comparing computation, i.e., the computational complexity of comparing computation may randomly change according to whether the matched CT could be quickly found or not. Therefore, we propose a method for precisely measuring the computational complexity of the GCAM-based deadlock recovery strategy.
Definition 9.
(Expected value) Given a finite set of random variables
and each of them has probability
of occurring. The expected value of
would be
.
Definition 10.
(Efficiency evaluation) Given an RG
and its GCAM
, with the set of legal markings
and deadlock ones
. The efficiency of comparing computations is defined as follows:
5. Experimental Results
In this section, we introduce two typical PN models of FMS to demonstrate the proposed recovery policy.
Example 1.
Given the PN model of FMS in Figure 1, there are some software tools for generating the corresponding RG, e.g., INA [55] and PNTools [56] are used in this paper. The detailed properties of the PN model can be presented via the incidence matrix, which is shown in Equation (2). First of all, the model’s RG analysis is implemented, and 20 reachable markings are obtained, such that the entire RG and relationship between each marking can be illustrated. In Figure 2, all markings belonging to RG are denoted as single nodes and connected by directed arrows, representing the transition that transforms the system from one marking into another. Then, the contents of the set of , , and can be further identified where , and . Accordingly, the corresponding GCAM of the first iteration can be built as a matrix, which is shown in Equation (9).
After the whole comparison computation, the optimal CT can be verified, implying that this CT can solve two deadlock markings and in the first iteration. For easy understanding, can be simplified as . The input nodes of are , and the output nodes are . The property of CT for the PN model shown in Figure 1 is presented in Table 2.

Table 2.
The property of each CT for PN model in Figure 5.
Then we add the subnet of to the original PN model, which is shown in Figure 5. The newly generated RG of Figure 5 is shown in Figure 6. The incidence matrix consists of the original model, and the subnet of CT is presented as Equation (10) in the following.
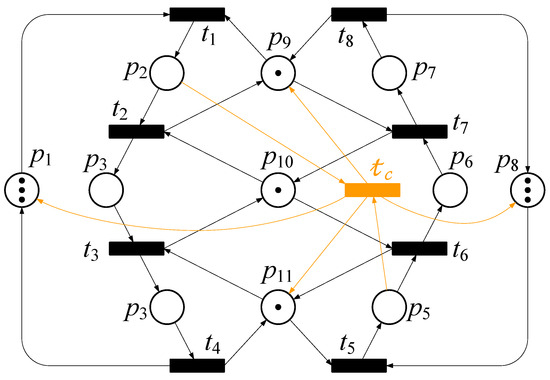
Figure 5.
The controlled net of PN model of Figure 1.
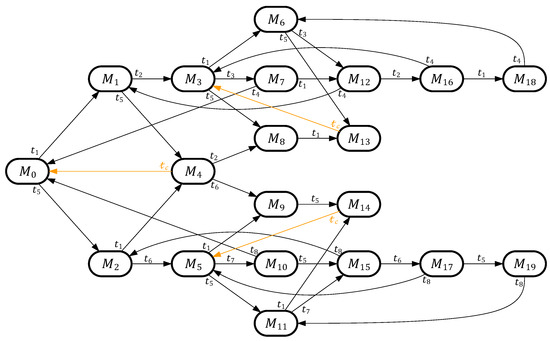
Figure 6.
The RG of PN model shown in Figure 5.
In the RG of Figure 6, there is not any deadlock marking or illegal zone, and the solved model is regarded as deadlock-free. Unlike other existing works, this transition-based recovery policy can solve the deadlock problem and provide maximal liveness.
In this paper, we introduce some techniques to reduce the computational cost and redundancy defined in Section 3.3. These techniques are also used to improve the existing GCAM-based method [40]. In Section 4, we developed an efficiency evaluation approach for comparing GCAM-based deadlock recovery policy computation. The evaluation approach shows that the proposed control policy has the equivalent recovering ability and lower computational cost. A comparison between GCAM-based deadlock recovery policies is presented in Table 3.

Table 3.
Efficiency evaluation of comparing computation of GCAM-based deadlock recovery policy.
Example 2.
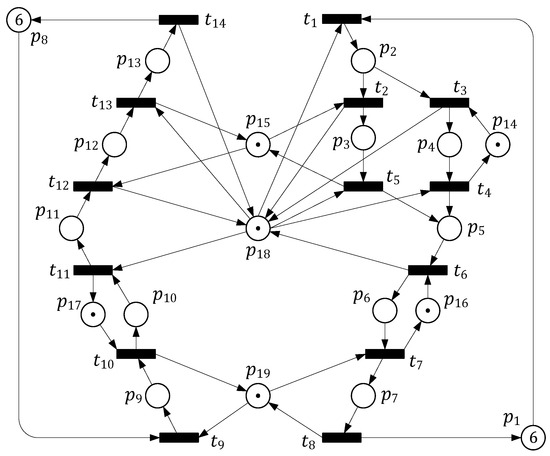

Figure 7.
A typical example of PN model of FMS.
Next, we consider another typical PN model of more complex FMS, shown in Figure 7. Here is a summarized description of its structure: there are a total of 19 places and 14 transitions. Its incidence matrix can be presented as a matrix, as Equation (12) in the following. The initial marking is .
After generating the corresponding RG of Figure 7, a total of 282 markings are obtained, including 205 legal markings, 61 quasi-deadlock markings, and 16 deadlock markings. Then its GCAM, a matrix, can be further generated. Due to space limitations, the detailed contents of all reachable markings and CT could not be listed here.
Via the first iteration of comparing computations, there are a total of five CTs with maximal obtained in this iteration. Each of them can recover eight deadlock markings, including , , , , and . In the experiment of [40], there are a total of 40 CTs obtained in the first iteration, where those are just the repetition of these 5 CTs, i.e., the same results are obtained by the proposed method. Then the next iteration will be run because some deadlock markings are still not solved.
After adopting as the main CTs in the first iteration, the second iteration begins with eight deadlock markings removed from . In the newly generated RG, there are eight deadlock markings left. Through comparing computations, there are a total of five optimal CTs obtained. Each of them can solve five deadlock markings, including , , , , and . In the second iteration of [40], there are a total of 25 CTs obtained. For the same reason mentioned above, it is actually the same experimental result as the proposed one in this paper.
By generating a new RG in the third iteration, there are still three deadlock markings in . There are 81 CTs identified after comparing computation, where they all can solve these three deadlock markings. The CT is chosen as the third CT in . The property of all CTs is shown in Table 4. Then, the set of CTs is added to the original PN model, where the new incidence matrix is shown as Equation (13).

Table 4.
The property of each CT for PN model in Figure 7.
According to the experimental results above, the proposed deadlock recovery method can actually obtain the same results and achieve equivalent controlling ability. Table 5 compares the proposed method and other existing deadlock recovery methods. There is no doubt that the proposed one is an optimal deadlock recovery policy, which can solve all deadlock markings and keep all legal markings reachable.

Table 5.
Comparison with other research on deadlock recovery.
As mentioned above, this paper aims to improve the existing GCAM-based deadlock recovery policy [40]. To measure the improvement precisely, Section 4 gives an efficiency evaluation approach for evaluating the computational performance of the GCAM-based methods. The comparison is shown in Table 6, where it is evident that the computational efficiency of the proposed method is much lower than the existing one [40]. Here also gives the execution time of comparing computation of experiments in Table 7, which are run on a computer with an Intel Core i5-3210M CPU running at 2.50 GHz using 8 GB of RAM, running Windows 7 operating system. According to Table 7, it is known that the proposed method can reduce the total execution time of the comparing computation of Example 2 from 3.618 s to 0.234 s.

Table 6.
Comparing results of GCAM-based deadlock recovery policies.

Table 7.
Efficiency evaluation of comparing computation of GCAM-based deadlock recovery policy.
6. Conclusions
In the deadlock domain, we all know that seeking optimal controllers for solving flexible manufacturing systems (FMS) is a challenging issue. In particular, how to enhance the computational efficiency seems even more difficult work. In this paper, we develop an optimal deadlock recovery policy based on Pan [40] and further improve its computational efficiency by reducing redundancy. We also introduce an approach to evaluate the operating efficiency. Through two typical examples of the PN model of FMS, the evaluation results show that the proposed method provides higher computational efficiency and the same recovering ability. The system deadlock problem is a PSPACE-complete problem and always takes much higher computational consumption. In our future works, we will consider another typical PN model of FMS [4], which has a more complex structure, or other models.
Author Contributions
Conceptualization, C.-Y.T.; Methodology, C.-Y.T.; Software, J.-C.C.; Validation, Y.-L.P.; Formal analysis, C.-Y.T. and Y.-L.P.; Investigation, C.-Y.T.; Resources, Y.-L.P. and J.-C.C.; Data curation, Y.-L.P. and J.-C.C.; Writing—Original draft, C.-Y.T.; Writing—Review & editing, Y.-L.P.; Visualization, C.-Y.T.; Supervision, Y.-L.P. and J.-C.C.; Project administration, Y.-L.P. and J.-C.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available in the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bullers, W.I.; Nof, S.Y.; Whinston, A.B. Artificial Intelligence in Manufacturing Planning and Control. AIIE Trans. 1980, 12, 351–363. [Google Scholar] [CrossRef]
- Kustak, A. Flexible Manufacturing Systems: A Structural Approach. Int. J. Prod. Res. 1985, 23, 1057–1073. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.K.; Midha, S.; Murli Krishna, V. A Heuristic Procedure for Loading Problems in Flexible Manufacturing Systems. Int. J. Prod. Res. 1992, 30, 2213–2228. [Google Scholar] [CrossRef]
- Ezpeleta, J.; Colom, J.M.; Martinez, J. A Petri Net Based Deadlock Prevention Policy for Flexible Manufacturing Systems. IEEE Trans. Robot. Autom. 1995, 11, 173–184. [Google Scholar] [CrossRef]
- Zhou, M.; Kurapati, V. Modeling, Simulation, and Control of Flexible Manufacturing System: A Petri Net Approach; World Scientific: Singapore, 1999. [Google Scholar]
- Košťál, P.; Sobrino, D.R. Flexible Manufacturing System for Drawingless Manufacturing. Key Eng. Mater. 2013, 581, 527–532. [Google Scholar] [CrossRef]
- Manu, G.; Vijay Kumar, M.; Nagesh, H.; Jagadeesh, D.; Gowtham, M.B. Flexible Manufacturing Systems (FMS), a Review. Int. J. Mech. Prod. Eng. Res. Dev. 2018, 8, 323–336. [Google Scholar] [CrossRef]
- Javaid, M.; Haleem, A.; Singh, R.P.; Suman, R. Enabling Flexible Manufacturing System (FMS) through the Applications of Industry 4.0 Technologies. Internet Things Cyber-Phys. Syst. 2022, 2, 49–62. [Google Scholar] [CrossRef]
- Liu, D.; Li, Z.; Zhou, M. Hybrid Liveness-Enforcing Policy for Generalized Petri Net Models of Flexible Manufacturing Systems. IEEE Trans. Syst. Man Cybern. Syst. 2013, 43, 85–97. [Google Scholar] [CrossRef]
- Chen, Y.; Li, Z.; Zhou, M. Optimal Supervisory Control of Flexible Manufacturing Systems by Petri Nets: A Set Classification Approach. IEEE Trans. Autom. Sci. Eng. 2014, 11, 549–563. [Google Scholar] [CrossRef]
- Ghaffari, A.; Rezg, N.; Xie, X. Design of a Live and Maximally Permissive Petri Net Controller Using the Theory of Regions. IEEE Trans. Robot. Autom. 2003, 19, 137–142. [Google Scholar] [CrossRef]
- Huang, Y.-S.; Pan, Y.-L.; Zhou, M. Computationally Improved Optimal Deadlock Control Policy for Flexible Manufacturing Systems. IEEE Trans. Syst. Man Cybern.-Part A Syst. Hum. 2012, 42, 404–415. [Google Scholar] [CrossRef]
- Chao, D.Y.; Pan, Y.-L.; Liao, W.-H. Structure Based Derived Uniform Formula for Siphon, Its Complementary Set and T-Characteristic Vectors. IFAC Proc. Vol. 2013, 46, 301–306. [Google Scholar] [CrossRef]
- Liu, G. Petri Nets: Theoretical Models and Analysis Methods for Concurrent Systems; Springer: Singapore, 2022. [Google Scholar]
- Row, T.-C.; Lee, S.-C.; Pan, Y.-L. Identifying the Saturated Line Based on the Number of Idle Places: Achieving Precise Maximal Permissiveness without Deadlocks Using Control Transitions or Control Places. Processes 2023, 11, 2325. [Google Scholar] [CrossRef]
- Cong, X.; Gu, C.; Uzam, M.; Chen, Y.; Al-Ahmari, A.M.; Wu, N.; Zhou, M.; Li, Z. Design of Optimal Petri Net Supervisors for Flexible Manufacturing Systems via Weighted Inhibitor Arcs. Asian J. Control 2017, 20, 511–530. [Google Scholar] [CrossRef]
- Kaid, H.; Al-Ahmari, A.; Li, Z.; Davidrajuh, R. Single controller-based colored petri nets for deadlock control in automated manufacturing systems. Processes 2020, 8, 21. [Google Scholar] [CrossRef]
- Hu, H.; Liu, Y.; Yuan, L. Supervisor Simplification in FMSs: Comparative Studies and New Results Using Petri Nets. IEEE Trans. Control Syst. Technol. 2016, 24, 81–95. [Google Scholar] [CrossRef]
- Feng, Y.; Xing, K.; Gao, Z.; Wu, Y. Transition Cover-Based Robust Petri Net Controllers for Automated Manufacturing Systems with a Type of Unreliable Resources. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 3019–3029. [Google Scholar] [CrossRef]
- Yue, H.; Xing, K.; Hu, Z. Robust Supervisory Control Policy for Avoiding Deadlock in Automated Manufacturing Systems with Unreliable Resources. Int. J. Prod. Res. 2013, 52, 1573–1591. [Google Scholar] [CrossRef]
- Wang, F.; Xing, K.-Y.; Zhou, M.-C.; Xu, X.-P.; Han, L.-B. A Robust Deadlock Prevention Control for Automated Manufacturing Systems with Unreliable Resources. Inf. Sci. 2016, 345, 243–256. [Google Scholar] [CrossRef]
- Kaid, H.; Al-Ahmari, A.; El-Tamimi, A.M.; Nasr, E.A.; Li, Z. Design and Implementation of Deadlock Control for Automated Manufacturing Systems. S. Afr. J. Ind. Eng. 2019, 30, 1–23. [Google Scholar] [CrossRef]
- Alzalab, E.A.; El-Sherbeeny, A.M.; El-Meligy, M.A.; Rauf, H.T. Trust-Based Petri Net Model for Fault Detection and Treatment in Automated Manufacturing Systems. IEEE Access 2021, 9, 157997–158009. [Google Scholar] [CrossRef]
- Chen, C.; Hu, H. Extended Place-Invariant Control in Automated Manufacturing Systems Using Petri Nets. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 1807–1822. [Google Scholar] [CrossRef]
- Xing, K.; Wang, F.; Zhou, M.C.; Lei, H.; Luo, J. Deadlock Characterization and Control of Flexible Assembly Systems with Petri Nets. Automatica 2018, 87, 358–364. [Google Scholar] [CrossRef]
- Kaid, H.; Al-Ahmari, A.; Li, Z.; Davidrajuh, R. Intelligent Colored Token Petri Nets for Modeling, Control, and Validation of Dynamic Changes in Reconfigurable Manufacturing Systems. Processes 2020, 8, 358. [Google Scholar] [CrossRef]
- Tricas, F.; Ezpeleta, J. Computing Minimal Siphons in Petri Net Models of Resource Allocation Systems: A Parallel Solution. IEEE Trans. Syst. Man Cybern.-Part A: Syst. Hum. 2006, 36, 532–539. [Google Scholar] [CrossRef]
- Huang, Y.-S.; Chung, T.-H.; Su, P.-J. Synthesis of Deadlock Prevention Policy Using Petri Nets Reachability Graph Technique. Asian J. Control 2010, 12, 336–346. [Google Scholar] [CrossRef]
- Chen, Y.F.; Li, Z.W.; Zhou, M.C. Behaviorally Optimal and Structurally Simple Liveness-Enforcing Supervisors of Flexible Manufacturing Systems. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 2012, 42, 615–629. [Google Scholar] [CrossRef]
- Abdul-Hussin, M.H. On Structural Conditions of S3PR Based Siphons to Prevent Deadlocks in Manufacturing Systems. Int. J. Simul. Syst. Sci. Technol. 2016, 17, 32-1. [Google Scholar] [CrossRef]
- Guo, X.; Wang, S.; You, D.; Li, Z.; Jiang, X. A Siphon-Based Deadlock Prevention Strategy for S3PR. IEEE Access 2019, 7, 86863–86873. [Google Scholar] [CrossRef]
- Zhuang, Q.; Dai, W.; Wang, S.; Du, J.; Tian, Q. An MIP-Based Deadlock Prevention Policy for Siphon Control. IEEE Access 2019, 7, 153782–153790. [Google Scholar] [CrossRef]
- Pan, Y.-L.; Tai, C.-W.; Tseng, C.-Y.; Huang, J.-C. Enhancement of Computational Efficiency in Seeking Liveness-Enforcing Supervisors for Advanced Flexible Manufacturing Systems with Deadlock States. Appl. Sci. 2020, 10, 2620. [Google Scholar] [CrossRef]
- Huang, Y.-S.; Pan, Y.-L.; Su, P.-J. Transition-Based Deadlock Detection and Recovery Policy for FMSS Using Graph Technique. ACM Trans. Embed. Comput. Syst. 2013, 12, 1–13. [Google Scholar] [CrossRef]
- Zhang, X.; Uzam, M. Transition-Based Deadlock Control Policy Using Reachability Graph for Flexible Manufacturing Systems. Adv. Mech. Eng. 2016, 8, 168781401663150. [Google Scholar] [CrossRef]
- Chen, Y.F.; Li, Z.W.; Al-Ahmari, A.; Wu, N.Q.; Qu, T. Deadlock Recovery for Flexible Manufacturing Systems Modeled with Petri Nets. Inf. Sci. 2017, 381, 290–303. [Google Scholar] [CrossRef]
- Bashir, M.; Liu, D.; Uzam, M.; Wu, N.; Al-Ahmari, A.; Li, Z. Optimal enforcement of liveness to flexible manufacturing systems modeled with Petri nets via transition-based controllers. Adv. Mech. Eng. 2018, 10, 168781401775070. [Google Scholar] [CrossRef]
- Row, T.-C.; Pan, Y.-L. Maximally Permissive Deadlock Prevention Policies for Flexible Manufacturing Systems Using Control Transition. Adv. Mech. Eng. 2018, 10, 168781401878740. [Google Scholar] [CrossRef]
- Dong, Y.; Chen, Y.; Li, S.; El-Meligy, M.A.; Sharaf, M. An Efficient Deadlock Recovery Policy for Flexible Manufacturing Systems Modeled with Petri Nets. IEEE Access 2019, 7, 11785–11795. [Google Scholar] [CrossRef]
- Pan, Y.-L. One Computational Innovation Transition-Based Recovery Policy for Flexible Manufacturing Systems Using Petri Nets. Appl. Sci. 2020, 10, 2332. [Google Scholar] [CrossRef]
- Row, T.-C.; Syu, W.-M.; Pan, Y.-L.; Wang, C.-C. One Novel and Optimal Deadlock Recovery Policy for Flexible Manufacturing 582 Systems Using Iterative Control Transitions Strategy. Math. Probl. Eng. 2019, 2019, 4847072. [Google Scholar] [CrossRef]
- Tseng, C.-Y.; Chen, J.-C.; Pan, Y.-L. A Novel and Advantageous Recovery Solution for Deadlock Problem of Flexible Manufacturing Systems Based on Petri Nets Modeling Theory. In Proceedings of the 2023 9th International Conference on Applied System Innovation (ICASI), Chiba, Japan, 21–25 April 2023; pp. 95–97. [Google Scholar] [CrossRef]
- Elsayed, M.S.; Kefi, K.; Li, Z. An Optimal Transition-Based Recovery Policy for Controlling Deadlock within Flexible Manufacturing Systems Using Graph Technique. IEEE Access 2023, 11, 51723–55173. [Google Scholar] [CrossRef]
- Barkaoui, K.; Pradat-Peyre, J.-F. On Liveness and Controlled Siphons in Petri Nets. In Application and Theory of Petri Nets 1996; Springer: Berlin/Heidelberg, Germany, 1996; pp. 57–72. [Google Scholar] [CrossRef]
- Piroddi, L.; Cordone, R.; Fumagalli, I. Selective Siphon Control for Deadlock Prevention in Petri Nets. IEEE Trans. Syst. Man Cybern.-Part A Syst. Hum. 2008, 38, 1337–1348. [Google Scholar] [CrossRef]
- Piroddi, L.; Cordone, R.; Fumagalli, I. Combined Siphon and Marking Generation for Deadlock Prevention in Petri Nets. IEEE Trans. Syst. Man Cybern.-Part A Syst. Hum. 2009, 39, 650–661. [Google Scholar] [CrossRef]
- Hou, Y.F.; Al-Ahmari, A.M.; Li, Z.W. Optimal Controllability of 2-Composed Siphons in a Class of Petri Nets. Electron. Lett. 2012, 48, 1535–1537. [Google Scholar] [CrossRef]
- Hou, Y.; Li, Z.; Zhao, M.; Liu, D. Extended Elementary Siphon-Based Deadlock Prevention Policy for a Class of Generalised Petri Nets. Int. J. Comput. Integr. Manuf. 2013, 27, 85–102. [Google Scholar] [CrossRef]
- Chao, D.Y.; Pan, Y.-L. Uniform Formulas for Compound Siphons, Complementary Siphons and Characteristic Vectors in Deadlock Prevention of Flexible Manufacturing Systems. J. Intell. Manuf. 2013, 26, 13–23. [Google Scholar] [CrossRef]
- Abdul-Hussin, M.H. Elementary Siphons of Petri Nets and Deadlock Control in FMS. J. Comput. Commun. 2015, 3, 57921. [Google Scholar] [CrossRef]
- Wang, S.; You, D.; Zhou, M. A Necessary and Sufficient Condition for a Resource Subset to Generate a Strict Minimal Siphon in S 4PR. IEEE Trans. Autom. Control 2017, 62, 4173–4179. [Google Scholar] [CrossRef]
- Wang, S.; Duo, W.; Guo, X.; Jiang, X.; You, D.; Barkaoui, K.; Zhou, M. Computation of an Emptiable Minimal Siphon in a Subclass of Petri Nets Using Mixed-Integer Programming. IEEE/CAA J. Autom. Sin. 2020, 8, 219–226. [Google Scholar] [CrossRef]
- Hu, M.; Yang, S.; Chen, Y. Partial Reachability Graph Analysis of Petri Nets for Flexible Manufacturing Systems. IEEE Access 2020, 8, 227925–227935. [Google Scholar] [CrossRef]
- Liu, G. Complexity of the Deadlock Problem for Petri Nets Modeling Resource Allocation Systems. Inf. Sci. 2016, 363, 190–197. [Google Scholar] [CrossRef]
- INA (Integrated Net Analyzer). A Software Tool for Analysis of Petri Nets. Version 2.2. Available online: https://www2.informatik.hu-berlin.de/~starke/ina.html (accessed on 19 October 2022).
- PN-Tools, A. Petri Net Analysis Tool, Version 1.0; Pedagogical Univ. Rzeszów: Warsaw, Poland, 1987.
- Reisig, W. Understanding Petri Nets Modeling Techniques, Analysis Methods, Case Studies; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Murata, T. Petri Nets: Properties, Analysis and Applications. Proc. IEEE 1989, 77, 541–580. [Google Scholar] [CrossRef]
- Peterson, J.L. Petri Net Theory and the Modeling of Systems; Prentice-Hall: Englewood Cliffs, NJ, USA, 1981. [Google Scholar]
- Desel, J.; Esparza, J. Free Choice Petri Nets; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Shanlin, Y.; Jie, Z.; Jun, G. Inverse Petri Nets: Properties and Applications. IFAC Proc. Vol. 1991, 24, 91–95. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).