Abstract
Photovoltaic (PV) generation systems that are partially shaded have a non-linear operating curve that is highly dependent on temperature and irradiance conditions. Shading from surrounding objects like clouds, trees, and buildings creates partial shading conditions (PSC) that can cause hot spot formation on PV panels. To prevent this, bypass diodes are installed in parallel across each panel, resulting in a global maximum power point (GMPP) and multiple local maximum power points (LMPPs) on the power-voltage (P-V) curve. Traditional methods for maximum power point tracking (MPPT), such as perturb and observe (P&O) and incremental conductance (INC), converge for LMPPs on the P-V curve, but metaheuristic algorithms can track the GMPP effectively. This paper proposes a new, efficient, and robust GMPP tracking technique based on a nature-inspired algorithm called Ali Baba and the Forty Thieves (AFT). Utilizing the AFT algorithm for MPPT in PV systems has several novel features and advantages, including its adaptability, exploration-exploitation balance, simplicity, efficiency, and innovative approach. These characteristics make AFT a promising choice for enhancing the efficiency of PV systems under varied circumstances. The performance of the proposed method in tracking the GMPP is evaluated using a simulation model under MATLAB/Simulink environment, the achieved simulation results are compared to particle swarm optimization (PSO). The proposed method is also tested in real-time using the Hardware-in-the-loop (HIL) emulator to validate the achieved simulation results. The findings indicate that the proposed AFT-based GMPP tracking method performs better under complex partial irradiance conditions than PSO.
1. Introduction
Solar energy receives special attention because of its long-term viability, abundant supply, pollution-free nature, and lack of carbon emissions. Photovoltaic (PV) systems are now used in over 100 nations for both independent and grid-connected applications. PV power, which includes both off-grid remote power supply and grid-connected systems, is the fastest-growing electricity-generating technology, with current annual growth rates of approximately 40%. Numerous devices, including drones, cars, satellites, embedded systems, sensors, and residential and commercial buildings, employ the PV-based power source [1]. The world installed an unprecedented 168 GW of power in 2021. Due to technological advancements in PV cells [2,3], declining PV cell costs [4], and government incentives [5,6], PV-based energy has recently gained popularity.
Several traditional single-stage algorithms have been developed, including hill climbing (HC) [7], incremental conductance (InC) [8], and perturb and observe (P&O) [9]. Although these algorithms successfully determine the maximum power point (MPP) of a photovoltaic (PV) array under uniform irradiance conditions, they fail to converge to the global maximum power point (GMPP) when the PV array is partially shaded (PSC). Furthermore, in the perturb and observe (P&O) and hill climbing methods, the algorithms exhibit oscillations around the MPP, resulting in power losses [10]. For maximum power point tracking (MPPT), AI-based techniques [11,12,13] have been used to overcome these problems. These soft computing techniques have demonstrated promising performance in tracking the maximum power using prior experiences as the basis for the search criterion. However, as more data are used, the complexity of these algorithms rises. The training process can be hampered by the lack of previous data, and anomalies in the available data could produce inaccurate findings. The storage demand is also increased by the substantial amount of data that these algorithms require [14].
To resolve such problems researchers have suggested stochastic search-based metaheuristic algorithms for maximum power point tracking (MPPT). These algorithms take their cues from natural occurrences like ant colonies, bird swarms, and flower pollination. For instance, under partial shading conditions (PSCs), algorithms like cuckoo search [15], grey wolf optimization [16], and the flower pollination algorithm [17] have shown the capacity to precisely track the global maximum power point (GMPP). However, because these algorithms use random elements in their search process, they often require significant computational time. In recent years, the use of metaheuristic algorithms has increased in solving various optimization problems due to their efficient convergence properties. These algorithms mimic behaviors such as hunting, reproduction, food foraging, and breeding found in plants and animals. There have been many different metaheuristic algorithms proposed in the literature [9,14,17,18,19,20,21,22]. One of the key benefits of metaheuristic algorithms is their exploratory nature, which enables them to cover the whole search space and locate the best answer while avoiding local peaks. Additionally, because these algorithms do not require specific training data, they are easier on processor memory. Not all metaheuristic algorithms, nevertheless, perform as well. They fluctuate based on a number of performance factors, including the time required to reach the true maximum power point, how often power fluctuates while tracking, the impact on processor memory, and other factors. An ideal approach would therefore minimize CPU burden while maximizing system performance based on the previously described parameters. In order to improve existing MPPT systems and make them more cost-effective, metaheuristic algorithms with improved performance and simplified structures are required.
The simplicity and exploratory capabilities of Particle Swarm Optimization (PSO) [23] make it a popular swarm-intelligence metaheuristic algorithm. Various modifications have been implemented to PSO over time to track the GMPP [20,24,25,26]. Being stochastic, PSO relies on random coefficients to track the maximum power point (MPP) under various shading conditions. When the algorithm looks for maxima, this stochasticity, however, presents difficulties. Conventional PSO relies on random parameter selection and has slow convergence rates, requiring more iterations to find the optimal point. Longer settling times and higher fluctuations are caused by an increased iteration rate, which results in power losses. PSO also faces challenges with premature convergence because of its stochastic nature. An adaptive PSO was suggested by the authors of [27] as a solution to the problem of becoming trapped in local peaks. However, because of the algorithm’s constrained capacity for decision-making for convergence, the problem of power losses arising from steady-state oscillations continued. The Jaya method, with its more straightforward structure, was discovered to be suitable for tracking the MPP by the authors of [28,29]. This method has two parts to its updating equation: a best-enhancing component (BEC) that moves it toward the best value and a worst-avoiding component (WAC) that keeps it separate from the worst options. However, the WAC becomes extremely large for lower values of the global best, pushing the solution away from the real global best and increasing tracking time and oscillations that result in power losses. In addition to these algorithms, authors have employed several human-based algorithms in their works. In [30], the musical chairs algorithm was presented, which produced significantly superior results when compared to other algorithms.
In this article, we utilize a novel algorithm for MPPT known as the Ali Baba and the Forty Thieves Algorithm (AFT) [31]. The AFT algorithm improves efficiency by addressing the drawbacks of other metaheuristic algorithms, AI, and other conventional algorithms.
AFT, which takes its inspiration from the tale of Ali Baba and the Forty Thieves, is categorized as a human-based algorithm. The thieves stand in for the search agents, the environment is the search space, each town position is a potential solution, Ali Baba’s house is the objective function, and Ali Baba is a metaphor for the global solution. The story is search-based in nature involving a group of 40 thieves who pursue Ali Baba. Their primary objective is to seek revenge and retrieve their stolen treasure by capturing Ali Baba. The search conducted by the gang for Ali Baba follows an iterative approach, consisting of multiple rounds that build upon the solutions found in previous iterations. In the proposed algorithm, the population is a representation of the thieves’ collective behavior, reflecting their search process. Throughout the tale, the main character, Marjaneh, takes countermeasures to thwart the gang’s search mission at each iteration. Her actions and strategies prevent the gang from accomplishing their objective, adding an element of challenges and complexity to the search process.
The convergence process is aided by the inclusion of numerous factors in AFT that facilitate exploration and exploitation. When looking for Ali Baba, the thieves (search agents) in AFT modify their positions using a mathematical model and tuning criteria while taking into account three potential scenarios.
The tracking range and perception potential are the two crucial parameters in AFT. With the help of these factors, AFT may efficiently explore the search space and find optimal or suboptimal solutions. AFT also uses clever deception techniques inspired by Marjaneh (Ali Baba’s maid), which boosts the chance of finding better answers in potential areas by encouraging the thieves to investigate other locations and directions. Across a variety of test functions, AFT has high reliability and effectiveness in obtaining close to ideal or optimal solutions.
The AFT algorithm for MPPT in PV systems appears to offer several novel features and benefits compared to existing MPPT algorithms:
- Tracking Range and Perception Potential: AFT utilizes the tracking range and perception potential as crucial parameters. This suggests that it has a dynamic approach to exploring the search space and adapting to changing environmental conditions, potentially making it more robust and adaptable than traditional MPPT algorithms.
- Clever Deception Techniques: AFT incorporates deception techniques inspired by Marjaneh, which encourage the thieves (representing the algorithm) to investigate other locations and directions. This implies that AFT can actively explore alternative solutions, potentially leading to better MPPT results, even in challenging conditions.
- Balanced Exploration and Exploitation: AFT employs a random search strategy for the thieves, striking a balance between exploration (diversifying the population) and exploitation (converging toward optimal solutions). This balance can result in quicker convergence while maintaining diversity, which is crucial for robust MPPT.
- Minimal Parameter Set: AFT uses a minimal set of parameters, indicating simplicity in implementation and tuning. This simplicity can make it more accessible and easier to deploy in practical PV systems.
Overall, the novelty and benefits of using the AFT algorithm for MPPT in PV systems include its adaptability, exploration-exploitation balance, simplicity, efficiency, and innovative approach. These qualities position AFT as a promising option for optimizing the performance of PV systems in various conditions.
The following is how the paper is set up: A summary of the PV cell’s single diode model is given in Section 2. Section 3 elaborates on the metaheuristic algorithms utilized in this research and their implementation. In Section 4, the obtained results from MATLAB/Simulink simulations are evaluated and compared. Section 5 presents the outcomes from the real-time Hardware-in-the-Loop (HIL) implementation of the proposed AFT algorithm for MPPT. The paper is finally concluded in Section 6, which summarizes the study’s major conclusions and contributions.
2. Modeling of the PV Cell
A parallel diode, a series resistance, and a current source that produces light comprise a PV cell. Typically, PV modules made of a collection of PV cells are coupled in series and parallel to produce the desired output power. Table 1 displays the specification of the PV cell employed in the simulation and Figure 1 shows the single-diode model of the PV cell.

Table 1.
Specifications of the photovoltaic (PV) cell.
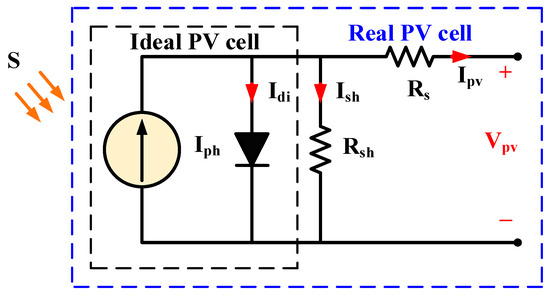
Figure 1.
Single-diode model of the photovoltaic (PV) cell.
The relationship between the output current and voltage can be stated using Ns and Np to denote the number of PV cells arranged in series and parallel, respectively.
The sun irradiation influences the produced photocurrent in the manner described below:
Additionally, the saturation current of the PV cell fluctuates with temperature in accordance with the following relationship:
According to Equations (1)–(3), the current produced by the PV array is simultaneously dependent on temperature and solar irradiation.
Now, take into consideration the PV cell model, which has no series loss and no leakage to ground, i.e., the cell’s series resistance , and the cell’s shunt resistance . The PV solar cell equivalent circuit mentioned above can be reduced to the following:
When all the parameters and voltage are known, Equation (4) transforms the output current into an explicit equation that can be calculated directly.
3. Metaheuristic Optimization Algorithm Based MPPT
Metaheuristic algorithms have been used for MPPT in PV generation systems to capture the GMPP and move beyond the constraints of conventional approaches. Through their exploitation skills, metaheuristic algorithms have the capacity to thoroughly explore the search space and select the best local optimal solution from among the global optimal solutions. Therefore, the optimization method is crucial to the MPPT controller’s effectiveness. Certain characteristics must be taken into account while designing an MPPT controller that is both cost- and power-efficient. These specifications include:
- Low failure rate: There should be very little chance of early convergence or failure for the MPPT algorithm.
- Fast convergence: To reduce the number of computing iterations necessary for an economical MPP tracker, the MPPT algorithm should reach the MPP quickly.
- Stable fluctuations: The MPPT algorithm needs to be capable of trustworthy exploration and exploitation in order to avoid needless search space traversal, which minimizes power fluctuations and related losses.
4. Ali Baba and the Forty Thieves (AFT) Algorithm-Based MPPT
The proposed AFT algorithm, based on global maximum power point tracking in a photovoltaic system, takes inspiration from the famous story of Ali Baba and the 40 thieves. The aim of this study is to introduce a novel optimization technique that mimics the story of Ali Baba and the 40 thieves, using a coordinated social behavior model to replicate human behavior. The underlying presumptions of this algorithm are as follows:
- The 40 thieves work together in a bevy and receive directions from someone, or from one of the thieves, to locate Ali Baba’s house. These directions may or may not be accurate.
- The 40 thieves travel a certain distance from their starting point until they locate Ali Baba’s house.
- Marjaneh can deceive the thieves several times with clever tactics to protect Ali Baba by a certain percentage.
As mentioned above, the search for Ali Baba by the thieves can result in three fundamental scenarios. In each of these cases, it is assumed that the thieves are conducting an efficient search of their surrounding environment, while also accounting for the proportion of the situation that is influenced by Marjaneh’s intelligence. This aspect forces the thieves to look in unexpected places. By modeling the behaviors of the thieves and Marjaneh, they can be related to an objective function that can be optimized.
4.1. Ali Baba and the Forty Thieves (AFT) Algorithm
The AFT algorithm encompasses several parameters that contribute to exploitation and exploration, outlined below as:
- Tracking distance parameter (): As the iterations progress, the emphasis on exploration diminishes while exploitation becomes more important. Lower values of focus on localized searches in propitious regions of search space. Consequently, in the later iterations, facilitates local search around the finest solution, resulting in exploitation. This specification regulates the amount of exploration in AFT by determining how far the new locations of thieves are from Ali Baba’s house. is defined using Equation (5) as:
- Perception potential parameter (): The degree of exploitation is regulated by , which quantifies the amount of comprehensive search around the finest solution. As iterations progress, the exploitation phase intensifies with comparatively larger values of this parameter. This specification emphasizes the exploration capability of AFT, particularly when it has comparatively small values. It is constantly increased during the iterative operation of AFT to avert getting stuck in local optima and approach the global optima. is defined using Equation (6) as:
- : This specification determines the direction of exploitation and exploration in AFT. As follows a uniform distribution between 0 and 1, the likelihood of obtaining positive and negative signs becomes equal.
- Marjaneh intelligence plans: This specification can directly enhance AFT exploration ability. The searching behavior of AFT can be represented mathematically as given below:
Case 1: If the thieves receive information from a source to help them locate Ali Baba, then their new locations can be determined using Equation (7) as follows:
where stands for the position of thief at iteration ), is the position of Ali Baba relative to the thief at iteration , is the best position attained by the thief up to iteration , denotes the global best position obtained by any thief up to the iteration, represents the tracking distance of the thieves at iteration , and denotes the perception potential of the thieves to Ali Baba at iteration .
The level of Marjaneh intelligence () used to camouflage the thief at iteration is calculated based on Equation (8).
where represents the wisdom of Marjaneh concerning the thief and the dimension, and it is characterized as a randomly generated number falling within the range of 0 to 1.
The parameter in can be characterized by Equation (9), given below.
where denotes a vector comprising random numbers that are uniformly scattered within the interval [0, 1], and n is the element number.
Case 2: If the thieves find out that they have been tricked, they may start exploring the search space for Ali Baba in a random manner. In such a scenario, the new positions of the thieves can be obtained using Equation (10), given below.
where and denote the lower and upper limits of the search space in the dimension, respectively.
4.2. MPPT Using AFT Algorithm
The flowchart of the AFT algorithm-based MPPT method is presented in Figure 2. In Figure 2, the duty ratio (D) sent to the DC-DC boost converter is analogous to the position of the thief in the AFT algorithm. The duty ratio is updated iteratively in each iteration using Equations (7), (9), and (10). The AFT algorithm implemented in the microcontroller dynamically adjusts the duty ratio in each iteration, mirroring its approach to optimizing the performance of each thief. Within each iteration, the algorithm assesses power levels and stores the duty ratio associated with the higher power output. When the power difference is less than 5% or the duty ratio difference is less than 2%, only the optimal duty ratio is transmitted to the switch.
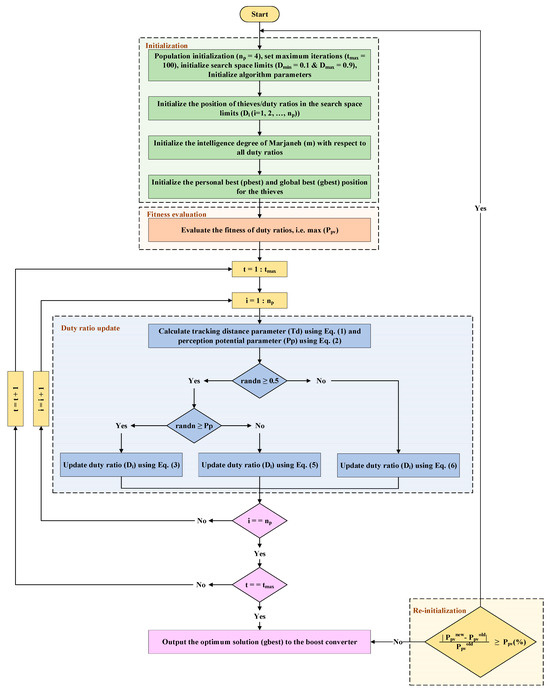
Figure 2.
Application of Ali Baba and the Forty Thieves (AFT) algorithm for MPPT.
The global best duty ratio () represents the duty ratio value that maximizes the power output. Furthermore, variations in radiation levels over time can cause the GMPP to fluctuate [32]. If the difference between the current power level and the previous one is less than 1% (indicating a change in insolation), the system triggers a reinitialization of all duty ratios and other relevant parameters.
The process of MPPT using AFT is detailed below:
- 1.
- Duty Ratio Initialization: The duty ratios within the AFT algorithm serve as control signals to regulate the converter, drawing an analogy to the position of the thieves. To initiate the optimization process, the duty ratios must be initialized within a predefined search space, constrained by two critical values: a maximum value ( = 0.9) and a minimum value ( = 0.1). These restrictions are imposed to confine the optimization within a secure and operationally feasible range of duty ratios.
- 2.
- Iterative Optimization Process: The AFT algorithm unfolds through an iterative optimization process inspired by the tale of Ali Baba and the 40 thieves. The search for Ali Baba by the thieves can lead to three fundamental scenarios. In each scenario, the thieves conduct an efficient search of their surroundings while considering the influence of Marjaneh’s intelligence, which compels them to explore unexpected locations. By modeling the behaviors of both the thieves and Marjaneh, these behaviors can be linked to an objective function that is amenable to optimization.
- 3.
- Obtaining the Optimum Duty Ratio: Through the iterative process, the AFT algorithm continually updates the duty ratio positions until it converges to a point where the optimal duty ratio, representing the global maximum power point (GMPP), is determined. Subsequently, this optimal duty ratio is transmitted to the converter, facilitating the adjustment of power conversion to operate at the peak power output of the PV system ().
The flowchart of the AFT algorithm-based MPPT method is presented in Figure 2. In Figure 2, the duty ratio (D) sent to the DC-DC boost converter is analogous to the position of the thief in AFT. The duty ratio is updated iteratively in each iteration using Equations (7), (9), and (10). After that, from the updated duty ratio, the best duty ratio () and the global best duty ratio () are evaluated. The optimal answer to the optimization problem is ultimately determined by the thieves’ best location.
5. Simulation and Analysis
For simulation analysis, the model of a photovoltaic system was developed, as given in Figure 3. It was constructed of four modules that were linked in series to form an array. A DC-DC boost converter then supplied power to the load. The PV module’s specifications are given in Table 2. The parameters for the DC-DC boost converter were derived as mentioned in [33,34,35]. The parameters used in different algorithms used in the paper are shown in Table 3. In this section, the simulation analysis of the proposed AFT algorithm is performed. The boost converter specifications were as follows: inductance (L) = 1.5 mH, load resistance (R) = 10, input capacitance (C1) = 47 F, and output capacitance (C2) = 470 F.
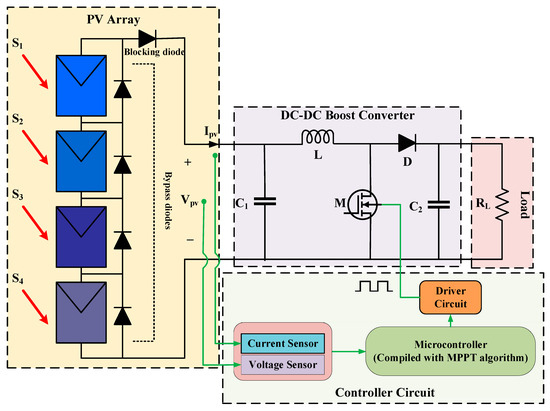
Figure 3.
Simulation model of the four-module photovoltaic system.

Table 2.
Ratings of components used in the PV model simulation.

Table 3.
Parameters values used in Particle Swarm Optimization (PSO), Adaptive Jaya (A-JAYA), and Ali Baba and the Forty Thieves (AFT) MPPT algorithms.
For analysis purposes, four alternative partial shading conditions (PSCs) were analyzed. For the first condition, a 1000 W/m2 of uniform insolation scenario was considered. The panels received (1000, 1000, 1000, 400) W/m2 and (1000, 1000, 600, 200) W/m2 accordingly for the second and third situations. Finally, a heavy shading scenario of (1000, 750, 400, 300) W/m2 was applied. The analysis of the performance of the three algorithms was performed on the basis of the maximum power tracked (), the tracking time (), and the efficiency () of the power tracked. The efficiency was calculated based on Equation (12).
5.1. Static Shading Conditions
5.1.1. Condition 1
The panels were given a consistent insolation of 1000 W/m2 in the first scenario. Figure 4 depicts the comparison results under this condition. The AFT tracking time for the 86.60 W MPP in this insolation was 0.2353 s. In comparison to the other algorithms with no steady-state oscillation, the suggested method’s tracking speed was also noticeably faster for condition 1. A-JAYA, on the other hand, tracked the MPP of 85.96 W with a 0.70 s tracking time. PSO tracked the MPP of 85.57 W in 2.23 s. AFT, A-JAYA, and PSO had efficiency rates of 99.15%, 98.4%, and 97.97%, respectively.
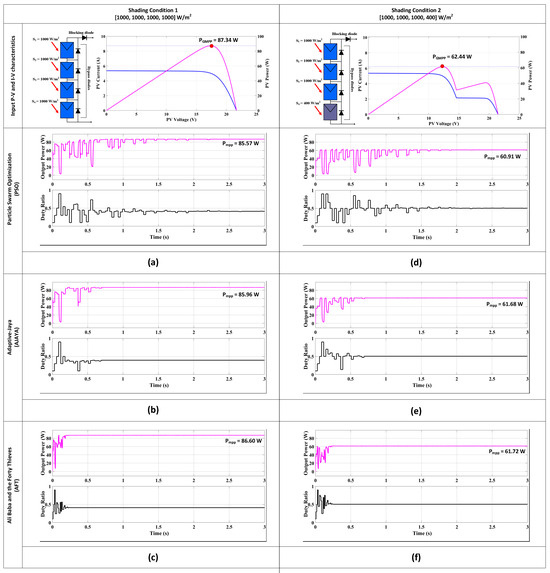
Figure 4.
Input Power-Voltage (P-V) and Current-Voltage (I-V) plots and output power and duty ratio plots of Particle Swarm Optimization (PSO), Adaptive Jaya (A-JAYA), and Ali Baba and the Forty Thieves (AFT) algorithm for (a–c) shading condition 1 and (d–f) shading condition 2.
5.1.2. Condition 2
In this case, the panels received (1000, 1000, 1000, 400) W/m2 insolation. Whereas PSO took longer to stabilize and caused steady-state oscillations even after the MPP had finally converged, AFT outperformed different algorithms with regard to settling time and efficiency. The tracking time of AFT, as seen from the result, was 0.25 s for tracking the MPP of 61.72 W. On the other hand, the tracking time of A-JAYA and PSO was observed to be 0.70 and 1.92 s for tracking the power of 61.68 W and 60.91 W, respectively. AFT was also seen to have a better efficiency of 98.84% as compared to A-JAYA (98.78%) and PSO (97.54%).
5.1.3. Condition 3
The panels were given an isolation of (1000, 1000, 600, 200) W/m2 in this situation. Figure 5 depicts the comparison results under this condition. In every respect, including settling time, oscillation, and frequency, AFT performed better compared to PSO and A-JAYA. The MPP of 41.50 W could be tracked by AFT in 0.2171 s, whereas A-JAYA and PSO needed 0.94 and 1.33 s, respectively, to track the MPP of 41.09 and 40.97 W. AFT’s efficiency in this scenario was observed to be 99.73%, A-JAYA’s efficiency was observed to be 98.75%, and PSO’s efficiency was observed to be 98.46%.
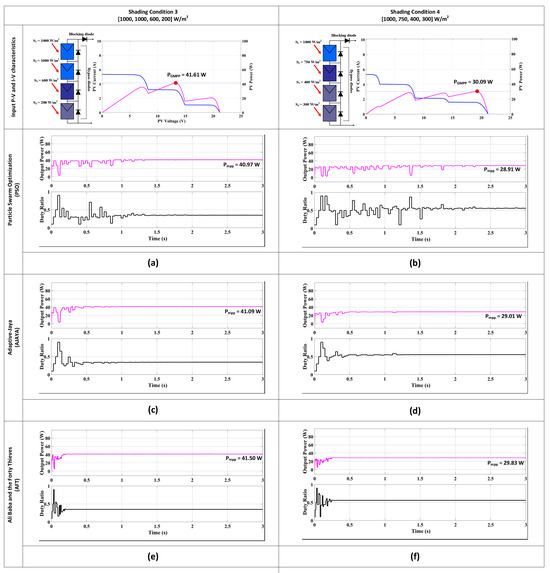
Figure 5.
Input Power-Voltage (P-V) and Current-Voltage (I-V) plots and output power and duty ratio plots of Particle Swarm Optimization (PSO), Adaptive Jaya (A-JAYA), and the Ali Baba and the Forty Thieves (AFT) algorithm for (a,c,e) shading condition 3 and (b,d,f) shading condition 4.
5.1.4. Condition 4
In this case, a comparison among AFT, PSO, and A-JAYA was depicted for the heavy shading scenario. The MPP was successfully traced by all three techniques, but the tracking time of A-JAYA took 1.18 s to track the MPP of 29.01 W, and PSO took 2.29 s to track the MPP of 28.91 W. On the other hand, AFT took just 0.2584 s for the MPP of 29.83 W. The efficiency of A-JAYA was found to be 96.07%, and the efficiency of PSO was observed to be 96.41%, whereas AFT had a greater efficiency of 99.13%. In the case of PSO, higher fluctuations and delayed convergence decisions led to decreased power efficiency.
The tracking time obtained from the AFT algorithm () was compared with the tracking time obtained by applying the A-JAYA and PSO algorithms. The performance improvement factor () is defined as Equation (13):
where is and .
Table 4 presents a qualitative analysis of the results for four distinct insolation scenarios. As can be seen, the AFT algorithm had a 99.2% average efficiency rating and an average tracking time of 0.235 s. In contrast, the A-JAYA algorithm’s average tracking time and efficiency was 0.88 s and 98.08%, respectively. The average tracking time and efficiency reported by the PSO algorithm was 1.94 s and 97.5%, respectively.

Table 4.
Quantitative analysis of simulation results.
Figure 6 graphically displays the PIF for the AFT algorithm in contrast to PSO and A-JAYA as established by the simulation study. As determined by the simulation study, Figure 7 graphically compares the efficiency of AFT to that of PSO and A-JAYA. The aforementioned results demonstrate that the suggested AFT algorithm performs significantly better than both the PSO and A-JAYA algorithms. This advantage is brought about by the AFT algorithm’s ability to boost the PV system’s efficiency by promoting faster convergence and minimizing fluctuations.
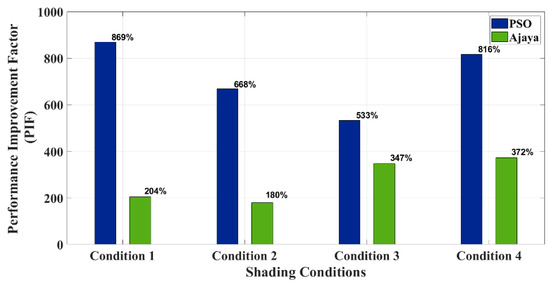
Figure 6.
Performance improvement factor (PIF) obtained from the simulation study for the Ali Baba and the Forty Thieves (AFT) algorithm with respect to Particle Swarm Optimization (PSO) and Adaptive Jaya (A-JAYA).
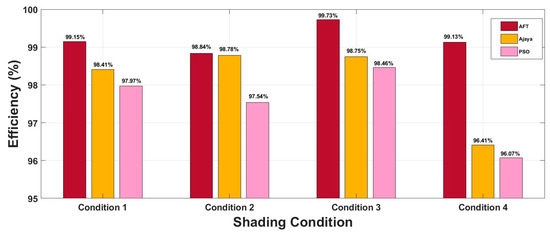
Figure 7.
Efficiency (%) obtained from the simulation study for the Ali Baba and the Forty Thieves (AFT) algorithm with respect to Adaptive Jaya (A-JAYA) and Particle Swarm Optimization (PSO).
5.2. Dynamic Shading Conditions
In the practical scenarios, there is a dynamic change in insolation conditions. Hence, this criterion was chosen to demonstrate the efficacy of the proposed method practical scenario. The shade patterns were changed over time to reflect changes in the sun’s position and cloud movement in order to imitate a dynamic setting. Every two seconds, the shade pattern was modified. The two situations below are displayed in contrast. Both the first and second cases were classified as dynamic insolation (varying insolation) and dynamic insolation (PS attenuation), respectively. The following is a description of the outcomes under both conditions. Figure 8 shows the irradiance profile under dynamic simulation.
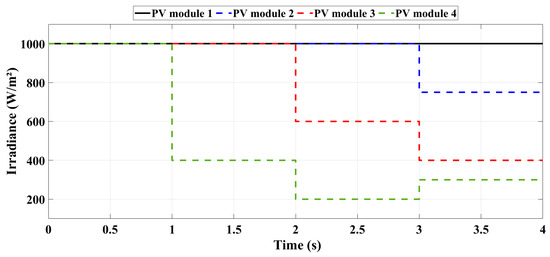
Figure 8.
Irradiance profile under dynamic simulation of the Ali Baba and the Forty Thieves (AFT)-based MPPT algorithm.
The code will re-initialize in the event of a power change brought on by an irradiance change. Equation (14) mentions the condition for re-initialization.
The outcome for AFT is displayed in Figure 9 under dynamic insolation with variation in irradiance values in the range of (1000, 1000, 1000, 1000), (1000, 1000, 1000, 400), (1000, 1000, 600, 200), (1000, 750, 400, 300). It is clear from the observation that the AFT algorithm tracked the MPP successfully for every instant. In AFT, each instant convergence time and fluctuation count were significantly smaller. The time for convergence for AFT at different insolations was 0.2353, 0.2502, 0.2171, and 0.2584 s, respectively. The advantage of change is clearly demonstrated by the fact that the proposed method monitored the MPP under dynamic situations effectively with significantly less convergence time as compared to other algorithms.
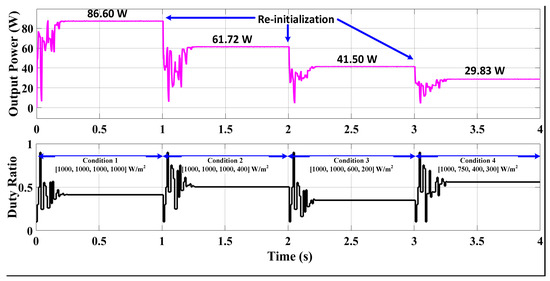
Figure 9.
Output power and duty ratio obtained using the Ali Baba and the Forty Thieves (AFT) algorithm when dynamic changes in irradiance occurred.
5.3. Impact of Search Agent Count on AFT Algorithm Performance
In this section, simulations were conducted using different numbers of search agents (3, 4, and 5) under consistent irradiance levels (1000, 900, 750, and 400 W/m2) applied to four PV panels. As illustrated in Figure 10a, with three search agents, the AFT algorithm achieved convergence to the MPP at 50.25 W within 0.20 s. The optimal duty ratio (Dbest) sent to the converter stabilized at 0.4285 s throughout the runtime, and the total number of iterations was four. The initial significant fluctuation observed was attributed to the initialization process and was not taken into account.
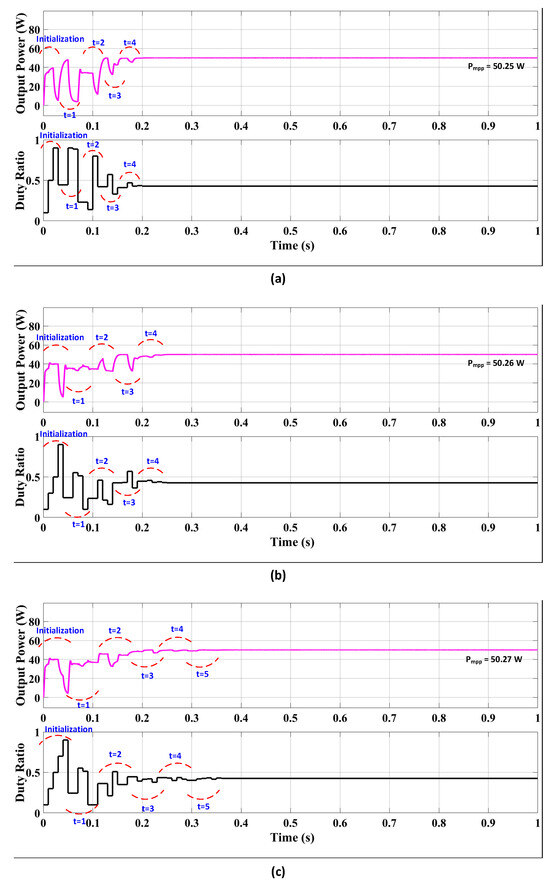
Figure 10.
Performance of the AFT algorithm when using (a) 3, (b) 4, and (c) 5 search agents.
Figure 10b demonstrates that with four search agents, the AFT algorithm converged to the MPP of 50.26 W within 0.24 s. The Dbest value sent to the converter stabilized at 0.4277 for the entire runtime, and the total number of iterations remained four.
In Figure 10c, when employing five search agents, the AFT algorithm reached the MPP of 50.27 W in 0.31 s. The Dbest value sent to the converter settled at 0.4264 for the duration of the runtime, and the total number of iterations increased to five.
As depicted in the figures, the iteration step varied for different swarm sizes, resulting in a slightly delayed convergence time as the number of particles increased. However, it is noteworthy that a smaller number of particles led to more frequent and larger fluctuations. Overall, the maximum power tracking efficiency remained consistent across varying swarm sizes. Therefore, the AFT algorithm demonstrates robust performance, capable of achieving accurate MPP tracking regardless of the number of search agents utilized.
6. Comparative Analysis of Algorithm Convergence
Under partial irradiance conditions of 1000, 900, 750, and 400 W/m2, simulations were conducted for the three algorithms: AFT (Figure 11a), A-JAYA (Figure 11b), and PSO (Figure 11c).
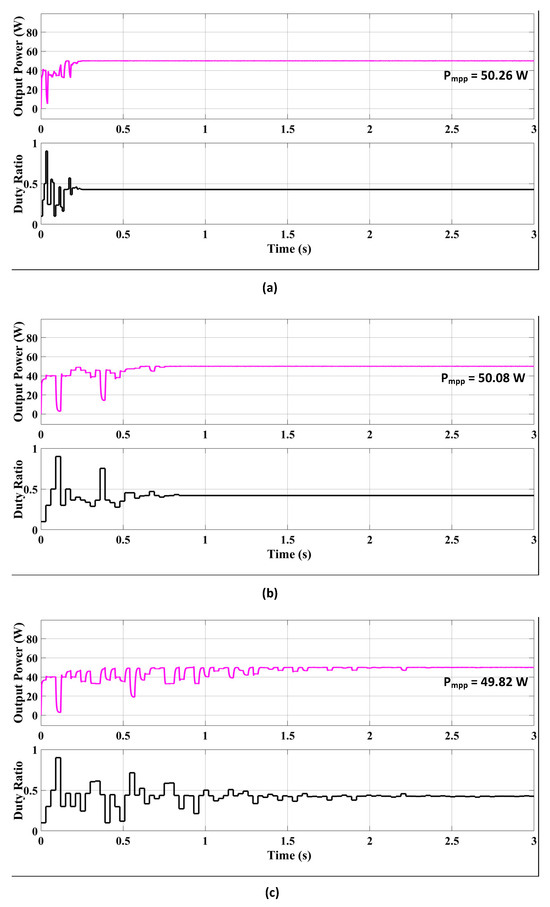
Figure 11.
Convergence analysis of (a) AFT, (b) A-JAYA, and (c) PSO algorithms under 1000, 900, 750, and 400 W/m2 irradiance condition.
The AFT algorithm demonstrated rapid convergence to the MPP, achieving 50.26 W within 0.25 s. The optimal duty ratio (Dbest) stabilized at 0.4277 throughout the runtime, and the total number of iterations was four. AFT achieved an outstanding maximum power tracking efficiency of 99.03% under these conditions.
In contrast, the A-JAYA algorithm also reached the MPP effectively, delivering 50.08 W within 0.76 s. The Dbest value stabilized at 0.4205, with a total of six iterations. The maximum power tracking efficiency for A-JAYA was 98.67%.
The PSO algorithm exhibited slightly slower convergence, attaining 49.82 W in 2.24 s. The Dbest remained stable at 0.4259 over 17 iterations, resulting in a maximum power tracking efficiency of 98.16%.
It is important to note that the number of steps corresponds to the number of iterations. In each step, all three algorithms evaluated four particles. However, the iteration steps varied between algorithms, as depicted in Figure 11. The duration of each step depended on the specific characteristics of the algorithm. This led to variations in the performance of the three algorithms, as detailed in Table 5.

Table 5.
Convergence analysis of the AFT, A-JAYA, and PSO algorithms.
Due to the reduced number of fluctuations and shorter tracking times observed in AFT when compared to A-JAYA and PSO, the overall system power losses were minimized in the AFT algorithm. This highlights the superior performance of AFT in terms of convergence time and efficiency under these conditions.
7. Implementation of the Proposed AFT Algorithm Using Real-Time HIL
Real-time HIL results are given in this section to validate the performance of AFT over PSO and A-JAYA. The PV system requirements for HIL implementation were the same as those specified in Table 2. The summary of insolation for the four PV panels is given in Table 6. Figure 12 illustrates the circuit incorporating the boost converter and various sensors interconnected within the circuit. Figure 13 portrays the Typhoon HIL emulation setup. The AFT algorithm was integrated into the microcontroller, which subsequently received input data in the form of voltage and current readings from the PV source. It then calculated the appropriate duty ratio value.
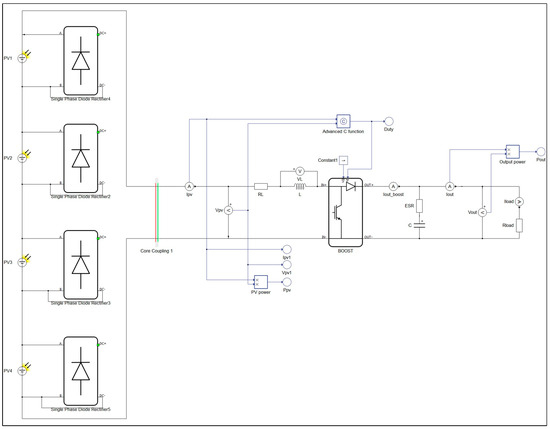
Figure 12.
Typhoon Hardware-in-the-Loop (HIL) simulation circuit integrating boost converter and interconnected sensors.

Figure 13.
Digital storage oscilloscope (DSO), Typhoon HIL-402 emulator, and host computer.
The AFT algorithm, embedded within the microcontroller, iteratively updated the duty ratio during its execution. During each iteration, the algorithm compared the power output with its previous value and retained the duty ratio associated with the higher power output. When the difference in power output was less than 5% or the difference in duty ratio was less than 2%, only the optimal duty ratio was communicated to the switch. Figure 14 shows the Input Power-Voltage (P-V) and Current-Voltage (I-V) plots of the photovoltaic (PV) array for shading conditions 1–5.
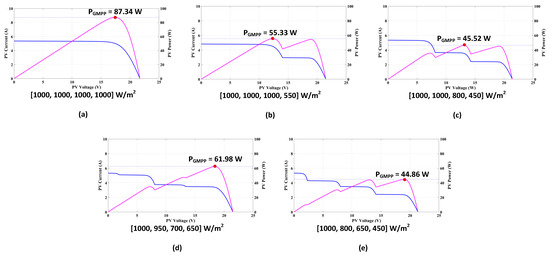
Figure 14.
Input Power-Voltage (P-V) and Current-Voltage (I-V) plots of the photovoltaic (PV) array for (a) shading condition 1; (b) shading condition 2; (c) shading condition 3; (d) shading condition 4; and (e) shading condition 5. (magenta plot: P-V, dark blue plot: I-V).
7.1. Static Shading Conditions
7.1.1. Shading Condition 1
The comparison of AFT with A-JAYA and PSO for shading condition 1 is shown in Figure 15a–c. Whereas A-JAYA and PSO tracked the MPP of 86.97 W and 86.60 W in 1.4 s and 4.8 s, respectively, the suggested algorithm settled to the MPP of 87.08 W in less time (0.9 s). Therefore, it is clear that the suggested AFT tracked the MPP faster. Additionally, the suggested algorithm’s efficiency was observed to be 99.70%, compared to A-JAYA and PSO’s 99.57% and 99.15%, respectively. Compared to when A-JAYA and PSO were used for MPP tracking, the shorter AFT reduced tracking time helped minimize power losses and boost the efficiency of the system’s power output.
7.1.2. Shading Condition 2
Figure 15d–f illustrates the comparison results when one out of four PV modules was shaded. Given that three PV modules received full insolation, this is a scenario with light shading conditions. The suggests that the AFT method reached its maximum power of 55.05 W in 0.9 s. A-JAYA and PSO reached their respective MPPs of 54.24 W and 45.32 W after 1.4 s and 4.0 s of convergence, respectively. In comparison to A-JAYA (98.03%) and PSO (97.95%), the efficiency of the suggested method for this shading situation was observed to be 99.49%. As a result, AFT followed a higher MPP value more quickly, and there was no significant fluctuation seen. Conversely, PSO caused a number of significant fluctuations that led to power losses.
7.1.3. Shading Condition 3
The comparative outcomes for shading condition 3 are displayed in Figure 15g–i. The suggested method could track the MPP of 45.32 W under this situation in 0.6 s, whereas A-JAYA and PSO settled for a lesser value of 44.83 W and 44.37 W, respectively, for the MPP. In comparison to the AFT, A-JAYA and PSO had substantially longer settling times and larger size variations. Again, for this circumstance, the combined impact of slower monitoring speed and considerable size variations greatly lowered the PV system’s overall efficiency.
7.1.4. Shading Condition 4
The comparison findings are shown in Figure 15j–l when three of the four PV modules are shaded. Only one PV module received complete insolation, indicating heavy shading conditions. For this circumstance, the suggested method could track the MPP of 61.22 W in 0.9 s compared to A-JAYA’s 1.8 s for 60.91 W and PSO’s 4.6 s for 60.56 W. The three algorithms under comparison were as follows in terms of efficiency: AFT (98.77%), A-JAYA (98.27%), and PSO (97.70%).
7.1.5. Shading Condition 5
For shading condition 5, the results obtained are shown in Figure 15m–o. The proposed algorithm tracked the MPP of 44.37 W in 0.8 s. A-JAYA tracked the MPP 44.22 W in 2.4 s, while PSO tracked the MPP 43.97 W in 3.6 s. The efficiency of AFT was observed to be 98.90%, while A-JAYA and PSO had an efficiency of 98.57% and 98.01%, respectively.
A qualitative examination of the data for five different insolation conditions is presented in Table 5. The AFT algorithm had an average tracking time of 0.8 s and an average efficiency rating of 99.2%, as shown. The average tracking time and average efficiency for the A-JAYA algorithm, in contrast, were 1.68 s and 98.5%, respectively. The PSO algorithm, meanwhile, reported an average tracking time of 3.96 s with a corresponding average efficiency of 98%.
The Performance Improvement Factor (PIF) for the AFT algorithm in comparison to PSO and A-JAYA, as determined by Hardware-in-the-Loop (HIL) analysis, is shown graphically in Figure 16. Figure 17 graphically illustrates the efficiency of the AFT algorithm in comparison to PSO and A-JAYA as determined by Hardware-in-the-Loop (HIL) analysis. The aforementioned findings make it clear that the proposed AFT algorithm greatly outperforms both PSO and A-JAYA algorithms in terms of performance. This superiority is due to the AFT algorithm’s capacity to increase the PV system’s efficiency by facilitating faster convergence and reducing fluctuations.
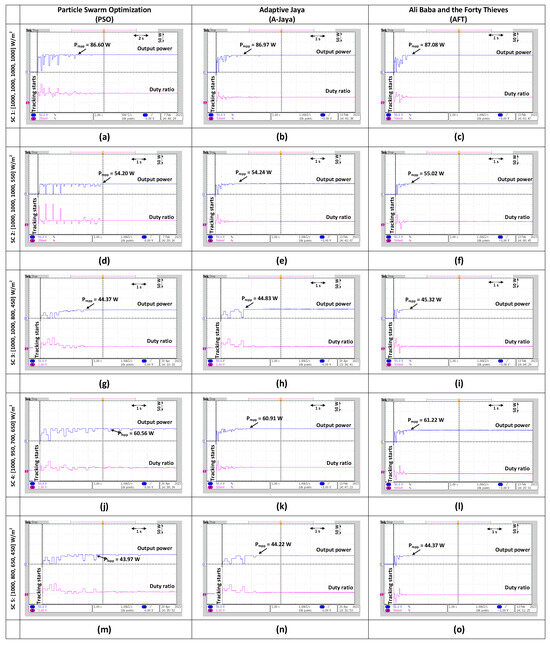
Figure 15.
Hardware-in-the-Loop (HIL) outcomes showing the output power and duty ratio for Particle Swarm Optimization (PSO), Adaptive Jaya (A-JAYA) and Ali Baba and the Forty Thieves (AFT) for (a–c) shading condition 1; (d–f) shading condition 2; (g–i) shading condition 3; (j–l) shading condition 4; and (m–o) shading condition 5.

Table 6.
Quantitative analysis of Hardware-in-the-Loop (HIL) outcomes.
Table 6.
Quantitative analysis of Hardware-in-the-Loop (HIL) outcomes.
| Shading Condition (SC) | ) | Method | (W) | (W) | (%) | (s) | |||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1000 | 1000 | 1000 | 1000 | AFT | 87.34 | 87.08 | 99.70 | 0.9 |
| A-JAYA | 86.97 | 99.57 | 1.4 | ||||||
| PSO | 86.60 | 99.15 | 4.8 | ||||||
| 2 | 1000 | 1000 | 1000 | 550 | AFT | 55.33 | 55.05 | 99.49 | 0.9 |
| A-JAYA | 54.24 | 98.03 | 1.4 | ||||||
| PSO | 54.20 | 97.95 | 4.0 | ||||||
| 3 | 1000 | 1000 | 800 | 450 | AFT | 45.52 | 45.32 | 99.56 | 0.6 |
| A-JAYA | 44.83 | 98.48 | 1.4 | ||||||
| PSO | 44.37 | 97.47 | 2.8 | ||||||
| 4 | 1000 | 950 | 700 | 650 | AFT | 61.98 | 61.22 | 98.77 | 0.8 |
| A-JATA | 60.91 | 98.27 | 1.8 | ||||||
| PSO | 60.56 | 97.70 | 4.6 | ||||||
| 5 | 1000 | 800 | 650 | 450 | AFT | 44.86 | 44.37 | 98.90 | 0.8 |
| A-JAYA | 44.22 | 98.57 | 2.4 | ||||||
| PSO | 43.97 | 98.01 | 3.6 | ||||||
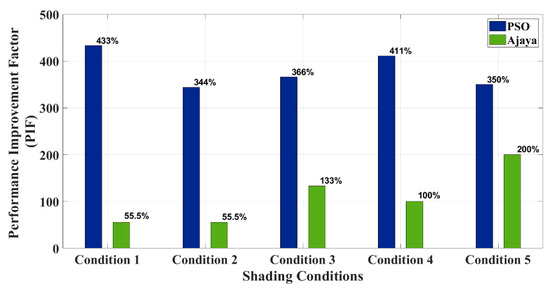
Figure 16.
Performance improvement factor (PIF) obtained from Hardware-in-the-Loop (HIL) analysis for Ali Baba and the Forty Thieves (AFT) algorithm with respect to Particle Swarm Optimization (PSO) and Adaptive Jaya (A-JAYA).
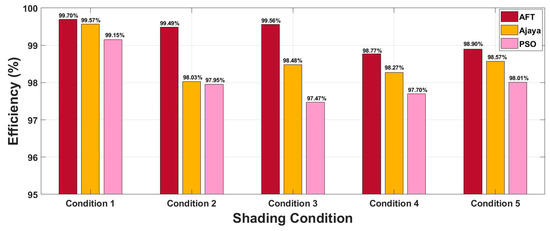
Figure 17.
Efficiency (%) obtained from Hardware-in-the-Loop (HIL) analysis for Ali Baba and the Forty Thieves (AFT) algorithm with respect to Adaptive Jaya (A-JAYA) and Particle Swarm Optimization (PSO).
7.2. Dynamic Shading Conditions
The AFT algorithm’s adaptability to dynamically changing situations is shown in this section to provide a more useful analysis after its performance has been validated. This scenario depicts variations in shading patterns that could happen as a result of shifting clouds or shifting sun position over time. Real-time results were generated using the HIL emulator. Figure 18 displays the AFT performance curves under various shading scenarios. The figure depicts how dynamic insolation affected the PV array, simulating how a cloud first partially shaded the array before dissipating over time to reveal or obscure the surface.
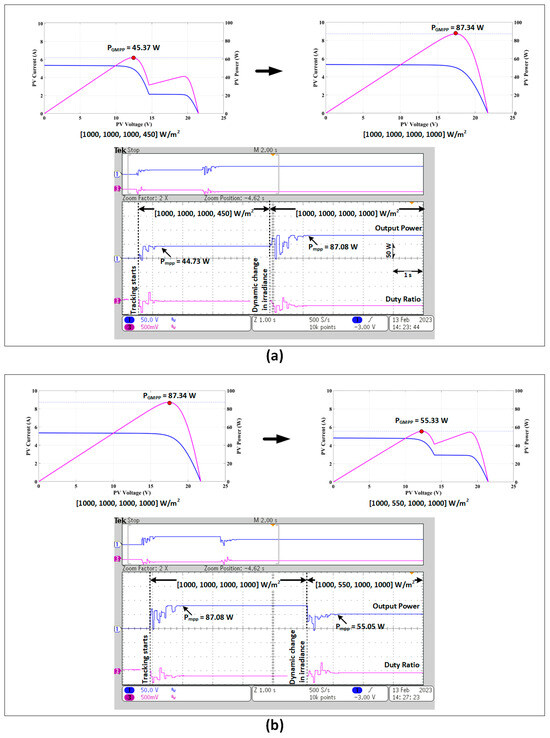
Figure 18.
Hardware-in-the-Loop (HIL) outcomes showing output power and duty ratio for (a) dynamic irradiance scenario 1 and (b) dynamic irradiance scenario 2.
Figure 18a shows the transition from condition 1, which was a light partial shading condition with full insolation for Panels 1, 2, and 3, to condition 2, which was a full insolation condition. For conditions 1 and 2, the AFT converged to the MPP in around 0.6 and 1.0 s, respectively. The MPPs being monitored had an efficiency of 98.58% and 99.70%, and they were 44.73 W and 87.08 W, respectively.
The transition from condition 2, which was full insolation, to condition 3, which was light shading (1000, 550, 1000, 1000), where panel 1, 3, and 4 received full insolation, is shown in Figure 18b. For conditions 2 and 3, the AFT settled in 1.0 s for both conditions However, the MPPs monitored under these circumstances were, respectively, 87.08 W and 55.05 W, with 99.70% and 99.49% efficiency.
8. Conclusions
This study’s goal was to develop an MPPT controller for photovoltaic (PV) arrays that is accurate, dependable, and minimizes fluctuations. To achieve this, a novel algorithm called the Ali Baba and Forty Thieves (AFT) algorithm was implemented in the MPPT controller using MATLAB/Simulink. The proposed AFT algorithm’s effectiveness was compared with that of the A-JAYA and PSO algorithms. The results of the comparison showed that the proposed AFT algorithm had many different types of advantages over A-JAYA and PSO, including a greater MPP tracking accuracy, a faster convergence rate, improved efficiency, and fewer fluctuations. Using Hardware-in-the-Loop (HIL) testing conducted in real time, the simulation results were further confirmed. The HIL findings showed that even in difficult situations, the proposed algorithm maintained reliable MPP tracking with barely any variations between global and local optima. The average tracking time for the AFT algorithm under the specified conditions was 0.82 s, and the average efficiency was 99.28%. The A-JAYA algorithm, in contrast, had an average tracking time and efficiency of 1.68 s and 98.5%, respectively. Meanwhile, the PSO algorithm estimated an average tracking time of 3.96 s and an associated average efficiency of 98%. Additionally, the effectiveness of the suggested algorithm was evaluated under static partial shade conditions, and its practical applicability in adapting to dynamically changing conditions was assessed. The findings suggest that the application of the AFT algorithm in the MPPT controller offers an optimal approach for efficient MPP tracking in industrial, commercial, and residential settings. Future studies can also investigate the creation of MPPT trackers utilizing improved algorithms to simplify computations and boost convergence speeds. This would aid in the development of MPPT technology moving forward.
Author Contributions
Conceptualization, K.U.R., I.S., A.S., F.I.B. and M.T.; Methodology, I.S. and A.S.; Software, K.U.R. and I.S.; Formal analysis, A.S. and S.A.; Investigation, A.S., C.-H.L. and S.A.; Writing—original draft, K.U.R., I.S. and A.S.; Writing—review & editing, K.U.R., I.S. and A.S.; Supervision, A.S. and M.T.; Funding acquisition, S.A., S.-D.L. and H.-D.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research has received funding from King Saud University through Researchers Supporting Project number RSP2023R387, King Saud University, Riyadh, Saudi Arabia.
Data Availability Statement
No data was used for the research described in the article.
Acknowledgments
The authors extend their appreciation to King Saud University for funding this work through Researchers Supporting Project number (RSP2023R387), King Saud University, Riyadh, Saudi Arabia.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mahto, R.; John, R. Modeling of Photovoltaic Module. In Solar Cells—Theory, Materials and Recent Advances; IntechOpen: London, UK, 2021. [Google Scholar] [CrossRef]
- Shubbak, M.H. Advances in solar photovoltaics: Technology review and patent trends. Renew. Sustain. Energy Rev. 2019, 115, 109383. [Google Scholar] [CrossRef]
- Garnett, E.C.; Ehrler, B.; Polman, A.; Alarcon-Llado, E. Photonics for Photovoltaics: Advances and Opportunities. ACS Photonics 2021, 8, 61–70. [Google Scholar] [CrossRef] [PubMed]
- Green, M.A. How Did Solar Cells Get So Cheap? Joule 2019, 3, 631–633. [Google Scholar] [CrossRef]
- Ding, H.; Zhou, D.Q.; Liu, G.Q.; Zhou, P. Cost reduction or electricity penetration: Government R&D-induced PV development and future policy schemes. Renew. Sustain. Energy Rev. 2020, 124, 109752. [Google Scholar]
- Singh, R.; Tripathi, P.; Yatendra, K. Impact of Solar Photovoltaic Penetration in Distribution Network. In Proceedings of the 2019 3rd International Conference on Recent Developments in Control, Automation Power Engineering (RDCAPE), Noida, India, 10–11 October 2019; pp. 551–556. [Google Scholar] [CrossRef]
- Zhu, W.; Shang, L.; Li, P.; Guo, H. Modified hill climbing MPPT algorithm with reduced steady—State oscillation and improved tracking efficiency. J. Eng. 2018, 2018, 1878–1883. [Google Scholar] [CrossRef]
- Srishti, D.; Samajdar, P.; Padhy, P.K. Incremental Conductance Based Model Predictive Control Algorithm for Solar PV Module for Tracking of MPP. In Proceedings of the 2023 IEEE Region 10 Symposium (TENSYMP), Canberra, Australia, 6–8 September 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Ali, A.I.; Mousa, H.H.; Mohamed, H.R.; Kamel, S.; Hassan, A.S.; Alaas, Z.M.; Mohamed, E.E.; Youssef, A.R. An Enhanced P&O MPPT Algorithm with Concise Search Area for Grid-Tied PV Systems. IEEE Access 2023, 11, 79408–79421. [Google Scholar] [CrossRef]
- El-sharawy, L.A.; El-helw, H.M.; Hasanien, H.M. Enhanced Grey Wolf optimization for GMPP Tracking of PV Systems under Partial Shading Condition. In Proceedings of the 2019 21st International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 17–19 December 2019; pp. 858–865. [Google Scholar] [CrossRef]
- Chaudhary, S.; Singh, A. Analysis of AI Techniques for Maximum Power Point Tracking under Partial Shading Conditions. In Proceedings of the 2020 IEEE 17th India Council International Conference (INDICON), New Delhi, India, 10–13 December 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Chaudhary, S.; Singh, A. Simplified Optimized Fuzzy Logic Controller for Maximum Power Point Tracking in PV Array under Partial Shading Conditions. In Proceedings of the 2021 IEEE Mysore Sub Section International Conference (MysuruCon), Hassan, India, 24–25 October 2021; pp. 279–284. [Google Scholar] [CrossRef]
- Rehman, U.U.; Faria, P.; Gomes, L.; Vale, Z. Artificial Neural Network Based Efficient Maximum Power Point Tracking for Photovoltaic Systems. In Proceedings of the 2022 IEEE International Conference on Environment and Electrical Engineering and 2022 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Prague, Czech Republic, 28 June–1 July 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Kumar, N.; Hussain, I.; Singh, B.; Panigrahi, B.K. Rapid MPPT for uniformly and partial shaded PV system by using JayaDE algorithm in highly fluctuating atmospheric conditions. IEEE Trans. Ind. Inform. 2017, 13, 2406–2416. [Google Scholar] [CrossRef]
- Anand, R.; Swaroop, D.; Kumar, B. Global Maximum Power Point Tracking for PV Array under Partial Shading using Cuckoo Search. In Proceedings of the 2020 IEEE 9th Power India International Conference (PIICON), Sonepat, India, 28 February–1 March 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Mohanty, S.; Subudhi, B.; Ray, P.K. A new MPPT design using grey Wolf optimization technique for photovoltaic system under partial shading conditions. IEEE Trans. Sustain. Energy 2016, 7, 181–188. [Google Scholar] [CrossRef]
- Ram, J.P.; Rajasekar, N. A Novel Flower Pollination Based Global Maximum Power Point Method for Solar Maximum Power Point Tracking. IEEE Trans. Power Electron. 2017, 32, 8486–8499. [Google Scholar]
- Fapi, C.B.N.; Tchakounté, H.; Hamida, M.A.; Wira, P.; Kamta, M. Experimental Implementation of Improved P&O MPPT Algorithm based on Fuzzy Logic for Solar Photovoltaic Applications. In Proceedings of the 2023 11th International Conference on Smart Grid (icSmartGrid), Paris, France, 4–7 July 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Li, W.; Zhang, G.; Pan, T.; Zhang, Z.; Geng, Y.; Wang, J. A Lipschitz Optimization-Based MPPT Algorithm for Photovoltaic System under Partial Shading Condition. IEEE Access 2019, 7, 126323–126333. [Google Scholar] [CrossRef]
- Obukhov, S.; Ibrahim, A.; Diab, A.A.Z.; Al-Sumaiti, A.S.; Aboelsaud, R. Optimal Performance of Dynamic Particle Swarm Optimization Based Maximum Power Trackers for Stand-Alone PV System under Partial Shading Conditions. IEEE Access 2020, 8, 20770–20785. [Google Scholar] [CrossRef]
- Teshome, D.F.; Lee, C.H.; Lin, Y.W.; Lian, K.L. A modified firefly algorithm for photovoltaic maximum power point tracking control under partial shading. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 661–671. [Google Scholar] [CrossRef]
- Kumar, B.; Kumar, R.; Kumar, P.; Kumar, R.; Singh, P.; Kumar, A. Analysis and Performance Evolution of Novel Global Modified Flower Pollination Algorithm for Photovoltaic System under Partial Shading Condition. In Proceedings of the 2022 2nd International Conference on Emerging Frontiers in Electrical and Electronic Technologies (ICEFEET), Patna, India, 24–25 June 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Nisa, M.; Andleeb, M.; Ilahi, B.F. Effect of Partial Shading on a PV Array and Its Maximum Power Point Tracking Using Particle Swarm Optimization. J. Phys. Conf. Ser. 2021, 1817, 12025. [Google Scholar] [CrossRef]
- Liu, Y.; Huang, S.; Huang, J.; Liang, W. A Particle Swarm Optimization-Based Maximum Power Point Tracking Algorithm for PV Systems operating under partially shaded conditions. IEEE Trans. Energy Convers. 2021, 27, 1027–1035. [Google Scholar] [CrossRef]
- Sangrody, R.; Taheri, S.; Cretu, A.-M.; Pouresmaeil, E. An Improved PSO-based MPPT Technique Using Stability and Steady State Analyses under Partial Shading Conditions. IEEE Trans. Sustain. Energy 2023, 1–10. [Google Scholar] [CrossRef]
- Lv, X.; Wang, Y.; Deng, J.; Zhang, G.; Zhang, L. Improved Particle Swarm Optimization Algorithm Based on Last-Eliminated Principle and Enhanced Information Sharing. Comput. Intell. Neurosci. 2018, 2018, 5025672. [Google Scholar] [CrossRef] [PubMed]
- Eltamaly, A.M.; Al-Saud, M.S.; Abokhalil, A.G.; Farh, H.M.H. Simulation and experimental validation of fast adaptive particle swarm optimization strategy for photovoltaic global peak tracker under dynamic partial shading. Renew. Sustain. Energy Rev. 2020, 124, 109719. [Google Scholar] [CrossRef]
- Huang, C.; Zhang, Z.; Wang, L.; Song, Z.; Long, H. A novel global maximum power point tracking method for PV system using jaya algorithm. In Proceedings of the 2017 IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 26–28 November 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Padmanaban, S.; Priyadarshi, N.; Bhaskar, M.S.; Holm-Nielsen, J.B.; Hossain, E.; Azam, F. A hybrid photovoltaic-fuel cell for grid integration with jaya-based maximum power point tracking: Experimental performance evaluation. IEEE Access 2019, 7, 82978–82990. [Google Scholar] [CrossRef]
- Ali, M.E. A novel musical chairs algorithm applied for MPPT of PV systems. Renew. Sustain. Energy Rev. 2021, 146, 111135. [Google Scholar] [CrossRef]
- Braik, M.; Ryalat, M.H.; Al-Zoubi, H. A novel meta-heuristic algorithm for solving numerical optimization problems: Ali Baba and the forty thieves. Neural Comput. Appl. 2022, 34, 409–455. [Google Scholar] [CrossRef]
- Eltamaly, A.M.; Farh, H.M.H.; Al Saud, M.S. Impact of PSO Reinitialization on the Accuracy of Dynamic Global Maximum Power Detection of Variant Partially Shaded PV Systems. Sustainability 2019, 11, 2091. [Google Scholar] [CrossRef]
- Rehman, H.; Sajid, I.; Sarwar, A.; Tariq, M.; Bakhsh, F.I.; Ahmad, S.; Mahmoud, H.A.; Aziz, A. Driving training-based optimization (DTBO) for global maximum power point tracking for a photovoltaic system under partial shading condition. IET Renew. Power Gener. 2023, 17, 2542–2562. [Google Scholar] [CrossRef]
- Sajid, I.; Gautam, A.; Sarwar, A.; Tariq, M.; Liu, H.-D.; Ahmad, S.; Lin, C.-H.; Sayed, A.E. Optimizing Photovoltaic Power Production in Partial Shading Conditions Using Dandelion Optimizer (DO)-Based MPPT Method. Processes 2023, 11, 2493. [Google Scholar] [CrossRef]
- Pervez, I.; Pervez, A.; Tariq, M.; Sarwar, A.; Chakrabortty, R.K.; Ryan, M.J. Rapid and Robust Adaptive Jaya (Ajaya) Based Maximum Power Point Tracking of a PV-Based Generation System. IEEE Access 2021, 9, 48679–48703. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).