Abstract
This article was conducted within the framework of project reg. no. CZ.11.4.120/0.0/0.0/16_013/0002594, programme, Interreg V-A Czech Republic-Poland, Microprojects Fund 2014–2020 in the Euroregion Silesia. It is focused in the area of modelling technological processes and the presentation of the main principles of these models. The modelling of technological processes is important in terms of its applicability to process prediction in industry. A complex of analytical and predictive metallurgical models was developed within VSB-TUO. The original mathematical model of coke degradation in a blast furnace makes it possible to calculate the minimum consumption of coke from the dynamic balance for different values of the ratio of direct and indirect reduction. As part of the graphic output, it determines the practically and theoretically achievable minimum coke consumption points. The use of the model enables the determination of a real reserve in reducing the amount of coke.
1. Introduction
One of the ways of increasing the efficiency of the blast furnace process is to optimise the charge for the production of pig iron, primarily from the viewpoint of achieving minimum coke consumption. In a series of works by leading blast furnace experts [1,2,3,4,5,6,7,8], it has been convincingly demonstrated that minimum coke consumption can be achieved with an optimal ratio of direct and indirect reduction. A realistic indicator forecast of the share of direct and indirect reduction makes it possible to increase the reporting quality of analytical diagrams and, using them, to compile a shaft that ensures the minimum level of energy demand. The solution to the mentioned problem was based on the study of a system consisting of a gaseous mixture of CO/CO2, coke, iron, and its oxides. Mathematically formulated relationships have been summarised; the task is often solved using mathematical models or enabling a simplified simulation of the kinetic side of reduction processes.
Models for the simulation of processes in a blast furnace address both the thermochemical area [9,10], the prediction of the thermal state of the hearth [11], the modelling of processes when injecting substitute fuels [12,13], and the countercurrent flow in the blast furnace [14].
Currently, the trend is directed towards the use of hydrogen as a substitute fuel. Shatokha, V, [15] simulated the operation of the VP with hydrogen injection into conventional tuyeres using a 1D steady-state zonal model. The maximum hydrogen injection rate was evaluated on the basis of the simulation of the vertical temperature pattern of the BF by focusing on the thermal reserve zone.
They used a mathematical model to predict the fuel consumption of a blast furnace, and this is presented by Cardoso, W. et al. [16]. Venkatesan, J. et al. [17], developed an advanced mathematical model. A model was developed to predict the carbon, coke, and fuel rates, oxygen rate, top gas composition, gas utilisation efficiency, and specific energy efficiency. The model simultaneously estimates the blast furnace process parameters. Qiang Wang, et al. have proven that numerical simulations within the replacement carbon composite briquettes save coke [18]. The new directions of simulations and modelling focus on the degree of utilisation of blast furnace gas. The latter is an important indicator parameter for expressing the energy consumption and smooth operation of the blast furnace. Authors Jiang, D. et al. [19] show the possibilities of predictive modelling of blast furnace gas utilisation rate. The aim of the present article is to present an original mathematical model of coke degradation in a blast furnace, which was developed within VŠB-TUO and gradually innovated/supplemented. Since the 1980s, blast furnaces in the Czech Republic have been assessed using the above methodology and the original thermodynamic model. Complementing the classic balance sheet assessment with the theoretical minimum coke consumption calculation (within the mathematical model of coke degradation in the blast furnace) enables a more comprehensive comparison of the technological level of individual blast furnaces as well as their real reserves in reducing coke consumption.
Balance, thermodynamic, and especially kinetic approaches in the modelling of metallurgical processes form the necessary basis for a continuous analysis of conditions where the assessed iron and steel technology can actually operate in limited technological states with the lowest achievable fuel consumption (reducing agents) and the highest achievable productivity [20].
Knowledge of physicochemical, thermal, and mechanical events during the blast furnace operation enables the compilation of mathematical formulations (mathematical models) of the relevant dependencies, which are processed by computer technology. The results will be forwarded either to the operator or directly to the regulatory authorities. This task has been discussed for many years, and many of these partial mathematical models have already been published in the professional literature, many of which are used in practise [20,21,22,23].
In addition to assessment and analytical purposes, the models designed in this way can also be used for variant prognostic calculations, enabling basic quantitative orientation on the impacts of the prepared rationalisation or intensification measures.
For these reasons, the Department of Metallurgy at VSB-TUO has developed a complex of analytical and predictive metallurgical models designed to assess the possibilities and benefits of intensified and modernised forms of iron and steel technology [14,24,25,26]. The basic scheme of mutual relations between individual models is presented [24] in Figure 1.
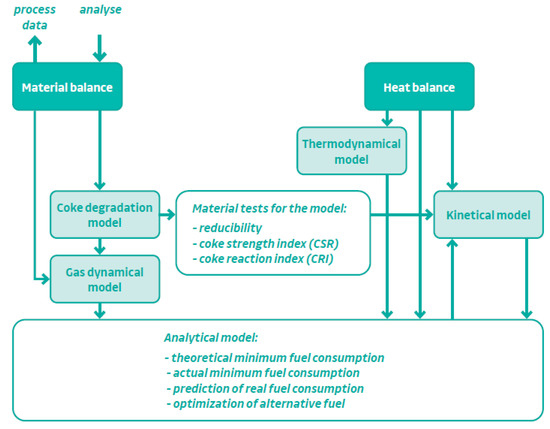
Figure 1.
Schematic diagram of the group of mathematical models for a blast furnace.
The original thermodynamic balance method for calculating the theoretical specific consumption of coke was later modified and generally extended by a graphical output in the form of Rist and later CDR diagrams. The theoretical minimum, from a thermodynamic viewpoint, is the limit-specific consumption of coke calculated here on the basis of the material and heat balance of the lower, so-called blast furnace production zone under the conditions of achieving thermodynamic equilibrium of reduction processes at gas outlets in this zone.
2. Materials and Methods
2.1. Method of Predictive Calculation of Specific Carbon Consumption
The permeability of the charge in the blast furnace is mainly dependent on its granulometric composition. In the layers of the input coke, which has not yet been granulometrically degraded during the descent in the blast furnace, the changes in breathability are not very significant [24]. In the seat and in the upper part of the hearth of the blast furnace, a liquid melt flows countercurrently with the rising gas. The flow of liquid phases reduces the free spaces between the coke pieces. The narrowing of the free spaces between the coke grains causes an increase in the gas flow rate and a loss of pressure. With a large amount of liquid smelting products, the spaces between the pieces of coke can become crowded and the gas flow interrupted.
The coke filling of the furnace in the lower part is composed of pieces of coke of various sizes with a significant proportion of small and fine grains, which are distributed in an undefinable manner in the layer [27]. To develop an objective mathematical description of the gas flow and charge drop in the blast furnace, the original causal relationships were compiled.
The value of the specific gas consumption at the reduction corresponds numerically to the specific carbon consumption required for the formation of such gas [21,24]. Therefore, the set of operating lines for a given charge indicates the relationship between specific carbon consumption and the degree of direct reduction for the respective residence time of the charge in the indirect gas reduction zone. Residence time can be determined in several ways, for example, by calculating the heat exchange intensity in the furnace preparation and operating volume or by direct measurement of the temperature profile in the furnace.
The model can also be applied to a multicomponent iron ore charge. This fact creates an important condition for future optimisation of the composition of the iron ore blast furnace charge under the specific conditions of the respective blast furnace unit. It represents a fundamental contribution of the model presented to the practical operational interpretation of standardised and special reducibility tests.
The graphical expression of carbon consumption in FeO reduction and carbon consumption to ensure the thermal side of the process depending on the share of direct reduction shows that the lowest carbon consumption corresponds to a certain, precisely defined ratio of both reductions. Any ratio other than optimal results in higher carbon consumption.
The relationship between specific carbon consumption and the degree of direct reduction achieved can be calculated using the indirect reduction model in the blast furnace shaft for variant calculations under different assumptions (conditions) of the indirect reduction process, such as different specific amounts of reducing gas or blast furnace process intensity. This degree corresponds to the proportion of wüstite in the reduced charge after the end of the indirect reduction.
From the dependence obtained kinetically between the specific consumption of the reducing gas and the degree of direct reduction, it is possible to determine the chemical-kinetic limit of carbon consumption for indirect reduction of iron oxides, which is expressed by the curve in Figure 2. However, from the enthalpy balance viewpoint, it is necessary to respect that the heat generated during the gasification of carbon into the reducing gas covers the necessary thermal needs of the process. The carbon required for heat also significantly depends on the degree of direct reduction.
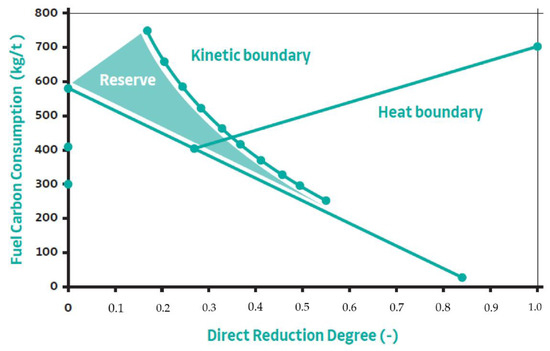
Figure 2.
The dependence of the specific consumption of reducing gas (carbon) on the degree of direct reduction.
Since indirect reduction is applied in the first phase of the blast furnace process, the extent of its course (with the long-term stable reactivity of the coke used) can be crucial for the resulting ratio of both types of reduction. Therefore, kinetic modelling of the course of indirect reduction of iron oxides plays a key role. This modelling result is the intersection of the thermal limit with the kinetic limit, determining the “optimal” degree of direct reduction rd,opt.
The optimal value of the coke’s reactivity can then be deduced from the optimal degree of direct reduction. Based on the innovative form of the CDR diagram shown in Figure 3, a technological analysis of the scope and effectiveness of individual technological measures can be performed to reduce the intensity of the fuel energy of the blast furnace process.
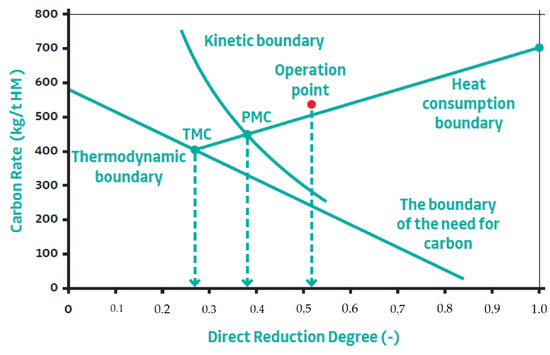
Figure 3.
A modified CDR diagram as the basis for technological control of blast furnace operation.
As part of the graphic output, it determines the practically achievable minimum coke consumption points (PMC) and theoretically achievable minimum coke consumption points (TMC). The use of the model enables the determination of a real reserve to reduce the amount of coke.
One of the basic functions of coke in a blast furnace is its ability to create sufficient space between the grains in the furnace, which is necessary for the flow of furnace gases and for the flow of liquid smelting products. This function can be decisive for coke consumption under certain conditions.
Therefore, it was highly desirable to develop procedures that included the effects of countercurrent gas conditions and the coke charge in the blast furnace when determining the theoretical minimum specific coke consumption.
The model algorithm principle uses Ergun equations to determine the conditions for the dynamic equilibrium of the countercurrent in the blast furnace, where the combustion gas flows from bottom to top and the coke and liquid smelting products (pig iron and slag) decrease in the opposite direction. If a certain limit value of the dynamic pressure of the gas is exceeded or the amount of flowing liquid products is excessive, the intermediate coke gaps are flooded.
The proposed mathematical model defines and describes the granulometric degradation of coke during its passage through the blast furnace. During its processing, knowledge about the behaviour of coke in a blast furnace, found in operating conditions and experimental work, was used. The mathematical model makes it possible to calculate the granulometric composition of the coke layer in the lower, critical part of the blast furnace, to determine the interstices of the “clean” coke layer, and to define the proportion of free spaces between the pieces found in the mass unit of coke. The model considers the effect of the specific amount of slag depending on the richness of the charge.
2.2. Mathematical Model of Coke Degradation in a Blast Furnace
To obtain an objective mathematical description of coke degradation during its descent in the blast furnace, we quantitatively compiled the original causal relationships that describe the degradation processes that act on coke in the blast furnace at VSB-TUO. Mathematical formulations were available for some of them, and for many, these dependencies were derived using available knowledge from the literature and from the results of experimental work.
Liquid smelting, consisting of slag and iron, flows in a countercurrent with the rising gas in the bosh and the top of the hearth. The flow of liquid phases reduces the free space between the coke pieces through which the gas flows.
The narrowing of the free space between the coke grains causes an increase in the velocity of the gas stream and its loss of pressure. The space between the coke pieces can be flooded, and the gas flow is interrupted by a large amount of liquid smelting products. This phenomenon can be manifested in cases where coke degradation reaches a point where the air-void content of the layer and, therefore, the extent of the free space between the pieces of coke are greatly reduced.
The coke charge of the furnace in its lower part consists of pieces of various sizes, with a significant proportion of small and fine grains that are indefinably distributed in the layer. Original causal relationships quantifying relevant events that take place in the blast furnace were compiled to develop an objective mathematical description of the gas flow and the decrease in the charge in the furnace with the simultaneous flow of liquid smelting products. Mathematical formulations were already available for some of them, but dependencies had to be derived for many others.
3. Results
3.1. Model Preparation Conditions
A summary of the main assumptions, arranged according to the logic of the model idea and the gradual application of degradation effects, is as follows:
- Coke changes its granulometric composition during loading and passing through a blast furnace. The result is a change in the bulk density of the coke and the air void content of the coke layer in the lower part of the furnace.
- The individual phases of coke degradation take place gradually and follow each other.
- Changes in coke granulometry caused by mechanical stress manifest themselves through fragmentation, breakage, and abrasion of the pieces; these changes are considered gradual.
- The volume by which the original volume of the coke pieces is reduced during the reaction of coke carbon with CO2 is proportional to the proportion of coke used for direct reduction.
- The reaction to the oxidation of coke carbon with CO2 takes place mainly on the surface of the pieces, resulting in a reduction in the apparent volume and size of the pieces. Upon descending the furnace, the reduced pieces approach each other until they touch each other
- The reaction of coke carbon with CO2 inside the pores results in a reduction in the apparent density of coke. The proportion of the reaction inside the pores in the total reaction of coke carbon with CO2 depends on temperature, coke porosity, and the shape of the pores.
- The reaction of coke carbon with CO2 on the surface of the pieces is manifested by the same reduction of the radial dimension of the piece, regardless of the original size.
- To calculate the reduction in the radial dimension, a spherical shape of the pieces and a uniform distribution according to their size in the entire range of granulometric groups are assumed.
- The following equation was derived for the decrease in apparent coke volume by reaction with CO2 (ΔV):
ΣVi − ΔV = ΣVi · (1 − Δd/di)3,
Vi—the original apparent volume of pieces of individual granulometric types
di—mean grain diameter
Δd—reduction of the radial dimension of the pieces
ΔV—decrease in apparent volume of coke during the reaction with CO2.
- 10.
- Abrasion of the damaged layers will also result in a further reduction in the radial dimension of the pieces in the individual groups. Similar to the reduction due to the reaction of coke carbon with CO2, the spherical shape of the pieces, their uniform size distribution over the entire range of the individual groups, and the same value of the reduction of the radial dimension of the pieces regardless of the original size are assumed here. Analogous assumptions also apply to the reduction of pieces by abrasion in the top part of the furnace.
- 11.
- The volume fraction of the surface layers of pieces disturbed by the reaction of coke carbon with CO2 depends on the proportion of reaction of coke carbon with CO2 inside the pores, the porosity of the input coke and its character, the reactivity of the coke mass, and increases in the volume fraction of a group by less than 10 mm.
- 12.
- As a result of the reduction in coke strength and the formation of cracks during high-temperature heating, some pieces of coke crack (along the cracks) and group 5 to 15 mm apart from the surface of larger pieces. The degree of high-temperature degradation depends on the temperature and its duration of action.
- 13.
- Iron carburization affects the reduction in the size of coke pieces. The proportion of carbon that is already dissolved in iron in the critical area of the bosh depends on the coke temperature in this part of the furnace.
3.2. Mathematical Model Structure
The model is based on the granulometric composition of the input coke, and the structure consists of the following sequence of changes:
- Change in granulometry due to fragmentation during loading
z1…..f1 (coke friability)
- Change in granulometry due to disintegration (breaking) of large pieces in the furnace top and furnace shaft
z2…..f2 (coke strength)
The character and course of disintegration (breakage) of large pieces of coke in the top and shaft of the furnace were derived on the basis of analogy with the course of coke degradation in the coke tank of the blast furnace. The proportion of broken and disintegrated pieces in both coarse-grained groups is characterised by a coefficient, the size of which was determined according to the above analogy.
For the disintegration of pieces over 80 mm, the assumption that the original pieces disintegrate into pieces of 60 to 80 mm and 20 to 40 mm in the ratio given by the third powers of the mean grain diameters of both classes was further applied, and the original relationships were derived. An analogous procedure also applies to the breakdown of pieces 60 to 80 mm and 40 to 60 mm.
- Change in granulometry due to abrasion in the furnace shaft
z3.....f3 (coke abrasion)
- Change in granulometry due to the reaction of coke carbon with CO2 on the surface of the pieces and carbonization of iron
z4…..f4
(degrees of direct reduction, porosity of coke, degree of carburization of pig iron)
- Change in granulometry due to coke surface rupture after reaction with CO2
z5…..f5
(degrees of direct reduction, proportion of the reaction of C with CO2 within the coke pieces, and coke porosity)
- Change in granulometry due to high-temperature decomposition of coke
z6…..f6 (coke temperatures in bosh)
- Determination of the interstices of the coke layer based on the resulting granulometric composition of the coke in the saddle
ε = f6 (granulometric composition of coke)
- Determination of the interstices of the real coke layer in the bosh
εr = f7
(coke interstices in bosh, coke density, amount of coke burned in tuyeres, specific amount of slag)
4. Discussion
The technological level indicator of blast furnace work characterises the degree of approximation of the actual specific consumption of coke to its theoretical average under the relevant production and raw material conditions for individual furnaces. The difference between the theoretical minimum and the actual specific consumption of coke characterises the internal technological reserve of the process.
A graphic assessment in the form of a CDR diagram has a different display according to different users; a similar method is used by BFI Düsseldorf [28] and ThyssenKrupp [29]. The ArcelorMittal group is also involved in the development of models for modelling processes in a blast furnace [30].
The foundations were laid by a leading expert within VŠB-TUO, Prof. Brož, whose original proposal for a mathematical model of the theoretical minimum specific consumption of coke was refined and refined by the scientific team led by prof. Bilík [10,25]. The original version of the model had previously been used in former Czechoslovakian blast furnace parts for annual technological analyses of blast furnace work. At present, the model is being modified for use in a specific blast furnace within the framework of a Czech metallurgical plant.
5. Conclusions
Today’s test methods make it possible to model the actual process of reduction in a blast furnace to a large extent. The models presented for the blast furnace process represent another level of mathematical formulation of the blast furnace process. In addition to the equations for the reaction rate and the rate of heat transfer under counterflow conditions, they also include the effects of the relatively slow progress of the raw materials on the temperature differences between the flowing gas and the cores of the reduced pieces of raw materials, on the speed of individual reactions, and on the degree of their approach to thermodynamic equilibrium.
The presented model is applied to a number of variant prognostic calculations. The theoretical minimum consumption of coke from the dynamic balance can be calculated in variants for different values of the direct and indirect reduction ratios. This allows the “breathability limit” to be determined in the CDR diagram. This is of fundamental importance in the use of alternative fuels in blast furnaces.
The use of the model enables the calculation/determination of the practically achievable minimum coke consumption (PMC), which is still about 20–40 kg higher than the theoretically achievable minimum coke consumption (TMC).
By using the model, the operation point can also be established—a real working point whose position relative to the PMC and TMC can be defined.
The model enables a forecast of the maximum possible replacement fuel seepage for a specific blast furnace.
Author Contributions
Conceptualization, J.B.; Methodology, S.J.; Project administration, A.K.; Validation, E.K.; Writing—review & editing, P.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research did not receive external funding.
Data Availability Statement
Not applicable.
Acknowledgments
The article was implemented with the support of the project “Czech-Polish exchange of experience with the adaptation of teaching for online tertiary education in the CZ-PL border region”, project reg. no.: CZ.11.4.120/0.0/0.0/16_013/0002594, which is co-financed by the European Fund for Regional Development within the INTERREG V-A Czech Republic—Poland programme through the 2014–2020 Microprojects Fund in Euroregion Silesia.
Conflicts of Interest
The authors declare no conflict to interest.
References
- Bartusch, H.; Ana María, F.S.; Magnus, F.; Frank, S.; Frank, S. Erhöhung der Energie- und Ressourceneffizienz und Reduzierung der Treibhausgasemissionen in der Eisen, Stahl und Zinkindustrie. Produktion und Energie; KIT Scientific Publishing: Karlsruhe, Germany, 2013; p. 190. ISBN 978-3-86644-857-5. [Google Scholar]
- Danloy, G. Modelling of the blast furnace internal state with MOGADOR. Rev. Métallurgie–CIT 2009, 106, 382–386. [Google Scholar] [CrossRef]
- Jeschar, R.; Bittner, H.G. A theoretical model coupling kinetic of ore reduction and coke gasification in blast furnaces. In Proceedings of the European Ironmaking Congress, Aachen, Germany, 14-17 September 1986; Volume 3, p. PII/1, Verlag Stahleisen. [Google Scholar]
- Tappeiner, T.; Kepplinger, W.L. Modell zur Ermittlung des Reduktionsmittelbedarf bei der Roheisenerzeugung. Stahl Eisen 2010, 5, 43–49. [Google Scholar]
- Lehmann, J. Thermodynamics, precipitation kinetic, coupled models development: Three main axes of research in physical chemistry at ArcelorMittal global r&d Maizieres process. Steel Res. Int. 2010, 81, 772–777. [Google Scholar]
- Kulinich, V.I. Thermodynamic Modeling of Blast-furnace Smelting of Hot Metal. Steel Transl. 2007, 37, 356–361. [Google Scholar] [CrossRef]
- Bernasowski, M.; Ledzki, A.; Stachura, R.; Klimczyk, A. Basic structure of the fuel rate optimization model and its practical use at the blast furnace technology. In Proceedings of the Metal 2014: International Conference on Metallurgy and Materials, Brno, Czech Republic, 21–23 May 2014; ISBN 978-80-87294-54-3. [Google Scholar]
- Li, M.; Wang, X.; Yao, H.; Saxén, H.; Yu, Y. Analysis of particle size distribution of coke on blast furnace belt using object detection. Processes 2022, 10, 1902. [Google Scholar] [CrossRef]
- Gasparini, V.M.; de Castro, L.F.A.; Quintas, A.C.B.; de Souza Moreira, V.E.; Viana, A.O.; Andrade, D.H.B. Thermo-chemical model for blast furnace process control with the prediction of carbon consumption. J. Mater. Res. Technol. 2017, 6, 220–225. [Google Scholar] [CrossRef]
- Roubicek, V.; Bilik, J.; Janik, I. Coke and ferrous raw quality for Ironmaking in the specific conditions of the Czech Rebublic. ICSTI/Ironmak. Conf. Proc. 1998, 57, 1679–1685. [Google Scholar]
- Bol’shakov, V.I.; Murav’eva, I.G.; Semenov, Y.S.; Shuliko, S.T.; Shumel’chik, E.I. Predicting the thermal state of the blast-furnace hearth. Steel Transl. 2009, 39, 402–405. [Google Scholar] [CrossRef]
- Liu, Y.; Shen, Y. Modelling and optimisation of biomass injection in ironmaking blast furnaces. Prog. Energy Combust. Sci. 2021, 87. [Google Scholar] [CrossRef]
- Li, Z.; Qi, Z.; Wang, Z.; Zhang, L.; Liang, D.; Dong, Q. Numerical investigation of coke oven gas (COG) injection into an ironmaking blast furnace (BF). Int. J. Hydrogen Energy 2022, 47, 31109–31128. [Google Scholar] [CrossRef]
- Pustejovska, P.; Tuma, J.; Stanek, V.; Kristal, J.; Jursova, S.; Bilik, J. Using a mathematical model of counter-current flow in a blast furnace to evaluate reducibility of iron-ore-bearing raw materials. Steel Res. Int. 2015, 86, 320–328. [Google Scholar] [CrossRef]
- Shatokha, V. Modeling of the effect of hydrogen injection on blast furnace operation and carbon dioxide emissions. Int. J. Miner. Metall. Mater. 2022, 29, 1851–1861. [Google Scholar] [CrossRef]
- Cardoso, W.; Di Felice, R.; Baptista, R. Mathematical Modelling to Predict Fuel Consumption in a Blast Furnace Using Artificial Neural Networks. In IEMAICLOUD 2021: International Conference on Intelligent Emerging Methods of Artificial Intelligence & Cloud Computing; Springer: Cham, Switzerland, 2021; pp. 1–10. [Google Scholar] [CrossRef]
- Venketesan, J.; Mrunmaya, K.P.; Ubayadullah, M.; Voona, S. Blast Furnace Mathematical Model to Evaluate the Impact of Variations in Process Parameters and its Effect on Fuel Rate & Energy Efficiency. Steel Tech. 2020, 14, 15–19. [Google Scholar]
- Wang, Q.; Liu, Z.; Tang, H.; Guo, Z. Experimental and Numerical Investigations on Charging Carbon Composite Briquettes in a Blast Furnace. Metals 2021, 11, 1669. [Google Scholar] [CrossRef]
- Jiang, D. Predictive Modeling of Blast Furnace Gas Utilization Rate Using Different Data Pre-Processing Methods. Metals 2022, 12, 535. [Google Scholar] [CrossRef]
- Bilík, J.; Schutzenhofer, W.; Hiebler, H. Einsatz der mathematischen modellierung in der reduktionsmetallurgie. Berg Hüttenmännische Mon. 1998, 143, 166–169. [Google Scholar]
- Bilík, J.; Schutzenhofer, W.; Lužný, R. Analytické modely vysokopecního pochodu v současné vysokopecní praxi. Hutnické Listy. LIV 1999, 7–8, 13–16. [Google Scholar]
- Brannbacka, J.; Torrkulla, J.; Saxen, H. Simple simulation model of blast furnace hearth. Ironmak. Steelmak. 2005, 32, 479–486. [Google Scholar] [CrossRef]
- Beppler, E.; Grosspietsch, K.H.; Hermann, W.; Lungen, H.B. Evaluation of coke quality in the past five decades to meet the requirements of the blast furnace operators. Cokemak. Int. 2000, 10, 54–61. [Google Scholar]
- Bilík, J.; Pustejovska, P.; Jursová, S. Modelování, Analýza a Predikce Pochodů Výroby Železa z Hlediska Současných Energetických a Ekologických Požadavků. Monografie; Akademické Nakladatelství CERM: Brno, Germany, 2013; p. 130. ISBN 978-80-7204-854-0. [Google Scholar]
- Kret, J.; Pustejovska, P. Predikce kvality surového železa s využitím expertních systémů. In Mozliwosc Ekonomizacji Produkcji w Wydzalach Wielkich Piecow i Spiekalni w Okrese Restrukturyzacji Hutnictwa; Miedzynarodowa Konferencja Naukowo-Techniczna: Warsaw, Poland, 1996; pp. 5–11. ISBN 83-87745-42-1. [Google Scholar]
- Babich, A.; Dieter, S.; Heinrich Wilhelm, G.; Kostas, M. Ironmaking (Textbook); RWTH Aachen University, Department of Ferrous Metallurgy, Wissenschaftsverlag Mainz in Aachen: Aachen, Germany, 2008; p. 402. ISBN 386-13-099-71. [Google Scholar]
- Gerdees, M.; Chaigneau, R.; Lingiardi, O.; Molenaar, R.; van Opbergen, R.; Sha, Y.; Warren, J. Modern Blast Furnace Ironmaking; Verlag Stahleisen GmbH: Düsseldorf, Germany, 2004; p. 118. ISBN 978-1-60750-040-7. [Google Scholar]
- Hauck, T. Neue Wege fűr die Verbesserte Prozessanfűhrung am Hochofen; BFI Kolloguium: Dűsseldorf, Germany, 2008. [Google Scholar]
- Thybas—Thyssen Blast Furnace Automation System. Firemní materiál Thyssen Krupp Stahl AG, Edition 2008.
- Zaimi, S.A. Blast furnace models development and application in ArcelorMittal group. Rev. Métallurgie–CIT 2009, 3, 105–111. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).