Multimode Wind Tunnel Flow Field System Monitoring Based on KPLS
Abstract
:1. Introduction
2. Methodology
2.1. Mean Matrix KPLS Regression Model
- Initialize u randomly.
- .
- .
- .
- Repeat steps 2–5 until convergence.
- .
- Return to 2, until all latent variables are calculated.
2.2. Mach Number Monitoring Based on KPLS
3. Illustration and Discussion
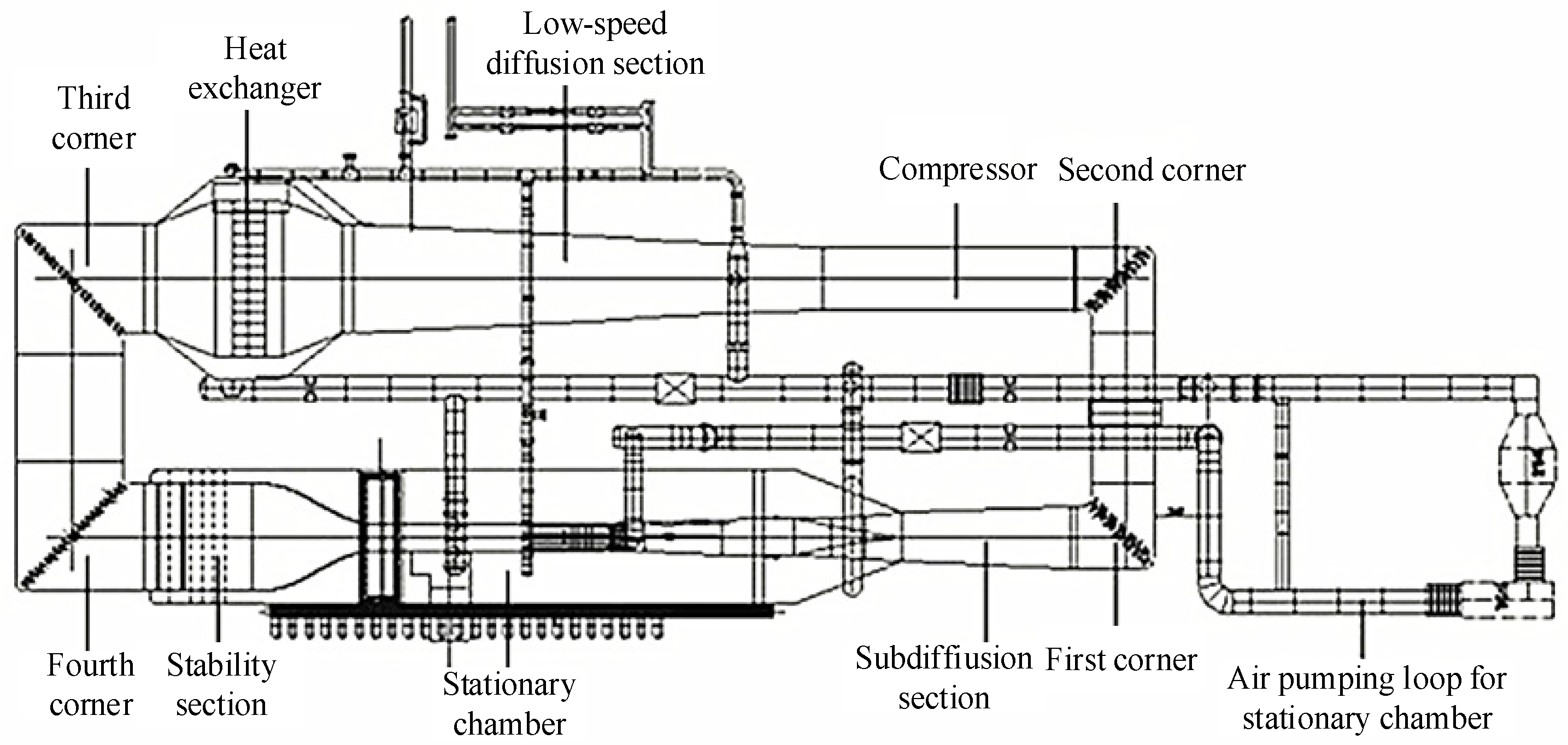
3.1. Wind Tunnel System
3.2. Mach Number Prediction Based on KPLS Model
- A.
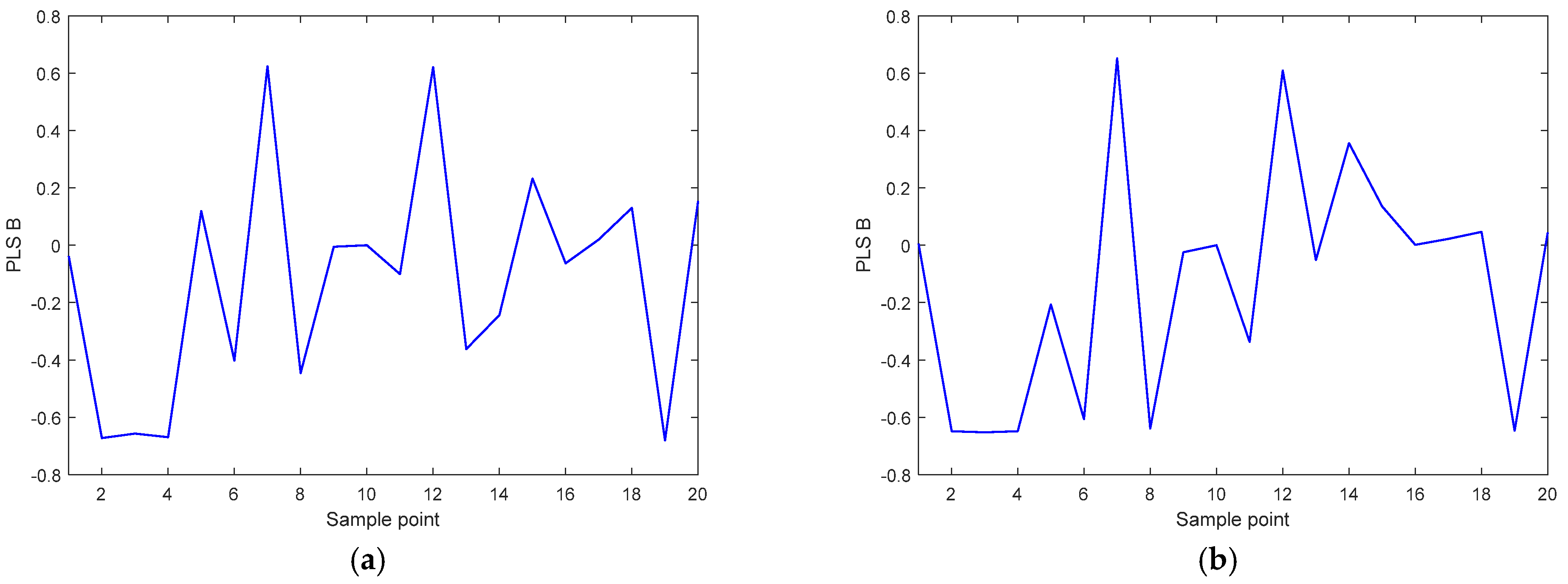
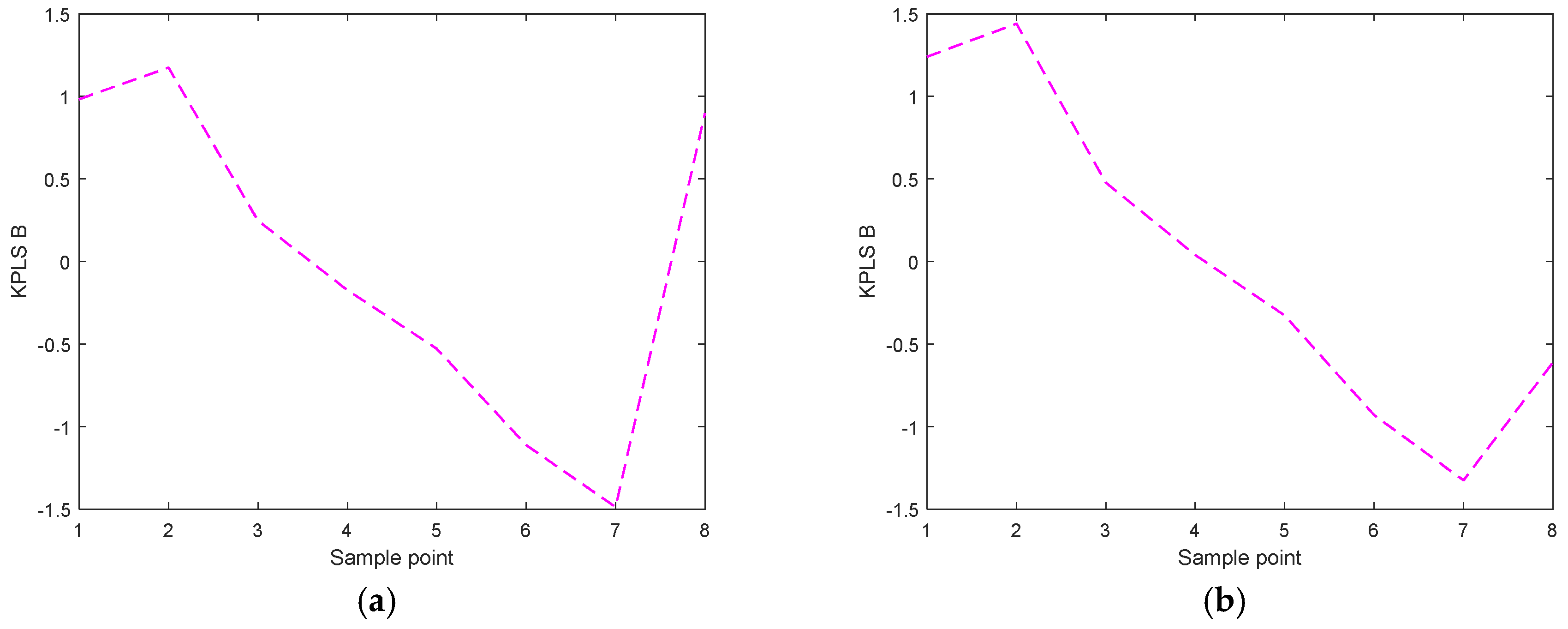
- Single-mode prediction
- B.
- Multimode prediction
3.3. Mach Number Monitoring
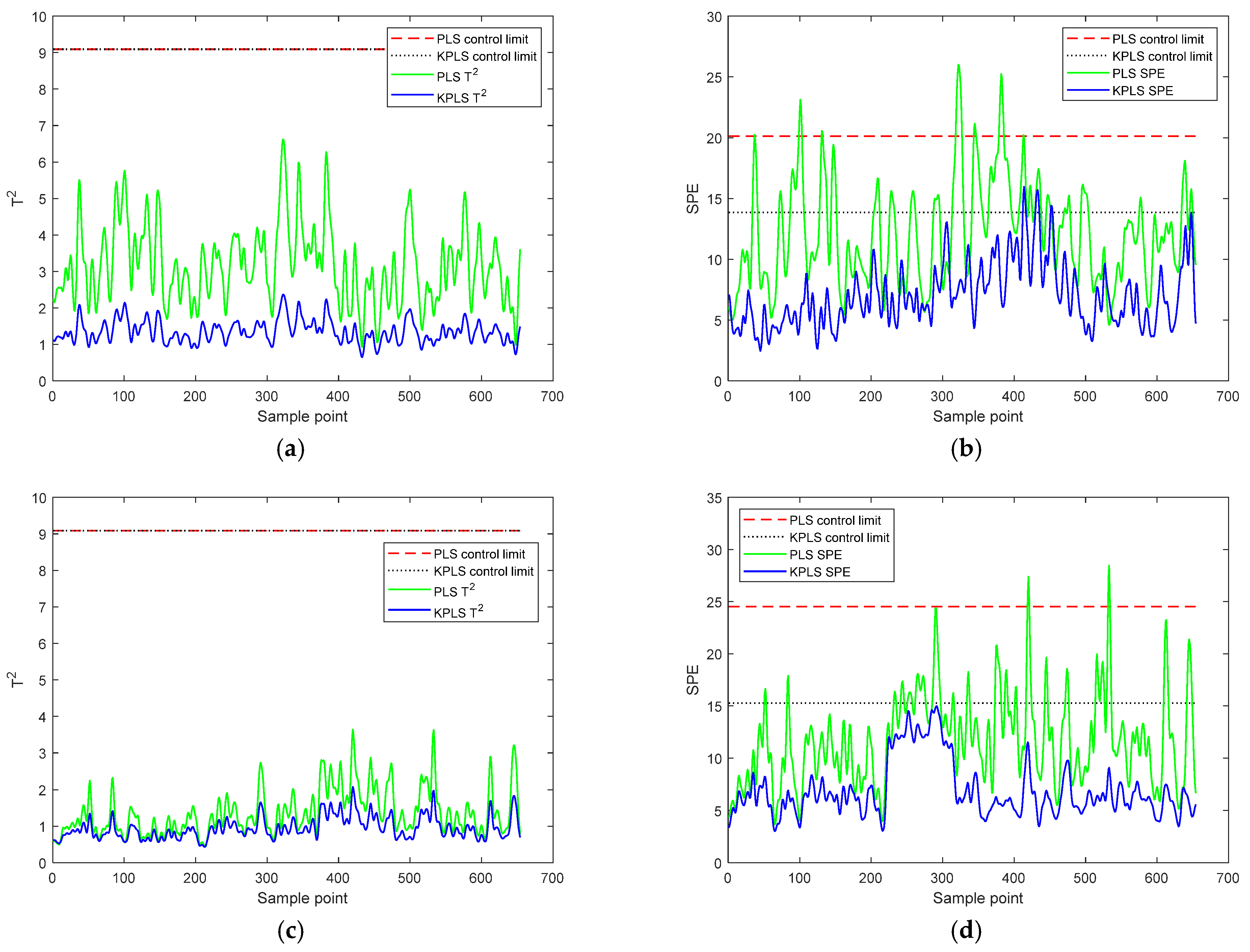
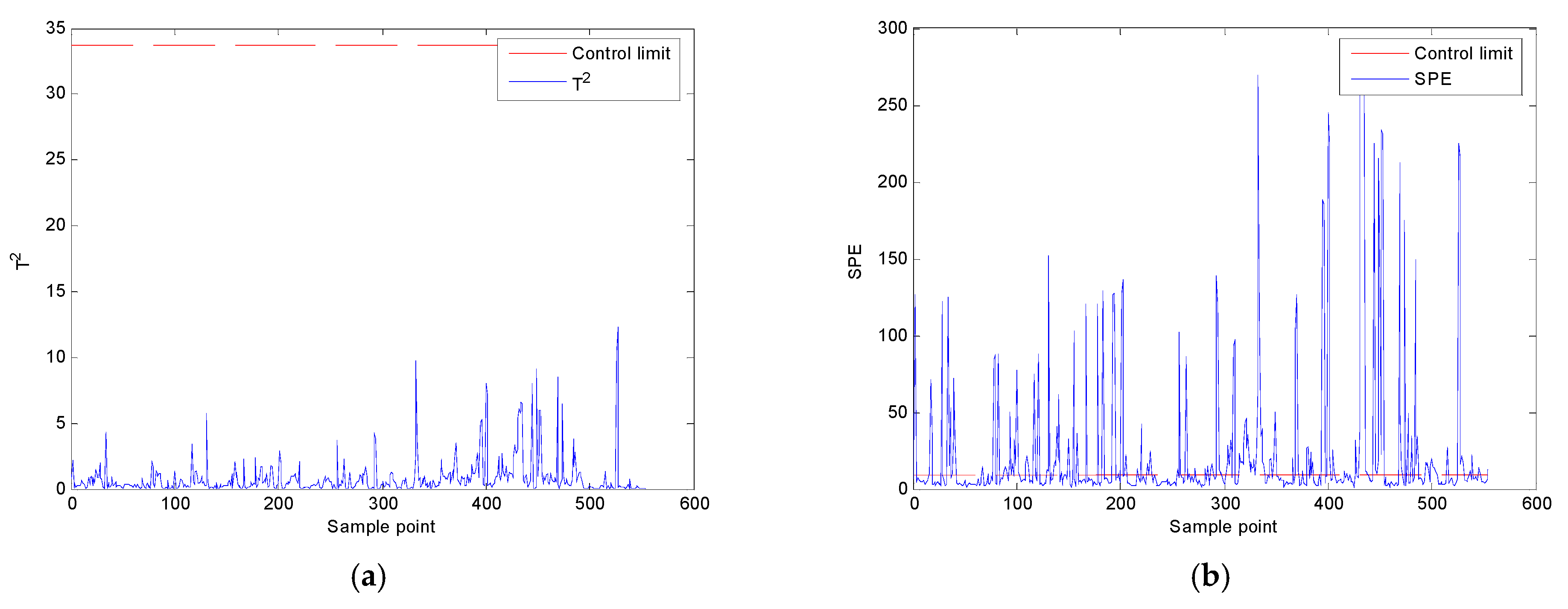
- A.
- Single-mode monitoring
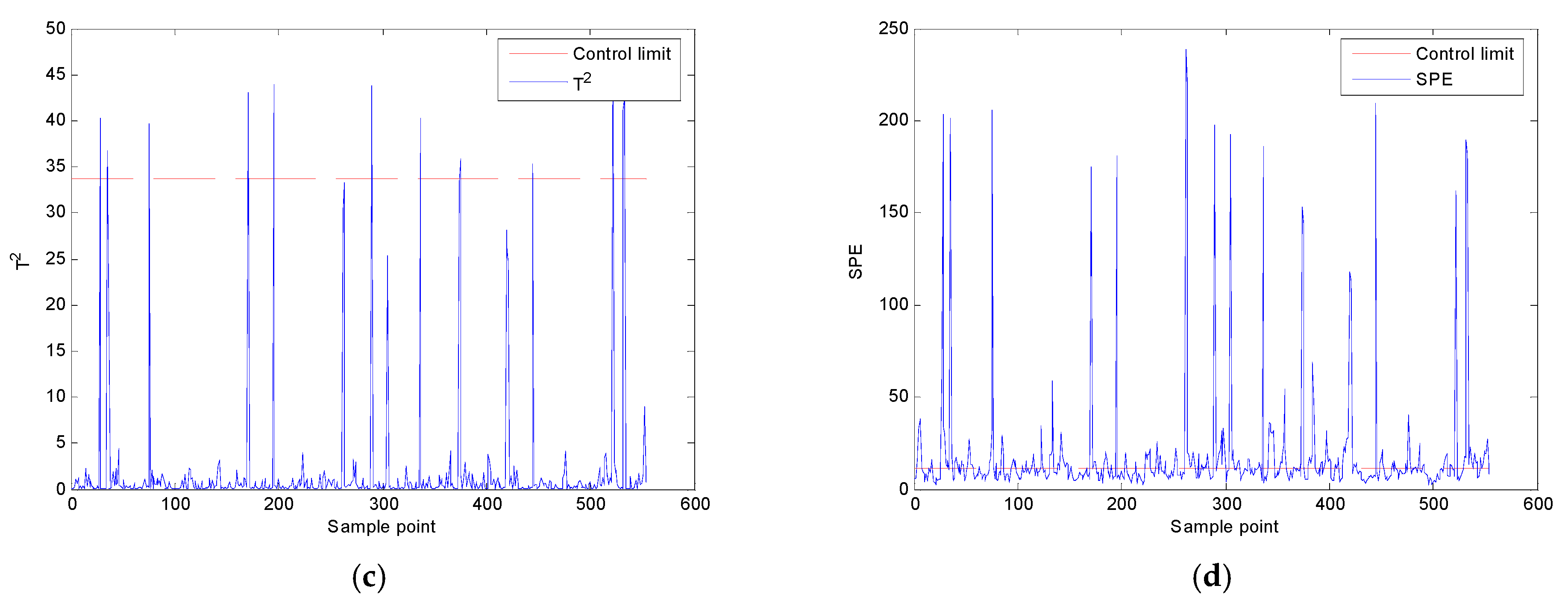
- B.
- Multimode monitoring
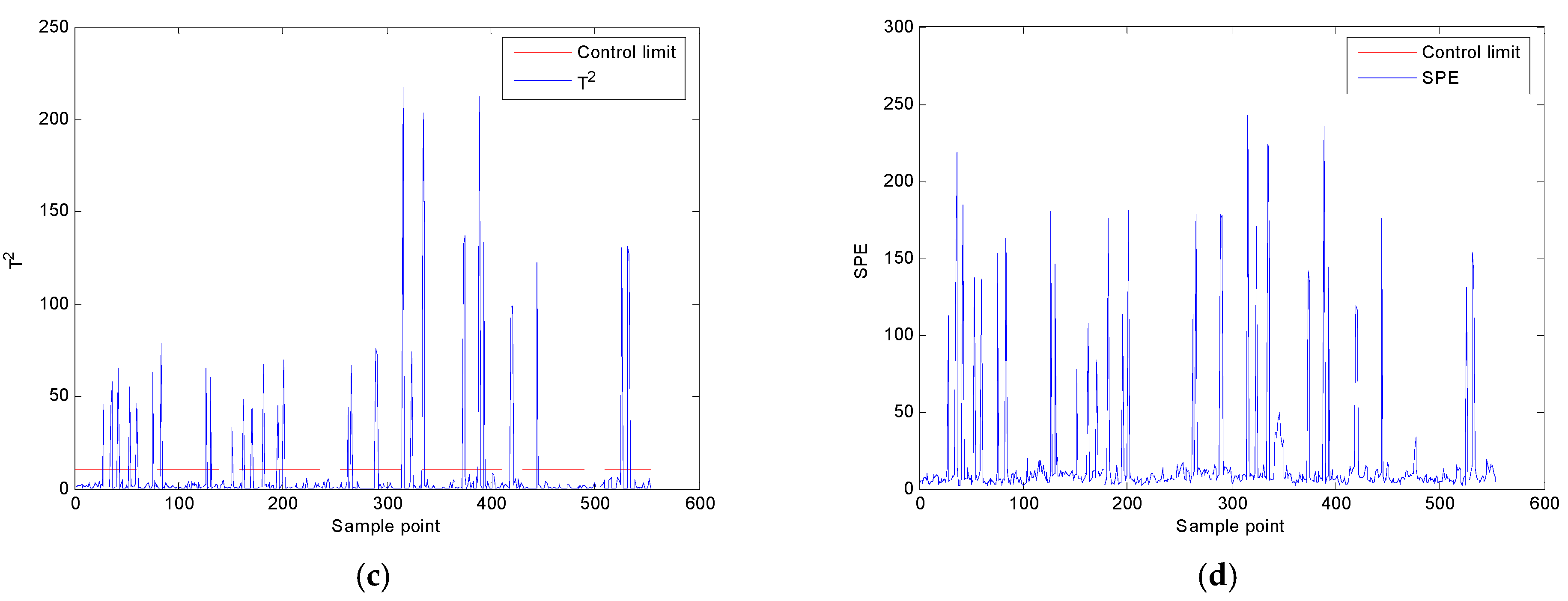
- C.
- Fault monitoring
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ju, X.F.; Wang, X.L.; Gao, Y. Wind tunnel flow field model predictive control based on multi-model. Control Eng. China 2018, 25, 1830–1835. [Google Scholar]
- Zhang, T.F.; Mao, Z.Z.; Yuan, P. Modeling of wind tunnel system based on nonlinear block-oriented model. Control Theory Appl. 2016, 33, 413–421. [Google Scholar]
- Yu, F.; Yuan, P.; Mao, Z.Z. Recursive identification of stagnation pressure in wind tunnel system. In Proceedings of the 35th Chinese Control Conference, Chengdu, China, 27–29 July 2016. [Google Scholar]
- Wang, X.J.; Yuan, P.; Mao, Z.Z.; Du, N. Wind tunnel Mach number prediction model based on random forest. Acta Aeronaut. Astronaut. Sin. 2016, 37, 1494–1505. [Google Scholar]
- Du, N.; Jiang, J.Y.; Yu, W.S.; Chen, L. Application of Ensemble Neural Network in the Prediction of Mach Number in 2.4 m Transonic Wind Tunnel. Ordnance Ind. Autom. 2015, 34, 56–58. [Google Scholar]
- Guo, J.; Zhang, R.; Cui, X.C.; Huang, X.; Zhao, L.P. Mach number prediction and analysis of multi-mode wind tunnel system. In Proceedings of the 2020 Chinese Automation Congress (CAC), Shanghai, China, 6–8 November 2020; pp. 6895–6900. [Google Scholar]
- Yuan, P.; Zhao, L.P. KPLS-based Mach number prediction for multi-mode wind tunnel flow system. Processes 2022, 10, 1718. [Google Scholar] [CrossRef]
- Geladi, P.; Kowalshi, B.R. Partial least squares regression: A tutorial. Anal. Chim. Acta 1986, 185, 1–17. [Google Scholar] [CrossRef]
- Kourti, T.; MacGregor, J.F. Process analysis, monitoring and diagnosis, using multivariate projection methods. Chemom. Intell. Lab. Syst. 1995, 28, 3–21. [Google Scholar] [CrossRef]
- Wang, X.Z. Data Mining and Knowledge Discovery for Process Monitoring and Control; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Gurden, S.P.; Westerhuis, J.A.; Bro, R.; Smilde, A.K. A comparison of multiway regression and scaling methods. Chemom. Intell. Lab. Syst. 2001, 59, 121–136. [Google Scholar] [CrossRef]
- Wang, H.W. Partial Least Squares Regression Method and Its Application; National Defense Industry Press: Beijing, China, 1999. [Google Scholar]
- Nomikos, P.; MacGregor, J.F. Multi-way partial least squares in monitoring batch processes. Chemom. Intell. Lab. Syst. 1995, 30, 97–108. [Google Scholar] [CrossRef]
- Wangen, L.E.; Kowalski, B.R. A multiblock partial least squares algorithm for investigating complex chemical systems. J. Chemom. 1988, 3, 3–20. [Google Scholar] [CrossRef]
- MacGregor, J.F.; Jackle, C.; Kiparissides, C. Process monitoring and diagnosis by multiblock PLS methods. AIChE J. 1994, 40, 826–838. [Google Scholar] [CrossRef]
- Rosipal, R.; Trejo, L.J. Kernel partial least squares regression in reproducing kernel Hilbert space. J. Mach. Learn. Res. 2001, 2, 97–123. [Google Scholar]
- Zhang, X.; Kano, M.; Li, Y. Locally weighted kernel partial least squares regression based on sparse nonlinear features for virtual sensing of nonlinear time-varying processes. Comput. Chem. Eng. 2017, 104, 164–171. [Google Scholar] [CrossRef]
- Lee, J.M.; Yoo, C.K.; Sang, W.C.; Vanrolleghem, P.A.; Lee, I.B. Nonlinear process monitoring using kernel principal component analysis. Chem. Eng. Sci. 2004, 59, 223–234. [Google Scholar] [CrossRef]
- Zhou, P.; Liu, J.P.; Liang, M.Y.; Zhang, R.Y. KPLS robust reconstruction error based monitoring and anomaly dentification of fuel ratio in blast furnace ironmaking. Acta Autom. Sin. 2021, 47, 1661–1671. [Google Scholar]
- Jia, R.D.; Mao, Z.Z.; Wang, F.L. KPLS model based product quality control for batch processes. CIESC J. 2013, 64, 1332–1339. [Google Scholar]
- Lu, N.Y.; Gao, F.R. Stage-based process analysis and quality prediction for batch processes. Ind. Eng. Chem. Res. 2005, 44, 3547–3555. [Google Scholar] [CrossRef]
- Jategaonkar, R. Flight Vehicle System Identification: A Time Domain Methodology; AIAA: Reston VA, USA, 2015. [Google Scholar]






| No. | Process Variable | Unit |
|---|---|---|
| 1 | Total pressure | Bar |
| 2 | Stable static pressure | Bar |
| 3 | Test static pressure | Bar |
| 4 | Outlet static pressure | Bar |
| 5 | Temperature | °C |
| 6 | Humidity | % |
| 7 | Test section flow | m3/s |
| 8 | Attack angle | ° |
| 9 | Speed | m/s |
| 10 | Blade angle | ° |
| 11 | Main output pressure | Bar |
| 12 | Main inlet pressure | Bar |
| 13 | Main output temperature | °C |
| 14 | Main inlet temperature | °C |
| 15 | Auxiliary angle | ° |
| 16 | Auxiliary inlet pressure | Bar |
| 17 | Auxiliary output temperature | °C |
| 18 | Mass flow of auxiliary outlet | m3/s |
| 19 | Mass flow of auxiliary inlet | m3/s |
| 20 | Auxiliary gas flow | m3/s |
| Data Blocks | Mach Number | Speed | Initial Attack Angle | Target Attack Angle | Attack Angle Step | Mode |
|---|---|---|---|---|---|---|
| 1 | 0.7813 | 1800 | −4 | −2 | 2 | Mode 1 |
| 2 | 0.7831 | 1800 | −2 | 0 | 2 | |
| 3 | 0.7803 | 1800 | 0 | 2 | 2 | |
| 4 | 0.7726 | 1800 | 2 | 4 | 2 | |
| 5 | 0.7684 | 1800 | 4 | 5 | 1 | Mode 2 |
| 6 | 0.7647 | 1800 | 5 | 6 | 1 | |
| 7 | 0.7613 | 1800 | 6 | 7 | 1 | |
| 8 | 0.7581 | 1800 | 7 | 8 | 1 | |
| 9 | 0.7539 | 1800 | 8 | 9 | 1 |
| Cases | Mean Matrix PLS Model | Mean Matrix KPLS Model |
|---|---|---|
| Test data 1 using the single-mode model | 2.730 × 10−3 | 0.204 × 10−3 |
| Test data 2 using the single-mode model | 1.781 × 10−3 | 0.251 × 10−3 |
| Test data 1 using the multimode model | 2.595 × 10−3 | 0.254 × 10−3 |
| Test data 2 using the multimode model | 2.878 × 10−3 | 0.357 × 10−3 |
| Cases | Mean Matrix PLS Model | Mean Matrix KPLS Model |
|---|---|---|
| Test data 1 using the single-mode model | 0.3938 | 0.9921 |
| Test data 2 using the single-mode model | 0.4123 | 0.9994 |
| Test data 1 using the multimode model | 0.4425 | 0.9978 |
| Test data 2 using the multimode model | 0.4425 | 0.9961 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, J.; Zhang, R.; Cui, X.; Ma, W.; Zhao, L. Multimode Wind Tunnel Flow Field System Monitoring Based on KPLS. Processes 2023, 11, 178. https://doi.org/10.3390/pr11010178
Guo J, Zhang R, Cui X, Ma W, Zhao L. Multimode Wind Tunnel Flow Field System Monitoring Based on KPLS. Processes. 2023; 11(1):178. https://doi.org/10.3390/pr11010178
Chicago/Turabian StyleGuo, Jin, Ran Zhang, Xiaochun Cui, Weitong Ma, and Luping Zhao. 2023. "Multimode Wind Tunnel Flow Field System Monitoring Based on KPLS" Processes 11, no. 1: 178. https://doi.org/10.3390/pr11010178
APA StyleGuo, J., Zhang, R., Cui, X., Ma, W., & Zhao, L. (2023). Multimode Wind Tunnel Flow Field System Monitoring Based on KPLS. Processes, 11(1), 178. https://doi.org/10.3390/pr11010178







