Highlights
- What are the main findings?
- Machine learning algorithms perform more efficiently than deep learning methods in classifying gas-liquid flow regimes in pipelines.
- Extreme gradient boosting is the best-performing algorithm for the six-class flow regime classification problem.
- What is the implication of the main findings?
- The current model can be implemented for the accurate classification of gas-liquid flow patterns in industrial pipelines with greater confidence.
Abstract
Gas–liquid flow is a significant phenomenon in various engineering applications, such as in nuclear reactors, power plants, chemical industries, and petroleum industries. The prediction of the flow patterns is of great importance for designing and analyzing the operations of two-phase pipeline systems. The traditional numerical and empirical methods that have been used for the prediction are known to result in a high inaccuracy for scale-up processes. That is why various artificial intelligence-based (AI-based) methodologies are being applied, at present, to predict the gas–liquid flow regimes. We focused in the current study on a thorough comparative analysis of machine learning (ML) and deep learning (DL) in predicting the flow regimes with the application of a diverse set of ML and DL frameworks to a database comprising 11,837 data points, which were collected from thirteen independent experiments. During the pre-processing, the big data analysis was performed to analyze the correlations among the parameters and extract important features. The comparative analysis of the AI-based models’ performances was conducted using precision, recall, F1-score, accuracy, Cohen’s kappa, and receiver operating characteristics curves. The extreme gradient boosting method was identified as the optimum model for predicting the two-phase flow regimes in inclined or horizontal pipelines.
1. Introduction
Gas–liquid two-phase flow in horizontal or inclined pipelines is one of the common issues encountered in several engineering applications, such as nuclear reactors, power plants, chemical industries, and petroleum industries. It is a complicated phenomenon due to the different types of phasic interactions, for example, interfacial structures, flooding, and deposition. A two-phase flow system can generate a number of geometrical and operational shapes, which are very important in determining the system properties [1]. Predicting the flow regime is a complex process as its formation is dependent on different process parameters. However, identification and prediction of the flow patterns created by the fluids are of great importance in analyzing and designing the operations of the pipeline systems used for the transmission of the gas–liquid multiphase flow. Most of the numerical and empirical methods that have been traditionally utilized to predict the flow patterns are capable of providing reasonably accurate predictions for the laboratory scale operations. Using such models to scale-up a lab-scale application to a field-level operation inevitably results in unknown degrees of uncertainties, i.e., imprecisions [2,3,4,5]. Different artificial intelligence-based (AI-based) modelling approaches have been previously adopted to minimize these prediction errors [6,7,8,9,10,11,12]. For the present study, the focus was on analyzing the comparative performance of machine learning (ML) and deep learning (DL) in predicting the two-phase flow regimes.
The multiphase flow patterns are usually detected by either visual observation or processing flow signals [13]. Even though the gas–liquid flow regimes are known to be strong functions of fluid properties, flow rates, and tube geometries, no universal functional relationship has been established as of now. That is, a flow regime map that was developed using lab-scale data cannot be used directly for designing field-scale pipeline systems. Only a prospective flow regime can be determined from the existing data and it should be modified using the pilot-scale data to establish a finalized flow regime map. In certain industrial operations, such as multiple pipe passages in oil-well sites or power plants, it is difficult, if not impossible, to measure the flow rates accurately. This kind of measurement requires involving expensive and complex multiphase flowmeter technology that is used to measure the critical flow attributes by integrating nodal analysis or data-driven methods with the measurement devices, such as a gamma-ray densitometer, Venturi meter, dual gamma-ray detector, and infra-red spectroscopic meter. Therefore, the automatic flow regime identification using ML models has attracted considerable research interest.
The gas–liquid two-phase flow regimes were classified in upward vertical pipes based on an experimental study [14]. The basic flow patterns were categorized as bubble, slug, churn, and annular flows. Later models were developed to identify the transition boundaries between these four basic flow regimes [15]. Compared to vertical and horizontal flow, fewer studies have been carried out on two-phase flow in inclined pipes. In one of the earliest studies that covered flow pattern classification in inclined pipes, the two-phase flow regimes were classified into the major categories of dispersed, stratified, intermittent, and annular bubbles [16,17]. They also proposed a unified model for the whole range of upward and downward pipe inclinations. Two-phase flows in a large pipe with a diameter of 15 centimeters were investigated by varying its inclinations from 0° (vertical) to 92° [18]. The flow pattern maps for water/gas, oil/water, and oil/water/gas systems were also generated as part of this study. A unified model that can predict liquid holdup, slug characteristics, pressure gradient, and flow patterns in upward and downward inclined pipes was proposed later [19]. The model was validated with experimental observations.
Traditionally, the two-phase flow regimes were identified directly through visual observation obtained with a camera or other imaging techniques [13,20]. However, the reliability of this method depends on the subjective judgement of the observer, particularly for flow pattern transitions [21]. Therefore, the method is also known as the subjective method. Conversely, in the objective or indirect determination method, the flow regimes are identified based on flow signal processing, statistical analysis, or experimentally measured raw data. The objective methods can be manual and automatic. Experiments are performed in manual methods to obtain data, which are then analyzed to extract features that are typical of each flow regime and the flow regimes are identified based on those features. For example, slug, plug, and separated flow regimes were identified by measuring the maximum velocity, maximum velocity difference ratio, and other parameters using ultrasound Doppler velocimetry (UDV) [22]. A flow regime map was proposed based on the image-processing techniques to calculate the void fraction and the corresponding probability density function (PDF) from the images recorded with a camera [23]. The characteristics of different flow regimes were obtained by employing the pressure and conductivity signals measurement, PDF, fast Fourier transform (FFT), and standard deviations (STD) analysis [24]. However, a significant amount of data needs to be analyzed and processed to find the suitable features of parameters for an accurate flow regime identification. Analyzing the difference between different flow regimes requires greater effort. Therefore, the manual determination method has a lower identification efficiency, which hinders its wider applications.
The development of AI facilitated the adoption of ML in the identification of two-phase flow regimes [25,26,27]. It utilizes the experimental data to realize and identify the flow regimes automatically. Application of ML for data classification is typically conducted in three main steps:
- (1)
- Data acquisition and pre-processing;
- (2)
- Feature extraction;
- (3)
- Model training and testing.
The ML method can further be divided into two categories:
- (1)
- Unsupervised learning;
- (2)
- Supervised learning.
In the unsupervised method, pre-existing labels are not required by the input data. Thereby, it eliminates the errors caused by the subjective judgement in classifying the flow regimes manually. An example of a typical unsupervised ML for two-phase flow regime identification is the self-organizing map-based (SOM-based) artificial neural network (ANN) [28,29]. SOM-ANN can provide greater accuracy by using PDF, such as statistical features extracted from void fraction signals, impedance meter signals, or statistical pixel features extracted from images for flow regime identification [30,31,32]. For supervised learning, input and output data pairs are contained in the training database. Flow regimes are considered as output data, which are determined by the researcher. One of the predominant supervised learning method is the supervised neural network, which is widely adopted for two-phase flow regime identification [21]. Neural networks can understand intricate relationships between input and output datasets, independent of the complex physics. Various types of neural networks, such as the back-propagation neural network (BPNN), radial basis function network (RBFN), and probabilistic neural network (PNN) were used for flow regime identification in the field of gas–liquid multiphase flow [33,34,35,36]. Attempts were also undertaken to capture the intricate input–output relationships that represent complex multiphase-flow dynamics by using physics-informed neural networks (PINNs) and interaction neural networks (INNs) [37,38]. PINNs incorporate numerical solvers for the main equations of state into the loss function optimization, while INNs learn physics-based representations of spatio-temporal fluid dynamics and interactions with governing medium when modelled and encoded as network graphs. However, the implementation of such complex algorithms is computationally expensive. Another effective classification algorithm is a support vector machine (SVM) that classifies data by finding linear decision boundaries or hyperplanes. This algorithm can be appropriately trained for two-phase flow regime identification by using different features, such as ultrasonic Doppler signals, ECT signals, or recorded images [25,39,40,41,42].
An ANN model was employed to determine flow patterns in horizontal air–water flows in one of the earliest studies on two-phase flow regime prediction with ML [43]. It was trained by stochastic features derived from turbulent absolute pressure signals under 366 measurements. The flow patterns identified by the network were claimed to be consistent with visual observations. Another ANN model was found to produce effective predictions based on conductivity probe signals [44]. ANN model was also developed using the measurements of an electrical resistivity probe for identifying the flow regimes to achieve a prediction accuracy of 96% [45]. A similar accuracy was attained by using power spectral density (PSD) from pressure difference data as inputs to train the ANN model [46]. The ANN model provided the best performance with a back-propagation algorithm in predicting the flow regimes in vertical two-phase flow tests, where two conductivity probes were installed for input data collections [47]. An ANN model capable of producing 80% accurate predictions was developed by extracting acoustic attenuation data as inputs from vertical oil-continuous multiphase flows [48]. By using signals from an ultrasonic Doppler sensor as inputs, an ANN model was trained and it scored 87–96% accuracy in flow patterns testing against a multilayer perceptron neural network [49]. The gas–liquid flow regimes were classified into three major categories of unstable, irregular, and stable flow regime using a SVM classifier and taking the input variables from the combination of multiple differential pressure signals at the different positions of a riser [50]. A visualization experiment was performed in swirling gas–liquid flow where the liquid holdup was measured with the image processing technique [51]. The data were statistically analyzed using PDF and cumulative PDF (CPDF). The CPDF was then utilized along with a self-organizing neural network (SONN) to develop the swirling flow regimes maps. A neural network was used based on the multi-scale wavelet analysis of differential pressure signal to investigate the recognition of two-phase flow regimes in a pipeline-riser system [52]. ANN was also applied on the dimensionless variables to develop a model by analyzing 9029 datasets [27,53]. The predicting accuracy was significantly improved by using ML on the dimensionless variables.
A new method was proposed for the quantitative two-dimensional assessment of fluid mixing in slug flow using the volume of fraction (VOF) algorithm [54]. The method could quantitatively distinguish the differences in the fluid-mixing capabilities among the systems. Both SVM and ANN were used to recognize stable flow and severe slugging in a pipeline-riser system [55]. The experiment used accelerometer signals for differentiating the flow regimes. The neural network was adopted to identify the four flow patterns of the stable state, two types of severe slugging, and an irregular transition state between severe slugging and dual-frequency severe slugging. Six different algorithms were tested to analyze the data obtained from two-phase experiments conducted using a horizontal 30 mm pipeline [56]. All the evaluated algorithms were reported to provide over 90% recognition accuracies. It was recommended to use the signals from scintillation detectors in gamma-ray absorption as inputs for creating ML models. While applying multiple ML algorithms in classifying two-phase flow regimes based on the measurement of pressure drops, the recognition rate of the flow regimes was found to be influenced by the positions of the pressure sensors in a 1657 m long pipeline consisting of horizontal, vertical, inclined, and S-shaped riser section [57,58,59].
The ML provides potential solutions in non-linear systems by generating its own rules for learned examples. One of its branches is DL that was developed by assembling the connected nodes comparable to the arrangement of neurons in biological systems. Similar to ML models, different DL models, such as convolutional neural network (CNN), fully convolutional network (FCN), theory guided neural network (TgNN), and deep neural network (DNN) were applied in classifying gas–liquid flow regimes based on the process conditions [60,61,62,63,64,65]. Table 1 summarizes a list of related studies on flow regime identification with ML and DL.

Table 1.
Summary of ML applications to predict gas–liquid two-phase flow regimes.
Even though a number of studies were conducted earlier in the field of classifying gas–liquid two-phase flow regimes, a significant fraction of those investigations targeted similar types of flow patterns. The ML models were trained by feeding input features generated from the signals of advanced measuring instruments. The majority of the previous studies employed different types of ANN and SVM for automatic flow regime identification. In most cases, the process of selecting the ML model was not validated; rather, the process was subjectively dependent on the features of the selected algorithm. Only a few of the previous studies reported the details of the validation. However, they compared limited sets of analogous models’ performances for the validations. A thorough comparative study with the application of ML and DL models for identifying gas–liquid flow regimes was not focused earlier. It should also be mentioned that the sizes of the experimentally measured data samples that were used for the previous studies were typically small. In the present study, a diverse set of algorithms were applied on a large dataset in predicting two-phase flow regimes to identify the best performer. The best performing algorithm was then applied to classify the flow regimes based on input parameters. The research contributions of this study are as follows:
- (1)
- The effectivity of the state-of-the-art ML models for classifying flow regime patterns into three different classification frameworks were investigated for the original dataset without any attempt of incorporating artificial data points in order to balance the class distribution.
- (2)
- The database used for the current study comprises 11,837 experimental measurements.
- (3)
- Six ML and three DL frameworks were designed and tested to model the flow patterns.
- (4)
- The feature importance analysis was performed thoroughly.
- (5)
- The best performing model was compared to the relevant models available in the literature.
2. Materials and Methods
2.1. Data Classification
The current database was compiled based on the results of 12 different experimental studies [53,66,67]. The experiments were conducted in different geographical locations around the world, starting from 1982. The major fraction of the current database was collected from 10 independent experimental investigations [53]. Two other sets of experiments were conducted using similar setups [66,67]. The details of the data with statistics are presented in Table 2. The current database consists of 11,837 data points (DP) with six basic flow regime features:

Table 2.
Summary of the experiments conducted to produce the current database.
- (1)
- Dispersed bubble (DB): 830 DP;
- (2)
- Stratified smooth (SS): 638 DP;
- (3)
- Stratified wavy (SW): 1516 DP;
- (4)
- Annular (A): 2138 DP;
- (5)
- Intermittent (I): 6354 DP;
- (6)
- Bubble (B): 362 DP.
We further classified the data points by aggregating the categorization into three and two classes based on the flow characteristics. In a three-class problem, the ‘SS’, ‘SW’, and ‘A’ are combined to form the ‘stratified flow’ (‘ST’) class, the ‘DB’ and ‘B’ classes are aggregated to form the ‘dispersed flow’ (‘DS’) class. Using this categorization, 4292 samples belong to ‘ST’, the ‘DS’ class has 1192 samples, and the ‘I’ class has 6354 samples. For the two-class problem, all the classes except ‘I’ (intermittent flow) are combined to form the ‘non-I’ (non-intermittent flow) regime. The ‘non-I’ class has 5484 samples, while the ‘I’ class has 6354 samples. The distributions of flow regime samples for six, three, and two class problems are depicted in Figure 1.
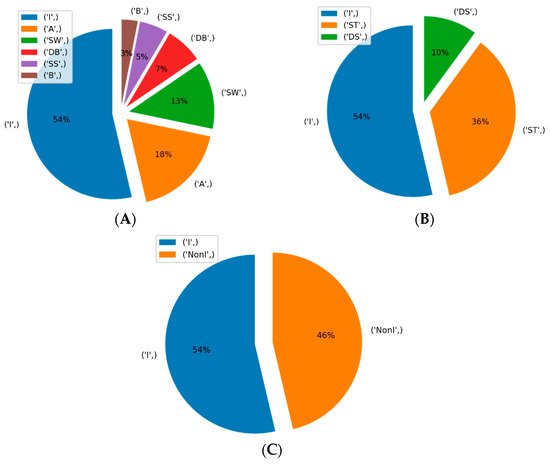
Figure 1.
(A) Class distribution of flow patterns for six classes; (B) Class distribution of flow patterns for three classes (ST stands for segregated flow, ST = SS + SW + A; DS stands for dispersed flow, DS = DB + B; I denotes intermittent flow); (C) Class distribution of flow patterns for two classes (Non-I denotes non-Intermittent flow, Non-I = SS + SW + A + DB + B).
2.2. Feature Normalization
Data normalization is an important step in feature pre-processing. The dataset was normalized for the current study using z-score standardization. It enables different features to be represented on the same scale. Each column, i.e., feature, in the dataset is normalized such that the mean and standard deviation of all the values become zero (0) and one (1), respectively. The z-score normalization of the features is expressed with , where, is the new normalized value, x is the original value, is the mean of the column, and is the standard deviation of the column. A positive normalized value indicates the data are above the mean, whereas a negative value indicates that the corresponding data are below the mean.
2.3. Feature Relevance and Importance Analysis
We performed feature importance analysis using two different techniques:
- (a)
- Feature importance analysis by extra tree (ET) classifier;
- (b)
- Principle component analysis.
The ET classifier performs feature selection while fitting the data to the model. It assigns the numerical importance in the range between 0 and 1 to the features playing the most significant role in predicting the output labels. The reported feature importance scores by the ET classifier are listed in Figure 2 in descending order. The heat map, as presented in Figure 3, shows the output of the principle component analysis (PCA) of flow-regime features.
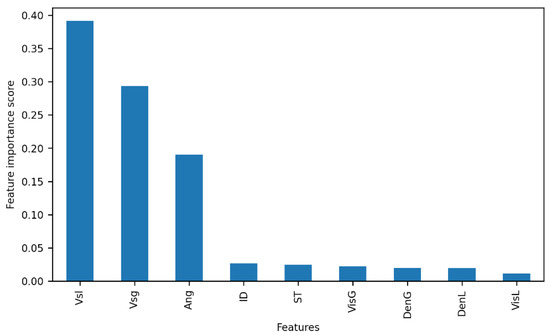
Figure 2.
Feature plot ranked by ET classifier reported importance score.
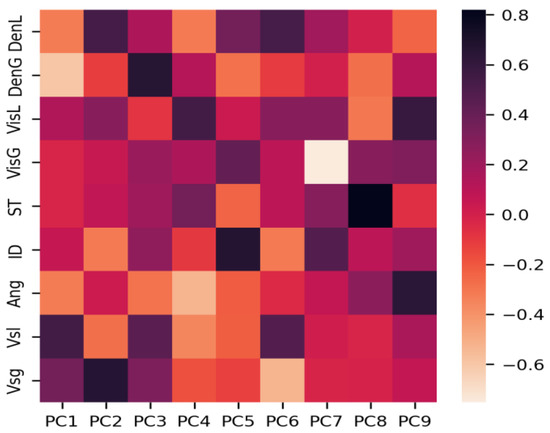
Figure 3.
The heat map of principle component analysis of flow-regime features. The correlations between principle components and feature variables are indicated with the color palette in the heat map.
Analyzing the relationships among features and outcome variable(s) is an essential step for ML modelling. It is usually followed by the feature importance study. The features that correlate well with the outcomes have a higher probability to be found as important predictors. These features also reveal the linearity nature of the problem. Therefore, the correlation between the flow regime features and flow pattern is analyzed, followed by the feature selection step. The heat map that is presented in Figure 4 shows the outcomes of the correlation coefficient analysis using Pearson’s method. The higher the correlation, the stronger the linear relationship among the variables. The positive correlation indicates the values of the variables are developing in the same direction, whereas the negative correlation indicates the development to go in the opposite direction. The correlation coefficient range [−0.27, 0.20], in the resulting analysis, indicates that a weak linear trend exists between the features and the flow pattern outcome. A pair-plot analysis was also performed using ET classifier reported top four features (Figure 5). As an exploratory data analysis technique, the pair-plot is used to explain the relationship between the variables and the univariate distribution for each attribute is shown as a histogram in the main-diagonal subplots. This pair-plot analysis indicates that the assumption of linearity among features in the context of flow pattern multi-class outcome is not practical, rather that the features are non-linearly related.
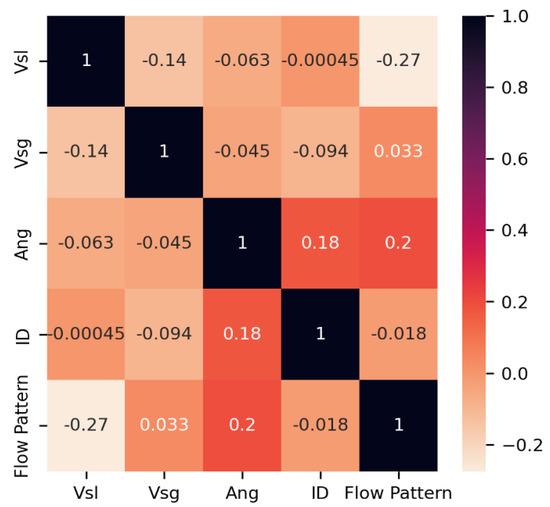
Figure 4.
Heat map of correlation coefficient analysis between flow patterns and flow regime experimental features. Vsl, Vsg, Ang, and ID represent the superficial velocities of liquid, gas, angular inclinations, and pipe diameter, respectively.
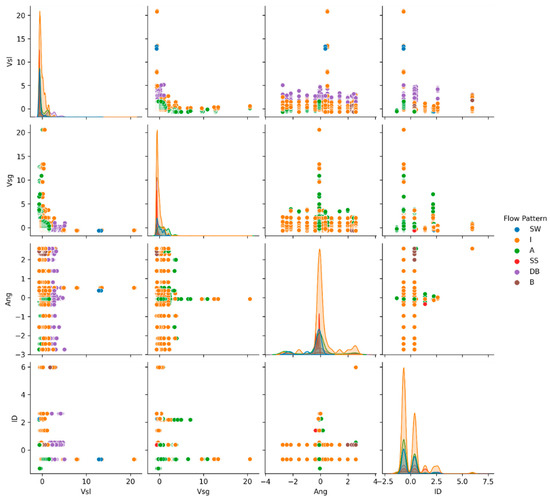
Figure 5.
Pair-plot for exploratory data analysis of top four feature variables (Vsl, Vsg, Ang, and ID).
2.4. Machine-Learning Algorithms
We have used six state-of-the-art supervised machine-learning algorithms to model the flow regime pattern using nine different features. The algorithms are random forest (RF), extra tree (ET), Extreme Gradient Boosting method (XGBoost), support vector machine (SVM), k-nearest neighbor (KNN), and AdaBoost (AB).
2.4.1. RF
The RF algorithm is an ensemble of decision trees (DT), which creates a forest with several individual trees [68]. In this forest, each tree is constructed in parallel on bootstrapped training samples using a random subset of features with information gain or the Gini index approach as the learning criterion. Based on the training on a subset of attributes, each tree produces a classification and the forest yields the class, with the majority votes as the final result of the classifier. The randomness in RF often yields better accuracy than traditional DT and helps to avoid overfitting by improving model generalization performances.
2.4.2. ET
The ET classifier works in a similar manner as RF by fitting several randomized DTs on various sub-samples and subset of features of the dataset. Additionally, it has more randomness in selecting decision thresholds for individual features during the model training. The ET model uses averaging to produce better accuracy and to regulate over-fitting [69].
2.4.3. Extreme GBM
The general concept of boosting is to use an ensemble of weak learners sequentially in order to create a more accurate predictor. In GBM, many individual decision trees are combined in a series, and each tree attempts to minimize the prediction errors made by the previous tree. The GBM algorithm is usually slower to learn due to its sequential nature; however, it yields moderately accurate predictions [70]. The Extreme GBM (XGBoost) is an efficient and effective implementation of the GBM algorithm.
2.4.4. SVM
The SVM is a popular ML algorithm for solving linear and non-linear classification problems. The basic strategy is to find a decision hyperplane that can separate the data points while keeping the boundary as far as possible from the closest data points [71]. For solving a non-linear classification problem, it uses kernel functions for feature mapping, and then finds a linear separator between classes in the modified feature space. The SVM creates a number of binary classifiers and uses a majority voting scheme to solve a multi-class classification problem.
2.4.5. KNN
The KNN is a supervised algorithm to address classification and regression problems. It works by calculating the distances between a query and all other data points, picking a set of examples (K), defining a neighborhood that is closest to the query, and, finally, voting for the most frequent label to be assigned to the query [72].
2.4.6. AB
The AB or adaptive boosting works by fitting a sequence of base learners on different weighted training data. It starts predicting the original dataset by assigning equal weight to each observation. If there is a misprediction by the initial learner, a higher weight is assigned to the corresponding sample. As an iterative algorithm, it keeps adding the learners until the desired accuracy is achieved or a specific number of models has reached [73].
2.5. Deep-Learning Algorithms
In addition to six general ML algorithms, three DL algorithms were also used for the present study. The algorithms are deep neural network, convolutional neural network, and bi-directional long-short-term memory (Bi-LSTM) recurrent neural network (RNN).
2.5.1. DNN
The DNN refers to the ANN system with multiple layers. It consists of several dense or fully connected (FC) layers followed by a classification or an output layer. Each of the FC layers contains several hidden neurons. The DNN used for this study is similar to the fully connected layers employed in the CNN architecture, as shown in Figure 6.
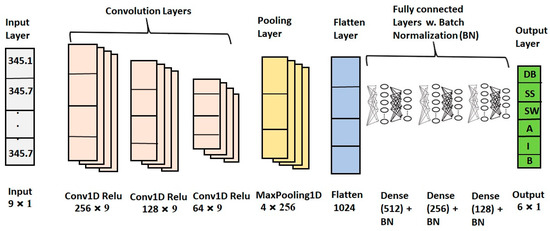
Figure 6.
CNN model architecture for six-class classification.
2.5.2. CNN
The CNN is a deep-learning framework that is primarily used in the task of pattern recognition within images. However, it can also be used to encode and feed numerical features into the architecture, making the network suitable for binary or multi-classification tasks. A one-dimensional (1D) CNN framework comprises neurons organized in two, rather than three, dimensions. A feature extraction stage and a classification stage are generally the parts of the framework [74]. The feature extraction stage, made of 1D convolution layers with several filters, can extract meaningful features at a deeper level. The classification stage includes one or several FC layers and an output layer. The proposed CNN architecture that is designed for six-class classification of flow patterns is depicted in Figure 6.
2.5.3. Bi-LSTM RNN
The RNN is another deep-learning framework suitable for sequence data [75]. However, it is used in the current study for non-sequence data of numerical features. The long short term memory (LSTM) is a variant of RNN that is capable of learning long-term dependencies among the input data by maintaining a memory state over time. In the Bi-LSTM network, each input row is presented forward and backward as two separate RNNs, leading to the same output layer. The current Bi-LSTM RNN model is constructed using several LSTM units, pooling and flatten layer, FC layers with batch normalization, and the classification layer in sequence. The activation functions used are ‘ReLU’ and ‘softmax’ in the dense and the classification layers, respectively. A similar architecture, like CNN (Figure 6), was used to design the custom RNN model for the six-class classification problem. However, the convolution layers were replaced with the Bi-LSTM layers having the similar number of hidden units.
2.6. Machine-Learning Model Training
The flow regime pattern classification models were trained through the hyperparameter optimization of six different ML models. A grid search was applied within specific ranges for a set of hyperparameters corresponding to each ML algorithm in order to find their optimal values that can best predict the flow regime class using either all or a selected set of features. This training was performed in a threefold cross-validation (CV) framework. After the models were trained, they were assessed on an independent dataset using a set of evaluation metrics suitable for an imbalanced multi-class classification problem. The training and testing framework of the ML models is explained with a flow diagram, as presented in Figure 7.
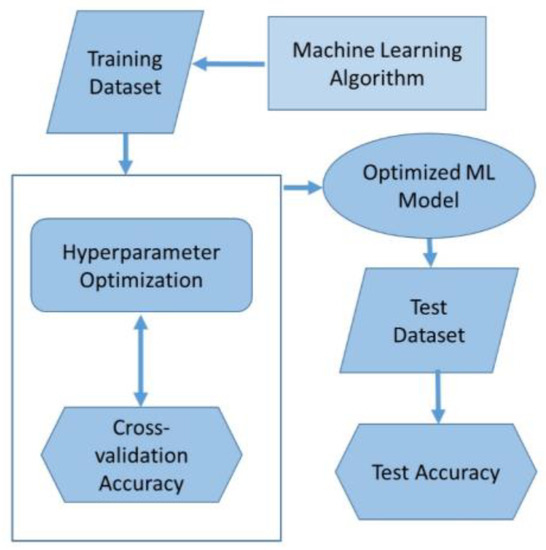
Figure 7.
General framework of ML classification system.
2.7. Evaluation Metrics for Model Assessment
The performances of the multi-class classification models in the present study was assessed with a set of evaluation metrics: accuracy, precision, recall, F1-score, Cohen’s kappa, confusion matrix (CM), and area under the curve (AUC)—receiver operating characteristics (ROC) curve. The values of the statistical parameters were calculated as weighted average using four parameters: true positives (TP), false positives (FP), false negatives (FN), and true negatives (TN). The micro average form of all the evaluation metrics was considered to ensure an unbiased assessment of the models. In a multi-class classification problem, the micro average is preferable in the existence of an imbalance class. This approach takes the class distribution into account and weighs the evaluation measure according to the corresponding distribution.
2.7.1. Accuracy
The accuracy can be measured as the ratio of the correct predictions over the total number of samples as follows:
2.7.2. Precision
Precision indicates the fraction of correctly predicted true patterns from the total predicted true classes. The following equation was used to calculate it:
2.7.3. Recall
Recall calculates the fraction of true classes that are correctly predicted. It is also known as the sensitivity and is a useful metric for an imbalanced class problem. It can be defined as follows:
2.7.4. F1-Score
F1-score represents the harmonic mean between precision and recall. It is a recommended metric to evaluate the models for imbalanced class problem. It is calculated as follows:
2.7.5. Cohen’s Kappa
Cohen’s kappa, or simply the kappa-score, measures the observed agreement for categorical data. This metric can handle both multi-class classification and imbalanced class problems. It can be calculated as follows:
where, is the observed agreement and is the expected agreement. The kappa-score can be less than 0 and equal to 1.
2.7.6. Confusion Matrix
The CM shows the number of actual and predicted patterns in each class in a tabulated form. The tabular layout provides the summary of the classification performances of the models and contains the prediction results, such as TP, FP, FN, and TN to calculate the various evaluation metrics. The CM is also used to realize which classes are being predicted correctly and the types of errors being made by the classifier.
2.7.7. AUC-ROC Curve
The AUC-ROC curve is a performance measurement technique for multi-class classifiers at various threshold settings. ROC is a probability curve, and AUC represents the degree of separability. It helps to visualize how well models are capable of distinguishing different classes. In the AUC-ROC graph for the multi-class classifier, a curve is plotted with true positive rate (TPR) against the false positive rate (FPR) for each class along with the AUC score for a specific confidence interval (CI).
3. Results
3.1. Feature Importance and Non-Linearity
One of the important aspects of the classification problem is to identify important features, which usually play the most significant role in predicting the output labels. The objective is to exclude the least significant variables from the dataset without hindering the performance of the ML model and to utilize the most relevant variables in building the model. We used the ET classifier reported feature importance score to rank the features in descending order. The higher the rank, the more important the feature is. As we can see in Figure 2, the top four important features reported by the ET classifier were the superficial velocity of liquid (Vsl), superficial velocity of gas (Vsg), inclination angle of the pipeline (Ang), the and internal diameter of the pipe (ID). The PCA analysis of the features is also presented in Figure 3. The correlation coefficient and pair-plot analyses (see Figure 4 and Figure 5) of these features confirm that the classes are non-linearly separable in the dataset.
3.2. Machine-Learning Model Training
Finding the optimal values of hyperparameters that best learn the patterns in the training data is an important step in statistical model learning. The optimization of selected hyperparameters with a specific range of values was performed on the training data (consists of 80% of samples) in a threefold cross-validation framework for three multi-class classification problems. The best hyperparameters were recorded when the model achieved the best accuracy on the validation set during the training. The different hyperparameters of the ML models and their optimized values which were obtained during the cross-validated training and are listed in Table 3. The models were then fitted with the training data using optimized hyperparameters. The fitted models were finally evaluated with the test data (comprising 20% of samples). The test accuracy and the cross-validated training accuracy of the models are presented in Table 4, Table 5 and Table 6. All ML model trainings were performed in the Google Colab non-GPU environment.

Table 3.
A set of hyperparameters for six ML models, the ranges used for model optimization, and the best values obtained for three classification problems.

Table 4.
Machine-learning model performances on training and test sets for six-class classification using all the features. The best performances are highlighted in bold.

Table 5.
Machine-learning model performances on training and test sets for three-class classification using all the features. The best performances are highlighted in bold.

Table 6.
Machine-learning model performances on training and test sets for two-class classification using all the features. The best performances are highlighted in bold.
3.3. Deep-Learning Model Training
The proposed CNN model has three 1D-convolutions with 256, 128, and 64 filters made of kernels of size three and ‘ReLU’ as the activation function. A max pooling layer and a flatten layer were used to reshape the features to feed to the FC layer in the classification stage. The ‘ReLU’ and ‘Softmax’ activation functions were used in the FC and output layer of the multi-class classification stage of the CNN. The RNN has a similar configuration as the CNN for feature extraction and classification stage, except the 1D-convolutions substituted with the bi-directional LSTM layers. The DNN is basically the classification stage of CNN, which was trained separately without the feature extraction stage of CNN.
All three deep-learning models were trained using 700 epochs with a batch size of 200. An early stopping with the parameter setting as patience = 200, monitor = “val_loss”, and mode = “min”, was used to avoid overfitting, while the models with the best validation accuracy were saved at regular intervals. The training of the DDN required 400 epochs, the CNN model used 323 epochs, and finally, the RNN model fitting used approximately 400 epochs until the loss on the validation set stops decreasing. The accuracy vs. epoch and loss vs. epoch plots for three DL model trainings are shown in Figure 8, Figure 9 and Figure 10. All DL model trainings were performed in the Google Colab GPU runtime environment.
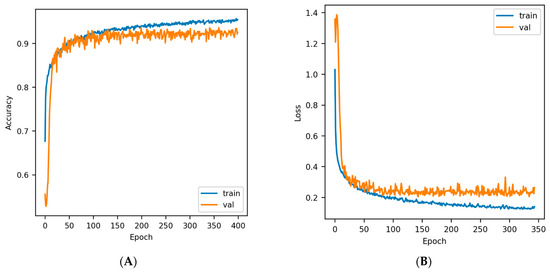
Figure 8.
DNN training curves (A) Accuracy vs. Epoch; (B) Loss vs. Epoch.
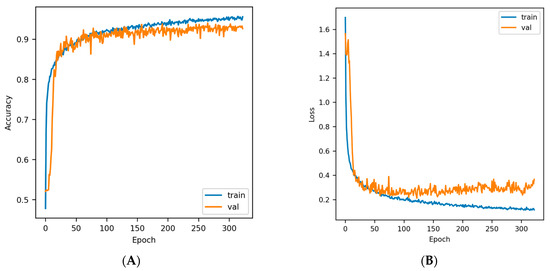
Figure 9.
CNN training curves (A) Accuracy vs. Epoch; (B) Loss vs. Epoch.
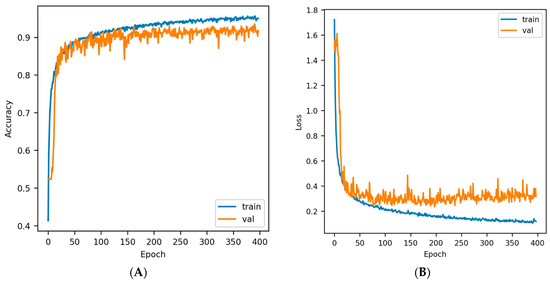
Figure 10.
Bi-LSTM RNN training curves (A) Accuracy vs. Epoch; (B) Loss vs. Epoch.
3.4. Classification Performance
The classification performances of the DL models are summarized in Table 7 and Table 8. Table 9 shows the performances of the ML models using the important features identified in the feature selection step. The confusion matrix and the classification report for the XGBoost method, using six classes for the test dataset, are shown in Figure 11.

Table 7.
Deep-learning model performances on training and test sets for six-class classification using all the features. The best performances are highlighted in bold.

Table 8.
Deep-learning model performances on training and test sets for three-class classification using all the features. The best performances are highlighted in bold.

Table 9.
Machine-learning model performances on the test set for six-class classification using the top four important features. The best performances are highlighted in bold.
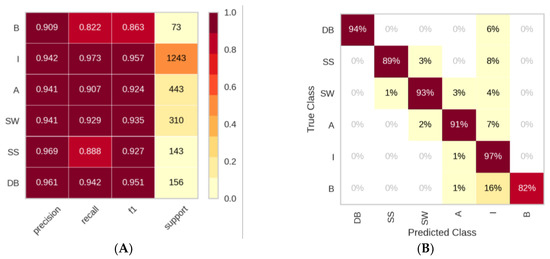
Figure 11.
Classification report (A) and the confusion matrix (B) resulting from the best classification model XGBoost for six-class classification.
3.5. Hyperparameter Optimization
A set of hyperparameters of the different ML algorithms were optimized for three classification problems with six (6), three (3), and two (2) classes in a threefold cross-validation framework. The optimized parameter values are listed in Table 3.
3.6. AUC-ROC Curves with Confidence Interval
The AUC-ROC curves with 95% CI for the two best algorithms from ML and DL family, XGBoost, and CNN classification models are shown in Figure 12, Figure 13, Figure 14 and Figure 15.
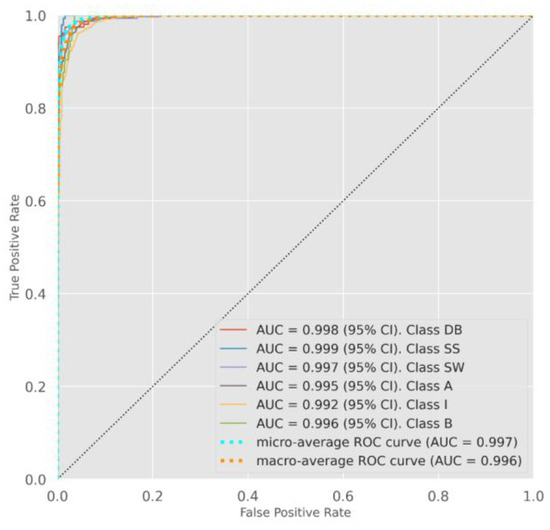
Figure 12.
ROC curves of XGBoost classifier for six classes (‘DB’, ‘SS’, ‘SW’, ‘A’, ‘I’, ‘B’).
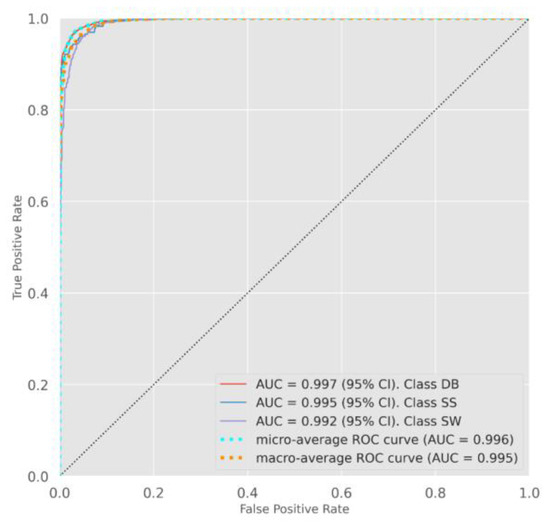
Figure 13.
ROC curves of XGBoost Classifier for three classes (‘ST’, ‘DS’, ‘I’).
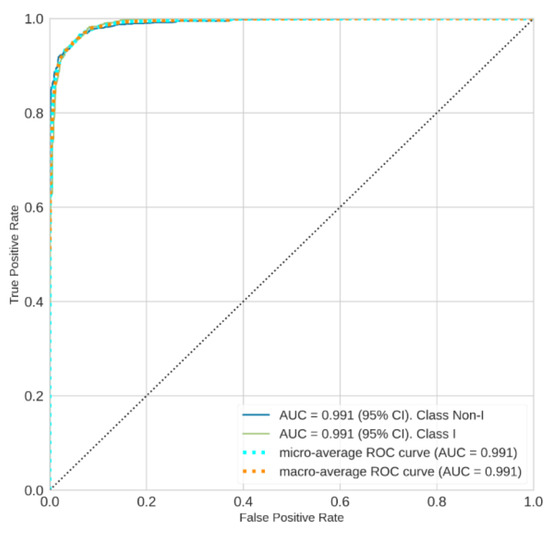
Figure 14.
ROC curves of XGBoost Classifier for two classes (‘I’ vs. ‘Non-I’).
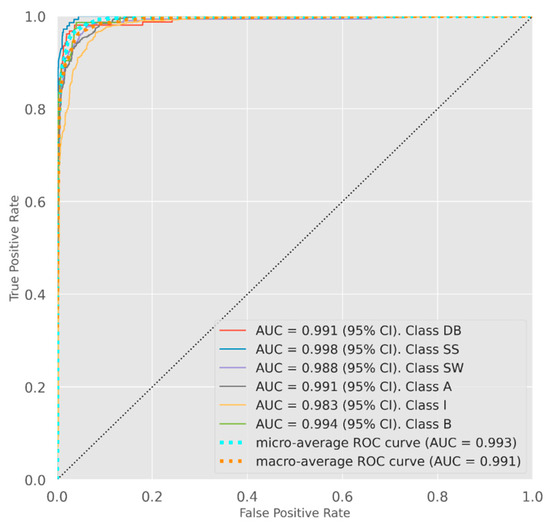
Figure 15.
ROC curves for CNN classifier for six classes.
3.7. Comparative Analysis
A comparative analysis of the best-performing ML and DL models with the similar models proposed in [65,76] are presented in Table 10 and Table 11.

Table 10.
Comparative analysis of the peer models on the flow regime dataset used in the current study comprising 11,838 data points. The accuracies are reported for individual model in each column. The best performances are highlighted in bold.

Table 11.
Comparative analysis of the proposed models on the peer database (Pereyra et al. [61]) consisting 9029 samples. The accuracies are reported for individual model in each column. The best performances are highlighted in bold.
4. Discussion
A multi-class classification problem of flow regime identification was investigated in the current study by selecting important features, designing multi-class classification systems, finding the best performing ML- and DL-based classifiers, and assessing the models with appropriate evaluation metrics. As the first step of classification system design, we analyzed the class distribution of the data points. To the best of our knowledge, the present database is larger than any other dataset used previously for similar classification problem. However, it is largely disproportioned in terms of class distribution. As Figure 1 depicts, class ‘I’ is evidently the majority class in the six-class and three-class classification problems, whereas the classes ‘B’, ‘SS’, and ‘DB’, each consist of less than 10% of the samples, representing the minority group. For three-class classification, there are less than half of the data points under the ‘DS’ and ‘ST’ categories, making them minority classes. This kind of disproportional distribution of data demonstrates the imbalanced nature of the current dataset.
The classification system design using ML algorithms involves several steps, such as splitting the data for training and testing, learning the model, i.e., optimizing hyperparameters based on the training data, and model evaluation on the test data (Figure 7). After feature selection and normalization, the flow regime dataset was divided into 80% training and 20% test for the current classification problems. The ML models were learned through hyperparameter optimization in a threefold cross-validated training framework. The optimized algorithmic parameters are reported in Table 3. The training was performed using all features as well as the top four important features. The classification accuracy of six-class classification using the important features was marginally lower than that of using all the features (92% vs. 94%). The probable reason could be that the top ranked four features could not capture the variability of the data completely, rather the variance was distributed among all nine features.
In general, the key factors to measure the effectivity of the classification model are the model’s performance on the independent test data and its convergence time, that is, the required time to train the model on the dataset. The ability of classifiers to process large data sets within a reasonable time is an important issue besides the accuracy in the era of Big Data. In terms of the performance on the test data, the best performing ML algorithm is XGBoost for all three classifications and using all nine features (see Table 4, Table 5 and Table 6). The second and third best-performing algorithms are ET and RF. In case of using a limited number of features, specifically top four important variables (refer to Table 9), the ET outperformed all other models. The supremacy of gradient boosting with improved loss functions, i.e., XGBoost and the ensembles of decision tree-like models, such as ET and RF, is evident in all three classification results, whether using all nine features or top four important features. Specifically, the XGBoost produced robust and highly accurate predictions. The SVM and KNN produced comparable results and came in the next two positions. The AB was the worst-performing algorithm as it was the simplest among the ML algorithms selected for the current study. In terms of its convergence time, the randomized decision tree family algorithms were again found to be very effective, as the average training time was approximately 100 s, while the SVM and KNN took approximately 400 and 500 s, respectively, in the Google Colab.
On the basis of performance and convergence time, the ML models tested for the current study can be arranged as follows in order of their effectivity in predicting gas–liquid flow regimes: XGBoost > ET > RF > SVM > KNN > AB. The advanced boosting and bagging algorithms demonstrate an evident supremacy over the other types of ML algorithms. The optimum algorithm was identified as XGBoost. It is a more regularized form of the traditional GBM. Similar to gradient boosting, the XGBoost exploits an ensemble of weak learners in a sequential manner by assigning a higher importance to the misclassified examples from the previous weak learner while minimizing a stepwise gradient loss. In addition, it comes with a powerful regularization technique that combines L1 and L2 norms, which effectively reduces overfitting and helps achieve better generalization capabilities than the general GBM.
As bagging algorithms, RF and ET use a strong modelling technique that runs multiple decision trees in parallel either on bootstrapped or whole original samples, using a randomly chosen subset of features with optimum or randomized split points. Consequently, all these features enable the RF and ET models to effectively reduce errors due to existent bias and variance in the input data, which improves the classification performance and the generalization capability of the models. Moreover, RF and ET models are inherently suitable for multi-class training data. These two models solve the non-linearity problem by finding a hyper-rectangle in the decision space. On the other hand, the SVMs are generally applicable to the binary classification and solve the multi-class classification by using several binary classifiers with a majority voting approach. The better generalization performances of ensemble classifiers demonstrate that a collection of classifiers can produce a more robust and confident classification as opposed to a single classifier, and this is where the power of ensemble learning lies in. Another important point to note is that the ensemble classifiers suffered the least due to the extreme imbalance of the dataset in the current study. This is because these models have the ability to incorporate higher weights into the minority class by making them cost-sensitive and, thereby, penalizing the misclassification of the low-representative class. These algorithms also merge the sampling technique and ensemble learning. They under-sample the majority class and grow trees on a more balanced dataset.
The CNN was the best performer with a 92% accuracy among the proposed DL architectures for the six-class classification (Table 7), while the DNN proved to be the best performer with a 94% accuracy for the three-class problem (Table 8). However, the differences in accuracies among these three DL models are not statistically significant. It is interesting to observe that the performance of the DNN is either superior or close to that of the CNN with a lesser sign of overfitting. A DNN is practically comprised of only the classification layer of the CNN. The performances of the RNN and CNN were also comparable. That is, the large networks of CNN and RNN failed to provide significantly better performance than the DNN. The learning curves shown in Figure 8, Figure 9 and Figure 10 exhibit that none of the DL models suffer from extreme overfitting due to the early-stopping applied for the trainings. The DL models performed better than a few ML models, such as SVM, KNN, and AB; however, their performances were inferior to the randomized decision tree and advanced boosting. The current analysis suggests that the heavy-weight DL algorithms, especially the CNN and RNN, may not be the suitable choice for the multi-class classification problem of identifying the flow regimes in the pipelines used for transmitting gas–liquid two-phase flows. They introduce excessive complexity in modelling the data and fail to generalize the problem. These algorithms are computationally expensive to train and test as they require a GPU machine for a reasonable convergence and prediction time. It can make them inefficient for industrial-scale data analysis, which usually involve millions of observations.
After identifying XGBoost as the optimum model for classifying gas–liquid two-phase flow regimes in pipelines, experiments were conducted to evaluate its shortcomings. The detailed classification report and the confusion matrix of the XGBoost model for six-class classification are illustrated in Figure 11. The classification report describes the class-specific precision, recall, and F1-scores for the model. As anticipated, the minority classes of ‘B’ and ‘SS’, which comprise less than 5% of total samples individually, have lower recall or sensitivity; whereas, the highest recall is for the majority class, ‘I’ that contains 54% of total samples. In the confusion matrix, class ‘B’ has the highest FN, i.e., 16% of ‘B’ class samples are wrongly predicted as class ‘I’. The second-highest FN is reported for the class ‘SS’. Approximately 8% of samples of this category are falsely classified as ‘I’. The misclassification rates for these two classes are 16% and 11%, respectively. The XGBoost model shows a deficiency in generalization because there are a limited number of training samples available for the minority classes, which causes the model to either fail in extracting any useful pattern for these classes or makes the learning biased towards the majority class. Nevertheless, a comparatively worse trend was observed for the ET classifier that was reported as the best performing ML model by Arteaga et al. (2021) for the current dataset. Their best model yields not only lower recalls of 84% and 88% for the ‘B’ and ‘SS’ classes, but also only 87% of the recall for the third-most minority group, ‘DB’, which includes 7% of total samples. On the contrary, the XGBoost produces 96% of precision, 94% of recall, and 95% of the F1-score values for this particular low-representative class. That is, the XGBoost is more resilient to the class imbalance problem; however, it may hinder the model’s performance gradually in case the imbalance is extreme (≤5%).
In addition to standard classification reports, other effective evaluation metrics for the imbalanced multi-class classification problems, such as the F1-score, Cohen’s kappa, and ROC-AUC curves, were used to assess the performance of the classifiers. The ROC curves for the XGBoost classifier are presented in Figure 12, Figure 13 and Figure 14 with AUC scores calculated for each class with a 95% confidence interval. Among the classification problems investigated in the current study, the three-class classification has the highest accuracy (96%) and F1-score. The Cohen’s kappa scores achieved for the six-class, three-class and two-class classifications are 91%, 92%, and 90%, respectively. Similarly, the AUC scores of 99.7% and 99.6% were achieved for both the six-class and three-class classification performances. As the AUC score indicates the degree of separability by plotting the TPR against the FPR, the ROC-AUC curves of the XGBoost classifier indicate the model’s capability of distinguishing the data points for the six-class or three-class categorizations with high confidence and accuracy. It is pertinent to note that all evaluation metrics were developed based on the micro-average form, which is suitable for an imbalanced class distribution.
A comparative analysis of the currently developed models to other similar models was performed as part of their evaluation. The primary objective of conducting this set of experiments was to investigate the effectiveness of the models in comparison to the peers’ models developed earlier independently. The best-performing models reported in [65] and [76] were specifically selected for the comparison as those were developed using a subset of the current database, i.e., the dataset that was reported in [53]. It ensured fair comparisons among the systems in terms of classification performances and provided the opportunity for the cross-application of the models to different datasets. The respective results of the analyses are presented in Table 10 and Table 11. The optimum ML and DL models realized in the course of the present study demonstrate better performances irrespective of the data size. It should be noted that we used the peers’ models with the reported parametric configurations and did not attempt to further optimize them on the respective databases. This objective analysis demonstrates the efficacy and robustness of the current models, which are unaffected by the database size and class imbalance.
It should be underscored that there was no attempt to balance the dataset for the present study. Only the original samples were used without over-sampling the minority classes with synthetic data points or duplicating the entries while testing the efficacy of the ML classifiers. This is because over-sampling can lead to overfitting and lowering the generalizability of the models on unseen data. Similarly, the under-sampling of the majority classes reduces the size of the training data resulting in the under-fitting of the models. The primary target was to achieve an unbiased and objective accuracy for the current flow regime dataset, which is imbalanced in nature. It is also important to note that the flow regime categorization in the consolidated experimental datasets comes from visual observation and manual assignment of flow patterns to the samples. Human error and visual limitation could introduce misassignment of the pattern type to flow regime samples, which can influence the AI models’ learning and could deteriorate the models’ generalization performances.
5. Conclusions
A large dataset including 11,838 data points is used in the current study to develop AI-based flow regime classification systems using state-of-the-art ML and DL algorithms. To the best of the authors’ knowledge, it is the largest dataset used to date for predicting gas–liquid two-phase flow regimes based on AI. The best performing ML algorithm is the XGBoost, with micro-average accuracies of 94%, 96%, and 95% for the six-class, three-class, and two-class classification problems, respectively. The Cohen’s kappa score of 89% and the AUC score of 99.6% at a 95% confidence interval are achieved for the six-class classification by the XGBoost classifier. A feature importance analysis reveals the superficial velocity of liquid (Vsl), the superficial velocity of gas (Vsg), the angular inclination of the pipeline (Ang), and the pipe’s internal diameter (ID) as the most important features. The ET classifier attains the highest six-class classification accuracy of 93% using these top four important features. Among the DL algorithms, the CNN model achieved the highest accuracy of 92% with Cohen’s kappa of 88% and AUC scores of 99.3%. Despite the imbalanced nature of the multi-class dataset employed in the current study, the effective designs of the classification systems ensure high levels of accuracies, F1-scores, Cohen’s kappa, and AUC scores. The present study provides a powerful AI approach to classify the multi-phase flow patterns in industrial pipelines with a high accuracy and confidence level.
Author Contributions
Conceptualization, N.H. and S.R.; methodology, N.H. and S.R.; software, N.H.; validation, N.H.; formal analysis, N.H. and S.R.; investigation, N.H. and S.R.; resources, N.H.; data curation, S.R. and H.Y.; writing—original draft preparation, N.H., S.R. and H.Y.; writing—review and editing, N.H. and S.R.; visualization, N.H.; supervision, N.H. and S.R.; project administration, N.H. and S.R.; funding acquisition, N.H. and S.R. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported through the Annual Funding track by the Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research, King Faisal University, Saudi Arabia [Project No. AN000279].
Data Availability Statement
The data used for the current study are available in [53,66,67].
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ghanbarzadeh, S.; Pedram, H.; Said, M. Intelligent image-based gas-liquid two-phase flow regime recognition. J. Fluids Eng. 2012, 134, 061302. [Google Scholar] [CrossRef]
- Strand, A.; Smith, I.E.; Unander, T.E.; Steinsland, I.; Hellevik, L.R. Uncertainty Propagation through a Point Model for Steady-State Two-Phase Pipe Flow. Algorithms 2020, 13, 53. [Google Scholar] [CrossRef]
- Bjørlo, I. Uncertainty in Multiphase Flow Estimates for a Field Development Case. Master’s Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2013. Available online: https://ntnuopen.ntnu.no/ntnu-xmlui/bitstream/handle/11250/235160/648709_FULLTEXT01.pdf?sequence=1&isAllowed=y (accessed on 1 January 2023).
- Klinkert, J. The Characterization of Uncertainty for Steady State Multiphase Flow Models in Pipelines. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2018. Available online: http://resolver.tudelft.nl/uuid:4968494c-464e-46f9-b635-5828cedaadfa (accessed on 1 January 2023).
- Posluszny, D.; Klavetter, K.; Cremaschi, S.; Sarica, C.; Subramani, H.J. Uncertainty Analysis of Multiphase Flow Modelling: A Case Study for Vertical Flows. In Proceedings of the 7th North American Conference on Multiphase Technology, Banff, AB, Canada, 2–4 June 2010. [Google Scholar]
- Duns, H.; Ros, N.C.J. Vertical Flow of Gas and Liquid Mixtures from Boreholes; Bataafse Internationale Petroleum Maatschappij, NV: The Hague, The Netherlands, 1963. [Google Scholar]
- Hagedorn, A.R.; Brown, K.E. Experimental study of pressure gradients occurring during continuous two-phase flow in small-diameter vertical conduits. J. Pet. Technol. 1965, 17, 475–484. [Google Scholar] [CrossRef]
- Aziz, K.; Govier, G.W. Pressure drop in wells producing oil and gas. J. Can. Pet. Technol. 1972, 11, PETSOC-72-03-04. [Google Scholar] [CrossRef]
- Beggs, D.H.; Brill, J.P. A study of two-phase flow in inclined pipes. J. Pet. Technol. 1973, 25, 607–617. [Google Scholar] [CrossRef]
- Mukherjee, H.; Brill, J.P. Pressure drop correlations for inclined two-phase flow. J. Energy Resour. Technol. 1985, 107, 549–554. [Google Scholar] [CrossRef]
- Asheim, H. MONA, an accurate two-phase well flow model based on phase slippage. SPE Prod. Eng. 1986, 1, 221–230. [Google Scholar] [CrossRef]
- Pucknell, J.K.; Mason, J.N.E.; Vervest, E.G. An Evaluation of Recent Mechanistic Models of Multiphase Flow for Predicting Pressure Drops in Oil and Gas Wells. In Proceedings of the SPE Offshore Europe, Aberdeen, UK, 7–10 September 1993. [Google Scholar] [CrossRef]
- Rouhani, S.Z.; Sohal, M.S. Two-phase flow patterns: A review of research results. Prog. Nucl. Energy 1983, 11, 219–259. [Google Scholar] [CrossRef]
- Hewitt, G.F.; Hall-Taylor, N.S. Annular Two-Phase Flow; Elsevier Ltd.: Amsterdam, The Netherlands, 1970. [Google Scholar] [CrossRef]
- Taitel, Y.; Bornea, D.; Dukler, A.E. Modelling flow pattern transitions for steady upward gas-liquid flow in vertical tubes. AIChE J. 1980, 26, 345–354. [Google Scholar] [CrossRef]
- Barnea, D.; Shoham, O.; Taitel, Y. Flow pattern characterization in two phase flow by electrical conductance probe. Int. J. Multiph. Flow 1980, 6, 387–397. [Google Scholar] [CrossRef]
- Barnea, D.; Shoham, O.; Taitel, Y.; Dukler, A.E. Flow pattern transition for gas-liquid flow in horizontal and inclined pipes. Comparison of experimental data with theory. Int. J. Multiph. Flow 1980, 6, 217–225. [Google Scholar] [CrossRef]
- Oddie, G.; Shi, H.; Durlofsky, L.J.; Aziz, K.; Pfeffer, B.; Holmes, J.A. Experimental study of two and three phase flows in large diameter inclined pipes. Int. J. Multiph. Flow 2003, 29, 527–558. [Google Scholar] [CrossRef]
- Zhang, H.Q.; Wang, Q.; Sarica, C.; Brill, J.P. Unified model for gas-liquid pipe flow via slug dynamics—Part 1: Model development. J. Energy Resour. Technol. 2003, 125, 266–273. [Google Scholar] [CrossRef]
- Dreyer, W.J.; Bennett, J.C. The molecular basis of antibody formation: A paradox. Proc. Natl. Acad. Sci. USA 1965, 54, 864. [Google Scholar] [CrossRef] [PubMed]
- Cong, T.; Su, G.; Qiu, S.; Tian, W. Applications of ANNs in flow and heat transfer problems in nuclear engineering: A review work. Prog. Nucl. Energy 2013, 62, 54–71. [Google Scholar] [CrossRef]
- Wang, S.Q.; Xu, K.W.; Kim, H.B. Slug flow identification using ultrasound Doppler velocimetry. Int. J. Heat Mass Transf. 2020, 148, 119004. [Google Scholar] [CrossRef]
- Peddu, A.; Chakraborty, S.; Das, P.K. Visualization and flow regime identification of downward air–water flow through a 12 mm diameter vertical tube using image analysis. Int. J. Multiph. Flow 2018, 100, 1–15. [Google Scholar] [CrossRef]
- Chen, S.W.; Lin, M.S.; Kuo, F.J.; Chai, M.L.; Liu, S.Y.; Lee, J.D.; Pei, B.S. Experimental investigation and identification of the transition boundary of churn and annular flows using multi-range differential pressure and conductivity signals. Appl. Therm. Eng. 2017, 114, 1275–1286. [Google Scholar] [CrossRef]
- Hobold, G.M.; da Silva, A.K. Machine learning classification of boiling regimes with low speed, direct and indirect visualization. Int. J. Heat Mass Transf. 2018, 125, 1296–1309. [Google Scholar] [CrossRef]
- Manjrekar, O.N.; Dudukovic, M.P. Identification of flow regime in a bubble column reactor with a combination of optical probe data and machine learning technique. Chem. Eng. Sci. X 2019, 2, 100023. [Google Scholar] [CrossRef]
- Mask, G.; Wu, X.; Ling, K. An improved model for gas-liquid flow pattern prediction based on machine learning. J. Pet. Sci. Eng. 2019, 183, 106370. [Google Scholar] [CrossRef]
- Julia, J.E.; Ozar, B.; Jeong, J.J.; Hibiki, T.; Ishii, M. Flow regime development analysis in adiabatic upward two-phase flow in a vertical annulus. Int. J. Heat Fluid Flow 2011, 32, 164–175. [Google Scholar] [CrossRef]
- Paranjape, S.; Chen, S.W.; Hibiki, T.; Ishii, M. Flow regime identification under adiabatic upward two-phase flow in a vertical rod bundle geometry. J. Fluids Eng. 2011, 133, 9. [Google Scholar] [CrossRef]
- Sawant, P.; Schelegel, J.; Paranjape, S.; Ozar, B.; Hibiki, T.; Ishii, M. Flow regime identification in large diameter pipe. Int. Conf. Nucl. Eng. 2008, 48167, 341–351. [Google Scholar]
- Tambouratzis, T.; Pázsit, I. Non-invasive on-line two-phase flow regime identification employing artificial neural networks. Ann. Nucl. Energy 2009, 36, 464–469. [Google Scholar] [CrossRef]
- Paranjape, S.; Ritchey, S.N.; Garimella, S.V. Electrical impedance-based void fraction measurement and flow regime identification in microchannel flows under adiabatic conditions. Int. J. Multiph. Flow 2012, 42, 175–183. [Google Scholar] [CrossRef]
- Mi, Y.; Ishii, M.; Tsoukalas, L.H. Vertical two-phase flow identification using advanced instrumentation and neural networks. Nucl. Eng. Des. 1998, 184, 409–420. [Google Scholar] [CrossRef]
- Sunde, C.; Avdic, S.; Pázsit, I. Classification of two-phase flow regimes via image analysis and a neuro-wavelet approach. Prog. Nucl. Energy 2005, 46, 348–358. [Google Scholar] [CrossRef]
- Jing, C.; Bai, Q.; Liu, B. Improved Void Fraction Measurement by Flow Regime Identification for Gas Liquid Two-Phase Flows. In Proceedings of the Seventh International Symposium on Instrumentation and Control Technology: Measurement Theory and Systems and Aeronautical Equipment, Beijing, China, 16 November 2008; Volume 7128, pp. 352–357. [Google Scholar]
- Harirchian, T.; Garimella, S.V. Boiling heat transfer and flow regimes in microchannels—A comprehensive understanding. J. Electron. Packag. 2011, 133, 011001. [Google Scholar] [CrossRef]
- Fraces, C.G.; Tchelepi, H. Physics Informed Deep Learning for Flow and Transport in Porous Media. In Proceedings of the SPE Reservoir Simulation Conference, Demand, 26 October 2021. [Google Scholar] [CrossRef]
- Maucec, M.; Jalali, R. GeoDIN—Geoscience-Based Deep Interaction Networks for Predicting Flow Dynamics in Reservoir Simulation Models. SPE J. 2022, 27, 1671–1689. [Google Scholar] [CrossRef]
- Tan, C.; Dong, F.; Wu, M. Identification of gas/liquid two-phase flow regime through ERT-based measurement and feature extraction. Flow Meas. Instrum. 2007, 18, 255–261. [Google Scholar] [CrossRef]
- Wang, H.X.; Zhang, L.F. Identification of two-phase flow regimes based on support vector machine and electrical capacitance tomography. Meas. Sci. Technol. 2009, 20, 114007. [Google Scholar] [CrossRef]
- Shanthi, C.; Pappa, N. An artificial intelligence based improved classification of two-phase flow patterns with feature extracted from acquired images. ISA Trans. 2017, 68, 425–432. [Google Scholar] [CrossRef] [PubMed]
- Nnabuife, S.G.; Pilario, K.E.S.; Lao, L.; Cao, Y.; Shafiee, M. Identification of gas-liquid flow regimes using a non-intrusive Doppler ultrasonic sensor and virtual flow regime maps. Flow Meas. Instrum. 2019, 68, 101568. [Google Scholar] [CrossRef]
- Cai, S.; Toral, H.; Qiu, J.; Archer, J.S. Neural network based objective flow regime identification in air-water two phase flow. Can. J. Chem. Eng. 1994, 72, 440–445. [Google Scholar] [CrossRef]
- Hernandez, L.; Juliá, J.E.; Chiva, S.; Paranjape, S.; Ishii, M. Fast classification of two-phase flow regimes based on conductivity signals and artificial neural networks. Meas. Sci. Technol. 2006, 17, 1511. [Google Scholar] [CrossRef]
- Rosa, E.S.; Salgado, R.M.; Ohishi, T.; Mastelari, N. Performance comparison of artificial neural networks and expert systems applied to flow pattern identification in vertical ascendant gas–liquid flows. Int. J. Multiph. Flow 2010, 36, 738–754. [Google Scholar] [CrossRef]
- Santoso, B.; Indarto, D.; Thomas, S.W. The identification of gas-liquid co-current two phase flow pattern in a horizontal pipe using the power spectral density and the artificial neural network (ANN). Mod. Appl. Sci. 2012, 6, 56–67. [Google Scholar] [CrossRef]
- Ghosh, S.; Pratihar, D.K.; Maiti, B.; Das, P.K. Identification of flow regimes using conductivity probe signals and neural networks for counter-current gas–liquid two-phase flow. Chem. Eng. Sci. 2012, 84, 417–436. [Google Scholar] [CrossRef]
- Figueiredo, M.M.F.; Goncalves, J.L.; Nakashima, A.M.V.; Fileti, A.M.F.; Carvalho, R.D.M. The use of an ultrasonic technique and neural networks for identification of the flow pattern and measurement of the gas volume fraction in multiphase flows. Exp. Therm. Fluid Sci. 2016, 70, 29–50. [Google Scholar] [CrossRef]
- Abbagoni, B.M.; Yeung, H. Non-invasive classification of gas–liquid two-phase horizontal flow regimes using an ultrasonic Doppler sensor and a neural network. Meas. Sci. Technol. 2016, 27, 84002. [Google Scholar] [CrossRef]
- Zou, S.; Guo, L.; Xie, C. Fast recognition of global flow regime in pipeline-riser system by spatial correlation of differential pressures. Int. J. Multiph. Flow 2017, 88, 222–237. [Google Scholar] [CrossRef]
- Liu, L.; Bai, B. Flow regime identification of swirling gas-liquid flow with image processing technique and neural networks. Chem. Eng. Sci. 2019, 199, 588–601. [Google Scholar] [CrossRef]
- Liu, W.; Xu, Q.; Zou, S.; Chang, Y.; Guo, L. Optimization of differential pressure signal acquisition for recognition of gas–liquid two-phase flow patterns in pipeline-riser system. Chem. Eng. Sci. 2021, 229, 116043. [Google Scholar] [CrossRef]
- Pereyra, E.; Torres, C.; Mohan, R.; Gomez, L.; Kouba, G.; Shoham, O. A methodology and database to quantify the confidence level of methods for gas–liquid two-phase flow pattern prediction. Chem. Eng. Res. Des. 2012, 90, 507–513. [Google Scholar] [CrossRef]
- Kihara, T.; Obata, H.; Hirano, H. Quantitative visualization of fluid mixing in slug flow for arbitrary wall-shaped microchannel using Shannon entropy. Chem. Eng. Sci. 2019, 200, 225–235. [Google Scholar] [CrossRef]
- Jung, S.; Yang, H.; Park, K.; Seo, Y.; Seong, W. Monitoring severe slugging in pipeline-riser system using accelerometers for application in early recognition. Sensors 2019, 19, 3930. [Google Scholar] [CrossRef]
- Hanus, R.; Zych, M.; Kusy, M.; Jaszczur, M.; Petryka, L. Identification of liquid-gas flow regime in a pipeline using gamma-ray absorption technique and computational intelligence methods. Flow Meas. Instrum. 2018, 60, 17–23. [Google Scholar] [CrossRef]
- Xu, Q.; Li, W.; Liu, W.; Zhang, X.; Yang, C.; Guo, L. Intelligent recognition of severe slugging in a long-distance pipeline-riser system. Exp. Therm. Fluid Sci. 2020, 113, 110022. [Google Scholar] [CrossRef]
- Xu, Q.; Zhou, H.; Zhu, Y.; Cao, Y.; Huang, B.; Li, W.; Guo, L. Study of identification of global flow regime in a long pipeline transportation system. Powder Technol. 2020, 362, 507–516. [Google Scholar] [CrossRef]
- Xu, Q.; Liu, C.; Wang, X.; Cao, Y.; Yu, H.; Li, W.; Guo, L. Machine learning classification of flow regimes in a long pipeline-riser system with differential pressure signal. Chem. Eng. Sci. 2021, 233, 116402. [Google Scholar] [CrossRef]
- Du, M.; Yin, H.; Chen, X.; Wang, X. Oil-in-water two-phase flow pattern identification from experimental snapshots using convolutional neural network. IEEE Access 2018, 7, 6219–6225. [Google Scholar] [CrossRef]
- Xu, Z.; Yang, X.; Chen, B.; Zhang, M.; Li, Y. Imaging of Flow Pattern of Gas-Oil Flows with Convolutional Neural Network. In Proceedings of the 2019 IEEE International Conference on Imaging Systems and Techniques (IST), Abu Dhabi, United Arab Emirates, 9–10 December 2019; pp. 1–6. [Google Scholar]
- Zhang, Y.; Azman, A.N.; Xu, K.W.; Kang, C.; Kim, H.B. Two-phase flow regime identification based on the liquid-phase velocity information and machine learning. Exp. Fluids 2020, 61, 212. [Google Scholar] [CrossRef]
- Kuang, B.; Nnabuife, S.G.; Rana, Z. Pseudo-image-feature-based identification benchmark for multi-phase flow regimes. Chem. Eng. J. Adv. 2021, 5, 100060. [Google Scholar] [CrossRef]
- Wang, N.; Zhang, D.; Chang, H.; Li, H. Deep learning of subsurface flow via theory-guided neural network. J. Hydrol. 2020, 584, 124700. [Google Scholar] [CrossRef]
- Lin, Z.; Liu, X.; Lao, L.; Liu, H. Prediction of two-phase flow patterns in upward inclined pipes via deep learning. Energy 2020, 210, 118541. [Google Scholar] [CrossRef]
- Abdul-Majeed, G.H. Liquid holdup in horizontal two-phase gas—Liquid flow. J. Pet. Sci. Eng. 1996, 15, 271–280. [Google Scholar] [CrossRef]
- Al-Dogail, A.S.; Gajbhiye, R.N. Effects of density, viscosity and surface tension on flow regimes and pressure drop of two-phase flow in horizontal pipes. J. Pet. Sci. Eng. 2021, 205, 108719. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef]
- Friedman, J.H. Stochastic gradient boosting. Comput. Stat. Data Anal. 2002, 38, 367–378. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Zhang, Z. Introduction to machine learning: K-nearest neighbors. Ann. Transl. Med. 2016, 4, 218. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.; Zou, H.; Rosset, S.; Hastie, T. Multi-class AdaBoost. Stat. Its Interface 2009, 2, 349–360. [Google Scholar] [CrossRef]
- O’Shea, K.; Nash, R. An Introduction to Convolutional Neural Networks. arXiv 2015, arXiv:1511.08458. [Google Scholar]
- Sherstinsky, A. Fundamentals of Recurrent Neural Network and Long Short-Term Memory Network. Phys. D Nonlinear Phenom. 2018, 404, 132306. [Google Scholar] [CrossRef]
- Arteaga-Arteaga, H.B.; Mora-Rubio, A.; Florez, F.; Murcia-Orjuela, N.; Diaz-Ortega, C.E.; Orozco-Arias, S.; Tabares-Soto, R. Machine learning applications to predict two-phase flow patterns. PeerJ Comput. Sci. 2021, 7, e798. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).