Experimental Analysis of Wind Pressure Characteristics in a Reduced-Scale Model of a Slab-Shaped High-Rise Building at Different Inflow Conditions with Various Wind Flow Directions
Abstract
:1. Introduction
2. Experimental Setting
2.1. Experimental Model
2.2. Test Cases
2.2.1. Wind Field in the Wind Tunnel
2.2.2. Test Scheme
3. Results
3.1. Time-Average Wind Pressure Coefficients
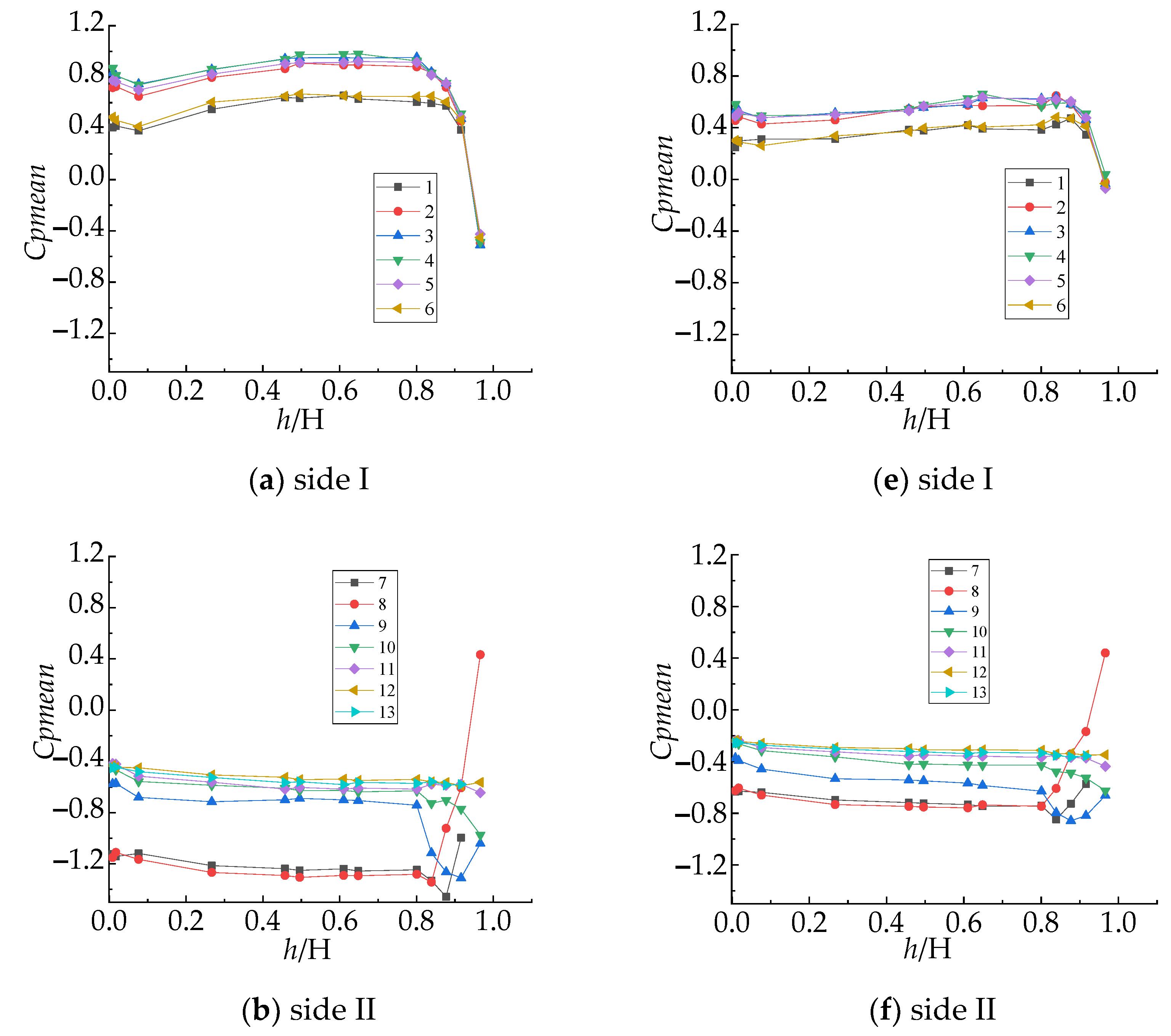
3.1.1. Distribution of Mean Wind Pressure Coefficient with Height
- (a)
- In Figure 4, comparing the average wind pressure coefficients Cpmean between the uniform flow and the boundary layer flow, the Cpmean value under the uniform flow field is generally slightly higher than that under the influence of the boundary layer flow, indicating that the effect of the regional wind environment in which the building is located cannot be ignored;
- (b)
- When focusing on the wind pressure coefficient of the building facades, it is found that the average wind pressure coefficients for the windward area (side I) show positive values (except the top point at layer N), and the highest measurements are found in the upper-middle part of building and gradually decrease along both sides. The average wind pressure coefficients of the measuring points for lines 1 and 6 are significantly lower than those for the middle measuring points (lines 2–5), both in the uniform flow and the boundary layer flow. The measuring points on the top floor of the building reflect negative pressures, indicating that the roof airflow is separated and that vortexes might occur;
- (c)
- The measurement values for sides II–IV are determined by negative pressure and the values are evenly distributed with the increasing height without significant differences. However, influenced by the concave and convex shape of the building, lines 7 and 8 contribute the maximum negative wind pressure on the building surface, while the values of lines 25 and 26 at the symmetrical position are more moderate.
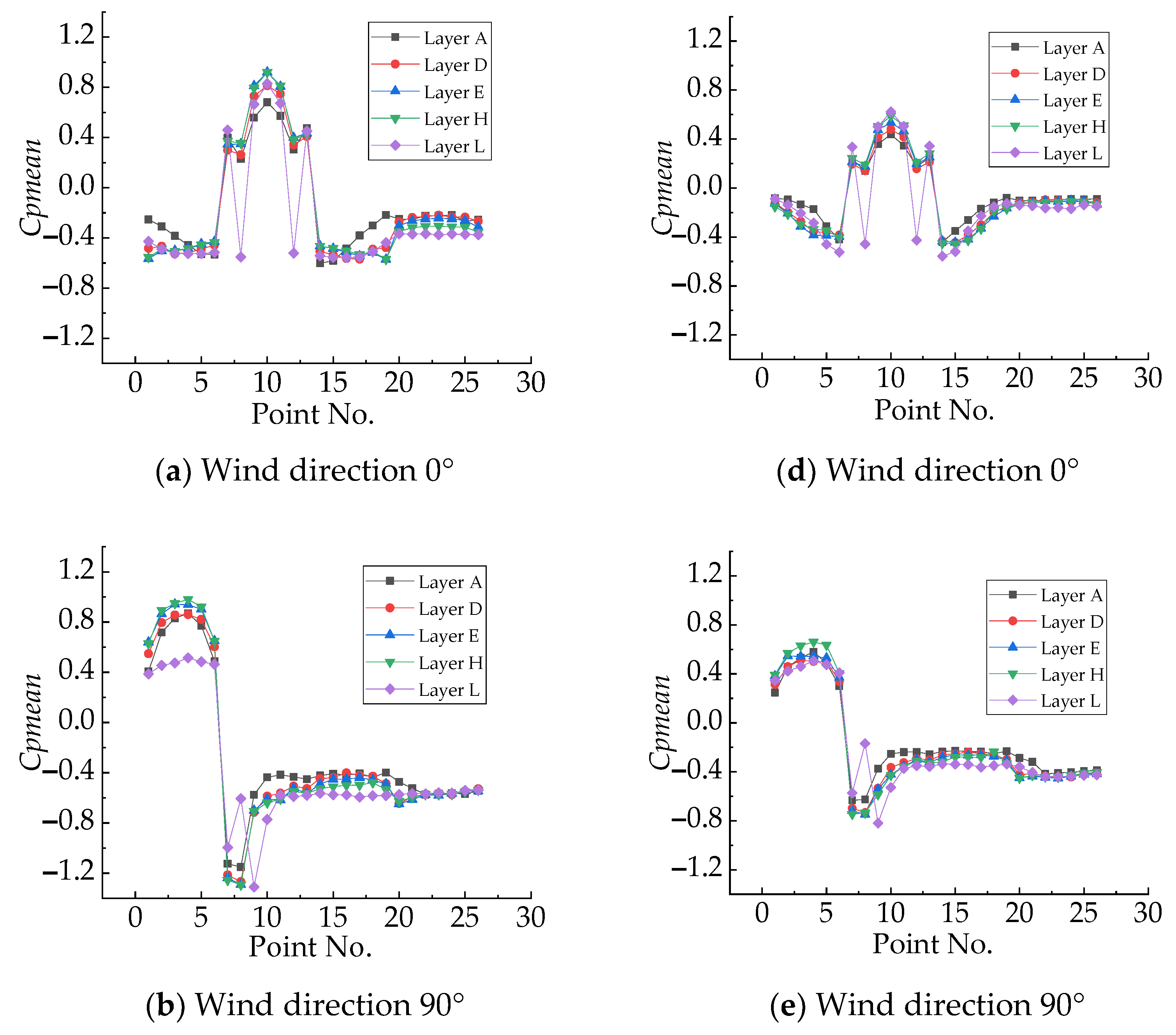
3.1.2. Distribution of Mean Wind Pressure Coefficient in the Horizontal Planes
- (a)
- Due to the existence of concave and convex areas in the building itself, the wind pressure distribution is different from that in conventional buildings. For example, when the wind direction angle is 0°, the curve of the top layer shows an obvious trend of jumping from positive pressure to negative pressure at points 8 and 12 (see Figure 6a,b). Based on the evaluation of the flow phenomenon around the building, the reason could be that, when the wind crosses the roof, as it is hindered by the raised part of the roof, the incoming wind blows across the roof more urgently, which causes obvious suction toward the 8 and 12 positions on the top layer;
- (b)
- Under both the uniform and the turbulent boundary layer inflow conditions, the overall trends for all working conditions are basically the same, but a discrepancy in the wind pressure data between these two inflow conditions could still be observed. For example, when the wind direction angle is 0°, the wind pressure values for the five horizontal layers selected in the uniform flow inflow condition (Figure 6a) are basically higher than the values in the boundary layer condition (Figure 6d). Furthermore, it is found that the maximum positive value occurs at point 10 on layers E and H in both Figure 6a,d, but the deviation reaches up to 0.2, which is a large gap for the wind pressure coefficient. Through the investigation of all the situations in Figure 6, the maximum deviation between these two inflow conditions is found to be close to 0.5, which appears at point 9 on layer L (see Figure 6b,e);
- (c)
- The maximum wind pressure coefficient on the windward side appears at the height of 2/3 H (layer H).
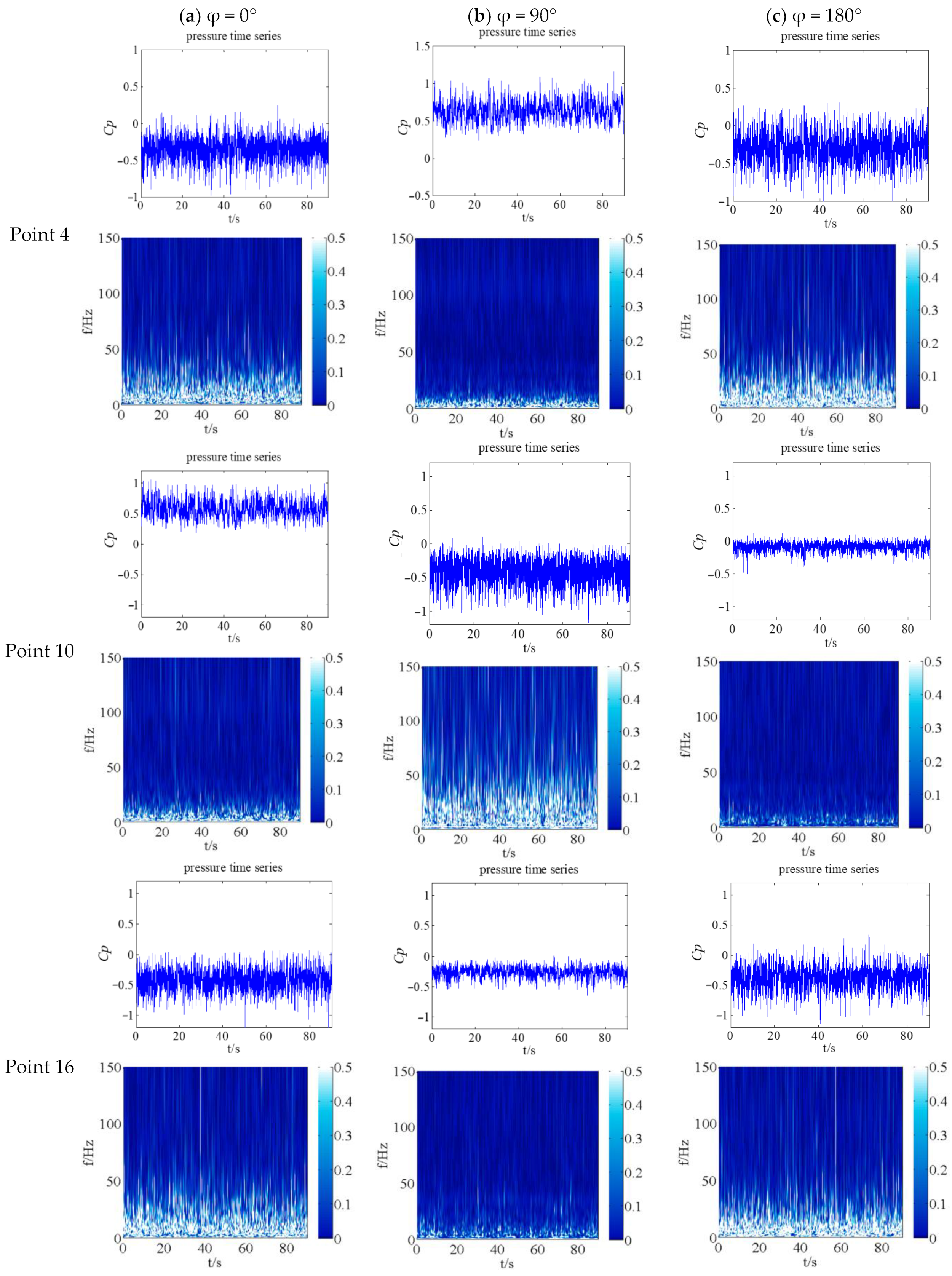
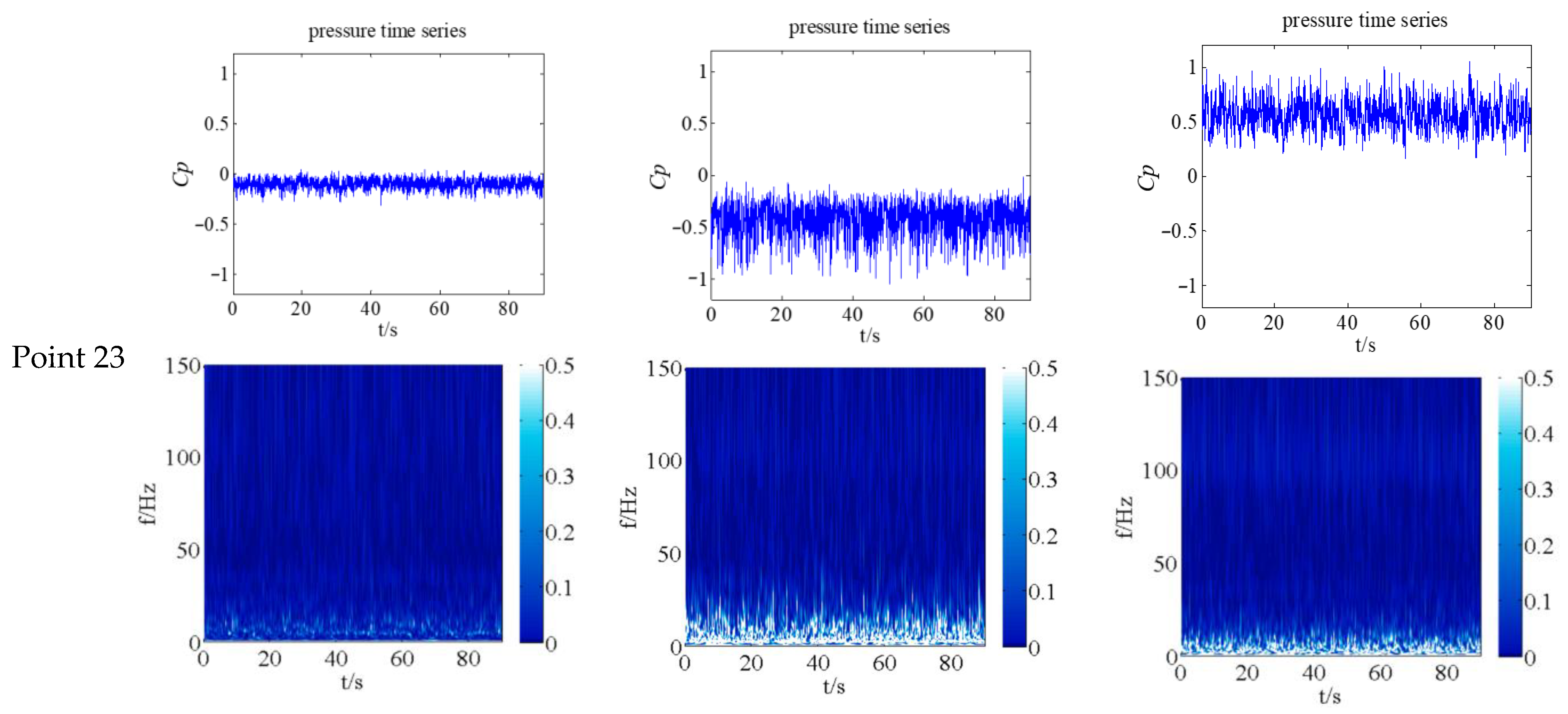
3.2. Instantaneous Wind Pressure Coefficients
4. Discussion
- (a)
- The distribution of the wind pressure coefficients of the building model is affected by the inflow condition. It is found that the average wind pressure coefficients in the uniform incoming condition are generally larger than those in the inflow condition with a turbulent boundary layer, which is close to the reality. The average deviation between these two inflow conditions is found to be nearly 0.15. However, because the uniform inflow condition is easy to realize, the results for some studies adopting the uniform inflow condition are bound to be different from the real situation. Therefore, in the study of the wind resistance characteristics of buildings, the incoming flow conditions must be confirmed and defined correctly.Furthermore, the influence of the different wind directions on the wind loads cannot be ignored either. For the slab-shaped building with significant concave and convex shapes involved in this study, there is a huge pressure gradient on the windward side with different wind directions; that is, the wind pressure decreases sharply over a short distance range until a relatively large negative pressure appears. This phenomenon is relatively rare in existing reports. The remarkable pressure gradients can cause further damage, which should also be paid attention to. It is best to conduct an all-wind-directions study.
- (b)
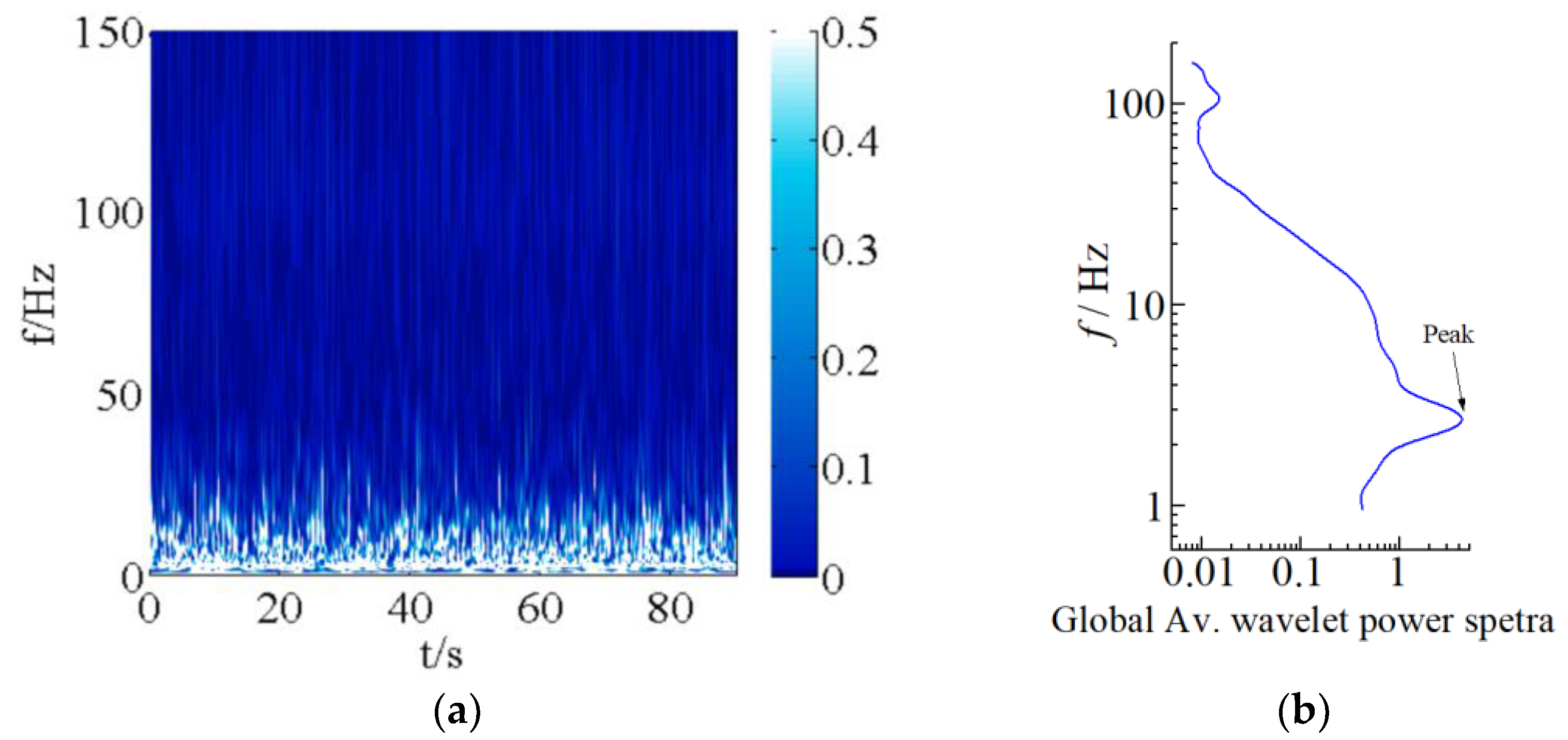
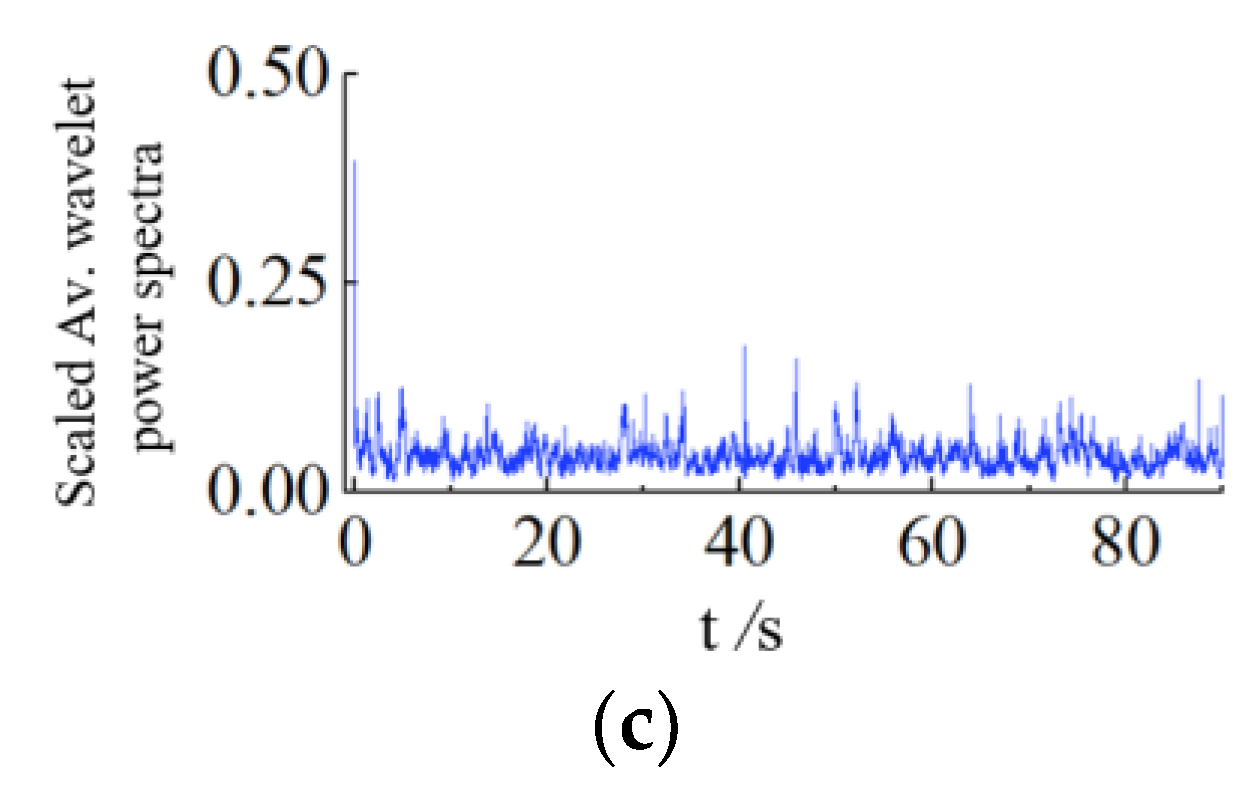
- The wind pressure acting on the building surface shows significant unsteady pulsating characteristics with a low dominant frequency. The dominant frequency of the wind pressure fluctuation was obtained using wind power spectra analysis and is roughly 3 Hz. Moreover, compared to the calculated values for first-order natural frequencies of different building structures based on empirical formulas [3] (14.89 Hz for a masonry structure; 3.99 Hz for a reinforced concrete frame structure; 15.69 Hz for a reinforced concrete shear structure), it can be seen that the dominant frequency of the rigid building model is very similar to the empirical values, especially the frequency of the reinforced concrete frame structure. Extending this finding to actual engineering, this phenomenon would trigger the wind-induced vibration of the structure. Accurate estimation of wind pressure pulsation characteristics is the premise of research on the wind-induced vibrations of structures and the guarantee of wind safety calculations.
- (c)
- The DTC Initium electronic scanning pressure measurement system, a high-precision system with a resolution of ± 0.003%FS, was adopted in the research, ensuring the accuracy of the measurement results to a large extent. However, there are still some factors that have to be considered in the test, such as the accuracy of the wind incoming flow, errors in testing location markings on the building surfaces, and so on.
5. Conclusions
- (a)
- The influence of inflow conditions around the building on the wind pressure cannot be ignored. The wind pressure on the building under these two conditions varies obviously, and the boundary layer inflow condition can be recommended in comparison to the uniform inflow condition. The wind incoming condition should be accurately evaluated when wind resistance design is undertaken;
- (b)
- Attention should be paid to the influence of the building shape on the wind pressure distribution. When there are obvious concave and convex surfaces in the architectural design, as in the building in this study, a remarkable pressure gradient appears and relatively large negative wind pressure occurs even on the windward sides. This also highlights the significance of conducting the research on the impact of different wind directions;
- (c)
- The wind pressure pulsates intensively, with the instantaneous pulsating energy changing significantly. This shows the unsteady nature of the wind loads acting on the building. Furthermore, the pulsations occur in the low-frequency band (0–50 Hz) and the global dominant frequency is found to be about 3 Hz. These characteristics may cause wind-induced structural vibration and should be considered during the design of buildings.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Hunt, A. Wind-tunnel measurements of surface pressures on building models at several scales. J. Wind Eng. Ind. Aerodyn. 1982, 10, 137–163. [Google Scholar] [CrossRef]
- Zhang, J.W.; Li, Q.S. Wind tunnel test and field measurement study of wind effects on a 600m high-super-tall building. Struct. Des. Tall Spec. Build. 2017, 26, e1385. [Google Scholar] [CrossRef]
- GB 50009-2012; Load Code for the Design of Building Structures. China Building Industry Press: Beijing, China, 2012.
- Wu, X.; Li, Q.S.; Li, Y. Test on surface wind pressure distributions and wind load characteristics for complex shape high-rise building. J. Archit. Civ. Eng. 2014, 1, 76–82. [Google Scholar]
- Yang, C. Study on Characteristic of High-Rise Buildings Wind Load with Numerical Simulation of Wind Tunnel. Master’s Thesis, Huazhong University of Science and Technology, Wuhan, China, 2016. [Google Scholar]
- Li, H. Experimental study on wind pressure of tall building. J. Exp. Mech. 2000, 2, 157–162. [Google Scholar]
- Li, Q.S.; Fu, J.Y.; Xiao, Y.Q.; Li, Z.N.; Ni, Z.H.; Xie, Z.N.; Gu, M. Wind tunnel and full-scale study of wind effects on China’s tallest building. Eng. Struct. 2006, 28, 1745–1758. [Google Scholar] [CrossRef]
- Li, Q.S.; Li, Y.G.; Zhi, L.H. Experimental study on wind pressure distribution characteristics of typical high-rise residential buildings. J. Hunan Univ. (Nat. Sci. Ed.) 2011, 4, 14–19. [Google Scholar]
- Grossmann, A.; Morlet, J. Decomposition of hardy functions into square integrable wavelets of constant shape. SIAM J. Math. Anal. 1984, 15, 723–736. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G.P. A practical guide to wavelet analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Geurts CP, W.; Hajj, M.R.; Tieleman, H.W. Continuous wavelet transform of wind and wind-induced pressures on a building in suburban terrain. J. Wind Eng. Ind. Aerodyn. 1998, 74–76, 609–617. [Google Scholar] [CrossRef]
- Gurley, K.R.; Kareem, A. First- and higher-order correlation detection using wavelet transforms. J. Eng. Mech. 2003, 2, 188–201. [Google Scholar] [CrossRef]
- Kareem, A.; Kijewski, T. Time-frequency analysis of wind effects on structures. J. Wind Eng. Ind. Aerodyn. 2002, 90, 1435–1452. [Google Scholar] [CrossRef]
- Li, H.N.; Yi, T.H.; Wang, G.X. Wavelet analysis and its application in structural wind engineering. J. Vib. Shock. 2008, 9, 11–16. [Google Scholar]
- Yamada, M.; Ohkitani, K. Orthonormal wavelet analysis of turbulence. Fluid Dyn. Res. 1991, 8, 101–115. [Google Scholar] [CrossRef]
- Zeldin, B.A.; Spanos, P.D. Random field representation and synthesis using wavelet bases. J. Appl. Mech. 1996, 63, 946. [Google Scholar] [CrossRef]
- Hajj, M.R.; Tieleman, H.W. Application of wavelet analysis to incident wind in relevance to wind loads on low-rise structure. Trans. ASME 1996, 128, 874–876. [Google Scholar] [CrossRef]
- Hajj, M.R.; Jordan, D.A.; Tieleman, H.W. Analysis of atmospheric wind and pressures on a low-rise building. J. Fluids Struct. 1998, 12, 537–547. [Google Scholar] [CrossRef]
- Jordan, D.A.; Hajj, M.R.; Tieleman, H.W. Wavelet analysis of the relation between atmospheric wind and pressure fluctuations on a low-rise building. J. Wind Eng. Ind. Aerodyn. 1997, 69, 647–655. [Google Scholar] [CrossRef]
- Dunyak, J.; Gilliam, X.; Peterson, R.; Smith, D. Coherent gust detection by wavelet transform. J. Wind Eng. Ind. Aerodyn. 1998, 77–78, 467–478. [Google Scholar] [CrossRef]
- Zhao, Y.; Cao, S.; Wu, Y.; Yukio, T.; Ozono, S. Comparison of several non-stationary methods for analysis of time history of non-stationary wind pressure. J. China Civ. Eng. 2011, 44, 51–57. [Google Scholar]
- Wang, H.; Xu, Z.; Teng, W.; Mao, J. Evolutionary power spectral density of recorded typhoons at Sutong Bridge using harmonic wavelets. J. Wind Eng. Ind. Aerodyn. 2018, 177, 197–212. [Google Scholar] [CrossRef]
- Pettit, C.L.; Jones, N.P.; Ghanem, R. Detection and simulation of roof-corner pressure transients. J. Wind Eng. Ind. Aerodyn. 2002, 90, 171–200. [Google Scholar] [CrossRef]
- Huang, X.; Gu, M. Wavelt analysis of pressure fluctuations on cantilevered arc roofs. J. Tongji Univ. (Natl. Sci.) 2008, 36, 586–591. [Google Scholar]
- Le, T.; Matsumoto, M.; Shirato, H. Spanwise coherent structure of wind turbulence and induced pressure on rectangular cylinders. Wind Struct. 2009, 12, 441–455. [Google Scholar] [CrossRef]
- Le, T.; Caracoglia, L. Rectangular prism pressure coherence by modified Morlet continuous wavelet transform. Wind. Struct. 2015, 20, 661–682. [Google Scholar] [CrossRef]
- Le, T.H.; Tamura, Y.; Matsumoto, M. Spanwise pressure coherence on prisms using wavelet transform and spectral proper orthogonal decomposition based tools. J. Wind Eng. Ind. Aerodyn. 2011, 99, 499–508. [Google Scholar] [CrossRef]
- Shen, J.; Li, C. Wavelet analysis for coherence of full-scale measured wind pressure on a super tall building. J. Vib. Shock. 2010, 29, 162–168. [Google Scholar]
- Jin, M.; Li, C. Non-Stationary Wind pressure prediction based on a hybrid decomposition algorithm of wavelet packet decomposition and variational mode decomposition. IOP Conf. Ser. Earth Environ. Sci. 2018, 189, 52038. [Google Scholar] [CrossRef]
- Karimpour, A.; Rahmatalla, S. Extended empirical wavelet transformation: Application to structural updating. J. Sound Vib. 2021, 500, 116026. [Google Scholar] [CrossRef]
- Hnaien, N.; Hassen, W.; Kolsi, L.; Mesloub, A.; Alghaseb, M.A.; Elkhayat, K.; Abdelhafez, M.H.H. CFD Analysis of Wind Distribution around Buildings in Low-Density Urban Community. Mathematics 2022, 10, 1118. [Google Scholar] [CrossRef]
- Liu, Y.G.; Liang, X.S.; Weisberg, R.H. Rectification of the bias in the wavelet power spectrum. J. Atmos. Ocean. Technol. 2007, 24, 2093–2102. [Google Scholar] [CrossRef]
- Ye, F.; Gu, M. Frequency characteristics of wind pressure on super-tall buildings. J. Tongji Univ. 2006, 34, 285–290. [Google Scholar]
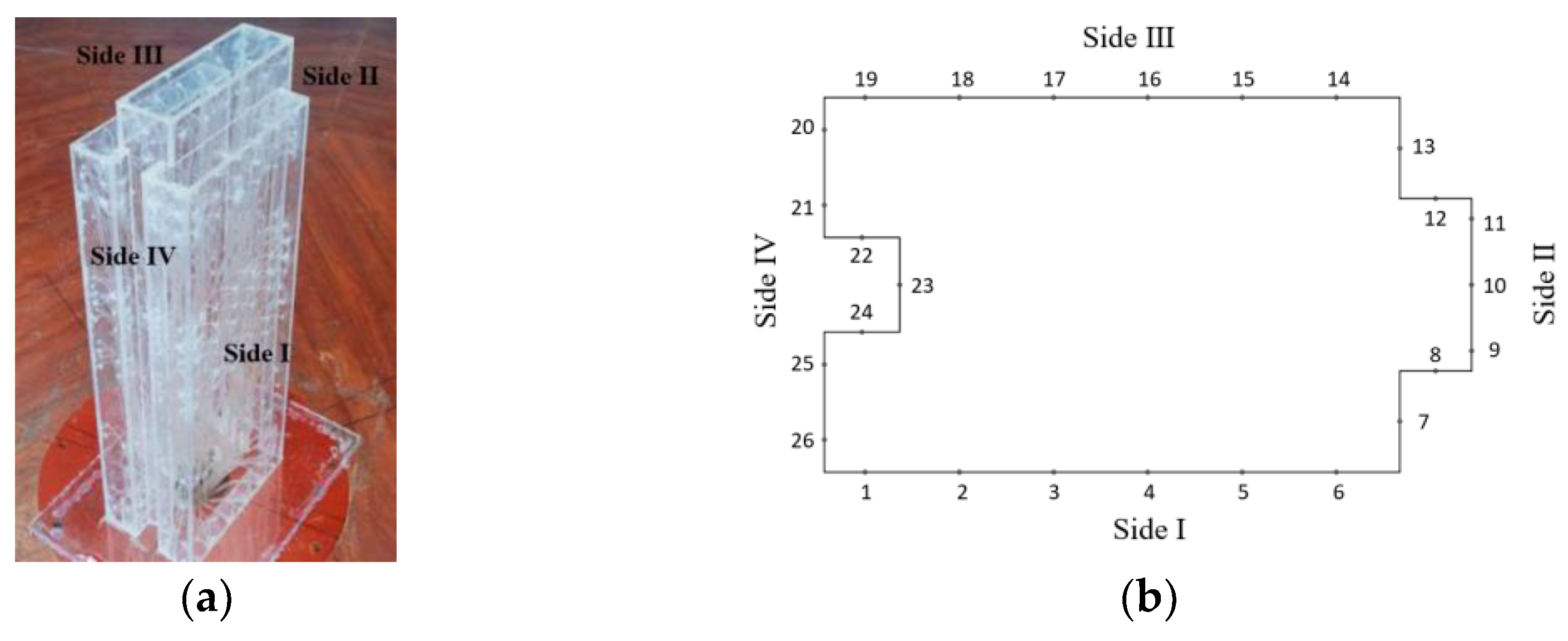

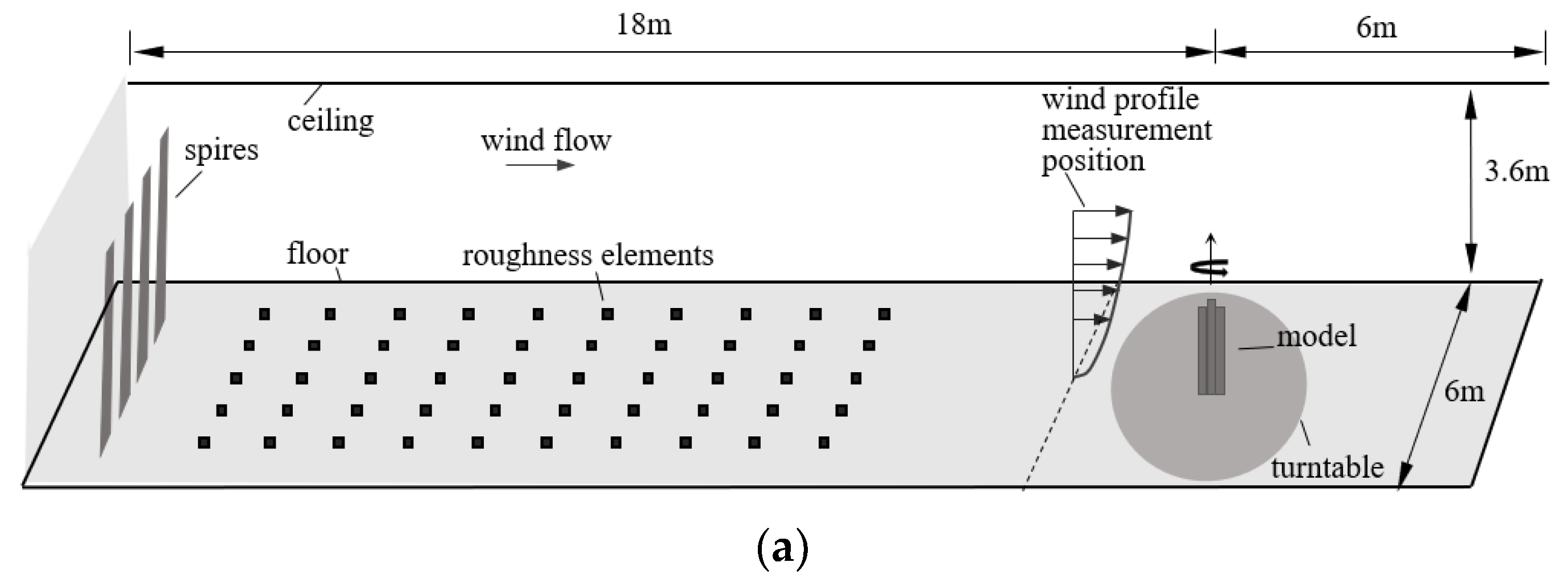
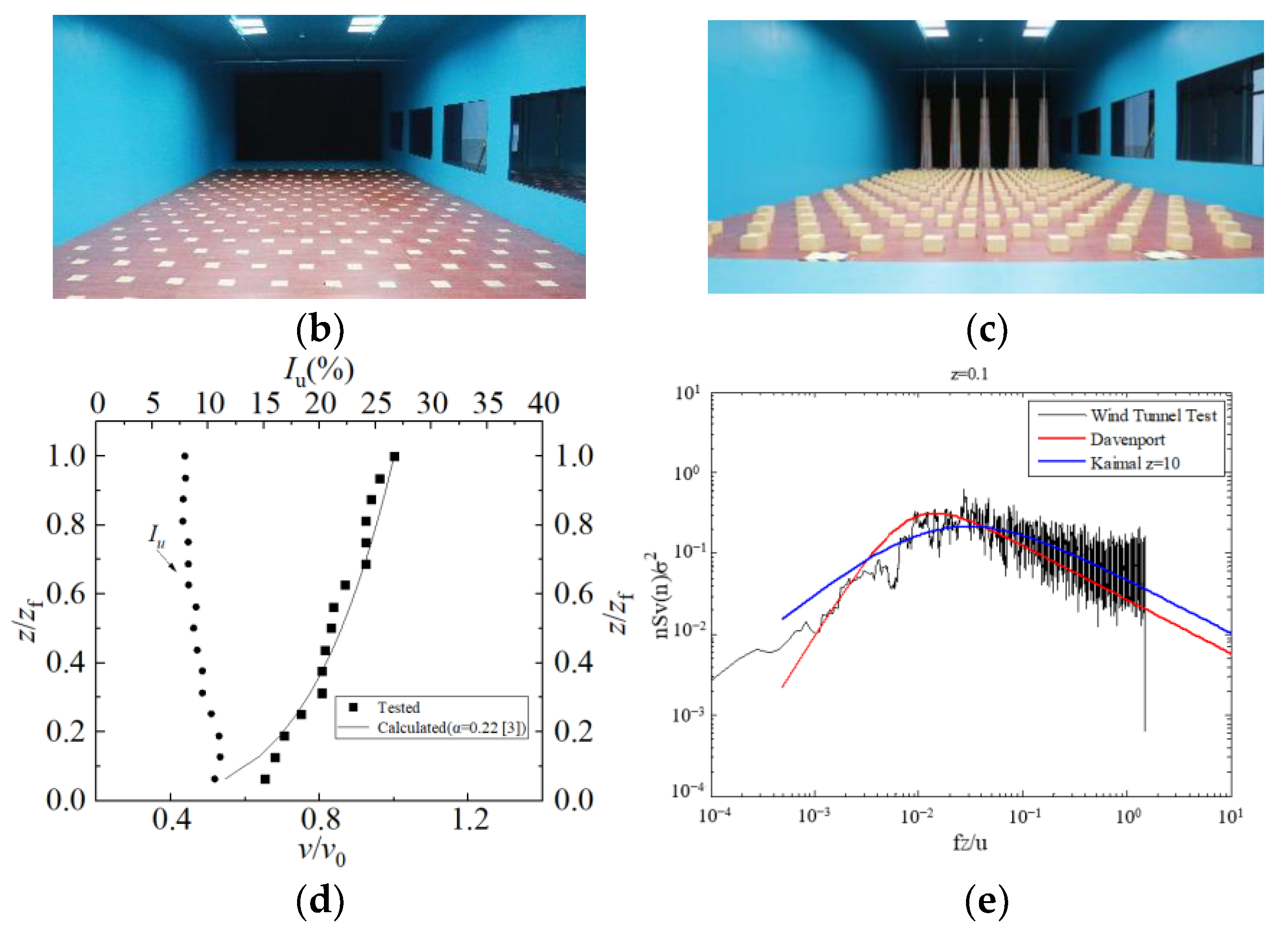
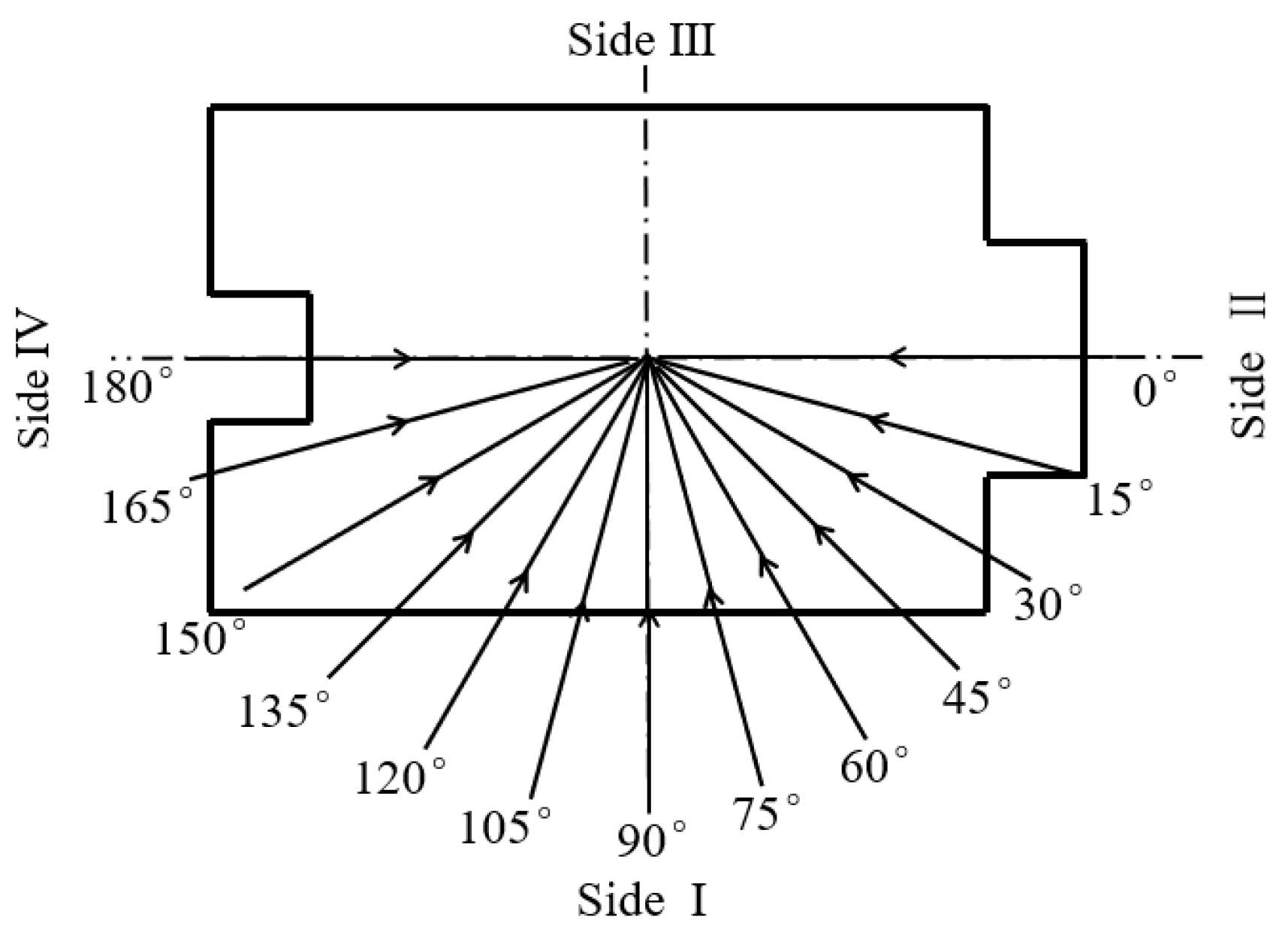



| Inflow Condition in the Wind Tunnel | Wind Speeds v (m/s) | Wind Directions φ |
|---|---|---|
| UF | 10 | 0°, 15°, 30°, 45°, 60°, 75°, 90°, 105°, |
| BL | 120°, 135°, 150°, 165°, 180° |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Q.; Zhang, X. Experimental Analysis of Wind Pressure Characteristics in a Reduced-Scale Model of a Slab-Shaped High-Rise Building at Different Inflow Conditions with Various Wind Flow Directions. Processes 2022, 10, 1645. https://doi.org/10.3390/pr10081645
Chen Q, Zhang X. Experimental Analysis of Wind Pressure Characteristics in a Reduced-Scale Model of a Slab-Shaped High-Rise Building at Different Inflow Conditions with Various Wind Flow Directions. Processes. 2022; 10(8):1645. https://doi.org/10.3390/pr10081645
Chicago/Turabian StyleChen, Qiuhua, and Xiaoxi Zhang. 2022. "Experimental Analysis of Wind Pressure Characteristics in a Reduced-Scale Model of a Slab-Shaped High-Rise Building at Different Inflow Conditions with Various Wind Flow Directions" Processes 10, no. 8: 1645. https://doi.org/10.3390/pr10081645
APA StyleChen, Q., & Zhang, X. (2022). Experimental Analysis of Wind Pressure Characteristics in a Reduced-Scale Model of a Slab-Shaped High-Rise Building at Different Inflow Conditions with Various Wind Flow Directions. Processes, 10(8), 1645. https://doi.org/10.3390/pr10081645





