Optimization of Two-Dimensional Extended Warranty Scheme for Failure Dependence of a Multi-Component System with Improved PSO–BAS Algorithm
Abstract
:1. Introduction
- (1)
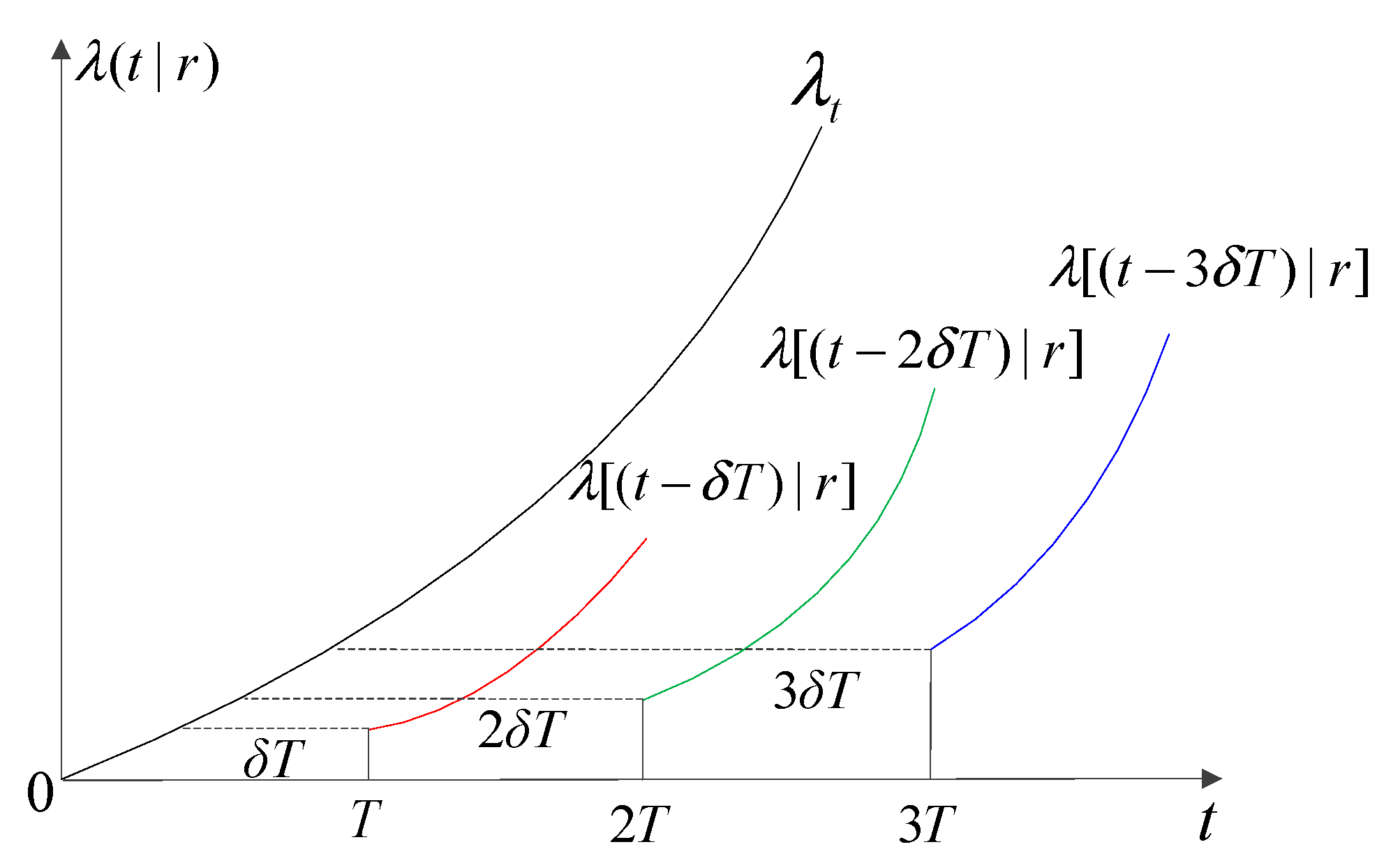
- For a multi-component system with unidirectional failure dependence, the present study attempts to develop a failure rate model through a failure-dependence analysis for the system. The protocols for both preventive (imperfect) maintenance and corrective (minimum) maintenance are introduced, and their repair effects are described using the virtual age method and minimum maintenance theory, respectively. Meanwhile, the non-homogeneous Poisson process (NHPP) theory was adopted for establishing a model for the number of system failures in a period of time, which provides an important basis for the model of warranty cost and for system availability.
- (2)
- For a failure-dependence system with a 2D warranty, under the case that the system is replaced when the warranty expires, models of warranty cost per unit time and the availability were established. In the case study, an optimal 2D EW scheme for the gearbox of an EMU system was determined via the PSO–BAS algorithm, with the minimum warranty cost as the decision objective and the availability acceptable to users as the constraint. The warranty scheme (decision variables) included the optimal 2D EW period and the preventive maintenance interval.
2. Related Work
2.1. 2D Warranty
2.2. Extended Warranty
2.3. Availability
2.4. The Failure Dependence
3. Model Description and Assumptions
3.1. Failure-Dependence Analysis
3.2. Model Description
3.3. Model Assumptions
- (1)
- The components of the system are connected in series;
- (2)
- The failure rate of the components increases with time and utilization rate;
- (3)
- The preventive maintenance cost does not alter with the preventive maintenance time;
- (4)
- The cost for a single corrective maintenance action does not change with the time and frequency of the maintenance, and the component failure rate is not altered by such maintenance.
4. Optimization Model Construction
4.1. Failure Rate Model
4.2. Imperfect Preventive Maintenance Strategy
4.3. Corrective Maintenance Strategy
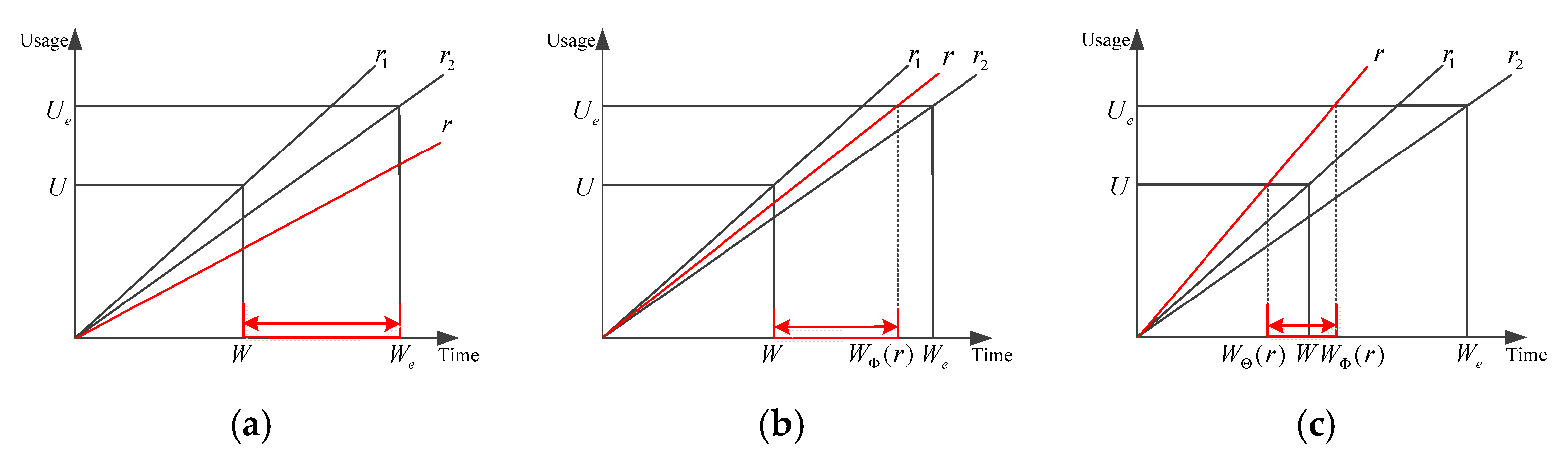
4.4. 2D EW Cost Model
- (1)
- As shown in Figure 3a, when , the total expected cost of the minimum maintenance for the studied system within the interval of the th preventive maintenance is:where stands for the minimum maintenance cost of the key component, and indicates the minimum maintenance cost of the subsystem.
- (2)
- As shown in Figure 3b, when , the total expected expenditure for the studied system’s minimum maintenance within the th preventive maintenance interval is:
- (3)
- As shown in Figure 3c, when , the total expected expenditure for the system’s minimum maintenance within the interval of the th preventive maintenance is:
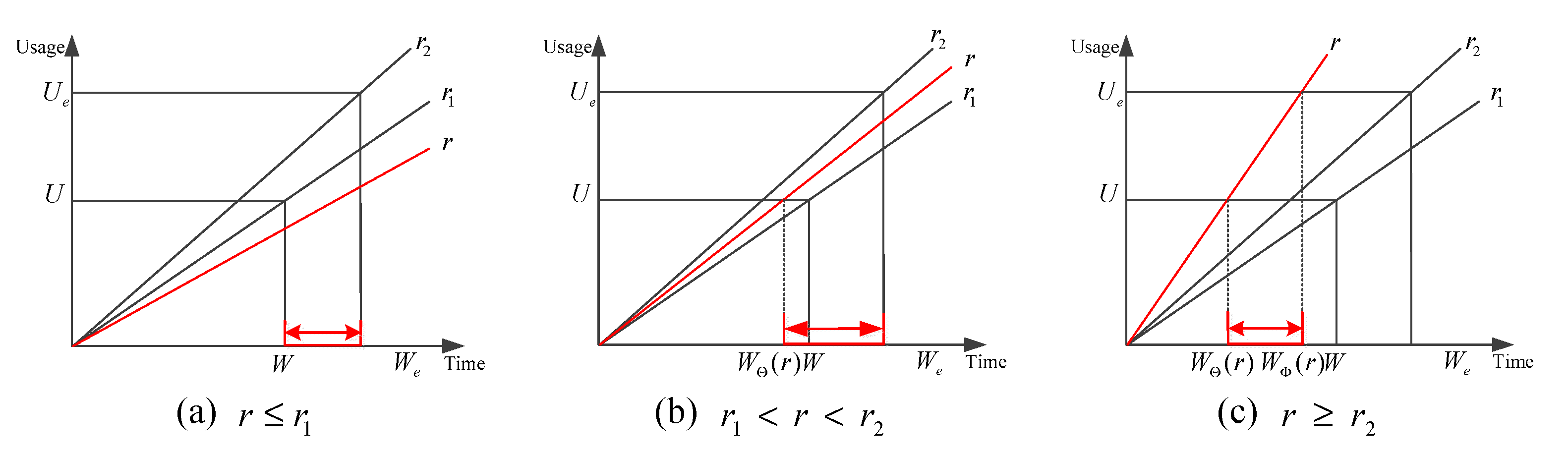
- (1)
- As shown in Figure 4a, when , the total expected expenditure for the system’s minimum maintenance within the th preventive maintenance interval is:
- (2)
- As shown in Figure 4b, when , the total expected expenditure for the system’s minimum maintenance within the th preventive maintenance interval is:
- (3)
- As shown in Figure 4c, when , the total expected expenditure for the system’s minimum maintenance within the th preventive maintenance interval is:
4.5. 2D EW Availability Model
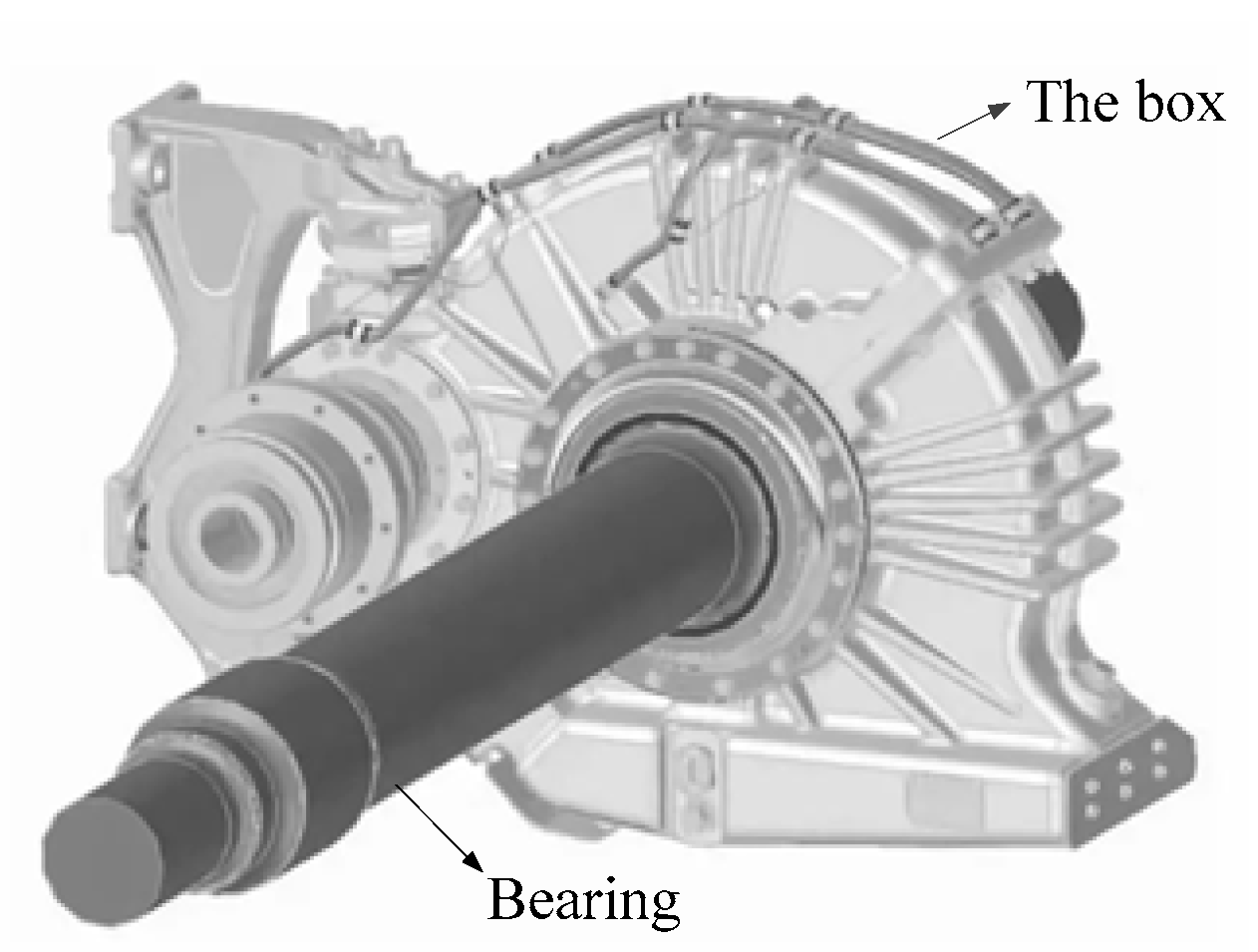
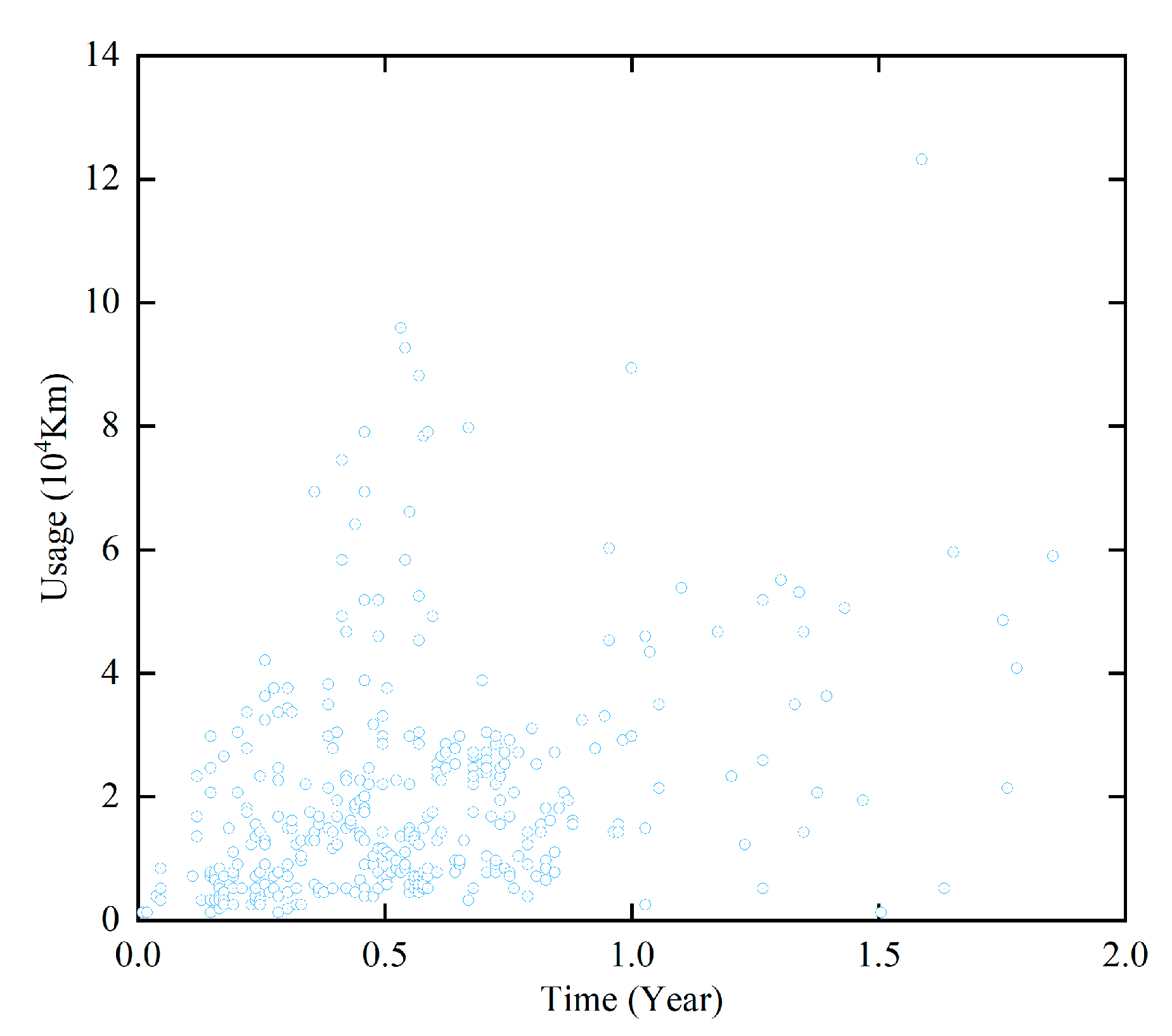
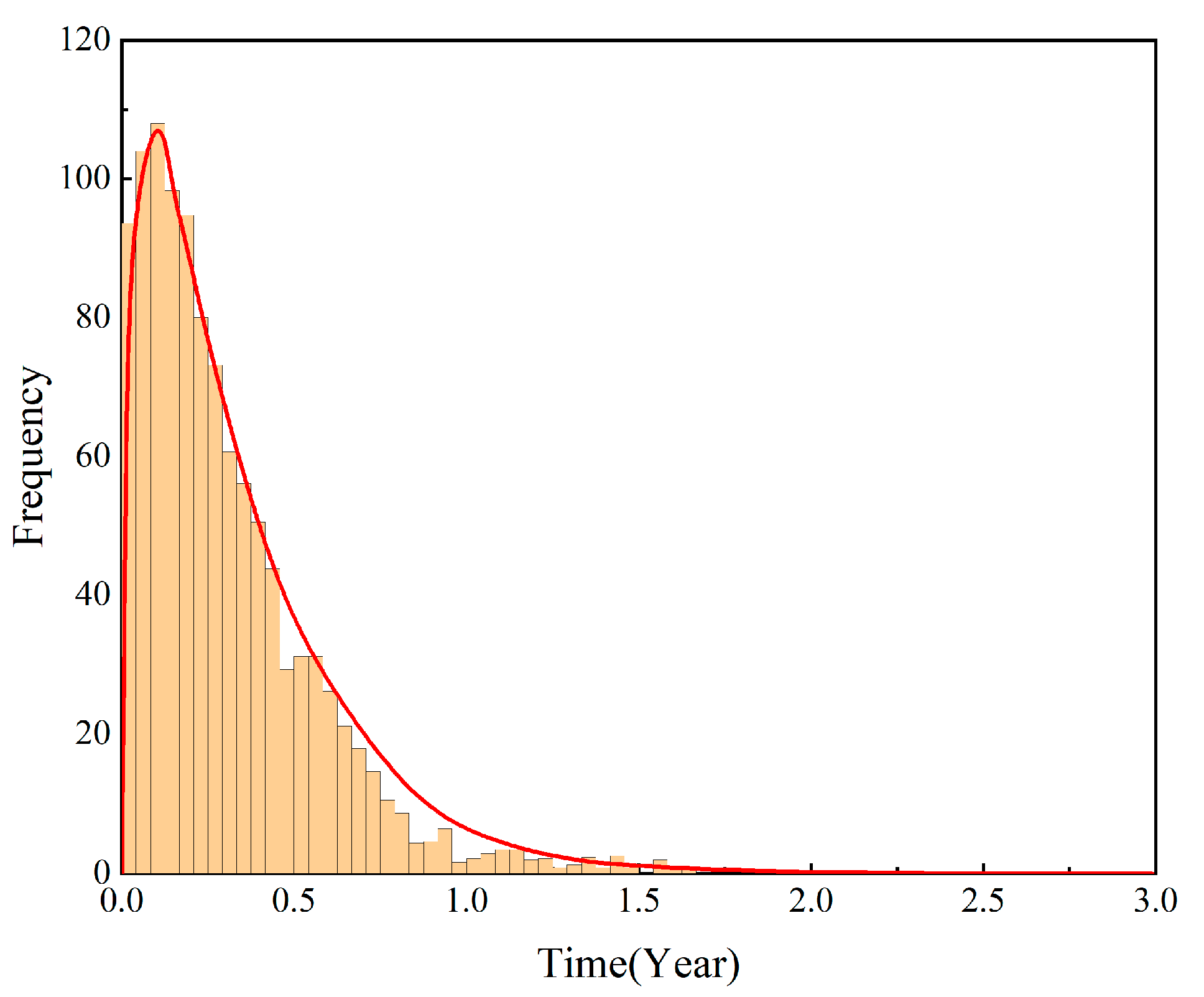
5. Case Analysis
5.1. Problem Description
5.2. Model Solution
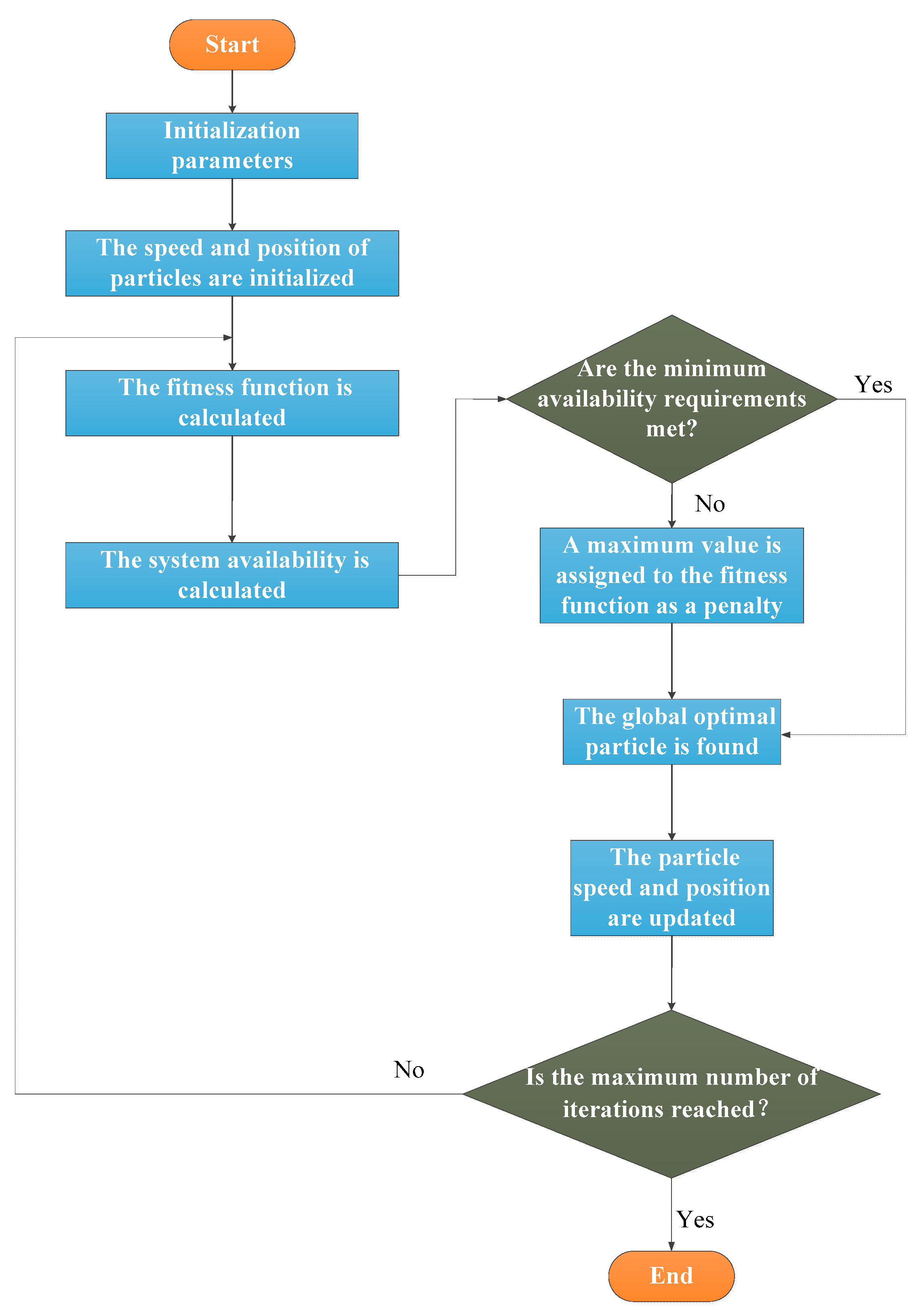
5.2.1. The Grid Search Method
5.2.2. The PSO–BAS Algorithm
5.3. Result Analysis
5.3.1. Dimension Reduction Analysis
5.3.2. Comparative Analysis
- (1)
- According to the analysis in Section 4.2, the 2D EW period was (8.4 years, 7.2 × 104 KM), and the preventive maintenance interval was 0.3 years. To verify the impact of imperfect preventive maintenance on reducing the EW cost and improving system availability, this paper compared the EW cost and the system availability of the gearbox system when only adopting corrective maintenance, and the gearbox system when adopting both corrective maintenance and imperfect preventive maintenance. When the system did not carry out preventive (imperfect) maintenance within the EW duration, i.e., the preventive maintenance interval was set to 8.4 years, the corresponding EW cost per unit time and the system availability were as follows:
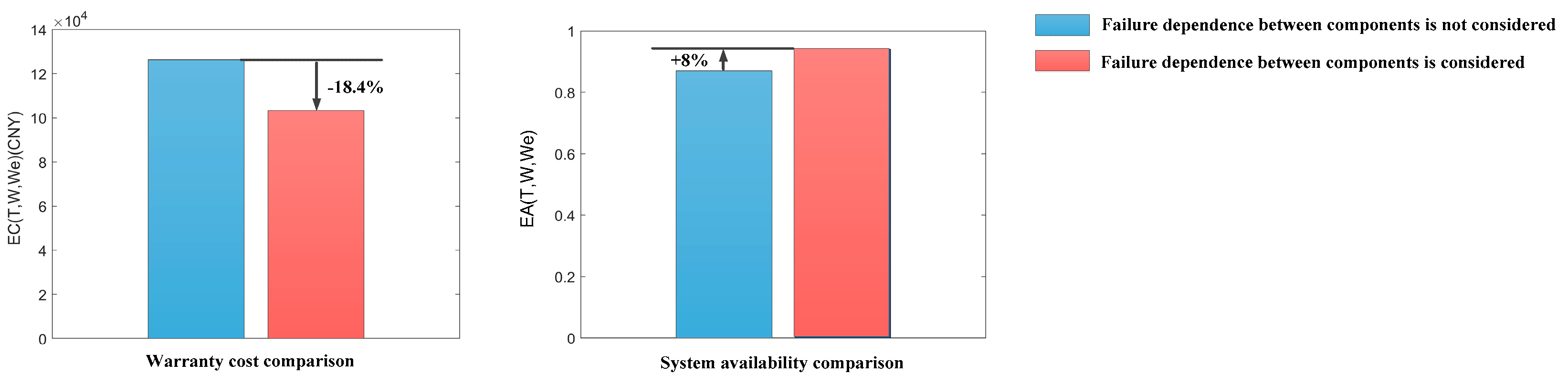
- (2)
- This paper considered the failure dependence between the bearing and the gear. If the failure dependence between the components was ignored, assuming that , the EW period and the preventive maintenance interval that minimized the EW cost per unit time could be calculated according to the model. The EW cost per unit time and the system availability under this scheme were as follows:
5.4. Sensitivity Analysis
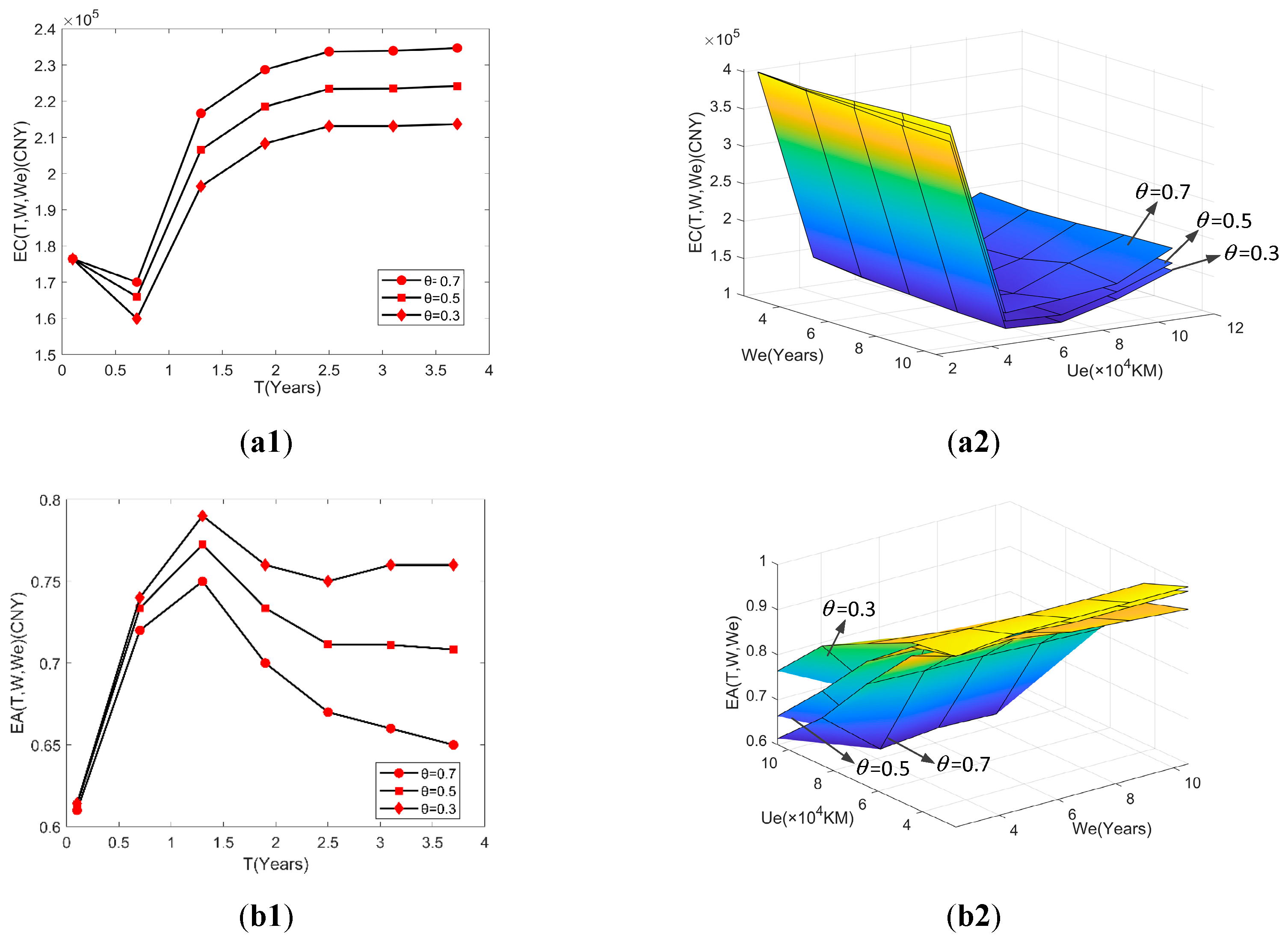
5.4.1. Failure-Dependence Coefficient Impact Analysis
5.4.2. Improvement Factor Impact Analysis
6. Conclusions
- (1)
- More complex failure dependencies between system components should be considered, such as common cause failure, interactive failure, and retained redundancy.
- (2)
- The failure dependence and economic dependence among multiple components should be considered comprehensively to make warranty decisions.
- (3)
- Considering market factors, the joint decision making of two-dimensional extended warranty schemes and pricing should be carried out.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Variables | |
| Basic warranty period of time dimension under design utilization | |
| Basic warranty period of usage dimension under design utilization | |
| Extended warranty period of time dimension under design utilization | |
| Extended warranty period of usage dimension under design utilization | |
| The interval of preventive (imperfect) maintenance | |
| The calendar time | |
| Component of system utilization | |
| The time of the first failure based on the design rate of utilization | |
| The time of the first failure based on the real rate of | |
| Imperfect preventive maintenance improvement factor | |
| Failure-dependence coefficient | |
| Scale parameter of the failure probability density function | |
| The AFT parameter | |
| Failure times of the key component within the interval of the kth preventive maintenance | |
| Functions | |
| The start time of the EW period for the utilization rate | |
| Probability density function of utilization | |
| Two-dimensional extended warranty cost in (a, b) | |
| The key component failure rate within the in-terval of the kth preventive maintenance for the utilization rate | |
| The subsystem failure rate within the interval of the kth preventive maintenance for the utilization rate | |
| Failure probability density function for the utili-zation rate | |
| Reliability function for the utilization rate | |
| The end time of the EW period for the utilization rate | |
| The real failure rate of the component a for the utilization rate | |
References
- Huang, Y.S.; Fang, C.C.; Lu, C.M.; Tseng, T.L.B. Optimal Warranty Policy for Consumer Electronics with Dependent Competing Failure Processes. Reliab. Eng. Syst. Saf. 2022, 222, 108418. [Google Scholar] [CrossRef]
- Huang, Y.S.; Huang, C.D.; Ho, J.W. A customized two-dimensional extended warranty with preventive maintenance. Eur. J. Oper. Res. 2017, 257, 525–535. [Google Scholar] [CrossRef]
- Mitra, A. Warranty parameters for extended two-dimensional warranties incorporating consumer preferences. Eur. J. Oper. Res. 2021, 219, 971–978. [Google Scholar] [CrossRef]
- Dong, E.; Cheng, Z.; Wang, R. Two-Dimensional Extended Warranty Strategy for an Economic Dependence Multi-Component Series System with Grid Search Algorithm. IEEE Access 2022, 10, 26876–26894. [Google Scholar] [CrossRef]
- Abeygunawardane, S.K.; Jirutitijaroen, P. Application of Probabilistic Maintenance Models for Selecting Optimal Inspection Rates Considering Reliability and Cost Tradeoff. IEEE Trans. Power Deliv. 2014, 29, 178–186. [Google Scholar] [CrossRef]
- Wang, J.X.; Lin, B.L.; Jin, J.C. Optimizing the Shunting Schedule of Electric Multiple Units Depot Using an Enhanced Particle Swarm Optimization Algorithm. Comput. Intell. Neurosci. 2016, 2016, 5804626. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mao, B.; Xie, Z.; Wang, Y.; Handroos, H.; Wu, H.; Shi, S. A hybrid differential evolution and particle swarm optimization algorithm for numerical kinematics solution of remote maintenance manipulators. Fusion Eng. Des. 2017, 124, 587–590. [Google Scholar] [CrossRef]
- Pereira, C.M.; Lapa, C.M.; Mol, A.C.; Da Luz, A.F. A Particle Swarm Optimization (PSO) approach for non-periodic preventive maintenance scheduling programming. Prog. Nucl. Energy 2010, 52, 710–714. [Google Scholar] [CrossRef]
- Jiang, X.Y.; Li, S. BAS: Beetle Antennae Search Algorithm for Optimization Problems. Int. J. Robot. Control. 2017, 1, 10724. [Google Scholar] [CrossRef]
- Wang, X.; Xie, W. Two-dimensional warranty: A literature review. Proc. Inst. Mech. Eng. Part O J. Risk Reliab. 2017, 232, 284–307. [Google Scholar] [CrossRef]
- Iskandar, B.P.; Murthy, D.N.P.; Jack, N. A new repair–replace strategy for items sold with a two-dimensional warranty. Comput. Oper. Res. 2005, 32, 669–682. [Google Scholar] [CrossRef]
- Cheng, Z.H.; Yang, Z.Y.; Zhao, J.M.; Wang, Y.B.; Li, Z.W. Preventive maintenance strategy optimizing model under twodimensional warranty policy. Eksploat. Niezawodn. 2015, 17, 365–373. [Google Scholar] [CrossRef]
- Cheng, Z.H.; Yang, Z.Y.; Yang, H.B. Optimization model of equipment two-dimensional warranty strategy under preventive maintenance. Ind. Eng. J. 2017, 20, 79–86. [Google Scholar]
- Chen, T.; Popova, E. Maintenance policies with two-dimensional warranty. Reliab. Eng. Syst. Saf. 2002, 77, 61–69. [Google Scholar] [CrossRef]
- Jack, N.; Murthy, D.N.P.; Iskandar, B.P. Comments on “Maintenance policies with two-dimensional warranty”. Reliab. Eng. Syst. Saf. 2003, 82, 105–109. [Google Scholar] [CrossRef]
- Su, C.; Wang, X. Optimal upgrade policy for used products sold with two-dimensional warranty. Qual. Reliab. Eng. Int. 2016, 32, 2889–2899. [Google Scholar] [CrossRef]
- Varnosafaderani, S.; Chukova, S. A two-dimensional warranty servicing strategy based on reduction in product failure intensity. Comput. Math. Appl. 2012, 63, 201–213. [Google Scholar] [CrossRef] [Green Version]
- Peng, S.; Jiang, W.; Zhao, W. A preventive maintenance policy with usage-dependent failure rate thresholds under two-dimensional warranties. Iise Trans. 2021, 53, 1231–1243. [Google Scholar] [CrossRef]
- Baik, J.; Murthy, D.N.P.; Jack, N. Two-dimensional failure modeling with minimal repair. Nav. Res. Logist. 2003, 51, 345–362. [Google Scholar] [CrossRef]
- Wang, X.; Li, L.; Xie, M. An unpunctual preventive maintenance policy under two-dimensional warranty. Eur. J. Oper. Res. 2020, 282, 304–318. [Google Scholar] [CrossRef]
- Zheng, R.; Su, C. A flexible two-dimensional basic warranty policy with two continuous warranty regions. Qual. Reliab. Eng. Int. 2020, 36, 2003–2018. [Google Scholar] [CrossRef]
- He, Z.; Wang, D.; He, S.; Zhang, Y.; Dai, A. Two-dimensional extended warranty strategy including maintenance level and purchase time: A win-win perspective. Comput. Ind. Eng. 2020, 141, 106294. [Google Scholar] [CrossRef]
- Wang, Q.; Cheng, Z.; Gan, Q.; Bai, Y.; Zhang, J. Cost Optimization of Two-Dimensional Warranty Products under Preventive Maintenance. Math. Probl. Eng. 2021, 2021, 2538050. [Google Scholar] [CrossRef]
- Wang, R.; Cheng, Z.; Wang, Q. Research on Availability Model of Two-dimensional Warranty Products Based on Incomplete Maintenance. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1043, 032046. [Google Scholar] [CrossRef]
- Zhu, H.H. Two Dimensional Warranty Modeling and Optimization Based on Preventive Maintenance; Shijiazhuang Railway University: Shaoxing, China, 2020. [Google Scholar]
- Dai, A.; Zhang, Z.; Hou, P.; Yue, J.; He, S.; He, Z. Warranty Claims Forecasting for New Products Sold with a Two-Dimensional Warranty. J. Syst. Sci. Syst. Eng. 2019, 28, 715–730. [Google Scholar] [CrossRef]
- Peng, T.; Chunling, L. Designing differential service strategy for two-dimensional warranty based on warranty claim data under consumer-side modularisation. Proc. Inst. Mech. Eng. Part O J. Risk Reliab. 2019, 234, 550–561. [Google Scholar] [CrossRef]
- Lin, K.; Chen, Y. Analysis of two-dimensional warranty data considering global and local dependence of heterogeneous marginals. Reliab. Eng. Syst. Saf. 2021, 207, 107327. [Google Scholar] [CrossRef]
- Tong, P.; Song, X.; Zixian, L. A maintenance strategy for two-dimensional extended warranty based on dynamic usage rate. Int. J. Prod. Res. 2017, 55, 5743–5759. [Google Scholar] [CrossRef]
- Wang, D.; He, Z.; He, S.; Zhang, Z.; Zhang, Y. Dynamic pricing of two-dimensional extended warranty considering the impacts of product price fluctuations and repair learning. Reliab. Eng. Syst. Saf. 2021, 210, 107516. [Google Scholar] [CrossRef]
- Wang, X.; Ye, Z.-S. Design of customized two-dimensional extended warranties considering use rate and heterogeneity. IISE Trans. 2020, 53, 341–351. [Google Scholar] [CrossRef]
- Yang, G.E.; Gao, Q.; Huang, Z.X. Maintenance Interval Period Optimization Method of Complex System Based on Availability. Fire Control. Command. Control. 2013. [Google Scholar]
- Pariaman, H.; Garniwa, I.; Surjandari, I.; Sugiarto, B. Availability Analysis of the Integrated Maintenance Technique based on Reliability, Risk, and Condition in Power Plants. Int. J. Technol. 2017, 8, 497. [Google Scholar] [CrossRef]
- Qiu, Q.; Liu, B.; Lin, C.; Wang, J. Availability analysis and maintenance optimization for multiple failure mode systems considering imperfect repair. Proc. Inst. Mech. Eng. Part O J. Risk Reliab. 2021, 235, 982–997. [Google Scholar] [CrossRef]
- Ahn, S.; Kim, W. On determination of the preventive maintenance interval guaranteeing system availability under a periodic maintenance policy. Struct. Infrastruct. Eng. 2011, 7, 307–314. [Google Scholar] [CrossRef]
- Wang, R.; Cheng, Z.; Rong, L.; Bai, Y.; Wang, Q. Availability Optimization of Two-dimensional Warranty Products Under Imperfect Preventive Maintenance. IEEE Access 2021, 9, 8099–8109. [Google Scholar] [CrossRef]
- Dong, E.; Cheng, Z.; Wang, R.; Zhang, X. Availability Optimization of Multicomponent Products with Economic Dependence under Two-Dimensional Warranty. Discret. Dyn. Nat. Soc. 2021, 2021, 2492430. [Google Scholar] [CrossRef]
- Su, C.; Cheng, L. Two-dimensional preventive maintenance optimum for equipment sold with availability-based warranty. Proc. Inst. Mech. Eng. Part O J. Risk Reliab. 2019, 233, 648–657. [Google Scholar] [CrossRef]
- Peng, W.; Zhang, X.; Huang, H. A failure rate interaction model for two-component systems—Based on copula function with shock damage interaction. J. Risk Reliab. 2016, 230, 278–284. [Google Scholar]
- Sun, Y. Reliability Prediction of Complex Repairable Systems: An Engineering Approach; Queensland University of Technology: Brisbane, Australia, 2006. [Google Scholar]
- Sun, Y.; Ma, L.; Mathew, J.; Zhang, S. An analytical model for interactive failures. Reliab. Eng. Syst. Saf. 2006, 91, 495–504. [Google Scholar] [CrossRef]
- Zhang, N.; Fouladirad, M.; Barros, A.; Zhang, J. Condition-based maintenance for a K-out-of-N deteriorating system under periodic inspection with failure dependence. Eur. J. Oper. Res. 2020, 287, 159–167. [Google Scholar] [CrossRef]
- Dong, E.; Cheng, Z.; Wang, R.; Zhang, Y. Extended warranty decision model of failure dependence wind turbine system based on cost-effectiveness analysis. Open Phys. 2022, 20, 616–631. [Google Scholar] [CrossRef]
- Qian, Q.; Jiang, Z.H. Preventive maintenance strategy and maintenance time of multi-component system. Ind. Eng. 2020, 23, 95–100. [Google Scholar]
- Wang, H.; Du, W.; Liu, Z.; Yang, X.; Li, Z. Multi component system maintenance of EMU based on joint fault and economic correlation. J. Shanghai Jiaotong Univ. 2016, 50, 660–667. [Google Scholar]
- Keizer MC, O.; Flapper SD, P.; Teunter, R.H. Condition-based maintenance policies for systems with multiple dependent components: A review. Eur. J. Oper. Res. 2017, 261, 405–420. [Google Scholar] [CrossRef]
- Lawless, J.; Hu, J.; Cao, J. Methods for the estimation of failure distributions and rates from automobile warranty data. Lifetime Data Anal. 1995, 1, 227–240. [Google Scholar] [CrossRef] [PubMed]
- Tong, P.; Liu, Z.; Men, F.; Cao, L. Designing and pricing of two-dimensional extended warranty contracts based on usage rate. Int. J. Prod. Res. 2014, 52, 6362–6380. [Google Scholar] [CrossRef]
- Zhao, X.; Xie, M. Using accelerated life tests data to predict warranty cost under imperfect repair. Comput. Ind. Eng. 2017, 107, 223–234. [Google Scholar] [CrossRef]
- Pham, H.; Wang, H. Imperfect maintenance. Eur. J. Oper. Res. 1996, 94, 425–438. [Google Scholar] [CrossRef]
- Shaomin, W.; Zuo, M.J. Linear and Nonlinear Preventive Maintenance Models. IEEE Trans. Reliab. 2010, 59, 242–249. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Liu, Z.; Liu, Y. Optimal preventive maintenance strategy for repairable items under two-dimensional warranty. Reliab. Eng. Syst. Saf. 2015, 142, 326–333. [Google Scholar] [CrossRef]






| Symbol | Expression | ||
|---|---|---|---|
| Algorithm—Basic Steps of GS |
 |
| Function: PSO–BAS pseudo code in this example |
| Note: this example aims to solve the minimum value |
| Parameter: N is the population size |
 |
| Parameters | Value |
|---|---|
| SwarmSize | 30 |
| 0.6 | |
| Inertia weight | 0.9 |
| SelfAdjustmentWeight | 1.49 |
| SocialAdjustmentWeight | 1.49 |
| MaxIterations K | 175 |
| Algorithm | Variables, Results, or Evaluation Indicators | |||||
|---|---|---|---|---|---|---|
| We | Ue | T | EC | EA | Operation Time | |
| Grid search method | 8.5 | 6.5 | 0.1 | 128708 | 0.8584 | 266 s |
| PSO | 8.4 | 6.9 | 0.1 | 127812 | 0.8601 | 140 s |
| PSO–BAS | 8.4 | 7.2 | 0.3 | 126305 | 0.87 | 121 s |
| Ue/×104 KM | We/Years | ||||
|---|---|---|---|---|---|
| 2.5 | 4.5 | 6.5 | 8.5 | 10.5 | |
| 2.5 | 0.7 | 3.1 | 2.5 | 3.1 | 3.7 |
| 4.5 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 |
| 6.5 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 |
| 8.5 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 |
| 10.5 | 0.7 | 0.7 | 0.7 | 0.7 | 0.7 |
| Ue/×104 KM | We/Years | ||||
|---|---|---|---|---|---|
| 2.5 | 4.5 | 6.5 | 8.5 | 10.5 | |
| 2.5 | 39.57 | 39.14 | 39.11 | 39.11 | 39.10 |
| 4.5 | 13.83 | 13.19 | 13.14 | 13.13 | 13.13 |
| 6.5 | 13.62 | 12.94 | 12.89 | 12.87 | 12.88 |
| 8.5 | 15.55 | 14.92 | 14.88 | 14.87 | 14.86 |
| 10.5 | 16.36 | 16.25 | 15.87 | 16.60 | 16.49 |
| Ue/×104 KM | We/Years | ||||
|---|---|---|---|---|---|
| 2.5 | 4.5 | 6.5 | 8.5 | 10.5 | |
| 2.5 | 0.9896 | 0.9932 | 0.9915 | 0.9914 | 0.9917 |
| 4.5 | 0.9543 | 0.9502 | 0.9463 | 0.9445 | 0.9425 |
| 6.5 | 0.8762 | 0.8713 | 0.8678 | 0.8621 | 0.8584 |
| 8.5 | 0.7653 | 0.6610 | 0.6632 | 0.6587 | 0.7712 |
| 10.5 | 0.7538 | 0.7306 | 0.7851 | 0.7336 | 0.7413 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, E.; Cheng, Z.; Wang, R.; Zhao, J. Optimization of Two-Dimensional Extended Warranty Scheme for Failure Dependence of a Multi-Component System with Improved PSO–BAS Algorithm. Processes 2022, 10, 1479. https://doi.org/10.3390/pr10081479
Dong E, Cheng Z, Wang R, Zhao J. Optimization of Two-Dimensional Extended Warranty Scheme for Failure Dependence of a Multi-Component System with Improved PSO–BAS Algorithm. Processes. 2022; 10(8):1479. https://doi.org/10.3390/pr10081479
Chicago/Turabian StyleDong, Enzhi, Zhonghua Cheng, Rongcai Wang, and Jianmin Zhao. 2022. "Optimization of Two-Dimensional Extended Warranty Scheme for Failure Dependence of a Multi-Component System with Improved PSO–BAS Algorithm" Processes 10, no. 8: 1479. https://doi.org/10.3390/pr10081479
APA StyleDong, E., Cheng, Z., Wang, R., & Zhao, J. (2022). Optimization of Two-Dimensional Extended Warranty Scheme for Failure Dependence of a Multi-Component System with Improved PSO–BAS Algorithm. Processes, 10(8), 1479. https://doi.org/10.3390/pr10081479






