Abstract
Jet loop reactors are standard multiphase reactors used in chemical, biological and environmental processes. The strong liquid jet provided by a nozzle enforces both internal circulation of liquid and gas as well as entrainment and dispersion of the gas phase. We present a one-dimensional compartment model based on a momentum balance that describes the internal circulation of gas and liquid phase in the jet loop reactor. This model considers the influence of local variations of the gas volume fraction on the internal circulation. These local variations can be caused by coalescence of gas bubbles, additional gas-feeding points and gas consumption or production. In this work, we applied the model to study the influence of a gas-consuming reaction on the internal circulation. In a comprehensive sensitivity analysis, the interaction of different parameters such as rate of reaction, power input through the nozzle, gas holdup, reactor geometry, and circulation rate were investigated. The results show that gas consumption can have a significant impact on internal circulation. Industrially relevant operating conditions have even been found where the internal circulation comes to a complete standstill.
1. Introduction
Jet loop reactors (JLRs) are multiphase reactors often used in chemical, biological and environmental processes [1]. The JLR operates with a continuous liquid phase and depending on the process with one or several dispersed phases, e.g., gas bubbles and/or solid particles. Therefore, it is applied for instance for heterogeneously or homogeneously catalyzed gas–liquid reactions (e.g., hydrogenation or hydroformylation reactions [2]), or for multiphase biotechnology processes (e.g., wastewater treatment with bacteria [2,3]).
Generally, the JLR consists of a nozzle, a draft tube and a baffle plate so that the column can be divided into four distinct sections: headspace, bottom space, space in the annular gap and inside the draft tube [4]. The JLR is characterized by the internal circulation flow that is caused by a strong liquid jet. The liquid jet is generated by a nozzle. If the nozzle is mounted above the draft tube, the liquid jet can be used to entrain gas from the headspace into the liquid phase and to disperse the gas. This results in a circulating co-current gas–liquid bubble flow in the JLR. Thus, no stirrer or other moving internals are needed inside the reactor, leading to a simple reactor design. Therefore, the JLR is well suited for solid-laden processes [2]. Another advantage of this type of reactor is that it allows a slim design. In addition, the pump that is required to drive the liquid jet is easier to seal compared to stirred tank reactors (CSTRs). Hence, the JLR is well suited for applications at high pressures [5]. Because of the high power input through the liquid jet, high gas–liquid interfacial area and large internal circulation flow rates are found in JLRs. Thus, they provide good mass and heat transfer characteristics as well as very high back-mixing [2]. The latter is advantageous for reaction systems with unwanted parallel side reactions of higher reaction order than the main reaction [5].
To describe the behavior of a JLR, in principle a model is required that considers both the complex multiphase fluid dynamics and the chemical reactions. This forms a challenging modeling problem as both the fluid dynamics and chemical reactions are strongly coupled and influence each other via property data (e.g., gas solubility), mass and heat transfer, and via back-mixing (that is, the internal circulation flow rate), which affects the internal concentration and temperature profiles in the different phases. In addition, the reactor cannot be considered independently of the other process steps in many cases, but it must be at least partially integrated into the overall process simulation. Reasons for that are, for example, external recirculation flows of unconverted reactants or inerts which occur in many industrial processes and which influence the internal concentration profiles and thus also the reaction rates.
Some attempts have been made to simulate the JLR using three-dimensional computational fluid dynamics (CFD) [6,7,8,9,10]. These models are limited to single-phase or multiphase systems without mass transfer or chemical reactions. To describe the influence of the internal flow velocities on the gas–liquid mass transfer, a combination of population balance equation (PBE) with CFD, which considers phenomena such as bubble breakage or coalescence, can be applied. This approach was applied, for example, by Qi et al. [11] but they did not consider reactions and mass transfer.
However, even if a multiphase CFD that incorporates the PBE, reactions, mass and heat transfer between phases, and full property data (like temperature and composition dependence of phase equilibria, phase density, viscosity and surface tension) were available, a single simulation would require tremendous computational effort. This circumstance limits the application of such a CFD-based modeling approach for the investigation of JLRs. This is especially true at an early stage of process development, in which large parameter spaces need to be checked quickly to capture favorable operating and design parameters (such as flow rate through the jet, reactor diameter and height). In addition, the integration of such a detailed model into a large process simulation is not yet possible due to the computational effort.
For that reason, often a two-step sequential modeling procedure is applied for the design of JLRs. First, the fluid dynamics in the reactor are considered without chemical reaction. Second, the chemical reactions are accounted for but the internal flow is fixed. By means of the fluid dynamic modeling, the interplay between geometry of the reactor and flow rate as well as velocity of the liquid jet for different operation conditions such as gas holdup is investigated. This simulation aims at identifying design and process parameters that ensure stable internal circulation with large flow rates, which results in good mixing as well as good heat and mass transfer in the reactor.
To carry out the simulations in the sequential process, the model according to Zehner and coworkers [12,13,14] or Blenke and coworkers [4,15,16,17] are usually used to describe the internal circulation flow and reactor geometry. These models are based on an integral balance of momentum or energy, exploiting the spatial separation of the flow in a JLR into an upward and downward part as a key simplification.
For the description of the gas holdup, which is the integral gas volume fraction of the gas in the gasified liquid, empirical correlations were developed, for example, by [18,19,20,21]. A detailed summary of modeling concepts and correlations can be found in [2,22].
After the fluid dynamic consideration, the information on the internal circulation flow obtained from the fluid dynamic model is translated into a reactor model that considers the chemical reactions. This model is used to calculate the interaction of, for example, feed composition and temperature on the composition and yield of target products. The reactor model can be a compartment model that reflects the residence time distribution, and internal concentration and temperature profiles, respectively. Alternatively, the JLR reactor can be considered as perfectly back-mixed so that a simple CSTR model can be used. These simple reactor models can be easily incorporated in large process simulations.
This sequential modeling procedure (first fluid dynamics then chemical reactions) has the disadvantage that direct feedback of reaction on internal fluid dynamics cannot be taken into account. The consumption or production in gas by reaction, however, can lead to strong variations of the gas volume fraction within the JLR that can slow down or accelerate the internal circulation flow. If this feedback is not considered in the model, significant differences between model prediction and behavior of the real production reactor, for example, with regard to conversion, selectivity or deactivation of catalyst can occur [5].
In principle, coupling between reaction and fluid dynamics can be reproduced by repeating the sequential process described above several times. This procedure, however, is very tedious and time-consuming. For that reason, we developed in previous work a simple model approach that interlinks directly the gas consumption or production by reaction with the fluid dynamic model describing the internal circulation flow [5]. The model developed by Bey and von Harbou [5] is based on an integral balance of momentum for the draft tube and the annular gap. The gas consumption is taken into account in the balance of momentum via the gas holdup in the draft tube and the annular gap. The gas consumption itself is calculated by means of the analytical solution of the local conversion rate for first order reactions in a recycle reactor. This model, however, has the disadvantage that the integral consideration is a strong simplification, especially if large local variations of the rate of gas consumption occur. Furthermore, the model can only be applied to simple isothermal reactions for which an analytic solution of the local conversion rates in recycle reactors occurs. In addition, local variation of the gas volume fraction caused, for example, by additional gas-feeding points or by changes in the velocity of gas bubbles due to coalescence cannot be represented by the model.
Therefore, we present in this paper an extension of our model approach [5]. Instead of an integral, a one-dimensional differential balance of momentum is applied to describe the internal circulation flow in JLRs. The model enables locally resolved calculation of the volume fraction of the phases, the pressure, the concentration of species and the velocity of the phases in the JLR. Certain properties of the multiphase flow, such as the bubble size distribution, are deliberately not considered in the model. The goal of the model is not to get a precise representation of the state of the multiphase flow in the JLR but to enable quick testing of different scenarios of possible interactions of reaction and internal circulation. Therefore, we applied the developed model for extensive sensitivity studies based on a case adapted from industry. To the best of the authors’ knowledge, the interaction between reaction and multiphase fluid dynamics in JLR as well as in similar reactors has not been systematically studied in the literature. The reaction is indeed frequently included in the calculation [23,24,25,26,27], but a systematic investigation and the effect on the operating behavior and reactor design is mostly missing. This is the gap we would like to close with our model and parameter studies.
In the first study, the influence of different process parameters such as power input and rate of reaction constant on the internal circulation flow is investigated for a given reactor design. In the second study, the impact of variation of the reactor design on the internal circulation flow is assessed. In the third study, both the process and the design parameters were varied simultaneously.
We found that the internal circulation flow can be very sensitive to gas consumption in a broad and industrially relevant range of process and design parameters. These results show that the sensitivity studies carried out with help of the model developed in this work provide comprehensive insights into the complex interplay between reaction and fluid dynamics in JLRs. From these insights, important conclusions can be drawn for the reliable design, and robust and safe operation of multiphase reactors.
2. The Principle of the Jet Loop Reactor
A wide variety of designs of JLRs exist. A good overview can be found in [12,14,17,22]. In this paper, we look at a design where the liquid is injected from the top, see Figure 1. However, the model developed in this work is not limited to this particular design, but can easily be adapted to other designs such as airlift reactors, reactors with liquid injection from the bottom or with additional gas-feeding points.
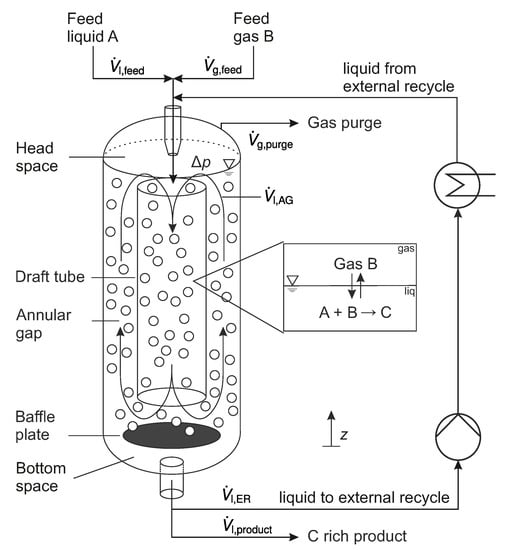
Figure 1.
Schematic drawing of a jet loop reactor.
In this work, two phases are considered: a continuous liquid phase (l) and a dispersed gas phase (g). The vessel (R) of the JLR contains the nozzle (N) at the top, the draft tube (DT) and the baffle plate (BP). The liquid is fed into the reactor via the nozzle with the volume flow rate . In the nozzle, the liquid flow is accelerated so that it is injected with high velocity into the liquid phase present in the reactor. Due to the high velocity of the jet, gas is drawn from the gaseous headspace into the circulating flow and dispersed, resulting in a downward bubble flow in the draft tube . At the baffle plate, the flow is divided. One part goes upward through the annular gap (AG) . The other part of the flow goes continuously downwards into the bottom space (BS) and is removed at the bottom of the reactor from where it is fed back into the reactor via the external liquid recycle (ER). The external liquid recycle is driven by a pump .
The gas phase flows dispersed as bubbles in co-current with the continuous liquid phase. However, not all gas bubbles follow the redirection into the draft tube at the top; some leave the surface into the gaseous headspace of the reactor. From there, the gas is either driven back into the liquid phase by the liquid jet or it leaves the reactor through the gas purge . The gas purge is needed to prevent accumulation of non-condensable gaseous inerts.
Typically, the reactor diameter is chosen so that the flow velocity of the liquid phase in the bottom space (especially in the gap between the baffle plate and the reactor wall) is smaller than the rise velocity of the gas bubbles. In this way, entrainment of gas bubbles into the external liquid recycle and into the pump, respectively, is minimized.
JLRs are commonly used for hydrogenation, carbonylation, hydroformylation and oxygenation. In simplified form, the reactions that take place can be represented as a single irreversible gas-consuming reaction that takes place in the liquid phase. The brutto reaction can be written as:
In our example, species A is a high-boiling reactant and species C a high-boiling product. Both are mainly present in the liquid phase. B is a gaseous species, for example, hydrogen or carbon monoxide that must be absorbed into the liquid phase upon reaction. In this work, it is assumed for the sake of simplicity that the liquid phase consists only of reactants A and B (dissolved from the gas phase), product C and an inert solvent. The gas phase consists of species B as only species B can change the phase. Note that the model could easily be extended to the system with more complicated phase behavior. The reactants are fed via the two-phase nozzle . The liquid product is withdrawn from the external recycle as shown in Figure 1. As these types of reactions are typically exothermic reactions, a heat exchanger is installed in the external liquid recycle to control the temperature of the reaction mixture.
A special feature of this design of JLR is that the gas holdup in the reactor can be controlled. If the flow rate of the product stream is increased for a short time, the liquid holdup in the reactor decreases and therefore also the gassed height. This increases the distance between the surface of the gasified liquid and the tip of the nozzle. The increased distance leads to an intensification of entrainment of gas by the jet into the liquid phase. As a result, the gas holdup in the circulating liquid phase increases and the gassed height rises again until an equilibrium is reached between entrainment, discharge and consumption of gas bubbles so that the gas holdup stays constant.
3. Modelling and Simulation
3.1. Governing Equations
The model used to describe the internal flow in the JLR is based on a one-dimensional balance of momentum along the internal circulation flow path of the liquid phase. The internal circulation flow path or just flow path starts at the inlet of the draft tube and leads further in the negative z-direction to the outlet of the draft tube . The flow path continues then in the annular gap in the positive z-direction. The end of the flow path coincides with the outlet of the annular gap . That is, the flow path describes one complete circulation. The following assumptions were made to simplify the balance of momentum:
- Stationary process;
- Constant property data (e.g., density and viscosity of liquid phase);
- No viscous effects;
- Only gravity acts as a body force;
- No momentum transfer between the liquid and gas phase, resulting in the zero-slip condition between gas bubbles and the liquid phase;
- No change in momentum due to phase change;
- Only friction forces act on the interface of the liquid phase.
Applying these assumptions, the balance of momentum of the liquid phase in the vertical z-direction is
where , and denote the mass density, the velocity and the volume fraction of phase k (liquid: , gas: ). Furthermore, p is the pressure, g the gravitational acceleration constant and the friction force per unit volume acting on the liquid phase, with
Here, is the hydraulic diameter of the compartment i (the compartments are introduced in Section 3.2), is the pressure loss coefficient that describes friction in the draft tube and annular gap as well as the 180° redirection. The pressure loss coefficient is a function of the given geometry and the velocity of the liquid phase. In this work, is calculated with the model presented by Zehner [28]. Details are given in the Supplementary Information S2.1 [29]. The volume fraction, the volume flow rate () and the velocity of the phases are coupled via Equation (3).
is the cross-sectional area of compartment i. It is assumed that the liquid volume flow rate is constant within each compartment i (see Section 3.2).
The balance of momentum of the gas phase is not considered in this work. The gas phase is described with closing conditions: the gas volume fraction results from the volume fraction constrain given in Equation (4), the velocity of the gas phase is obtained from the zero-slip condition (see Equation 5).
It is important to note that the model approach is not limited to the zero-slip condition but can be easily extended with models describing the gas–liquid slip velocity. This extension, however, was not in the scope of the present work and will be considered in further work.
The change in molar concentration of reactant A in the liquid phase along the flow path is calculated with a kinetic model assuming plug flow behavior [30], see Equation (6).
where is the molar concentration of species A in the liquid phase, is the stoichiometric coefficient of species A in Reaction (R1) and is the rate of reaction per unit volume of Reaction (R1). It is assumed that the rate of reaction follows a simple power law:
where is the rate of reaction constant. The power law is of first order with respect to the molar concentration of liquid species A and of zeroth order with respect to the gaseous species B. This type of reaction kinetics can be found in systems in which the gas–liquid mass transfer is fast so that the liquid phase is always saturated with dissolved gaseous species. In this work, this simplification is justified as our focus is to study the general influence of a gas-consuming reaction on the internal circulation flow. However, it is important to note that the presented model approach is not limited to this simplification but can be easily extended both with more complicated kinetic models and with models describing mass transfer between gas and liquid phases.
The consumption of gas along the flow path of the gas phase is reflected as a reduction in the internal volume flow rate of the gas phase. It is calculated directly from the conversion of the liquid species A according to the stoichiometry of the given chemical reaction (see Reaction (R1)).
Here, is the initial position in the direction of the flow path of compartment i and is the molar mass of species B.
3.2. Compartment Model of the Jet Loop Reactor
To describe the JLR with its internal circulation flow with the one-dimensional model equations presented above, the reactor is divided into compartments as shown in Figure 2. Where, is the height of compartment i, with . The balance of momentum is only considered in those compartments in which gas–liquid flow is present. Those are: draft tube (DT) and annular gap (AG). The conversion of species A, which only takes place in the liquid phase, is considered in all compartments including the external recycle (ER) and the bottom space (BS). As shown in Equation (6), plug flow (PFR) behavior is assumed in the draft tube, the annular gap and the external recycle. The bottom space (BS) is described as ideally mixed (CSTR). It is assumed that the mixing of the liquid feed , the liquid jet ( and the internal circulation flow is instantaneous. Note that the head space (HS), the upper flow redirection (HR) and the lower flow redirection (BR) are not modeled.
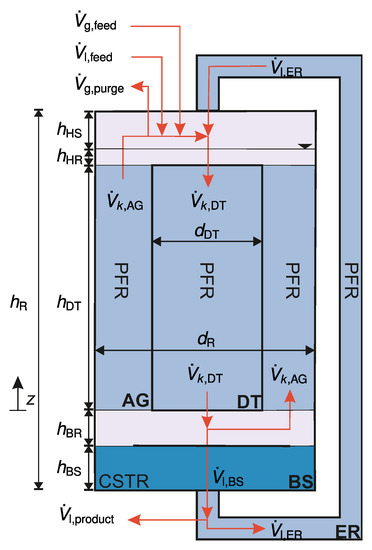
Figure 2.
Compartment model of the jet loop reactor. The abbreviations denote: AG annular gap, DT draft tube, BS bottom space, HS head space, ER external liquid recycle, BR lower flow redirection, HR upper flow redirection, R reactor, CSTR continuous stirred tank reactor, and PFR plug flow reactor.
3.3. Implementation and Simulation
3.3.1. Boundary Conditions
Using Equations (1)–(8), the gas and liquid volume fractions , the pressure , the molar concentration of species A in the liquid phase and the velocity of the gas and liquid phase can be calculated as functions of the flow path z. The possibility of representing the influence of the reaction on the gas volume fraction and expressing the gas volume fraction as a function of the location in the JLR is the main difference of this model approach to the so-far well established integral models of JLRs of, for example, Zehner and coworkers [12,13,14].
When all geometry parameters including the diameter of the nozzle mouth are given, the following process parameters (i.e., boundary conditions) have to be specified to close the system of Equations (1)–(8):
- , the volume flow rate of liquid jet, which is equivalent to the volume flow rate of the external liquid recycle;
- , the volume flow rate at the entry of the draft tube and the annular gap;
- , the volume flow rate of liquid feed;
- , the pressure in the headspace of the JLR.
The volume flow rate of the liquid jet can be calculated using a simple pressure drop correlation and the definition of the volume flow rate (see Equation (3)):
is the diameter of the nozzle mouth, is the pressure drop over the nozzle and is the pressure loss coefficient of the nozzle, whose value is assumed to be constant with . Instead of the pressure drop over the nozzle, the (specific) power input can also be specified,
P is the power introduced into the reactor by the liquid jet and is the reactor volume. Thus, we have four parameters and two Equations (9) and (10), resulting in a degree of freedom of two. Hence, when two parameters are specified, the other two are fixed. All values specified in this work are summarized in the Supplementary Information S1.
The volume flow rate of the liquid feed is specified in this work so that a space-time yield in the reactor is obtained that is typical for industrial reactors.
The volume flow rate of the gas phase at the inlet of the draft tube must be specified to calculate the volume flow rate of the gas phase along the flow path (see Equation (8)). It is the sum of the volume flow rate of gas that is entrained by the liquid jet and of gas bubbles recirculated from the flow through the annular gap. The volume flow rate of the gas that is entrained by the liquid jet into the liquid phase depends on the distance of the nozzle mouth to the surface of the gassed liquid. The volume flow rate of recirculated gas bubbles depends on many parameters such as reactor geometry and properties of the fluids. Both flow rates are not explicitly calculated in this work. Instead, the volume flow rate of the gas phase at the inlet of the draft tube is specified using the volume flow rate of the gas feed, see Equation (12). The gas feed is calculated from the stoichiometric amount required to enable (at least theoretically) full conversion of species A, which is fed via the liquid phase into the reactor (see Equation (11)). Two factors are used: and . They are defined in the interval . is the stoichiometric excess factor applied to ensure that more gas is fed into the liquid phase than the maximum that can be consumed in the reaction. The factor reflects the internal recycle of gas bubbles from the annular gap into the draft tube.
As no additional gas is fed into the annular gap, the volume flow rate of the gas phase at the inlet of the annular gap is the same as the volume flow rate at the outlet of the draft tube, see Equation (13).
Further details on the modeling can be found in the Supplementary Information S2.
3.3.2. Method of Solution
The solution of the differential equation of the balance of momentum (Equation (1)) is achieved with the finite volume method. Because of the simple kinetic model, the species balance can be solved for each compartment analytically (for details, see Supplementary Information S2.2).
The discretized system of non-linear equations is solved with a damped Newton algorithm implemented in MATLAB® in the Version R2019a (9.6.0.1072779) from the publisher The MathWorks Inc. (Natick, MA, USA). For details on the implementation see Supplementary Information S.4.
3.3.3. Definition of the Simulation Studies
Three different simulation studies are carried out in this work: (I) variation of process parameter, (II) variation of design parameter and (III) variation of process and design parameter.
In the variation of process parameter study, the reactor design (including the design of the nozzle) is given and the following process parameters are varied: the rate of reaction constant and the specific power input. This study represents the case of optimizing the process conditions such as internal circulation flow or conversion of reactants for an existing reactor. In real processes, a variation of the rate of reaction constant can be achieved, e.g., by varying the amount of catalyst or the temperature of the reacting mixture. For a given design, the variation of the specific power input can only be realized by varying the volume flow rate of liquid phase through the nozzle (i.e., by varying the power output of the pump). Variations of the volume flow rate results directly in variations of the pressure drop over the nozzle. Table S.2 in the Supplementary Information gives details on the varied parameters of this study.
The variation of design parameter study reflects the case in which the specifications for the reaction process are given and the internal design of the reactor is chosen, for example, to achieve maximum internal circulation. Specifications for the reaction process are typically the space-time yield, the production rate or feed rate, respectively, and the composition of the feed. The space-time yield and production rate result in a defined reactor volume. When the reactor volume is given, the following design parameters that determine the internal geometry of the reactor can be varied: ratio of diameter of draft tube to diameter of reactor (short: diameter ratio), ratio of reactor height to reactor diameter (short: slenderness ratio). To study the influence of the consumption of gas on the internal circulation flow, the rate of reaction constant was also varied in this study. Tables S.3 and S.4 in the Supplementary Information give details on the varied parameters of this study.
To get deep insights into the complex interactions of both design and process parameters, the following parameters were varied in the last study (variation of process and design parameter): ratio of diameter of draft tube to diameter of reactor, specific power input, the rate of reaction constant and the gas holdup in the reactor. Table S.5 in the Supplementary Information gives details on the varied parameters of this study.
The constant parameters, e.g., property data applied for all the simulation studies are listed in Table S.1 in the Supplementary Information.
3.3.4. Output Parameters
For the evaluation of the simulation results, the following output parameters are defined:
- : circulation number;
- : gas holdup in the annular gap;
- : difference of gas holdup in draft tube and annular gap
- : molar concentration of species A in the liquid phase at the inlet of the draft tube;
- : molar concentration of species A in the liquid phase at the outlet of the draft tube
- : molar concentration of species A in the liquid phase along the flow path;
- : volume fraction of gas along the flow path.
The circulation number describes the ratio of the liquid volume flow rate of the internal circulation flow to the external recycle :
The gas holdup in the annular gap or in the draft tube is the volume weighted average of the gas volume fraction in that section.
The gas holdup difference between the draft tube and the annular gap is
For brevity, in the following the output parameter is called gas holdup difference.
4. Simulation Results
4.1. Variation of Process Parameter
Figure 3A depicts the circulation number and the molar concentration of A in the liquid phase at the inlet of the draft tube as a function of the rate of reaction constant for different power inputs . Figure 3B shows the gas holdup in the annular gap and the gas holdup difference as a function of the rate of reaction constant for different power inputs . The effect of the variation of the rate of reaction constant and the specific power input on a given reactor design is investigated here at a low excess of gas (), that is a low gas holdup. The influence of the gas holdup on the internal circulation is discussed in Section 4.2.
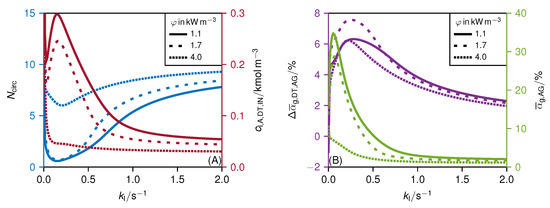
Figure 3.
(A) Circulation number (blue) and molar concentration of A in the liquid phase at the inlet of the draft tube (red), and (B) gas holdup difference (purple) and gas holdup in the annular gap (green), as a function of the rate of reaction constant . Variation of the specific power input (line style). Applied parameter see Tables S.1 and S.2.
If no reaction takes place , no gas is consumed and is constant along the whole flow path. Because of the injection of liquid at the top and removal at the bottom, the volume flow rate of liquid in the draft tube is larger than in the annular gap. Therefore, the gas holdup in the draft tube is smaller than in the annular gap (i.e., ). Hence, the hydrostatic pressure in the draft tube is larger than in the annular gap. This pressure gradient promotes the internal circulation flow in the JLR. Thus, a high circulation number at is found for all power inputs.
With the onset of the reaction, gas is consumed. Due to the larger cross-sectional area and the lower liquid volume flow rate in the annular gap, the residence time in the annular gap is longer than in the draft tube. Consequently, more gas is consumed in the annular gap than in the draft tube so that the gas holdup decreases in the annular gap with increasing rate of reaction constant. The result is that the gas holdup difference becomes positive . Now, the hydrostatic pressure gradient acts against the direction of the internal circulation flow. Thus, the circulation number decreases rapidly with the increasing rate of reaction constant. Surprisingly, the gas holdup in the annular gap initially increases. The explanation for this observation is that the internal circulation flow decreases faster at low rate of reaction constants than the gas volume flow rate in the annular gap. Only when the reaction becomes even faster and the gas consumption in the annular gap increases further does the gas holdup in the annular gap also decrease.
If the reaction rate continues to increase, there is no more consumption of gas in the annular gap but only in the draft tube. This reduces the difference of the gas holdup again and the decelerating effect of the hydrostatic pressure difference on the internal circulation flow diminishes. Thus, the circulation number increases again. If the reaction is so fast that the reactants are completely converted immediately after being injected into the draft tube, the gas consumption has no effect on the circulation number and it is similar to that of the non-reactive case.
The strong variation of the circulation number depending on the rate of reaction constant also affects the concentration profiles within the JLR. If the circulation number is large, back-mixing is enhanced. Thus, the spatial concentration gradients of the reacting species along the flow path are small within the reactor. In contrast, a reduction in the internal circulation number leads to lower back-mixing, which results in larger concentration gradients along the flow path. This behavior shows how important it is that the gas consumption is considered in the model so that the internal circulation flow is properly captured by the model. Whereby in future work, the model predictions should be confirmed by experiments to prevent an overestimation of the influence of a reaction on the fluid dynamics by the model. However, the observations from industrial processes described in [5] support the model predictions.
If the influence of gas consumption on the internal circulation flow does not account for in the fluid dynamic model of the JLR, the internal circulation number and thus also the back-mixing can be significantly overestimated in the design of the reactor compared to the real behavior of the JLR. In the case of reaction systems in which unwanted side reactions occur that are of higher order with respect to the reactants, the reduction in internal back-mixing decreases the selectivity, or the increase in the concentration of reactants at the reactor inlet can cause an increase in the deactivation rate of the catalyst. Furthermore, reduction in back-mixing means that the rate of reaction, and thus also the required gas–liquid mass transfer, is significantly higher at the inlet of the JLR than that at the upper end of the annular gap. If this increased demand for mass transfer was not considered when designing the reactor with a power input chosen to be too low (because the model did not consider these effects), it may result in a deficiency of dissolved gas species. In many cases, this deficiency of reactants results in an increased rate of formation of unwanted side-products. For the case of internal heat exchanger surfaces, similar problems could arise. If the degree of back-mixing is smaller in reality than expected in the design of the reactor, hot spots may arise at the reactor entrance (top of the draft tube) due to the high concentration of reactants and therefore high rate of reactions. These examples show that negligence of the influence of gas consumption on the internal circulation during the design of the reactor can lead to the reactor not reaching the desired target values (e.g., conversion of reactants, selectivity to target products) later in operation.
As demonstrated above, many operation conditions can be found in which the consumption of gas influences the internal circulation in the JLR. This means that the results of non-reactive test runs in real JLRs (e.g., runs without catalyst or with inert gas), which are carried out during start-up (e.g., for calibration of instruments, understanding of reactor behavior), may not provide information that can be directly transferred to reactive operation when gas is consumed.
Figure 3 shows clearly that high power inputs mitigate the influence of the rate of reaction constant and the gas consumption, respectively, on the internal circulation. At high power inputs, the accelerating or decelerating contribution of the hydrostatic pressure difference is small compared to the input of momentum of the liquid jet. For this reason, variations of the hydrostatic pressure difference due to gas consumption are less significant when the power input is large.
As expected, the sensitivity of the internal circulation for the power input is largest in the range of rate of reaction constants (–) where the decelerating effect of the hydrostatic pressure difference is largest and the internal circulation number reaches a minimum. In the following, this region is called the “sensitive reactive” range.
The influence of the power input on the internal circulation is not linear in the sensitive reactive range. For power inputs smaller than , a small change in the power leads to a significant change in the internal fluid dynamics. It is most likely that the strong reduction in the internal circulation flow of the liquid phase in the sensitive reactive range for power inputs less than () would lead to a complete collapse of the circulation in reality. In the simulation, the low internal circulation flow is only possible because the zero-slip condition between gas and liquid phases is assumed. For small liquid velocities, the slip velocity of the gas phase (that is, the rise velocity of the gas bubbles) is significant, especially when coalescence of gas bubbles occurs at large values of the gas holdup. In addition, at high gas volume fractions and low liquid velocities, complex two-phase flows and flow patterns can occur [31]. The prediction of the collapse of the internal circulation flow, however, was not in the scope of this paper and will be considered in future work. For the design of JLRs, the information provided by the model presented in this work is sufficient to identify sensitive regions. For JLRs used in industry, robust operation must be ensured. Therefore, the reactor should be operated far outside these sensitive regions.
4.2. Variation of Design Parameter
4.2.1. Variation of the Draft Tube to Reactor Diameter Ratio
Figure 4A shows the circulation number and the gas holdup difference as a function of the diameter ratio for different rate of reaction constants . Thereby, the investigated rate of reaction constants, based on the findings from the previous section, stand for: (I) non-reactive case (i.e., ), (II) non-sensitive reactive case (i.e., ) and (III) sensitive reactive case (i.e., ). Figure 4B illustrates the molar concentration of A in the liquid phase at the inlet of the draft tube and at its outlet as a function of the diameter ratio for different rate of reaction constants.
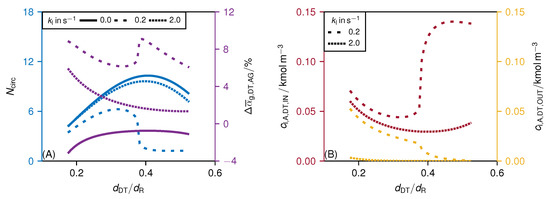
Figure 4.
(A) Circulation number (blue) and gas holdup difference (purple), and (B) molar concentration of A in the liquid phase at the inlet (red) and outlet (yellow) of the draft tube as a function of diameter ratio . Variation of the rate of reaction constant (line style). Applied parameter see Tables S.1 and S.3 with .
In the non-reactive case, the circulation number shows a convex shape with a maximum at a diameter ratio of 0.42. Blenke et al. [15] determined semi-empirical 0.59 for a single-phase case and Gao et al. [10] determined CFD-based 0.66 for a two-phase case. Both cases are non-reactive and in contrast to our work, the nozzle is located in the bottom space, which may explain the discrepancy with our non-reactive case. The maximum of the circulation number is caused by a minimum of the overall frictional losses in the reactor that are dominated by losses from the redirection of the internal flow at the inlet () and the outlet of the draft tube (). In the non-sensitive reactive case with very high rate of reaction constants , a similar pattern is observed as in the non-reactive case, though the circulation number is somewhat smaller in the reactive case. As already described in the previous section (see Section 4.1), the reaction has little effect on the internal fluid dynamics for very fast reactions where the gas consumption takes place only in the upper part of the draft tube. The reduction in the circulation number observed for the non-sensitive reactive case is caused by consumption of gas. This leads to a positive gas holdup difference as shown in Figure 4A, which in turn decelerates the internal circulation flow.
As in the previous section, the results show a clear influence of gas consumption on internal circulation number when the rate of reaction constant is in the sensitive reactive range (here: ). After the circulation number has reached a maximum at a diameter ratio of about 0.34, the circulation number decreases abruptly to a constant value of about 1.2. To get a better understanding for the cause of the significant change in the circulation number, the gas volume fraction is plotted as a function of the flow path and the diameter ratio in Figure 5. The length of the flow path is normalized with its total length of .
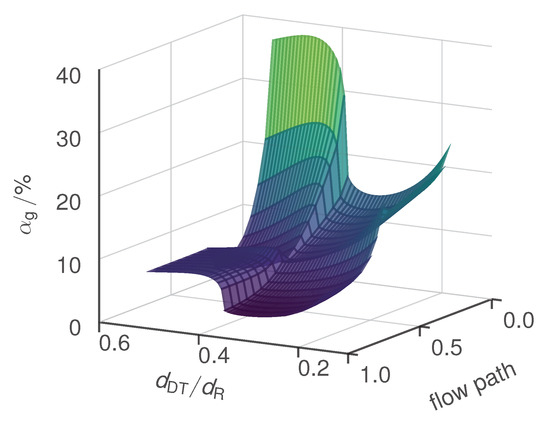
Figure 5.
Gas volume fraction as a function of the diameter ratio and the normalized flow path. Applied parameter see Tables S.1 and S.3 with and where the reactor volume was kept constant.
At low values of the diameter ratio, the circulation number increases with increasing diameter ratio (see Figure 4A). As in the other two cases, this trend is initially due to the decrease in internal friction. Because the gas flow entrained by the nozzle remains constant in the simulation, the gas volume fraction at the inlet of the draft tube decreases as the circulation number increases (see Figure 4A). Consequently, the gas holdup difference decreases. Simultaneously, the increase in back-mixing leads to a reduction in the concentration of reactant A at the inlet of the draft tube (see Figure 4B); the complete plot of the concentration profile of reactant A as a function of the flow path is shown in the Supplementary Information. So far, the trend for both reactive cases (non-sensitive and sensitive) is the same. However, the decrease in the molar concentration of reactant A at the inlet of the draft tube reduces the rate of reaction and therefore also the gas consumption in that region of the reactor. Hence, in the sensitive case, the gas volume fraction starts to increase again at the value of the diameter ratio of about 0.31 where the circulation number reaches its maximum. This leads to an increase in the decelerating effect of the gas holdup difference (see Figure 4A) when the diameter ratio is increased further. In addition to that, the residence time of the liquid phase in the draft tube increases because both the volume of the draft tube increases compared to the volume of the annular gap and the internal circulation flow rate of the liquid phase decreases. Thus, the increase in the concentration of the reactant A at the inlet of the draft tube and the increase in the residence time in the draft tube caused by the reduction in the circulation number lead both to an unfavorable distribution of gas consumption and gas holdup between draft tube and annular gap. As a result, the gas holdup difference increases rapidly at a value of the diameter ratio of 0.38 (see Figure 4A) and so does its decelerating effect. Hence, the flow rate of the internal circulation is very small for values of the diameter ratio of more than 0.4. In this case, the draft tube acts almost like a PFR where all the conversion of reactant A takes place (see concentration difference between inlet and outlet of the draft tube plotted in Figure 4B). To summarize, in the sensitive reactive case, the reactor characteristics change in dependence of the diameter ratio (see Figure 5). For small diameter ratios, the circulation number is large; the reactor behaves like a CSTR with small local difference of the concentration of reactants and gas volume fraction. For large diameter ratios, however, the circulation number is small so that the draft tube acts as a PFR, which results in strong local gradients of the concentration of reactants and gas volume fraction. The strong differences between the behavior of the JLR for the non-reactive and the reactive (and kinetically sensitive) case demonstrate that the gas consumption can have a significant influence on the internal circulation flow.
4.2.2. Variation of the Reactor Height to the Reactor Diameter
Figure 6A shows the circulation number and the gas holdup difference as a function of the slenderness ratio. Figure 6B illustrates the molar concentration of A in the liquid phase at the inlet and the outlet of the draft tube as a function of the slenderness ratio. As in the previous section, three cases are considered: (I) non-reactive case (i.e., ), (II) non-sensitive reactive case (i.e., ) and (III) sensitive reactive case (i.e., ).
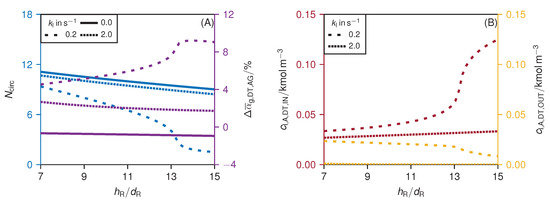
Figure 6.
(A) Circulation number (blue) and gas holdup difference (purple), and (B) molar concentration of A in the liquid phase at the inlet (red) and outlet (yellow) of the draft tube as a function of slenderness ratio . Variation of the rate of reaction constant (line style). Applied parameter see Tables S.1 and S.4 with .
For the non-reactive and the non-sensitive reactive case (i.e., ), the circulation number decreases with increasing because internal friction increases when the reactor becomes slimmer. The differences between the non-reactive and non-sensitive reactive case in terms of circulation number are due to gas consumption and its decelerating effect explained above.
Similar to the results presented in the previous study in which the diameter ratio is varied, the sensitive reactive case () deviates significantly from the two other cases (see Figure 6). In addition, a sharp drop in circulation number is observed here if the design parameter that is the slenderness ratio is increased over a certain value (about 13). The explanation for this behavior is basically the same as that we presented in the previous section. When the slenderness ratio is increased over a certain value, the internal circulation decreases and its feedback effect on the gas consumption caused by the increases in the concentration of reactants at the inlet of the draft tube (see Figure 6B) induces a change in the regime of the reactor behavior. Figure 7 depicts the concentration of reactant A as a function of the normalized length of flow path and of the slenderness ratio. While the local concentration gradients in the JLR are small at low slenderness ratios they become more than three times larger at high slenderness ratios. Thus, the reactor characteristics change from a well back-mixed system (CSTR) to the behavior of a PFR. The gas volume fraction shows similar trends (a figure is included in the Supplementary Information S3).
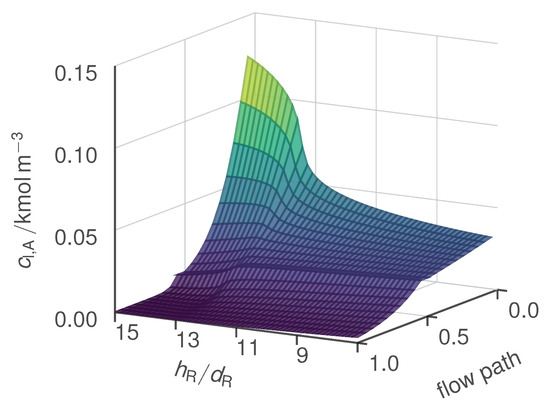
Figure 7.
Molar concentration of A in the liquid phase as a function of the slenderness ratio and the normalized flow path. Applied parameter see Tables S.1 and S.4 with , and diameter ratio where the reactor volume was kept constant.
In this study, however, it is noticeable that the change in circulation number is not as abrupt as in the case of the change in the diameter ratio (compare Figure 4 with Figure 6). While the increase in the diameter ratio causes a change in the regime of the reactor characteristics via two effects (back-mixing and ratio of residence time in draft tube and annular gap), in this case it only acts via the reduction in back-mixing caused by the reduction in the circulation flow rate.
4.3. Influence of Process and Design Parameters
In the simulation studies presented in the previous sections, the volume flow rate of entrained gas is kept at a constant value that results in a gas holdup of about 10%. Figure 8 summarizes the results of simulation studies in which the gas holdup (i.e., volume flow rate of entrained gas), the power input, the diameter ratio and the rate of reaction constant are varied. Note that in contrast to Section 4.1, the specific power input was adjusted by varying the nozzle diameter, resulting in variation of the pressure drop over the nozzle. The liquid volume flow rate through the nozzle (i.e., the flow rate of the external recycle) was kept constant so that the different reactor concepts remain comparable. The bottom row in Figure 8 shows the non-reactive case (). The results are in line with the expectation. High power input, low gas holdup and a diameter ratio of about 0.5 facilitate high circulation numbers. Similar trends are found for the non-sensitive reactive case (). In this case, only the absolute values of the circulation number are somewhat lower compared to the non-reactive case due to the decelerating effect of the gas consumption on the circulation (see explanation in Section 4.1).
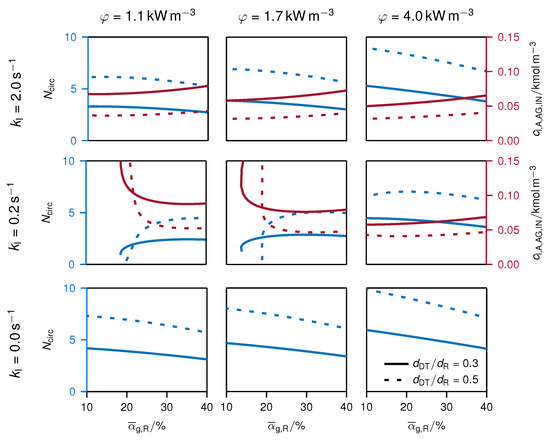
Figure 8.
Influence of rate of reaction constant , power input on the circulation number (blue line) and the molar concentration of component A in the liquid phase at the inlet of the draft tube (red line) as a function of the gas holdup at different diameter ratios (line style). Applied parameter see Tables S.1 and S.5 where the reactor volume was kept constant.
In the sensitive reactive case (), similar behavior compared to the other two cases is found but only if the gas holdup is large. If the gas holdup is decreased to values smaller than 20%, the circulation number drops sharply (for a diameter ratio of 0.5) and no solution is found by the solver (both diameter ratios). These results suggest that the internal circulation flow collapses at this point. Only with very high power input () can a stable circulation (for the given assumptions) be achieved. The drastic decreases (or even collapse) of the internal circulation observed for the sensitive reactive case at low values of the gas holdup correspond to the results shown in Figure 4. Obviously, a small gas holdup is not beneficial for the circulation flow in this case. As discussed in the previous sections, the unfavorable local distribution of gas consumption and the resulting differences between the gas holdup in the draft tube and in the annular gap have a decelerating effect on the internal circulation. However, at large values of the gas holdup, the flow rate of the circulating gas is much larger than stoichiometrically required for the reaction. Thus, the consumption of gas causes only small variations of the gas volume fraction along the flow path. Consequently, the influence of the reaction and gas consumption on the circulation flow diminishes at large values of the gas holdup.
The results show that the operating window of feasible gas holdups is significantly smaller for the sensitive reactive case than for the other two cases. It is also likely that commission of the JLR is more difficult in the sensitive reactive case. Here, operation with high power input or additional gas-feeding points in the draft tube are possible countermeasures that can be taken during operation or design of the JLR.
5. Conclusions and Outlook
A one-dimensional model of a jet loop reactor, which is based on a balance of momentum, is presented in this work. It facilitates the local resolution of important process variables such as species concentration, gas volume fraction, pressure and velocity of gas and liquid phases. For example, the influence of gas consumption by reaction on the gas volume fraction and its feedback on the internal circulation flow can be investigated with the model. Due to its simplicity, simulations with the model are fast and robust. Thus, large ranges of both process and design parameters can be studied with the model. We do not claim that our model predicts the real behavior of the reactor precisely. However, the presented model enables tests of different scenarios (that are different combination of process and design parameters). Thereby it provides insights into the complex interactions of the processes taking place simultaneously in the JLR.
Despite the simplification of the model, the influence of the reaction on the fluid dynamics is clearly evident. In general, gas consumption has a decelerating effect on the internal circulation. In addition to that, we found an unfavorable combination of process conditions (rate of reaction constant, gas holdup and power input) under which the gas consumption causes a drastic reduction in the internal circulation, which would lead in reality most likely to a complete collapse of the internal circulation. If a JLR is designed for a synthesis whose rate of reaction constant is in the sensitive reactive region, the strong influence of the gas consumption has to be considered. Most important, the operational window for possible gas holdups in the reactor is significantly narrowed down. Both at too high and at too low values of the gas holdup, the reactor cannot be operated in a stable manner. The results suggest that start-up of this reaction in the JLR has to be done with care. Even the reduction in internal circulation and back-mixing alone can have negative effects on the synthesis.
The results show that neglecting the influence of gas consumption on the internal circulation can lead to strong overestimation of the reactor performance (i.e., conversion of reactants and selectivity to target products). That means information gained either from non-reactive calibration and test runs in the production reactor or from laboratory kinetic studies carried out in well mixed stirred tank reactors cannot be transferred to the reactive case in the production scale.
The presented model enables not only identification of parameter regions in which strong sensitivity of the internal circulation on gas consumption can be expected, but also assessment of different countermeasures. For example the stabilizing effect of additional gas-feeding points or of an increase in power input on the internal circulation can be evaluated by means of the model.
Even though observations from industrial JLR support the findings of this work, no comprehensive experimental data basis exists so far that allows verification of the model predictions. These experimental studies will be carried out in future work. Furthermore, not only gas consumption but also coalescence of gas bubbles can influence the internal circulation. For example, internals such as cooling tubes can enhance coalescence. The structure of the model facilitates easy and quick extensions in future work, so that phase slip and coalescence can be accounted for in the model. Thereby, these industrially relevant phenomena could be included in sensitivity studies in the future.
The presented model closes the gap between the classical process model used, for example, in flow sheet simulators and detailed CFD simulations. Process models usually do not consider the balance of momentum and therefore cannot describe internal flow phenomena. CFD models enable deep insights into flow phenomena in reactors. However, they are computationally too expensive to cover large parameter spaces. This is where our model comes in. Even though it is not strictly predictive due to its simplicity, the model can be used to study the complex interactions that occur in gas–liquid reactors and apparatuses. Thereby, it gives valuable insights both for the design and scale-up as well as for the operation of these processes.
The aim of future studies will be to generalize the observations made in this paper with concrete example processes. The development and selection of suitable dimensionless indicators could be useful in this regard. Furthermore, an easy-to-calculate stability criterion of the internal circulation would be very helpful for users in industry as well as a validation of the performed simulation studies by experiments.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/pr10071297/s1, Table S.1: Left: Property data applied in the simulations. Center: Constant reactor geometry parameter. Right: Constant process conditions.; Table S.2: Applied parameters of study I.; Table S.3: Applied parameters of study II where the diameter ratio is varied.; Table S.4: Applied parameters of study II where the slenderness ratio is varied.; Table S.5; Applied parameters of study III.; Figure S.1: Molar concentration of species A in the liquid phase as a function of the diameter ratio and the normalized flow path using the parameters specified in Tables S.1 and S.3 with where the reactor volume where kept constant.; Figure S.2. Molar concentration of species A in the liquid phase as a function of the diameter ratio and the normalized flow path using the parameters specified Tables S.1 and S.3 with where the reactor volume where kept constant.; Figure S.3: Gas volume fraction as a function of the diameter ratio and the normalized flow path using the parameters specified in Tables S.1 and S.3 with where the reactor volume where kept constant.; Figure S.4: Gas volume fraction as a function of the diameter ratio and the normalized flow path using the parameters specified in Tables S.1 and S.3 with where the reactor volume where kept constant.; Figure S.5: Molar concentration of A in the liquid phase as a function of the slenderness ratio and the normalized flow path using the parameters specified in Tables S.1 and S.4 with whereby the diameter ratio and the reactor volume were kept constant.; Figure S.6: Molar concentration of A in the liquid phase as a function of the slenderness ratio and the normalized flow path using the parameters specified in Tables S.1 and S.4 with whereby the diameter ratio and the reactor volume were kept constant.; Figure S.7: Gas volume fraction as a function of the slenderness ratio and the normalized flow path using the parameters specified in Tables S.1 and S.4 with whereby the diameter ratio and the reactor volume were kept constant.; Figure S.8: Gas volume fraction as a function of the slenderness ratio and the normalized flow path using the parameters specified in Tables S.1 and S.4 with whereby the diameter ratio and the reactor volume were kept constant.; Figure S.9: Flowchart of the solution procedure.
Author Contributions
Conceptualization, F.B., E.v.H. and O.B.; methodology, F.B. and E.v.H.; software, F.B. and E.v.H.; validation, F.B., E.v.H. and O.B.; formal analysis, F.B.; investigation, F.B.; resources, E.v.H.; data curation, F.B.; writing—original draft preparation, F.B.; writing—review and editing, F.B., E.v.H. and O.B.; visualization, F.B.; supervision, E.v.H.; project administration, E.v.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
The following nomenclature is used in this manuscript:
| Latin letters | |||
| Ratio of the cross-sectional area of compartment i to the cross-sectional area of the reactor | |||
| Cross-sectional area of compartment i | |||
| Molar concentration of species A in the liquid phase in compartment i | |||
| Hydraulic diameter of compartment i | m | ||
| Recycling excess factor | |||
| Stoichiometric excess factor of species B | |||
| Friction force per unit volume acting on the liquid phase | |||
| g | Gravitational acceleration constant | ||
| Height of compartment i | m | ||
| Rate of reaction constant of Reaction I | |||
| Molar mass of spices j | |||
| Circulation number | |||
| Pressure in the headspace | bar | ||
| Pressure drop over the nozzle | Pa | ||
| p | Pressure | Pa | |
| P | Power introduced into the rector | W | |
| Rate of reaction per unit liquid volume of Reaction I | |||
| Velocity of phase k | |||
| Volume flow rate of phase k in compartment i | |||
| Volume of compartment i | |||
| z | Coordinate along the axial direction | m | |
| Inital postion in flow path direction of compartment i | m | ||
| Greek letters | |||
| Volume fraction of phase k | |||
| Difference between the gas holdup of compartment DT and AG; gas holdup difference | |||
| Gas holdup of phase k of compartment i, integral over along z | |||
| Pressure loss coefficient | |||
| Stoichiometric coefficient of chemical species j of the reaction I | |||
| Mass density of phase k | |||
| Specific power input per reactor volume; power input | |||
| Subscripts | |||
| circ | Circulation | ||
| feed | Feed stream | ||
| g | Gas phase index | ||
| i | Compartment index | ||
| IN | Inlet | ||
| I | Reaction I | ||
| j | Chemical species index | ||
| k | Phase index | ||
| l | Liquid phase index | ||
| OUT | Outlet | ||
| product | Product stream | ||
| purge | Purge stream | ||
| Abbreviations | |||
| A | High-boiling reactant A | ||
| AG | Annular gap | ||
| B | Chemical species B | ||
| BP | Baffle plate | ||
| BR | Lower flow redirection | ||
| BS | Bottom space | ||
| C | High-boiling product C | ||
| CFD | Computational fluid dynamics | ||
| CSTR | Continuous stirred tank reactor | ||
| DT | Draft tube | ||
| BR | External recycle | ||
| HR | Upper flow redirection | ||
| HS | Head space | ||
| JLR | Jet loop reactor | ||
| N | Nozzle | ||
| PBE | Population balance equation | ||
| PFR | Plug flow reactor | ||
| R | Reactor |
References
- Baerns, M. Technische Chemie, 2nd ed.; Wiley-VCH: Weinheim, Germany, 2013. [Google Scholar]
- Warmeling, H.; Behr, A.; Vorholt, A.J. Jet loop reactors as a versatile reactor set up—Intensifying catalytic reactions: A review. Chem. Eng. Sci. 2016, 149, 229–248. [Google Scholar] [CrossRef]
- Bloor, J.C.; Anderson, G.K.; Willey, A.R. High rate aerobic treatment of brewery wastewater using the jet loop reactor. Water Res. 1995, 29, 1217–1223. [Google Scholar] [CrossRef]
- Blenke, H. Loop reactors. In Advances in Biochemical Engineering; Springer: Berlin/Heidelberg, Germany, 1979; Volume 13. [Google Scholar]
- Bey, O.; von Harbou, E. Einfluss der Wechselwirkung von Reaktion und Fluiddynamik auf das Verhalten von Strahlschlaufenreaktoren. Chem. Ing. Tech. 2021, 93, 191–200. [Google Scholar] [CrossRef]
- Kang, D.Y.; Kim, M.R.; Lim, J.H.; Lee, T.Y.; Lee, J.K. Neutralization of Alkaline Wastewater with CO2 in a Continuous Flow Jet Loop Reactor. Korean Chem. Eng. Res. 2016, 54, 101–107. [Google Scholar] [CrossRef]
- Mier, P.; Kraume, M. Betriebsverhalten und Maßstabsübertragung von ein- und zweiphasig betriebenen Strahlschlaufenapparaten (CFD-Simulationen und Experimente). Chem. Ing. Tech. 2000, 72, 1067–1068. [Google Scholar] [CrossRef]
- Szafran, R.G.; Kmiec, A. Application of CFD Modelling Technique in Engineering Calculations of Three-Phase Flow Hydrodynamics in a Jet-Loop Reactor. Int. J. Chem. React. Eng. 2004, 2. [Google Scholar] [CrossRef]
- Mathpati, C.S.; Deshpande, S.S.; Joshi, J.B. Computational and experimental fluid dynamics of jet loop reactor. AIChE J. 2009, 55, 2526–2544. [Google Scholar] [CrossRef]
- Gao, Y.; Du, H.; Cheng, Y.; Wang, L.; Li, X. CFD simulation for up flow jet-loop reactors by use of bi-dispersed bubble model. Chem. Eng. Res. Des. 2019, 141, 66–83. [Google Scholar] [CrossRef]
- Qi, N.; Zhang, K.; Xu, G.; Yang, Y.; Zhang, H. CFD-PBE simulation of gas-phase hydrodynamics in a gas-liquid-solid combined loop reactor. Pet. Sci. 2013, 10, 251–261. [Google Scholar] [CrossRef][Green Version]
- Zehner, P. Modellbildung für Mehrphasenströmungen in Reaktoren. Chem. Ing. Tech. 1988, 60, 531–539. [Google Scholar] [CrossRef]
- Tebel, K.H.; Zehner, P. Fluid dynamic description of jet-loop reactors in multiphase operation. Chem. Eng. Technol. CET 1989, 12, 274–280. [Google Scholar] [CrossRef]
- Zehner, P.; Benfer, R. Modelling fluid dynamics in multiphase reactors. Chem. Eng. Sci. 1996, 51, 1735–1744. [Google Scholar] [CrossRef]
- Blenke, H.; Bohner, K.; Schuster, S. Beitrag zur optimalen Gestaltung chemischer Reaktoren. Chem. Ing. Tech. 1965, 37, 289–294. [Google Scholar] [CrossRef]
- Bohner, K.; Blenke, H. Gasgehalt und Flüssigkeitsumwälzung im zweiphasig betriebenen Schlaufenreaktor. Chem. Ing. Tech. 1972, 44, 373. [Google Scholar] [CrossRef]
- Blenke, H.; Bohner, K.; Pfeiffer, W. Hydrodynamische Berechnung von Schlaufenreaktoren für Einphasensysteme. Chem. Ing. Tech. 1971, 43, 10–17. [Google Scholar] [CrossRef]
- Gao, Y.; Du, H.; Lu, H.; Cheng, Y.; Wang, L.; Li, X. Gas holdup and liquid velocity distributions in the up flow jet-loop reactor. Chem. Eng. Res. Des. 2018, 136, 94–104. [Google Scholar] [CrossRef]
- Velan, M.; Ramanujam, T.K. Hydrodynamics in down flow jet loop reactor. Can. J. Chem. Eng. 1991, 69, 1257–1261. [Google Scholar] [CrossRef]
- Wagh, S.M.; Koranne, K.V.; Mankar, R.B.; Sonolikar, R.L. Gas holdup in a two-phase reversed flow jet loop reactor. Can. J. Chem. Eng. 2010, 88, 793–800. [Google Scholar] [CrossRef]
- Panchal, N.; Bhutada, S.; Pangarkar, V.G. Gas induction and hold up characteristics of liquid jet loop reactor using multi orifice nozzles. Chem. Eng. Commun. 1991, 102, 59–68. [Google Scholar] [CrossRef]
- Reschetilowski, W. Handbuch Chemische Reaktoren; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar] [CrossRef]
- Babajimopoulos, A.; Assanis, D.N.; Flowers, D.L.; Aceves, S.M.; Hessel, R.P. A fully coupled computational fluid dynamics and multi-zone model with detailed chemical kinetics for the simulation of premixed charge compression ignition engines. Int. J. Engine Res. 2005, 6, 497–512. [Google Scholar] [CrossRef]
- Harris, C.K.; Roekaerts, D.; Rosendal, F.; Buitendijk, F.; Daskopoulos, P.; Vreenegoor, A.; Wang, H. Computational fluid dynamics for chemical reactor engineering. Chem. Eng. Sci. 1996, 51, 1569–1594. [Google Scholar] [CrossRef]
- Jung, J.; Gamwo, I.K. Multiphase CFD-based models for chemical looping combustion process: Fuel reactor modeling. Powder Technol. 2008, 183, 401–409. [Google Scholar] [CrossRef]
- Kruggel-Emden, H.; Stepanek, F.; Munjiza, A. A Study on the Role of Reaction Modeling in Multi-phase CFD-based Simulations of Chemical Looping Combustion. Oil Gas Sci. Technol. Rev. D’IFP Energies Nouv. 2011, 66, 313–331. [Google Scholar] [CrossRef][Green Version]
- Zandie, M.; Ng, H.K.; Gan, S.; Muhamad Said, M.F.; Cheng, X. Review of the advances in integrated chemical kinetics-computational fluid dynamics combustion modelling studies of gasoline-biodiesel mixtures. Transp. Eng. 2022, 7, 100102. [Google Scholar] [CrossRef]
- Zehner, P. Flüssigkeits/Feststoff-Strömungen in Verfahrenstechnischen Apparaten: Fortschritt-Berichte VDI Reihe 3: Verfahrenstechnik Nr. 160; VDI-Verlag gmbH: Düsseldorf, Germany, 1988. [Google Scholar]
- Idel chik, I.E. Handbook of Hydraulic Resistance, 4th ed.; Begell House: Redding, CA, USA, 2007. [Google Scholar]
- Levenspiel, O. Chemical Reaction Engineering; John Wiley & Sons, Inc.: New York, NY, USA, 1999; Volume 3. [Google Scholar]
- Kelessidis, V.C.; Dukler, A.E. Modeling flow pattern transitions for upward gas-liquid flow in vertical concentric and eccentric annuli. Int. J. Multiph. Flow 1989, 15, 173–191. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).