Product-Property Guided Scale-Up of a Fluidized Bed Spray Granulation Process Using the CFD-DEM Method
Abstract
:1. Introduction
- Layering granulation, where particles quickly dry and the injected liquid leaves a solid residue that forms a shell or coating, and
- agglomeration, where the cohesive forces of the liquid cause the particles to remain in contact, resulting in the formation of larger granules after solidification of the liquid or sintering.
- the product moisture content,
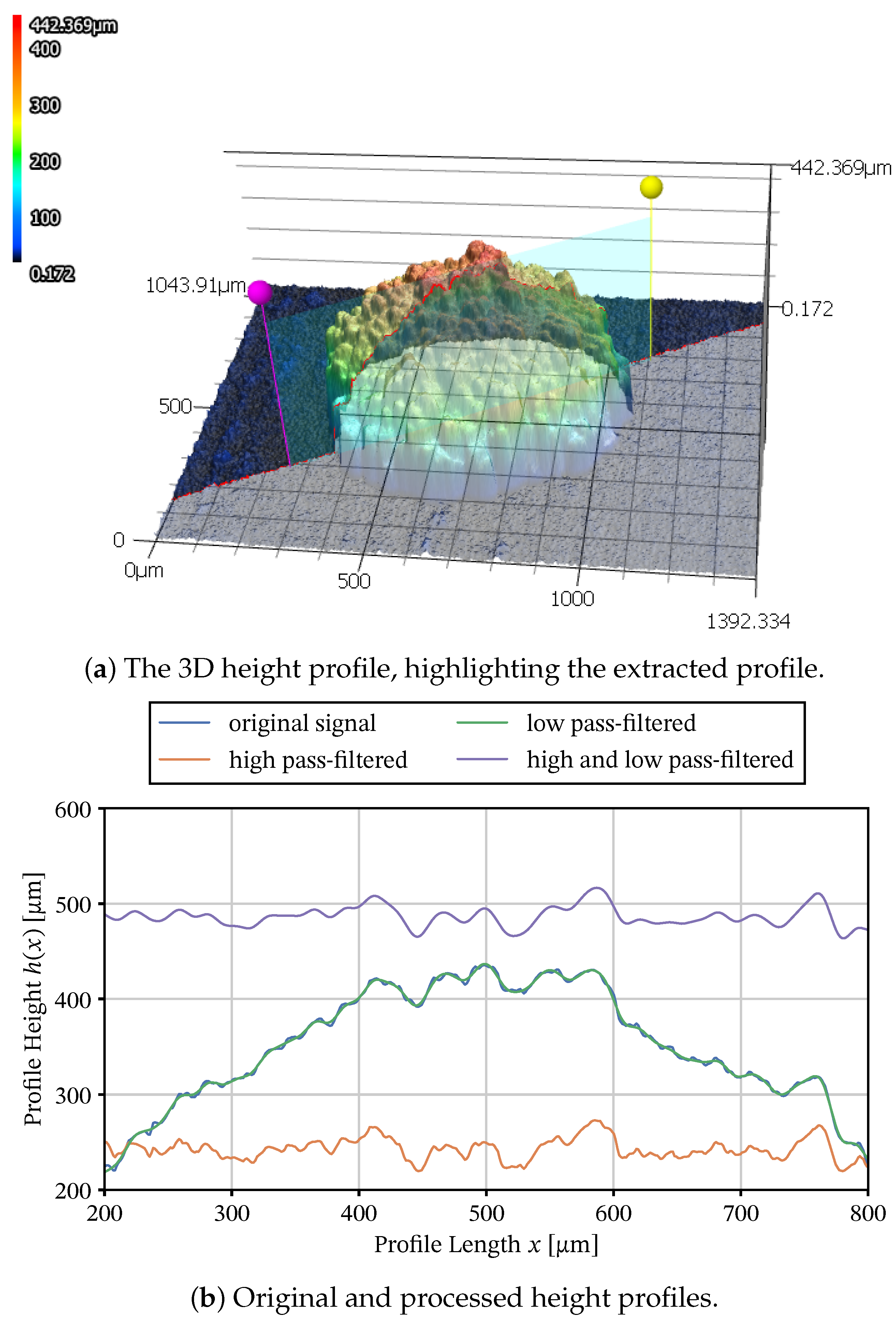
- the area surface roughness as analyzed by confocal microscopy,
- the modulus of elasticity using compression testing,
- the granule porosity using X-ray micro-computer tomography,
- the wetting behavior using the contact angle as given by the sessile drop experiment.
2. Materials and Methods
2.1. CFD-DEM Simulation
- droplet injection and transport in the gas phase,
- droplet evaporation,
- deposition of droplets onto the particle surface,
- evaporation of liquid on the particle surface,
- transport of energy/enthalpy in the gas phase and
- transport of a vapor species in the gas phase.
2.2. Tracked Quantities
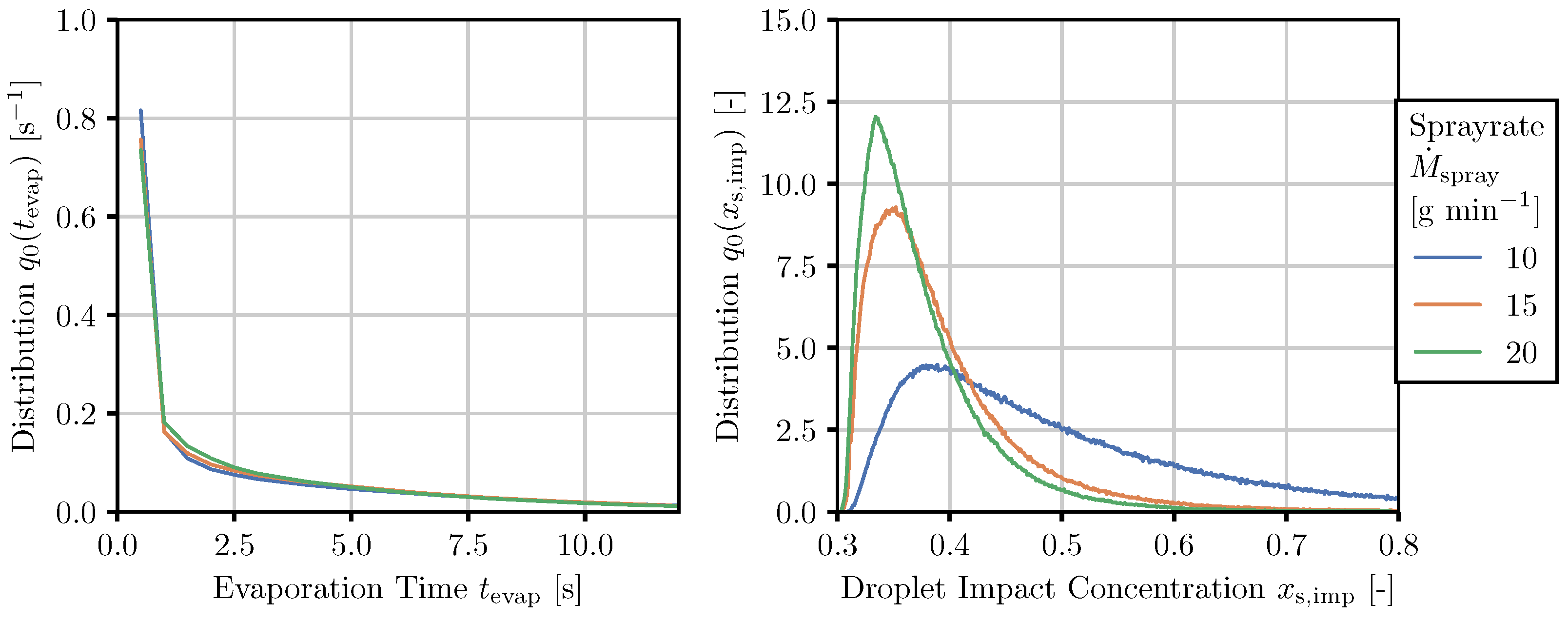
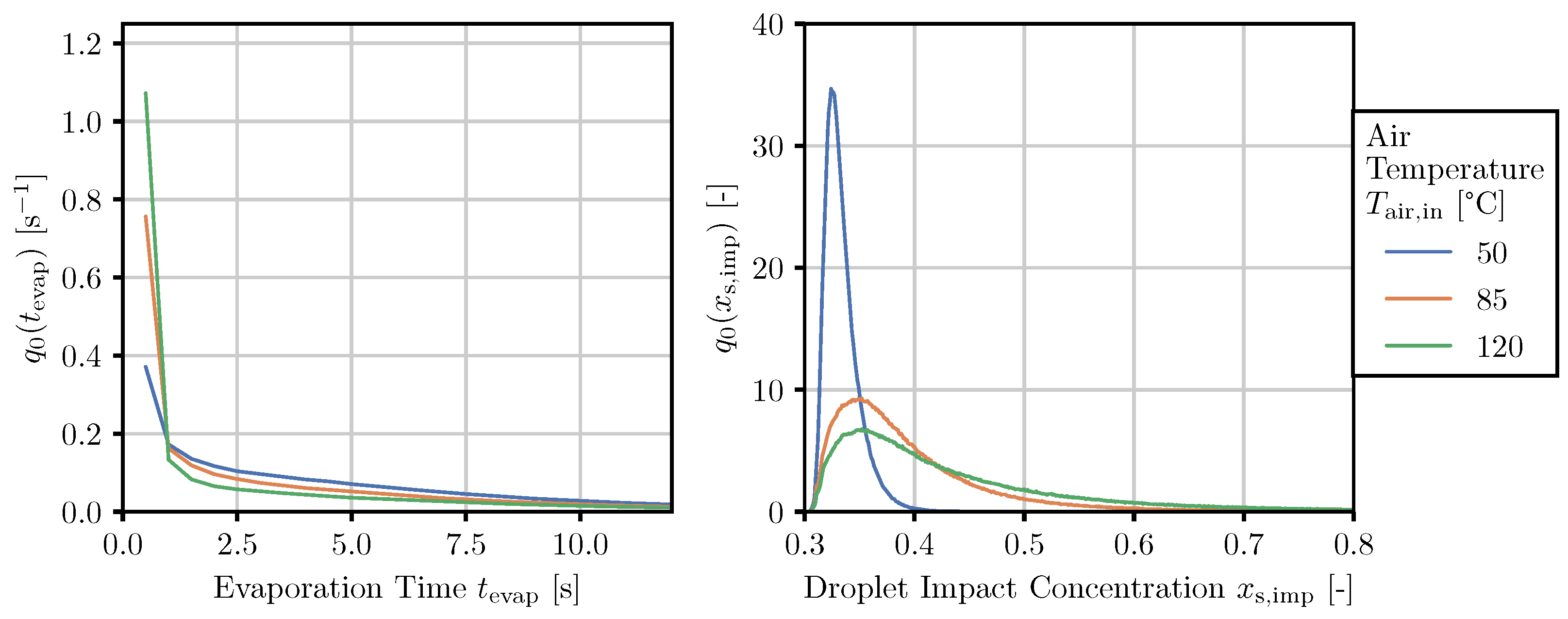
- Solids concentration in the droplets at impact: The concentration of the solid component of droplets upon impact is an indicator for the intensity of the drying conditions that occur—determining interplay of solvent removal and aggregation of the solid components by diffusion, relating to the time available for nucleation and crystallization to occur for solutions and aggregation to take place in the case of suspensions.
- Relative velocity at impact: The relative velocity between particle and droplet, together with viscosity and surface tension (both dependent on solids concentration), should correlate with the droplet interaction regime.
2.3. Product-Property Tracked Quantity Correlation
- Population-based: Distributions over all tracked quantities are analyzed separately. This has the key advantage of being easily automated and taking into consideration the spread of the entire population of particles.
- Particle-based: For single or selected particle populations, tracked quantities are correlated with each other to give a temporal sequence of events or states in which the particle is, e.g., periods of drying alternating with wetting. While this may be more intuitive to analyze, automatically scaling this analysis to the entire particle population is much more difficult.
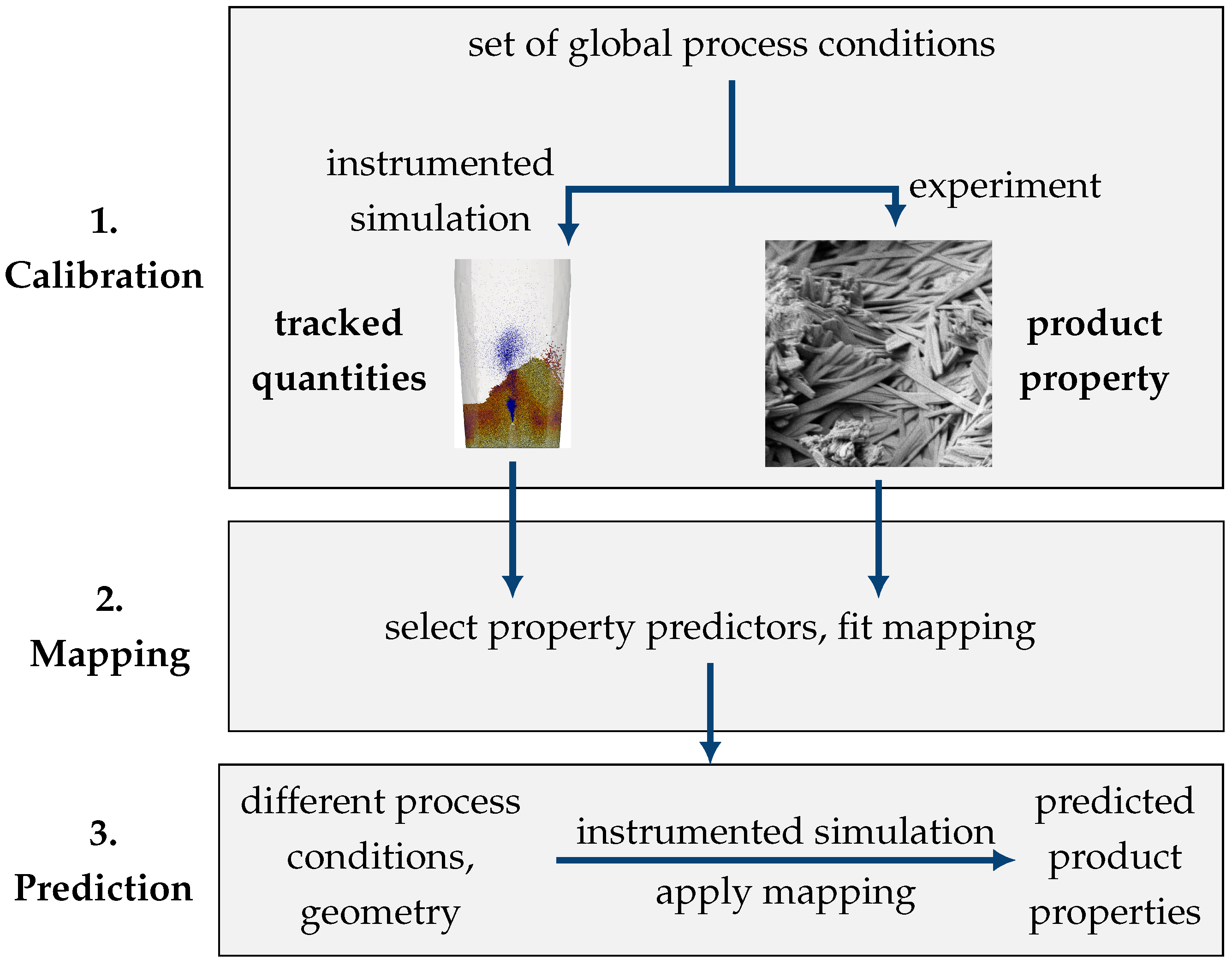
2.4. Workflow
- Calibration experiments,
- calibration simulations,
- evaluation of simulations and experiments, derivation of a mapping and
- predictive simulation.
2.5. Assumptions and Limitations
2.6. Laboratory-Scale Experiments
- Fluidization air flow rate,
- fluidization air temperature,
- liquid spray rate,
- atomization air pressure and
- nozzle air temperature.
2.7. Particle Roughness Quantification
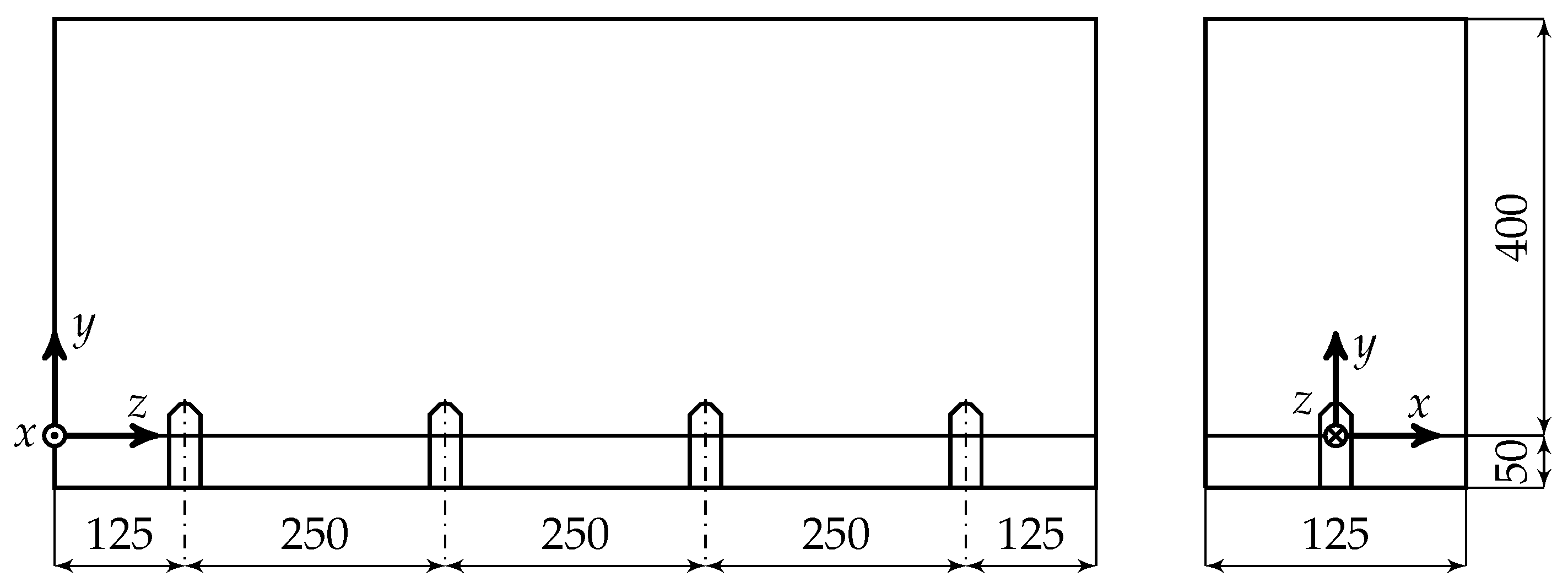
2.8. Pilot-Scale Experiments
- the gas velocity,
- the net spray rate per distributor area and
- the bed mass per distributor area
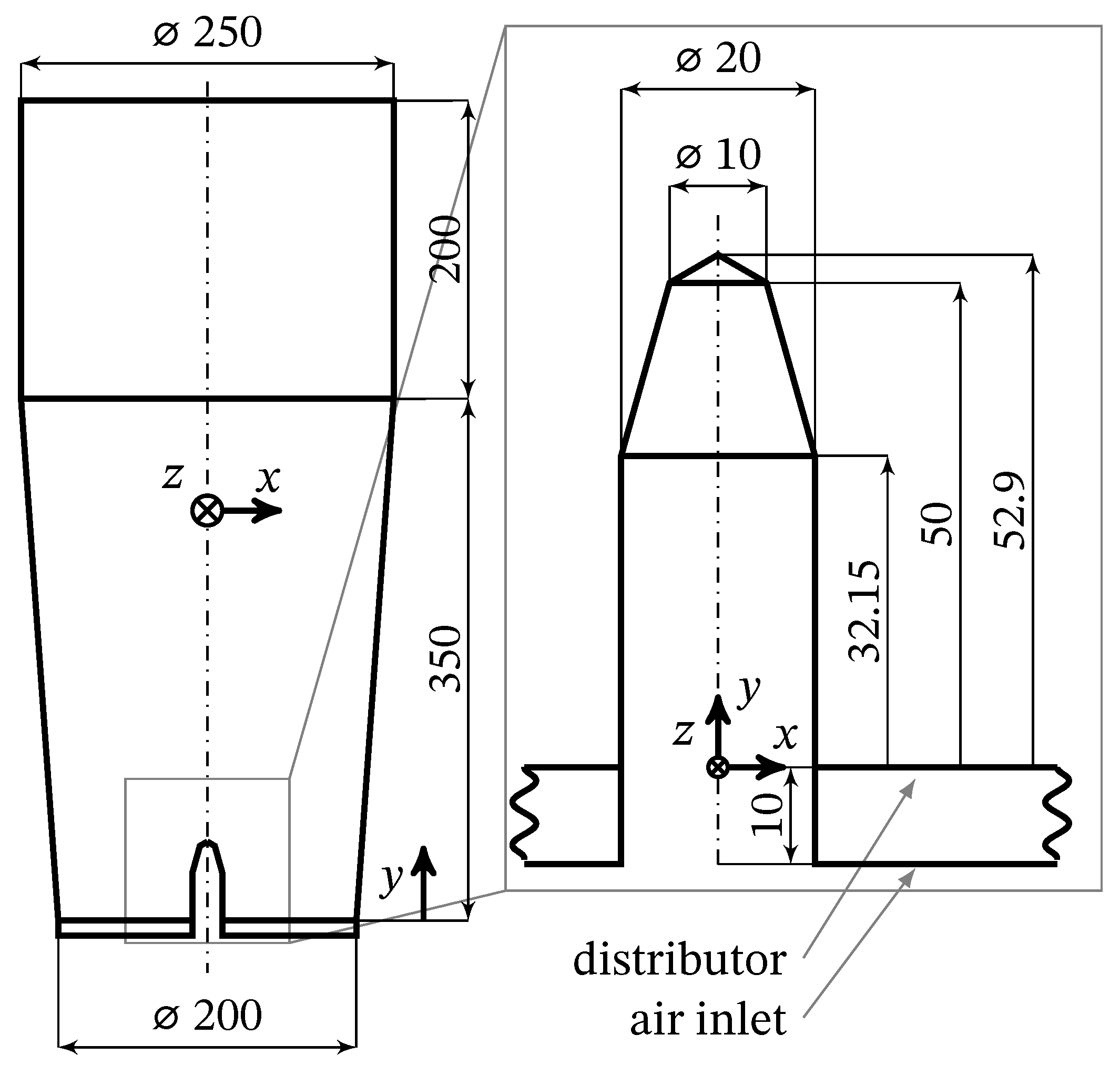
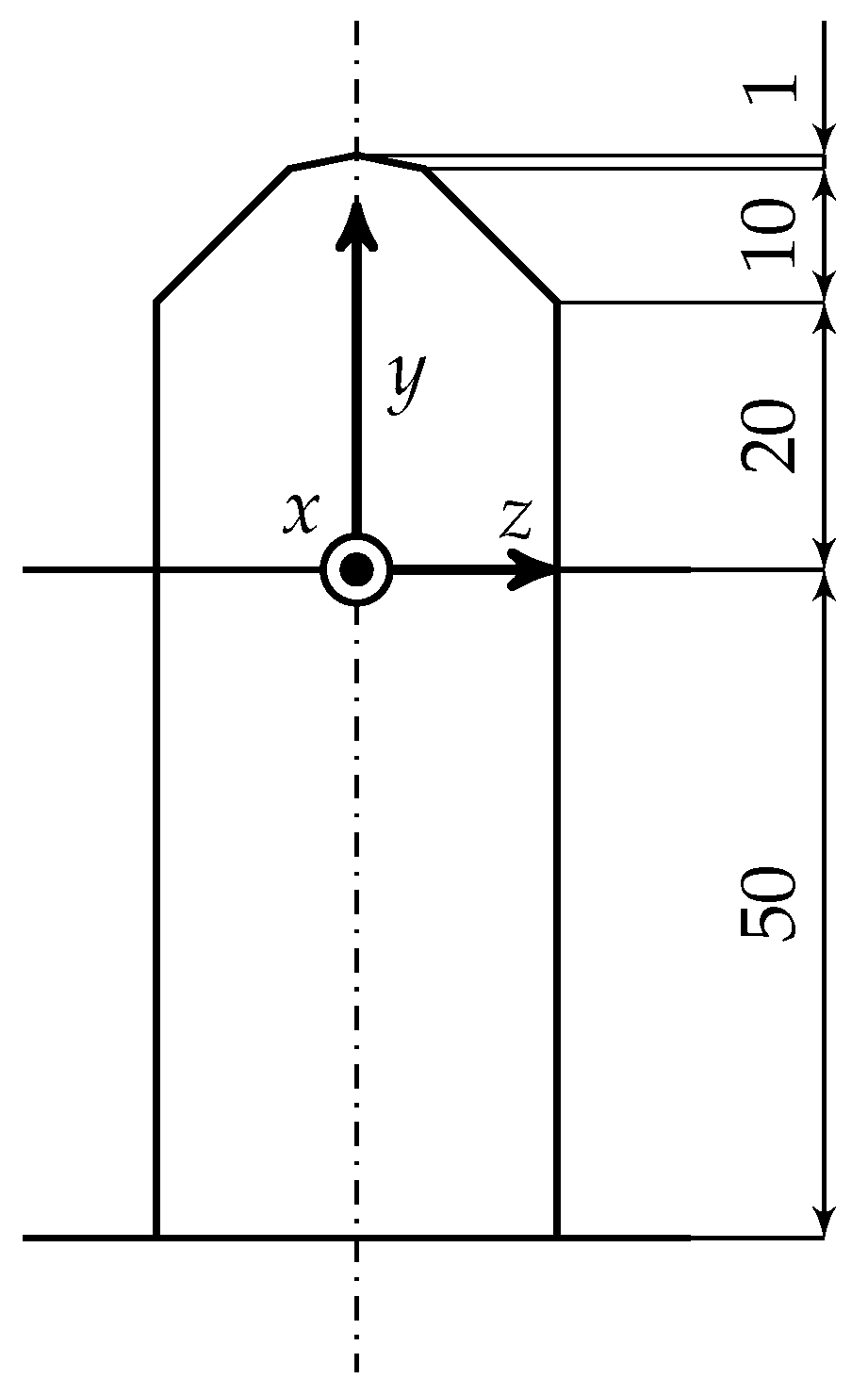
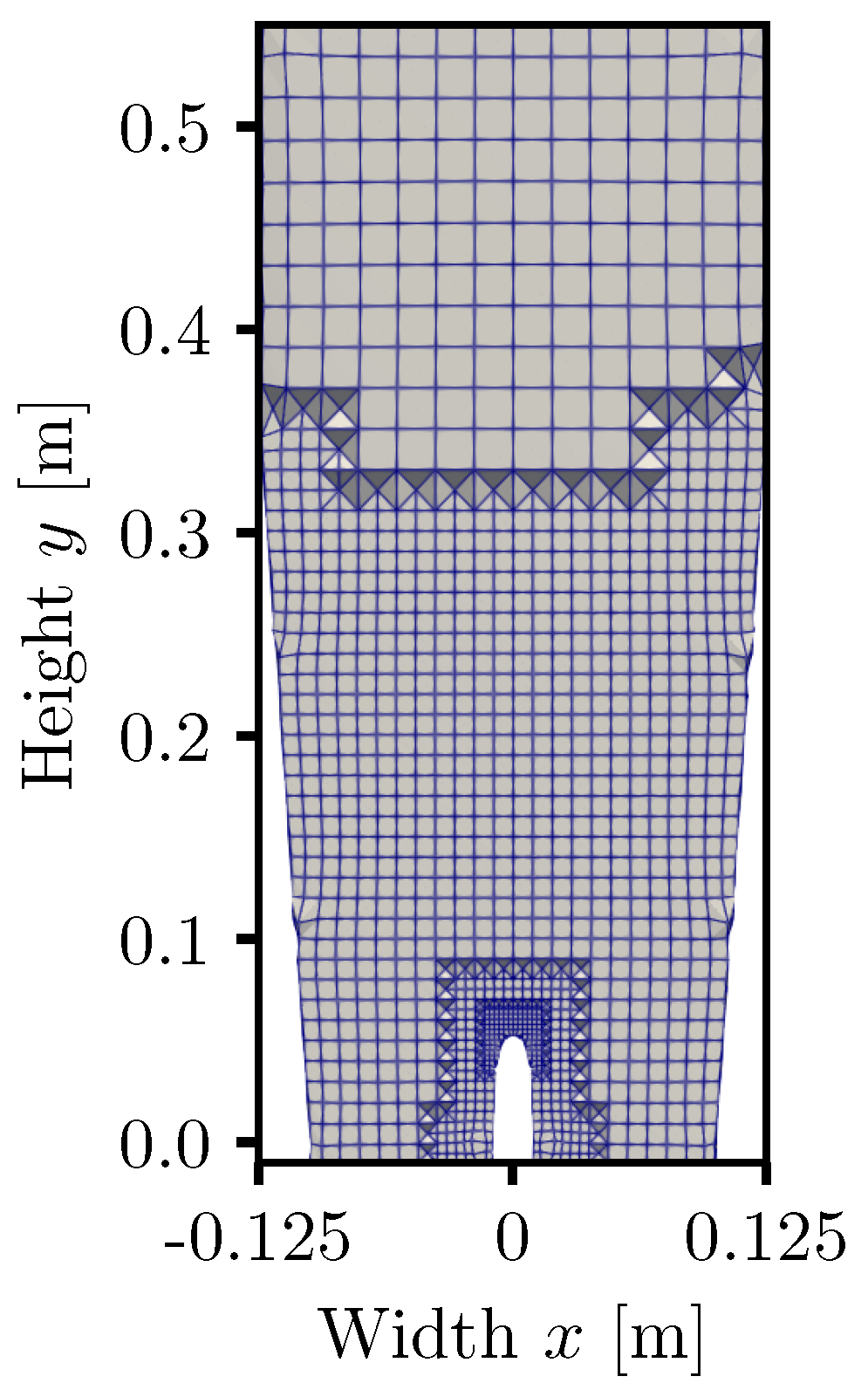
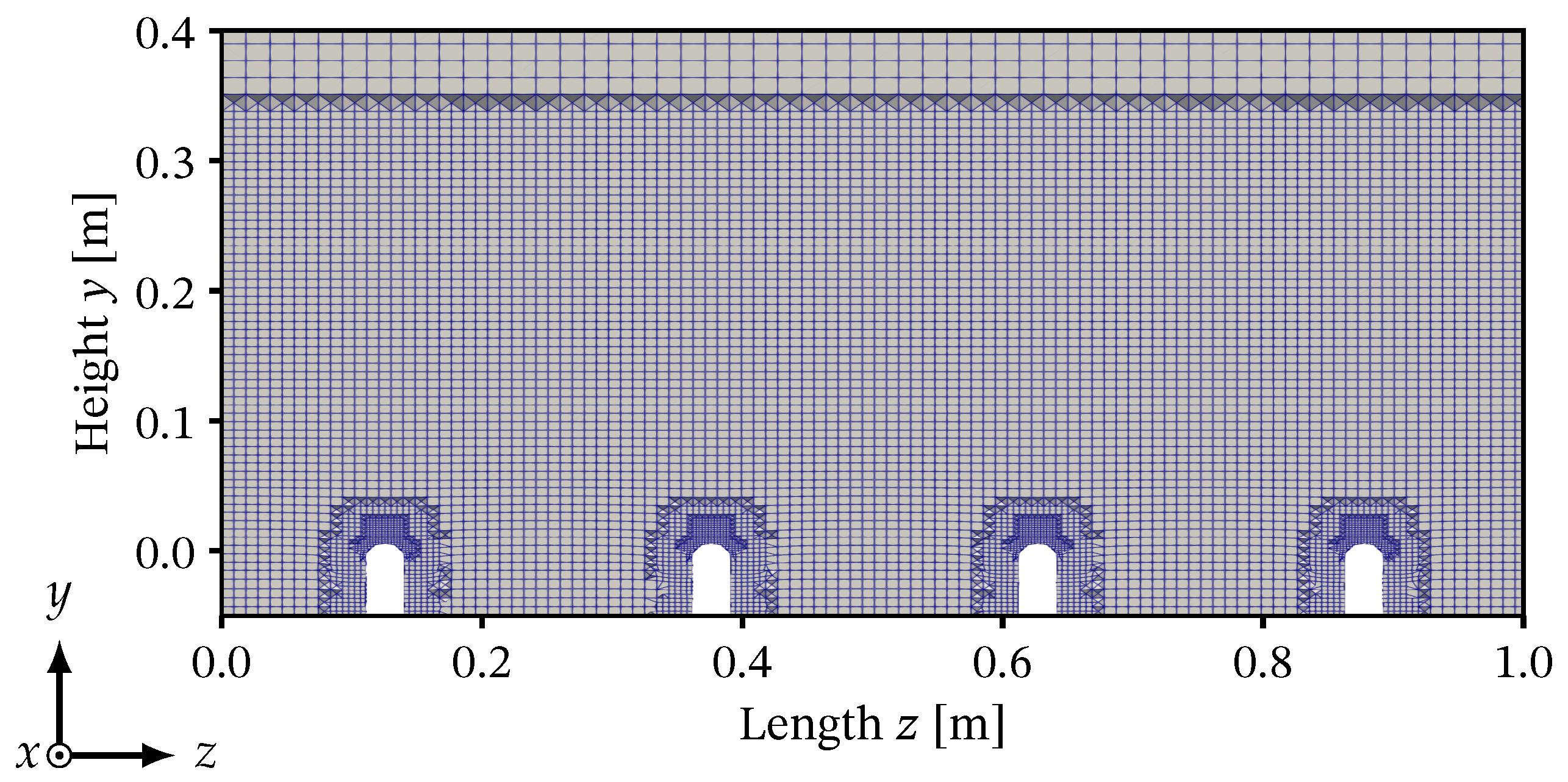
2.9. Simulation Setup
3. Results and Discussion
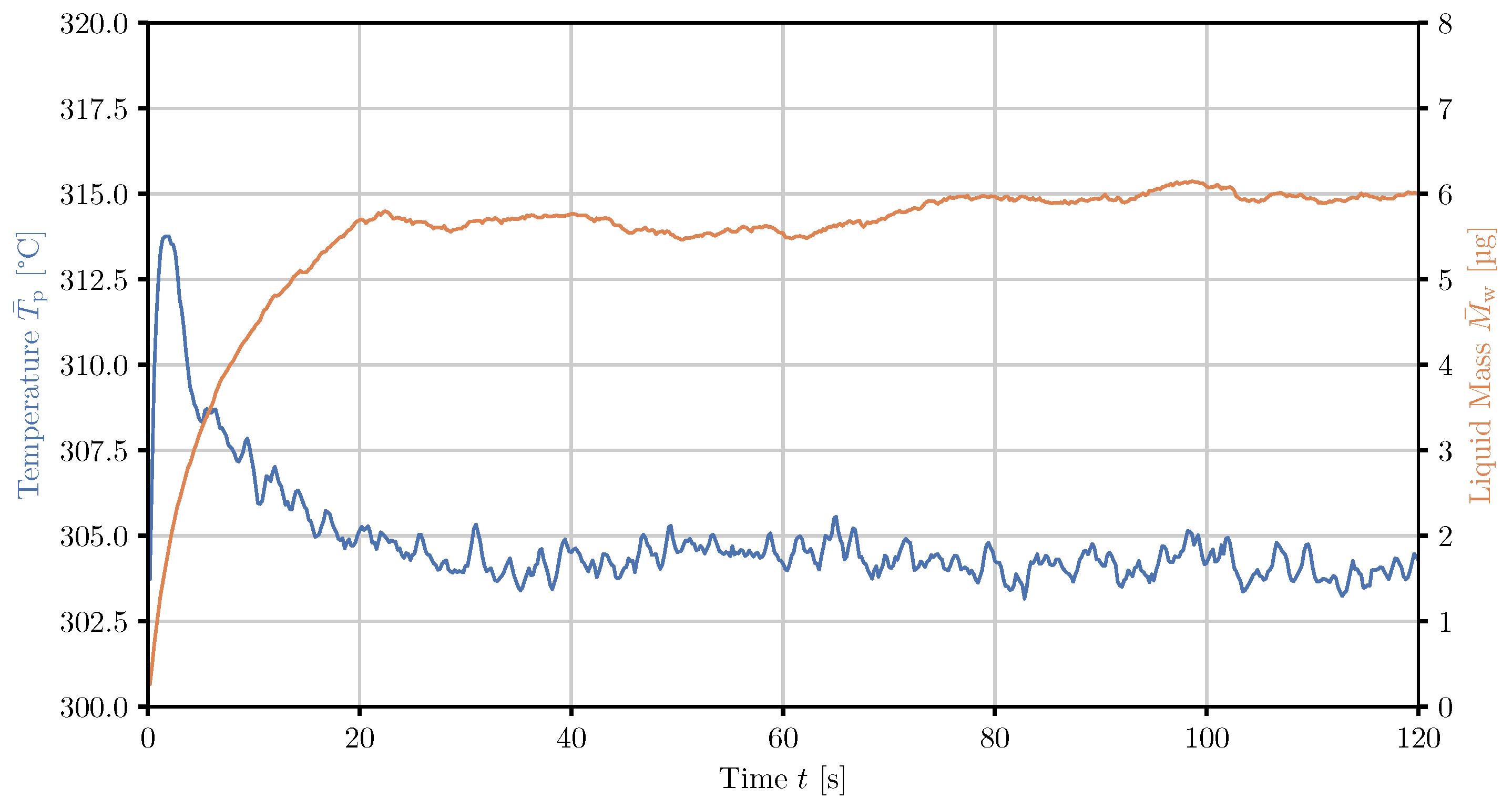
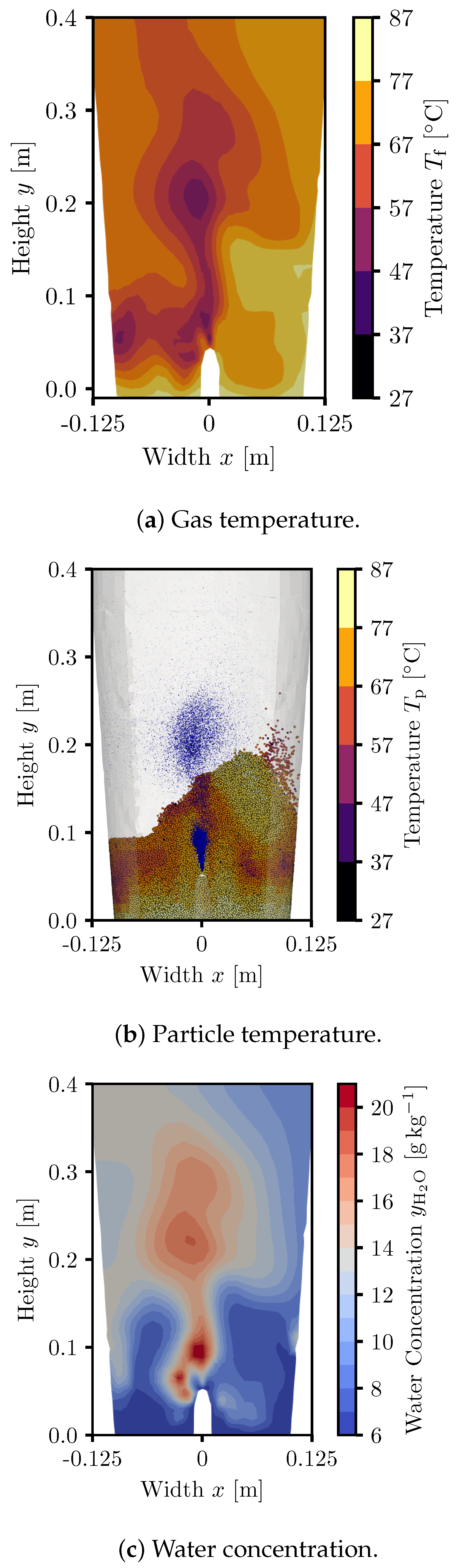
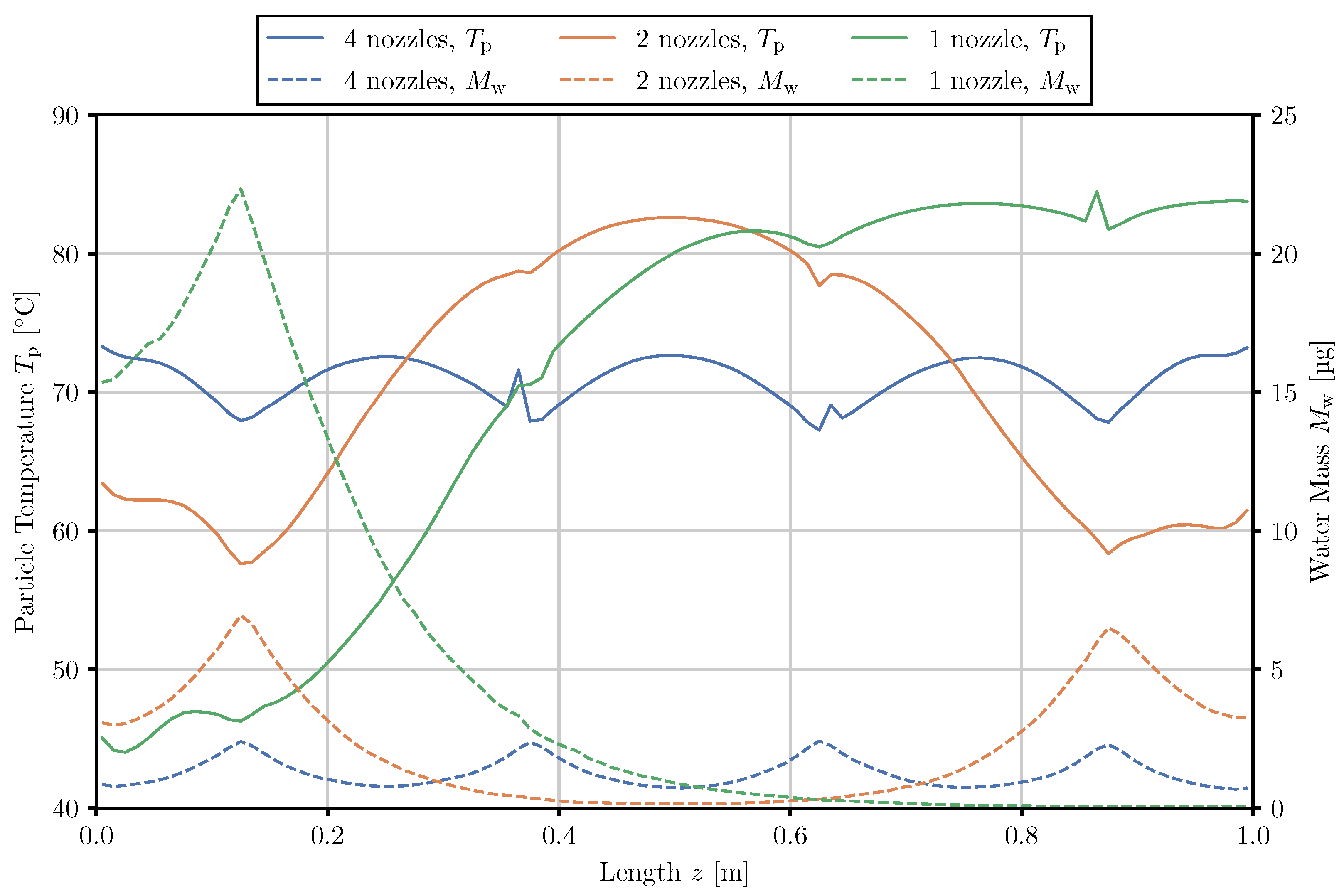
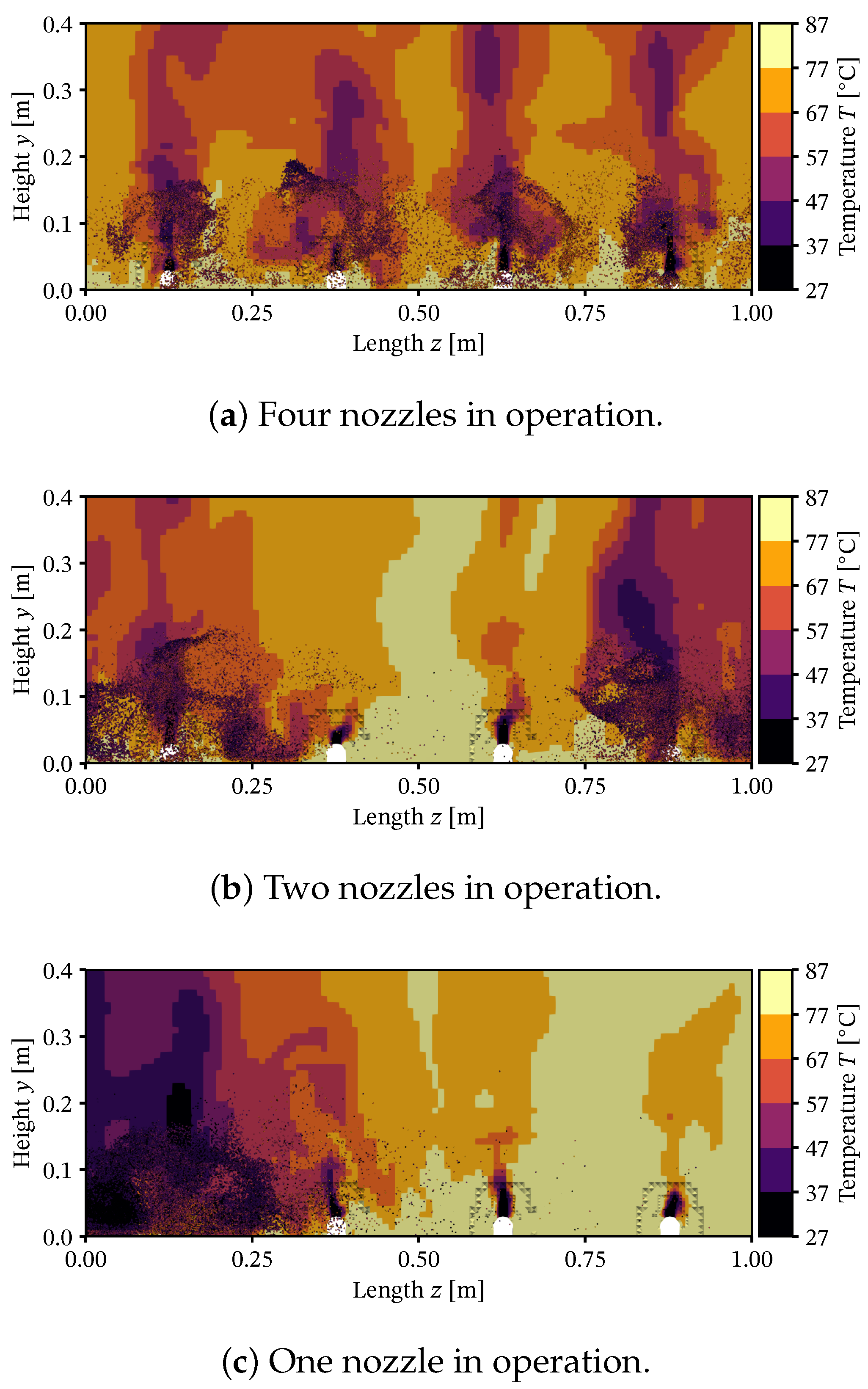
3.1. Laboratory-Scale Simulations
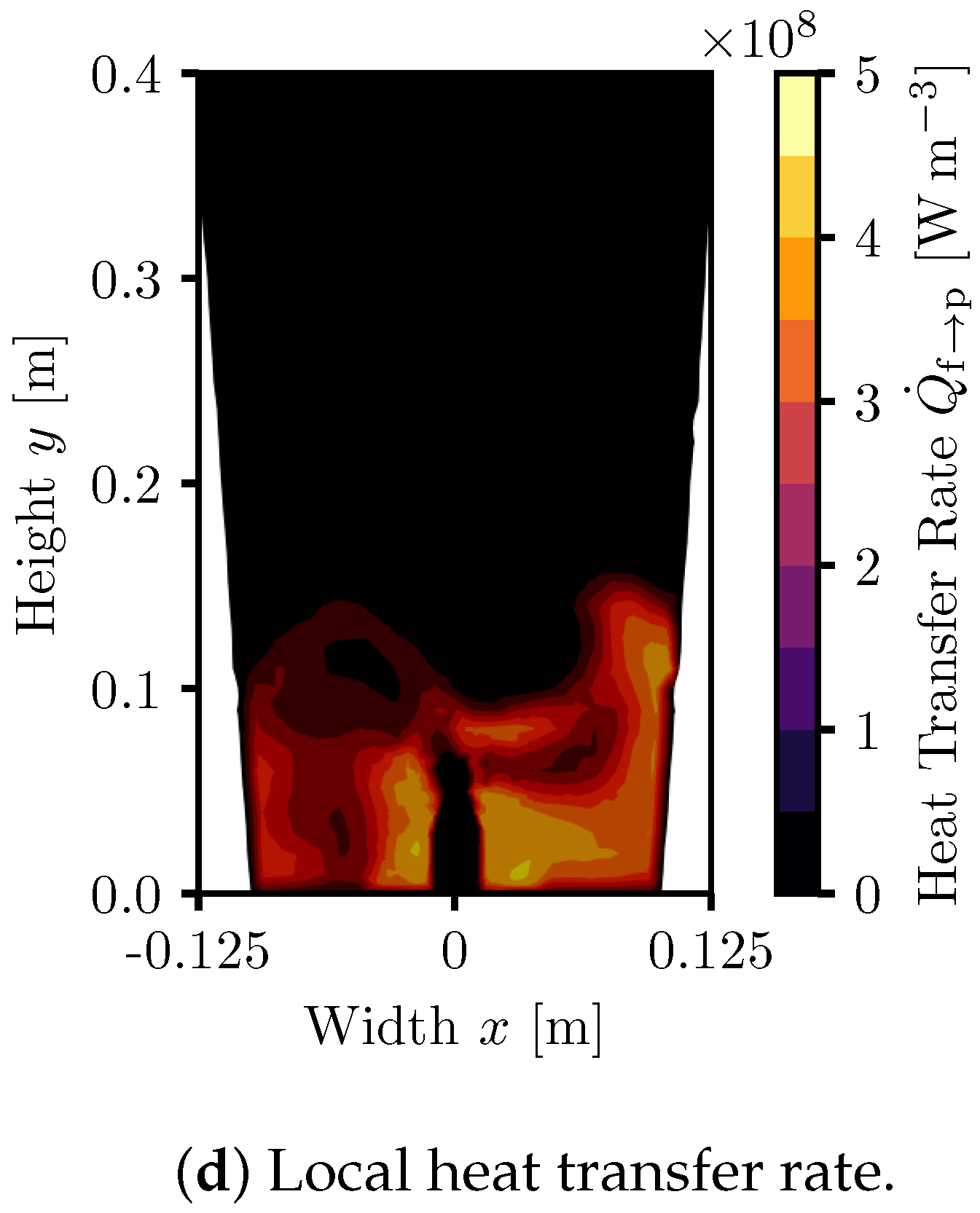
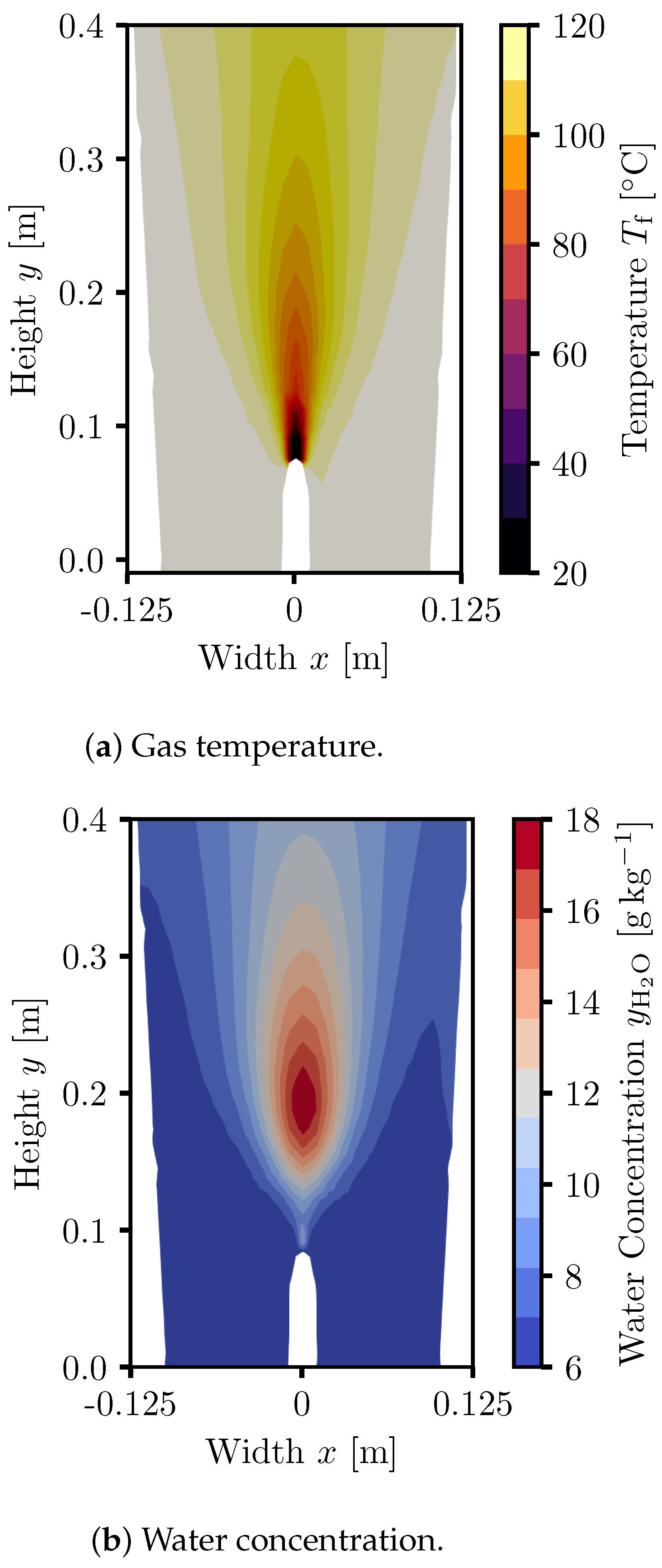
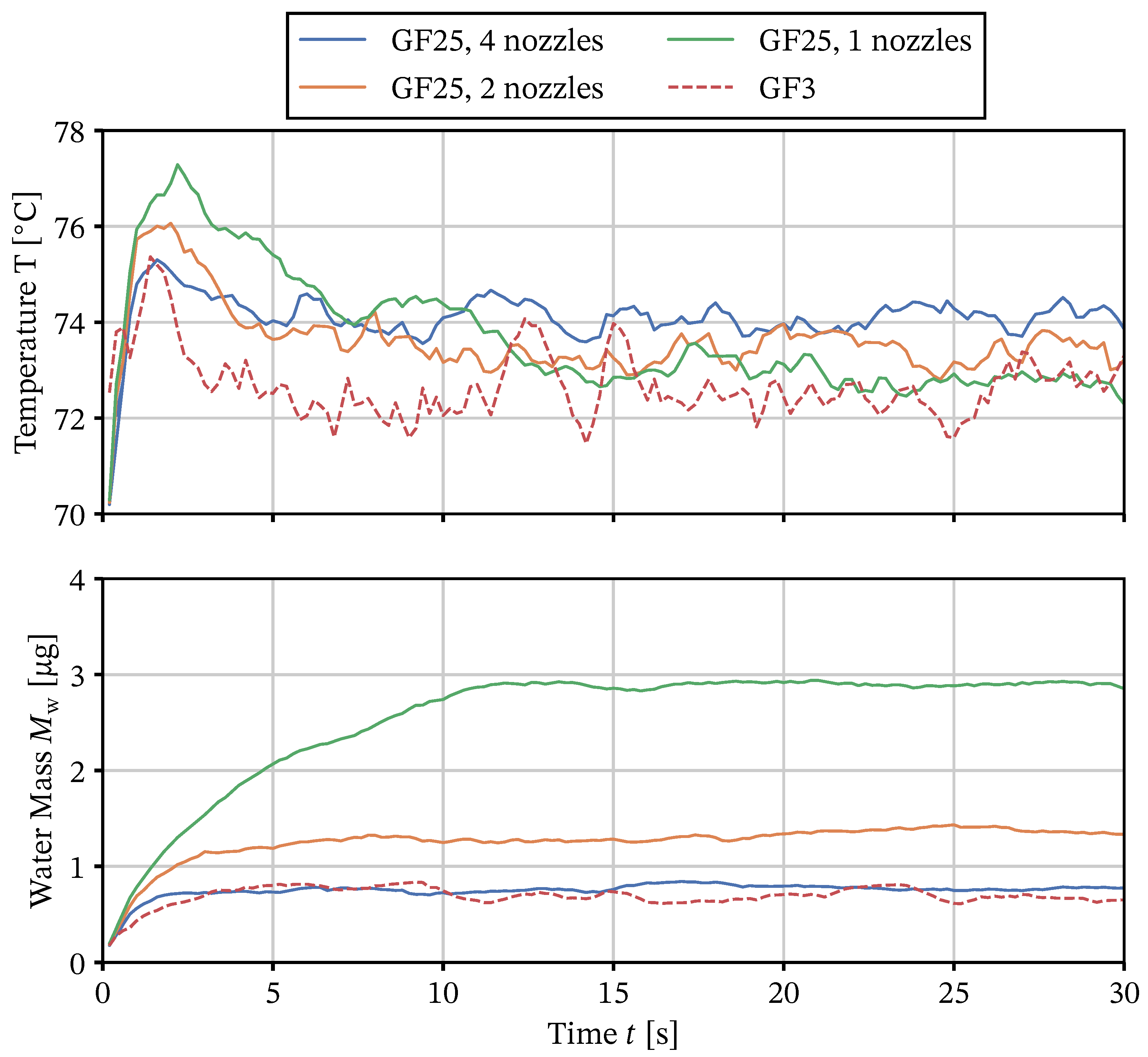
3.2. Pilot-Scale Simulations
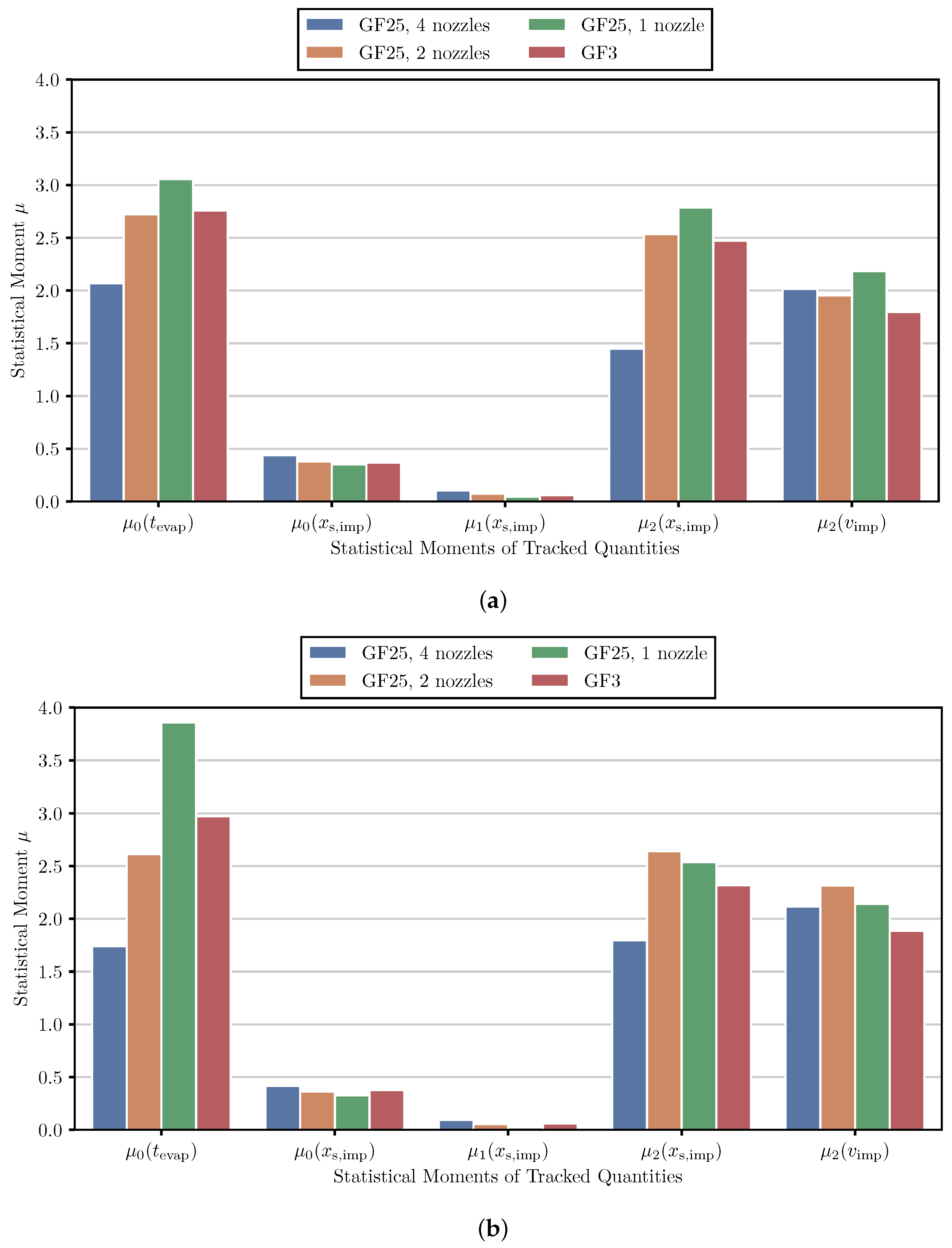
3.3. Product-Property Tracked Quantity Mapping
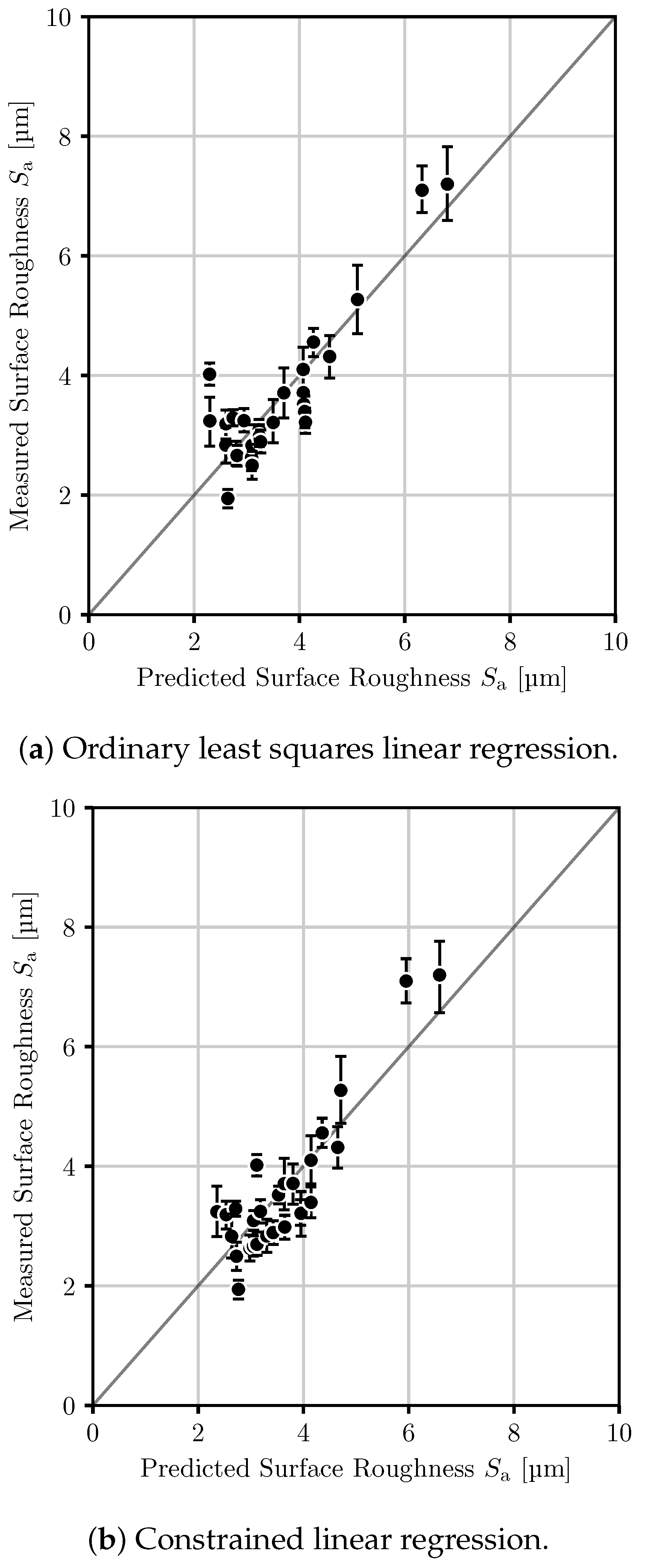
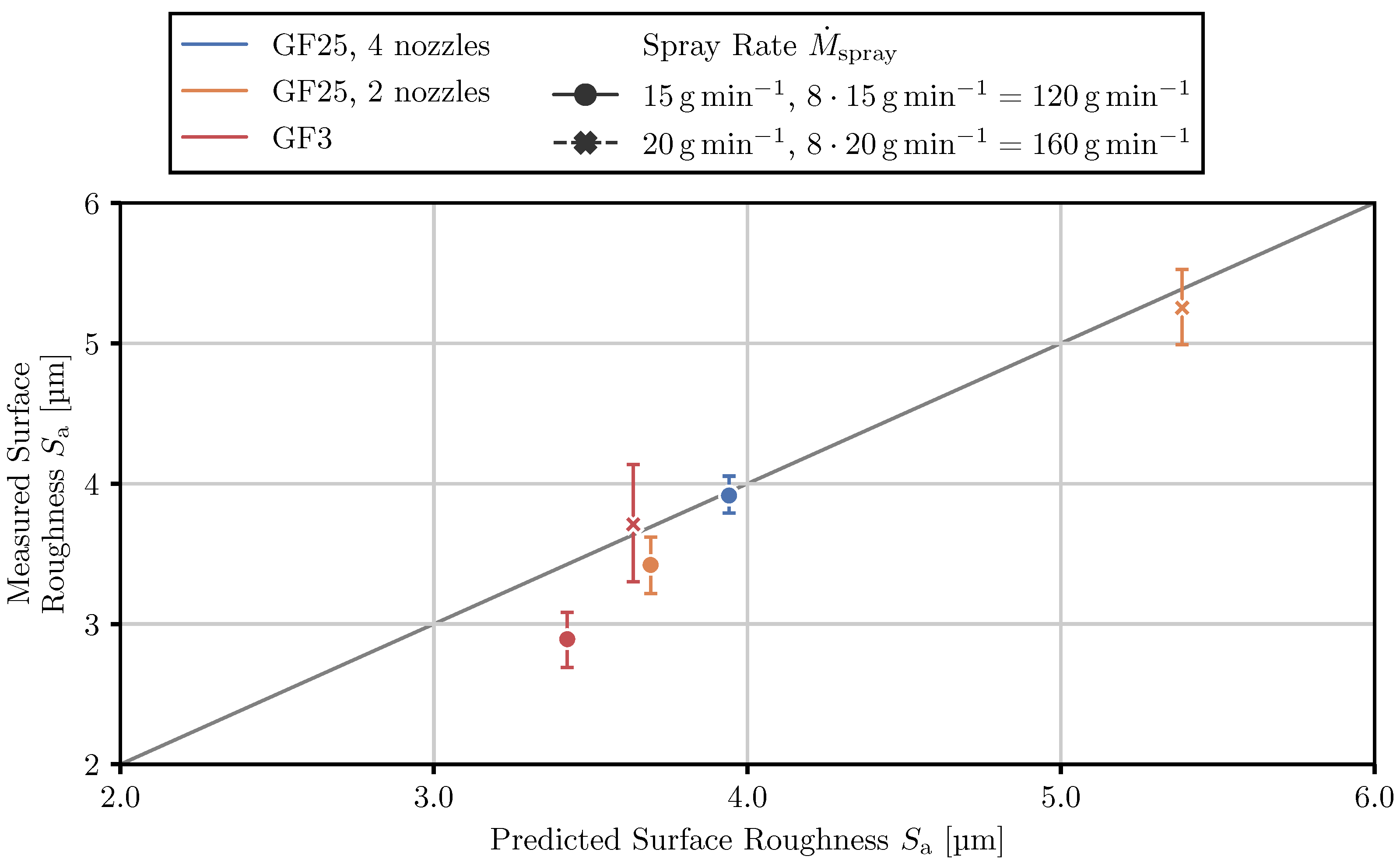
3.4. Prediction of Product Properties on the Pilot-Scale
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hoffmann, T.; Rieck, C.; Bück, A.; Peglow, M.; Tsotsas, E. Influence of Granule Porosity during Fluidized Bed Spray Granulation. Procedia Eng. 2015, 102, 458–467. [Google Scholar] [CrossRef] [Green Version]
- Rieck, C.; Hoffmann, T.; Bück, A.; Peglow, M.; Tsotsas, E. Influence of Drying Conditions on Layer Porosity in Fluidized Bed Spray Granulation. Powder Technol. 2015, 272, 120–131. [Google Scholar] [CrossRef]
- Schmidt, M.; Bück, A.; Tsotsas, E. Experimental Investigation of the Influence of Drying Conditions on Process Stability of Continuous Spray Fluidized Bed Layering Granulation with External Product Separation. Powder Technol. 2017, 320, 474–482. [Google Scholar] [CrossRef]
- Diez, E.; Meyer, K.; Bück, A.; Tsotsas, E.; Heinrich, S. Influence of Process Conditions on the Product Properties in a Continuous Fluidized Bed Spray Granulation Process. Chem. Eng. Res. Des. 2018, 139, 104–115. [Google Scholar] [CrossRef]
- Batista, J.; Santos, D.; Béttega, R. Determination of the Physical and Interaction Properties of Sorghum Grains: Application to Computational Fluid Dynamics–Discrete Element Method Simulations of the Fluid Dynamics of a Conical Spouted Bed. Particuology 2021, 54, 91–101. [Google Scholar] [CrossRef]
- Bahramian, A.; Olazar, M. Evaluation of Elastic and Inelastic Contact Forces in the Flow Regimes of Titania Nanoparticle Agglomerates in a Bench-Scale Conical Fluidized Bed: A Comparative Study of CFD-DEM Simulation and Experimental Data. Chem. Eng. Res. Des. 2021, 176, 34–48. [Google Scholar] [CrossRef]
- Kieckhefen, P. A Novel Method for Predicting Product Properties in Fluidized Bed Spray Granulation; Number 19 in SPE-Schriftenreihe; Cuvillier Verlag: Göttingen, Germany, 2021. [Google Scholar]
- Golshan, S.; Sotudeh-Gharebagh, R.; Zarghami, R.; Mostoufi, N.; Blais, B.; Kuipers, J. Review and Implementation of CFD-DEM Applied to Chemical Process Systems. Chem. Eng. Sci. 2020, 221, 115646. [Google Scholar] [CrossRef]
- Kieckhefen, P.; Pietsch, S.; Dosta, M.; Heinrich, S. Possibilities and Limits of Computational Fluid Dynamics–Discrete Element Method Simulations in Process Engineering: A Review of Recent Advancements and Future Trends. Annu. Rev. Chem. Biomol. Eng. 2020, 11, 397–422. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Goniva, C.; Kloss, C.; Deen, N.G.; Kuipers, J.A.; Pirker, S. Influence of Rolling Friction on Single Spout Fluidized Bed Simulation. Particuology 2012, 10, 582–591. [Google Scholar] [CrossRef]
- Kinaci, M.E.; Lichtenegger, T.; Schneiderbauer, S. A CFD-DEM Model for the Simulation of Direct Reduction of Iron-Ore in Fluidized Beds. Chem. Eng. Sci. 2020, 227. [Google Scholar] [CrossRef]
- Kieckhefen, P.; Lichtenegger, T.; Pietsch, S.; Pirker, S.; Heinrich, S. Simulation of Spray Coating in a Spouted Bed Using Recurrence CFD. Particuology 2018, 42, 92–103. [Google Scholar] [CrossRef]
- Gunn, D. Transfer of Heat or Mass to Particles in Fixed and Fluidised Beds. Int. J. Heat Mass Transf. 1978, 21, 467–476. [Google Scholar] [CrossRef]
- Kariuki, W.I.; Freireich, B.; Smith, R.M.; Rhodes, M.; Hapgood, K.P. Distribution Nucleation: Quantifying Liquid Distribution on the Particle Surface Using the Dimensionless Particle Coating Number. Chem. Eng. Sci. 2013, 92, 134–145. [Google Scholar] [CrossRef]
- Stull, D.R. Vapor Pressure of Pure Substances. Organic and Inorganic Compounds. Ind. Eng. Chem. 1947, 39, 517–540. [Google Scholar] [CrossRef]
- Lichtenegger, T.; Peters, E.; Kuipers, J.; Pirker, S. A Recurrence CFD Study of Heat Transfer in a Fluidized Bed. Chem. Eng. Sci. 2017, 172, 310–322. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-Learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Orth, M.; Kieckhefen, P.; Pietsch, S.; Heinrich, S. Correlating Granule Surface Structure Morphology and Process Conditions in Fluidized Bed Layering Spray Granulation. KONA Powder Part. J. 2021, 39, 230–239. [Google Scholar] [CrossRef]
- Sutherland, W. The Viscosity of Gases and Molecular Force. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1893, 36, 507–531. [Google Scholar] [CrossRef] [Green Version]
- Pietsch, S.; Kieckhefen, P.; Müller, M.; Schönherr, M.; Kleine Jäger, F.; Heinrich, S. Novel Production Method of Tracer Particles for Residence Time Measurements in Gas-Solid Processes. Powder Technol. 2018, 338, 1–6. [Google Scholar] [CrossRef]
- Kieckhefen, P.; Pietsch, S.; Höfert, M.; Schönherr, M.; Heinrich, S.; Kleine Jäger, F. Influence of Gas Inflow Modelling on CFD-DEM Simulations of Three-Dimensional Prismatic Spouted Beds. Powder Technol. 2018, 329, 167–180. [Google Scholar] [CrossRef]

| Parameter | Symbol | Unit | Values | ||
|---|---|---|---|---|---|
| Low | Mid | High | |||
| Fluidization air flow rate | 80 | 105 | 130 | ||
| Fluidization air temperature | 50 | 85 | 120 | ||
| Spray air pressure | 0.5 | 1.8 | 3.0 | ||
| Spray solution flow rate | 10 | 15 | 20 | ||
| Spray air temperature | 20 | 70 | 120 | ||
| Fluidization Air | Spray Air | ||||
|---|---|---|---|---|---|
| ID | Flow Rate [Nm3 h−1] | Temperature [°C] | Pressure [bar] | Solution Flow Rate [g min−1] | Temperature [°C] |
| 1 | 105 | 85 | 1.8 | 10 | 70 |
| 2 | 130 | 50 | 3.0 | 10 | 120 |
| 3 | 80 | 50 | 0.5 | 20 | 20 |
| 4 | 105 | 85 | 1.8 | 15 | 70 |
| 5 | 105 | 85 | 1.8 | 15 | 70 |
| 6 | 105 | 85 | 1.8 | 15 | 70 |
| 7 | 80 | 50 | 3.0 | 10 | 20 |
| 8 | 105 | 85 | 1.8 | 15 | 120 |
| 9 | 130 | 120 | 3.0 | 10 | 20 |
| 10 | 130 | 85 | 1.8 | 15 | 70 |
| 12 | 80 | 50 | 0.5 | 10 | 120 |
| 13 | 130 | 120 | 0.5 | 10 | 120 |
| 14 | 130 | 50 | 3.0 | 20 | 20 |
| 15 | 130 | 120 | 0.5 | 20 | 20 |
| 16 | 105 | 85 | 1.8 | 15 | 20 |
| 17 | 130 | 50 | 0.5 | 20 | 120 |
| 18 | 80 | 120 | 3.0 | 20 | 20 |
| 19 | 105 | 85 | 1.8 | 20 | 70 |
| 20 | 80 | 120 | 0.5 | 20 | 120 |
| 21 | 130 | 120 | 3.0 | 20 | 120 |
| 22 | 80 | 120 | 0.5 | 10 | 20 |
| 23 | 105 | 85 | 3.0 | 15 | 70 |
| 24 | 130 | 50 | 0.5 | 10 | 20 |
| 25 | 105 | 120 | 1.8 | 15 | 70 |
| 26 | 80 | 120 | 3.0 | 10 | 120 |
| 28 | 105 | 50 | 1.8 | 15 | 70 |
| 30 | 80 | 85 | 1.8 | 15 | 70 |
| 31 | 80 | 50 | 3.0 | 20 | 120 |
| 32 | 105 | 85 | 0.5 | 15 | 70 |
| Symbol | Unit | Glatt GF3 | Glatt GF25 | |
|---|---|---|---|---|
| Geometry | ||||
| Base Dimensions | ||||
| Base Area | 0.0314 | 0.25 | ||
| Fluidization Air | ||||
| Flow Rate | 105 | 840 | ||
| Temperature | 85 | 85 | ||
| Spray | ||||
| Atomization Pressure | 1.8 | 1.8 | ||
| Air Temperature | 20 | 20 | ||
| Solute Concentration | 0.3 | 0.3 | ||
| Bed Mass | 2 | 16 |
| Quantity | Symbol | Value |
|---|---|---|
| Numerics | ||
| Time Step | ||
| CFD | ||
| DEM | ||
| Coupling Interval | ||
| Scaling Factor (Coarse Graining) | 4 | |
| Particle | ||
| Diameter | ||
| Density | 1400 | |
| Young’s Modulus | ||
| Particle–Particle | ||
| Particle–Wall | ||
| Poisson Ratio | 0.22 | |
| Restitution Coefficient | ||
| Particle–Particle | 0.051 | |
| Particle–Wall | 0.051 | |
| Friction Coefficient | ||
| Particle–Particle | 0.3 | |
| Particle–Wall | 0.3 | |
| Rolling Friction Coefficient | ||
| Particle–Particle | 0.083 | |
| Particle–Wall | 0.028 | |
| Liquid | ||
| Density | 1000 | |
| Heat Capacity | 4186 | |
| Heat of Evaporation | ||
| Droplets per Parcel | 4 |
| Atomization Pressure | Atomization Air Flow Rate | Median Droplet Size |
|---|---|---|
| [bar] | kg h−1 | [m] |
| 0.5 | 2 | 42 |
| 1.8 | 4 | 32 |
| 3.0 | 5 | 22 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kieckhefen, P.; Pietsch-Braune, S.; Heinrich, S. Product-Property Guided Scale-Up of a Fluidized Bed Spray Granulation Process Using the CFD-DEM Method. Processes 2022, 10, 1291. https://doi.org/10.3390/pr10071291
Kieckhefen P, Pietsch-Braune S, Heinrich S. Product-Property Guided Scale-Up of a Fluidized Bed Spray Granulation Process Using the CFD-DEM Method. Processes. 2022; 10(7):1291. https://doi.org/10.3390/pr10071291
Chicago/Turabian StyleKieckhefen, Paul, Swantje Pietsch-Braune, and Stefan Heinrich. 2022. "Product-Property Guided Scale-Up of a Fluidized Bed Spray Granulation Process Using the CFD-DEM Method" Processes 10, no. 7: 1291. https://doi.org/10.3390/pr10071291
APA StyleKieckhefen, P., Pietsch-Braune, S., & Heinrich, S. (2022). Product-Property Guided Scale-Up of a Fluidized Bed Spray Granulation Process Using the CFD-DEM Method. Processes, 10(7), 1291. https://doi.org/10.3390/pr10071291







