Exponential Stabilization for a Class of Strict-Feedback Nonlinear Time Delay Systems via State Feedback Control Scheme
Abstract
:1. Introduction
2. Problem Description
3. Controller Design and Stability Analysis
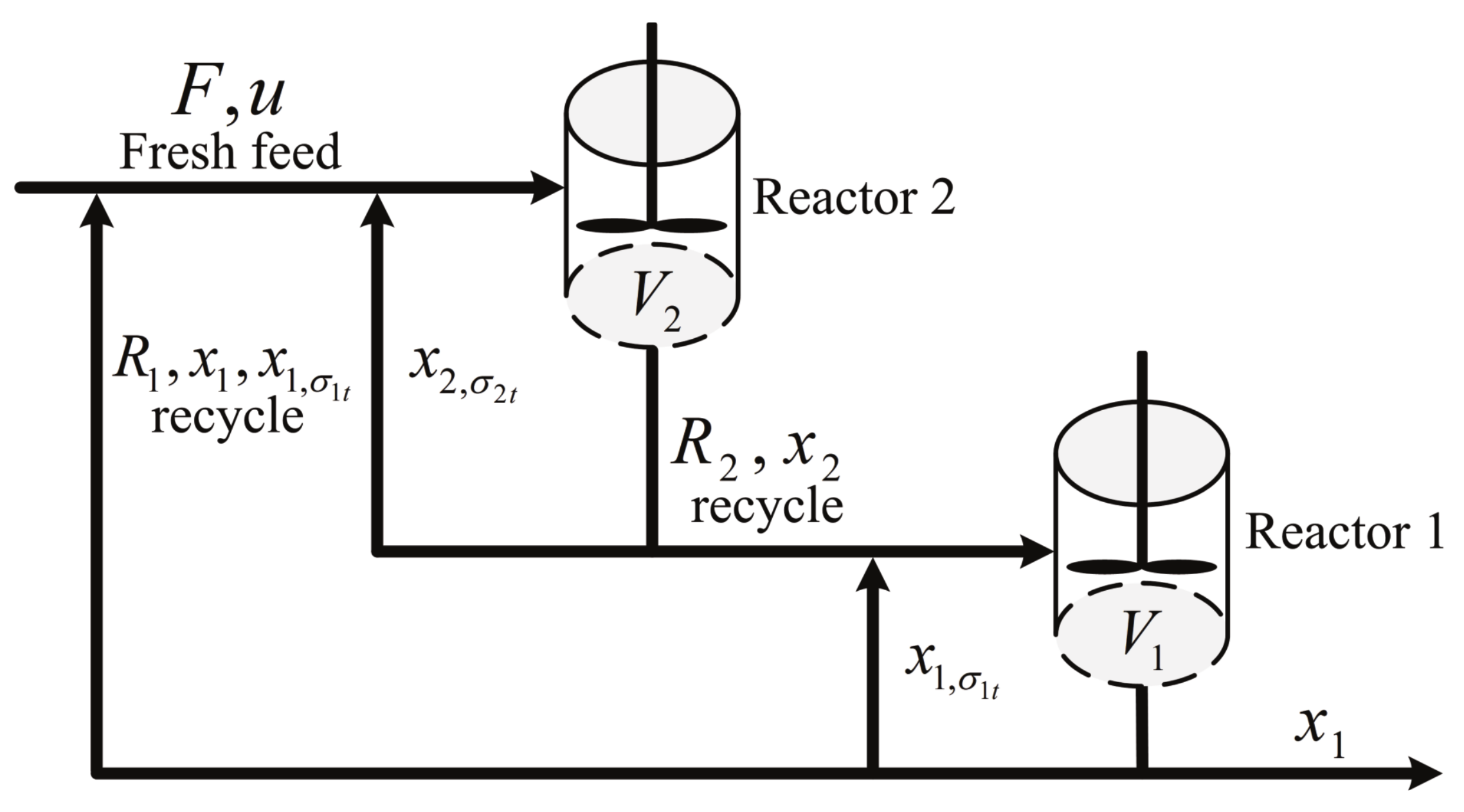
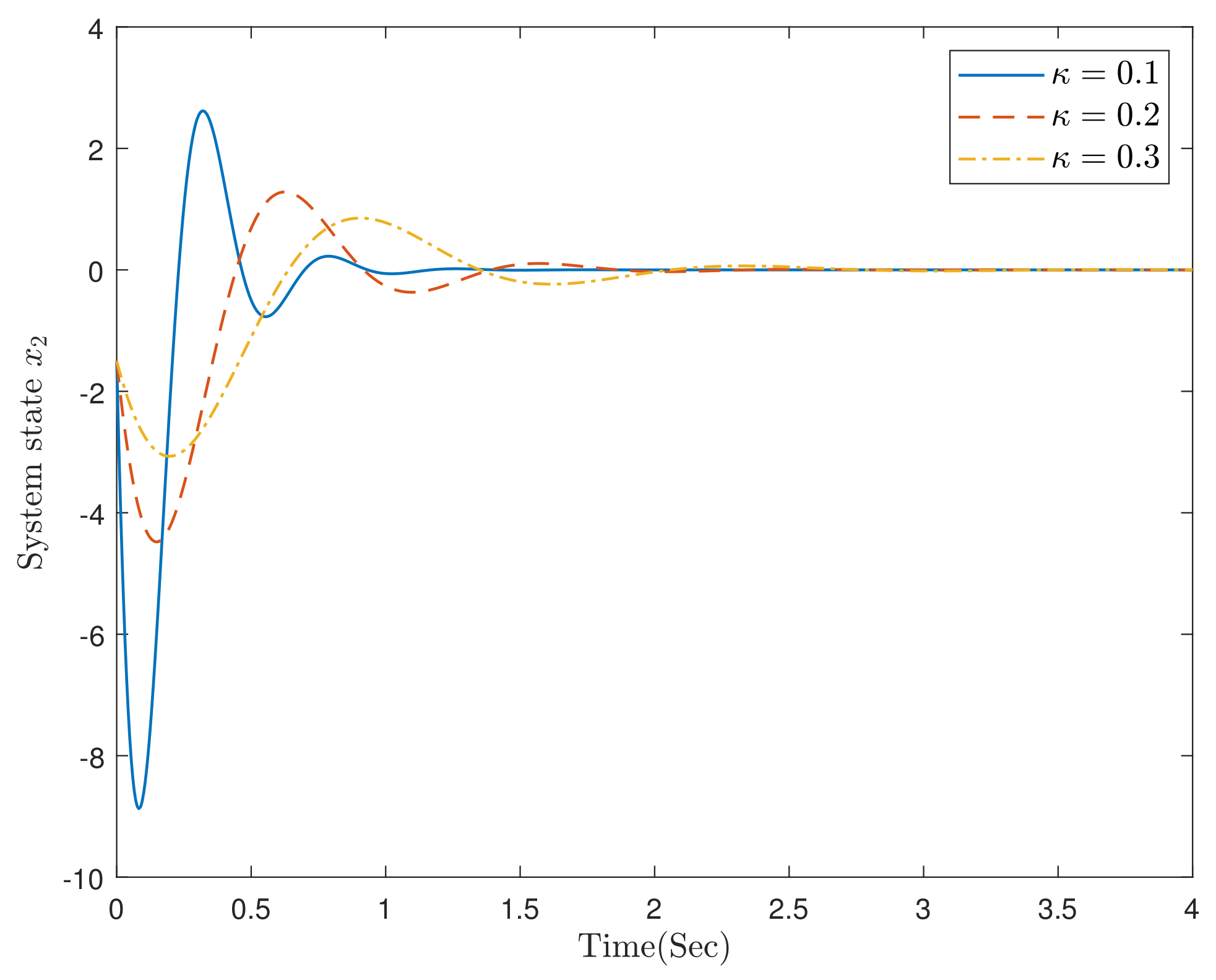
4. An Example
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, H.Y.; Wang, L.J.; Du, H.P.; Boulkroune, A. Adaptive fuzzy backstepping tracking control for strict-feedback systems with input delay. IEEE Trans. Fuzzy Syst. 2017, 25, 642–652. [Google Scholar] [CrossRef]
- Sun, W.; Yuan, W.X.; Shao, Y.; Sun, Z.Y.; Zhao, J.S.; Sun, Q. Adaptive fuzzy control of strict-feedback nonlinear time-delay systems with full-state constraints. Int. J. Fuzzy Syst. 2018, 20, 2556–2565. [Google Scholar] [CrossRef]
- Wang, T.; Wu, J.; Wang, Y.J.; Ma, M. Adaptive fuzzy tracking control for a class of strict-feedback nonlinear systems with time-varying input delay and full state constraints. IEEE Trans. Fuzzy Syst. 2020, 28, 3432–3441. [Google Scholar] [CrossRef]
- Wang, M.; Chen, B.; Shi, P. Adaptive neural control for a class of perturbed strict-feedback nonlinear time-delay systems. IEEE Trans. Syst. Cybern. Part B Cybern. 2008, 38, 721–730. [Google Scholar] [CrossRef]
- Wu, J.; Chen, W.S.; Yang, F.Z.; Li, J.; Zhu, Q. Global adaptive neural control for strict-feedback time-delay systems with predefined output accuracy. Inf. Sci. 2015, 301, 27–43. [Google Scholar] [CrossRef]
- Niu, B.; Li, L. Adaptive neural network tracking control for a class of switched strict-feedback nonlinear systems with input delay. Neurocomputing 2016, 173, 2121–2128. [Google Scholar] [CrossRef]
- Choi, Y.H.; Yoo, S.J. Neural-networks-based adaptive quantized feedback tracking of uncertain nonlinear strict-feedback systems with unknown time delays. J. Frankl. Inst. 2020, 357, 10691–10715. [Google Scholar] [CrossRef]
- Chehardoli, H.; Eghtesad, M. Robust adaptive control of switched nonlinear systems in strict feedback form with unknown time delay. IMA J. Math. Control Inf. 2015, 32, 761–779. [Google Scholar]
- Shi, X.C.; Xu, S.Y.; Li, Y.M.; Chen, W.M.; Chu, Y.M. Robust adaptive control of strict-feedback nonlinear systems with unmodelled dynamics and time-varying delays. Int. Control 2017, 90, 334–347. [Google Scholar] [CrossRef]
- Wu, H.S. Simple adaptive robust control schemes of uncertain strict-feedback nonlinear time-delay systems. IET Control Theory Appl. 2017, 11, 2222–2231. [Google Scholar] [CrossRef]
- Elmi, M.; Talebi, H.A.; Menhaj, M.B. Robust adaptive dynamic surface control of nonlinear time-varying systems in strict-feedback form. Int. J. Control Autom. Syst. 2019, 17, 1432–1444. [Google Scholar] [CrossRef]
- Oucheriah, S. Exponential stabilization of a class of uncertain time-delay systems with bounded controllers. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2000, 47, 606–609. [Google Scholar] [CrossRef]
- Hua, C.C.; Wang, Q.G.; Guan, X.P. Exponential stabilization controller design for interconnected time delay systems. Automatica 2008, 44, 2600–2606. [Google Scholar] [CrossRef]
- Dong, Y.L.; Wang, X.L.; Mei, S.W.; Li, W.X. Exponential stabilization of nonlinear uncertain systems with time-varying delay. J. Eng. Math. 2012, 77, 225–237. [Google Scholar] [CrossRef]
- Wu, A.L.; Zeng, Z.G. Exponential stabilization of memristive neural networks with time delays. IEEE Trans. Neural Networks Learn. 2012, 23, 1919–1929. [Google Scholar]
- Benabdallah, A.; Echi, N. Global exponential stabilization of a class of nonlinear time-delay systems. Int. J. Syst. Sci. 2016, 47, 3857–3863. [Google Scholar] [CrossRef]
- Li, Y.N.; Sun, Y.G.; Meng, F.W.; Tian, Y.Z. Exponential stabilization of switched time-varying systems with delays and disturbances. Appl. Math. Comput. 2018, 324, 131–140. [Google Scholar] [CrossRef]
- Li, X.F.; Fang, J.A.; Li, H.Y.; Duan, W.Y. Exponential stabilization of time-varying delayed complex-valued memristor-based neural networks via impulsive control. Asian J. Control 2018, 20, 2290–2301. [Google Scholar] [CrossRef]
- Sheng, Y.; Lewis, F.L.; Zeng, Z.G. Exponential stabilization of fuzzy memristive neural networks with hybrid unbounded time-varying delays. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 739–750. [Google Scholar] [CrossRef]
- Sheng, Y.; Huang, T.W.; Zeng, Z.G.; Li, P. Exponential stabilization of inertial memristive neural networks with multiple time delays. IEEE Trans. Cybern. 2021, 51, 579–588. [Google Scholar] [CrossRef]
- Sheng, Y.; Huang, T.W.; Zeng, Z.G. Exponential stabilization of fuzzy memristive neural networks with multiple time delays via intermittent control. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 3092–3101. [Google Scholar] [CrossRef]
- Khalil, H.K. Nonlinear Systems; Prentice Hall: Hoboken, NJ, USA, 2002. [Google Scholar]
- Nguang, S.K. Robust stabilization of a class of time-delay nonlinear systems. IEEE Trans. Autom. Control 2000, 45, 756–762. [Google Scholar] [CrossRef]
- Liu, L.; Yin, S.; Zhang, L.X.; Yin, X.Y.; Yan, H.C. Improved results on asymptotic stabilization for stochastic nonlinear time-delay systems with application to a chemical reactor system. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 195–204. [Google Scholar] [CrossRef]
- Cui, R.H.; Xie, X.J. Finite-time stabilization of stochastic low-order nonlinear systemswith time-varying orders and FT-SISS inverse dynamics. Automatica 2021, 125, 109418. [Google Scholar] [CrossRef]
- Cui, R.H.; Xie, X.J. Finite-time stabilization of output-constrained stochastic high-order nonlinear systems with high-order and low-order nonlinearities. Automatica 2022, 136, 110085. [Google Scholar] [CrossRef]
- Zhang, T.L.; Deng, F.Q.; Sun, Y.; Shi, P. Fault estimation and fault-tolerant control for linear discrete time-varying stochastic systems. Sci. China Inf. Sci. 2021, 64, 200201. [Google Scholar] [CrossRef]
- Jiang, X.S.; Zhao, D.Y. Event-triggered fault detection for nonlinear discrete-time switched stochastic systems: A convex function method. Sci. China Inf. Sci. 2021, 64, 200204. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kong, M.; Liu, L. Exponential Stabilization for a Class of Strict-Feedback Nonlinear Time Delay Systems via State Feedback Control Scheme. Processes 2022, 10, 1259. https://doi.org/10.3390/pr10071259
Kong M, Liu L. Exponential Stabilization for a Class of Strict-Feedback Nonlinear Time Delay Systems via State Feedback Control Scheme. Processes. 2022; 10(7):1259. https://doi.org/10.3390/pr10071259
Chicago/Turabian StyleKong, Mengru, and Liang Liu. 2022. "Exponential Stabilization for a Class of Strict-Feedback Nonlinear Time Delay Systems via State Feedback Control Scheme" Processes 10, no. 7: 1259. https://doi.org/10.3390/pr10071259
APA StyleKong, M., & Liu, L. (2022). Exponential Stabilization for a Class of Strict-Feedback Nonlinear Time Delay Systems via State Feedback Control Scheme. Processes, 10(7), 1259. https://doi.org/10.3390/pr10071259





