A Review of Lithium-Ion Battery Thermal Runaway Modeling and Diagnosis Approaches
Abstract
:1. Introduction
2. Basic Background on Thermal Runaway Mechanism
3. Lithium-Ion Battery Thermal Runaway Modeling
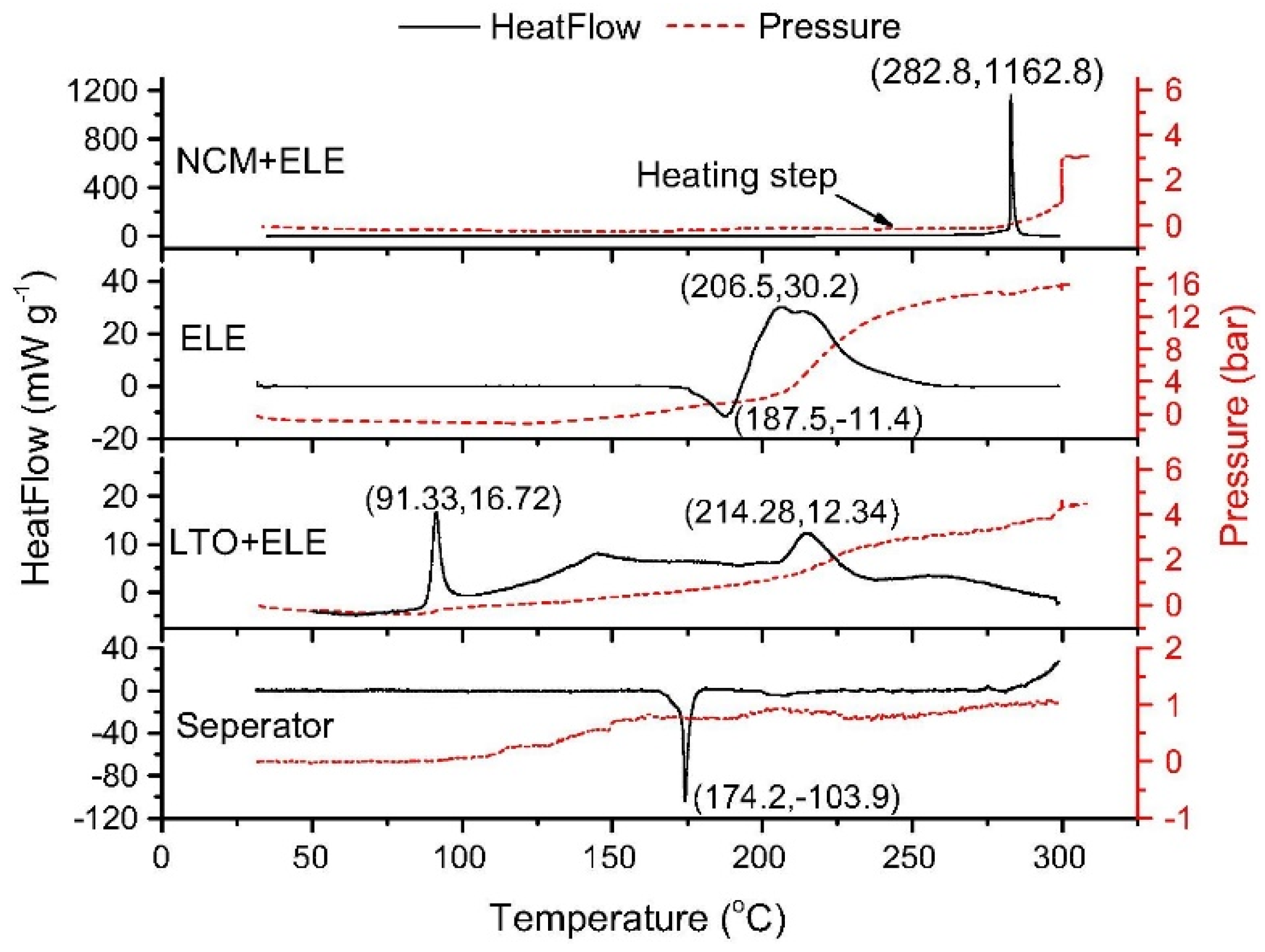
3.1. Review of Thermal Runaway Mechanisms and Modeling
3.2. Other Recent Notable Studies in Thermal Runaway Modeling
4. Lithium-Ion Battery Thermal Runaway Prognosis and Diagnosis
4.1. Lithium-Ion Battery Thermal Runaway Prediction
4.2. Lithium-Ion Battery Internal Short-Circuit Diagnosis
4.3. Lithium-Ion Battery Thermal Runaway Detection
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Tran, M.-K.; Sherman, S.; Samadani, E.; Vrolyk, R.; Wong, D.; Lowery, M.; Fowler, M. Environmental and Economic Benefits of a Battery Electric Vehicle Powertrain with a Zinc–Air Range Extender in the Transition to Electric Vehicles. Vehicles 2020, 2, 398–412. [Google Scholar] [CrossRef]
- Tran, M.-K.; DaCosta, A.; Mevawalla, A.; Panchal, S.; Fowler, M. Comparative Study of Equivalent Circuit Models Performance in Four Common Lithium-Ion Batteries: LFP, NMC, LMO, NCA. Batteries 2021, 7, 51. [Google Scholar] [CrossRef]
- Tran, M.-K.; Akinsanya, M.; Panchal, S.; Fraser, R.; Fowler, M. Design of a Hybrid Electric Vehicle Powertrain for Performance Optimization Considering Various Powertrain Components and Configurations. Vehicles 2021, 3, 20–32. [Google Scholar] [CrossRef]
- Tran, M.-K.; Cunanan, C.; Panchal, S.; Fraser, R.; Fowler, M. Investigation of Individual Cells Replacement Concept in Lithium-Ion Battery Packs with Analysis on Economic Feasibility and Pack Design Requirements. Processes 2021, 9, 2263. [Google Scholar] [CrossRef]
- Jiang, Z.Y.; Qu, Z.G.; Zhang, J.F.; Rao, Z.H. Rapid Prediction Method for Thermal Runaway Propagation in Battery Pack Based on Lumped Thermal Resistance Network and Electric Circuit Analogy. Appl. Energy 2020, 268, 115007. [Google Scholar] [CrossRef]
- Tran, M.-K.; Mathew, M.; Janhunen, S.; Panchal, S.; Raahemifar, K.; Fraser, R.; Fowler, M. A comprehensive equivalent circuit model for lithium-ion batteries, incorporating the effects of state of health, state of charge, and temperature on model parameters. J. Energy Storage 2021, 43, 103252. [Google Scholar] [CrossRef]
- IEA. Global EV Outlook. 2021. Available online: https://www.iea.org/reports/global-ev-outlook-2021 (accessed on 8 February 2022).
- Tran, M.-K.; Fowler, M. A Review of Lithium-Ion Battery Fault Diagnostic Algorithms: Current Progress and Future Challenges. Algorithms 2020, 13, 62. [Google Scholar] [CrossRef] [Green Version]
- Tran, M.-K.; Panchal, S.; Khang, T.D.; Panchal, K.; Fraser, R.; Fowler, M. Concept Review of a Cloud-Based Smart Battery Management System for Lithium-Ion Batteries: Feasibility, Logistics, and Functionality. Batteries 2022, 8, 19. [Google Scholar] [CrossRef]
- Tran, M.-K.; Fowler, M. Sensor Fault Detection and Isolation for Degrading Lithium-Ion Batteries in Electric Vehicles Using Parameter Estimation with Recursive Least Squares. Batteries 2020, 6, 1. [Google Scholar] [CrossRef] [Green Version]
- Xie, Y.; Li, H.; Li, W.; Zhang, Y.; Fowler, M.; Tran, M.-K.; Zhang, X.; Chen, B.; Deng, S. Improving thermal performance of battery at high current rate by using embedded heat pipe system. J. Energy Storage 2022, 46, 103809. [Google Scholar] [CrossRef]
- Feng, X.; Ouyang, M.; Liu, X.; Lu, L.; Xia, Y.; He, X. Thermal Runaway Mechanism of Lithium Ion Battery for Electric Vehicles: A Review. Energy Storage Mater. 2018, 10, 246–267. [Google Scholar] [CrossRef]
- Tran, M.-K.; Panchal, S.; Chauhan, V.; Brahmbhatt, N.; Mevawalla, A.; Fraser, R.; Fowler, M. Python-based scikit-learn machine learning models for thermal and electrical performance prediction of high-capacity lithium-ion battery. Int. J. Energy Res. 2021, 12, 2825. [Google Scholar] [CrossRef]
- Xiong, R.; Ma, S.; Li, H.; Sun, F.; Li, J. Toward a Safer Battery Management System: A Critical Review on Diagnosis and Prognosis of Battery Short Circuit. iScience 2020, 23, 101010. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; Wei, X.; Tang, X.; Zhu, J.; Chen, S.; Dai, H. Internal Short Circuit Mechanisms, Experimental Approaches and Detection Methods of Lithium-Ion Batteries for Electric Vehicles: A Review. Renew. Sustain. Energy Rev. 2021, 141, 110790. [Google Scholar] [CrossRef]
- Huang, L.; Liu, L.; Lu, L.; Feng, X.; Han, X.; Li, W.; Zhang, M.; Li, D.; Liu, X.; Sauer, D.U.; et al. A Review of the Internal Short Circuit Mechanism in Lithium-Ion Batteries: Inducement, Detection and Prevention. Int. J. Energy Res. 2021, 45, 15797–15831. [Google Scholar] [CrossRef]
- Liao, Z.; Zhang, S.; Li, K.; Zhang, G.; Habetler, T.G. A Survey of Methods for Monitoring and Detecting Thermal Runaway of Lithium-Ion Batteries. J. Power Sources 2019, 2019, 436. [Google Scholar] [CrossRef]
- Feng, X.; Zheng, S.; Ren, D.; He, X.; Wang, L.; Liu, X.; Li, M.; Ouyang, M. Key Characteristics for Thermal Runaway of Li-Ion Batteries. Energy Procedia 2019, 158, 4684–4689. [Google Scholar] [CrossRef]
- Yuan, C.; Wang, Q.; Wang, Y.; Zhao, Y. Inhibition Effect of Different Interstitial Materials on Thermal Runaway Propagation in the Cylindrical Lithium-Ion Battery Module. Appl. Therm. Eng. 2019, 153, 39–50. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q.; Jiang, B.; Li, B.; Yan, Y. A Critical Review of Thermal Management Models and Solutions of Lithium-Ion Batteries for the Development of Pure Electric Vehicles. Renew. Sustain. Energy Rev. 2016, 64, 106–128. [Google Scholar] [CrossRef]
- Bandhauer, T.M.; Garimella, S.; Fuller, T.F. A Critical Review of Thermal Issues in Lithium-Ion Batteries. J. Electrochem. Soc. 2011, 158, R1. [Google Scholar] [CrossRef]
- Ma, S.; Jiang, M.; Tao, P.; Song, C.; Wu, J.; Wang, J.; Deng, T.; Shang, W. Temperature Effect and Thermal Impact in Lithium-Ion Batteries: A Review. Prog. Nat. Sci. Mater. Int. 2018, 28, 653–666. [Google Scholar] [CrossRef]
- Huang, P.; Ping, P.; Li, K.; Chen, H.; Wang, Q.; Wen, J.; Sun, J. Experimental and Modeling Analysis of Thermal Runaway Propagation over the Large Format Energy Storage Battery Module with Li4Ti5O12 Anode. Appl. Energy 2016, 183, 659–673. [Google Scholar] [CrossRef]
- Liu, X.; Stoliarov, S.I.; Denlinger, M.; Masias, A.; Snyder, K. Comprehensive Calorimetry of the Thermally-Induced Failure of a Lithium Ion Battery. J. Power Sources 2015, 280, 516–525. [Google Scholar] [CrossRef]
- Feng, X.; Sun, J.; Ouyang, M.; He, X.; Lu, L.; Han, X.; Fang, M.; Peng, H. Characterization of Large Format Lithium Ion Battery Exposed to Extremely High Temperature. J. Power Sources 2014, 272, 457–467. [Google Scholar] [CrossRef]
- Li, H.; Duan, Q.; Zhao, C.; Huang, Z.; Wang, Q. Experimental Investigation on the Thermal Runaway and Its Propagation in the Large Format Battery Module with Li(Ni1/3Co1/3Mn1/3)O2 as Cathode. J. Hazard. Mater. 2019, 375, 241–254. [Google Scholar] [CrossRef] [PubMed]
- Coman, P.T.; Darcy, E.C.; Veje, C.T.; White, R.E. Numerical Analysis of Heat Propagation in a Battery Pack Using a Novel Technology for Triggering Thermal Runaway. Appl. Energy 2017, 203, 189–200. [Google Scholar] [CrossRef]
- Gachot, G.; Grugeon, S.; Armand, M.; Pilard, S.; Guenot, P.; Tarascon, J.M.; Laruelle, S. Deciphering the Multi-Step Degradation Mechanisms of Carbonate-Based Electrolyte in Li Batteries. J. Power Sources 2008, 178, 409–421. [Google Scholar] [CrossRef]
- Chen, H.; Buston, J.E.H.; Gill, J.; Howard, D.; Williams, R.C.E.; Read, E.; Abaza, A.; Cooper, B.; Wen, J.X. A Simplified Mathematical Model for Heating-Induced Thermal Runaway of Lithium-Ion Batteries. J. Electrochem. Soc. 2021, 168, 010502. [Google Scholar] [CrossRef]
- Esho, I.; Shah, K.; Jain, A. Measurements and Modeling to Determine the Critical Temperature for Preventing Thermal Runaway in Li-Ion Cells. Appl. Therm. Eng. 2018, 145, 287–294. [Google Scholar] [CrossRef]
- Feng, X.; He, X.; Ouyang, M.; Wang, L.; Lu, L.; Ren, D.; Santhanagopalan, S. A Coupled Electrochemical-Thermal Failure Model for Predicting the Thermal Runaway Behavior of Lithium-Ion Batteries. J. Electrochem. Soc. 2018, 165, A3748–A3765. [Google Scholar] [CrossRef]
- Ostanek, J.K.; Li, W.; Mukherjee, P.P.; Crompton, K.R.; Hacker, C. Simulating Onset and Evolution of Thermal Runaway in Li-Ion Cells Using a Coupled Thermal and Venting Model. Appl. Energy 2020, 268, 114972. [Google Scholar] [CrossRef]
- Ren, D.; Feng, X.; Lu, L.; Ouyang, M.; Zheng, S.; Li, J.; He, X. An Electrochemical-Thermal Coupled Overcharge-to-Thermal-Runaway Model for Lithium Ion Battery. J. Power Sources 2017, 364, 328–340. [Google Scholar] [CrossRef]
- Qi, C.; Zhu, Y.; Gao, F.; Yang, K.; Jiao, Q. Mathematical Model for Thermal Behavior of Lithium Ion Battery Pack under Overcharge. Int. J. Heat Mass Transf. 2018, 124, 552–563. [Google Scholar] [CrossRef]
- An, Z.; Shah, K.; Jia, L.; Ma, Y. Modeling and Analysis of Thermal Runaway in Li-Ion Cell. Appl. Therm. Eng. 2019, 160, 113960. [Google Scholar] [CrossRef]
- Drake, S.J.; Martin, M.; Wetz, D.A.; Ostanek, J.K.; Miller, S.P.; Heinzel, J.M.; Jain, A. Heat Generation Rate Measurement in a Li-Ion Cell at Large C-Rates through Temperature and Heat Flux Measurements. J. Power Sources 2015, 285, 266–273. [Google Scholar] [CrossRef]
- Hatchard, T.D.; MacNeil, D.D.; Basu, A.; Dahn, J.R. Thermal Model of Cylindrical and Prismatic Lithium-Ion Cells. J. Electrochem. Soc. 2001, 148, A755–A761. [Google Scholar] [CrossRef]
- Peng, P.; Jiang, F. Thermal Safety of Lithium-Ion Batteries with Various Cathode Materials: A Numerical Study. Int. J. Heat Mass Transf. 2016, 103, 1008–1016. [Google Scholar] [CrossRef]
- Chombo, P.V.; Laoonual, Y. Prediction of the Onset of Thermal Runaway and Its Thermal Hazards in 18650 Lithium-Ion Battery Abused by External Heating. Fire Saf. J. 2022, 129, 103560. [Google Scholar] [CrossRef]
- Ren, D.; Liu, X.; Feng, X.; Lu, L.; Ouyang, M.; Li, J.; He, X. Model-Based Thermal Runaway Prediction of Lithium-Ion Batteries from Kinetics Analysis of Cell Components. Appl. Energy 2018, 228, 633–644. [Google Scholar] [CrossRef]
- Coman, P.T.; Darcy, E.C.; Veje, C.T.; White, R.E. Modelling Li-Ion Cell Thermal Runaway Triggered by an Internal Short Circuit Device Using an Efficiency Factor and Arrhenius Formulations. J. Electrochem. Soc. 2017, 164, A587–A593. [Google Scholar] [CrossRef] [Green Version]
- Cai, T.; Stefanopoulou, A.G.; Siegel, J.B. Modeling Li-Ion Battery Thermal Runaway Using a Three Section Thermal Model. In Proceedings of the ASME 2018 Dynamic Systems and Control Conference, DSCC 2018, Atlanta, GA, USA, 30 September–3 October 2018; Volume 2. [Google Scholar]
- Hong, J.; Wang, Z.; Qu, C.; Ma, F.; Xu, X.; Yang, J.; Zhang, J.; Zhou, Y.; Shan, T.; Hou, Y. Fault Prognosis and Isolation of Lithium-Ion Batteries in Electric Vehicles Considering Real-Scenario Thermal Runaway Risks. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 1. [Google Scholar] [CrossRef]
- Hong, J.; Wang, Z.; Ma, F.; Yang, J.; Xu, X.; Qu, C.; Zhang, J.; Shan, T.; Hou, Y.; Zhou, Y. Thermal Runaway Prognosis of Battery Systems Using the Modified Multiscale Entropy in Real-World Electric Vehicles. IEEE Trans. Transp. Electrif. 2021, 7, 2269–2278. [Google Scholar] [CrossRef]
- Hong, J.; Wang, Z.; Yao, Y. Fault Prognosis of Battery System Based on Accurate Voltage Abnormity Prognosis Using Long Short-Term Memory Neural Networks. Appl. Energy 2019, 251, 113381. [Google Scholar] [CrossRef]
- Li, D.; Zhang, Z.; Liu, P.; Wang, Z.; Zhang, L. Battery Fault Diagnosis for Electric Vehicles Based on Voltage Abnormality by Combining the Long Short-Term Memory Neural Network and the Equivalent Circuit Model. IEEE Trans. Power Electron. 2021, 36, 1303–1315. [Google Scholar] [CrossRef]
- Li, D.; Zhang, Z.; Wang, Z.; Liu, P.; Liu, Z.; Lin, N. Timely Thermal Runaway Prognosis for Battery Systems in Real-World Electric Vehicles Based on Temperature Abnormality. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 1. [Google Scholar] [CrossRef]
- Li, D.; Liu, P.; Zhang, Z.; Zhang, L.; Deng, J.; Wang, Z.; Dorrell, D.G.; Li, W.; Sauer, D.U. Battery Thermal Runaway Fault Prognosis in Electric Vehicles Based on Abnormal Heat Generation and Deep Learning Algorithms. IEEE Trans. Power Electron. 2022, 37, 8513–8525. [Google Scholar] [CrossRef]
- Li, D.; Zhang, Z.; Liu, P.; Wang, Z. DBSCAN-Based Thermal Runaway Diagnosis of Battery Systems for Electric Vehicles. Energies 2019, 12, 2977. [Google Scholar] [CrossRef] [Green Version]
- Klink, J.; Hebenbrock, A.; Grabow, J.; Orazov, N.; Nylén, U.; Benger, R.; Beck, H.-P. Comparison of Model-Based and Sensor-Based Detection of Thermal Runaway in Li-Ion Battery Modules for Automotive Application. Batteries 2022, 8, 34. [Google Scholar] [CrossRef]
- Klink, J.; Grabow, J.; Orazov, N.; Benger, R.; Börger, A.; Ahlberg Tidblad, A.; Wenzl, H.; Beck, H.P. Thermal Fault Detection by Changes in Electrical Behaviour in Lithium-Ion Cells. J. Power Sources 2021, 490, 229572. [Google Scholar] [CrossRef]
- Dong, P.; Liu, Z.; Wu, P.; Li, Z.; Wang, Z.; Zhang, J. Reliable and Early Warning of Lithium-Ion Battery Thermal Runaway Based on Electrochemical Impedance Spectrum. J. Electrochem. Soc. 2021, 168, 090529. [Google Scholar] [CrossRef]
- Shah, K.; Jain, A. Prediction of Thermal Runaway and Thermal Management Requirements in Cylindrical Li-Ion Cells in Realistic Scenarios. Int. J. Energy Res. 2019, 43, 1827–1838. [Google Scholar] [CrossRef]
- Shah, K.; Chalise, D.; Jain, A. Experimental and Theoretical Analysis of a Method to Predict Thermal Runaway in Li-Ion Cells. J. Power Sources 2016, 330, 167–174. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Li, J.; Abdollahi, A.; Jones, T. Data-Driven Thermal Anomaly Detection for Batteries Using Unsupervised Shape Clustering. In Proceedings of the IEEE International Symposium on Industrial Electronics, Kyoto, Japan, 20–23 June 2021. [Google Scholar]
- Jiang, J.; Cong, X.; Li, S.; Zhang, C.; Zhang, W.; Jiang, Y. A Hybrid Signal-Based Fault Diagnosis Method for Lithium-Ion Batteries in Electric Vehicles. IEEE Access 2021, 9, 19175–19186. [Google Scholar] [CrossRef]
- Jiang, L.; Deng, Z.; Tang, X.; Hu, L.; Lin, X.; Hu, X. Data-Driven Fault Diagnosis and Thermal Runaway Warning for Battery Packs Using Real-World Vehicle Data. Energy 2021, 234, 121266. [Google Scholar] [CrossRef]
- Ren, D.; Feng, X.; Liu, L.; Hsu, H.; Lu, L.; Wang, L.; He, X.; Ouyang, M. Investigating the Relationship between Internal Short Circuit and Thermal Runaway of Lithium-Ion Batteries under Thermal Abuse Condition. Energy Storage Mater. 2021, 34, 563–573. [Google Scholar] [CrossRef]
- Kong, X.; Plett, G.L.; Scott Trimboli, M.; Zhang, Z.; Qiao, D.; Zhao, T.; Zheng, Y. Pseudo-Two-Dimensional Model and Impedance Diagnosis of Micro Internal Short Circuit in Lithium-Ion Cells. J. Energy Storage 2020, 27, 101085. [Google Scholar] [CrossRef]
- Gao, W.; Zheng, Y.; Ouyang, M.; Li, J.; Lai, X.; Hu, X. Micro-Short-Circuit Diagnosis for Series-Connected Lithium-Ion Battery Packs Using Mean-Difference Model. IEEE Trans. Ind. Electron. 2019, 66, 2132–2214. [Google Scholar] [CrossRef]
- Zheng, Y.; Luo, Q.; Cui, Y.; Dai, H.; Han, X.; Feng, X. Fault Identification and Quantitative Diagnosis Method for Series-Connected Lithium-Ion Battery Packs Based on Capacity Estimation. IEEE Trans. Ind. Electron. 2022, 69, 3059–3067. [Google Scholar] [CrossRef]
- Feng, X.; Pan, Y.; He, X.; Wang, L.; Ouyang, M. Detecting the Internal Short Circuit in Large-Format Lithium-Ion Battery Using Model-Based Fault-Diagnosis Algorithm. J. Energy Storage 2018, 18, 26–39. [Google Scholar] [CrossRef]
- Lai, X.; Yi, W.; Kong, X.; Han, X.; Zhou, L.; Sun, T.; Zheng, Y. Online Detection of Early Stage Internal Short Circuits in Series-Connected Lithium-Ion Battery Packs Based on State-of-Charge Correlation. J. Energy Storage 2020, 30, 101514. [Google Scholar] [CrossRef]
- Lai, X.; Yi, W.; Li, H.; Han, X.; Feng, X.; Li, S.; Zhou, L.; Zheng, Y. Online Internal Short Circuit Detection Method Considering Equalization Electric Quantity for Lithium-Ion Battery Pack in Electric Vehicles. Int. J. Energy Res. 2021, 45, 7326–7340. [Google Scholar] [CrossRef]
- Qiao, D.; Wang, X.; Lai, X.; Zheng, Y.; Wei, X.; Dai, H. Online Quantitative Diagnosis of Internal Short Circuit for Lithium-Ion Batteries Using Incremental Capacity Method. Energy 2022, 243, 123082. [Google Scholar] [CrossRef]
- Qiao, D.; Wei, X.; Fan, W.; Jiang, B.; Lai, X.; Zheng, Y.; Tang, X.; Dai, H. Toward Safe Carbon–Neutral Transportation: Battery Internal Short Circuit Diagnosis Based on Cloud Data for Electric Vehicles. Appl. Energy 2022, 317, 119168. [Google Scholar] [CrossRef]
- Schmid, M.; Kleiner, J.; Endisch, C. Early Detection of Internal Short Circuits in Series-Connected Battery Packs Based on Nonlinear Process Monitoring. J. Energy Storage 2022, 48, 103732. [Google Scholar] [CrossRef]
- Cai, T.; Pannala, S.; Stefanopoulou, A.G.; Siegel, J.B. Battery Internal Short Detection Methodology Using Cell Swelling Measurements. In Proceedings of the American Control Conference, Denver, CO, USA, 1–3 July 2020. [Google Scholar]
- Sun, Z.; Wang, Z.; Chen, Y.; Liu, P.; Wang, S.; Zhang, Z.; Dorrell, D.G. Modified Relative Entropy Based Lithium-Ion Battery Pack Online Short Circuit Detection for Electric Vehicle. IEEE Trans. Transp. Electrif. 2021, 8, 1710–1723. [Google Scholar] [CrossRef]
- Su, T.; Lyu, N.; Zhao, Z.; Wang, H.; Jin, Y. Safety Warning of Lithium-Ion Battery Energy Storage Station via Venting Acoustic Signal Detection for Grid Application. J. Energy Storage 2021, 38, 102498. [Google Scholar] [CrossRef]
- Li, B.; Parekh, M.H.; Pol, V.G.; Adams, T.E.; Fleetwood, J.; Jones, C.M.; Tomar, V. Operando Monitoring of Electrode Temperatures During Overcharge-Caused Thermal Runaway. Energy Technol. 2021, 9, 2100497. [Google Scholar] [CrossRef]
- Sheikh, M.; Elmarakbi, A.; Elkady, M. Thermal Runaway Detection of Cylindrical 18650 Lithium-Ion Battery under Quasi-Static Loading Conditions. J. Power Sources 2017, 370, 61–70. [Google Scholar] [CrossRef] [Green Version]
- Koch, S.; Birke, K.P.; Kuhn, R. Fast Thermal Runaway Detection for Lithium-Ion Cells in Large Scale Traction Batteries. Batteries 2018, 4, 16. [Google Scholar] [CrossRef] [Green Version]
- Cai, T.; Stefanopoulou, A.G.; Siegel, J.B. Early Detection for Li-Ion Batteries Thermal Runaway Based on Gas Sensing. ECS Trans. 2019, 89, 85–97. [Google Scholar] [CrossRef]
- He, D.; Sun, J.; Li, Y.; Tian, F.; Chen, Y.; Tong, G.; Chen, X.; Shen, Q.; Lian, Z. Thermal Runaway Warning Based on Safety Management System of Lithium Iron Phosphate Battery for Energy Storage. In Proceedings of the 2020 IEEE International Conference on Artificial Intelligence and Information Systems, ICAIIS 2020, Dalian, China, 20–22 March 2020. [Google Scholar]
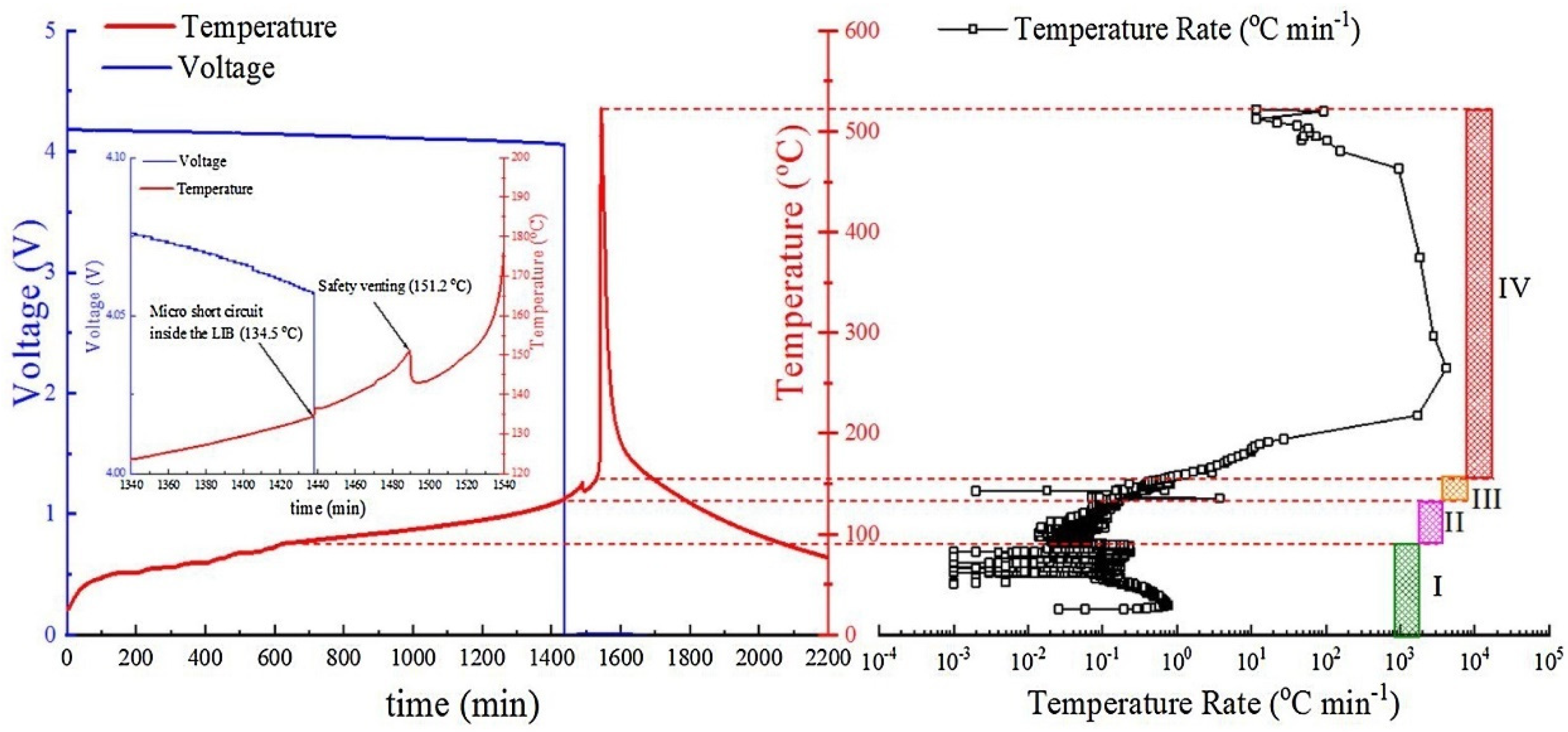
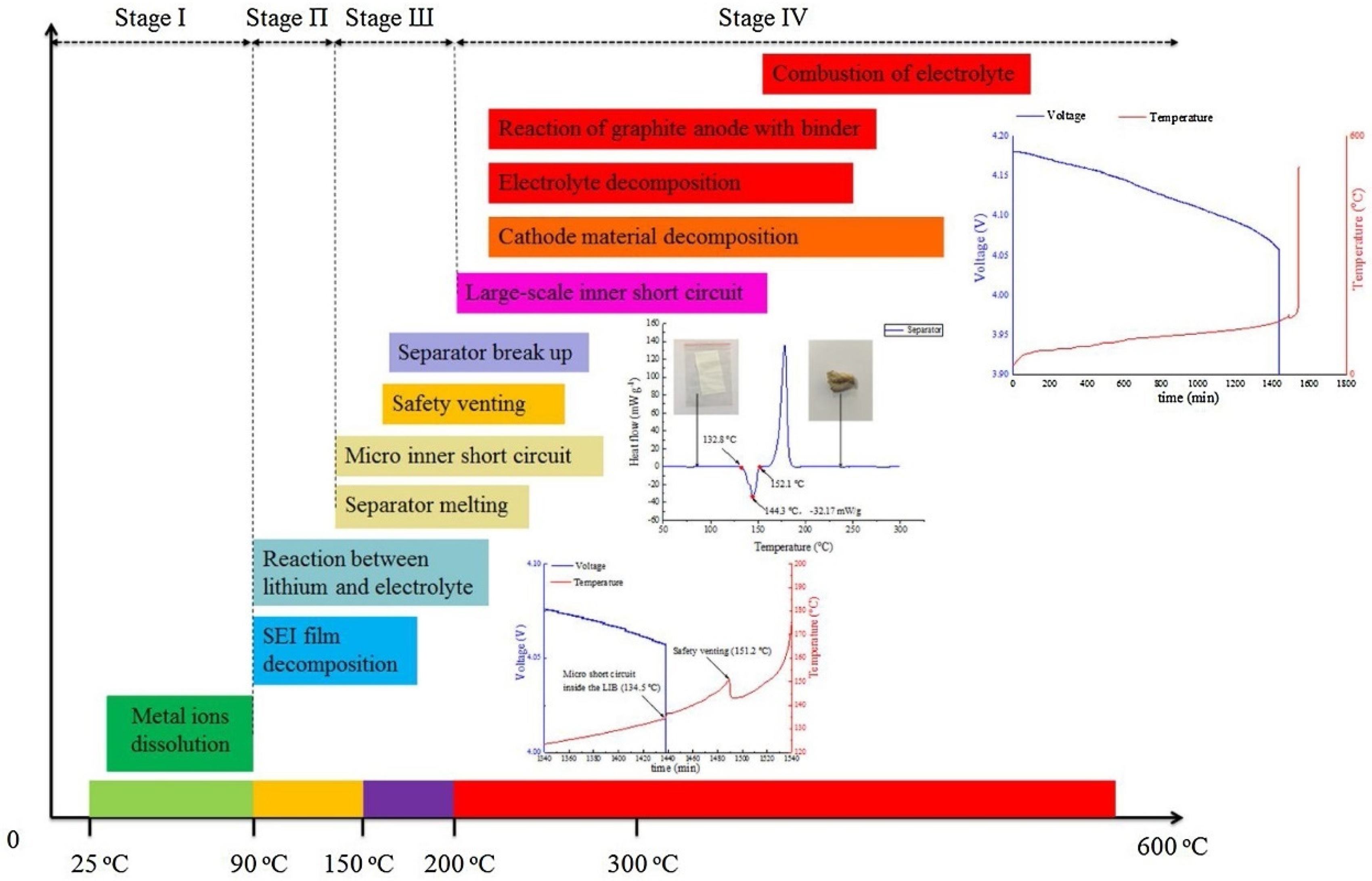
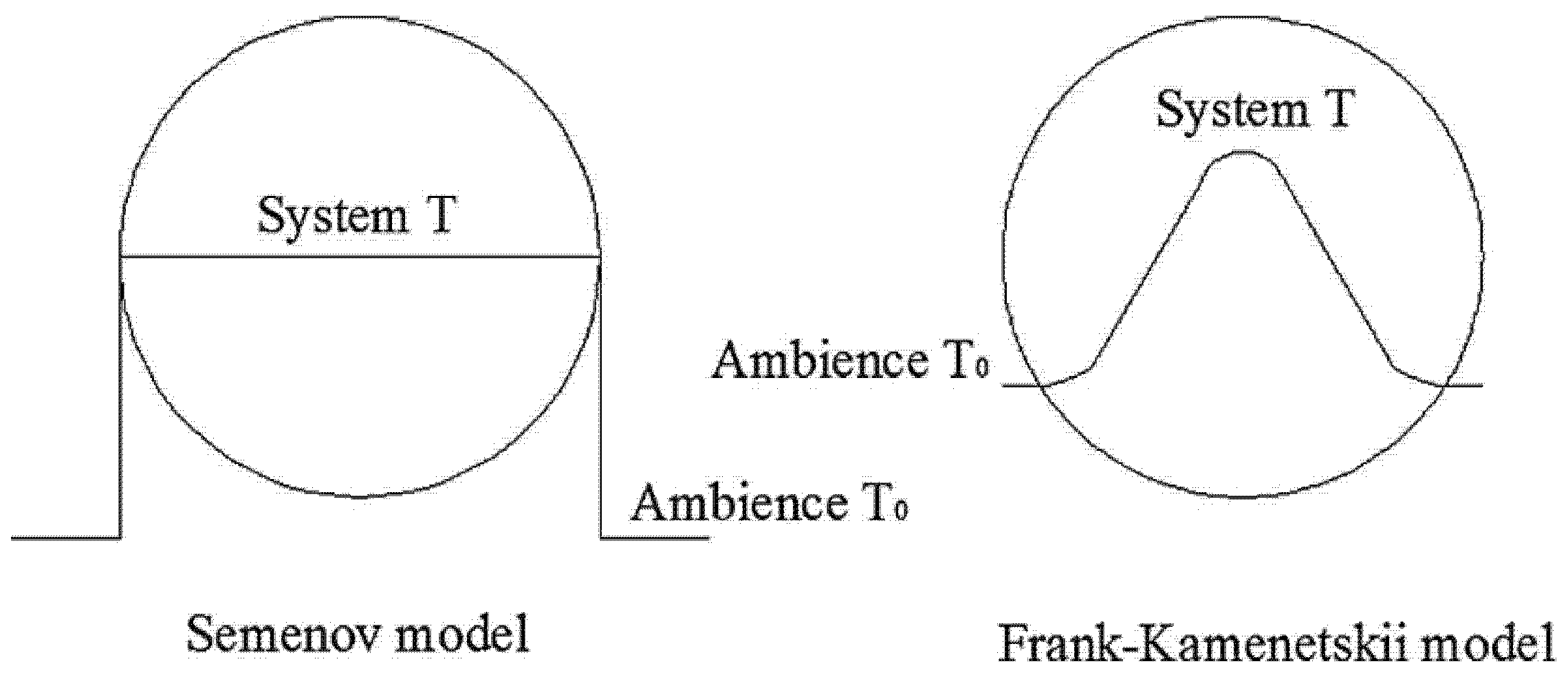
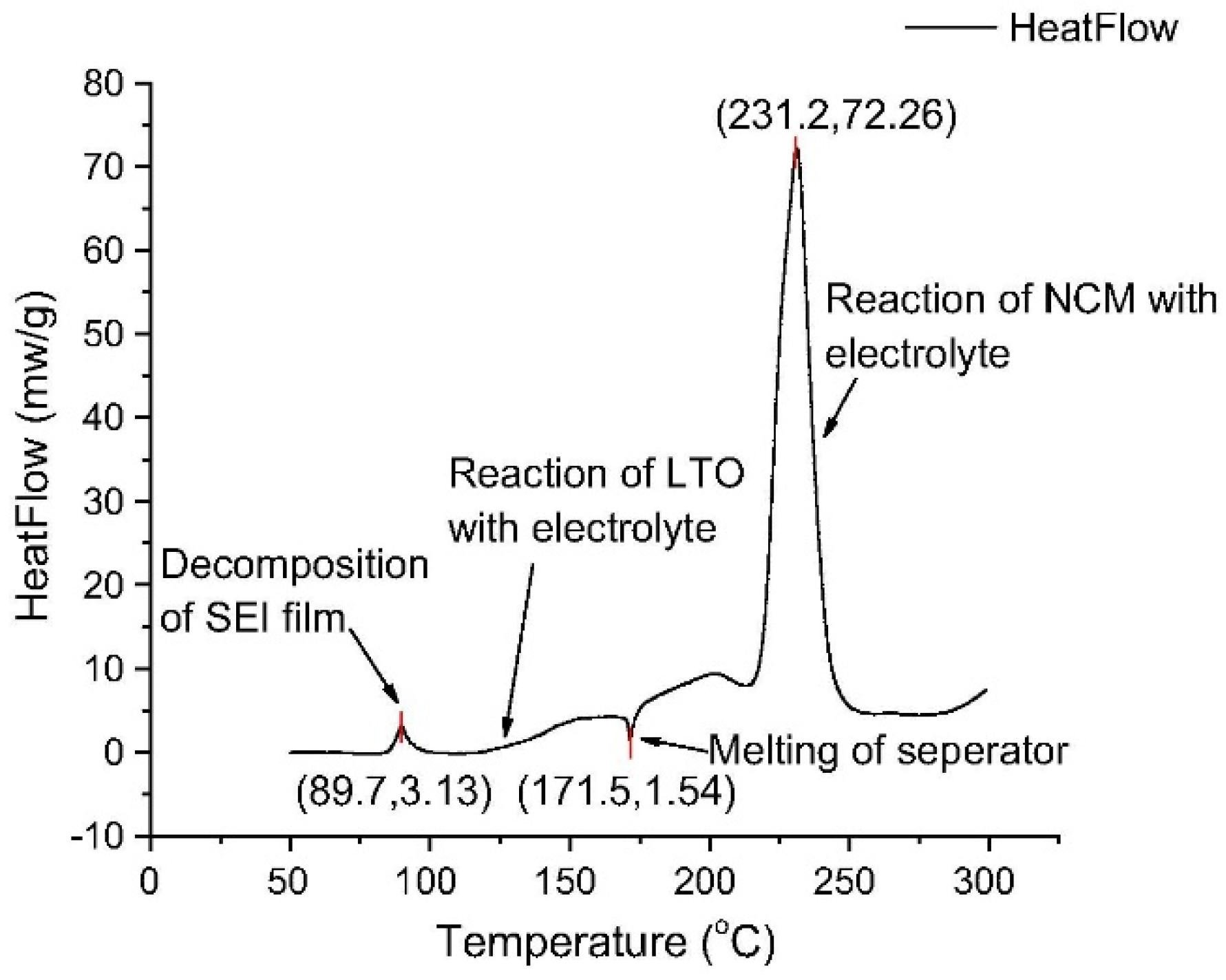
| SOC | T Onset (°C) | Propagation Time inside a Single Cell (s) | Propagation Time between Cells (s) |
|---|---|---|---|
| 100% | 154.1 | 10 | 87 |
| 50% | 96.3 | 39 | 307 |
| 0% | 90.6 | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tran, M.-K.; Mevawalla, A.; Aziz, A.; Panchal, S.; Xie, Y.; Fowler, M. A Review of Lithium-Ion Battery Thermal Runaway Modeling and Diagnosis Approaches. Processes 2022, 10, 1192. https://doi.org/10.3390/pr10061192
Tran M-K, Mevawalla A, Aziz A, Panchal S, Xie Y, Fowler M. A Review of Lithium-Ion Battery Thermal Runaway Modeling and Diagnosis Approaches. Processes. 2022; 10(6):1192. https://doi.org/10.3390/pr10061192
Chicago/Turabian StyleTran, Manh-Kien, Anosh Mevawalla, Attar Aziz, Satyam Panchal, Yi Xie, and Michael Fowler. 2022. "A Review of Lithium-Ion Battery Thermal Runaway Modeling and Diagnosis Approaches" Processes 10, no. 6: 1192. https://doi.org/10.3390/pr10061192
APA StyleTran, M.-K., Mevawalla, A., Aziz, A., Panchal, S., Xie, Y., & Fowler, M. (2022). A Review of Lithium-Ion Battery Thermal Runaway Modeling and Diagnosis Approaches. Processes, 10(6), 1192. https://doi.org/10.3390/pr10061192










