Abstract
The melting effect, a type of heat transferal process, is a fascinating mechanism of thermo-physics. It is related to phase change issues that occur in several industrial mechanisms. Glass treatment, polymer synthesis, and metal processing are among these. In view of this, the current investigation explicates the flow of a dusty nanofluid through a stretching cylinder in a porous medium by considering the effect of the melting heat transfer phenomenon. Using the required similarity transformations, the governing partial differential equations (PDEs) showing the energy transference and fluid motion in both the liquid and dust phases were translated into ordinary differential equations (ODEs). The numerical solutions for the acquired ODEs were developed using the Runge–Kutta–Fehlberg method of fourth–fifth order (RKF-45) and the shooting process. Graphical representations were used to interpret the effects of the governing parameters, including the porosity parameter, the Eckert number, and the stretching and melting parameters, on the respective velocity and temperature profiles for both the fluid and dust phases. The skin friction coefficient and the Nusselt number were also discussed and tabulated. The outcomes show that enhancing the porosity parameter will diminish the fluid- and dust-phase velocities. Fluid velocity, dust-phase velocity, and temperature improve with escalating values of the curvature parameter, whereas the melting effect reduces the thermal profiles of the fluid and dust phases. The surface drag force declines with an improvement in curvature and porosity constraints.
1. Introduction
Nanomaterials have undergone considerable developments in science and technology over the last few decades. These nanoscale-engineered materials are a significant part of nanotechnology, which has allowed for excellent efficiency enhancements to be achieved in several industry sectors. The base liquids, including air, oil, ethylene glycol, and water, have a lower heat-conductive efficiency than nanoliquids. The mixture of nano-sized particles and traditional liquids is referred to as a nanoliquid, and nanoparticles generally increase the thermal conduction efficacy of the base liquids. These liquids have had a great impact on the development of novel thermal transportation fluids, and fantastic efforts have been made in this area in recent years. Nanoliquids have a variety of applications in innovative nanotechnology and engineering disciplines, such as micro-manufacturing, nuclear reactor refrigerating, and many others. Moreover, modern technology has afforded new opportunities to improve heat transportation rates in a variety of industrial operations, such as pharmaceuticals, the petroleum and geothermal industries, and food industries. Because of their exceptional thermal transport abilities and promising applications in a wide range of fields, nanoliquids have stimulated the interest of many researchers [1,2,3,4,5]. On the other side, the scrutiny of bi-phase streams in which solid spherical particles are dispersed in a fluid is of importance for a variety of technological challenges, including blood rheology, the purification of crude oil, flow via packed beds, the pollution of the environment, powder technology, sedimentation, metal extrusion, particle centrifugal separation, and the drawing of copper wires. The steady flow of a two-phase dispersion past a diverse selection of geometries has been explored extensively in the literature. Recently, Hussain et al. [6] elucidated the characteristics of thermal radiation in a dusty nanoliquid past a porous stretchy surface. Rashed and Ahmed [7] examined the convective–radiative movement of a dusty nanoliquid inside a permeable enclosure. Ramzan et al. [8] investigated the bi-phase flow of a micropolar liquid containing dust particles across a stretchable surface. The features of dusty nanoliquid flow in magnetic and electrical fields were examined by Wahidunnisa et al. [9] with the consideration of the joule effect. Sowmya et al. [10] discussed the convective–radiative heat transference phenomenon of a liquid with dust particles using the Cattaneo–Christov heat flux model (CCHF).
Heat transference is one of the most prominent and widely discussed topics in scientific research, and its significance is magnified by the requirement for energy management and efficiency improvements. Developing effective solutions for reducing energy consumption and enhancing effectiveness is essential in this regard. Maximizing heat transmission facilities to advance thermal energy requires concentrating on apparatus miniaturization on the one hand, and intensifying the heat transmission per unit area on the other. Due to its structural system, a porous medium affords a massive heat transferal region in a specific volume. Porous media-manufactured strong thermal conductive components, such as metal foams, can also enhance heat transmission. The major reasons for the superior thermal effectiveness of porous media are increased fluid–solid interactions, caused by the irregular movement of fluid between the pore spaces of porous substances, and liquid mixing. In many engineering applications, such as electronic cooling, groundwater, drying processes, oil flow filtration, solar collectors, and all types of heat exchangers, such structures can be observed. They can also be found in geothermal engineering, combustion systems, porous bearings, cooling turbine blades, and thermal insulation where cooling or heating are required. As a result, investigators have paid special attention to the porous media approach. Wahid et al. [11] scrutinized the Marangoni movement of a hybrid nanoliquid through a disk in a porous medium. Furthermore, they performed a stability analysis and obtained dual solutions for the velocity and temperature equations. Khan and Alzahrani [12] inspected the radiative stream of a nanoliquid in a permeable medium with entropy optimization. Ramesh et al. [13] examined the aspect of mass and heat transference of a ternary nanoliquid flow in a permeable convergent–divergent channel, taking into account the heat source/sink. Ahmad et al. [14] considered the effect of a chemical reaction and discussed the dissipative stream of a hybrid nanoliquid past a permeable stretchy surface. The successive over-relaxation (SOR) methodology was used in their investigation to solve dimensionless ODEs numerically. Ali et al. [15] investigated the effect of a heat source on the flow of a hybrid nanoliquid via an extended surface in a permeable medium, where the set of ODEs was numerically solved using the SOR approach.
Melting heat transfer is a fascinating sub-discipline of thermo-physics. The melting phenomenon has a wide applicability, which includes energy recovery in geothermal stations, the silicon wafer process, heat engines, heat exchangers, thermocouples, permafrost melting, and hot extrusion. The melting heat transference problem is a poignant boundary problem in its most basic form, which necessitates the use of powerful computational methods to solve. However, another approach is to focus on the boundary-layer stream in melting phase-change problems, where the melting phenomenon may be represented as a boundary condition. Recently, Mabood et al. [16] explained the melting heat transmission and radiative flow of a hybrid nanofluid through a stretchable shape. Waqas et al. [17] expounded the production of entropy by the motion of a liquid containing more than one nanoparticle by considering the melting heat transfer phenomenon. Hayat et al. [18] researched the melting heat transfer properties of a hybrid nanoliquid using a cylindrical shape stretching at a uniform pace. Mallikarjuna et al. [19] explicated the aspects of melting heat transfer in a dusty nanoliquid past a permeable stretchy surface. Khan et al. [20] explored the melting impact and radiation heat modification on a nanoliquid stream past a Riga plate by considering the heat generation/sink.
The analysis of boundary layer flow and heat transmission through a stretchy surface has captivated the interest of many investigators due to its various engineering and industrial applications, especially in the production of paper and fiberglass, glass, polymers, rubber, and synthetic filaments, as well as the continuous stretching of plastic sheets, bar drawing, hot rolling, aerodynamic extrusion, and the condensation of liquid films. On the other hand, many manufacturing and physical processes have boundary surfaces that closely resemble a cylindrical configuration. The effects of heat transportation over cylindrically elongated surfaces are critical in such mechanisms, namely wire drawing, hot rolling, and fiber spinning. In view of this, numerous researchers have expounded the flow, heat, and mass transferences of various kinds of liquids through a stretching cylinder. Abbas et al. [21] investigated the flow behavior of a nanoliquid containing hybrid nanoparticles through a stretching cylinder with the impact of a magnetic field inclined at a specified angle. Waqas et al. [22] considered the use of the Cattaneo–Christov double-diffusion model for inspecting the bioconvective stream of a nanoliquid through an elongated cylinder. Kumar et al. [23] probed the two-phase stream of an incompressible liquid with dust particles past a cylindrical geometry stretching at a constant rate. Rashid et al. [24] described the heat transfer features of a hybrid nanoliquid and its flow over a stretchy cylinder. Madhukesh et al. [25] scrutinized the saddle and nodal point aspects of the flow of a hybrid nanofluid over a three-dimensional circular cylinder.
Based on the above literature reviews, no work has been conducted on the flow of a dusty nanofluid through a stretching cylinder in a porous medium while considering the melting heat transfer. In view of the many industrial applications of the melting effect and stretching cylinders, the present research explicates the flow of a dusty nanofluid through a stretching cylinder in a porous medium while considering the melting heat transfer phenomenon. Using the suitable similarity transformations, the PDEs were transformed into a set of ODEs. To achieve the numerical solutions for the reduced ODEs, the RKF-45 scheme was implemented with the shooting procedure. The impact of different control parameters on the fluid- and dust-phase velocities, the temperature, and the heat transfer rate is provided in graphs and tables and discussed afterwards with a physical explanation. The current research can be employed in a variety of disciplines, including heat engines, heat exchangers, thermocouples, permafrost melting, hot extrusion, oil flow filtration, solar collectors, and many others.
2. Mathematical Modeling
In the present study, we considered an incompressible, steady, 2D (two dimensional) dusty nanofluid motion through a stretching cylinder which is bounded the whole phenomenon graphically by the well-known curvilinear coordinates system () (see Figure 1). The axis of the cylinder is taken along the horizontal direction and the radial axis is taken normal or perpendicular to it. Further, assumed the surface velocity is denoted by , where axis is measured along the surface of the cylinder, is the reference length and is the positive stretching factor (). The impacts of melting and the porous medium were also included in the given model. In addition, and denoted the velocity components along the respective and axes and denoted the temperature of the fluid. Momentum and heat analyses were carried out for both the fluid and dust phases.
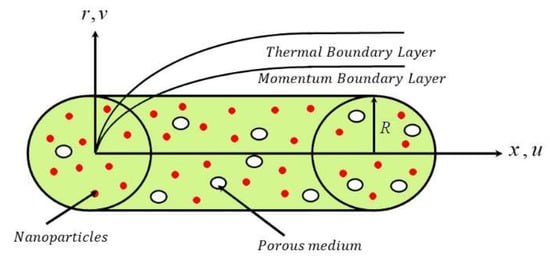
Figure 1.
Geometrical illustration of the problem.
The following are the governing equations that symbolize the nanofluid phase as well as the dust phase when the porous medium and the melting effect on a stretching cylinder are taken into account (see Manjunatha et al. [26], Waini et al. [27], and Singh et al. [28]).
In the above-mentioned equations, Equations (1)–(3) are for the fluid phase and the remaining equations are for the dust phase.
The appropriate boundary conditions for the above equations are specified as
and the melting phenomenon is given by (see Singh et al. [28])
For the Equations (1)–(8), is the axial coordinate, is the radial coordinate, and are the fluid phase velocity components, is the Stokes resistance, is the number density of particles, are the dust phase velocity components, is the permeability of the porous medium, is the kinematic viscosity, is the thermal conductivity, is the density, is the specific heat capacity of fluid, is the thermal equilibrium time, is the relaxation time for dust particles, is the density of the dust particles, is the mass of the dust particles, is the specific heat capacity of a dust particle, is the latent heat of the fluid, is the specific heat capacity of the solid surface, is the melting temperature.
The similarity variables are as follows (see Manjunatha et al. [26]):
Fluid phase:
Dust phase:
and
The following are the thermo-physical characteristics of a nanofluid (see Devi and Devi [29]):
By substituting the similarity transformations into the governing Equations (1)–(6) along with boundary conditions (7) and (8), we obtain:
Fluid phase:
Dust phase:
Subjected to the changed boundary conditions are
and
in which
Furthermore, the above equations comprise distinct, dimensionless, and distinguished parameters which can be symbolically demarcated as follows:
porosity parameter, mass concentration of particles, interaction parameter for velocity, interaction parameter for temperature, relaxation time of dust particles, ratio of specific heat, Eckert number, density of the dust particle, melting parameter, thermal equilibrium time, and is the curvature parameter.
Engineering coefficients and their reduced forms are as follows (see Ramzan et al. [30]):
where, denotes local Reynolds number.
3. Numerical Procedure and Validation
The reduced governing equations and boundary conditions were solved numerically with the help of the RKF-45 method and the shooting scheme. To provide a better understanding of this method, the structural outline for this technique is presented in Figure 2. To obtain the equation, the resultant equations were converted into first-order initial value problems. Consider
with
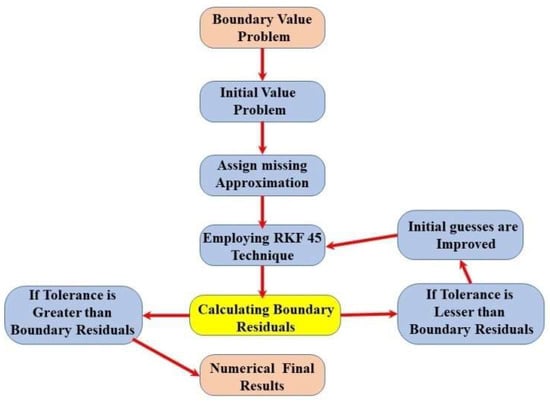
Figure 2.
Structural outline for the numerical procedure.
The initial value problem is represented by Equations (22) and (23). The unknown values are calculated using the shooting technique and numerically solved using the RKF-45 process with a step size of 0.01 and an error tolerance of around 10−6, which then satisfies the boundary condition at . The numerical solution to the problem is then computed using a computer program by varying the constraints’ values.
4. Results and Discussion
The numerical solution to the governing ODEs (13)–(16) with the boundary conditions (17)–(18) was achieved using the RKF-45 technique. Graphical depictions were utilized to analyze the impacts of the pertinent parameters, namely the curvature parameter , the porosity parameter , the Eckert number , and the melting parameter , on respective fluid- and dust-phase velocities . Fluid- and dust-phase temperature profiles are shown in Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8, while the streamline graphs are depicted in Figure 9a,b and Figure 10a,b, respectively. Moreover, the nature of the velocities and temperatures of both phases is examined in this segment and an appropriate explanation is provided here. The base liquid (H2O–Water) and nanoparticle (GO–Graphene oxide) thermo-physical characteristics are presented in Table 1 (see Chu et al. [31]). The results are also reported and compared (see Table 2) to the works of Gupta and Gupta [32], Ali [33], Grubka and Bobba [34], Eldahab and Aziz [35], and Abel and Mahesha [36] in certain reducing cases to verify the current numerical method. For the temperature gradient, the numerical values agree well with the published research, as exhibited in Table 2.The numerical values of the skin friction coefficient and Nusselt number in the presence and absence of the parameter are presented in Table 3. The value of decreases with decreases in and or increases in and . On the other hand, the value of decreases with an increase in or a decrease in the remaining parameters, as displayed in Table 3.
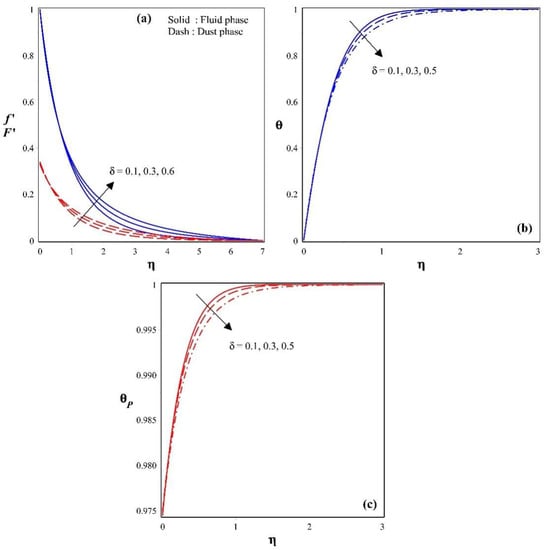
Figure 3.
(a): Impact of the curvature parameter on the fluid-phase velocity and dust-phase velocity profiles; (b): effect of the curvature parameter on the fluid-phase temperature profile; and (c):effect of the curvature parameter on the dust-phase temperature profile.
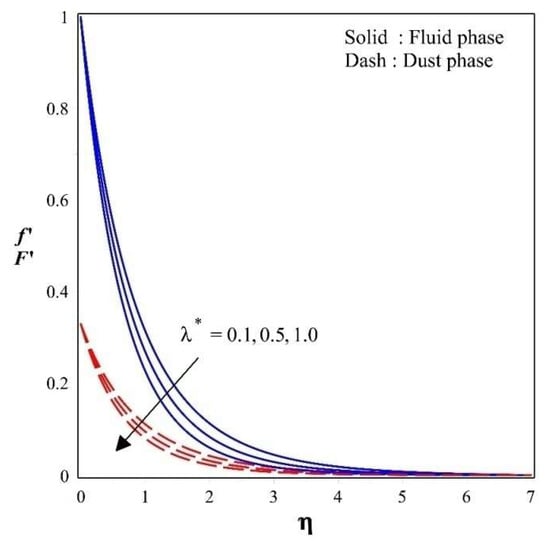
Figure 4.
Effect of the porosity parameter on the fluid- and dust-phase velocity profiles.
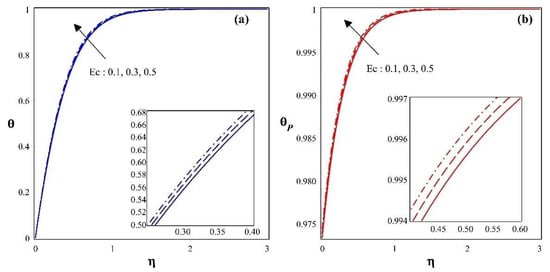
Figure 5.
(a): Effect of the Eckert number on the fluid-phase temperature profile and (b):effect of the Eckert number on the dust-phase temperature profile.
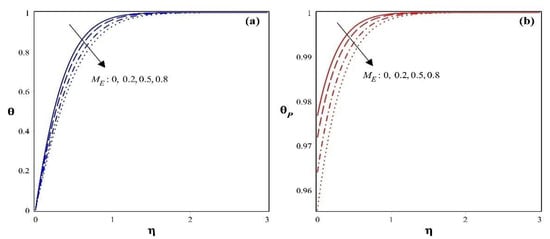
Figure 6.
(a): Consequence of the melting parameter on the fluid-phase temperature profile; (b): effect of the melting parameter on the dust-phase temperature profile.
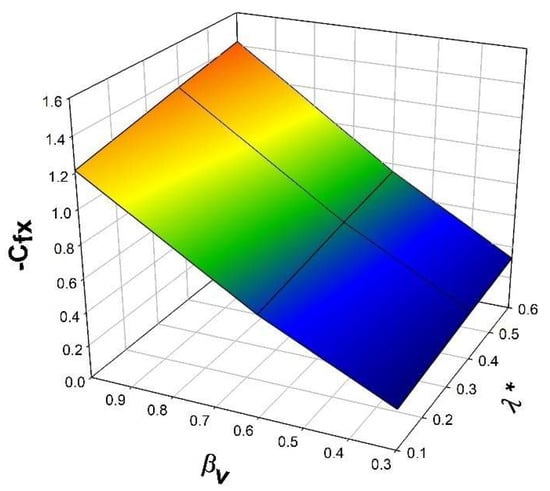
Figure 7.
Three-dimensional representation of with the impact of the interaction and porosity parameters.
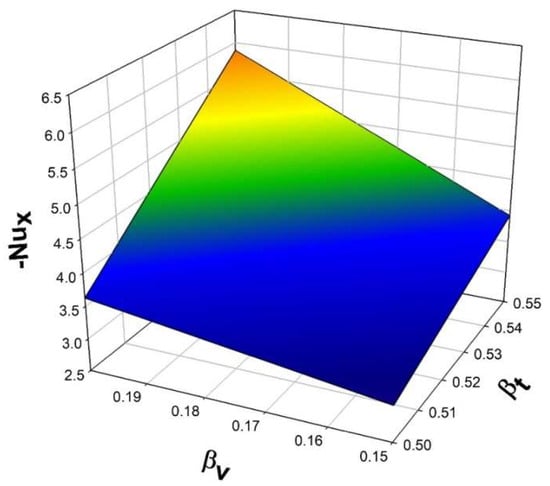
Figure 8.
Three-dimensional representation of with the impact of the interaction parameters for velocity and temperature.
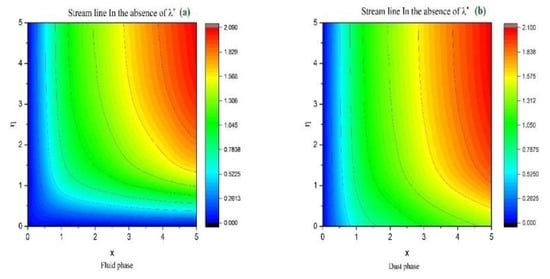
Figure 9.
Streamline representation for (a) the fluid phase and (b) the dust phase in the absence of .
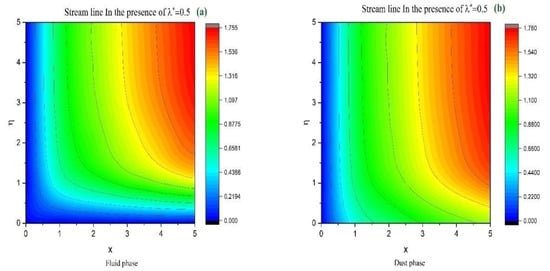
Figure 10.
Streamline representation for (a) the fluid phase and (b) the dust phase in the presence of .

Table 1.
Base liquid and nanoparticle thermo-physical characteristics.

Table 2.
Comparison of non-dimensional temperature gradients in the absence of , , , , ,, when .

Table 3.
Computational values of and for various dimensionless parameters keeping other constraints and .
The significant effect of the curvature parameter on the velocity profiles of fluid and dust particles is displayed in Figure 3a. As the magnitude of the curvature parameter increases, the fluid-phase velocity and the dust-phase velocity enhance remarkably. It is evident from Figure 3(a) that the fluid acceleration is the same as the dust velocity, especially in comparison to , and the upsurge of expands the velocity within the boundary layer. Furthermore, when , the problem is limited to a flat surface. As a result of the cylinder, the flow rate inside the boundary layer is larger than that of a level plane. This signifies that the intensifying velocity within the boundary layer is caused by expansion in the cylinder measurement. As predicted, the velocity and momentum increase and the thickness of the boundary layer decreases towards the cylinder’s surface, whereas the reverse effect is observed when distant from it. This is because the opposition supplied in aggregate by viscous forces near the cylinder’s surface is substantially larger than those distant from it. Furthermore, when the curvature parameter increases, the radius of the cylinder decreases, resulting in a reduced resistance to fluid motion and hence an increased fluid velocity. When compared to the liquid state, the inclination of the velocity gradient is significantly quicker in the dust stage. Figure 3b exhibits the variations in the fluid temperature profile, while Figure 3c shows the nature of the dust-phase temperature profile for increased scales of the curvature parameter. As the curvature parameter increases, the radius of the cylinder decreases, resulting in less resistance to fluid motion. Hence, heat distribution decreases in both the fluid and dust phases. These figures unveil that both the fluid- and dust-phase temperature profiles upsurge with an enhancement in the magnitude of curvature parameter.
The variations in the fluid- and dust-phase velocity profiles for the diverse magnitudes of porosity parameter are indicated in Figure 4. The fluid-and dust-phase velocity gradient drops gradually with an augmentation in the value of the porosity parameter. An upsurge in the value of the porosity parameter is the major cause of lower permeability, which results in a reduction in velocity. From a physical point of view, the permeability of a porous medium depends on both the porosity and particle size. A rise in the porosity parameter causes the porous medium to restrict the flow of liquid, decelerating its movement. As a result, the thickness of the boundary layer is diminished and thereby the velocity profiles of both phases drop rapidly.
Figure 5a indicates the impact of the Eckert number on the fluid-phase temperature profile, while Figure 5b shows the impact for the dust-phase temperature profile. In both the figures, one can perceive that the temperature profile increases with a rise in the Eckert number . Increments in the Eckert number strengthen the intermolecular movement and kinetic energy in liquids. As a result, the thermal variation, including both stages and the associated boundary layer, is enhanced by this intermolecular tension.
Figure 6a indicates the variations in the fluid thermal gradient, whereas Figure 6b manifests the nature of the dust particle temperature profile by considering the impact of the melting parameter . An enhancement in the melting parameter results in a reduction in the temperature profile for both stages. This is attributed to the fact that an increment in the melting parameter enhances the melting intensity, and as the melting strengthens, the geometry gradually transforms to a liquid, ultimately causing the velocity gradients to develop rapidly. This results in a decrease in the temperature gradient and its related boundary layer thickness. It can be observed that the thermal distribution is greater without the influence of the melting parameter, as opposed to in the presence of the melting parameter.
Figure 7 denotes the variations in with the impact of porosity and the velocity interaction parameter . The surface drag force decreases as the porosity parameter increases, as this creates opposition to the fluid flow due to an increase in the medium’s pore size, and the velocity interaction parameter reduces the fluid flow owing to the presence of the porous material.
An impression of the interaction parameters for velocity and temperature on the Nusselt number is exhibited through a 3D representation, as shown in Figure 8.Due to the presence of the thermal equilibrium time and thermal relaxation time for dust particles, the thermal distribution is enhanced by an increase in the values of the interaction parameters.
Figure 9a,b and Figure 10a,b show the streamline patterns with the impact of the porosity parameter. In the absence of the porosity parameter, Figure 9a indicates the streamline variations for the fluid phase, whereas the streamline pattern in the presence of the porosity parameter for the dust phase is exhibited in Figure 9b. Figure 10a,b show the streamline plots drawn to show the impact of the porosity parameter for both the fluid and dust phases, respectively.
5. Final Remarks
In this investigation, the characteristics of the melting effect phenomenon in the heat transference and flow of a dusty nanofluid through a permeable stretching cylinder were elucidated. The governing PDEs signifying energy transference and fluid motion in both the liquid and dust phases were converted into ODEs and numerically solved using the RKF-45 scheme with the shooting procedure. The major outcomes of this investigation are as follows:
- ❖ The fluid- and dust-phase velocities showed decreasing trends with an increase in the porosity parameter.
- ❖ The fluid- and dust-phase velocities improved with an increase in the curvature parameter. The same trend was observed in the fluid- and dust-phase temperature profiles.
- ❖ For lower values of the melting parameter, the temperature field for both the dust and liquid phases was enhanced significantly.
- ❖ The temperature profile for both the fluid and dust phases improves as the Eckert number increases.
- ❖ The surface drag force reduces when the porosity and interaction parameters are increased.
- ❖ The rate of heat dispersal increases as the values of the interaction parameters increase.
Many practical scenarios, such as heat engines, heat exchangers, thermocouples, permafrost melting, hot extrusion, oil flow filtration, solar collectors, energy recovery in geothermal stations, and the silicon wafer process require the use of porous materials and the melting phenomenon. Thermal efficiency and consistency may be greatly adjusted by employing the appropriate parameters examined in the present study.
Author Contributions
Conceptualization, M.U., J.M. and U.K.; methodology, M.U. and J.M.; software, M.U., J.M. and U.K.; validation, M.U., J.M., U.K. and S.R.; formal analysis, S.R., A.Z. and A.M.G.; investigation, A.M.G., A.Z. and S.R.; resources, A.M.G.; data curation, A.Z.; writing—original draft preparation, M.U., U.K., J.M. and S.R.; writing—review and editing, A.Z., Z.R., A.M.G. and S.R.; visualization, A.Z., J.M., Z.R. and S.R.; supervision, A.Z.; project administration, Z.R. and A.M.G.; funding acquisition, Z.R. and A.M.G. All authors have read and agreed to the published version of the manuscript.
Funding
The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University, Abha, Saudi Arabia, for funding this work through the Research Group Project under the grant number RGP.1/254/42.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The author, Z. Raizah, extends their appreciation to Scientific Research at King Khalid University, Abha, Saudi Arabia, for funding this work through the Research Group Project under the grant number RGP.1/254/42. We would like to thank the reviewers for their thoughtful comments and efforts towards improving our paper.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Cartesian coordinate (m) | |
| Coordinate in the radial direction (m) | |
| Reference length (m) | |
| Radius of the cylinder (m) | |
| Uniform stretching velocity (ms−1) | |
| Stretching velocity (ms−1) | |
| & | Fluid-phase velocity components (ms−1) |
| & | Dust-phase velocity components (ms−1) |
| Temperature (K) | |
| Stokes resistance | |
| The number density of particles | |
| Kinematic viscosity (m2s−1) | |
| Porous medium permeability (m2) | |
| Thermal conductivity (kgms−3K−1) | |
| Density (kgm−3) | |
| The density of the dust particle (kgm−3) | |
| Specific heat capacity of fluid (m−2s−2K−1) | |
| Specific heat capacity of the solid surface (m−2s−2K−1) | |
| Latent heat of the fluid | |
| The temperature of the dust particle (K) | |
| Wall temperature (K) | |
| Melting temperature (K) | |
| Ambient temperature (K) | |
| Thermal equilibrium time | |
| The relaxation time of dust particles | |
| Mass of the dust particle (kg) | |
| Dynamic viscosity (kgm−1s−1) | |
| Solid volume fraction (-) | |
| Nanofluid | |
| Eckert number (-) | |
| Ratio of specific heat (-) | |
| Melting parameter (-) | |
| Pr | Prandtl number |
| Curvature parameter (-) | |
| Skin friction coefficient | |
| Nusselt number coefficient | |
| Local Reynolds number | |
| Dimensionless velocities of fluid phase | |
| Dimensionless velocities of dust phase | |
| Dimensionless temperature | |
| Dimensionless temperature for the dust particle | |
| Interaction parameter for velocity | |
| Interaction parameter for temperature |
References
- Abbas, S.Z.; Khan, M.I.; Kadry, S.; Khan, W.A.; Israr-Ur-Rehman, M.; Waqas, M. Fully developed entropy optimized second order velocity slip MHD nanofluid flow with activation energy. Comput. Methods Programs Biomed. 2020, 190, 105362. [Google Scholar] [CrossRef]
- Madhukesh, J.K.; Ramesh, G.K.; Aly, E.H.; Chamkha, A.J. Dynamics of water conveying SWCNT nanoparticles and swimming microorganisms over a Riga plate subject to heat source/sink. Alex. Eng. J. 2022, 61, 2418–2429. [Google Scholar] [CrossRef]
- Muhammad, T.; Waqas, H.; Manzoor, U.; Farooq, U.; Rizvi, Z.F. On doubly stratified bioconvective transport of Jeffrey nanofluid with gyrotactic motile microorganisms. Alex. Eng. J. 2021, 61, 1571–1583. [Google Scholar] [CrossRef]
- Ramesh, G.K.; Madhukesh, J.K.; Prasannakumara, B.C.; Shehzad, S.A.; Abbasi, F.M. Thermodynamics Examination of Fe3O4-CoFe2O4/Water + EG Nanofluid in a Heated Plate: Crosswise and Stream-wise Aspects. Arab. J. Sci. Eng. 2021, 1–10. [Google Scholar] [CrossRef]
- Xu, Y.-J.; Bilal, M.; Al-Mdallal, Q.; Khan, M.A.; Muhammad, T. Gyrotactic micro-organism flow of Maxwell nanofluid between two parallel plates. Sci. Rep. 2021, 11, 15142. [Google Scholar] [CrossRef]
- Hussain, S.A.; Ali, G.; Muhammad, S.; Shah, S.I.A.; Ishaq, M.; Khan, H. Dusty Casson Nanofluid Flow with Thermal Radiation Over a Permeable Exponentially Stretching Surface. J. Nanofluids 2019, 8, 714–724. [Google Scholar] [CrossRef]
- Rashed, Z.Z.; Ahmed, S.E. Unsteady three dimensional radiative-convective flow and heat transfer of dusty nanofluid within porous cubic enclosures. J. Dispers. Sci. Technol. 2021, 0, 1–15. [Google Scholar] [CrossRef]
- Ramzan, M.; Gul, H.; Baleanu, D.; Nisar, K.S.; Malik, M.Y. Role of Cattaneo–Christov heat flux in an MHD Micropolar dusty nanofluid flow with zero mass flux condition. Sci. Rep. 2021, 11, 19528. [Google Scholar] [CrossRef]
- Wahidunnisa, L.; Suneetha, S.; Reddy, S.; Reddy, P.B.A. Comparative study on electromagnetohydrodynamic single-wall carbon nanotube–water dusty nanofluid in the presence of radiation and Ohmic heating. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2021, 235, 950–958. [Google Scholar] [CrossRef]
- Sowmya, G.; Saleh, B.; Punith Gowda, R.J.; Naveen Kumar, R.; Varun Kumar, R.S.; Radhika, M. Analysis of radiative nonlinear heat transfer in a convective flow of dusty fluid by capitalizing a non-Fourier heat flux model. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2021, 09544089211041192. [Google Scholar] [CrossRef]
- Wahid, N.S.; Arifin, N.M.; Khashi’ie, N.S.; Pop, I. Marangoni hybrid nanofluid flow over a permeable infinite disk embedded in a porous medium. Int. Commun. Heat Mass Transf. 2021, 126, 105421. [Google Scholar] [CrossRef]
- Khan, M.I.; Alzahrani, F. Free convection and radiation effects in nanofluid (Silicon dioxide and Molybdenum disulfide) with second order velocity slip, entropy generation, Darcy-Forchheimer porous medium. Int. J. Hydrogen Energy 2021, 46, 1362–1369. [Google Scholar] [CrossRef]
- Ramesh, G.K.; Madhukesh, J.K.; Shehzad, S.A.; Rauf, A. Ternary nanofluid with heat source/sink and porous medium effects in stretchable convergent/divergent channel. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2022, 09544089221081344. [Google Scholar] [CrossRef]
- Ahmad, S.; Ali, K.; Rizwan, M.; Ashraf, M. Heat and mass transfer attributes of copper–aluminum oxide hybrid nanoparticles flow through a porous medium. Case Stud. Therm. Eng. 2021, 25, 100932. [Google Scholar] [CrossRef]
- Ali, K.; Ahmad, S.; Nisar, K.S.; Faridi, A.A.; Ashraf, M. Simulation analysis of MHD hybrid Cu-Al2O3/H2O nanofluid flow with heat generation through a porous media. Int. J. Energy Res. 2021, 45, 19165–19179. [Google Scholar] [CrossRef]
- Mabood, F.; Yusuf, T.A.; Khan, W.A. Cu–Al2O3–H2O hybrid nanofluid flow with melting heat transfer, irreversibility analysis and nonlinear thermal radiation. J. Therm. Anal. Calorim. 2021, 143, 973–984. [Google Scholar] [CrossRef]
- Waqas, H.; Muhammad, T.; Noreen, S.; Farooq, U.; Alghamdi, M. Cattaneo-Christov heat flux and entropy generation on hybrid nanofluid flow in a nozzle of rocket engine with melting heat transfer. Case Stud. Therm. Eng. 2021, 28, 101504. [Google Scholar] [CrossRef]
- Hayat, T.; Muhammad, K.; Alsaedi, A. Numerical study of melting heat transfer in stagnation-point flow of hybrid nanomaterial (MWCNTs+Ag+kerosene oil). Int. J. Numer. Methods Heat Fluid Flow 2021, 31, 2580–2598. [Google Scholar] [CrossRef]
- Mallikarjuna, H.B.; Nirmala, T.; Punith Gowda, R.J.; Manghat, R.; Varun Kumar, R.S. Two-dimensional Darcy–Forchheimer flow of a dusty hybrid nanofluid over a stretching sheet with viscous dissipation. Heat Transf. 2021, 50, 3934–3947. [Google Scholar] [CrossRef]
- Khan, S.A.; Khan, M.I.; Alzahrani, F. Melting heat transportation in chemical reactive flow of third grade nanofluid with irreversibility analysis. Int. Commun. Heat Mass Transf. 2021, 129, 105696. [Google Scholar] [CrossRef]
- Abbas, N.; Nadeem, S.; Saleem, A.; Malik, M.Y.; Issakhov, A.; Alharbi, F.M. Models base study of inclined MHD of hybrid nanofluid flow over nonlinear stretching cylinder. Chin. J. Phys. 2021, 69, 109–117. [Google Scholar] [CrossRef]
- Waqas, H.; Manzoor, U.; Muhammad, T.; Hussain, S. Thermo-bioconvection transport of nanofluid over an inclined stretching cylinder with Cattaneo–Christov double-diffusion. Commun. Theor. Phys. 2021, 73, 075006. [Google Scholar] [CrossRef]
- Varun Kumar, R.S.; Punith Gowda, R.J.; Naveen Kumar, R.; Radhika, M.; Prasannakumara, B.C. Two-phase flow of dusty fluid with suspended hybrid nanoparticles over a stretching cylinder with modified Fourier heat flux. SN Appl. Sci. 2021, 3, 384. [Google Scholar] [CrossRef]
- Rashid, U.; Liang, H.; Ahmad, H.; Abbas, M.; Iqbal, A.; Hamed, Y.S. Study of (Ag and TiO2)/water nanoparticles shape effect on heat transfer and hybrid nanofluid flow toward stretching shrinking horizontal cylinder. Results Phys. 2021, 21, 103812. [Google Scholar] [CrossRef]
- Madhukesh, J.K.; Ramesh, G.K.; Roopa, G.S.; Prasannakumara, B.C.; Shah, N.A.; Yook, S.-J. 3D Flow of Hybrid Nanomaterial through a Circular Cylinder: Saddle and Nodal Point Aspects. Mathematics 2022, 10, 1185. [Google Scholar] [CrossRef]
- Manjunatha, P.T.; Gireesha, B.J.; Prasannakumara, B.C. Effect of Radiation on Flow and Heat Transfer of MHD Dusty Fluid Over a Stretching Cylinder Embedded in a Porous Medium in Presence of Heat Source. Int. J. Appl. Comput. Math. 2017, 3, 293–310. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Unsteady flow and heat transfer past a stretching/shrinking sheet in a hybrid nanofluid. Int. J. Heat Mass Transf. 2019, 136, 288–297. [Google Scholar] [CrossRef]
- Singh, K.; Pandey, A.K.; Kumar, M. Melting heat transfer assessment on magnetic nanofluid flow past a porous stretching cylinder. J. Egypt. Math. Soc. 2021, 29, 1. [Google Scholar] [CrossRef]
- Devi, S.P.A.; Devi, S.S.U. Numerical Investigation of Hydromagnetic Hybrid Cu – Al2O3/Water Nanofluid Flow over a Permeable Stretching Sheet with Suction. Int. J. Nonlinear Sci. Numer. Simul. 2016, 17, 249–257. [Google Scholar] [CrossRef]
- Ramzan, M.; Shaheen, N.; Chung, J.D.; Kadry, S.; Chu, Y.-M.; Howari, F. Impact of Newtonian heating and Fourier and Fick’s laws on a magnetohydrodynamic dusty Casson nanofluid flow with variable heat source/sink over a stretching cylinder. Sci. Rep. 2021, 11, 2357. [Google Scholar] [CrossRef]
- Chu, Y.-M.; Nisar, K.S.; Khan, U.; Kasmaei, H.D.; Malaver, M.; Zaib, A.; Khan, I. Mixed Convection in MHD Water-Based Molybdenum Disulfide-Graphene Oxide Hybrid Nanofluid through an Upright Cylinder with Shape Factor. Water 2020, 12, 1723. [Google Scholar] [CrossRef]
- Gupta, P.S.; Gupta, A.S. Heat and mass transfer on a stretching sheet with suction or blowing. Can. J. Chem. Eng. 1977, 55, 744–746. [Google Scholar] [CrossRef]
- Ali, M.E. On thermal boundary layer on a power-law stretched surface with suction or injection. Int. J. Heat Fluid Flow 1995, 16, 280–290. [Google Scholar] [CrossRef]
- Grubka, L.J.; Bobba, K.M. Heat Transfer Characteristics of a Continuous, Stretching Surface with Variable Temperature. J. Heat Transf. 1985, 107, 248–250. [Google Scholar] [CrossRef]
- Abo-Eldahab, E.M.; El Aziz, M.A. Blowing/suction effect on hydromagnetic heat transfer by mixed convection from an inclined continuously stretching surface with internal heat generation/absorption. Int. J. Thermal Sci. 2004, 43, 709–719. [Google Scholar] [CrossRef]
- Abel, M.S.; Mahesha, N. Heat transfer in MHD viscoelastic fluid flow over a stretching sheet with variable thermal conductivity, non-uniform heat source and radiation. Appl. Math. Model. 2008, 32, 1965–1983. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).