An Unsupervised Clustering Method for Selection of the Fracturing Stage Design Based on the Gaussian Mixture Model
Abstract
:1. Introduction
2. Methodology
2.1. Calculation of Three Quality Indexes Based on Logging Data
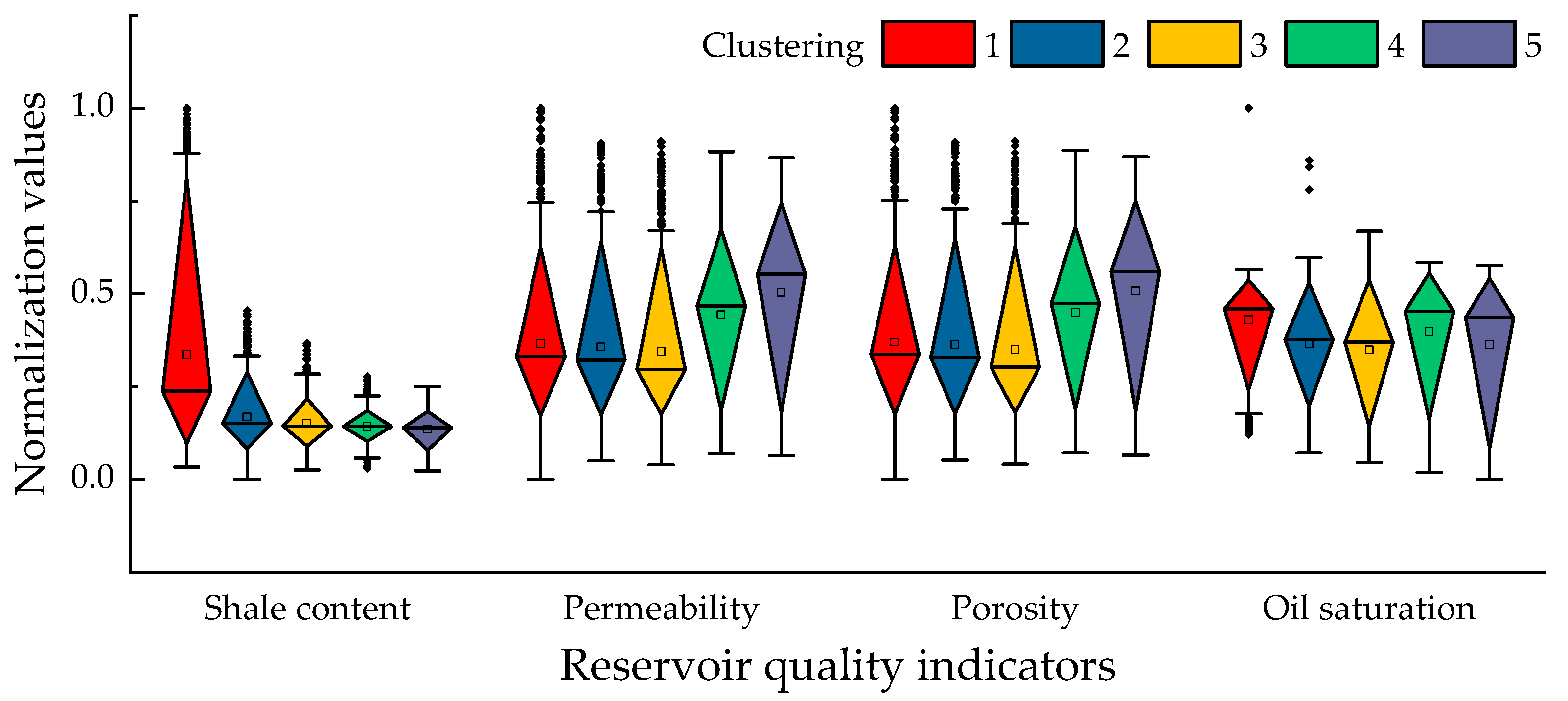
2.1.1. Calculation of Reservoir Quality Index
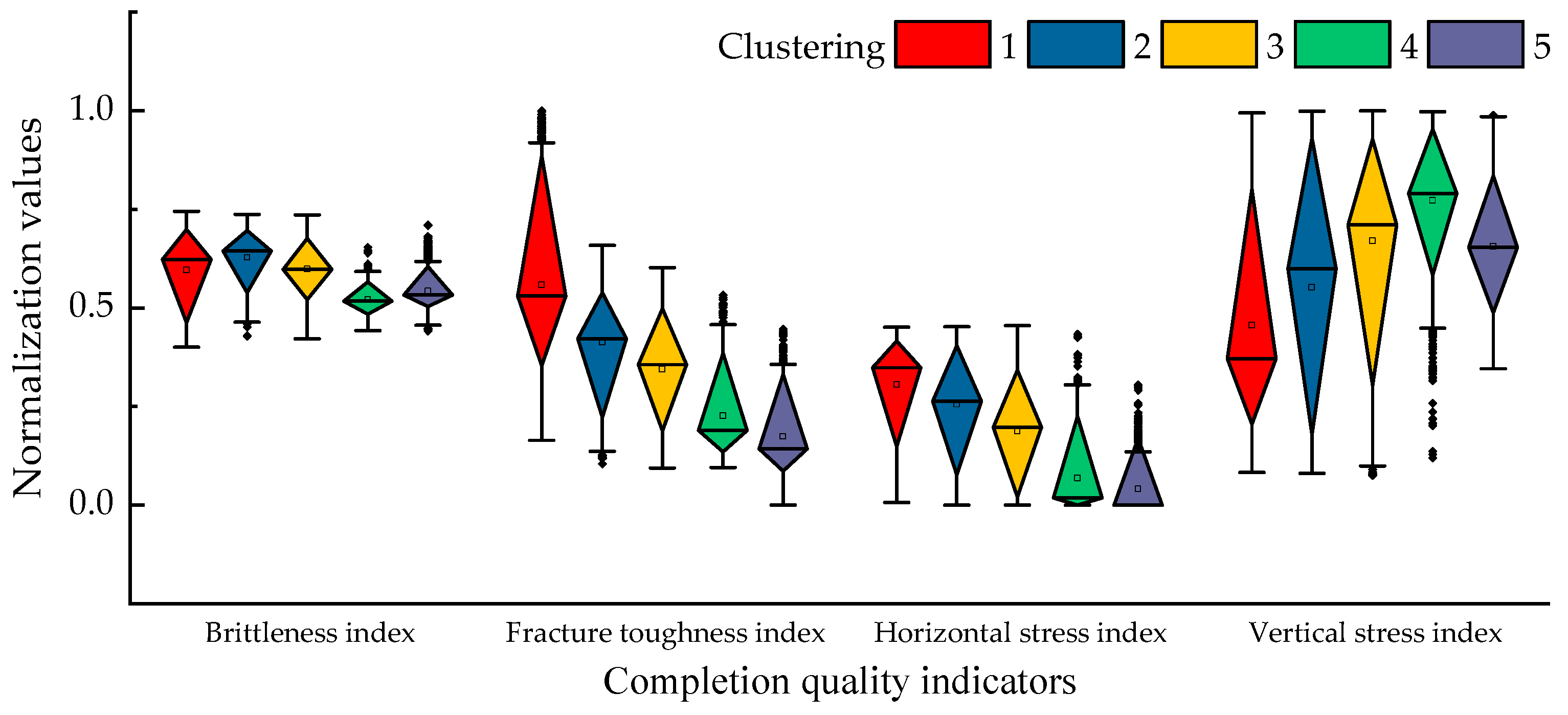
2.1.2. Calculation of the Completion Quality Index
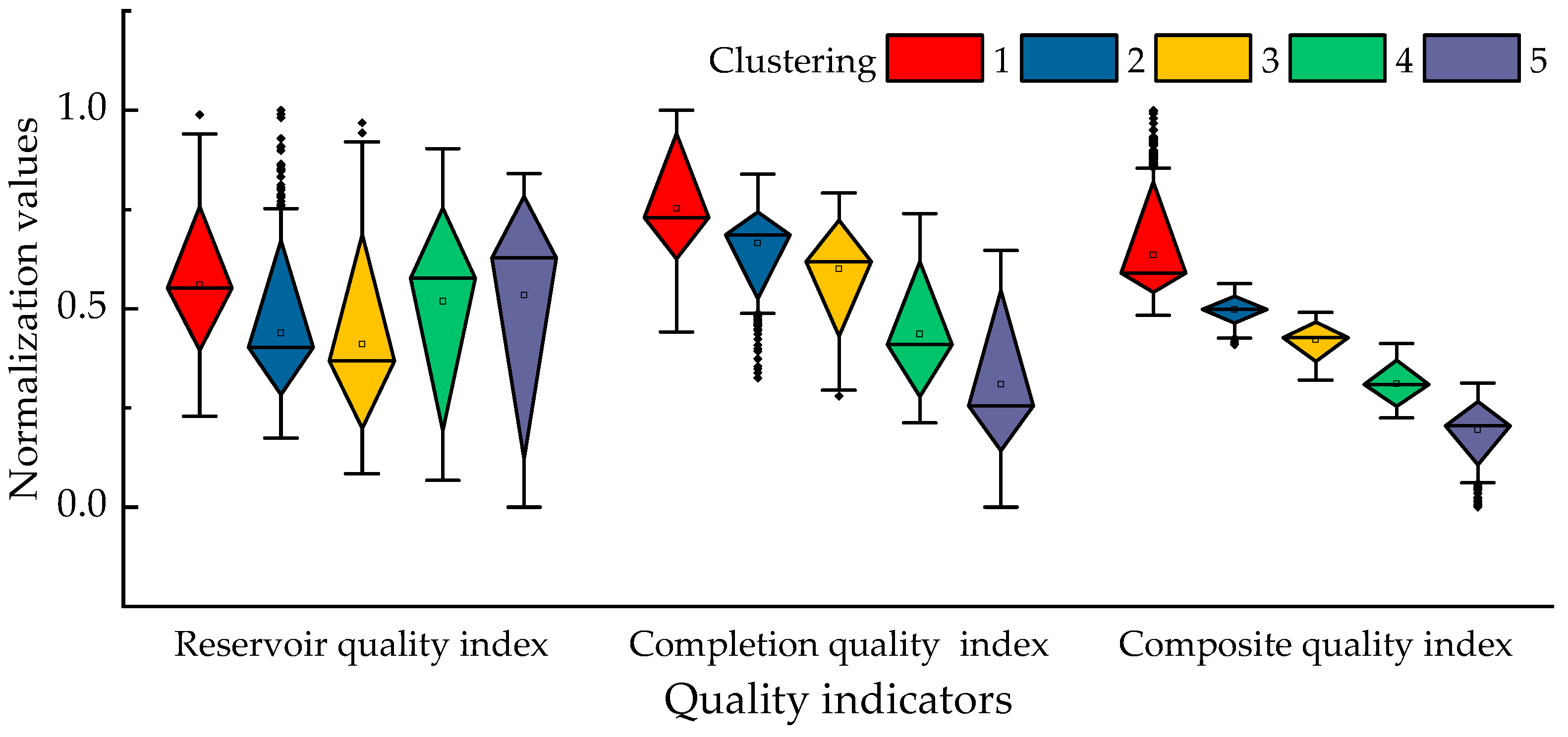
2.1.3. Calculation of the Composite Quality Index
2.2. Coupled Evaluation Model of the Entropy Weight Method and Analytic Hierarchy Process
2.2.1. The Entropy Weight Method (EWM)
2.2.2. The Analytic Hierarchy Process (AHP)
2.2.3. Establishment of the Coupled Evaluation Model Entropy Weight Method and Analytic Hierarchy Process
2.3. Gaussian Mixture Model (GMM) Clustering Algorithms
2.3.1. Standardization of Original Data
2.3.2. GMM Clustering Algorithms
2.4. Flowchart of the Identification of the Fracturing Grades
3. Case Study and Discussion
3.1. Analysis of the Coupled Evaluation Model of EMW and AHP
3.2. Determination of Clustering Number Value
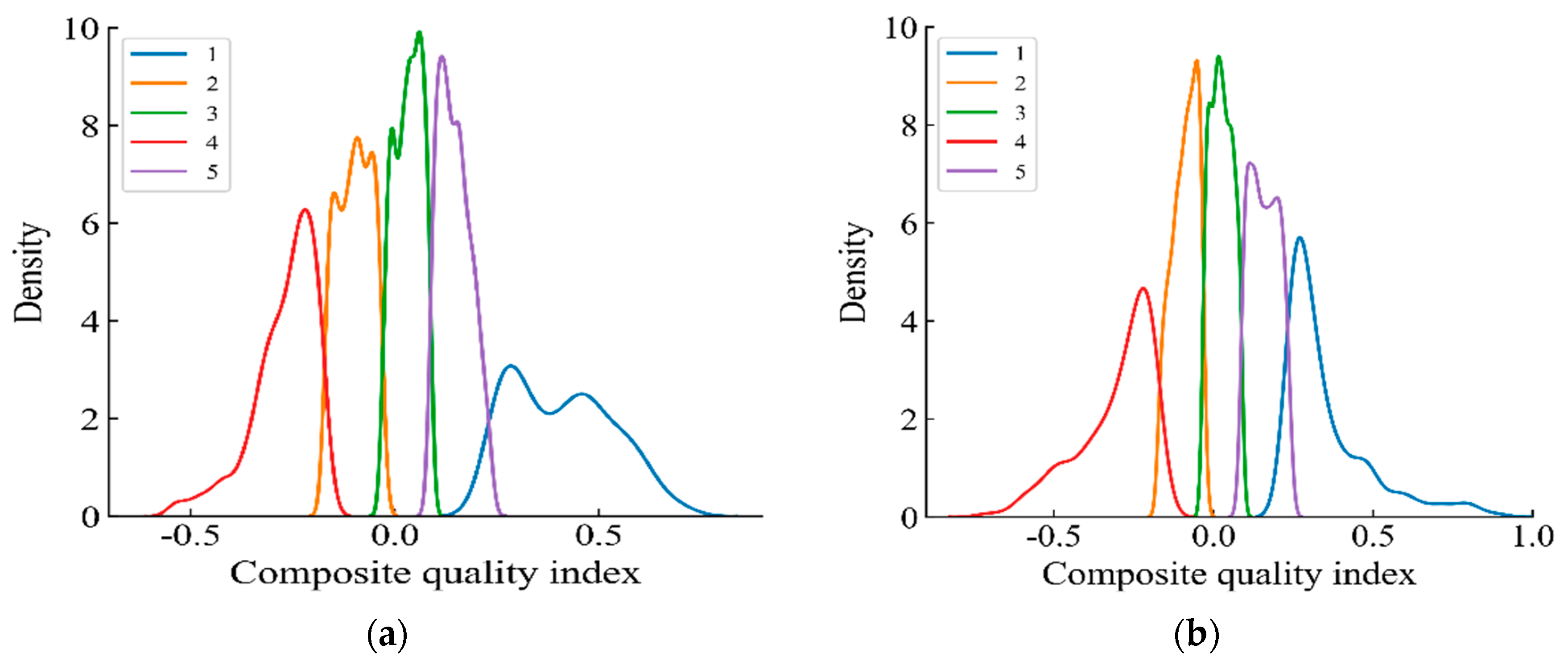
3.3. Cluster Simulation Experiment
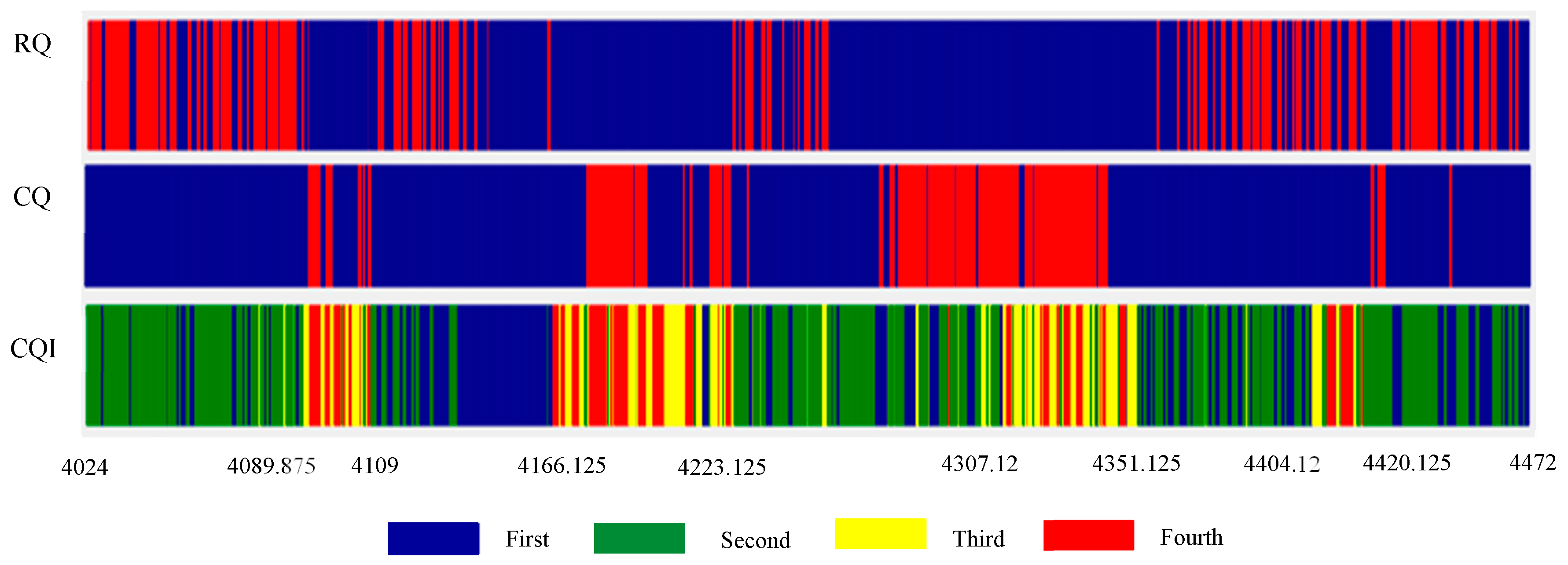
3.4. Cluster Test Experiment
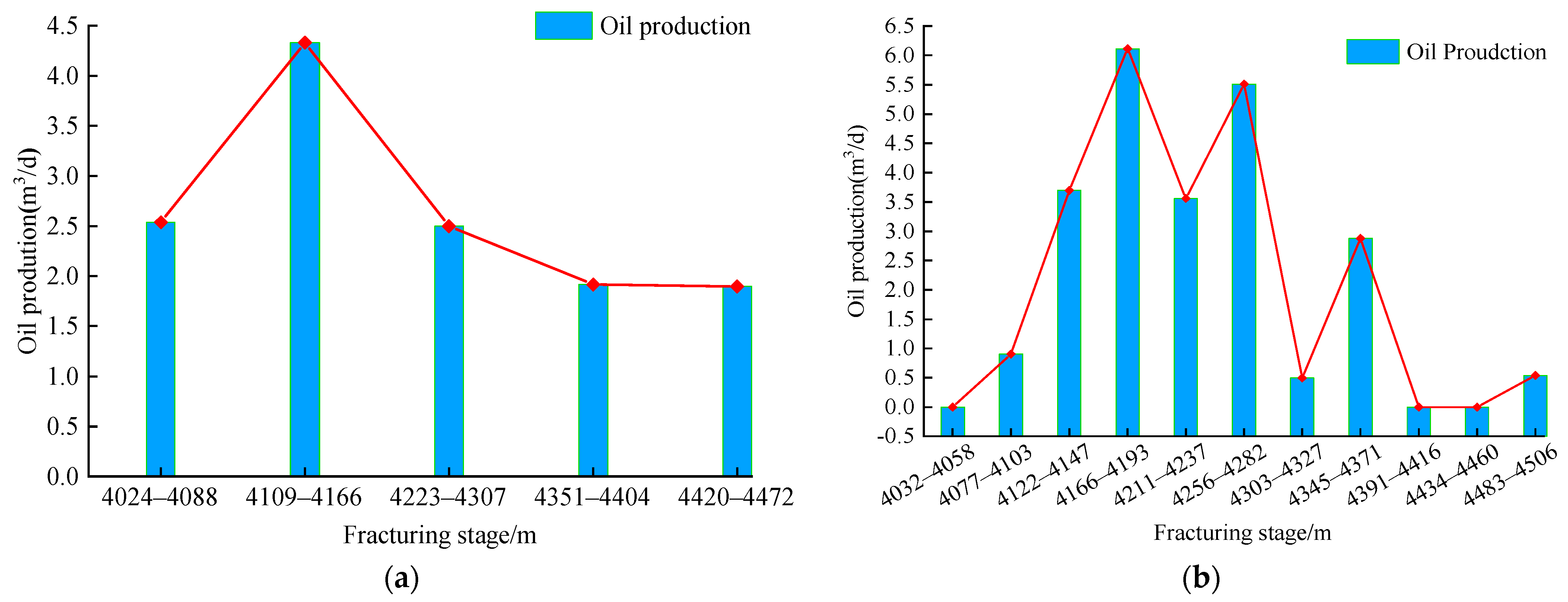
3.5. Cluster Prediction Test
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hu, W.; Wei, Y.; Bao, J. Development of the theory and technology for low permeability reservoirs in China. Pet. Explor. Dev. 2018, 45, 646–656. [Google Scholar] [CrossRef]
- Lei, Q.; Guan, B.; Cai, B.; Wang, X.; Xu, Y.; Tong, Z.; Wang, H.; Fu, H.; Liu, Z.; Wang, Z. Technological progress and prospects of reservoir stimulation. Pet. Explor. Dev. 2019, 46, 580–587. [Google Scholar] [CrossRef]
- Li, Q.; Ma, X.; Gao, B.; Chen, X. Progress and Enlightenment of Exploration and Development of Major Shale Oil Zones in the USA. Xinjiang Pet. Geol. 2021, 42, 630–640. [Google Scholar]
- Lei, Q.; Xu, Y.; Cai, B.; Guan, B.; Wang, X.; Bi, G.; Li, H.; Li, S.; Ding, B.; Fu, H.; et al. Progress and prospects of horizontal well fracturing technology for shale oil and gas reservoirs. Pet. Explor. Dev. 2022, 49, 166–172. [Google Scholar] [CrossRef]
- Li, G.; Liu, G.; Hou, Y.; Zhao, X.; Wu, J.; Li, S.; Xian, C.; Liu, H. Optimization method of favorable lithofacies and fracturing parameter for continental shale oil. Acta Pet. Sin. 2021, 42, 1405–1416. [Google Scholar]
- Chen, G.; Bai, Y.; Chen, X.; Xu, B.; Zhu, Y.; Feng, R.; Chen, L. A new identification method for the longitudinal integrated shale oil/gas sweet spot and its quantitative evaluation. Acta Pet. Sin. 2016, 37, 1337–1342. [Google Scholar]
- Miller, C.; Waters, G.; Rylander, E. 2011: Evaluation of Production Log Data from Horizontal Wells Drilledin Organic Shales. In Proceedings of the North American Unconventional Gas Conference and Exhibition, The Woodlands, TX, USA, 14–16 June 2011. [Google Scholar]
- Wigger, E.; Viswanathan, A.; Fisher, K.; Slocombe, R.W.; Kaufman, P.; Chadwick, C. Logging Solutions for Completion Optimization in Unconventional Resource Plays; Society of Petroleum Engineers: Danbury, CT, USA, 2014. [Google Scholar]
- Suarez-Rivera, R.; Deenadayalu, C.; Chertov, M.; Hartanto, R.N.; Gathogo, P.; Kunjir, R. Improving horizontal completions on heterogeneous tight shales. In Proceedings of the Canadian Unconventional Resources Conference, Calgary, AB, Canada, 15–17 November 2011. [Google Scholar]
- Suarez-Rivera, R.; Vaaland Dahl, G.; Borgos, H.; Paddock, D.; Handwerger, D. Seismic-based heterogeneous Earth model improves mapping reservoir quality and completion quality in tight shales. In Proceedings of the Unconventional Resources Conference and Exhibition—USA, The Woodlands, TX, USA, 10–12 April 2013. [Google Scholar]
- Zou, C.; Dong, D.; Wang, Y.; Li, X.; Huang, J.; Wang, S.; Guan, Q.; Zhang, C.; Wang, H.; Liu, H.; et al. Shale gas in China: Characteristics, challenges and prospects (II). Pet. Explor. Dev. 2016, 43, 166–178. [Google Scholar] [CrossRef]
- Lei, Q.; Weng, D.; Xiong, S.; Liu, H.; Guan, B.; Deng, Q.; Yan, X.; Liang, H.; Ma, Z. Progress and development directions of shale oil reservoir stimulation technology of China National Petroleum Corporation. Pet. Explor. Dev. 2021, 48, 1035–1042. [Google Scholar] [CrossRef]
- Liu, G. Challenges and countermeasures of log evaluation in unconventional petroleum exploration. Pet. Explor. Dev. 2021, 48, 891–902. [Google Scholar] [CrossRef]
- Zhang, D.; Yu, Y.; Li, S.; Chen, Y.; Xu, J. Staging optimization of multi-stage perforation fracturing based on unsupervised machine learning. J. China Univ. Pet. 2021, 45, 59–66. [Google Scholar]
- Slocombe, R.; Acock, A.; Fisher, K.; Viswanathan, A.; Chadwick, C.; Reischman, R.; Wigger, E. Eagle Ford Completion Optimization Using Horizontal Log Data. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 30 September–2 October 2013. [Google Scholar]
- Cipolla, C.; Weng, X.; Onida, H.; Nadaraja, T.; Ganguly, U.; Malpani, R. New Algorithms and Integrated Workflow for Tight Gas and Shale Completions. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 30 October–2 November 2011. [Google Scholar]
- Atanayev, A.; Nadezhdin, S.; Al Zeidi, O.; Batmaz, T.; Kurniadi, S.D. An Advanced Workflow for Determining Fracture Geometry in Complex Tight Oil Formations in the Sultanate of Oman; Society of Petroleum Engineers: Danbury, CT, USA, 2016. [Google Scholar]
- Cipolla, C.L.; Lewis, R.E.; Maxwell, S.C.; Mack, M.G. Appraising Unconventional Resource Plays: Separating Reservoir Quality from Completion Effectiveness. In Proceedings of the International Petroleum Technology Conference, Bangkok, Thailand, 15–17 November 2011. IPTC 14677. [Google Scholar]
- Ejofodomi, E.A.; Varela, R.A.; Cavazzoli, G.; Velez, E.I.; Peano, J. Development of an Optimized Completion Strategy in the Vaca Muerta Shale with an Anisotropic Geomechanical Model. In Proceedings of the European Unconventional Conference and Exhibition, Vienna, Austria, 25–27 February 2014. [Google Scholar]
- Salah, M.; Ibrahim, M. Engineered Fracture Spacing Staging and Perforation Cluster Spacing Optimization for Multistage Fracturing Horizontal Wells. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 24–26 September 2018. [Google Scholar]
- Li, H.; Liu, C.; Lu, Y.; Jiang, B.; Du, X. New Method of Tight Oil Horizontal Well Multi-cluster Perforation Design and Its Application. Well Logging Technol. 2018, 42, 362–366. [Google Scholar]
- Xia, H.; Lai, J.; Li, G.; Yang, B. Sweet Spot Prediction of Shale Oil Reservoir Based on Logging Data. J. Southwest Pet. Univ. 2021, 43, 199–207. [Google Scholar]
- Zeng, W. Logging Interpretation Techniques for Determining Permeability. Well Logging Technol. 1979, 3, 1–11. [Google Scholar]
- Li, Q.; Zhou, R.; Zhang, J.; Wu, H.; Li, X. Relations between Archie’s formula and reservoir pore structure. Oil Gas Geol. 2002, 4, 364–367. [Google Scholar]
- Jin, X.; Shah, S.N.; Roegiers, J.C.; Zhang, B. An integrated petrophysics and geomechanics approach for fracability evaluation in shale reservoirs. Soc. Pet. Eng. J. 2015, 20, 518–526. [Google Scholar] [CrossRef]
- Rickman, R.; Mullen, M.J.; Petre, J.E.; Grieser, W.V.; Kundert, D. Apracticaluse of shale petrophysics for stimulation design optimization: All shale plays are not clones of the Barnett Shale. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 21–24 September 2008; Society of Petroleum Engineers: Danbury, CT, USA, 2008. [Google Scholar]
- Li, N.; Zou, Y.; Zhang, S.; Ma, X.; Zhu, X.; Li, S.; Cao, T. Rock brittleness evaluation based on energy dissipation under triaxial compression. J. Pet. Sci. Eng. 2019, 183, 106349. [Google Scholar] [CrossRef]
- Jin, Y.; Chen, M.; Zhang, X. Determination of Fracture Toughness for Deep Well Rock with Geophysical Logging Data. Chin. J. Rock Mech. Eng. 2001, 4, 454–456. [Google Scholar]
- Jin, Y.; Chen, M.; Wang, H.; Ruan, Y. Study on prediction method of fracture toughness of rock mode II by logging data. Chin. J. Rock Mech. Eng. 2008, S2, 3630–3635. [Google Scholar]
- Song, L.; Liu, Z.; Li, C.; Hu, S. Geostress logging evaluation method of tight sandstone based on transversely isotropic model. Acta Pet. Sin. 2015, 36, 707–714. [Google Scholar]
- Yang, Y. Evaluation and analysis of weight assignment method in multi-index comprehensive evaluation. Stat. Decis. 2006, 13, 17–19. [Google Scholar]
- Chuan, Y. Entropy-based weights on decision makers in group decision-making setting with hybrid preference representations. Appl. Soft Comput. 2017, 60, 737–749. [Google Scholar]
- Deng, X.; Li, J.; Zeng, H. Research on Computation Methods of AHP Wight Vector and Its Applications. Math. Pract. Theory 2012, 42, 93–100. [Google Scholar]
- Mai, T.; Mortari, D. Theory of functional connections applied to quadratic and nonlinear programming under equality constraints. J. Comput. Appl. Math. 2021, 406, 113912. [Google Scholar] [CrossRef]
- Huang, Z.; Xiang, Y.; Zhang, B.; Wang, D.; Liu, X. An Efficient Method for K-Means Clustering. Pattern Recognit. Artif. Intell. 2010, 23, 516–521. [Google Scholar]
- Lloyd, S. Least squares quantization in PCM. IEEE Trans. Inf. Theory 1982, 28, 129–137. [Google Scholar] [CrossRef] [Green Version]
- Weber, C.M.; Ray, D.; Valverde, A. Gaussian mixture model clustering algorithms for the analysis of high precision mass measurements. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2022, 1027, 166299. [Google Scholar] [CrossRef]
- Patel, E.; Kushwaha, D.S. Clustering Cloud Workloads: K-Means vs Gaussian Mixture Model. Procedia Comput. Sci. 2020, 171, 158–167. [Google Scholar] [CrossRef]
- Zhang, B.; Shin, Y.C. An Adaptive Gaussian Mixture Method for Nonlinear Uncertainty Propagation in Neural Networks. Neurocomputing 2021, 458, 170–183. [Google Scholar] [CrossRef]


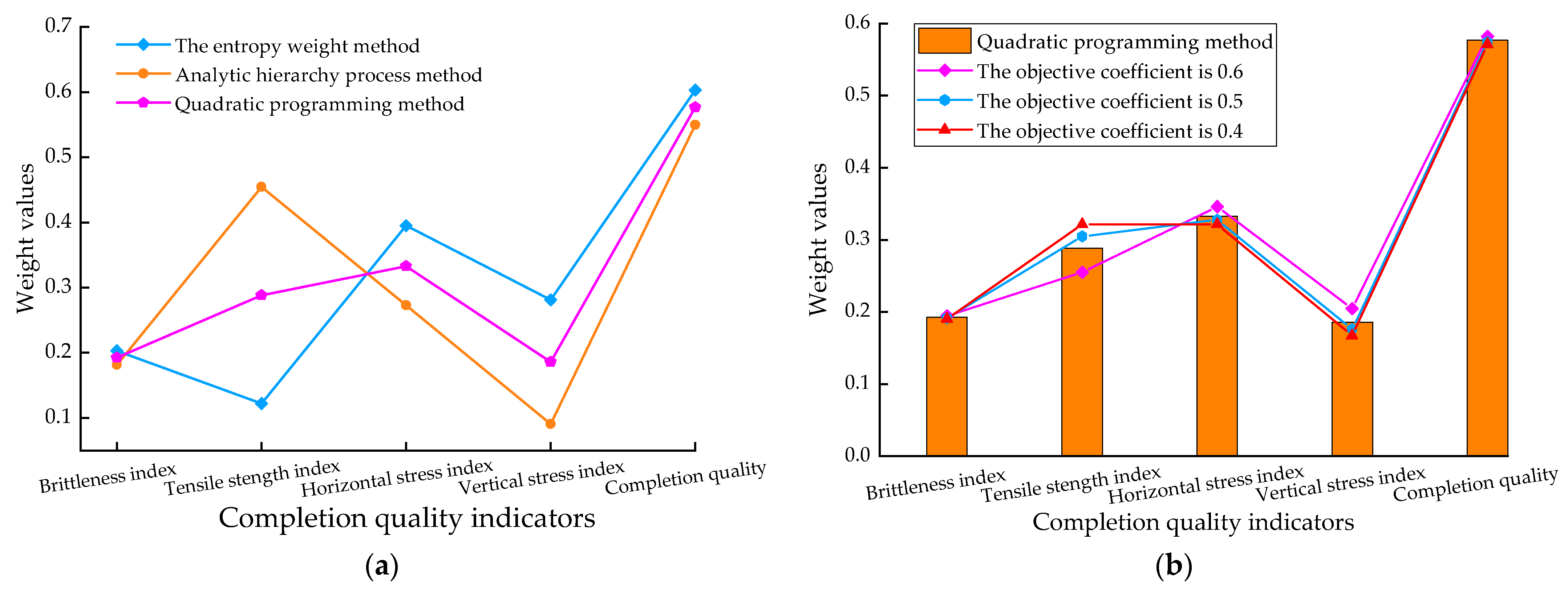


| Indicator | The Weight of Each Indicator | ||
|---|---|---|---|
| EWM | AHP | Quadratic Programming | |
| 0.39 | 0.055 | 0.2225 | |
| 0.209 | 0.1178 | 0.1634 | |
| 0.213 | 0.2634 | 0.2382 | |
| 0.187 | 0.5638 | 0.3754 | |
| 0.397 | 0.4500 | 0.4235 | |
| Indicator | The Weight of Each Indicator | ||
|---|---|---|---|
| EWM | AHP | Quadratic Programming | |
| 0.203 | 0.1818 | 0.1927 | |
| 0.122 | 0.4545 | 0.2885 | |
| 0.395 | 0.2727 | 0.333 | |
| 0.281 | 0.0909 | 0.1857 | |
| 0.603 | 0.550 | 0.5765 | |
| Fracturing Stages of GMM | Actual Fracturing Stages and Production | ||
|---|---|---|---|
| Fracturing stages/m | Grade | Fracturing stages/m | Oil production m3/d |
| 4024.0~4089.9 | 2 | 4024.0~4088.0 | 2.536 |
| 4089.9~4109.0 | 4 | Null | 0 |
| 4109.0~4166.1 | 1 | 4109.0~4166.0 | 4.331 |
| 4166.1~4223.1 | 4 | Null | 0 |
| 4223.1~4307.3 | 2 | 4223.0~4307.0 | 2.499 |
| 4307.1~4351.1 | 3 | Null | 0 |
| 4351.2~4404.1 | 2 | 4351.0~4404.0 | 1.915 |
| 4404.1~4420.1 | 4 | Null | 0 |
| 4420.1~4472.0 | 2 | 4420.0~4472.0 | 1.896 |
| Fracturing Stages of GMM | Actual Fracturing Stages and Production | ||||||
|---|---|---|---|---|---|---|---|
| Fracturing stages/m | Grade | Fracturing stages/m | Grade | Fracturing stages/m | Oil production m3/d | Fracturing stages/m | Oil production m3/d |
| 4032.0~4057.0 | 4 | 4281.8~4302.5 | 4 | 4032.0~4058.0 | 0 | Null | 0 |
| 4057.0~4075.4 | 3 | 4302.5~4327.3 | 2 | Null | 0 | 4303.0~4327.0 | 0.493 |
| 4075.4~4101.9 | 2 | 4327.3~4342.5 | 3 | 4077.0~4103.0 | 0.907 | Null | 0 |
| 4101.9~4120.8 | 3 | 4342.5~4370.0 | 1 | Null | 0 | 4345.0~4371.0 | 2.876 |
| 4120.8~4146.8 | 1 | 4370.0~4389.5 | 3 | 4122.0~4147.0 | 3.698 | Null | 0 |
| 4146.8~4165.9 | 4 | 4389.5~4410.9 | 3 | Null | 0 | 4391.0~4416.0 | 0 |
| 4165.9~4192.9 | 1 | 4410.9~4424.1 | 4 | 4166.0~4193.0 | 6.116 | Null | 0 |
| 4192.9~4211.1 | 3 | 4424.1~4462.5 | 4 | Null | 0 | 4434.0~4460.0 | 0 |
| 4211.1~4237.5 | 2 | 4462.5~4480.8 | 4 | 4211.0~4237.0 | 3.561 | Null | 0 |
| 4237.5~4255.9 | 3 | 4480.8~4506.0 | 2 | Null | 0 | 4483.0~4506.0 | 0.539 |
| 4255.9~4281.8 | 2 | 4256.0~4282.0 | 5.509 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Yang, L.; Fan, M.; Zou, Y.; Wang, W. An Unsupervised Clustering Method for Selection of the Fracturing Stage Design Based on the Gaussian Mixture Model. Processes 2022, 10, 894. https://doi.org/10.3390/pr10050894
Wang X, Yang L, Fan M, Zou Y, Wang W. An Unsupervised Clustering Method for Selection of the Fracturing Stage Design Based on the Gaussian Mixture Model. Processes. 2022; 10(5):894. https://doi.org/10.3390/pr10050894
Chicago/Turabian StyleWang, Xin, Lifeng Yang, Meng Fan, Yushi Zou, and Wenchao Wang. 2022. "An Unsupervised Clustering Method for Selection of the Fracturing Stage Design Based on the Gaussian Mixture Model" Processes 10, no. 5: 894. https://doi.org/10.3390/pr10050894
APA StyleWang, X., Yang, L., Fan, M., Zou, Y., & Wang, W. (2022). An Unsupervised Clustering Method for Selection of the Fracturing Stage Design Based on the Gaussian Mixture Model. Processes, 10(5), 894. https://doi.org/10.3390/pr10050894






