Techno-Economic Power Dispatching of Combined Heat and Power Plant Considering Prohibited Operating Zones and Valve Point Loading

Abstract

Co-generation units (i.e., combined heat and power plants—CHPs) are playing an important role in fulfilling the heat and power demand in the energy system. Due to the depletion of fossil fuels and rising carbon footprints in the environment, it is necessary to develop some alternatives as well as energy efficient operating strategies. By utilising the waste heat from thermal plants, cogeneration units help to decrease energy generation costs as well as reduce emitted pollutants. The combined heat and power economic dispatch (CHPED) operation strategy is becoming an important optimisation task in the energy efficient operation of a power system. The optimisation of CHPED is quite complex due to the dual dependence of heat and power in the cogeneration units. The valve point loading effect and prohibited operating zones of a thermal power unit make the objective function non-linear and non-convex. In this work, to address these issues more effectively, the viable operational area of the CHP and power system network losses are considered for the optimal allocation of power output and heat generation. A metaheuristic optimisation algorithm is proposed to solve the CHPED to minimize the fuel supply, thus satisfying the constraints. To handle equality and inequality constraints, an external penalty factor-based constraint handling technique is used. The success of the proposed CHPED algorithm is tested on three considered cases. In all the cases, the results show the effectiveness in terms of solution accuracy and better convergence.

1. Introduction

Smart energy networks need intelligent operation for optimally managing electrical and thermal energy requirements. The electrical and thermal energy demands can be managed through combined heat and power (CHP) plants. CHP plants are effectively contributing to the efficient operation of electrical and thermal energy networks as well as to the reduction in carbon emissions, facilitating an increasing penetration of intermittent renewable energy sources. CHPs are designed and operated to provide stable thermal and electrical energy supplies, and they are capable to overcome the load dynamics. Over the years, the most pressing challenges in electric power system operation have been the economic load dispatches from conventional power plants [1,2]. The energy efficiency of combined cycle plants is around 50–60%, since a majority of the energy is lost during the energy conversion process. The cogeneration system needs to be implemented in thermal power plants for utilizing the waste heat in a useful way to reduce the overall energy cost and increase the environmental benefits. In the utility market, cogeneration units are used as district power plants for supplying the electrical and thermal energy demands as well as to facilitate intermittent renewable energy sources. The use of a CHP system can increase fuel proficiency around 90%, reduce the operating charges by 10–40%, and decrease carbon emissions around 13–18% [3,4].

As a result, CHP economic dispatch (CHPED) can play an important role in increasing an overall system’s energy efficiency. The CHPED needs to be optimized considering different operational strategies (e.g., thermal or electrical prioritized operations, steam turbine operational limits, etc.). The CHEPD objective function becomes non-linear and non-convex due to the valve point loading (VPL) effect and prohibited operating zones (POZs) of a traditional thermal power system. Due to mutual dependency of heat and power in a cogeneration unit, the CHPED optimisation problem faces some technical challenges [5,6]. To better understanding, the feasible operating region of the cogeneration unit and transmission losses should be taken into consideration [7].

Several optimisation strategies are proposed to resolve the CHPED problem, and they are classified in two types: mathematical and meta-heuristic. Mathematical methods consist of duel and quadratic programming [8], Lagrangian relaxation [9], two-layer Lagrangian relaxation algorithm [10], branch and bound algorithms [11], etc. These methods are not sufficiently suitable to address the non-convex, discontinues, and non-differentiable fuel cost functions. Therefore, there is a significant challenge to resolve CHPED problems. As a result, new metaheuristic strategies for CHPED problem formulation can be used to solve these shortcomings. These metaheuristic algorithms demonstrate the ability to locate optimal solutions through a global search. As a result, researchers applied several swarm intelligence optimisation techniques to resolve CHPED complications and find better solutions. Initially, researchers used a metaheuristic algorithm to solve the CHPED problem on a small scale. For example, in [12], genetic algorithm with multiplier updating technique has been proposed with a penalty value to solve the CHPED issue. A stochastic model is introduced with improved particle swarm optimisation to solve CHPED in a real situation [13]. In [14], a self-adaptive real-coded GA (SARGA) based on mutation and crossover phenomena has been proposed for CHEPD, and, to address the equality and inequality constraints, a penalty mechanism has been implemented. In [15], the authors have proposed a harmony search (HS) algorithm for minimising the fuel cost function by adjusting the pitch of basic search operators. In [16], author(s) have employed the firefly algorithm (FA), influenced by the behaviour of fireflies, as they attract each other at different rates depending on the intensity of the light. Therefore, this intensity of the light is a good analogy to optimise any objective function value. In [17], the authors have suggested a genetic algorithm based on an enhanced penalty function technique; to realize an equilibrium between exploration and probability, a distance-based constraint handling approach has been included to solve the CHPED problem. In [18], the authors have proposed cuckoo search optimisation (CSO) algorithm with penalty factor to minimise the overall fuel cost function accurately. However, in [19], the bender decomposition algorithm the CHPED problem has divided into master and sub-problem. The subproblem generates the bender cuts, which has been used to update the master problem. In [20], a new variant of PSO has been proposed, where only the largest particle is chosen whose fitness is greater than the average fitness value. Whereas in [21], the hybridization of genetic algorithm and harmony search has been introduced to solve the CHPED problem. In [22], non-convexity has been replaced by convex formulations by using the two binary variables. However, in [23], the authors have proposed simulated annealing with basic bio-geography-based optimisation, which increases the convergence capability and avoids finding local minima. The main disadvantage of mentioned algorithms is that they do not consider the valve point loading effects including losses. However, differential evolution (DE) and bee colony optimisation (BCO) overcome these drawbacks [24,25]. Similarly, in [26], the authors have proposed novel self-adaptive learning method to solve the CHPED problem considering VPL, ramp rate limit, reserve constraints, and network losses.

In [27], the authors have been proposed cuckoo search algorithm (CSA) to resolve the CHPED issue. CSA is relatively easy to implement and provides better alternatives for CHPED problems due to its fewer control parameters and computational timings. In [28], the authors have used the gravity search algorithm (GSA) to explain the CHPED issue. The gravitation law of moving particles inspired GSA, which includes various physical quantities such as the gravitational constant, mass, Euclidean distance, gravitation, acceleration, and velocity. GSA gives a better solution for the CHPED problem, having minimal fuel prices by dynamic adjustment of control parameters. In [29], cuckoo optimisation has been applied as a powerful and robust solution technique for large scale units. An improved differential evolution algorithm has been proposed, which enhances the performance of basic DE with a modified repair process to handle equality constraints [30]. In [31], the authors have suggested a new optimisation method for analysing heat and power demand uncertainties using information gap decision theory and interval analysis to explain the CHPED optimisation process. In [32], a Lagrangian-relaxation-based alternative approach has used to divide the non-convex area of the CHP unit into several convex regions using the Big M method to solve the CHPED issue efficiently.

To improve system performance and accuracy, several other studies have been projected to explain the CHPED optimisation task. For example, in [33], the acceleration constants have dynamically altered to increase the optimum search and avoid premature convergence during CHPED optimisation. However, in [34], the authors have suggested an oppositional teaching learning-based (OTLBO) algorithm to improve CHP plant solution accuracy and speed of convergence. In [35], to solve CHPED effectively, the authors have suggested a crisscross optimisation algorithm in which two exploration operator crossings exist, flat and perpendicular. Whereas in [36], a real coded genetic algorithm (RCGA) through progressive transformation evolution has been applied on six benchmark systems of the CHP plant, considering VPL and network losses.

Thermal power plant’s prohibited operating zones (POZs) make the system more challenging due to the discontinuous nature of fuel supply. It increases the complexity to solve the CHPED system. To solve CHPED with POZs, only a few optimisation algorithms have been implemented. In [37,38], the author proposed group search optimisation to reduce the operating cost as well as enhance the solution accuracy of the CHP economic dispatch problem. To handle the non-convex CHPED problem, an oppositional-based group search optimisation based on guess and opposite guess has been developed [39]. The authors of [40] have suggested a heat transfer search technique that included three stages: conduction, convection, and radiation. In contrast, the authors of [41] have reported enhanced GA, employing unique crossover and mutation techniques. To recover mutation offspring and assist them in reaching a feasible range, an effective constraint handling technique has been used to resolve the CHPED issue. To address the CHPED problem with different constraints, a bio-geography-based learning particle swarm optimisation is developed, which uses migration operator to attain the best position [42]. In [43], the authors have proposed a modified PSO, where Gaussian random variables are taken to improve the global search of particles. However, in [44], a self-regulating PSO has given the higher speed of convergence, when considering VPL and POZs. Differential evolution with a dual population has been planned to solve the CHPED problem for multifuel selections of generating units [45]. In [46], differential evolution with migrating variables has been used to increase the direction of search and replace those variables that were targeted earlier. A mesh adaptive direct search algorithm has been used in CHP dispatch in [47], but it has not sufficiently covered impacts of POZs. Similarly, presented algorithms in [48,49] for CHP dispatching, POZs and VPLs have not been adequately considered for finding operations’ of CHPs.

It is required to investigate a more effective metaheuristic algorithm, which can solve a large and complex non-linear and non-convex CHPED problem. Metaheuristic algorithm can only provide the global optimum solutions. They cannot give accurate solutions. Most of the techniques explained by the different authors are complicated due to consideration of a large number of parameters. This paper focuses on the use of a simple algorithm to solve the CHPED problem, and it is based on [50]. In the considered algorithm, a random communication occurs between all the candidates throughout the iteration process. The simplicity of the considered algorithm is that there are only two design parameters such as population size and number of iterations. To address the CHPED problem more accurately, the feasible operating region of the cogeneration unit and network losses are taken into account with the objective of minimizing fuel cost. To handle equality and inequality constraints, a suitable penalty factor-based constraint handling strategy has introduced. The VPL and POZs are used for considering the feasible operating region of a CHP plant.

The CHEPD formulations have been presented in [51,52,53,54,55] and they have used in their presented soft computing techniques for CHP dispatch. The VPLs description have been provided in [56], but not covered sufficiently role of POZs. Also, some computing techniques have been described in [57,58,59,60] with CHP operations’ constraints for maintaining the heat and power balance operation within the considered energy network.

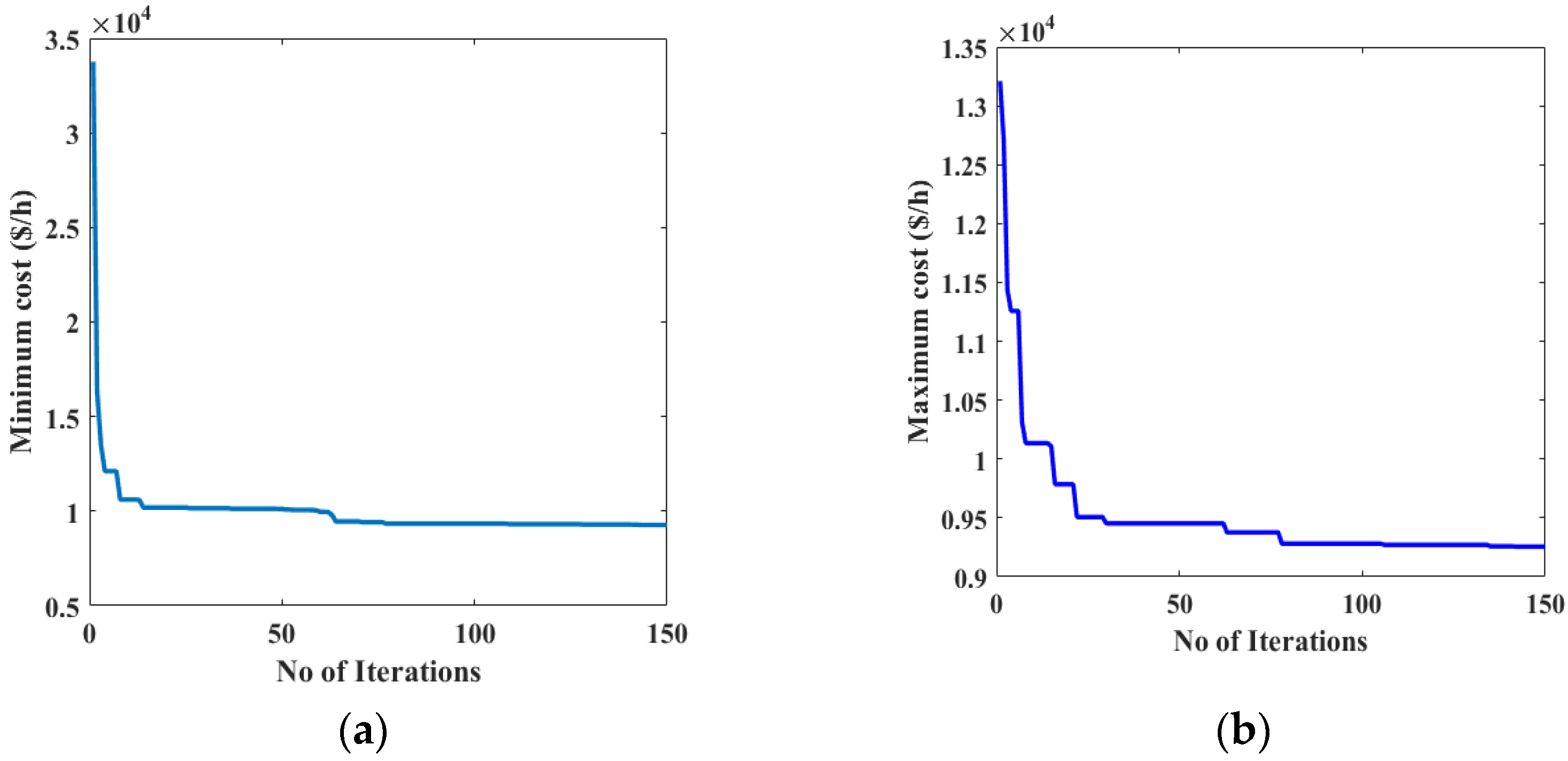
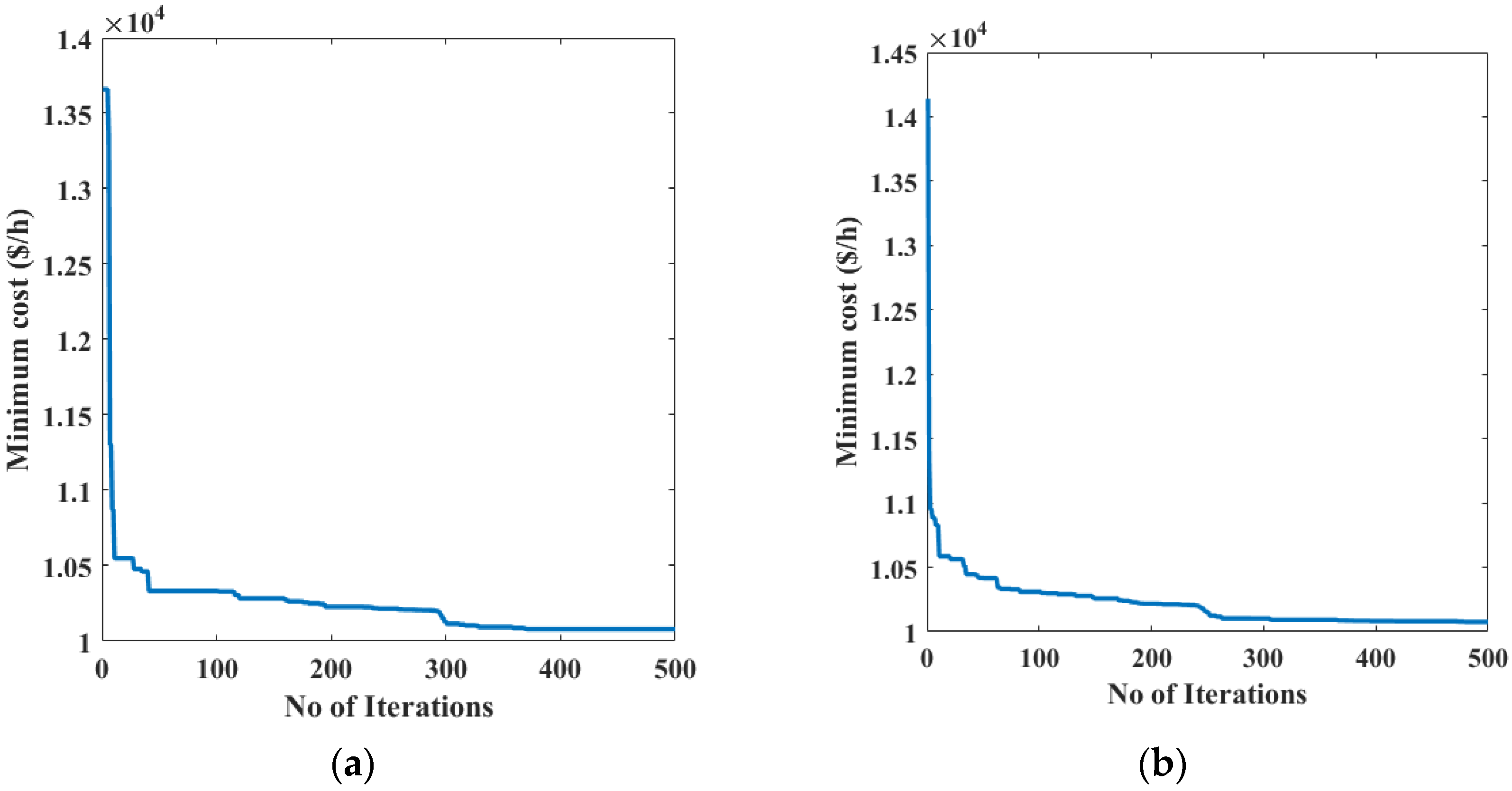
In this work, to validate the proposed algorithm, three typical test case systems, including 4-units, 7-units, and 24-units, are considered. The results of these cases are compared with the well-established algorithm to show the superiority among them. The following sections of the article are structured as: (i) Section 2 presents the mathematical modelling of the CHP economic dispatch optimisation problem; (ii) Section 3 represents the proposed algorithm; (iii) Section 4 provides the analysis of considered three cases; And (iv) finally, the conclusion and future scope of the article are given in Section 5.

2. Mathematical Modelling of CHPED

2.1. Objective Function

The main objective of the CHPED is to identify the most cost-effective way to schedule power and heat generation, to fulfil both the heat and power demand while satisfying all constraints. The mathematical equation, which is based on [18,33,56,59,60] for total operating cost function, is expressed in Equation (1).

$$\mathrm{Min} \mathrm{C} ={\displaystyle \sum }_{\mathrm{i}=1}^{{\mathrm{N}}_{\mathrm{TH}}}{\mathrm{C}}_{\mathrm{i}}({\mathrm{P}}_{\mathrm{i}}^{\mathrm{TH}})+{\displaystyle \sum }_{\mathrm{j}=1}^{{\mathrm{N}}_{\mathrm{CHP}}}{\mathrm{C}}_{\mathrm{j}}\left({\mathrm{P}}_{\mathrm{J}}^{\mathrm{CHP}},{ \mathrm{h}}_{\mathrm{j}}^{\mathrm{CHP}} \right)+{\displaystyle \sum }_{\mathrm{k}=1}^{{\mathrm{N}}_{\mathrm{H}}}{\mathrm{C}}_{\mathrm{k}}({\mathrm{P}}_{\mathrm{k}}^{\mathrm{H}}) \left(\$/\mathrm{h}\right)$$

(1)

where, C is entire operating price, ${\mathrm{C}}_{\mathrm{i}}\left({\mathrm{P}}_{\mathrm{i}}^{\mathrm{TH}}\right)$ is the fuel cost function of the $\mathrm{i}\mathrm{th}$ thermal power unit, ${\mathrm{C}}_{\mathrm{j}}\left({\mathrm{P}}_{\mathrm{J}}^{\mathrm{CHP}},{ \mathrm{h}}_{\mathrm{j}}^{\mathrm{CHP}} \right)$ is cost function of the $\mathrm{j}\mathrm{th}$ CHP unit, ${\mathrm{C}}_{\mathrm{k}}\left({\mathrm{P}}_{\mathrm{k}}^{\mathrm{H}}\right)$ is the cost function of the $\mathrm{k}\mathrm{th}$ heat-only unit, N_TH, N_CHP, N_H are the number of thermal power, cogeneration, and heat units. ${\mathrm{P}}_{\mathrm{i}}^{\mathrm{TH}}$ is the power output of the $\mathrm{i}\mathrm{th}$ conventional thermal power unit, ${\mathrm{P}}_{\mathrm{J}}^{\mathrm{CHP}}$ and ${\mathrm{h}}_{\mathrm{j}}^{\mathrm{CHP}}$ are the power and heat outputs of the $\mathrm{j}\mathrm{th}$ CHP unit, and ${\mathrm{P}}_{\mathrm{k}}^{\mathrm{H}}$ is the heat output of the kth heat unit.

The quadratic cost function (based on [18,33,56,59,60],) of the thermal power unit is expressed in Equation (2).

$${\displaystyle \sum }_{\mathrm{i}=1}^{{\mathrm{N}}_{\mathrm{TH}}}{\mathrm{C}}_{\mathrm{i}}({\mathrm{P}}_{\mathrm{i}}^{\mathrm{TH}})={\displaystyle \sum }_{\mathrm{i}=1}^{{\mathrm{N}}_{\mathrm{TH}}}[{\mathrm{a}}_{\mathrm{i}}+{\mathrm{b}}_{\mathrm{i} }{\mathrm{P}}_{\mathrm{I}}^{\mathrm{TH}}+{\mathrm{C}}_{\mathrm{i} }{\mathrm{P}}_{\mathrm{i}}^{{\mathrm{TH}}^2}] \left(\$/\mathrm{h}\right)$$

(2)

where, ${\mathrm{a}}_{\mathrm{i}},{\mathrm{b}}_{\mathrm{i}}, \mathrm{and} {\mathrm{C}}_{\mathrm{i}}$ are its cost coefficients of the thermal power unit.

Due to VPL (i.e., valve-point loading) effects, objective function becomes nonconvex, nonlinear, and discontinuous, creating several local minima. A rectified sinusoidal function is needed to include in the cost function for the accurate modelling of VPL effects [53,54,56]. The mathematical equation of cost function, including VPL, is expressed in Equation (3).

$${\displaystyle \sum }_{\mathrm{i}=1}^{{\mathrm{N}}_{\mathrm{TH}}}{\mathrm{C}}_{\mathrm{i}}({\mathrm{P}}_{\mathrm{i}}^{\mathrm{TH}})={\displaystyle \sum }_{\mathrm{i}=1}^{{\mathrm{N}}_{\mathrm{TH}}}[{\mathrm{a}}_{\mathrm{i}}+{\mathrm{b}}_{\mathrm{i} }{\mathrm{P}}_{\mathrm{I}}^{\mathrm{TH}}+{\mathrm{C}}_{\mathrm{i} }{\mathrm{P}}_{\mathrm{i}}^{{\mathrm{TH}}^2}+|{\mathrm{e}}_{\mathrm{i} }\sin \left\{{\mathrm{f}}_{\mathrm{i}}\left({\mathrm{P}}_{\mathrm{i}}^{{\mathrm{TH}}^{\min }}-{\mathrm{P}}_{\mathrm{I}}^{\mathrm{TH}}\right)\right\} |] \left(\$/\mathrm{h}\right)$$

(3)

where, e_i and f_i are the cost coefficient of the $\mathrm{i}\mathrm{th}$ unit for valve point loading in a conventional thermal power unit.

The mathematical equation of the cost function for the cogeneration unit and heat-only unit is expressed in Equations (4) and (5), and it is based on [18,33,56].

$${\displaystyle \sum }_{\mathrm{j}=1}^{{\mathrm{N}}_{\mathrm{CHP}}}{\mathrm{C}}_{\mathrm{j}}\left({\mathrm{P}}_{\mathrm{J}}^{\mathrm{CHP}},{ \mathrm{h}}_{\mathrm{j}}^{\mathrm{CHP}} \right)={\displaystyle \sum }_{\mathrm{j}=1}^{{\mathrm{N}}_{\mathrm{CHP}}}[{\mathrm{a}}_{\mathrm{j}}+{\mathrm{b}}_{\mathrm{j} }{\mathrm{P}}_{\mathrm{j}}^{\mathrm{CHP}}+{\mathrm{c}}_{\mathrm{J}}{\mathrm{P}}_{\mathrm{J}}^{{\mathrm{CHP}}^2}+{\mathrm{d}}_{\mathrm{J}}{\mathrm{h}}_{\mathrm{J}}^{\mathrm{CHP}}+{ \mathrm{e}}_{\mathrm{J}}{\mathrm{h}}_{\mathrm{J}}^{{\mathrm{CHP}}^2}+{ \mathrm{f}}_{\mathrm{j} }{\mathrm{P}}_{\mathrm{j}}^{\mathrm{CHP}}{ \mathrm{h}}_{\mathrm{j}}^{\mathrm{CHP}}] \left(\$/\mathrm{h}\right)$$

(4)

$${\displaystyle \sum }_{\mathrm{k}=1}^{{\mathrm{N}}_{\mathrm{H}}}{ \mathrm{C}}_{\mathrm{k}}\left({\mathrm{h}}_{\mathrm{k}}^{\mathrm{H}}\right)={\displaystyle \sum }_{\mathrm{k}=1}^{{\mathrm{N}}_{\mathrm{H}}}{\mathrm{a}}_{\mathrm{k}}+{\mathrm{b}}_{\mathrm{k}}{\mathrm{h}}_{\mathrm{k}}^{\mathrm{H}}+{\mathrm{c}}_{\mathrm{k} }{\mathrm{h}}_{\mathrm{k}}^{\mathrm{H}2}\left(\$/\mathrm{h}\right)$$

(5)

where, ${\mathrm{C}}_{\mathrm{j}}\left({\mathrm{P}}_{\mathrm{J}}^{\mathrm{CHP}},{ \mathrm{h}}_{\mathrm{j}}^{\mathrm{CHP}} \right)$ is the cost function of the $\mathrm{j}\mathrm{th}$ cogeneration unit; ${\mathrm{a}}_{\mathrm{j}},{\mathrm{b}}_{\mathrm{j}},{\mathrm{c}}_{\mathrm{j}},{\mathrm{d}}_{\mathrm{j}},{\mathrm{e}}_{\mathrm{j}},{\mathrm{f}}_{\mathrm{j}}$ are the cost coefficient of the $\mathrm{j}\mathrm{th}$ cogeneration unit; ${\mathrm{C}}_{\mathrm{k}}\left({\mathrm{h}}_{\mathrm{k}}^{\mathrm{H}}\right)$ is the cost of the $\mathrm{k}\mathrm{th}$ heat-only units, and ${\mathrm{a}}_{\mathrm{k}},{\mathrm{b}}_{\mathrm{k}},{ \mathrm{and} \mathrm{c}}_{\mathrm{k}}$ are the cost coefficient of the $\mathrm{k}\mathrm{th}$ heat-only unit.

2.2. Constraints

2.2.1. Power Output Balance

The entire power generation of the thermal power and cogeneration units should be equal to the total power demand. If any network losses are existing, they would be added to the power demand shown in Equation (6), based on [18,33,56].

$${\displaystyle \sum }_{\mathrm{i}=1}^{{\mathrm{N}}_{\mathrm{TH}}}{\mathrm{P}}_{\mathrm{i}}^{\mathrm{TH} }+{\displaystyle \sum }_{\mathrm{j}=1}^{{\mathrm{N}}_{\mathrm{CHP}}}{\mathrm{P}}_{\mathrm{j}}^{\mathrm{CHP}}={\mathrm{P}}_{\mathrm{d} }+{\mathrm{P}}_{\mathrm{loss} }$$

(6)

where ${\mathrm{P}}_{\mathrm{d} }$ is generated power demand, ${ \mathrm{P}}_{\mathrm{loss}}$ is transmission line losses, determined by Kron’s loss formulation [55], and it is expressed by Equation (7), based on [18,33,56].

$${\mathrm{P}}_{\mathrm{loss}}={\displaystyle \sum }_{\mathrm{i}=1}^{{\mathrm{N}}_{\mathrm{TH}}}{\displaystyle \sum }_{\mathrm{j}=1}^{{\mathrm{N}}_{\mathrm{TH}}}{\mathrm{P}}_{\mathrm{i}}^{\mathrm{TH}}{\mathrm{B}}_{\mathrm{ij}}{\mathrm{P}}_{\mathrm{j}}^{\mathrm{TH}}+{\displaystyle \sum }_{\mathrm{i}=1}^{{\mathrm{N}}_{\mathrm{TH}}}{\displaystyle \sum }_{\mathrm{j}=1}^{{\mathrm{N}}_{\mathrm{CHP}}}{\mathrm{P}}_{\mathrm{i}}^{\mathrm{TH}}{\mathrm{B}}_{\mathrm{ij}}{\mathrm{P}}_{\mathrm{j}}^{\mathrm{CHP}}+{\displaystyle \sum }_{\mathrm{i}=1}^{{\mathrm{N}}_{\mathrm{CHP}}}{\displaystyle \sum }_{\mathrm{j}=1}^{{\mathrm{N}}_{\mathrm{CHP}}}{\mathrm{P}}_{\mathrm{i}}^{\mathrm{CHP}}{\mathrm{B}}_{\mathrm{ij}}{\mathrm{P}}_{\mathrm{j}}^{\mathrm{CHP}}+{\displaystyle \sum }_{\mathrm{i}=1}^{{\mathrm{N}}_{\mathrm{TH}}}{\mathrm{P}}_{\mathrm{i}}^{\mathrm{TH}}{\mathrm{B}}_{\mathrm{oi}}+{\displaystyle \sum }_{\mathrm{j}=1}^{{\mathrm{N}}_{\mathrm{CHP}}}{\mathrm{P}}_{\mathrm{i}}^{\mathrm{CHP}}{\mathrm{B}}_{\mathrm{oi}}+{\mathrm{B}}_{\mathrm{oo}}$$

(7)

where ${\mathrm{B}}_{\mathrm{ij}},{\mathrm{B}}_{\mathrm{o}\mathrm{i}},{\mathrm{B}}_{\mathrm{oo}}$ are the B-matrix coefficient of the transmission line.

2.2.2. Heat Production Balance

The entire heat produced through the cogeneration and heat unit should be equivalent to total heat demand, expressed in Equation (8), based on [18,33,56].

$${\displaystyle \sum }_{\mathrm{j}=1}^{{\mathrm{N}}_{\mathrm{CHP}}}{\mathrm{h}}_{\mathrm{i}}^{\mathrm{CHP}}+{\displaystyle \sum }_{\mathrm{k}=1}^{{\mathrm{N}}_{\mathrm{H}}}{\mathrm{h}}_{\mathrm{k}}^{\mathrm{H}}={\mathrm{h}}_{\mathrm{d} }$$

(8)

where ${\mathrm{h}}_{\mathrm{i}}^{\mathrm{CHP}}$ is the heat output of the $\mathrm{i}\mathrm{th}$ CHP unit, ${\mathrm{h}}_{\mathrm{k}}^{\mathrm{H}}$ is the heat output of the $\mathrm{k}\mathrm{th}$ heat unit, and ${\mathrm{h}}_{\mathrm{d} }$ is heat demand.

2.2.3. Capacity Limits of Thermal Power Unit

The capacity limits of thermal power units are required and expressed in Equation (9), based on [18,33,56].

$${\mathrm{P}}_{\mathrm{i}}^{{\mathrm{TH}}^{\min } }\le {\mathrm{P}}_{\mathrm{i}}^{\mathrm{TH} }\le {\mathrm{P}}_{\mathrm{i}}^{{\mathrm{TH}}^{\max } };\mathrm{where} \mathrm{i}=1,\dots \dots ..{\mathrm{N}}_{\mathrm{TH}}$$

(9)

where ${\mathrm{P}}_{\mathrm{i}}^{{\mathrm{TH}}^{\min } }$ and ${\mathrm{P}}_{\mathrm{i}}^{{\mathrm{TH}}^{\max } }$ show the lower and higher limits of the $\mathrm{i}\mathrm{th}$ thermal power unit in MW.

2.2.4. Capacity Limits of Cogeneration Unit

The capacity limits of CHP units are required and expressed in Equations (10) and (11), and they are based on [18,33,56].

$${\mathrm{P}}_{\mathrm{j}}^{\mathrm{CHP},\min }\left({\mathrm{h}}_{\mathrm{j}}^{\mathrm{CHP}}\right)\le {\mathrm{P}}_{\mathrm{j}}^{\mathrm{CHP}}\le {\mathrm{P}}_{\mathrm{j}}^{\mathrm{CHP},\max }\left({\mathrm{h}}_{\mathrm{j}}^{\mathrm{CHP}}\right) ; \mathrm{where} \mathrm{j}=1,\dots \dots \dots {\mathrm{N}}_{\mathrm{CHP}}$$

(10)

$${\mathrm{h}}_{\mathrm{j}}^{\mathrm{CHP}, \min }\left({\mathrm{P}}_{\mathrm{j}}^{\mathrm{CHP}}\right)\le {\mathrm{h}}_{\mathrm{j}}^{\mathrm{CHP}}\le {\mathrm{h}}_{\mathrm{j}}^{\mathrm{CHP}, \max }\left({\mathrm{P}}_{\mathrm{j}}^{\mathrm{CHP}}\right) ; \mathrm{where} \mathrm{j}=1,\dots \dots \dots {\mathrm{N}}_{\mathrm{CHP} }$$

(11)

where ${\mathrm{P}}_{\mathrm{j}}^{\mathrm{CHP}, \min }\left({\mathrm{h}}_{\mathrm{j}}^{\mathrm{CHP}}\right)$ and ${\mathrm{P}}_{\mathrm{j}}^{\mathrm{CHP}, \max }\left({\mathrm{h}}_{\mathrm{j}}^{\mathrm{CHP}}\right)$ are the lower and higher limits of the power generation of the $\mathrm{j}\mathrm{th}$ cogeneration unit in MW, and the function of heat generation given by ${\mathrm{h}}_{\mathrm{j}}^{\mathrm{CHP}}$, ${\mathrm{h}}_{\mathrm{j}}^{\mathrm{CHP}, \min }\left({\mathrm{P}}_{\mathrm{j}}^{\mathrm{CHP}}\right),$ and ${\mathrm{h}}_{\mathrm{j}}^{\mathrm{CHP}, \max }\left({\mathrm{P}}_{\mathrm{j}}^{\mathrm{CHP}}\right)$ are the min and max heat produced by the $\mathrm{j}\mathrm{th}$ CHP unit in MWth and the function of generated power given by ${\mathrm{P}}_{\mathrm{j}}^{\mathrm{CHP}}$.

2.2.5. Capacity Limits of Heat Init

The capacity limits of only heat units are required and expressed in Equation (12), based on [18,33,56].

$${\mathrm{h}}_{\mathrm{k}}^{\mathrm{H},\min }\le {\mathrm{h}}_{\mathrm{k}}^{\mathrm{H}}\le {\mathrm{h}}_{\mathrm{k}}^{\mathrm{H},\max } ; \mathrm{where} \mathrm{k}=1,\dots \dots \dots ,{\mathrm{h}}_{\mathrm{k} }$$

(12)

where, ${\mathrm{h}}_{\mathrm{k}}^{\mathrm{H},\min }$ and ${\mathrm{h}}_{\mathrm{k}}^{\mathrm{H},\max }$ show the minimum and maximum limit of the heat unit k, expressed in MWth.

2.2.6. Constraint of Prohibited Operating Zones (POZs)

Due to some problems in the machinery or its components, for example pumps or boilers, practical generating units include the forbidden operating zone. The input-output characteristic of a device having prohibited operation zones (POZs) is discontinuous [53,54]. The prohibited zones of thermal power units are expressed by Equation (13), based on [18,33,53,54,55,56].

$$\{\begin{array}{c}{\mathrm{P}}_{\mathrm{i}}^{{\mathrm{TH}}^{\min } }\le {\mathrm{P}}_{\mathrm{i}}^{\mathrm{TH} }\le {\mathrm{P}}_{\mathrm{i},1}^{{\mathrm{TH}}^{\mathrm{L}} }\\ {\mathrm{P}}_{\mathrm{i},\mathrm{m}-1}^{{\mathrm{TH}}^{\mathrm{U}} }\le {\mathrm{P}}_{\mathrm{i}}^{\mathrm{TH} }\le {\mathrm{P}}_{\mathrm{i},\mathrm{m}}^{{\mathrm{TH}}^{\mathrm{L}} }, \mathrm{where} \mathrm{m}=2,3,\dots \dots \dots \dots {\mathrm{Z}}_{\mathrm{i}}^{ } \\ {\mathrm{P}}_{\mathrm{i},\mathrm{zi}}^{{\mathrm{TH}}^{\mathrm{u}} }\le {\mathrm{P}}_{\mathrm{i}}^{\mathrm{TH} }\le {\mathrm{P}}_{\mathrm{i}}^{{\mathrm{TH}}^{\max } }\end{array}$$

(13)

where, ${\mathrm{P}}_{\mathrm{i},\mathrm{m}}^{{\mathrm{TH}}^{\mathrm{L}} }$ and ${\mathrm{P}}_{\mathrm{i},\mathrm{m}}^{{\mathrm{TH}}^{\mathrm{U}} }$ are the minimum and maximum limit of the $\mathrm{m}\mathrm{th}$ POZ of the $\mathrm{i}\mathrm{th}$ conventional thermal power unit. ${\mathrm{Z}}_{\mathrm{i}}^{ }$ represents the quantity of POZs for the $\mathrm{i}\mathrm{th}$ generation unit.

2.3. Constraint Handling Technique

For single-objective functions, handling equality and inequality restrictions are accomplished via external penalty parameters, which punish infeasible solutions throughout the iterative process of transforming the constrained CHPED issue into an unconstrained problem. After multiple trials, the right values of the static penalty factors must be carefully adjusted in order to achieve better optimal solutions, while adhering to the limitations [18]. This method is also known as the sequence of unconstrained minimization techniques. Since different constraints have different orders of magnitude [18,33,56], it is more appropriate to normalise each constraint; for example, the $\mathrm{i}\mathrm{th}$ equality constraint ${\mathrm{G}}_{\mathrm{i}}^{\prime }\left(\mathrm{Y}\right)-{\mathsf{\theta }}_{\mathrm{i}}\le 0$ and the $\mathrm{j}\mathrm{th}$ inequality constraint ${\mathrm{H}}_{\mathrm{j}}^{\prime }\left(\mathrm{Y}\right)-{\mathsf{\eta }}_{\mathrm{j}}\le 0$ can be normalised to ${\mathrm{G}}_{\mathrm{i}}\left(\mathrm{Y}\right)={\mathrm{G}}_{\mathrm{i}}^{\prime }\left(\mathrm{Y}\right)/{\mathsf{\theta }}_{\mathrm{i}}-1=0$ and ${\mathrm{H}}_{\mathrm{j}}\left(\mathrm{y}\right)={\mathrm{H}}_{\mathrm{j}}^{\prime }\left(\mathrm{Y}\right)/{\mathsf{\eta }}_{\mathrm{j}}-1 \le 0$. The optimisation issue can be written in compact form after normalising the constraints, where ${\mathsf{\theta }}_{\mathrm{i}}$ and ${\mathsf{\eta }}_{\mathrm{j}}$ are constants, and Y = (Y₁, Y₂, …………., Y_N) represent n number of state variables. The optimisation problem can be written in compact form after normalising the constraints in the following manner:

Min C (Y₁, Y₂, …………., Y_N)

Subject to constraints

$${\mathrm{G}}_{\mathrm{i}}({\mathrm{Y}}_1,{\mathrm{Y}}_2,\dots \dots \dots \dots ,{\mathrm{Y}}_{\mathrm{N}})=0 ; \mathrm{where} \mathrm{i}=1,2,\dots \dots \dots \dots \mathrm{Ne}$$

$${\mathrm{H}}_{\mathrm{j}}({\mathrm{Y}}_1,{\mathrm{Y}}_2,\dots \dots \dots \dots \dots ,{\mathrm{Y}}_{\mathrm{N}}) \le 0 ;\mathrm{where} \mathrm{j}=1,2,\dots \dots \dots \dots \mathrm{Nie}$$

$${\mathrm{Y}}_{\mathrm{k}}^{\min }\le {\mathrm{Y}}_{\mathrm{k}}\le {\mathrm{Y}}_{\mathrm{k}}^{\max } ; \mathrm{where} \mathrm{k}=1,\dots \dots \dots \mathrm{N}$$

where N, $\mathrm{Ne}$, $\mathrm{Nie}$ are the number of unknown state variables, equality constraints, and inequality constraints, respectively [18,33,53,54,55,56]. The modified objective function is expressed in Equation (14).

$$\mathrm{F}=\mathrm{Min} \mathrm{C}\left({\mathrm{Y}}_1,{\mathrm{Y}}_2,\dots ,{ \mathrm{Y}}_{\mathrm{N}}\right)+\mathrm{R} ({\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{Ne}}|{\mathrm{G} }_{\mathrm{i}}({\mathrm{Y} }_1,{\mathrm{Y} }_2,\dots \dots \dots ,{\mathrm{Y} }_{\mathrm{N}}){|}^2)+{\displaystyle \sum }_{\mathrm{j}=1}^{\mathrm{Nie}}|\mathrm{Max}\left(0,{ \mathrm{H} }_{\mathrm{j}}({\mathrm{Y} }_1,{\mathrm{Y} }_2,\dots \dots \dots ,{\mathrm{Y} }_{\mathrm{N}}\right)){|}^2)$$

(14)

where R is a suitable penalty value, and its suitable value is estimated after several trials to get the best solution.

3. Optimisation Algorithm

The issues (discussed in Section 2) need to be addressed more effectively. For the viable operational area of the CHP, power system network losses or an optimal allocation of power output and heat generation is required. In this work, a metaheuristic optimisation algorithm is proposed to solve the CHPED to minimise the fuel supply, thus satisfying the constraints. To handle equality and inequality constraints, an external penalty factor-based constraint handling technique is used. This paper focuses on use of a simple algorithm to solve the CHPED problem and it is based on [50]. The programming technique is outlined in the steps, given below. The algorithm flow chart is shown in the Figure 1.

Step 1. Design the fitness function: Formulate the mathematical equation as a fitness function f(x) to be minimised.

Step 2. Initialization of system input parameters: Input the CHPED designing variable for the power and heat units, electrical power demand and heat demand, population size, and termination criteria. Consider the number of design variables, and population size and candidate solution are set to be m and n, respectively.

Step 3. Select the required solutions: Find the minimum value of fuel cost F(X) of CHP economic dispatch for the best particle as F(X)_best and the maximum value of F(X) as F(X)_worst throughout the algorithm step. Identify the corresponding power and heat generation ${\mathrm{X}}_{\mathrm{j},\mathrm{k},\mathrm{i}}$ of the CHP plant, according to the minimum and maximum values of fuel cost. Where, ${\mathrm{X}}_{\mathrm{j},\mathrm{k},\mathrm{i}} \mathrm{is}$ the value of the $\mathrm{j}\mathrm{th}$ design variable during the $\mathrm{i}\mathrm{th}$ iteration for the $\mathrm{k}\mathrm{th}$ particle.

Step 4. Modify the solutions: Modify the solution based on the minimum and maximum fuel cost of the CHP system and the random interaction between the generated values of power and heat. Modifying the power and heat generation values, marked by the following Equation (15), which is based on [50]:

$${\mathrm{X}}_{\mathrm{j},\mathrm{k},\mathrm{i}}^{\prime }={\mathrm{X}}_{\mathrm{j}.\mathrm{k}.\mathrm{i} }+{\mathrm{r}}_{1,\mathrm{j},\mathrm{i}}\left({\mathrm{X}}_{\mathrm{j},\mathrm{best},\mathrm{i} }-\left|{\mathrm{X}}_{\mathrm{j},\mathrm{worst},\mathrm{i}}\right|\right)+{\mathrm{r}}_{2,\mathrm{j},\mathrm{i}} \left(\left|{ \mathrm{X}}_{\mathrm{j},\mathrm{k},\mathrm{i} }{ \mathrm{or} \mathrm{X}}_{\mathrm{j},\mathrm{l},\mathrm{i} }\left|-\right|{ \mathrm{X}}_{\mathrm{j},\mathrm{l},\mathrm{i} }{ \mathrm{or} \mathrm{X}}_{\mathrm{j},\mathrm{k},\mathrm{i} }\right|\right)$$

(15)

where ${\mathrm{X}}_{\mathrm{j},\mathrm{best},\mathrm{i} }$ is the best particle value for variable j during the $\mathrm{i}\mathrm{th}$ iteration, ${\mathrm{X}}_{\mathrm{j},\mathrm{worst},\mathrm{i}}$ is the worst particle value for variable j during the $\mathrm{i}\mathrm{th}$ iteration, ${\mathrm{X}}_{\mathrm{j},\mathrm{k},\mathrm{i}}^{\prime }$ is the updated value of ${\mathrm{X}}_{\mathrm{j}.\mathrm{k}.\mathrm{i} }$, and ${\mathrm{r}}_{1,\mathrm{j},\mathrm{i}}$ and ${\mathrm{r}}_{2,\mathrm{j},\mathrm{i}}$ are two random numbers for the $\mathrm{j}\mathrm{th}$ variable during the $\mathrm{i}\mathrm{th}$ iteration between (0,1).

${\mathrm{X}}_{\mathrm{j},\mathrm{k},\mathrm{i} }{ \mathrm{or} \mathrm{X}}_{\mathrm{j},\mathrm{l},\mathrm{i} }$ shows any particle result k is related with any randomly chosen particle solution i, and information is replaced based on their fitness value. If the objective function value of the $\mathrm{k}\mathrm{th}$ particle is better than the objective function value of the $\mathrm{i}\mathrm{th}$ solution, then ${\mathrm{X}}_{\mathrm{j},\mathrm{k},\mathrm{i} }{ \mathrm{or} \mathrm{X}}_{\mathrm{j},\mathrm{l},\mathrm{i} }$ is replaced with ${\mathrm{X}}_{\mathrm{j},\mathrm{k},\mathrm{i} }$. However, if the objective function value of the $\mathrm{i}\mathrm{th}$ solution is better than the objective function value of the $\mathrm{k}\mathrm{th}$ solution, then ${\mathrm{X}}_{\mathrm{j},\mathrm{l},\mathrm{i} }{ \mathrm{or} \mathrm{X}}_{\mathrm{j},\mathrm{k},\mathrm{i} }$ is replaced with ${\mathrm{X}}_{\mathrm{j},\mathrm{l},\mathrm{i} }$. Similarly, if the objective function value of the $\mathrm{k}\mathrm{th}$ solution is better than the objective function value of the $\mathrm{i}\mathrm{th}$ solution, then ${\mathrm{X}}_{\mathrm{j},\mathrm{l},\mathrm{i} }{ \mathrm{or} \mathrm{X}}_{\mathrm{j},\mathrm{k},\mathrm{i} }$ becomes ${\mathrm{X}}_{\mathrm{j},\mathrm{l},\mathrm{i} }$. On the other hand, if the objective function value of the $\mathrm{i}\mathrm{th}$ solution is better than the objective function value of the $\mathrm{k}\mathrm{th}$ solution, then “${\mathrm{X}}_{\mathrm{j},\mathrm{l},\mathrm{i} }{ \mathrm{or} \mathrm{X}}_{\mathrm{j},\mathrm{k},\mathrm{i}}$” becomes ${\mathrm{X}}_{\mathrm{j},\mathrm{k},\mathrm{i} }$.

Step 5. Report the required solutions: As a check, if the new value of fuel cost F(X)_new is corresponding to the modified value of power and heat generation ${\mathrm{X}}_{\mathrm{j},\mathrm{k},\mathrm{i}}^{\prime }$, then take the modified value in place of the previous value, otherwise, keep the previous value. Repeat the same process until the termination criteria has been satisfied and the optimum solution has been found out.

4. Results and Discussion

CHP units have their own feasible operating zones (FORs), and they are required for finding the operational points of them, considering the combination of power and thermal supplies. In this work, the four types of FOR of CHP units are considered, based on [18], and they are depicted in Figure 2. Figure 2a shows the FORs of a type-1 CHP unit. It includes the second unit of test system 1, the fifth unit of test system 2, and the fourteenth and sixteenth units of test system 3. Figure 2b shows the FORs of the type-2 CHP unit, which includes the third unit of test system 1, the sixth unit of test system 2, and the fifteenth and seventeenth units of test system 3. Figure 2c shows the FORs of the type-3 CHP unit, and it considers the eighteenth unit of test system 3. Figure 2d shows the FORs of type-4 CHP, and it includes the nineteenth unit of test system 3. Due to the random results of the stochastic algorithm, the effective solutions are receiving over 50 independent trials. The statistical simulation results of minimum cost, maximum cost, mean cost, and computational time are analysed. To prove the utility of the proposed optimisation technique, based on [50], for the CHPED issue, three case systems have been considered, and the results have been compared with other techniques available in the literature.

4.1. Test System 1

Test system 1 includes four units having one thermal power unit, two cogeneration units, and a heat unit. Test structure data has taken from [33]. The power demand ${\mathrm{P}}_{\mathrm{d} }$ and heat demand ${\mathrm{h}}_{\mathrm{d} }$ are 200 MW and 115 MWth, respectively. The two cases are used for analysing the proposed CHPED technique.

4.1.1. Case 1

The VPL effects have been considered in Case 1. The population size and maximum number of iterations are set to 50 and 150.

Table 1. Best allocation of power output and heat generation for case 1 of test system 1.

P1	0	P3	40	H3	75.2427
P2	159.9358	H2	39.8401	H4	0

shows the best allocation of power and heat generation from the proposed CHPED technique.

Table 2. Statistical analysis for case 1 of test system 1.

Algorithm	GA-PF [17]	FA [16]	MADS-LHS [47]	MADS-PSO [47]	MADS-DACE [47]	CSA [27]	TVAC-PSO [33]	MCSA [27]	GWO [37]	IGA-NCM [41]	Proposed CHPED Algorithm
Maximum cost ($/h)	-	-	10,005.3805	9997.6576	9260.4317	9303.183	-	-	-	9257.9014	9352.1458
Mean cost ($/h)	-	-	9547.9151	9551.277	9257.5148	9258.168	-	-	-	9257.1553	9295.0657
Minimum cost ($/h)	9267.28	9257.10	9277.1311	9301.357	9257.07	9257.07	9257.07	9257.07	9257.07	9257.075	9256.0075
Computational time (s)	-	-	7.0422	7.5594	2.3078	0.59	1.33	1.35	1.082	2.66	1.846

summarises the statistical study in terms of minimum, mean, maximum, and computational time, including those of GA-PF [17], FA [16], MADS-LHS [47], MADS-PSO [47], MADS-DACE [47], CSA [27], TVAC-PSO [33], MCSA [27], GWO [37], and IGA-NCM [41]. It is observed from Table 2, after applying the proposed CHPED algorithm, that the minimum cost obtained is 9256.0075 ($/h). Table 2 shows that the cost is the lowest of all the other approaches. The minimum fuel cost convergence curve found using the suggested CHPED algorithm is shown in Figure 3a.

4.1.2. Case 2

Both the VPL effects and POZs of conventional thermal power units are considered in Case 2. The test case 2 data for prohibited operating zones have been taken from [41]. Using proposed CHEPD algorithm, the results are analysed. The population size and maximum number of iterations are set to 50 and 150, respectively. The power output and heat generation towards minimum fuel cost is summarised in

Table 3. Best allocation of power output and heat generation for case 2 of test system 1.

P1	0	P3	40.2763	H3	74.3513
P2	159.7143	H2	40.6534	H4	0

. The minimum cost, mean cost, maximum cost, and computational time are shown in

Table 4. Statistical analysis for case 2 of test system 1.

Algorithm	GSO [38]	OGSO [39]	DEGM [51]	DE [51]	Proposed CHPED Algorithm
Maximum cost ($/h)	9292.6631	9290.7735	9290.5810	9292.4286	9477.2720
Mean cost ($/h)	9291.7326	9290.6026	9290.5331	9291.6290	9324.8554
Minimum cost ($/h)	9291.2717	9290.5459	9290.4804	9291.1375	9262.8770
Computational time (s)	1.5273	1.7309	1.2403	1.2173	1.988

, including those of GSO [38], OGSO [39], DEGM [51], and DE [51]. It is clear from Table 4, after applying the proposed CHEPD algorithm, that the obtained minimum cost is 9262.8770 ($/h), which is less when compared to other reported results. Figure 3b shows the fuel cost convergence characteristic.

4.2. Test System 2

Test system 2 includes four thermal power unit, two cogeneration units, and a heat unit. Moreover, transmission network losses are considered in test system 2. Test system 2 data have been taken from [33]. The power demand and heat demand are 600 MW and 150 MWth. Two cases are selected for test system 2, and the considered transmission line loss matrix coefficients are based on [56].

4.2.1. Case 1

The VPL effect of thermal power unit is considered in case 1. The population size and maximum number of iterations are set to 50 and 500.

Table 5. Best allocation of power output and heat generation for case 1 of test system 2.

P1	47.4057	P3	112.6816	P5	91.9780	H5	27.6816	H7	49.2903
P2	98.7887	P4	209.1485	P6	40	H6	72.9333

shows the best values of power and heat generation obtained from the proposed CHPED algorithm.

Table 6. Statistical analysis for case 1 of test system 2.

Algorithm	BCO [25]	TVAC-PSO [33]	TLBO [34]	OTLBO [34]	AIS [48]	EP [48]	PSO [48]	CSA [27]	OGSO [39]	IGA-NCM [41]	Proposed CHEPD Algorithm
Maximum cost ($/h)	-	-	10,133.6130	10,106.8314	-	-	-	12,602.920	10,097.3801	10,108.6241	10,107.6677
Mean cost ($/h)	-	-	10,114.1539	10,099.4057	-	-	-	10,878.882	10,095.8455	10,108.0481	10,090.9149
Minimum cost ($/h)	10,317	10,100.3164	10,094.8384	10,094.3529	10,355	10,390	10,613	10,177.6	10,094.2407	10,107.9071	10,079.2151
Computational time (s)	5.1563	3.25	2.86	3.06	5.2956	5.3274	-	1.2	2.5681	7.69	8.023

summarises the statistical summary in terms of minimum cost, mean cost, maximum cost, and computational time, including those of BCO [25], TVAC-PSO [33], TLBO [34], OTLBO [34], AIS [48], EP [48], PSO [48], CSA [27], OGSO [39], and IGA-NCM [41]. It is observed from Table 6, after applying the proposed CHPED algorithm, the minimum cost obtained is 10,079.2151 ($/h). Table 6, shows that the cost is the lowest of all the other approaches. The minimum fuel cost convergence curve is depicted in Figure 4a.

4.2.2. Case 2

Both the VPL effect and POZs of the thermal power unit are considered in Case 2. The test case data of POZs have been taken from [41]. The population size and maximum number of iterations are set to 50 and 500. The power output and heat generation towards minimum fuel cost is summarised in

Table 7. Best allocation of power output and heat generation for case 2 of test system 2.

P1	47.0388	P3	112.5798	P5	92.0439	H5	28.7711	H7	46.0278
P2	98.5481	P4	209.8352	P6	40.0004	H6	75.1990

.

Table 8. Statistical analysis for case 2 of test system 2.

Algorithm	GSO [38]	OGSO [39]	IGA-NCM [41]	BLPSO [42]	Proposed CHEPD Algorithm
Maximum cost ($/h)	10,103.7203	10,102.3585	10,116.3042	10,102.1864	10,080.2645
Mean cost ($/h)	10,102.2168	10,101.8566	10,115.0872	10,101.5626	10,077.4625
Minimum cost ($/h)	10,101.3483	10,101.3160	10,114.8410	10,101.3079	10,075.3202
Computational time (s)	2.5903	2.8073	8.17	6.18	9.536

compares the statistical results of minimum cost, mean cost, maximum cost, and computational time of the proposed CHPED algorithm and other algorithms, including those of GSO [38], OGSO [39], IGA-NCM [41], and BLPSO [42]. It is clear from Table 8, after applying the proposed CHPED algorithm, the minimum cost obtained is 10,075.3202 ($/h), which is less when compared to other reported results. The minimum fuel cost convergence curve is shown in Figure 4b.

4.3. Test System 3

Test system 3 is a combination of twenty-four thermal power units, six cogeneration units, and five heat units. The test data have been taken from [33]. The power demand ${\mathrm{P}}_{\mathrm{d} }$ and heat demand ${\mathrm{h}}_{\mathrm{d} }$ are 2350 MW and 1250 MWth. The following two cases are considered.

4.3.1. Case 1

The VPL effects of thermal power units are considered. Here, the population size and the maximum number of iterations are 50 and 1000.

Table 9. Best allocation of power output and heat generation for case 1 of test system 3.

P1	628.3130	P11	40.0243	h15	81.0654
P2	359.9973	P12	55.0398	h16	105.4930
P3	0.0045	P13	55.0067	h17	77.3073
P4	159.7227	P14	81.0460	h18	40.5253
P5	109.8682	P15	40.0038	h19	20.7161
P6	60.0000	P16	81.0009	h20	459.2565
P7	159.7445	P17	40.0119	h21	59.9983
P8	159.7982	P18	10.0000	h22	59.9780
P9	159.6977	P19	35.0186	h23	120.0000
P10	115.7025	h14	105.6650	h24	119.9832

shows the best allocation of power and heat generation.

Table 10. Statistical analysis for case 1 of test system 3.

Algorithm	CPSO [33]	TVAC-PSO [33]	TLBO [34]	GSA [28]	GSO [49]	Proposed CHEPD Algorithm
Maximum cost ($/h)	60,076.6903	58,359.5520	58,038.5273	-	58,453.9227	57,864.0758
Mean cost ($/h)	59,853.478	58,198.3106	58,014.3685	-	58,217.0254	57,862.6973
Minimum cost ($/h)	59,736.2635	58,122.7460	58,006.9992	58,121.8640	58,122.7068	57,861.1978
Computational time (s)	53.36	52.25	5.67	26.483	54.31	10.469

gives the statistical analysis in terms of the minimum cost, mean cost, maximum cost, and computational time obtained from the proposed CHPED algorithm, including those of CPSO [33], TVAC-PSO [33], TLBO [34], GSA [28], and GSO [49]. Figure 5a depicts the minimum fuel cost convergence curve obtained from the proposed CHPED algorithm hm. Table 10 shows that the minimum fuel cost 57,861.1978 ($/h), obtained from the proposed CHPED algorithm, is minimal when compared to other algorithms.

4.3.2. Case 2

The VPL and POZs of the thermal power unit are considered in case 2. The test case data of the prohibited operating zones have been taken from [41]. The population size and maximum number of iterations are set to 50 and 1000. The power output and heat generation towards minimum fuel cost is summarised in

Table 11. Best allocation of power output and heat generation for case 2 of test system 3.

P1	628.9019	P11	77.3854	h15	79.2938
P2	359.7078	P12	55.0000	h16	105.8367
P3	0.0210	P13	118.2993	h17	78.4357
P4	109.8662	P14	81.0225	h18	40.8931
P5	159.7324	P15	40.0000	h19	21.0661
P6	60.0000	P16	81.0000	h20	454.0547
P7	109.8561	P17	40.0293	h21	59.9989
P8	109.9098	P18	10.0000	h22	59.9983
P9	159.7088	P19	35.0000	h23	120.0000
P10	114.5164	h14	109.9887	h24	120.0000

. The minimum cost, mean cost, maximum cost, and computational time is shown in

Table 12. Statistical analysis for case 2 of test system 3.

Algorithm	GSO [38]	OGSO [39]	CSO-PPS [52]	HTS [40]	Proposed CHPED Algorithm
Maximum cost ($/h)	58,119.1635	57,953.3522	57,945	57,960.73	57,897.8129
Mean cost ($/h)	58,114.6060	57,946.0934	57,940	57,959.92	57,896.7356
Minimum cost ($/h)	58,110.090	57,942.5577	57,935	57,959.41	57,895.6050
Computational time (s)	5.8017	5.9869	4.43	6.6877	11.271

, including those of GSO [38], OGSO [39], CCO-PPS [52], and HTS [40]. It is clear from Table 12, after applying the proposed CHPED algorithm, that the minimum cost found is 57,895.6050 ($/h), which is less when compared to other reported results. The minimum fuel cost convergence curve obtained from the proposed CHPED algorithm is shown in Figure 5b.

The presented methodology can be used in a power system network integrated with thermal power plants, CHP plants, and heat supply units, for providing heat and power demand within the considered network. The CHPED algorithm can be implemented in coordinating the economic dispatch of power and heat from the power plants, considering the technical constraints as well as transmission network’s line loss coefficients.

5. Conclusions and Future Scope

In this work, the combined heat and power economic dispatches of thermal and power supplies, from the combinations of power units, have used the proposed CHPED optimisation algorithm. The proposed CHPED algorithm is used to find thermal and power dispatches, considering the valve point loading effects as well as prohibited operating zones of conventional thermal power units, feasible operating region of cogeneration units, and transmission network losses. The considered three case systems have been analysed for the CHPED, and the obtained results have demonstrated the effectiveness of the proposed algorithm. The obtained results of three case systems are compared with the well-established algorithms, and it is observed that the proposed CHPED algorithm provides the best results for the economic dispatch of thermal and power supplies from the combinations of different power units. To achieve the feasible optimum results in the CHPED problem, all equality and inequality constraints are handled by the exterior static penalty method considered in the proposed CHEPD algorithm. Through considered for different test systems and case studies, it is observed that the presented method for CHEPD is suitable for small- and large-scale power units. The research work presented in this article is limited to combined heat and power dispatching that consider the VPL and POZs of a thermal power unit.

Therefore, the presented work can be further enhanced for integrating the combined heat and power units with intermittent renewable energy resources, for the optimum dispatching of power to maintain secure and reliable energy supplies. Moreover, the other constraints of thermal power units, such as ramp rate limit and reserve constraints, can be included for making operation more reliable and stable.