A Novel Point-to-Point Trajectory Planning Algorithm for Industrial Robots Based on a Locally Asymmetrical Jerk Motion Profile
Abstract
:1. Introduction
2. Proposed Trajectory Model
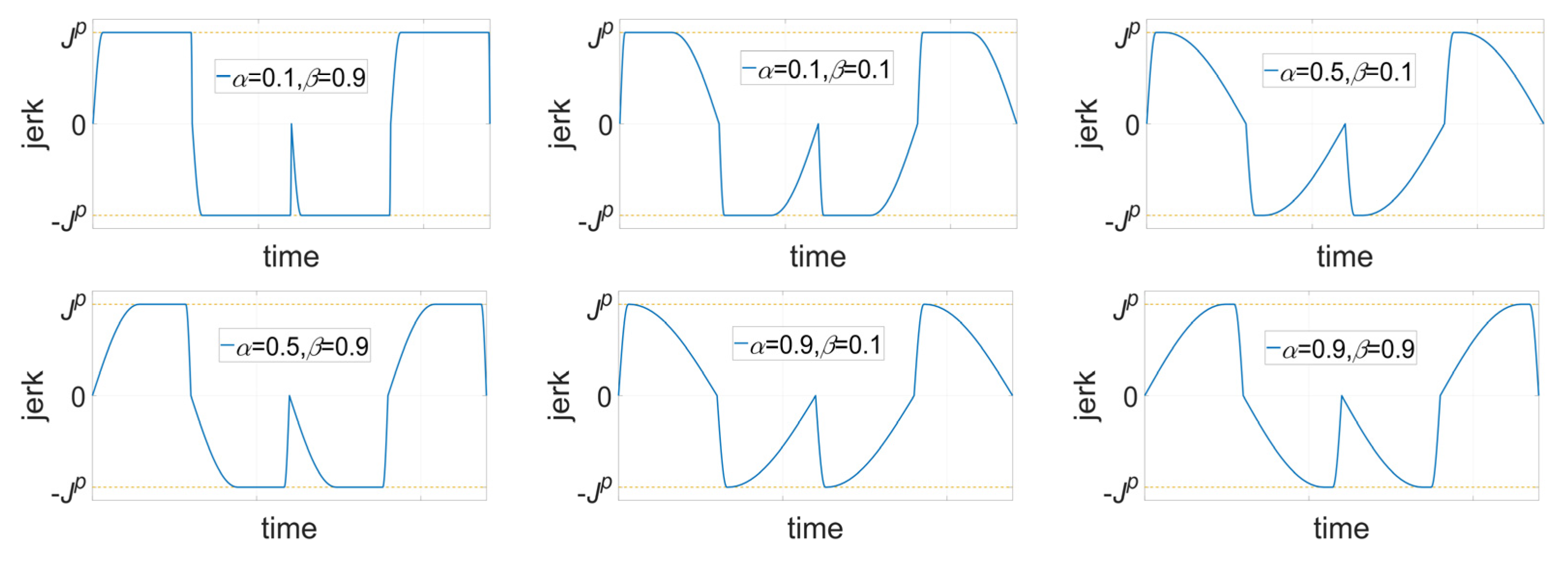
2.1. Locally Asymmetrical Jerk Motion Profile
2.2. Shape Coefficients
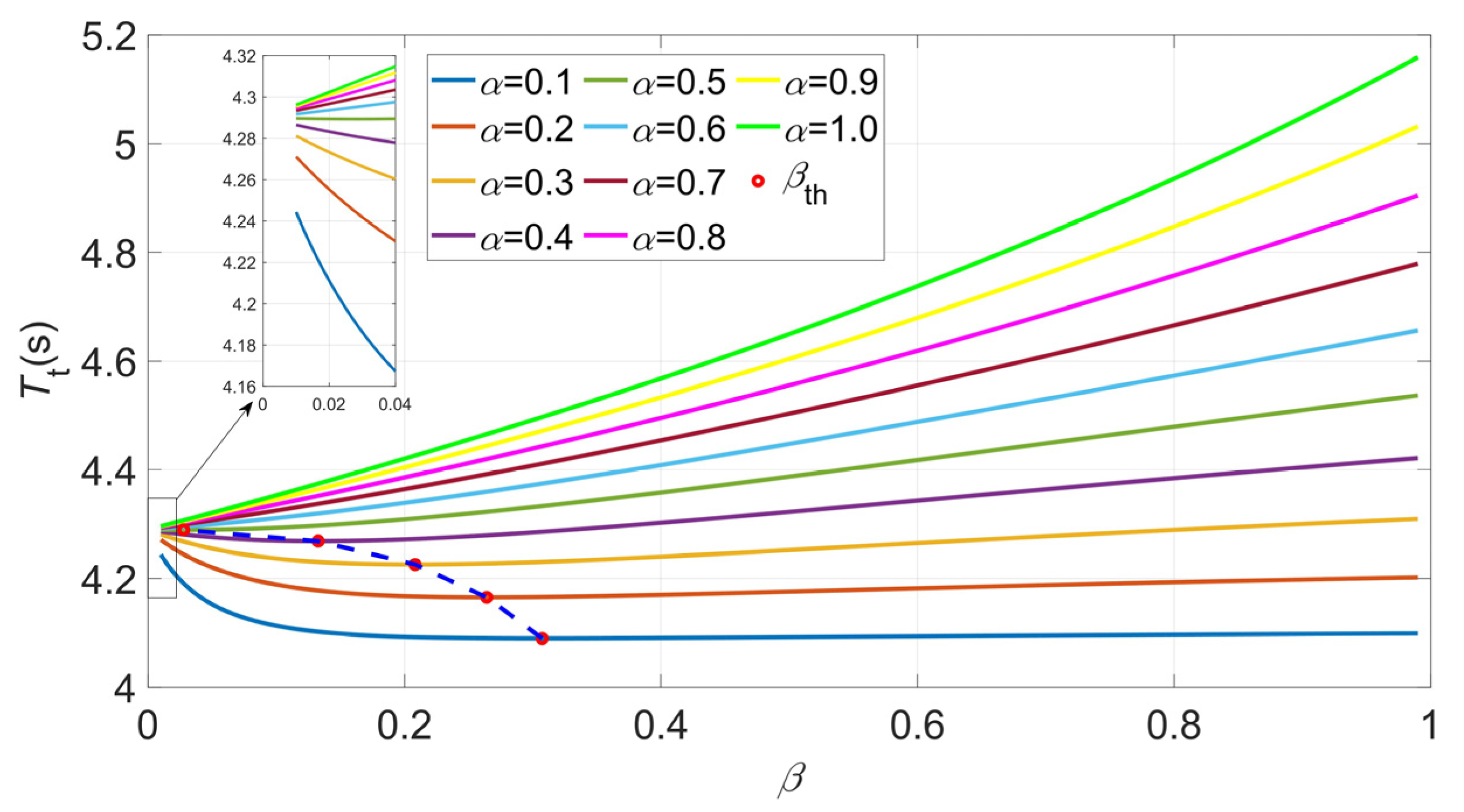
3. Optimal Problem Formulation
4. Point-to-Point Trajectory Planning Algorithm
| Algorithm 1: PTPA |
| Input:θinitial, θgoal, Vmax, Amax, Jmax, α and β |
| Output:Ω |
| Start |
| Generate the displacements Df = θgoal − θinitial |
| Compute the thresholds Vamax, Damax, Dvmax1, Dvmax2 using Equations (18), (19), (23) and (26) |
| forg = 1 to n do |
| ifVgamax < Vgmax |
| if Dgf > Dgvmax1 |
| Compute T1,g, T2,g, T3,g, T4, g and T8,g according to Type I |
| else if Dgamax < Dgf ≤ Dgvmax1 |
| T8,g = 0 |
| Compute T1,g, T2,g, T3,g and T4,g according to Type II |
| end if |
| else ifDgf > Dgvmax2 |
| T4,g = 0 |
| Compute T1,g, T2,g, T3,g and T8,g according to Type III |
| else |
| T4,g = 0, T8,g = 0 |
| Compute T1,g, T2,g and T3,g according to Type IV |
| end if |
| end for |
| Generate the execution time τ using Equation (28) |
| Compute the scaling coefficient k using Equation (29) |
| Synchronize the motion profiles of each joint trajectory |
| end |
4.1. Minimum Time
4.2. Synchronization of Motion Profiles
5. Results
5.1. Numerical Simulation
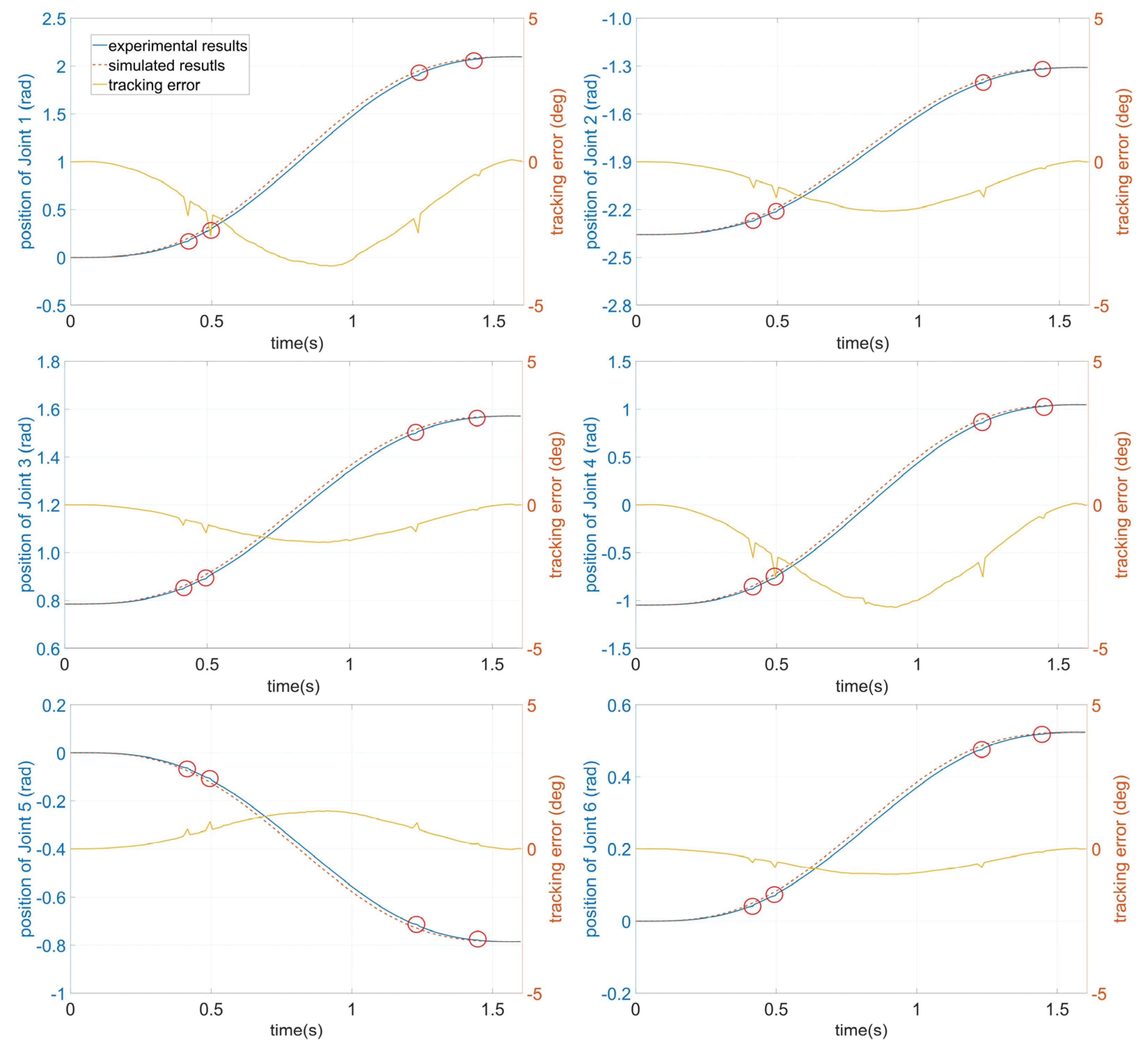
5.2. Experimental Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Yin, G.T.; Zhu, Z.H.; Gong, H.; Lu, Z.F.; Yong, H.S.; Liu, L.; He, W. Flexible punching system using industrial robots for automotive panels. Robot. Comput. Integr. Manuf. 2018, 52, 92–99. [Google Scholar] [CrossRef]
- Lin, W.Y.; Ren, X.Y.; Zhou, T.T.; Cheng, X.J.; Tong, M.S. A novel robust algorithm for position and orientation detection based on cascaded deep neural network. Neurocomputing 2018, 308, 138–146. [Google Scholar] [CrossRef]
- Çakır, M.; Hekimoğlu, B.; Deniz, C.M. Path Planning for Industrial Robot Milling Applications, Procedia Comput. Sci. 2019, 158, 27–36. [Google Scholar] [CrossRef]
- Malhan, R.K.; Shembekar, A.V.; Kabir, A.M.; Bhatt, P.M.; Shah, B.; Zanio, S.; Nutt, S.; Gupta, S.K. Automated planning for robotic layup of composite prepreg. Robot. Comput. Integr. Manuf. 2021, 67, 102020. [Google Scholar] [CrossRef]
- Brossog, M.; Bornschlegl, M.; Franke, J. Reducing the energy consumption of industrial robots in manufacturing systems. Int. J. Adv. Manuf. Technol. 2015, 78, 1315–1328. [Google Scholar] [CrossRef]
- Rubioa, F.; Llopis-Albert, C.; Valero, F.; Suñer, J.L. Industrial robot efficient trajectory generation without collision through the evolution of the optimal trajectory. Robot. Auton. Syst. 2016, 86, 106–112. [Google Scholar] [CrossRef] [Green Version]
- Perumaal, S.S.; Jawahar, N. Automated trajectory planner of industrial robot for pick-and-place Task. Int. J. Adv. Robot. Syst. 2013, 10, 100. [Google Scholar] [CrossRef]
- Moghaddam, M.; Nof, S.Y. Parallelism of Pick-and-Place operations by multi-gripper robotic arms. Robot. Comput. Integr. Manuf. 2016, 42, 135–146. [Google Scholar] [CrossRef]
- Duque, D.A.; Prietob, F.A.; Hoyos, J.G. Trajectory generation for robotic assembly operations using learning by demonstration. Robot. Comput. Integr. Manuf. 2019, 57, 292–302. [Google Scholar] [CrossRef]
- Ha, C.W.; Lee, D. Analysis of embedded prefilters in motion profiles. IEEE Trans. Ind. Electron. 2018, 65, 1481–1489. [Google Scholar] [CrossRef]
- Gasparetto, A.; Zanotto, V. A new method for smooth trajectory planning of robot manipulators. Mech. Mach. Theory 2007, 42, 455–471. [Google Scholar] [CrossRef]
- Biagiotti, L.; Melchiorri, C. Trajectory Planning for Automatic Machines and Robots; Springer: Berlin/Heidelberg, Germany, 2008; pp. 15–50. [Google Scholar]
- Jond, H.B.; Nabiyev, V.V.; Benveniste, R. Trajectory planning using high-order polynomials under acceleration constraint. J. Opt. Ind. Eng. 2017, 21, 1–6. [Google Scholar] [CrossRef]
- Boryga, M.; Graboś, A. Planning of manipulator motion trajectory with higher-degree polynomials use. Mech. Mach. Theory 2009, 44, 1400–1419. [Google Scholar] [CrossRef]
- Fang, Y.; Hu, J.; Qi, J.; Liu, W.H.; Wang, W.M.; Peng, Y.H. Planning trigonometric frequency central pattern generator trajectory for cyclic tasks of robot manipulators. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 4014–4031. [Google Scholar] [CrossRef]
- Rymansaib, Z.; Iravani, P.; Sahinkaya, M.N. Exponential trajectory generation for point to point motions. In Proceedings of the 2013 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Wollongong, Australia, 9–12 July 2013. [Google Scholar] [CrossRef]
- Müller-Karger, C.M.; Mirena, A.L.G.; López, J. Hyperbolic trajectories for pick-and-place operations to elude obstacles. IEEE Trans. Robot. Autom. 2000, 16, 294–300. [Google Scholar] [CrossRef]
- Savsani, P.; Jhala, R.L.; Savsani, V.J. Optimized trajectory planning of a robotic arm using teaching learning based optimization (TLBO) and artificial bee colony (ABC) optimization techniques. In Proceedings of the 2013 IEEE International Systems Conference (SysCon), Orlando, FL, USA, 15–18 April 2013. [Google Scholar] [CrossRef]
- Kazem, B.I.; Mahdi, A.I.; Oudah, A.T. Motion Planning for a Robot Arm by Using Genetic Algorithm. Jjmie 2008, 2, 131–136. [Google Scholar]
- Yue, S.G.; Henrich, D.; Xu, W.L.; Tso, S.K. Point-to-Point Trajectory Planning of Flexible Redundant Robot Manipulators Using Genetic Algorithms. Robotica 2002, 20, 269–280. [Google Scholar] [CrossRef] [Green Version]
- Bureerat, S.; Pholdee, N.; Radpukdee, T.; Jaroenapibal, P. Self-adaptive MRPBIL-DE for 6D robot multi-objective trajectory planning. Expert Syst. Appl. 2019, 136, 133–144. [Google Scholar] [CrossRef]
- Chettibi, T.; Lehtihet, H.E.; Haddad, M.; Hanchi, S. Minimum cost trajectory planning for industrial robots. Eur. J. Mech. A/Solids 2004, 23, 703–715. [Google Scholar] [CrossRef]
- Huang, J.S.; Hu, P.F.; Wu, K.Y.; Zeng, M. Optimal time-jerk trajectory planning for industrial robots. Mech. Mach. Theory 2018, 121, 530–544. [Google Scholar] [CrossRef]
- Yoon, H.; Chung, S.; Kang, H.; Hwang, M. Trapezoidal motion profile to suppress residual vibration of flexible object moved by robot. Electronics 2019, 8, 30. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.D.; Luo, X.; Xu, S.J.; Luo, Q.S.; Han, B.L.; Liang, G.H.; Jia, Y. A planning method for multi-axis point-to-point synchronization based on time constraints. IEEE Access 2020, 8, 85575–85604. [Google Scholar] [CrossRef]
- Nguyen, K.D.; Ng, T.C.; Chen, I.M. On algorithms for planning S-curve motion profiles. Int. J. Adv. Robot. Syst. 2008, 5, 99–106. [Google Scholar] [CrossRef]
- Wang, H.; Wang, H.; Huang, J.H.; Zhao, B.; Quan, L. Smooth point-to-point trajectory planning for industrial robots with kinematical constraints based on high-order polynomial curve. Mech. Mach. Theory 2019, 139, 284–293. [Google Scholar] [CrossRef]
- Lee, D.; Ha, C.W. Optimization process for polynomial motion profiles to achieve fast movement with low vibration. IEEE Trans. Control Syst. Technol. 2020, 28, 1892–1901. [Google Scholar] [CrossRef]
- Perumaal, S.; Jawahar, N. Synchronized trigonometric S-curve trajectory for jerk-bounded time-optimal pick and place operation. Int. J. Robot. Autom. 2012, 27, 385–395. [Google Scholar] [CrossRef]
- Valente, A.; Baraldo, S.; Carpanzano, E. Smooth trajectory generation for industrial robots performing high precision assembly processes. CIRP Ann. 2017, 66, 17–20. [Google Scholar] [CrossRef]
- Fang, Y.; Qi, J.; Hu, J.; Wang, W.; Peng, Y.H. An approach for jerk-continuous trajectory generation of robotic manipulators with kinematical constraints. Mech. Mach. Theory 2020, 153, 103957. [Google Scholar] [CrossRef]
- Fang, Y.; Liu, W.; Shao, Q.; Qi, J.; Peng, Y.H. Smooth and time-optimal s-curve trajectory planning for automated robots and machines. Mech. Mach. Theory 2019, 137, 127–153. [Google Scholar] [CrossRef]
- Lee, A.Y.; Choi, Y. Smooth trajectory planning methods using physical limits. J. Mech. Eng. Sci. 2015, 229, 2127–2143. [Google Scholar] [CrossRef]
- Bailón, W.P.; Cardiel, E.B.; Campos, I.J.; Paz, A.R. Mechanical energy optimization in trajectory planning for six DOF robot manipulators based on eighth-degree polynomial functions and a genetic algorithm. In Proceedings of the 2010 7th International Conference on Electrical Engineering Computing Science and Automatic Control, Tuxtla Gutierrez, Mexico, 8–10 September 2010. [Google Scholar] [CrossRef]
- Fung, R.F.; Cheng, Y.H. Trajectory planning based on minimum absolute input energy for an LCD glass-handling robot. Appl. Math. Model. 2014, 38, 2837–2847. [Google Scholar] [CrossRef]
- Macfarlane, S.; Croft, E.A. Jerk-Bounded Manipulator Trajectory Planning: Design for Real-Time Applications. IEEE Trans. Robot. Autom. 2003, 19, 42–52. [Google Scholar] [CrossRef] [Green Version]
- Kucuk, S. Optimal trajectory generation algorithm for serial and parallel manipulators. Robot. Comput. Integr. Manuf. 2017, 48, 219–232. [Google Scholar] [CrossRef]





| Joint No. | |||||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| Position | Initial position (rad) | 0 | −π/6 | 0 | −π/3 | 0 | 0 |
| Goal position (rad) | 2π/3 | π/6 | π/4 | π/3 | −π/4 | π/6 | |
| Kinematic limits | Velocity (rad/s) | 8 | 10 | 10 | 5 | 5 | 5 |
| Acceleration (rad/s2) | 10 | 12 | 12 | 8 | 8 | 8 | |
| Jerk (rad/s3) | 30 | 40 | 40 | 20 | 20 | 20 | |
| Work | Trajectory Model | Performance Measure | |
|---|---|---|---|
| Ex. Time (s) | Max. Jerk (rad/s3) | ||
| Chettibi et al. [22] | Cubic polynomial | 2.675 | 30.56 (joint 2) |
| Perumaal et al. [29] | 3-segment sine jerk (sync acc/dec) | 2.5133 | 6.63 (joint 1, 4) |
| Valente et al. [30] | 3-segment sine jerk (async acc/dec) | 1.7395 | 20 (joint 4) |
| Fang et al. [32] | 15-segment sigmoid jerk | 1.8760 (Smax = 150rad/s4) | 20.3 (joint 1) |
| Fang et al. [31] | Symmetrical 15-segment sine jerk | 1.5309 (α = 0.1) 1.6414 (α = 0.5) 1.7396 (α = 1) | 20 (joint 1, 4) 20 (joint 1, 4) 20 (joint 1, 4) |
| Present | Locally asymmetrical 15-segment sine jerk | 1.5301 (α = 0.1, β = 0.3) 1.6062 (α = 0.5, β = 0.1) 1.6286 (α = 1, β = 0.1) | 20 (joint 1, 4) 20 (joint 1, 4) 20 (joint 1, 4) |
| Different Phases | Test task 1 | Contrastive Task 2 | ||
|---|---|---|---|---|
| Valente et al. [30] | Present (α = 0.5, β = 0.1) | Valente et al. [30] | Present (α = 0.5, β = 0.1) | |
| AP (s) | 0.87 | 0.80 | 0.90 | 0.69 |
| CVP (s) | 0.00 | 0.00 | 0.38 | 0.59 |
| DP (s) | 0.87 | 0.80 | 0.90 | 0.69 |
| Total (s) | 1.74 | 1.60 | 2.18 | 1.97 |
| PR (%) | - | 8.05 | - | 9.63 |
| Degradation Mode | Work | Performance Measure | |
|---|---|---|---|
| Ex. Time (s) | Max. Jerk (rad/s3) | ||
| Degraded J4, jerk limit 20→5 rad/s3 | Valente et al. [30] | 2.7613 | 5 (joint 4) |
| Fang et al. [31] (α = 0.5) | 2.6056 | 5 (joints 1, 4) | |
| Present (α = 0.5, β = 0.1) | 2.5497 | 5 (joints 1, 4) | |
| Degraded J3, acc. limit 12→1 rad/s2 | Valente et al. [30] | 2.5066 | 6.6843 (joints 1, 4) |
| Fang et al. [31] (α = 0.5) | 1.8058 | 40 (joint 3) | |
| Present (α = 0.5, β = 0.1) | 1.8023 | 40 (joint 3) | |
| Degraded J1, vel. limit 8→0.5 rad/s | Valente et al. [30] | 4.5124 | 30 (joint 1) |
| Fang et al. [31] (α = 0.5) | 4.4854 | 30 (joint 1) | |
| Present (α = 0.5, β = 0.1) | 4.4759 | 30 (joint 1) | |
| Error | Joint 1 | Joint 2 | Joint 3 | Joint 4 | Joint 5 | Joint 6 |
|---|---|---|---|---|---|---|
| Max. abs. error (deg) | 2.96 | 1.45 | 1.08 | 2.90 | 1.10 | 0.73 |
| Terminal error (deg) | 3.96 × 10−2 | −7.35 × 10−3 | 3.02 × 10−3 | 8.40 × 10−3 | 4.11 × 10−3 | −4.19 × 10−3 |
| Terminal error variance | 1.94 × 10−6 | 2.02 × 10−6 | 6.54 × 10−7 | 1.71 × 10−6 | 3.84 × 10−7 | 1.56 × 10−7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Z.; Chen, J.; Bao, T.; Wang, J.; Zhang, L.; Xu, F. A Novel Point-to-Point Trajectory Planning Algorithm for Industrial Robots Based on a Locally Asymmetrical Jerk Motion Profile. Processes 2022, 10, 728. https://doi.org/10.3390/pr10040728
Wu Z, Chen J, Bao T, Wang J, Zhang L, Xu F. A Novel Point-to-Point Trajectory Planning Algorithm for Industrial Robots Based on a Locally Asymmetrical Jerk Motion Profile. Processes. 2022; 10(4):728. https://doi.org/10.3390/pr10040728
Chicago/Turabian StyleWu, Zhijun, Jiaoliao Chen, Tingting Bao, Jiacai Wang, Libin Zhang, and Fang Xu. 2022. "A Novel Point-to-Point Trajectory Planning Algorithm for Industrial Robots Based on a Locally Asymmetrical Jerk Motion Profile" Processes 10, no. 4: 728. https://doi.org/10.3390/pr10040728
APA StyleWu, Z., Chen, J., Bao, T., Wang, J., Zhang, L., & Xu, F. (2022). A Novel Point-to-Point Trajectory Planning Algorithm for Industrial Robots Based on a Locally Asymmetrical Jerk Motion Profile. Processes, 10(4), 728. https://doi.org/10.3390/pr10040728





