Abstract
This paper reviews the current research status of rolling bearing fault diagnosis technology for railway vehicles. Several domains are covered, including vibration fault diagnosis, acoustic signal fault diagnosis, and temperature prediction diagnosis methods on train rolling bearing test principles and related research. The application scenarios, system diagnosis accuracies, and model structures of various studies in the literature are also compared and analyzed. Furthermore, the main technical points to be improved and the analysis of the possible research directions are proposed, which provide new research ideas for subsequent fault diagnosis methods and system innovation research and development.
1. Introduction
Highlights:
- The mainstream methods and combinations for the vibration signal are analyzed.
- The wayside acoustic diagnosis approaches with features are reviewed.
- Temperature forecasting methods with spatial analysis are displayed.
- The future directions and challenges of railway bearings are discussed.
With the development of the railway industry, the railway passenger and freight volume maintained a continuous growth trend. Based on the speed increase of railway vehicles and the construction of the transportation networks, various types of trains kept the high-frequency operation, which has brought increasingly prominent operational safety issues [1]. As one of the most important components in the train bogie machinery equipment, the rolling bearings have the function of bearing and transmitting loads, whose categories mainly include axle box bearings, traction motor bearings, and gearbox bearings. These types of bearings are operated in a complex environment with a variety of loads and abrasions, which are also components with an intensely high damage rate in rotating machinery, and the costs and accuracy requirements are relatively high [2,3]. Therefore, it is meaningful to investigate the performance of rolling bearings on railway vehicles.
Although the rolling bearing fault detection of railway vehicle traction system can be classified into the category of fault detection of mechanical system, there are obvious differences between them, mainly as follows: (a) the traditional mechanical fault diagnosis systems are normally fixed and aimed at a single fault system, while the railway vehicles need accurate fault information, and, more importantly, the future trends of major faults and information should be transmitted to the driver [4,5]. (b) The operating conditions of the traditional mechanical system are quite stable, while the running state of the bearing of the railway vehicles varies greatly with the operating speed and railway line conditions, and the coupling effect between the rail and the vehicles cannot be ignored [6,7]. (c) The traditional mechanical systems present no relative motion tracks, while the tracks of railway vehicles vary with the locations and time of operation. Therefore, the vibration and sound signals of the rolling bearing when running at variable speed contain abundant characteristic information of rail transit vehicles than the operation in constant speed [8,9]. Figure 1 displays the axial and radial load distribution on the axles slew bearing in electric locomotives.

Figure 1.
The axial and radial loads on the axles slew bearing in electric locomotives.
In the situation of variable speed, heavy load, and various complex operation and climatic conditions, the defects such as wear, corrosion, and cracks, will cause the loss of rotation accuracy of the bearing, increase the vibration and generate the noise and rotational resistance, which lead to the failure of the entire wheel-rail mechanical system, and, more seriously, cause major vehicle safety accidents [10,11,12]. Under the faulty condition, the internal vibration and friction of the bearing will raise the generated heat, resulting in a higher temperature than the temperature fluctuation range of the normal bearing [13,14]. Moreover, the sound signal emitted by the running of the faulty bearings also contains a wealth of status information. The identification and diagnosis technology of the above faults can effectively ensure the safe operation of the train transmission system while improving the reliability and economic benefits of the system, and reducing the accident rate [15].
For the incipient detection of bearings, condition monitoring and prognosis methods could effectively monitor failures and predict remaining life to offer accurate evaluation of mechanical systems [16,17]. When the abnormality can be detected timely and effectively in the incipient failure stage, a catastrophic accident caused by the failure to the later stage can be avoided [18,19]. The major types of the incipient faults diagnosis methods can be divided into data-based and model-based methods [20]. Due to the large amount of historical data for fault detection, the computing costs of the data-based methods cannot be ignored. On the contrary, the model-based methods also present excellent performance by the geometrical systematical descriptions. Based on different systems and signals, the open-loop and closed-loop methods should be analyzed and compared to choose the appropriate approaches [20]. The features of nonlinearity and non-stationary variations in the data will be arduous for diagnosis that the incipient fault diagnosis approaches for nonlinear non-Gaussian closed-loop systems under noisy environment are still worth further investigation [21]. In the fault diagnosis application of railway vehicles, the physical modeling is complicated due to the different influences of complex climatic and environmental factors around various railway lines on vehicles [22,23]. In addition, with the large amount of data generated by the long-term operation of the trains, it is intensely convenient to use the algorithm combination to analyze the train bearing status based on the data, and the evaluation standards for vehicles operation on different lines can also be relatively consistent [24].
The research experience has proved that fault diagnosis can extend the operating life of the equipment and reduce the cost of regular maintenance before the secondary damage or major damage to the equipment [25,26]. The different types of faults could reflect the different aspects of the faulty components [27,28,29]. The review mainly introduces various related tests and algorithms from the aspects of vibration, acoustic signal fault diagnosis, and temperature prediction diagnosis, which are widely utilized in rolling bearing research and the application of railway vehicles. The evaluation and comparison to the characteristics of various diagnosis methods are also given. Ultimately, combined with the application status, the future development directions and challenges of the bearing fault diagnosis methods are summarized.
2. Fault Diagnosis of the Vibration Signals on Train Bearings
2.1. The Vibration Signals of Railway Vehicle Bearings
With the continuous increase of the running speed, the complicated structure, and the changing driving status of railway vehicles, the fault diagnosis methods of vibration systems present obvious differences to the general mechanical vibration fault detection methods [30]. The traditional mechanical vibration fault diagnosis system is aiming at a single fault system with quite stable operating conditions, while railway vehicles should predict feasible failures and feedback information to the drivers with the rail line conditions [31]. Based on the above analysis of the particularity of the vibration of railway vehicles, it can be seen that the rolling bearings of railway vehicles possess nonlinear and nonstationary specialties, which require suitable approaches to support the investigation [32,33].
The vibration signals research is a common method in the fault diagnosis of train bearings. A large amount of signal data is collected through sensors and analyzed to obtain corresponding systematic fault information [34]. The process mainly includes the collection of fault information, the analysis of nonlinear and nonstationary information, and status recognition [35,36]. The failure information of train components can be obtained by measuring or building a vibration test bench, as shown in Figure 2. The damage to the surface of the bearing components can cause shock pulse force, in which the information is generally weak in energy [37]. The vibration signal collected under the operation status usually contains other interference signals, so that the target fault signals can be easily submerged inside [38]. As a consequence, the methods to explore the extraction of fault feature information and status recognition are of great significance to the fault diagnosis of the train bearings [39].
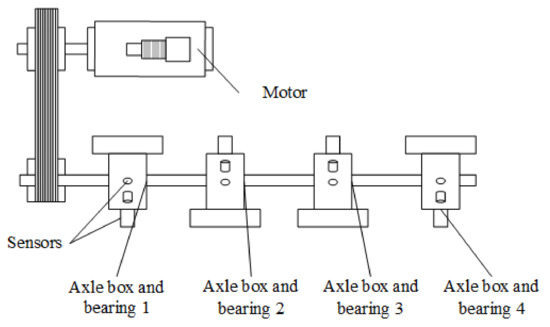
Figure 2.
Schematic diagram of the test bench.
In response to the above-mentioned research requirements, the researchers recently applied various fault identification methods for the collected nonlinear and nonstationary bearing vibration signals and established corresponding fault diagnosis models for analysis based on actual on-board bearings. Žvokelj et al. proposed the multiscale kernel principal component analysis (MSKPCA) to process the vibration signals, which is more suitable for acquiring complex multiscale non-linear information with different time-frequency features [40]. In another research, the multivariate independent component analysis (ICA) was also used to deal with complex large-scale and widely dynamic signals in slewing bearing systems, providing the effectiveness in changeable operating and background conditions [41]. Shao et al. designed a tracking depth wavelet autoencoder (TDWAE) method, in which the Gaussian wavelet function was used as the activation function to integrate multiple wavelet autoencoder and an adaptive tracking learning algorithm could further improve the diagnostic performance [42]. Compared with the traditional methods, the hybrid model could reach an accuracy of over 98%. Zhao et al. employed improved a harmonic product spectrum (IHPS) to explore and test multiple modulation sources submerged in the vibration signals, which could extract fault-related pulse characteristics, eliminate the impact caused by non-faulty modulation, and accurately determine the best resonance band where the fault pulse is most pronounced [43]. Cheng et al. utilized an improved minimum entropy deconvolution method to optimize the performance of the filter to enhance the pulse component of the fault signal in the train rolling bearings [44]. Caesarendra et al. proposed a study on the time-series feature prediction based on the fuzzy inference system (PANFIS), which was regarded as a data-driven methods [45]. The prediction performance has been proved by experiments with benchmark algorithms. Yang et al. established a multi-objective optimized wavelet filter to adaptively extract the fault characteristics of locomotive wheel-set bearings [46]. The model performed multi-objective optimization of wavelet parameters and designed a multi-objective fitness function. The Kurtosis can effectively find transient components and their positions in the frequency domain from species containing strong noise signals, thereby accurately identifying the fault characteristics of rolling bearings and effectively diagnosing faults [47]. Liu et al. applied the adaptive correlated kurtogram (ACK) to handle the analysis of wheel-bearings, which would conclude the resonant frequency bands and keep the special periodic impulses by correlated kurtosis to improve the effectiveness of feature information from identifying frequency [48]. Since the vibration response signal of the bearing has significant non-stationarity, it can be regarded as a cyclostationary signal. Based on the theoretical survey on cyclostationary signal, Feng and Chu studied the method of bearing fault diagnosis by cyclostationary analysis, and the validity of the method was verified by experiments [49].
The rapid development of artificial intelligence (AI) in recent years has brought new research algorithms and practical application tools to fault diagnosis technology [50,51]. Combining the characteristics of traffic machinery big data and the advantages of artificial intelligence learning, many researchers applied artificial intelligence classification algorithms for fault analysis and diagnosis that the nonlinear and nonstationary vibration signals could be deeply analyzed and the deep changing trend of the raw datasets could be better presented. For predictive maintenance in engineering applications, the users will construct the corresponding fault diagnosis model by the actual research object, and then modify the model through the vibration classification. The commonly used algorithms in train bearing fault diagnosis models are data decomposition, feature extraction, optimization integration algorithms, etc. The rest of this section will mainly analyze and discuss the application of these algorithms.
2.2. Application of Data Decomposition Algorithms
At present, to raise the diagnosis accuracy of the non-stationary and non-linear train bearing vibration signals, the data decomposition algorithms are commonly used for preprocessing, then the obtained feature vector sets will be decomposed into training and test sample sets, and the classification algorithms are employed for identification [52]. Normal data decomposition methods in the fault diagnosis of train rolling bearings are wavelet transform (WT), wavelet packet decomposition (WPD), empirical mode decomposition (EMD), ensemble empirical mode decomposition (EEMD), variational mode decomposition (VMD), empirical wavelet transform (EWT), etc. [53,54,55,56,57,58]. In comparison with wavelet decomposition, wavelet packet decomposition can resolve the low-frequency part of the signal and the high-frequency part as the secondary decomposition, so they have relatively stronger signal analysis capabilities [59]. Zhuo et al. chose wavelet packets to denoise and extract signal features, and the results were considered as sample inputs. The backpropagation neural network (BPNN) was applied as the classifier, in which feedforward multilayer network structure was employed to transmit information forward and to feedback the network error for the diagnosis result [60,61]. Wang et al. applied WPD to decompose the vibration signal of the axle box bearing into multiple frequency bands [62]. The frequency band will be extracted with the largest energy factor and reconstructed as a time-domain signal. The complexity of the reconstructed signal was regarded as the feature vector and input to the support vector machine model for identification, which was firstly proposed by Vapnik [63].
EMD is based on the adaptive decomposition of the signals, which decomposes the signals into the sum of the basic mode components (IMF) [64]. EMD could effectively decompose the nonlinear and non-stationary signals of rail vehicles, and perform feature extraction [65]. Li et al. developed a fault feature extraction method combining wavelet denoising and EMD for the vibration signal of axle gearbox bearings [66]. The denoised vibration signals were firstly decomposed by using the EMD algorithm, and then the obtained basic mode components were selected by the correlation coefficient method to eliminate the error information. Finally, the BPNN was used for fault identification, and the accuracy rate was over 90%, whereas EMD also has the problem of modal aliasing, and the extraction of fault feature vectors is not sufficiently thorough. EEMD adds the white noise signal to the original signal and then decomposes it. The noise will be neutralized interactively, and the final result can be achieved based on retaining more information [67,68]. Li et al. presented the EEMD to replace EMD and combine the SVM as the hybrid framework [69]. The sub-sequence weights were assigned through the correlation coefficients between the multi-sensor vibration signals and the trained SVM was utilized as a classifier for bearing fault diagnosis. The specific model calculation steps are described in Figure 3. Figure 4 shows the typical waveforms in the time domain of original signals and decomposed IMF components by the EEMD decomposing algorithm. The decomposed IMFs could be later applied as the input for the classifier in the hybrid structure.
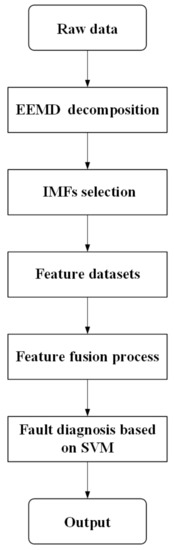
Figure 3.
Main steps of the proposed method in [69].
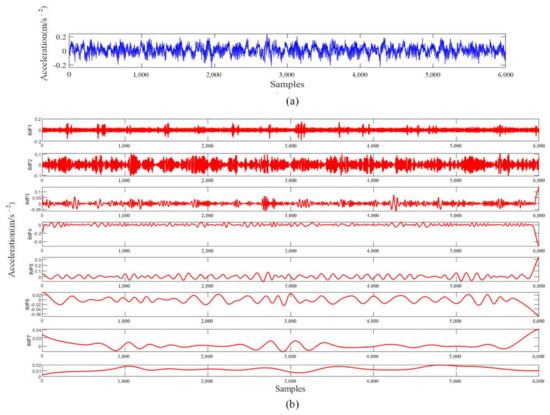
Figure 4.
(a) the original fault signals and (b) the first 8 IMF components after EEMD.
Unlike EMD-based methods, VMD can solve the problems of end effects and modal component aliasing, reduce the non-stationarity of complex original data, and outcome relatively stable sub-sequences with different frequency scales [70]. Huang et al. applied the scale-space representation and binary clustering and Jiang et al. used the IMF evaluation index (SIEI) based on the conjoint analysis of relatedness and kurtosis to improve VMD, both of which demonstrated that the results were better than traditional EMD, EEMD, and VMD [71,72]. The EWT method combines the classic wavelet with the EMD decomposition, which is quite suitable to process the non-stationary vibration signals [73]. Cao et al. proposed EWT for vibration signal analysis and fault diagnosis of wheel bearings, the results fully verified the effectiveness of EWT under different failure conditions [74]. Deng and Liu created a new self-adaptive frequency window EWT method to extract weak fault information for wheelset bearing with strong background noise [75]. The proposed model can not only suppress the complex background noise interference, but also enhance the capacity to extract weak fault features.
The application of the decomposition methods could greatly reduce the non-stationary of the bearing vibration series and improve the classification accuracy of the hybrid models. The bearing vibration series have a large number of fluctuations by the high and low-frequency data, which makes it arduous to learn the features completely. The experiment results prove the effectiveness of the decomposition algorithm on improving the nonlinearity and volatility and selecting the subseries with abundant information in the hybrid modeling.
2.3. Application of Feature Extraction and Machine Learning Methods
The datasets in the train bearings are normally collected from on-board sensors or through simulating the operation speed of the train that the bearings could be set under the normal rotation speed. These datasets usually contain abundant rich bearing vibration information, but there are also requirements for deep information extraction and noise reduction to improve the accuracy of incipient fault classification and identification [76,77]. The machine learning algorithms are popular in data classification with feature extraction methods that these types of techniques could extract meaningful features from collected data. Saki et al. used the discrete Fourier transform (DFT) for time-frequency conversion and trained the least square support vector machine (LSSVM) for the fault identification [78]. The cyclic correntropy spectrum (CCES) can process the train bearing fault signals in impulsive noise background [79]. Li et al. constructed a hybrid diagnosis model with the vibration signals from axle box bearing based on symmetric alpha-stable (SαS) distribution feature extraction and least squares support vector machines (LS-SVM) [80]. The fast nonlocal means (FNLM) was also applied for denoising. The structure diagram of the fault diagnosis algorithm is displayed in Figure 5.
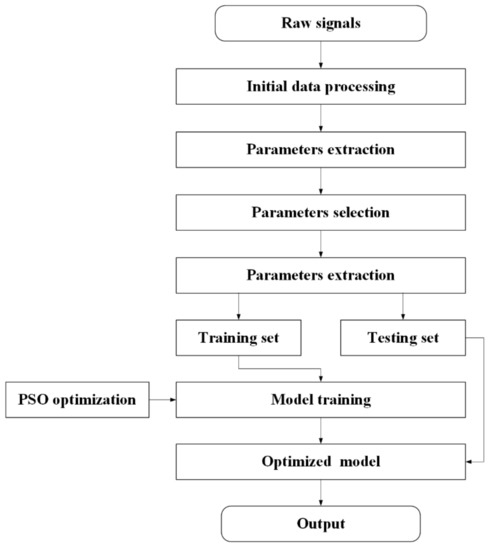
Figure 5.
Main steps of the proposed method in [80].
Deep learning algorithms are generally based on deep neural network structures of learning and training data. The traditional method solves the problem by adding more neurons, and the purpose of deep learning is to extract more features by using more hidden layers and a large amount of training data for modeling [81,82]. The commonly applied deep learning algorithms in rolling bearing vibration signal analysis include convolutional neural network (CNN) and deep belief network (DBN) [83,84]. The CNN model integrates feature extractors and features classifiers in its structure, in which both functions can be realized. The basic structure of CNN is displayed in Figure 6. Yang et al. developed a feature-based transfer neural network (FTNN), which used laboratory data and equipment diagnostic training to identify the health status of bearings during locomotive operation [85]. CNN was employed to extract the transferable features of the original vibration data (data collected by the motor bearings in the laboratory and the bearings of the locomotive gearbox). Li et al. also constructed the hybrid feature extraction by the CNN and the fully-connected layer [86]. Peng et al. proposed a deeper 1D convolutional neural network (Der-1DCNN), in which the CNN was set as the classifier [87]. The model contained the structure of residual learning, which extracted deep features to alleviate the problems of training difficulty and performance degradation of the network. The accuracy of the model was close to 100%. Shao et al. adopted a convolutional deep confidence network (CDBN) method for fault diagnosis of electric locomotive bearings [88]. Zhao et al. designed a bearing fault diagnosis algorithm based on VMD, Hilbert Transform (HT), and DBN [89]. The time-domain signals were decomposed by VMD for a series of intrinsic mode functions IMF, and the Hilbert envelope spectrum was obtained through HT to construct the characteristic matrix, which was set as the input of the DBN network to obtain the fault diagnosis model.
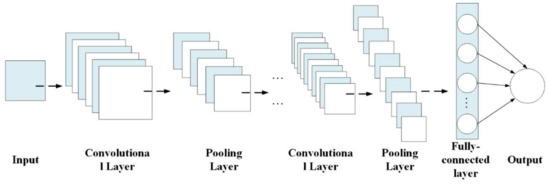
Figure 6.
The basic structure of the CNN algorithm.
The extracted features with the vibration data collection conditions are presented in Table 1. The hybrid combination of the feature extraction and deep learning classifier can also efficiently analyze the data features of each subseries and improve the modeling accuracy, which enables them to select the optimal feature of each subseries by the fluctuation characteristics and obtain the best results. Moreover, deep neural networks possess multiple hidden layers, which raise the ability to identify the deep wave information of bearing series.

Table 1.
Partial extracted features in the research.
2.4. Application of Optimization and Ensemble Algorithms
Based on the effectiveness of the simple diagnosis model and data processing method, the train bearing fault diagnosis model could be optimized in terms of structure to further improve its performance. The basic structure of the optimization algorithm and ensemble algorithm currently applied is shown in Figure 7. Li et al. proposed an enhanced selective integration deep learning method based on the long-horned beetle search algorithm (BAS) using locomotive bearing data, which constructed an enhanced weighted combination strategy with specific category thresholds to achieve selective integration, and employed the BAS algorithm to optimize specific category threshold [91]. Cheng et al. applied the particle swarm optimization algorithm (PSO) to optimize the filter coefficients of the deconvolution problem for fault diagnosis of high-speed rail rolling bearings [92]. The filter coefficient of the deconvolution problem was solved by the PSO algorithm, which was derived from a simulation of a simplified social model by Kennedy and Eberhart [93]. Experimental simulation results verified that the PSO-based method had positive deconvolution performance and robustness. In addition, the modification of the model structure of train bearing diagnosis has also been reflected in recent papers. The common modeling enhancement iterative algorithm is an adaptive enhancement (AdaBoosting). The principle of Boosting is to transform multiple weak classifiers into strong classifiers by constructing a set of ensemble algorithms [94]. After each iteration, a new learner will be generated and the samples will be recognized. Cai et al. proposed an EMD-GNN-AdaBoost model combining EMD with a genetic algorithm (GA) for fault diagnosis of bearing vibration [94]. To test the effectiveness of the GA-BPNN-AdaBoost model, the experimental results of EMD-GNN-AdaBoost and GA-BPNN were also verified, in which the former had significantly higher efficiency and accuracy in diagnosis. The experiments of Han et al. also tested the advanced performance of an improved AdaBoost algorithm that outperformed other benchmark models like BPNN and SVM in the reliability and practicability [95].
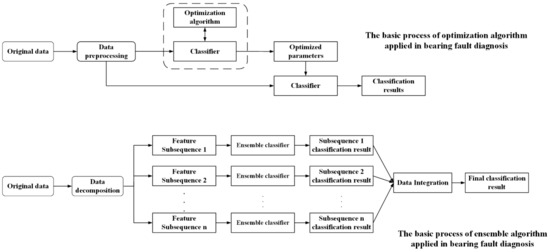
Figure 7.
Basic structures of optimization algorithms and ensemble algorithms.
At present, the algorithm compositions in various fault diagnosis models are growing complicated. Partial models and accuracy of fault diagnosis models are listed in Table 2. In addition to the above algorithms listed in the article, other existing deep learning and optimization algorithms are also tested in subsequent research, such as gated recurrent unit, reinforcement learning, etc. [96,97,98]. The ensemble learning methods have stronger adaptability than the single models. The excellent optimization decisions for the weight of the ensemble approaches are based on the current features of the bearing vibration time series with different amplitudes and fluctuations, which can fully integrate the advantages of the single algorithms and optimize the performance from different aspects. The integration of the deep networks with decomposition and feature extraction methods and strengthen the adaptability of the models. Correspondingly, with the growing complexity of the model structure, the balance between the operational efficiency and diagnosis accuracy demand further increase.

Table 2.
Partial models and accuracy of fault diagnosis for the rolling bearing of railway vehicles.
3. Fault Diagnosis of Wayside Acoustic Features on Train Bearings
The noise formation of rolling bearings is a continuous process. Due to the continuous rotation and rolling of the rolling elements, the structure of the components is deformed by the interaction with other components. So that periodic vibration is generated, which, in turn, causes the vibration of the air to produce waveforms [99]. As long as the bearing vibrates and reaches a certain frequency, the noise will be generated [100]. The rolling bearing inspection of trains is mainly divided into static monitoring and dynamic monitoring [101]. Static monitoring needs to be carried out when the train is stopped. It would take up the scheduling time of the train, while the detection speed is slow and the labor intensity of the maintenance workers is exceedingly high [101]. The dynamic monitoring, however, can complete the state monitoring of the bearing during the running of the train and provide real-time feedback of the bearing status to realize online monitoring [102]. The monitoring methods realize a high degree of automation. Therefore, the dynamic monitoring technology of train bearings has become the current popular research direction.
Depending on the install position of monitoring equipment, the dynamic monitoring systems can be divided into an on-board monitoring system and trackside monitoring system. For the vehicle monitoring system, the advantage could be that the collected signal is closer to the actual signal source and is less affected by the environment [103]. However, its disadvantages are also obvious that various monitoring systems for all crucial train equipment directly lead to the high cost of the on-board monitoring system and also increase the complexity of the system [15].
The acoustic wayside identification system was proposed by the Association of American Railroads (AAR), which was later developed widely in railway research [104]. Different from the on-board monitoring system, the wayside monitoring systems are favored by scholars owing to the low costs, a wide range of monitoring objects, and low maintenance costs [105]. The fault diagnosis technology of train wayside acoustics is mainly to install non-contact sensors (such as microphone arrays, etc.) on the trackside to collect bearing-related signals when the train passes through the experimental area [106]. Due to the complexity of the collection environment, strong interference, and steep distortion of the sound signal, this type of method should further reduce the error and improve the accuracy of signal feature extraction based on the static experimental methods [107]. Amini et al. proposed time spectral kurtosis (TSK) to reduce the background noises and identify the axle-bearing defects [108]. To effectively extract the trackside-bearing acoustic signal, Zhang et al. used an improved singular value decomposition (ISVD) and resonance-based signal sparse decomposition (RSSD) to form the hybrid ISVD-RSSD [109]. The ISVD method could be utilized to eliminate the background noise in the roadside acoustic signal, and the RSSD method is suitable for the decomposition of the denoised signal and the elimination of harmonic components. Christos et al. applied a complex shifted morlet wavelets (CSMW) method to handle the acoustic Doppler signals [110]. Other Doppler effect reduction methods include the models that combine multi-scale chirplet path tracing (MSCPP) and variable digital filter (VDF), and motion parameter estimation methods to avoid the Doppler effect and obtain a residual signal without harmonic interference, which contain the enhanced spline-kernelled chirplet transform (ESCT) model to extract the main harmonic components and the corresponding instantaneous frequency (IF) [111,112]. Another Doppler correction method is the hybrid structure of a short-time multiple signal classification (MUSIC) and angle interpolation resampling (AIR) in the microphone array signals [113]. The structure is quite simple and barely needs initial knowledge, and the results also prove the applicable potential to remove the Doppler distortion. As further exploration for spatial filtering effect to a trackside bearing acoustic signal, Zhang et al. designed a time-varying spatial filtering rearrangement (TSFR) model [114]. The time-varying spatial filters were used to extract signals from different sources. The Doppler distortion was corrected by interpolation and rearrangement. The reconstruction of the separated signal and the envelope spectrum analysis of the corrected signal were lately conducted. The applied acoustic features are presented in the Table 3.
For the fault signal from serious background noises, Peng et al. utilized the kurtosis-optimization-based wavelet packet (KWP) and finished a comparative experiment with existing algorithms EMD and high-frequency resonance technique (HFR), which fully proved the effectiveness of the algorithm [115]. Dybała and Radkowski employed similar experiments to directly measure the railway vehicles, which was based on the Hilbert transform and the method of analytical description [116]. Zhang et al. proposed a Doppler feature matching search algorithm (DFMS) based on the fusion time-frequency distribution (TFD) of a raw signal to solve the Doppler distortion problem [117]. Kilinc and Vagner combined the support vector machine (SVM) and fisher linear discriminant analysis (FLDA) for the defect classification [118]. The test results have verified the availability of the model in multi-source acoustic diagnosis for defective train bearings. The schematic diagram of the above tests is described in Figure 8.
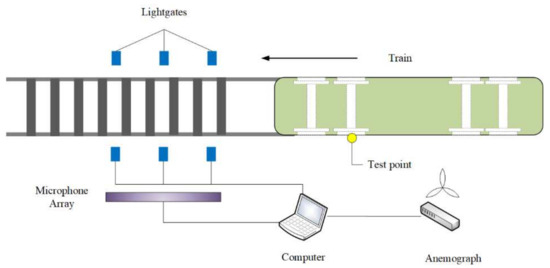
Figure 8.
Schematic diagram of the wayside acoustic detection system.

Table 3.
Partial applied acoustic features in the research.
Table 3.
Partial applied acoustic features in the research.
| Reference | Applied Features | Corresponding Techniques | Authors |
|---|---|---|---|
| [108] | Time and frequency domain | TSK | Amini et al. |
| [109] | Time domain waveform, Envelope spectrum | ISVD-RSSD | Zhang et al. |
| [110] | Frequency domain, acoustic Doppler signal | CSMW | Christos et al. |
| [111] | Time domain waveform, Envelope spectrum | MSCPP | Zhang et al. |
| [114] | Time domain waveform, Envelope spectrum, TFD | TSFR | Zhang et al. |
| [116] | Frequential domain features | Hilbert transform, analytical description | Dybała and Radkowski |
| [118] | Time-domain features (TDF) | FLDA/SVM | Kilinc and Vagner |
Shen et al. proposed a new Doppler transient model combining Laplacian wavelet and spectral correlation evaluation, which was for the diagnosis of locomotive bearing faults [119]. The main function was to extract transient pulse components, match actual bearing fault pulses, and construct the model structure. The first step of similar experiments was to use the static bearing test platform to collect the relevant sound signals of the faulty bearing when the load vehicle is running. Then the obtained data were set as a sound file with a full-range speaker, playing it on the car as the sound source of the train bearing [120,121]. Through a uniform linear motion, the microphone arrays are fixed on the roadside collects the sound signal, as shown in Figure 9.
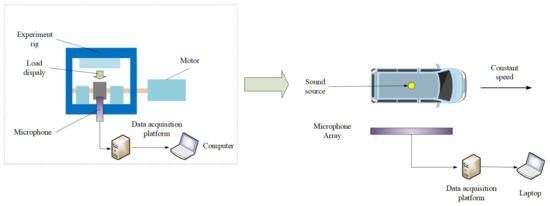
Figure 9.
The Doppler signal acquisition experiment.
Innovative methods integrating microphone arrays and matching tracking algorithms also help to achieve similar results [122]. Liu et al. combined traditional time-domain interpolation with kinematic parameter estimation and proposed an iterative algorithm based on least-squares theory [123]. They indicated that the interval between the microphone array and the middle of the track should be maintained steady to reduce the amount of calculation of additional parameters. The increase in train speed would also cause distortion and more interference of the sound signal, thereby raising the difficulty of feature extraction. In addition, the application areas of bearing fault diagnosis based on the trackside acoustic principle should be limited, which requires fixed-point execution and improved system robustness.
The performance of the Doppler Effect reduction approaches is greatly dependent on the accuracy of instantaneous frequencies (IFs) extraction results. The authentic railway background noise in the collected signal also should not be ignored to estimate IFs, and the relationships among fault degree, speed, and load should be further assessed. Improved extraction and de-noising methods could be a direction of future research. The above wayside acoustic fault diagnosis methods can be extended to the application of other railway vehicle components, such as wheels and axles [124,125]. In addition, multi-category detection and diagnosis methods are integrated and further applied. Various train rolling bearing diagnosis technologies have different advantages and limitations. The simultaneous measurement results from the onboard and roadside monitoring systems are integrated into one platform, and the measurement data results can be also correlated with the bearing health status, which might contribute to effective vehicle health assessment for vehicle operation and maintenance [126,127].
4. Fault Diagnosis of Temperature Features on Train Bearings
The temperature change of the train bearing system comes from the friction of the bearing and the heat dissipation capacity of the system [128]. The abnormal heat transfer in the friction between the bearing parts may cause the bearing overheat, which will present a negative impact on the reliability and service duration of the train system [129]. Researchers mainly choose the onboard contacting bearing temperature monitoring system to reflect the axle bearing temperature information of the changing trend, and realize the prediction and evaluation of the train status.
Liu et al. proposed a multilayer long short-term memory–isolation forest model (MLSTM-iForest) [130]. The time-series data of bearing temperature was applied as the input of MLSTM in the axle box bearing temperature forecasting. Then they calculated the deviation index of the obtained temperature data and input the results into the iForest algorithm for unsupervised classification to determine whether the bearing is faulty. The experimental results of the high-speed EMU dataset tested the effectiveness of the model in the early warning of the axle box bearing with the best performance (accuracy 98.4%) in comparison to other machine learning algorithms. To solve the train health detection based on bearing temperature, Sun and Zhang proposed a hybrid model of bearing temperature prediction integrating improved hierarchical Dirichlet model (HDP) and hidden Markov model (HMM) [131]. The non-parametric properties of the HDP process were employed to infer the number of hidden states and compensate for the defects of HMM. Meanwhile, to handle the nonlinear characteristics of the bearing performance degradation process, the greedy kernel principal component analysis (GKPCA) extracted the characteristics of bearing degradation. Cheng et al. presented a local outlier factor (LOF) detection algorithm based on the bearing temperature obtained by the non-contact measurement of the wireless transmission system, including a variety of factors related to bearing failure [132]. The test results verified the availability of the method in the situation and forecasted all seven quintessential temperature-related abnormal behaviors on the train axle box bearings. Márquez et al. proposed condition-based maintenance (CBM) solution, which applies the predictive analysis to design a CBM plan for train axle bearings to increase the preventive maintenance interval and reliability [133]. In the experiment, the artificial neural network (ANN) prediction model and the temperature data set training model of different bearing positions were selected.
In similar real-time bearing temperature trend prediction research, the long-term short-term memory network (LSTM), which was proposed in 1997, is often employed as a predictor to predict and compare EMU bearing temperature changes and identify failure modes [134,135,136]. Chen et al. combined multi-objective learning (MTL) with LSTM to analyze the bearing temperature features at different positions under the same conditions, thereby describing the time and space correlation between the traction motor bearings of the electric multiple unit (EMU) and various sensors at different positions to reduce the data loss, noise, and overfitting [137]. Gu and Huang established the bearing temperature prediction model MTL-LSTM based on a statistical analysis of the Wuhan–Guangzhou high-speed train operating status, line characteristics, and environmental data in a year [138]. The train operation status data was classified within the train, and the difference between the forecasting value and the actual value from the MTL-LSTM model was tested to diagnose the abnormal bearing temperature. Wang et al. further proposed a spatio-temporal correlation Seq2seq model based on spatial correlation [139]. The structure is composed of an encoder with a spatial attention mechanism and a decoder with temporal attention. In the encoder, spatial attention can acquire the dynamic inter-sensor correlation presented in the sensor data by dealing with the former hidden status of the encoder and the preset value of the sensor. The temporal attention algorithm can adaptively choose appropriate compensation for time series prediction, and the prediction accuracy is increased by 29.28% in comparison with single LSTM. The sensor distribution and time–space correlation on the bogie wheels are described in Figure 10 and Figure 11.
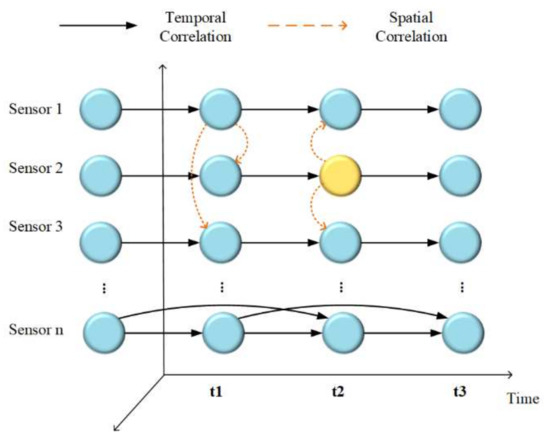
Figure 10.
The temporal and spatial correlation in sensor data of axle bearing temperature.
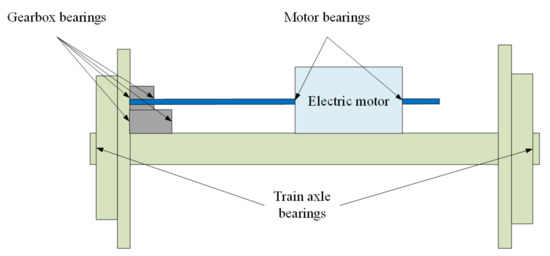
Figure 11.
The distribution position of bearing sensors on the bogie.
The abovementioned models can be applied by forecasting bearing temperature results. Partial temperature forecasting models are listed in Table 4. With the multi-objective and spatial algorithm analysis, it can be found that the hybrid models can often obtain higher accuracy than the single models. Furthermore, the speed of the vehicles, the duration of the vehicle’s continuous operation, and the ambient temperature all can affect the temperature rise of the train bearings. Moreover, the running speed of the train has a certain hysteresis relative to the temperature rise of the bearing, and the bearing in different operation stages has different temperature change trends. Therefore, in the process of spatiotemporal correlation analysis, it is indispensable to fully consider various influencing factors to reduce the false alarm rate of abnormal monitoring and improve prediction accuracy.

Table 4.
Partial temperature forecasting models in the research.
5. Discussion
To sum up the analysis, the main directions in the research of the train bearing fault diagnosis are vibration fault diagnosis, trackside acoustic fault diagnosis, and temperature prediction. The characteristics are listed in Table 5.

Table 5.
Comparative performance of different fault diagnosis techniques.
The trend of the methods applied in railway bearings is obvious and decomposition is the commonly used method among data processing. From the comparative analysis of the above sections, it could also indicate that feature extraction, ensemble learning, and spatiotemporal models also contribute to the modeling accuracy. The data in the vibration fault diagnosis is mainly obtained from a fixed vibration test bench. The measurement accuracy is high, but the test location and operation requirements are also high. Through literature analysis, it can be found that the vibration fault diagnosis model has made many application achievements in recent years, especially the diagnosis and classification methods such as recognition algorithms, data decomposition, deep learning, and optimized integration algorithms. These algorithms improved the accuracy of the diagnosis system and also brought an increase in the complexity of the algorithm structure, which has an impact on the computational efficiency.
In comparison with vibration diagnosis, wayside acoustic fault diagnosis has the advantage of non-contact measurement. The experimental devices are arranged more conveniently, but it is also carried out at fixed measuring locations, and the setting of the trackside experiment area is limited. Furthermore, the effect of using the vehicle simulation dynamic test and the elimination of environmental interference needs further verification. The temperature diagnosis and prediction technology directly analyze the data obtained by real-time monitoring through the onboard temperature sensors. At the same time, the methods reduce the costs of test equipment and maintenance and realize the prediction of the bearing temperature change trend in the long-distance operation. Conversely, the false alarm of system temperature in real-time detection is unavoidable, which often affects the accuracy of diagnosis. In addition, the latest research shows that the spatial correlation between the temperature changes of bearings at multiple positions on the train bogie can’t be ignored. Based on time series prediction, it is feasible to increase the diagnosis of the train space temperature for improvement in train health monitoring.
6. Conclusions and Future Work
This paper mainly reviewed the related application scenarios, comprehensive performance, and development potential of vibration fault diagnosis, wayside acoustic fault diagnosis, and temperature prediction of train rolling bearings. Vibration fault diagnosis methods are currently used quite frequently, while the corresponding model structure is complex, and the spatiotemporal correlation analysis brought by multi-bearing measurement in temperature prediction has great potential for further research. Furthermore, it is also indispensable to enhance the anti-interference ability in the data measurement for acoustic fault diagnosis. For the application of the new algorithm, the consideration of the balance between its operation efficiency and diagnosis accuracy should not be ignored. In the future, train rolling bearing diagnosis technology will also integrate a variety of sensor data and systems, especially under the increased capacity and complex operating conditions. Further screening and extracting for effective information from the perspective of data application is necessary, which contributes to reliable railway vehicle maintenance and comprehensive decision-making.
From the operation principle, technical characteristics, and application scope of mainstream types of the train bearing fault diagnosis conducted in recent years, it can be concluded that the future trends of various rolling bearing fault diagnosis technologies as the following points:
- (1)
- Fault diagnosis algorithm and integrated application. To fulfill the various data processing requirements of the trains, other existing algorithms can also be gradually adopted, such as gated recurrent units, reinforcement learning, graph neural networks, etc. [96,97]. The integration of train rolling bearing diagnosis technologies and the integration of different types of data can be further strengthened to improve the train failure database [140];
- (2)
- Anti-interference processing. From various tests in the fault diagnosis research, it is obvious that the noise reduction of the complex environment and strong interference in train operation directly affects the quality of the sensor data. Regardless of vibration or temperature research, certain processing or quantification of environmental interference is required for the accuracy of data input. The improvement of feature extraction methods is the key to raising the overall fault diagnosis accuracy of train bearings;
- (3)
- Spatio-temporal correlation analysis. In the train, especially the multi-bearing structure in the bogie, the spatial and time-dependent temperature data change phenomenon is worthy of in-depth study. The potential information will affect the fault diagnosis modeling method and contribute to the analysis of the changes in the monitoring data of the train operation areas and the correlation between the internal train components. The changes of temperature data of multiple components in spatio-temporal series may play a positive role in the analysis of the whole train driving and braking system, and the prediction of the life cycle of the train mechanical system will effectively promote the maintenance work of the railway department;
- (4)
- Big data management application. In some literature in the review, the amount of train bearing data is already close to 100,000. With the increase in train operation time, the continuous accumulation and expansion of rolling bearing data, comprehensively recording fault data, and a large-scale data-parallel calculation are paramount to raise the performance of the fault diagnosis system. For example, the Apache Spark framework can be conducted to process large sample test data. Through centralized and distributed programs, the computing efficiency would be greatly raised to realize rolling bearing health detection and historical data analysis, which can accurately evaluate the safety of different railway vehicles and conduct in-depth mining of the relevance in the operation networks and maintenance.
Author Contributions
Conceptualization, G.Y. and Y.B.; methodology, G.Y. and J.C.; software, G.Y. and C.Y. (Chengqing Yu); validation, G.Y., C.Y. (Chengming Yu) and C.Y. (Chengqing Yu); formal analysis, G.Y. and Y.B.; investigation, J.C.; resources, G.Y. and Y.B.; data curation, G.Y. and J.C.; writing—original draft preparation, G.Y. and Y.B.; writing—review and editing, G.Y., C.Y. (Chengming Yu) and C.Y. (Chengqing Yu); visualization, G.Y., C.Y. (Chengming Yu) and C.Y. (Chengqing Yu); supervision, Y.B.; project administration, G.Y.; funding acquisition, G.Y. and Y.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
This study is fully supported by the National Natural Science Foundation of China (Grant No. 61902108) and the Natural Science Foundation of Hebei Province (Grant No. F2019208305).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Pennacchi, P.; Chatterton, S.; Vania, A.; Massocchi, D. Definition of Damage Indices for Railway Axle Bearings: Results of Long-Lasting Tests. Machines 2021, 9, 12. [Google Scholar] [CrossRef]
- Cheng, Y.; Zou, D.; Zhang, W.; Wang, Z. A Hybrid Time-Frequency Analysis Method for Railway Rolling-Element Bearing Fault Diagnosis. J. Sens. 2019, 2019, 8498496. [Google Scholar] [CrossRef]
- Jiang, W.; Wang, C.; Zou, J.; Zhang, S. Application of Deep Learning in Fault Diagnosis of Rotating Machinery. Processes 2021, 9, 919. [Google Scholar] [CrossRef]
- Huang, H.; Liu, F.; Geng, L.; Liu, Y.; Ren, Z.; Zhao, Y.; Lei, X.; Lu, X. Fault diagnosis accuracy improvement using wayside rectangular microphone array for health monitoring of railway-vehicle wheel bearing. IEEE Access 2019, 7, 87410–87424. [Google Scholar] [CrossRef]
- Čamaj, J.; Brumerčíková, E.; Hranický, M.P. Information System and Technology Optimization as a Tool for Ensuring the Competitiveness of a Railway Undertaking—Case Study. Sustainability 2020, 12, 8915. [Google Scholar] [CrossRef]
- Wang, Z.; Mei, G.; Xiong, Q.; Yin, Z.; Zhang, W. Motor car–track spatial coupled dynamics model of a high-speed train with traction transmission systems. Mech. Mach. Theory 2019, 137, 386–403. [Google Scholar] [CrossRef]
- Bernal, E.; Spiryagin, M.; Cole, C. Onboard condition monitoring sensors, systems and techniques for freight railway vehicles: A review. IEEE Sens. J. 2018, 19, 4–24. [Google Scholar] [CrossRef]
- Chen, B.; Yan, Z.; Chen, W. Defect detection for wheel-bearings with time-spectral kurtosis and entropy. Entropy 2014, 16, 607–626. [Google Scholar] [CrossRef] [Green Version]
- Morys, B.J.J.o.S. Enlargement of out-of-round wheel profiles on high speed trains. J. Sound Vib. 1999, 227, 965–978. [Google Scholar] [CrossRef]
- Yi, C.; Wang, D.; Fan, W.; Tsui, K.-L.; Lin, J. EEMD-based steady-state indexes and their applications to condition monitoring and fault diagnosis of railway axle bearings. Sensors 2018, 18, 704. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Liang, X.; Lin, J.; Chen, Y.; Liu, J. Train axle bearing fault detection using a feature selection scheme based multi-scale morphological filter. Mech. Syst. Signal Processing 2018, 101, 435–448. [Google Scholar] [CrossRef]
- Amasorrain, J.I.; Sagartzazu, X.; Damian, J. Load distribution in a four contact-point slewing bearing. Mech. Mach. Theory 2003, 38, 479–496. [Google Scholar] [CrossRef]
- Symonds, N.; Corni, I.; Wood, R.; Wasenczuk, A.; Vincent, D. Observing early stage rail axle bearing damage. Eng. Fail. Anal. 2015, 56, 216–232. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Chang, Q.; Luo, J.; Man, J.; Chen, Q.; Shen, Y. Comprehensive Evaluation Model of Bearing Transportation Protection Effect of Bogie Traction Motor under Data Imbalance. J. Sens. 2021, 2021, 4690369. [Google Scholar] [CrossRef]
- Entezami, M.; Roberts, C.; Weston, P.; Stewart, E.; Amini, A.; Papaelias, M. Perspectives on railway axle bearing condition monitoring. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2020, 234, 17–31. [Google Scholar] [CrossRef]
- Wang, S.; Chen, J.; Wang, H.; Zhang, D. Degradation evaluation of slewing bearing using HMM and improved GRU. Measurement 2019, 146, 385–395. [Google Scholar] [CrossRef]
- Caesarendra, W.; Tjahjowidodo, T.; Kosasih, B.; Tieu, A.K. Integrated condition monitoring and prognosis method for incipient defect detection and remaining life prediction of low speed slew bearings. Machines 2017, 5, 11. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.; Jiang, B.; Chen, W.; Yi, H. Data-driven detection and diagnosis of incipient faults in electrical drives of high-speed trains. IEEE Trans. Ind. Electron. 2018, 66, 4716–4725. [Google Scholar] [CrossRef]
- Oliveira, D.F.; Vismari, L.F.; de Almeida, J.R.; Cugnasca, P.S.; Camargo, J.B.; Marreto, E.; Doimo, D.R.; de Almeida, L.P.; Gripp, R.; Neves, M.M. Evaluating unsupervised anomaly detection models to detect faults in heavy haul railway operations. In Proceedings of the 2019 18th IEEE International Conference On Machine Learning And Applications (ICMLA), Boca Raton, FL, USA, 16–19 December 2019; pp. 1016–1022. [Google Scholar]
- Safaeipour, H.; Forouzanfar, M.; Casavola, A. A survey and classification of incipient fault diagnosis approaches. J. Process Control 2021, 97, 1–16. [Google Scholar] [CrossRef]
- Safaeipour, H.; Forouzanfar, M.; Ramezani, A. Incipient fault detection in nonlinear non-Gaussian noisy environment. Measurement 2021, 174, 109008. [Google Scholar] [CrossRef]
- Połom, M.; Tarkowski, M.; Puzdrakiewicz, K. Urban transformation in the context of rail transport development: The case of a newly built railway line in Gdańsk (Poland). J. Adv. Transp. 2018, 2018, 1218041. [Google Scholar] [CrossRef]
- Rosique, F.; Navarro, P.J.; Fernández, C.; Padilla, A. A systematic review of perception system and simulators for autonomous vehicles research. Sensors 2019, 19, 648. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cheng, C.; Qiao, X.; Luo, H.; Wang, G.; Teng, W.; Zhang, B. Data-driven incipient fault detection and diagnosis for the running gear in high-speed trains. IEEE Trans. Veh. Technol. 2020, 69, 9566–9576. [Google Scholar] [CrossRef]
- Xu, G.; Hou, D.; Qi, H.; Bo, L. High-speed train wheel set bearing fault diagnosis and prognostics: A new prognostic model based on extendable useful life. Mech. Syst. Signal Processing 2021, 146, 107050. [Google Scholar] [CrossRef]
- Corni, I.; Symonds, N.; Birrell, C.E.; Katsamenis, O.L.; Wasenczuk, A.; Vincent, D. Characterization and mapping of rolling contact fatigue in rail-axle bearings. Eng. Fail. Anal. 2017, 82, 617–630. [Google Scholar] [CrossRef]
- Liu, F.; He, Q.; Kong, F.; Liu, Y. Doppler effect reduction based on time-domain interpolation resampling for wayside acoustic defective bearing detector system. Mech. Syst. Signal Processing 2014, 46, 253–271. [Google Scholar] [CrossRef]
- Ghasemi, A.; Hodkiewicz, M.R. Estimating mean residual life for a case study of rail wagon bearings. IEEE Trans. Reliab. 2012, 61, 719–730. [Google Scholar] [CrossRef]
- Luo, H.; Bo, L.; Peng, C.; Hou, D. Fault diagnosis for high-speed train axle-box bearing using simplified shallow information fusion convolutional neural network. Sensors 2020, 20, 4930. [Google Scholar] [CrossRef]
- Gómez, M.J.; Castejón, C.; Corral, E.; García-Prada, J.C. Railway axle condition monitoring technique based on wavelet packet transform features and support vector machines. Sensors 2020, 20, 3575. [Google Scholar] [CrossRef]
- Fraga-Lamas, P.; Fernández-Caramés, T.M.; Castedo, L. Towards the Internet of smart trains: A review on industrial IoT-connected railways. Sensors 2017, 17, 1457. [Google Scholar] [CrossRef] [Green Version]
- Savoskin, A.; Vlasevskii, S. Aspects of Railway Vehicles Vibrations with Nonlinear Spring Suspension Characteristics. In International Scientific Siberian Transport Forum; Springer: Cham, Switzerland, 2019; pp. 109–116. [Google Scholar]
- Trilla, A.; Gratacòs, P. Maintenance of bogie components through vibration inspection with intelligent wireless sensors: A case study on axle-boxes and wheel-sets using the empirical mode decomposition technique. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2016, 230, 1408–1414. [Google Scholar] [CrossRef]
- Zhuang, Z.; Ding, J.; Tan, A.C.; Shi, Y.; Lin, J. Fault detection of high-speed train wheelset bearing based on impulse-envelope manifold. Shock Vib. 2017, 2017, 2104720. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Q.; Ding, J.; Zhao, W. An adaptive boundary determination method for empirical wavelet transform and its application in wheelset-bearing fault detection in high-speed trains. Measurement 2021, 171, 108746. [Google Scholar] [CrossRef]
- Ahn, G.; Lee, H.; Park, J.; Hur, S. Development of indicator of data sufficiency for feature-based early time series classification with applications of bearing fault diagnosis. Processes 2020, 8, 790. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, S.; Wang, B.; Habetler, T.G. Deep learning algorithms for bearing fault diagnostics—A comprehensive review. IEEE Access 2020, 8, 29857–29881. [Google Scholar] [CrossRef]
- Chen, L.; Qin, N.; Dai, X.; Huang, D. Fault diagnosis of high-speed train bogie based on capsule network. IEEE Trans. Instrum. Meas. 2020, 69, 6203–6211. [Google Scholar] [CrossRef]
- Zhang, B.; Miao, Y.; Lin, J.; Yi, Y. Adaptive maximum second-order cyclostationarity blind deconvolution and its application for locomotive bearing fault diagnosis. Mech. Syst. Signal Processing 2021, 158, 107736. [Google Scholar] [CrossRef]
- Žvokelj, M.; Zupan, S.; Prebil, I. Non-linear multivariate and multiscale monitoring and signal denoising strategy using kernel principal component analysis combined with ensemble empirical mode decomposition method. Mech. Syst. Signal Processing 2011, 25, 2631–2653. [Google Scholar] [CrossRef]
- Žvokelj, M.; Zupan, S.; Prebil, I. EEMD-based multiscale ICA method for slewing bearing fault detection and diagnosis. J. Sound Vib. 2016, 370, 394–423. [Google Scholar] [CrossRef]
- Shao, H.; Jiang, H.; Zhao, K.; Wei, D.; Li, X. A novel tracking deep wavelet auto-encoder method for intelligent fault diagnosis of electric locomotive bearings. Mech. Syst. Signal Processing 2018, 110, 193–209. [Google Scholar]
- Zhao, M.; Lin, J.; Miao, Y.; Xu, X. Detection and recovery of fault impulses via improved harmonic product spectrum and its application in defect size estimation of train bearings. Measurement 2016, 91, 421–439. [Google Scholar] [CrossRef]
- Cheng, Y.; Zhou, N.; Zhang, W.; Wang, Z. Application of an improved minimum entropy deconvolution method for railway rolling element bearing fault diagnosis. J. Sound Vib. 2018, 425, 53–69. [Google Scholar] [CrossRef]
- Caesarendra, W.; Pratama, M.; Kosasih, B.; Tjahjowidodo, T.; Glowacz, A. Parsimonious network based on a fuzzy inference system (PANFIS) for time series feature prediction of low speed slew bearing prognosis. Appl. Sci. 2018, 8, 2656. [Google Scholar] [CrossRef] [Green Version]
- Yang, S.; Gu, X.; Liu, Y.; Hao, R.; Li, S. A general multi-objective optimized wavelet filter and its applications in fault diagnosis of wheelset bearings. Mech. Syst. Signal Processing 2020, 145, 106914. [Google Scholar] [CrossRef]
- Udmale, S.S.; Singh, S.K.; Bhirud, S.G. A bearing data analysis based on kurtogram and deep learning sequence models. Measurement 2019, 145, 665–677. [Google Scholar] [CrossRef]
- Liu, Z.; Yang, S.; Liu, Y.; Lin, J.; Gu, X. Adaptive correlated Kurtogram and its applications in wheelset-bearing system fault diagnosis. Mech. Syst. Signal Processing 2021, 154, 107511. [Google Scholar] [CrossRef]
- Feng, Z.; Chu, F. Cyclostationary analysis for gearbox and bearing fault diagnosis. Shock Vib. 2015, 2015, 542472. [Google Scholar] [CrossRef] [Green Version]
- Daniyan, I.; Mpofu, K.; Oyesola, M.; Ramatsetse, B.; Adeodu, A. Artificial intelligence for predictive maintenance in the railcar learning factories. Procedia Manuf. 2020, 45, 13–18. [Google Scholar] [CrossRef]
- Saufi, S.; Ahmad, Z.; Leong, M.; Lim, M. An intelligent bearing fault diagnosis system: A review. In Proceedings of the Engineering Application of Artificial Intelligence Conference 2018 (EAAIC 2018), Sabah, Malaysia, 3–5 December 2018; p. 06005. [Google Scholar]
- Qiao, Z.; Lei, Y.; Li, N. Applications of stochastic resonance to machinery fault detection: A review and tutorial. Mech. Syst. Signal Processing 2019, 122, 502–536. [Google Scholar] [CrossRef]
- Arneodo, A.; Grasseau, G.; Holschneider, M. Wavelet transform of multifractals. Phys. Rev. Lett. 1988, 61, 2281. [Google Scholar] [CrossRef]
- Lindsey, A.R.; Dill, J.C. Wavelet packet modulation: A generalized method for orthogonally multiplexed communications. In Proceedings of the Twenty-Seventh Southeastern Symposium on System Theory, Starkville, MS, USA, 12–14 March 1995; pp. 392–396. [Google Scholar]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Processing 2013, 62, 531–544. [Google Scholar] [CrossRef]
- Gilles, J. Empirical wavelet transform. IEEE Trans. Signal Processing 2013, 61, 3999–4010. [Google Scholar] [CrossRef]
- Zhao, L.; Wang, L.; Yan, R. Rolling bearing fault diagnosis based on wavelet packet decomposition and multi-scale permutation entropy. Entropy 2015, 17, 6447–6461. [Google Scholar] [CrossRef] [Green Version]
- Werbos, P.J. Backpropagation through time: What it does and how to do it. Proc. IEEE 1990, 78, 1550–1560. [Google Scholar] [CrossRef] [Green Version]
- Zhuo, W.; Yu, Z. Research on rolling bearing fault diagnosis of high-speed train. J. Phys. Conf. Ser. 2019, 1314, 012086. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Lu, Z.; Wei, J.; Zhang, Y. Fault diagnosis for rail vehicle axle-box bearings based on energy feature reconstruction and composite multiscale permutation entropy. Entropy 2019, 21, 865. [Google Scholar] [CrossRef] [Green Version]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Liu, X.; Bo, L.; Luo, H. Bearing faults diagnostics based on hybrid LS-SVM and EMD method. Measurement 2015, 59, 145–166. [Google Scholar] [CrossRef]
- Guo, T.; Deng, Z. An improved EMD method based on the multi-objective optimization and its application to fault feature extraction of rolling bearing. Appl. Acoust. 2017, 127, 46–62. [Google Scholar] [CrossRef]
- Li, X.; Jia, L.; Yang, X. Fault diagnosis of train axle box bearing based on multifeature parameters. Discret. Dyn. Nat. Soc. 2015, 2015, 846918. [Google Scholar] [CrossRef]
- Wang, C.; Sha, C.; Su, M.; Hu, Y. An algorithm to remove noise from locomotive bearing vibration signal based on self-adaptive EEMD filter. J. Cent. South Univ. 2017, 24, 478–488. [Google Scholar] [CrossRef] [Green Version]
- Yi, C.; Lin, J.; Zhang, W.; Ding, J. Faults diagnostics of railway axle bearings based on IMF’s confidence index algorithm for ensemble EMD. Sensors 2015, 15, 10991–11011. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jiang, F.; Zhu, Z.; Li, W.; Ren, Y.; Zhou, G.; Chang, Y. A fusion feature extraction method using EEMD and correlation coefficient analysis for bearing fault diagnosis. Appl. Sci. 2018, 8, 1621. [Google Scholar] [CrossRef] [Green Version]
- Yan, G.; Yu, C.; Bai, Y. Wind Turbine Bearing Temperature Forecasting Using a New Data-Driven Ensemble Approach. Machines 2021, 9, 248. [Google Scholar] [CrossRef]
- Huang, Y.; Lin, J.; Liu, Z.; Wu, W. A modified scale-space guiding variational mode decomposition for high-speed railway bearing fault diagnosis. J. Sound Vib. 2019, 444, 216–234. [Google Scholar] [CrossRef]
- Jiang, F.; Zhu, Z.; Li, W. An improved VMD with empirical mode decomposition and its application in incipient fault detection of rolling bearing. IEEE Access 2018, 6, 44483–44493. [Google Scholar] [CrossRef]
- Liu, Q.; Yang, J.; Zhang, K. An improved empirical wavelet transform and sensitive components selecting method for bearing fault. Measurement 2022, 187, 110348. [Google Scholar] [CrossRef]
- Cao, H.; Fan, F.; Zhou, K.; He, Z. Wheel-bearing fault diagnosis of trains using empirical wavelet transform. Measurement 2016, 82, 439–449. [Google Scholar] [CrossRef]
- Deng, F.; Liu, Y. An adaptive frequency window empirical wavelet transform method for fault diagnosis of wheelset bearing. In Proceedings of the 2018 Prognostics and System Health Management Conference (PHM-Chongqing), Chongqing, China, 26–28 October 2018; pp. 1291–1294. [Google Scholar]
- Rao, X.; Sheng, C.; Guo, Z.; Yuan, C. A review of online condition monitoring and maintenance strategy for cylinder liner-piston rings of diesel engines. Mech. Syst. Signal Processing 2022, 165, 108385. [Google Scholar] [CrossRef]
- Caesarendra, W.; Tjahjowidodo, T. A review of feature extraction methods in vibration-based condition monitoring and its application for degradation trend estimation of low-speed slew bearing. Machines 2017, 5, 21. [Google Scholar] [CrossRef]
- Saki, M.; Abolhasan, M.; Lipman, J. A novel approach for big data classification and transportation in rail networks. IEEE Trans. Intell. Transp. Syst. 2019, 21, 1239–1249. [Google Scholar] [CrossRef]
- Zhao, X.; Qin, Y.; Jia, L.; Liu, Z. Fault Feature Extraction based on Cyclic Correntropy for Train Axle Bearings in Impulsive Noise. In Proceedings of the 2020 Asia-Pacific International Symposium on Advanced Reliability and Maintenance Modeling (APARM), Vancouver, BC, Canada, 20–23 August 2020; pp. 1–5. [Google Scholar]
- Li, Y.; Zhang, W.; Xiong, Q.; Lu, T.; Mei, G. A novel fault diagnosis model for bearing of railway vehicles using vibration signals based on symmetric alpha-stable distribution feature extraction. Shock Vib. 2016, 2016, 5714195. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.; Jin, W.; Ren, J.; Sun, Z. A multi-perspective architecture for high-speed train fault diagnosis based on variational mode decomposition and enhanced multi-scale structure. Appl. Intell. 2019, 49, 3923–3937. [Google Scholar] [CrossRef]
- Han, S.; Oh, S.; Jeong, J. Bearing Fault Diagnosis Based on Multiscale Convolutional Neural Network Using Data Augmentation. J. Sens. 2021, 2021, 6699637. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y. Convolutional networks for images, speech, and time series. Handb. Brain Theory Neural Netw. 1995, 3361, 1995. [Google Scholar]
- Xie, J.; Li, T.; Yang, Y.; Jin, W. Learning features from high speed train vibration signals with deep belief networks. In Proceedings of the 2014 International Joint Conference on Neural Networks (IJCNN), Beijing, China, 6–11 July 2014; pp. 2205–2210. [Google Scholar]
- Yang, B.; Lei, Y.; Jia, F.; Xing, S. An intelligent fault diagnosis approach based on transfer learning from laboratory bearings to locomotive bearings. Mech. Syst. Signal Processing 2019, 122, 692–706. [Google Scholar] [CrossRef]
- Li, X.; Zhang, W.; Ding, Q.; Sun, J. Multi-layer domain adaptation method for rolling bearing fault diagnosis. Signal Processing 2019, 157, 180–197. [Google Scholar] [CrossRef] [Green Version]
- Peng, D.; Liu, Z.; Wang, H.; Qin, Y.; Jia, L. A novel deeper one-dimensional CNN with residual learning for fault diagnosis of wheelset bearings in high-speed trains. IEEE Access 2018, 7, 10278–10293. [Google Scholar] [CrossRef]
- Shao, H.; Jiang, H.; Zhang, H.; Liang, T. Electric locomotive bearing fault diagnosis using a novel convolutional deep belief network. IEEE Trans. Ind. Electron. 2017, 65, 2727–2736. [Google Scholar] [CrossRef]
- Zhao, H.; Liu, H.; Xu, J.; Guo, C.; Deng, W. Research on a fault diagnosis method of rolling bearings using variation mode decomposition and deep belief network. J. Mech. Sci. Technol. 2019, 33, 4165–4172. [Google Scholar] [CrossRef]
- Zhu, H.; He, Z.; Wei, J.; Wang, J.; Zhou, H. Bearing fault feature extraction and fault diagnosis method based on feature fusion. Sensors 2021, 21, 2524. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Jiang, H.; Niu, M.; Wang, R. An enhanced selective ensemble deep learning method for rolling bearing fault diagnosis with beetle antennae search algorithm. Mech. Syst. Signal Processing 2020, 142, 106752. [Google Scholar] [CrossRef]
- Cheng, Y.; Wang, Z.; Zhang, W.; Huang, G. Particle swarm optimization algorithm to solve the deconvolution problem for rolling element bearing fault diagnosis. ISA Trans. 2019, 90, 244–267. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Cai, G.; Yang, C.; Pan, Y.; Lv, J. EMD and GNN-AdaBoost fault diagnosis for urban rail train rolling bearings. Discret. Contin. Dyn. Syst.-S 2019, 12, 1471. [Google Scholar] [CrossRef] [Green Version]
- Han, L.; Yu, C.; Liu, C.; Qin, Y.; Cui, S. Fault diagnosis of rolling bearings in rail train based on exponential smoothing predictive segmentation and improved ensemble learning algorithm. Appl. Sci. 2019, 9, 3143. [Google Scholar] [CrossRef] [Green Version]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar]
- Kaelbling, L.P.; Littman, M.L.; Moore, A.W. Reinforcement learning: A survey. J. Artif. Intell. Res. 1996, 4, 237–285. [Google Scholar] [CrossRef] [Green Version]
- Dong, S.; Yu, C.; Yan, G.; Zhu, J.; Hu, H. A Novel Ensemble Reinforcement Learning Gated Recursive Network for Traffic Speed Forecasting. In Proceedings of the 2021 Workshop on Algorithm and Big Data, Fuzhou, China, 12–14 March 2021; pp. 55–60. [Google Scholar]
- Choe, H.C.; Wan, Y.; Chan, A.K. Neural pattern identification of railroad wheel-bearing faults from audible acoustic signals: Comparison of FFT, CWT, and DWT features. In Proceedings of the AeroSense’97, Orlando, FL, USA, 20–25 April 1997; pp. 480–496. [Google Scholar]
- Gasch, R. Dynamic behaviour of the Laval rotor with a transverse crack. Mech. Syst. Signal Processing 2008, 22, 790–804. [Google Scholar] [CrossRef]
- Asngali, B.; Susanto, A.; Subkhan, M.; Martinez, I.; Yamada, K.; Majedi, F. Static Analysis of Railway Axle using Finite Element Method and Monitoring of Railway Bearing Based on Vibration Analysis. J. Phys. Conf. Ser. 2021, 1845, 012037. [Google Scholar] [CrossRef]
- Shah, D.S.; Patel, V.N. A review of dynamic modeling and fault identifications methods for rolling element bearing. Procedia Technol. 2014, 14, 447–456. [Google Scholar] [CrossRef]
- Ngigi, R.; Pislaru, C.; Ball, A.; Gu, F. Modern techniques for condition monitoring of railway vehicle dynamics. J. Phys. Conf. Ser. 2012, 364, 012016. [Google Scholar] [CrossRef]
- Cline, J.E.; Bilodeau, J.R.; Smith, R.L. Acoustic wayside identification of freight car roller bearing defects. In Proceedings of the Proceedings of the 1998 ASME/IEEE Joint Railroad Conference, Philadelphia, PA, USA, 16 April 1998; pp. 79–83. [Google Scholar]
- Shirotori, T. A method for wayside bogie monitoring based on internal yard running vibration. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2021, 235, 440–449. [Google Scholar] [CrossRef]
- Zhang, A.; Shen, C.; He, Q.; Hu, F.; Liu, F.; Kong, F. Doppler distortion removal based on Dopplerlet transform and re-sampling for wayside fault diagnosis of train bearings. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2021, 235, 3407–3423. [Google Scholar] [CrossRef]
- Zvolenský, P.; Leštinský, L.; Ďungel, J.; Grenčík, J. Acoustic diagnostics of railway vehicles. Transp. Res. Procedia 2021, 55, 667–672. [Google Scholar] [CrossRef]
- Amini, A.; Entezami, M.; Huang, Z.; Rowshandel, H.; Papaelias, M. Wayside detection of faults in railway axle bearings using time spectral kurtosis analysis on high-frequency acoustic emission signals. Adv. Mech. Eng. 2016, 8, 1687814016676000. [Google Scholar] [CrossRef] [Green Version]
- Zhang, D.; Entezami, M.; Stewart, E.; Roberts, C.; Yu, D. Adaptive fault feature extraction from wayside acoustic signals from train bearings. J. Sound Vib. 2018, 425, 221–238. [Google Scholar] [CrossRef]
- Christos, Y.; Jedrzej, M.; Konstantinos, R.; Ioannis, A. Multicomponent decomposition of a time-varying acoustic Doppler signal generated by a passing railway vehicle using Complex Shifted Morlet Wavelets. Transp. Res. Part C Emerg. Technol. 2014, 44, 34–51. [Google Scholar] [CrossRef]
- Zhang, D.; Entezami, M.; Stewart, E.; Roberts, C.; Yu, D. A novel doppler effect reduction method for wayside acoustic train bearing fault detection systems. Appl. Acoust. 2019, 145, 112–124. [Google Scholar] [CrossRef]
- Zhang, D.; Entezami, M.; Stewart, E.; Roberts, C.; Yu, D.; Lei, Y. Wayside acoustic detection of train bearings based on an enhanced spline-kernelled chirplet transform. J. Sound Vib. 2020, 480, 115401. [Google Scholar] [CrossRef]
- Zhang, S.; He, Q.; Zhang, H.; Ouyang, K. Doppler correction using short-time MUSIC and angle interpolation resampling for wayside acoustic defective bearing diagnosis. IEEE Trans. Instrum. Meas. 2017, 66, 671–680. [Google Scholar] [CrossRef]
- Zhang, S.; He, Q.; Ouyang, K.; Xiong, W. Multi-bearing weak defect detection for wayside acoustic diagnosis based on a time-varying spatial filtering rearrangement. Mech. Syst. Signal Processing 2018, 100, 224–241. [Google Scholar] [CrossRef]
- Peng, C.; Ai, W.; Peng, J.; Gao, X. Wayside Acoustic Diagnosis of Axle Box Bearing Based on Fault Feature Extraction Algorithm. In Proceedings of the 2018 IEEE Far East NDT New Technology & Application Forum (FENDT), Xiamen, China, 6–8 July 2018; pp. 90–94. [Google Scholar]
- Dybała, J.; Radkowski, S. Reduction of Doppler effect for the needs of wayside condition monitoring system of railway vehicles. Mech. Syst. Signal Processing 2013, 38, 125–136. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, S.; He, Q.; Kong, F. The Doppler Effect based acoustic source separation for a wayside train bearing monitoring system. J. Sound Vib. 2016, 361, 307–329. [Google Scholar] [CrossRef]
- Kilinc, O.; Vagner, J. Wayside diagnosis of metro wheelsets using acoustic sensor data and one-period analysis. In Proceedings of the 23rd International Conference Engineering Mechanics 2017, Svratka, Czech Republic, 15–18 May 2017; pp. 458–461. [Google Scholar]
- Shen, C.; Liu, F.; Wang, D.; Zhang, A.; Kong, F.; Tse, P.W. A doppler transient model based on the laplace wavelet and spectrum correlation assessment for locomotive bearing fault diagnosis. Sensors 2013, 13, 15726–15746. [Google Scholar] [CrossRef] [Green Version]
- Liu, F.; Shen, C.; He, Q.; Zhang, A.; Liu, Y.; Kong, F. Wayside bearing fault diagnosis based on a data-driven Doppler effect eliminator and transient model analysis. Sensors 2014, 14, 8096–8125. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Qian, Q.; Liu, F.; Lu, S.; He, Q.; Zhao, J. Wayside bearing fault diagnosis based on envelope analysis paved with time-domain interpolation resampling and weighted-correlation-coefficient-guided stochastic resonance. Shock Vib. 2017, 2017, 3189135. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Hu, Z.; He, Q.; Zhang, S.; Zhu, J. Doppler distortion correction based on microphone array and matching pursuit algorithm for a wayside train bearing monitoring system. Meas. Sci. Technol. 2017, 28, 105006. [Google Scholar] [CrossRef]
- Liu, Y.; Qian, Q.; Liu, F.; Lu, S.; Fu, Y. Wayside acoustic fault diagnosis of train wheel bearing based on Doppler effect correction and fault-relevant information enhancement. Adv. Mech. Eng. 2017, 9, 1687814017732676. [Google Scholar] [CrossRef] [Green Version]
- Papaelias, M.; Huang, Z.; Amini, A.; Vallely, P.; Day, N.; Sharma, R.; Kerkyras, Y.; Kerkyras, S. Advanced wayside condition monitoring of rolling stock wheelsets. In Proceedings of the 11th European Conference on Non-Destructive Testing (ECNDT 2014), Prague, Czech Republic, 6–11 October 2014; pp. 6–10. [Google Scholar]
- Nenov, N.; Dimitrov, E.; Dodev, N.; Vasilev, V. Sensors and microsystems of Wayside Monitoring System for rolling stock in motion. In Proceedings of the 2016 39th International Spring Seminar on Electronics Technology (ISSE), Pilsen, Czech Republic, 18–22 May 2016; pp. 418–423. [Google Scholar]
- Vale, C.; Bonifácio, C.; Seabra, J.; Calçada, R.; Mazzino, N.; Elisa, M.; Terribile, S.; Anguita, D.; Fumeo, E.; Saborido, C. Novel efficient technologies in Europe for axle bearing condition monitoring–the MAXBE project. Transp. Res. Procedia 2016, 14, 635–644. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Xiong, W.; Zhang, S.; He, Q.; Kong, F. Nonstationary weak signal detection based on normalization stochastic resonance with varying parameters. Sādhanā 2016, 41, 621–632. [Google Scholar] [CrossRef] [Green Version]
- Choi, J.K. Thermal characteristics of the spindle bearing system with a gear located on the bearing span. Int. J. Mach. Tools Manuf. 1998, 38, 1017–1030. [Google Scholar] [CrossRef]
- Zhou, X.; Zhang, H.; Hao, X.; Liao, X.; Han, Q. Investigation on thermal behavior and temperature distribution of bearing inner and outer rings. Tribol. Int. 2019, 130, 289–298. [Google Scholar] [CrossRef]
- Liu, L.; Song, D.; Geng, Z.; Zheng, Z. A Real-Time Fault Early Warning Method for a High-Speed EMU Axle Box Bearing. Sensors 2020, 20, 823. [Google Scholar] [CrossRef] [Green Version]
- Sun, Z.; Zhang, N. Analysis of the health status of railway vehicle bearings based on improved HDP-HMM. In Proceedings of the 2018 5th International Conference on Systems and Informatics (ICSAI), Nanjing, China, 10–12 November 2018; pp. 507–513. [Google Scholar]
- Cheng, Y.; Wang, Z.; Zhang, W. A novel condition-monitoring method for axle-box bearings of high-speed trains using temperature sensor signals. IEEE Sens. J. 2018, 19, 205–213. [Google Scholar] [CrossRef]
- Márquez, A.C.; de la Fuente Carmona, A.; Marcos, J.A.; Navarro, J. Designing CBM Plans, Based on Predictive Analytics and Big Data Tools, for Train Wheel Bearings. Comput. Ind. 2020, 122, 103292. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Liu, L.; Song, D.; Zhang, W. Fault Pattern Recognition of Axle Box Bearings for High-speed EMU Based on Onboard Real-time Temperature Data. In Proceedings of the 2019 Prognostics and System Health Management Conference (PHM-Qingdao), Qingdao, China, 25–27 October 2019; pp. 1–5. [Google Scholar]
- Yang, X.; Dong, H.; Man, J.; Chen, F.; Zhen, L.; Jia, L.; Qin, Y. Research on temperature prediction for axles of rail vehicle based on lstm. In Proceedings of the International Conference on Electrical and Information Technologies for Rail Transportation, Qingdao, China, 25–27 October 2019; pp. 685–696. [Google Scholar]
- Chen, Y.; Zhang, C.; Zhang, N.; Chen, Y.; Wang, H. Multi-task learning and attention mechanism based long short-term memory for temperature prediction of EMU bearing. In Proceedings of the 2019 Prognostics and System Health Management Conference (PHM-Qingdao), Qingdao, China, 25–27 October 2019; pp. 1–7. [Google Scholar]
- Gu, J.; Huang, M. Fault Diagnosis Method for Bearing of High-Speed Train Based on Multitask Deep Learning. Shock Vib. 2020, 2020, 8873504. [Google Scholar] [CrossRef]
- Wang, X.; Liu, F.; Chen, Y. Application of Spatio-Temporal Attention Mechanism in Temperature Prediction of High-Speed Train Bogie. In Proceedings of the 2019 Prognostics and System Health Management Conference (PHM-Paris), Paris, France, 2–5 May 2019; pp. 327–331. [Google Scholar]
- Pappaterra, M.J.; Flammini, F.; Vittorini, V.; Bešinović, N. A Systematic Review of Artificial Intelligence Public Datasets for Railway Applications. Infrastructures 2021, 6, 136. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).