Abstract
Flash calculations, including phase split and phase classification for both n-octane/water blends and paraffinic aromatic synthetic naphtha (PASN)/water blends present significant computational challenges. Calculations to establish the two-phase and three-phase regions, as well as the transitions between regions, were addressed by a phase classification method proposed in a recent contribution involving machine learning (ML). This work focusses on the phase-split calculations, considering (a) the lack of numerical convergence of the traditional calculations and their related numerical issues for water/n-octane and PASN/water systems based on the Rachford–Rice derived surfaces and (b) the successful implementation of an ML approach based on a K-nearest-neighbor (KNN) algorithm, which uses the abundant experimental data obtained in a CREC-VL cell.
1. Introduction
Phase equilibrium calculations deal with two main problems [1]: (i) phase stability or the number of phases present, and (ii) phase split or the establishment of the composition and amount of each phase present. For water/hydrocarbon mixtures, conventional approaches to determine phase equilibrium are computationally expensive. Furthermore, the various analyses are penalized by the lack of good initial estimates of equilibrium phase ratios [2,3].
While the number of phases at thermodynamic equilibrium is an unknown condition, as considered in our previous work [4,5,6], experimental data from the CREC-VL cell can be used to determine whether two-phase or three-phase regions are present. This allows for, in combination with ML, an effective “a priori” classification of the number of phases. This also reduces the computational cost and gives better initial estimates of the phase-split calculation once the model is trained.
Traditionally, the designated Rachford–Rice equations [7] can be used to solve the phase-split calculations for a flash unit (Figure 1 and Figure 2). The equations for both two-phase and three-phase calculations are summarized in Equations (1)–(3).
where corresponds to the vapor mole fraction, zi is the molar fraction of component i, Ki stand for the equilibrium constants, and Hi is an auxiliary variable.
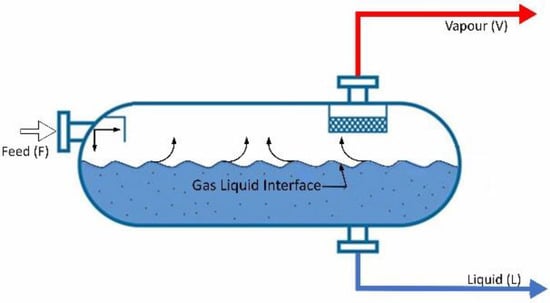
Figure 1.
Schematic representation of a flash system dealing with two phases.
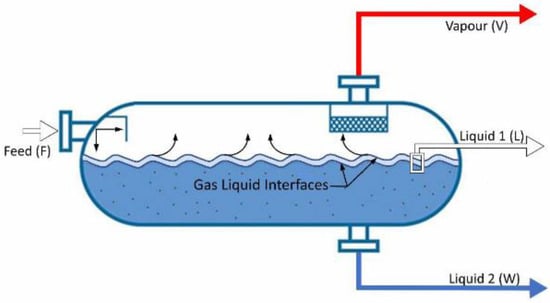
Figure 2.
Schematic representation of a flash system dealing with three phases.
Calculations using the Rachford–Rice equations may involve different numerical approaches as reported in the technical literature, such as successive substitution, quasi-Newton, Newton, steepest-descend, and their modifications and combinations [2].
In the present study, two-phase and three -flash calculations are specifically developed for water/n-octane and PASN/water blends using the Soave–Redlich–Kwong–Kabadi–Danner equation of state (SRKKD EoS). Following this, convergence calculations and numerical issues for water/n-octane and for PASN/water systems are established by using the resulting Rachford–Rice derived surfaces. Once this is accomplished, phase-split computations are compared with those from the ML approach in terms of vapor pressure. The outcome of this highlights the importance of an ML approach for accurate predictions, which is developed quite effectively by using the abundant research data available from the CREC-VL Cell experiments [8].
2. Mathematical Model
Soave–Redlich–Kwong–Kabadi–Danner (SRKKD) Equation of State
Traditionally, the Peng–Robinson (PR) equation of state (EoS) is one of the most popular EoSs, for calculating hydrocarbon-based PVT behavior, including vapor pressures [9]. When using simulation software, such as HYSYS V9 or Aspen Plus V9, it is considered one of the most improved thermodynamic models available, given its large binary interaction parameter database.
However, the PR EoS displays limitations when it is considered for water or aqueous hydrocarbon mixtures [10]. In these cases, as suggested by previous research from our CREC-UWO group [8], the PR EoS does not describe well the system under study, and a different EoS must be used. In binary systems, such as n-octane/water mixtures, an activity coefficient model can be used, as we proposed in our previous work [4].
Nevertheless, classical activity coefficient models are limited to low pressures (≤10 bar) with no C7+ species included. In the case of water and heavy hydrocarbons, such as naphtha or bitumen (C7+), as in the present study, a cubic equation of state is strongly suggested. In this work, the Soave–Redlich–Kwong (SRK) EoS with a Kabadi–Danner [11] modification is used. These authors suggested that the SRK EoS with Kabadi–Danner modification improves the VLLE calculations for water–hydrocarbon systems, particularly under highly diluted hydrocarbons in water, which is of great interest for this research.
Given the reported advantages of using the Kabadi–Danner modification with the Soave–Redlich–Kwong EoS (SRKKD EoS) for VLL equilibrium calculations for hydrocarbon–water blends [12,13], the SRKKD EoS was used in the present study. The SRKKD EoS can be defined by Equations (4)–(8) as follows:
where and .
The mixing rules required to determine the SRK EoS parameters are given by Equations (10) and (11), with the Kabadi–Danner modification being reported by Equations (9) and (12)–(14) [11].
With respect to , it can be calculated using group contribution methods, which account for the sum of the contributions of the different functional groups included in every hydrocarbon molecule. Values from various functional groups can be obtained from the table published by Kabadi–Danner (1985) [11]. The kij parameters used for the calculations reported in this work were taken from HYSYS V9 software.
Furthermore, to compute the fugacity coefficient with the SRKKD EoS, Equations (15) and (16) can be used [14] as follows:
3. Materials and Methods
3.1. Materials
Distilled water was used with a pH of 7 ± 0.05 and a total organic carbon of less than 0.1 ± 0.02 ppm for all experimental studies. In the case for the alkane compounds, Sigma-Aldrich HPLC assay purity reagents were used. The purity of those hydrocarbons was represented in mole percent as follows: n-hexane >97%, n-heptane >96%, n-octane >99%, n-decane >99%, n-dodecane >99%. The water content of the n-alkanes was 0% for n-octane and n-dodecane, 0.01% for n-hexane and n-decane, and 0.02% for n-heptane. Toluene was obtained from Fisher Scientific with a purity >99% and 0.008% water content.
3.2. CREC Vapor–Liquid Equilibrium Cell
The Chemical Reactor Engineering Center (CREC) developed a CREC VL-Cell [15] that allows for the measurement of VLL equilibrium (Figure 3). This unit uses a “dynamic method”. The temperature of the cell increases progressively by using a thermal ramp of 1.2 °C/min. As a result, every run provides plenty of vapor–liquid equilibrium data at 10 Hz every 0.01 s. Additional explanations about the cell operation are reported in [8,15].

Figure 3.
Representation of: (a) the CREC VL-Cell apparatus and (b) a schematic of the mixing patterns inside the CREC VL-Cell.
The CREC VL-Cell uses a marine type of impeller (propeller). The unit propeller helps to ensure a well dispersed and homogeneous blend of non-miscible liquids. This provides a good heat distribution inside the CREC VL-Cell. Furthermore, the special cell design allows one to directly analyze a process sample. It also avoids losses of light volatile components due to sample transfers.
The CREC VL-Cell has two thermocouples strategically located inside the CREC VL-Cell and connected to a temperature data acquisition unit. The thermocouples help to measure both the gas- and liquid-phase temperatures within the VL-Cell through a USB desktop computer port. As a result, experimental data can be stored and displayed in real time on a PC using Omega temperature data acquisition software.
In addition to these features, the CREC VL-Cell includes a pressure transducer placed alongside a pressure gauge. The combinations of two separate pressure instruments allows for simultaneous measurement and validation of the saturation vapor pressure. The pressure transducer is logged into a desktop USB port, allowing for observation and registration of the changes of pressure through the Omega software. Thus, one should note that the instrumentation implemented into the CREC VL-Cell delivers accurate temperature and pressure data [15]. In addition, the automatization of the CREC VL-Cell permits the collection of large amounts of vapor pressure data per experiment, which constitute a very valuable source of information for VLL equilibrium simulations and modeling.
4. Results and Discussion
4.1. Traditional Phase-Split Calculations
Traditionally, phase-split calculations are performed by solving Rachford–Rice (RR) equations involving phase equilibrium constants. Rachford–Rice equations are nonlinear functions obtained from the equal chemical potentials combined with species material balances [2].
In the case of the three-phase flash, the main equations (Equations (17)–(21)) are reported below, with the hydrocarbon phase used as a as reference [2,16].
Or
In this respect, the root-finding calculation is a complex one, given these equations present discontinuities at their extremes (division by zero) and may have an almost flat slope near their roots [17].
Additionally, in solving the Rachford–Rice equations, the choice of numerical method is influenced by the independent variables that are selected, such as component mole fractions, equilibrium ratios, or the logarithm of equilibrium ratios [18].
When equilibrium constant ratios or logarithms of equilibrium constants are considered, a Newton–Raphson method is typically applied. In the case of mole fractions, either a Newton method or a minimization of Gibbs free energy can be considered [19]. Logarithms of K calculations are usually preferred, given the use of mole fractions may create an ill-defined Jacobian, and the natural logarithm stabilizes the Newton method when K values of different orders of magnitude are involved [18].
Regarding multiphase flash-split calculations with three or more phases, they typically involve an outer loop, where the equilibrium constants are calculated, and an inner loop, where the mass balances (Rachford–Rice equations) are evaluated. The end goal is to determine the phase mole fractions and the compositions for a given set of K values [20]. This inner loop is known as “constant-K” flash [21].
Given the above, a general algorithm to solve multiphase flash calculations is described in Figure 4. It can be observed that within each successive substitution step, the Rachford–Rice equations designated as “constant-K” flash are solved independently.
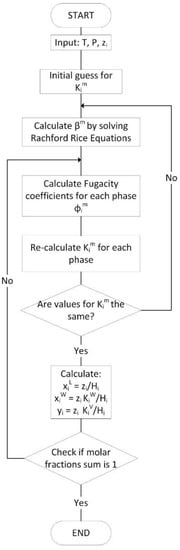
Figure 4.
Traditional algorithm for three-phase flash calculations. Adapted with permission from Ref. [23]. 2006, Saeid Mokhatab, William A. Poe, James G. Speight.
One should note that the solution of the two-phase constant-K flash calculation is a relatively easy one. However, and in the case where one has to account for a three-phase flash, these calculations may become extensive and challenging. This is due to the non-linearity of the objective resulting functions [18].
The “constant-K” flash is discussed in Section 4.2. In this respect, in phase-split calculations, good initial estimates increase the probability of finding the global minimum Gibbs free energy, with an initial guess from stability testing or the previous simulation timestep being an option [2]. To accomplish this, constraints for the initial estimates are usually needed, as suggested previously by Okuno et al. [20] and Leibovici and Neoschil [22].
4.2. Constant-K Flash Solution
The solution of the “constant-K flash” has been studied previously using two different approaches [24], which include (i) minimization techniques and (ii) direct solution of the RR equations. Tranenstein (1985) [19] proposed a constrained minimization of the Gibbs free energy to solve the two-phase problem, whereas Leibovicy and Jean (1995) [22] used a Newton procedure with a relaxation parameter to solve the multiphase problem. Furthermore, Okuno et al. (2010) [20] minimized the non-monotonic convex function using the independent-phase mole fractions. Haugen et al. (2011) [24] used a two-dimensional bisection method to provide good initial guesses for the Newton algorithm in the three-phase case. Li and Firoozabadi (2012) [2] employed stability testing as an initial guess for phase-split calculations with a two-dimensional bisection method for two and three phases. Yan and Stenby (2014) [25] proposed Householder’s high-order iteration method together with a method to improve the initial estimate for the two-phase problem. More recently, Fernandez-Martinez et al. (2020) [17] applied an associated polynomial to obtain all the roots of a two-phase isothermal flash.
One of the most popular approaches to solve the “constant-K” flash problem is to use a Newton–Raphson method to solve Rachford–Rice equations (Equations (17) and (18)), obtaining values for and . In that case, the Newton–Raphson method considered is given by Equations (23)–(27).
Or
The Newton–Raphson method solution can converge to a non-desired root value, with this being a function of the initial guest. It can also lead to numerical divergence, with this being an inherent characteristic of the non-linear equations being solved [18]. As shown by Hinojosa-Gomez et al. (2012) [26], Newton’s method fails to converge near the critical point and phase boundaries. Thus, good initial guesses are required for the phase fraction calculations, with poor initial estimates leading to incorrect roots or being unable to find a numerical solution [24,26].
In this respect, the initial guess for , should be constrained within the proper solution domain. In this sense, when approaching the numerical solution of the constant-K flash, it is advantageous to consider this as an iterative constrained minimization calculation instead of being a root-finding problem [20]:
refers to a convex function, as proven by Okuno et al., 2010 [20], with N linear constrains and with representing the gradient, with the condition of having a symmetric Jacobian matrix [20,27]. If this is the case, the scalar function involves a gradient vector, which represents the RR equations [20].
By integrating (Equations (20) and (21)) with respect to , one can obtain Equation (31), with the integration constant set to zero:
Or, alternatively:
When examining the possible mathematical solutions for a multiphase system at equilibrium with the number of phases larger than 2 (Np > 2), one can notice that the range of these solutions is wider than the space of the physical solutions [22]. To address this matter, Leibovicy and Neoschil (1995) [22] proposed that numerical solutions should be limited by hyperplanes defined by:
In this respect, it is important to notice that in Equation (31), the region is unbounded if the following applies: (a) the function is monotonic, (b) it does not have a minimum, and (c) there is no solution to the constant-K flash with Np phases [20].
In that sense, Okuno et al. [20] proposed a feasible solution region based on the non-negativity of phase-component mole fractions in a given phase, L (), such as:
Then, from Equation (34) and with positive phase-component mole fractions in phase L, it results:
And from Equations (35) and (36):
Equations (40), (44), and (47) can be summarized as follows:
For .
Okuno et al. [20] proposed a general definition of these thermodynamic parameters as: with , and .
The constant-K flash problem is solved by Equation (49).
In that sense, Equation (49) accounts for the “negative flash” case. One should note that when the iterative flash procedure yields β values in the or ranges, this leads to a “negative flash” [28]. These “negative flashes”, although “not physically acceptable” roots, can be preserved for the next calculation step. This is the case, given the anticipated function continuity. It is interesting to mention that Okuno et al.’s resulting algorithm performs better with initial negative roots than when the condition is complied from the very beginning in the first calculation step [28].
4.3. Algorithm to Solve the Flash Unit for Water/PASN Mixtures
After addressing the numerical solution of the constant-K flash problem, it is possible to complete the flash calculations as described in Figure 4. In this sense, the steps involved in the flash calculations are as follows:
- Input the operating and feed conditions: T, P, zi;
- Provide an initial guess for the K-values;
- Solve Rachford–Rice equations as discussed in Section 4.2, minimizing Equation (49);
- Calculate , , and from Equations (34)–(36);
- Calculate the fugacity coefficients from Equation (15);
- Calculate objective functions and compare with tolerance:
- Update K-values:
- Check that , , and .
The main problem with the proposed algorithm is that it may be computationally very expensive [1] as a function of the initial guesses chosen, as well as presenting both convergence and accuracy issues.
When applying the Newton–Raphson method (Equations (23)–(27)) using an initial estimate within the set boundaries (as presented in the following section), such as and , for the water/PASN, employing SRKKD EoS model and Python, the result is and root with four iterations only. In this respect, the HYSYS V9 results in this case were and , with the difference being much lower than 0.1%. In contrast and as expected, for the water/n-octane system, the calculation reaches the 10,000 maximum number of iterations with the obtained results not having physical meaning: and .
Given the above, the function (Equation (49)) for the water/PASN mixture was minimized using different methods within the minimize functions available in the Python Optimize library. Tolerance was set in the 10−8 range, with the percentage of difference for the calculated values being lower than 0.3%. Table 1 reports the various methods tested. Best results were obtained using the constrained optimization by linear approximation (COBYLA) method.

Table 1.
Results for water/PASN system using different methods for the minimize function of Scipy-Optimize package for Python.
However, in spite of this, none of the considered methods led us to meaningful physical solutions for water/n-octane blends, as reported in Table 2. Not even a genetic algorithm was able to numerically solve this case, arriving at a result of . Additional explanations of this matter are described in Section 4.4.

Table 2.
Results for water/n-octane system using different methods for the minimize function of Scipy-Optimize package for Python.
Regarding the VLLE for water/PASN, it can be calculated accordingly, as reported in Table 3. In this case, the bubble pressure (), which is of interest for this research, can be calculated using both Python and Hysis V9.

Table 3.
Pressure calculation results for water/PASN system in VLLE region (no air).
However, when comparing VLLE results from HYSYS V9 and results from SRKKD EoS implemented with Python, the described Python algorithm for water/PASN works better to calculate pressure results than HYSYS V9, as shown in Figure 5 and Figure 6, with SRKKD EoS implemented with Python achieving better agreement with experimental data from the CRE VL-Cell.
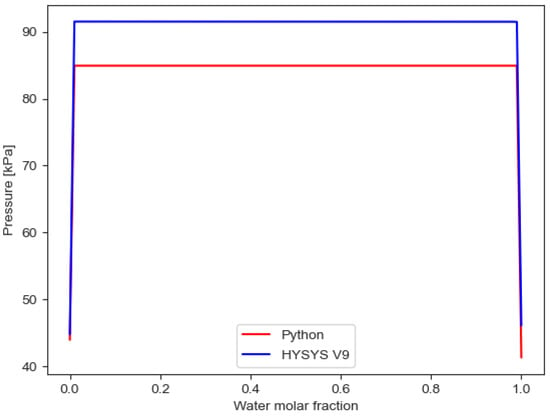
Figure 5.
Comparison of VLLE results for water/PASN using Python and HYSYS V9 (no air).
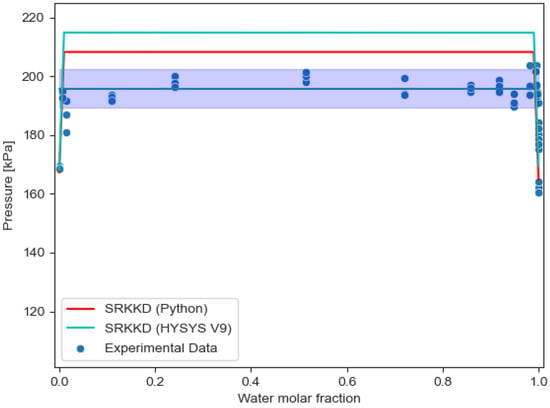
Figure 6.
Comparison of VLLE experimental results for water/PASN using Python and HYSYS V9 at 80 °C.
On the other hand, in the case of water/n-octane blends, the described algorithm presents convergence problems. To describe these issues, it is important to establish how the numerical Rachford–Rice equations (Equations (17)–(19)) influence these types of iterative calculations for both water/n-octane and water/PASN mixtures. To address this matter, the following section evaluates the approach proposed by Li and Firoozabadi [29] and the boundaries set by Okuno et al. [20].
4.4. Issues with Constant-K Solution Calculations
Li and Firoozabadi [29] reported some examples of how and surfaces (Rachford–Rice surfaces) change, whereas and are varied, with and parameters representing the vapor and water fraction, respectively. A display of one of the examples reported by Li and Firoozabadi for a general case [29] is shown in Figure 7 for and intersecting the z = 0 plane.
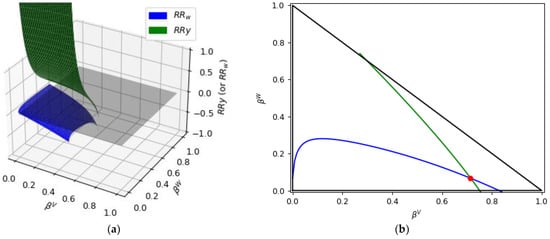
Figure 7.
(a) and surfaces intersecting the z = 0 plane highlighted in grey (Adapted from [29]), (b) The and lines at z = 0 plane. Note: The “red dot” represents the solution at and plane.
The triangle defined in Figure 7a by the vertices (0,1), (0, 0), and (1, 0) represents the solution domain [29], with the solution at and plane shown with a red dot.
In this regard, if one attempts to develop a similar Python-based calculation for an octane/water blend “constant-K” flash, one can observe that it is not possible to obtain a converging iterative solution. This is also true for a wide range of octane in water concentrations in the 0.5–99.75 wt.% range.
As a result, to provide a sound explanation of the findings, the following steps were followed:
- (a)
- The first step involves the SRKKD EoS model and HYSYS V9 with “constant-K” flash simulations. Equilibrium constants are approximated on this basis and used later for a thorough analysis of Rachford–Rice equations.
- (b)
- The second step considers a “constant-K” flash calculation using the equilibrium constant calculated in step 1. This helps to provide a good understanding of how the Rachford–Rice equations perform in such hydrocarbon/water mixtures.
4.4.1. Octane–Water Blends
To illustrate the calculations, a three-phase separator was specified in HYSYS V9 feeding a 100 kgmol/h blend with a 50% mol water/50% mol n-octane mixture for the first step. Working conditions for this three-phase separator were T = 80 °C and a vapor fraction of 0.1. In this case, the presence of air was not considered. Results obtained are reported in Table 4.

Table 4.
HYSYS V9 results for three-phase flash calculations at T = 80 °C using SRKKD.
In developing the second calculation step, using the and constants obtained from HYSYS V9 in Python, the RRy and RRw values were in a low-level range, as shown in Figure 8a. The values of and also changed in a restricted domain. Furthermore, if the value was higher than 0.63 or was higher than 0.58, the solution for and did not converge.
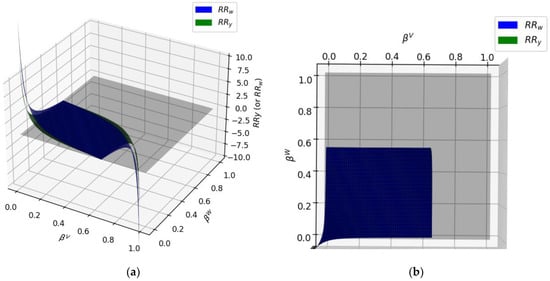
Figure 8.
and surfaces intersecting the z = 0 plane for 50%mole water/n-octane at T = 80 °C. (a) 3D surface, (b) top view.
Additionally, when RRy and RRw were considered at z = 0, the obtained for different values of led to two parallel and z = 0 plane-superimposed RRy and RRw straight lines, as shown in Figure 9. In contrast, an HYSYS V9 solution was obtained, as identified with a red dot in Figure 9.
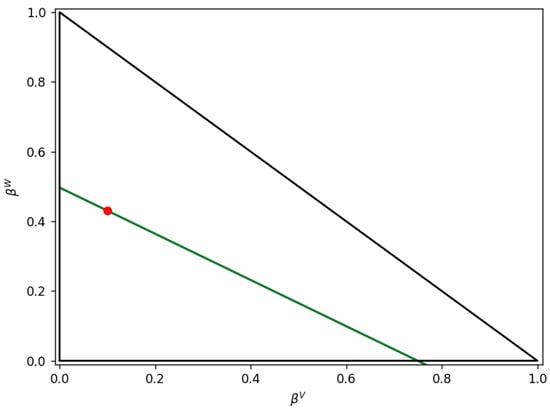
Figure 9.
Lines for and and T = 80 °C. Note: the red point represents HYSYS solution.
As a result of this and under these conditions, one can understand why the iterative calculations trying to find an intersection of the RRy and RRw lines fail and the “constant-K” solution remains unknown.
Regarding these results, Haugen and Firoozabadi [24] advanced that algorithms of this type solving RR equations can fail when the lines at RRy = 0 and RRw = 0 are parallel in the domain of interest. In this respect, these authors designated these conditions as the result of a “bicritical point” where two of the phases have very similar compositions. They identified three different kinds of “bicritical regions” [24]: (i) , (ii) or (iii), and . In this case, the K values for water/n-octane mixtures are as follows: and . As a result and given the conditions considered involving , they could be considered in partial agreement with case (iv) from the Haugen and Firoozabadi criteria [24].
For different temperatures (in this case, 110 °C) (Table 5), the behavior of n-octane/water mixtures displays similar calculation challenges, as can be observed in Figure 10 and Figure 11.

Table 5.
HYSYS V9 results for three-phase flash calculations at T = 100 °C using SRKKD.
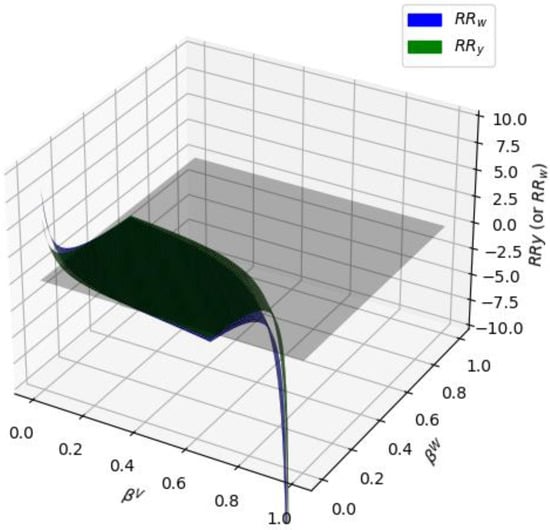
Figure 10.
and surfaces intersecting the z = 0 plane for 30% mole water/n-octane at T = 110 °C.
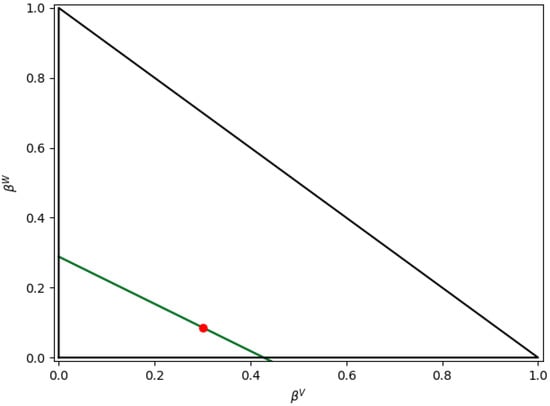
Figure 11.
Lines for and at T = 110 °C. Note: red point represents HYSYS solution.
Haugen et al. (2011) [24] described that the non-converging lines problem leads to a very large number of iterations, with the numerical solution becoming unacceptably expensive.
Thus, in the case of octane/water mixtures, the described and surfaces make it very challenging for a proposed algorithm, such as the SRKKD EoS model with Python algorithm, to converge towards a “constant-K” flash solution.
4.4.2. PASN/Water Blends
In contrast with the “non-convergence” results described in Section 4.3 and Section 4.4.1 for n-octane/water blends, the PASN/water mixtures evaluated with the SRKKD EoS model with Python can provide consistent “constant-K” flash-convergent simulations. This is the case when performing flash calculations for a 50%mole water/PASN mixture. Results after convergence are presented in Table 6.

Table 6.
PASN/water mixture three-phase flash calculations at T = 80 °C and P = 83.16 kPa using SRKKD model, the Rachford–Rice equations and the Python calculations of the present study.
Figure 12 reports the calculated RRy and RRw, using KiV and KiW from the SRKKD model using the Python calculations. In this case, values of and are smaller than 0.5, providing converging numerical solutions in all cases.
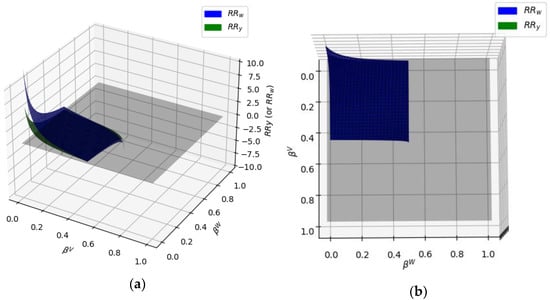
Figure 12.
and surfaces intersecting the z = 0 plane for 50 mol% water/PASN at T = 80 °C. (a) 3D surfaces, (b) top view.
Figure 13 further describes the “constant-K” flash solution for the and lines, displaying the numerical and solutions with convergence assured.
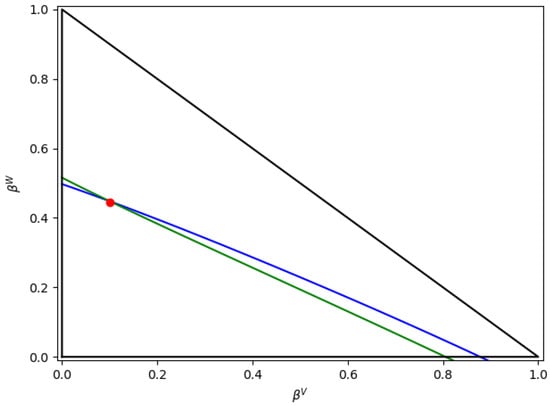
Figure 13.
Lines for and . Note: red point represents Python solution, the blue line is related to , and the green line is related to .
4.4.3. Boundary Conditions
Regarding the boundary conditions, if one considers the water/n-octane mixture with Ki approximated by HYSYS V9 (Figure 11), the boundary conditions proposed by Okuno et al. [20] result in Equations (54) and (55), with the hyperplanes superimposed to the lines for and , as presented in Figure 14.
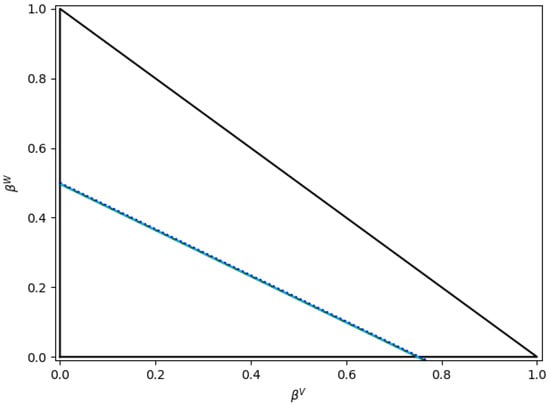
Figure 14.
Boundaries for and as poposed by Okuno et al. [20] for water/n-octane mixtures. Notes: (i) reported lines are for ; (ii) the two superimposed blue lines encompass both Equations (54) and (55) lines.
Furthermore, in applying the boundary conditions proposed by Okuno et al. [20] for the water/PASN blend, the hyperplanes related to Equations (56)–(62) can be represented as in Figure 15.
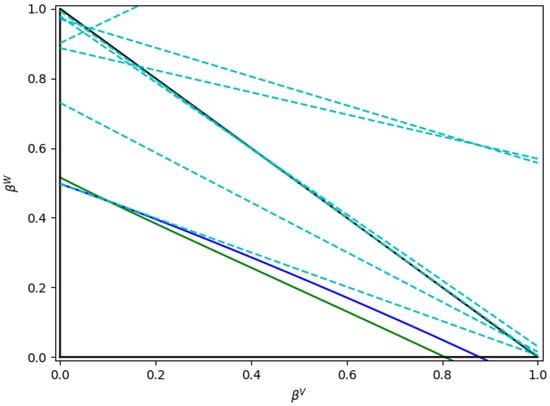
Figure 15.
Boundaries for and as poposed by Okuno et al. [20] for water/PASN mixtures. Notes: (i) the blue solid lines are related to , (ii) the green solid lines to , and (iii) the cyan broken lines represent the boundaries according to Equations (56)–(62).
4.4.4. Remarks
On the basis of results from “constant-K” flash calculations for n-octane/water and PASN/water blends, one can conclude that the composition of hydrocarbon/water blends is a key factor in allowing for a viable numerical calculation using the Rachford–Rice equations. Thus, to address possible calculation uncertainty and ambiguity resulting for octane/water blends, an alternate methodology to calculate the molar fractions and mixture pressure is proposed in the upcoming sections.
4.5. Liquid-Phase K-Values from Experimental Data for Water/n-Octane Mixtures
As discussed in the previous sections, the initial guess for K values affects the convergence of the flash calculation algorithm (Figure 4). Usually, Wilson correlation [30] (Equation (63)) is used as a first approximation for the K value in the hydrocarbon phase. For the K values in the water phase, Connolly et al. [1] suggested values based on the initial feed, as presented in Equation (64).
In this sense, another advantage of the CREC VL-Cell developed by CREC researchers is that it allows one to determine the solubility values based on the VLLE data obtained. The transition from the three-phase and two-phase regions defines the solubility limit. Figure 16 presents the solubility limit regions for a water/n-octane mixture at 110 °C. This region is characterized by the transition from three phases to two phases.
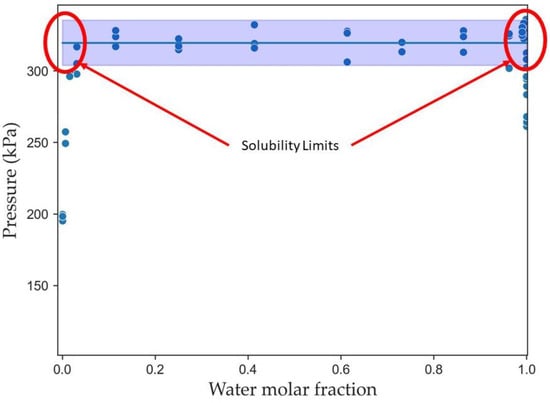
Figure 16.
Solubility limit regions for water/octane at 110 °C.
The applicability of the CREC-VL-Cell for establishing solubility and solubility limits is not restricted to any type of hydrocarbon/water blend. Thus, the CREC-VL-Cell can be of special value in dealing with hydrocarbon/water blends involving intrinsic convergence uncertainties observed by octane–water mixtures while using the Rachford–Rice equations (refer to Section 4.4).
Figure 17 shows that the solubility limit for an octane/water blend can be calculated from the intersection between the lines that define the three-phase and two-phase domain. The calculated solubilities at 110 °C are and , considering the 95% confidence interval defined by the blue region. Although the solubility of water in n-octane is in close agreement with calculated, the value using HYSYS V9 with SRKKD EoS and Rachford–Rice equations yields a solubility for n-octane in water two orders of magnitude higher compared with the Hysis V9-predicted value.
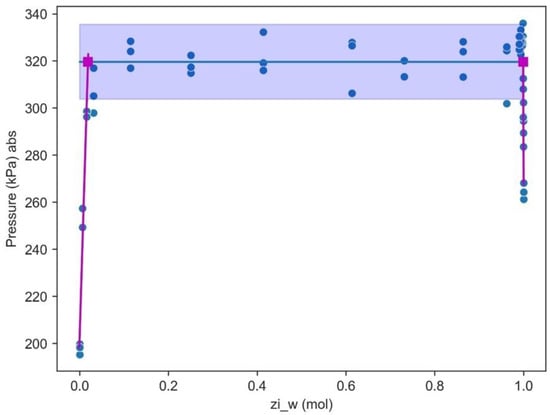
Figure 17.
Calculated solubility limit for water/octane at 110 °C. Note: magenta solid lines represent the two-phase region, whereas the blue solid line represents the three-phase region. Blue bands represent the 95% confidence interval.
As a result, once the solubility values are obtained from the CREC-VL-Cell, it is possible to calculate water-phase constants as . Furthermore, for the vapor phase species at equilibrium, one can obtain an approximative value using and . Assuming the vapor phase behaves as an ideal gas, then , and the obtained results are and .
The mean value obtained has a 16.04% difference from the value predicted by HYSYS V9 (). However, the HYSYS V9 value is within the range of the 95% confidence interval. Figure 18 and Figure 19 report the observed solubilities of water in n-octane and n-octane in water, respectively, as determined in the CREC VL-Cell and compared with the values reported by Maczynski et al. (2004) [31] for both water in n-octane and n-octane in water.
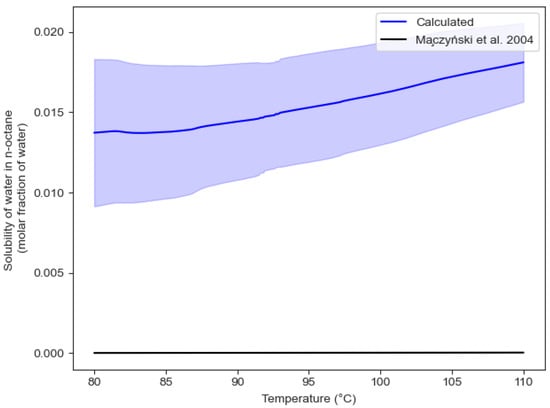
Figure 18.
Solubility of water in n-octane in the temperature range of interest. Note: blue bands represent the 95% confidence interval.
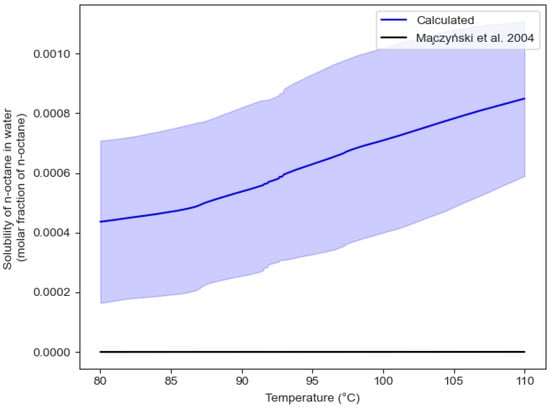
Figure 19.
Solubility of n-octane in water in the temperature range of interest. Note: blue bands represent the 95% confidence interval.
Furthermore, on the basis of the experimental data obtained in the CREC-VL-Cell, a correlation to obtain the K values for water/octane mixtures in the temperature range of interest and low pressure (1–3 atm) is proposed. This correlation is given by the following Equation (65), with the constants involved reported in Table 7. A comparison with calculated values from experimental results is also reported in Figure 20, showing the adequate fitting of the experimental values by this correlation.

Table 7.
Constants for K-value correlation of water/n-octane system.
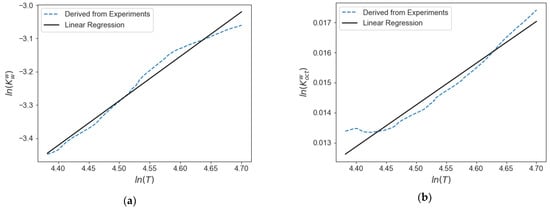
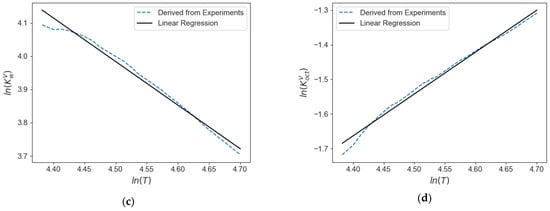
Figure 20.
K values calculated from experimental data in the CREC VL-Cell for water/n-octane mixtures: (a) K value for water in W phase, (b) K value for octane in W phase, (c) K value for water in V phase, (d) K value for octane in V phase.
Given the observed differences with the experimental points reported in Figure 6 and obtained in the CREC-VL-Cell, it is important to provide a more precise methodology to calculate the pressures at VLLE, accounting for the uncertainties related to the experimental values. This will be discussed in the following section.
4.6. Machine Learning Approach
As shown in the previous sections of this work (Section 4.1, Section 4.2, Section 4.3, Section 4.4, Section 4.5), traditional thermodynamic models for multiphase systems based on Rachford–Rice equations overpredict vapor pressure in cases unable to provide converging and meaningful solutions.
Thus, to implement machine learning, linear regression, KNN, SVM, and decision tree regressor (DTR) are considered. On this basis, the prediction errors, coefficients of determination (R2), mean squared errors (MSE), and mean absolute errors (MAE) are established. To accomplish this for each experimental condition, the following is considered: (a) the predicted number of phases together with the feed molar fraction and temperature as input parameters [4,6] and (b) the system pressure as target variable. Additional details of the classification methodology can be found in a recent publication of our research group [4].
In the case of KNN, SVM, and DTR, the parameters were tuned using a grid search with cross validation (GridSearchCV). This method allows for determination of the best set of parameters in each model based on the coefficient of determination (R2). The training set was selected by randomly splitting the sample into 80% for training and 20% testing (train_test_split function). Results for the grid search are summarized in Table 8, showing the best parameters for each method calculated by the GridSearchCV function by comparing R2.

Table 8.
Models selected for the prediction of pressure for water/n-octane.
Table 9 reports the coefficient of determination (R2), mean squared error (MSE), and mean absolute error (MAE) for the selected models (best score) for octane/water using the abundant testing dataset obtained in the CREC VL cell. Figure 21 describes a comparison for the pressures measured and the predicted values, showing that the KNN model provides the best approximation, with an R2 value of 0.99 and MSE values as low as 43.78 and 4.91 parameters. The KNN method is selected as the best model to predict the pressure of water/n-octane mixtures in the range of interest.

Table 9.
Metrics for the selected models. Note: calculated based on test dataset.
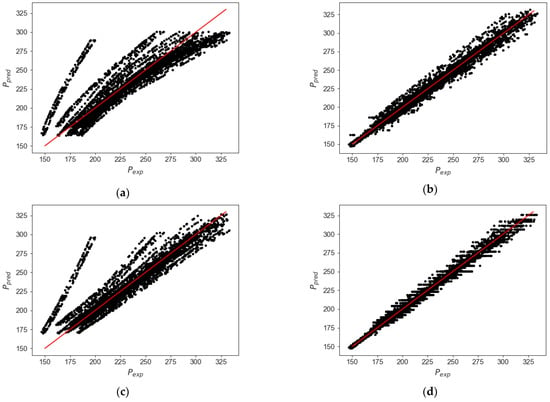
Figure 21.
Test pressure vs. calculated pressure for the different models are as follows: (a) linear regression, (b) KNN, (c) SVC, and (d) decision tree regressor. Note: red line represents a perfect prediction.
The best ML model to describe the behavior of pressure for n-octane/water blends is KNN, with this model overcoming the issues of the traditional thermodynamic models involving the Rachford–Rice equations, significantly reducing the uncertainty of any theoretically thermodynamically based algorithm.
In the same way, if a pseudo-binary mixture is assumed for PASN/water mixtures, a KNN model based on the experimental results can also be applied with an R2 = 0.9933 MSE = 34.24 and MAE = 4.41, as presented in Figure 22. The pseudo-component for the PASN is defined using the hydrocarbon blends reported in Table 6.
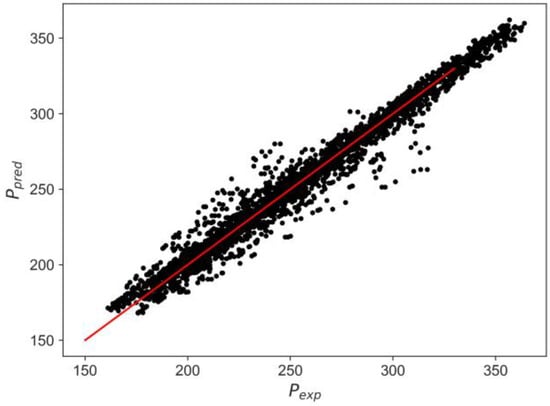
Figure 22.
Test pressure vs. calculated KNN of PASN/water blend. Note: red line represents a perfect prediction.
Although the ML model developed in the present study has the ability to predict vapor pressure efficiently, it requires a significant number of experimental data points allowing for both the training of the proposed model, as well as its validation. In this respect, the availability of laboratory equipment, such as the CREC VL-Cell, providing abundant phase equilibrium data, is critical for both ML model development and validation.
5. Conclusions
- (a)
- Flash calculations for n-octane/water and PASN/water systems can be described, in principle, using the SRKKD EoS and Rachford–Rice equations. However, the SRKKD EoS and Rachford–Rice equations involve convergence issues in the case of n-octane/water mixtures. These convergence issues were clarified considering the parallelism of the RRx and RRy (Rachford–Rice) planes for n-octane/water systems.
- (b)
- Flash calculations for synthetic naphtha/water (PASN/water) blends implemented using a Python-based algorithm showed numerical solutions free of converging issues, although with numerical solutions showing a lack of accurate prediction of naphtha–water solubility.
- (c)
- Data from the CREC VL-Cell can be used to propose correlations for the calculation of solubility of n-octane in water and water in n-octane, as well as the equilibrium constant values.
- (d)
- Data from the CREC VL-Cell and the developed ML approach with the KNN model showed the best performance with, an R2 = 0.9911, for accurately predicting the total pressure in water/n-octane mixtures, and R2 = 0.9933 in the case of PASN/water mixtures.
Author Contributions
Conceptualization, S.L.-Z. and H.d.L.; methodology, S.L.-Z., S.E. and H.d.L.; software studies, S.L.-Z.; validation, S.L.-Z. and S.E.; formal analysis, S.L.-Z. and H.d.L.; investigation, S.L.-Z.; resources, H.d.L.; data curation, S.E.; writing—original draft preparation, S.L.-Z.; writing—review and editing, H.d.L. and S.E.; visualization, S.L.-Z. and S.E.; supervision, H.d.L. and S.E.; project administration, H.d.L.; funding acquisition, H.d.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science and Engineering Research Council of Canada (NSERC) and Syncrude Canada Ltd., Calgary, AB, Canada, under the NSERC-CRD program.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data used in this study are openly available in https://ir.lib.uwo.ca/etd/7283/ accessed on 1 January 2021.
Acknowledgments
The authors would like to acknowledge Jeonghoon Kong for the execution of the experiments in the CREC VL-Cell and Sujit Bhattacharya from Syncrude Canada Ltd. for his valuable comments and advice during the development of this research. The authors would also like to thank the Natural Science and Engineering Research Council of Canada (NSERC) and the industrial sponsor, Syncrude Canada Ltd., for the financial support provided for this work under the NSERC-CRD program. Additionally, the authors would like to acknowledge Florencia de Lasa for her assistance with the editing of this manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
Symbols with Latin letter
| i | identifies component i of the solution |
| j | summation index running through all components |
| identifies a subgroup | |
| summation index running through all subgroups present in the solution | |
| number of subgroups, k, present in component i | |
| relative volume of subgroup k (tabulated) | |
| relative surface area of subgroup k (tabulated) | |
| interaction energy between subgroups m and k | |
| Acronyms | |
| ANN | Artificial neural network |
| EoS | Equation of state |
| FNN | Feedforward neural network |
| KNN | K -nearest-neighbor algorithm |
| logsig | Logarithmic sigmoid (activation function) |
| ML | Machine learning |
| NRU | Naphtha recovery unit |
| PASN | Paraffinic aromatic synthetic naphtha |
| PNN | Probabilistic neural network |
| PR-EoS | Peng–Robinson equation of state |
| SRKKD | Soave–Redlich–Kwong–Kabadi–Danner equation of state |
| RBF | Radial basis transfer |
| RVM | Relevance vector machines |
| SRK-EoS | Soave–Redlich–Kong equation of state |
| TPR | Three-phases region |
| tansig | Hyperbolic tangent sigmoid |
| VLE | Vapor–liquid equilibrium |
| VLLE | Vapor–liquid–liquid equilibrium |
References
- Connolly, M.; Pan, H.; Tchelepi, H. Three-Phase Equilibrium Computations for Hydrocarbon–Water Mixtures Using a Reduced Variables Method. Ind. Eng. Chem. Res. 2019, 58, 14954–14974. [Google Scholar] [CrossRef]
- Li, Z.; Firoozabadi, A. General Strategy for Stability Testing and Phase-Split Calculation in Two and Three Phases. SPE J. 2012, 17, 1096–1107. [Google Scholar] [CrossRef]
- Li, R.; Li, H.A. Improved Three-Phase Equilibrium Calculation Algorithm for Water/Hydrocarbon Mixtures. Fuel 2019, 244, 517–527. [Google Scholar] [CrossRef]
- Lopez-Zamora, S.; Kong, J.; Escobedo, S.; de Lasa, H. Thermodynamics and Machine Learning Based Approaches for Vapor-Liquid-Liquid Phase Equilibria in N-Octane/Water Blends, as a Naphtha-Water Surrogate in Water Streams. Processes 2021, 9, 413. [Google Scholar] [CrossRef]
- Lopez-Zamora, S.; Kong, J.; Escobedo, S.; de Lasa, H. Vapour-Liquid-Liquid and Vapour-Liquid Equilibrium of Paraffinic Aromatic Synthetic Naphtha/Water Blends: Prediction of The Number of Phases. Can. J. Chem. Eng. 2021, pp. 1–19. Available online: https://onlinelibrary-wiley-com.proxy1.lib.uwo.ca/doi/full/10.1002/cjce.24230 (accessed on 7 October 2021).
- Lopez-Zamora, S.M. Thermodynamic Vapor-Liquid Equilibrium in Naphtha-Water Mixtures; The University of Western Ontario: London, ON, Canada, 2021. [Google Scholar]
- Rachford, H.H.; Rice, J.D. Procedure for Use of Electronic Digital Computers in Calculating Flash Vaporization Hydrocarbon Equilibrium. J. Pet. Technol. 1952, 4, 19. [Google Scholar] [CrossRef]
- Kong, J. Multiphase Equilibrium in A Novel Batch Dynamic VL-Cell Unit with High Mixing: Apparatus Design and Process Simulation; The University of Western Ontario: London, ON, Canada, 2020. [Google Scholar]
- Castellanos Diaz, O. Measurement and Modelling Methodology for Heavy Oil and Bitumen Vapour Pressure; University of Calgary: Calgary, AB, Canada, 2012. [Google Scholar]
- Wu, J.; Prausnitz, J.M. Phase Equilibria for Systems Containing Hydrocarbons, Water, and Salt: An Extended Peng-Robinson Equation of State. Ind. Eng. Chem. Res. 1998, 37, 1634–1643. [Google Scholar] [CrossRef] [Green Version]
- Kabadi, V.N.; Danner, R.P. A Modified Soave-Redlich-Kwong Equation of State for Water-Hydrocarbon Phase Equilibria. Ind. Eng. Chem. Process Des. Dev. 1985, 24, 537–541. [Google Scholar] [CrossRef]
- Sadjadi, S.; Hosseinpour, M.; Mohammadnezhad, F.; Ahmadi, S.J.; Khazayi, M.A. Hydrogen-Deuterium Chemical Exchange in Supercritical Water: Thermodynamic Considerations for Optimizing the Synthesis of High Degree Deuterated Benzene. J. Supercrit. Fluids 2017, 125, 96–103. [Google Scholar] [CrossRef]
- Safamirzaei, M.; Modarress, H. Modeling and Predicting Solubility of N-Alkanes in Water. Fluid Phase Equilibria 2011, 309, 53–61. [Google Scholar] [CrossRef]
- Matsoukas, T. Fundamentals of Chemical Engineering Thermodynamics: With Applications to Chemical Processes; Pearson Education, Inc.: Livonia, MI, USA, 2013. [Google Scholar]
- Escobedo, S.; Kong, J.; Lopez-Zamora, S.; de Lasa, H. Synthetic Naphtha Recovery from Water Streams: Vapor-Liquid-Liquid Equilibrium (VLLE) Studies in a Dynamic VL-Cell Unit with High Intensity Mixing. Can. J. Chem. Eng. 2022, 100, 607–625. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, T.; Sun, S.; Gao, X. Accelerating Flash Calculation through Deep Learning Methods. J. Comput. Phys. 2019, 394, 153–165. [Google Scholar] [CrossRef] [Green Version]
- Fernández-Martínez, E.H.; López-López, E. Some Theoretical Results on Rachford-Rice Equation for Flash Calculations: Multi-Component Systems. Comput. Chem. Eng. 2020, 140, 106962. [Google Scholar] [CrossRef]
- Connolly, M. An Isenthalpic-Based Compositional Framework for Nonlinear Thermal Simulation; Stanford University: Stanford, CA, USA, 2018. [Google Scholar]
- Trangenstein, J.A. Minimization of Gibbs Free Energy in Compositional Reservoir Simulation. Soc. Pet. Eng. AIME SPE 1985, 233–246. [Google Scholar] [CrossRef]
- Okuno, R.; Johns, R.T.; Sepehrnoori, K. A New Algorithm for Rachford-Rice for Multiphase Compositional Simulation. SPE J. 2010, 15, 313–325. [Google Scholar] [CrossRef]
- Okuno, R. Modeling of Multiphase Behavior for Gas Flooding Simulation; The University of Texas at Austin: Austin, TX, USA, 2009. [Google Scholar]
- Leibovici, C.F.; Jean, N. A Solution of Rachford-Rice Equations for Multiphase Systems. Fluid Phase Equilibria 1995, 112, 217–221. [Google Scholar] [CrossRef]
- Mokhatab, S.; Poe, W.A.; Speight, J.G. Handbook of Natural Gas Transmission and Processing; Gulf Professional Publishing: Burlington, MA, USA, 2006; Volume 66. [Google Scholar]
- Haugen, K.B.; Firoozabadi, A.; Sun, L. Efficient and Robust Three-Phase Split Computations. AIChE J. 2011, 59, 2555–2565. [Google Scholar] [CrossRef]
- Yan, W.; Stenby, E.H. On Solving the Rachford-Rice Equation with Higher Order Methods. Fluid Phase Equilibria 2014, 363, 290–292. [Google Scholar] [CrossRef]
- Hinojosa-Gomez, H.; Solares-Ramırez, J.; Bazua-Rueda, E.R. An Improved Algorithm for the Three-Fluid-Phase VLLE Flash Calculation Humberto. AIChE J. 2012, 59, 215–228. [Google Scholar] [CrossRef]
- Bertsekas, D.P. Nonlinear Programming, 2nd ed.; Athena Scientific: Belmont, MA, USA, 1999; ISBN 9781886529007 1886529000. [Google Scholar]
- Whitson, C.H.; Michelsen, M.L. The Negative Flash. Fluid Phase Equilibria 1989, 53, 51–71. [Google Scholar] [CrossRef]
- Li, Z.; Firoozabadi, A. Initialization of Phase Fractions in Rachford-Rice Equations for Robust and Efficient Three-Phase Split Calculation. Fluid Phase Equilibria 2012, 332, 21–27. [Google Scholar] [CrossRef]
- Wilson, G.M. A Modified Redlich-Kwong Equation of State, Application to General Physical Data Calculations. In Proceedings of the 65th National AIChE Meeting, Cleveland, OH, USA, 4–7 May 1969. [Google Scholar]
- Ma̧czyński, A.; Wiśniewska-Gocłowska, B.; Góral, M. Recommended Liquid-Liquid Equilibrium Data. Part 1. Binary Alkane-Water Systems. J. Phys. Chem. Ref. Data 2004, 33, 549–577. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).