Characterization of Stressing Conditions in a High Energy Ball Mill by Discrete Element Simulations
Abstract
:1. Introduction
2. Materials and Methods
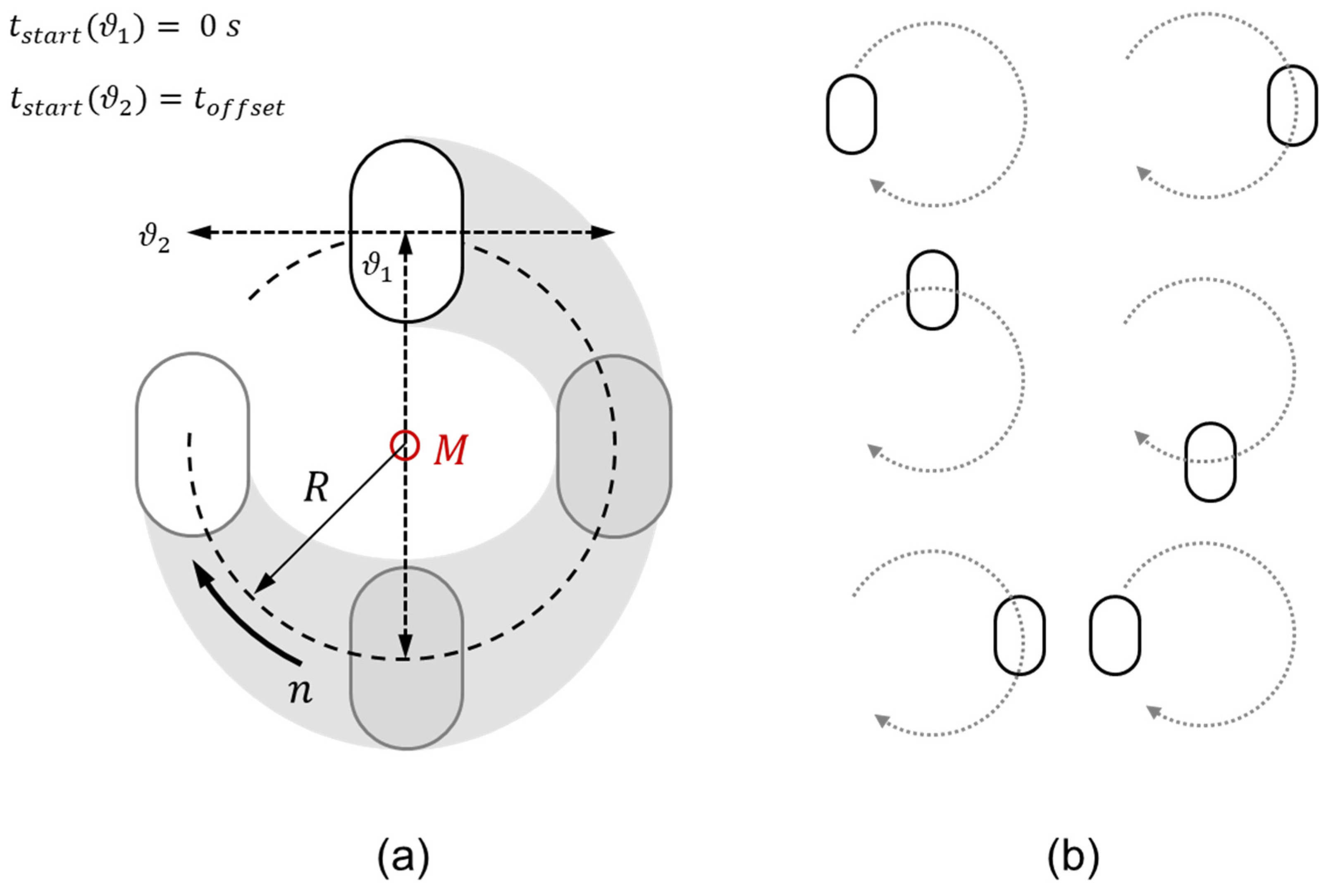
2.1. Simulation Set-Up
2.2. Simulation Model
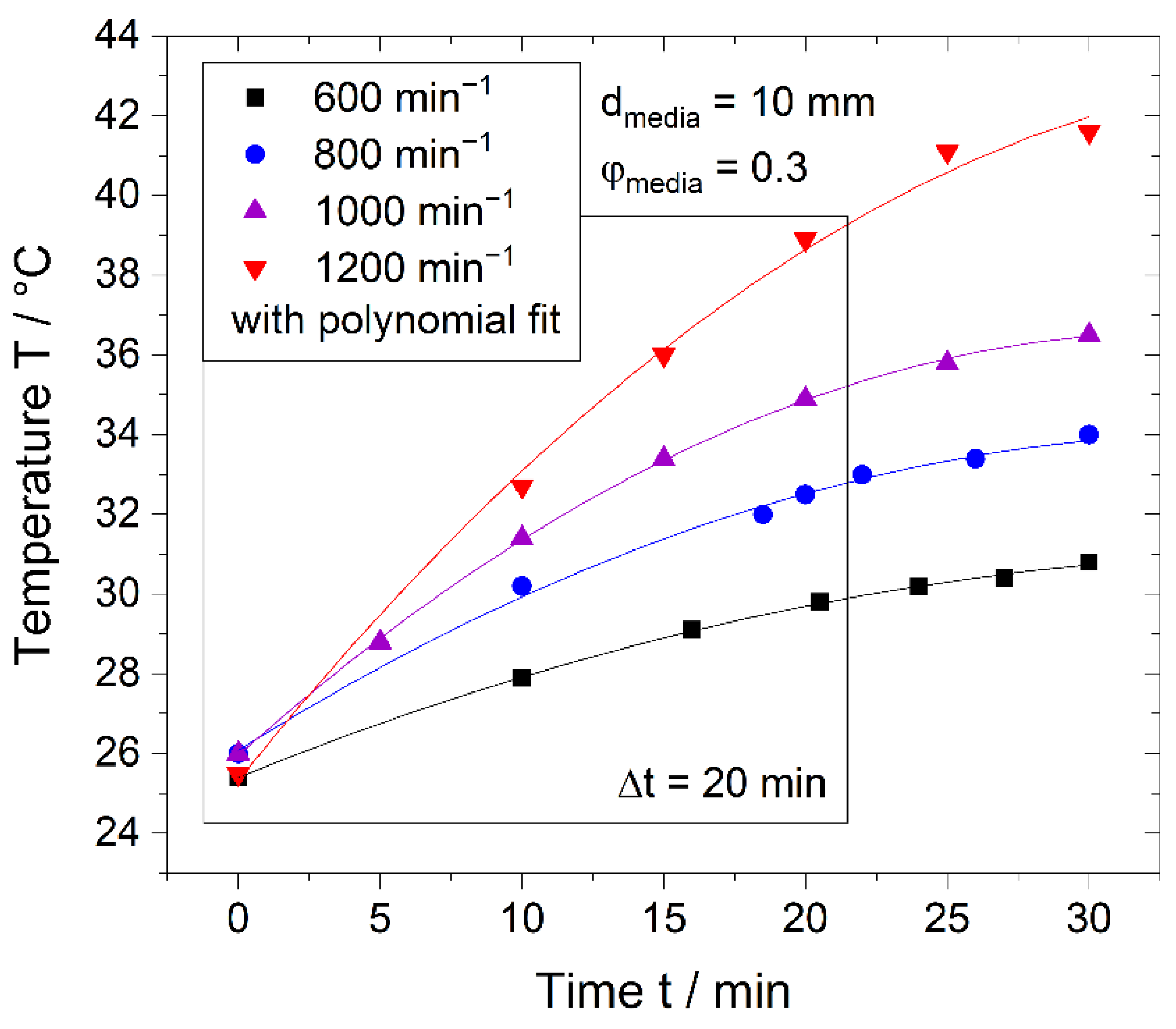
2.3. Simulation Validation via Thermal Energy
2.4. Simulation Operation Parameters
2.5. Comparison of High Energy Mill and Planetary Mill
2.6. Calculation of Energy Dissipation
3. Results and Discussion
3.1. Simulation Validation
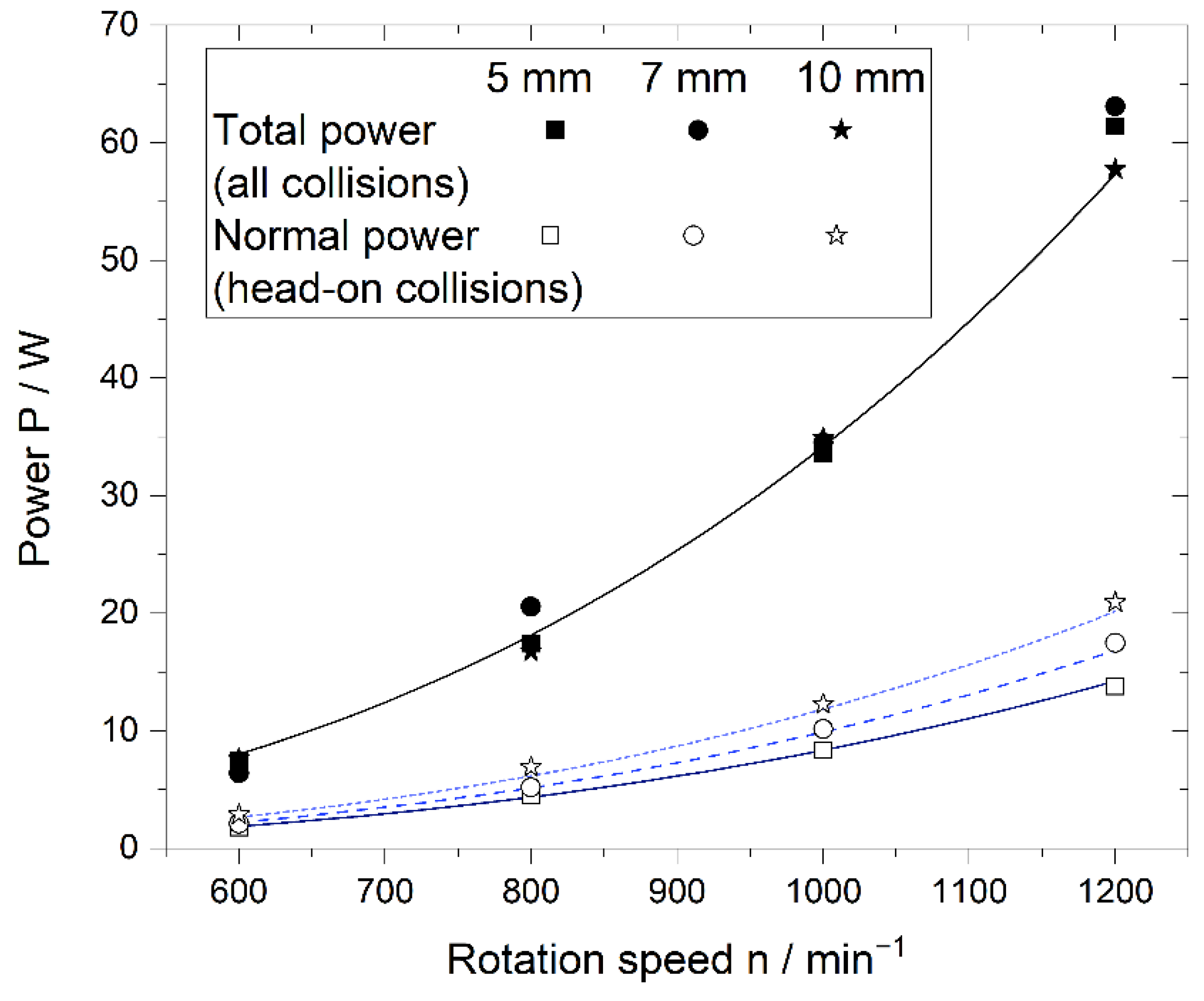
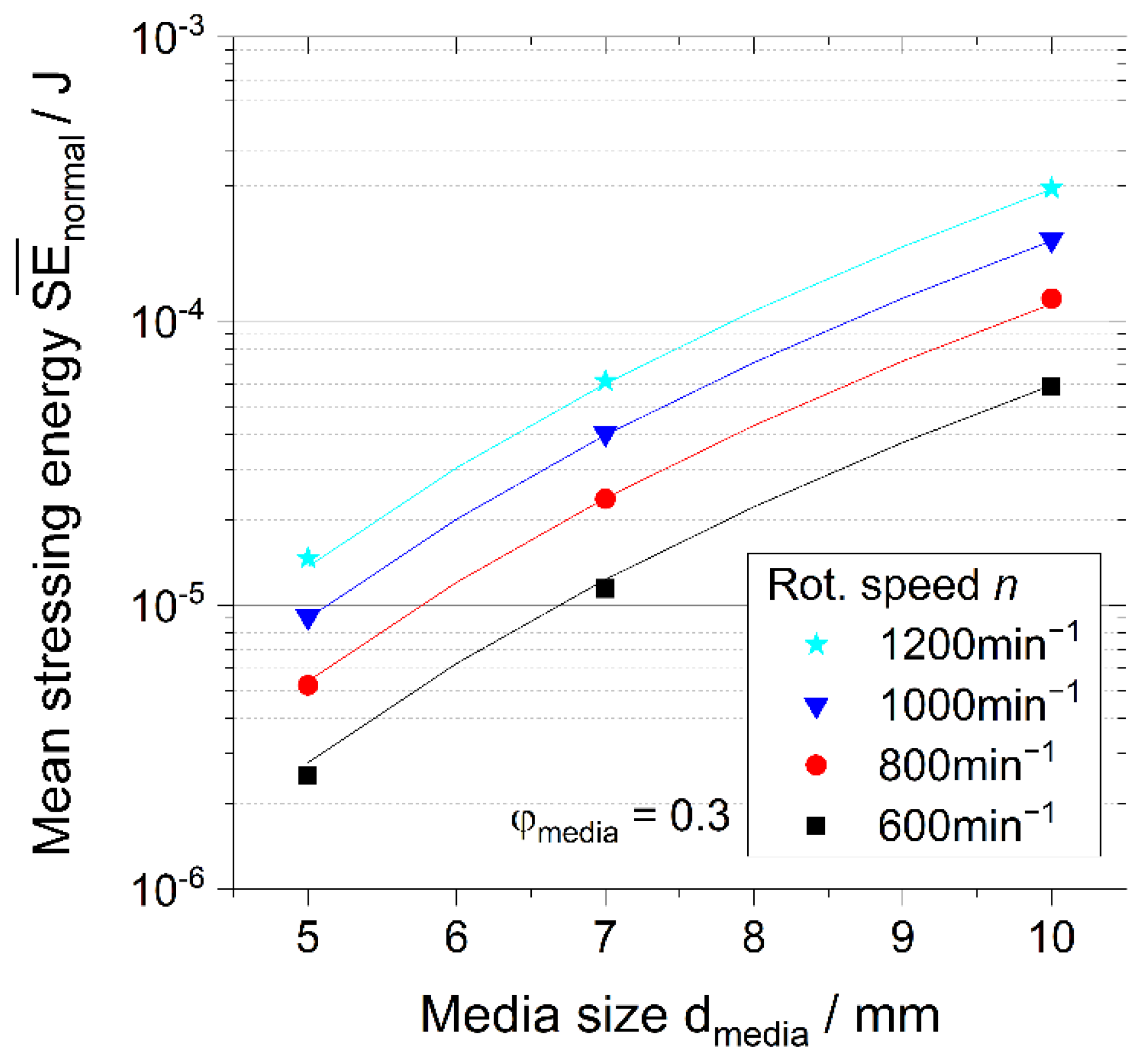
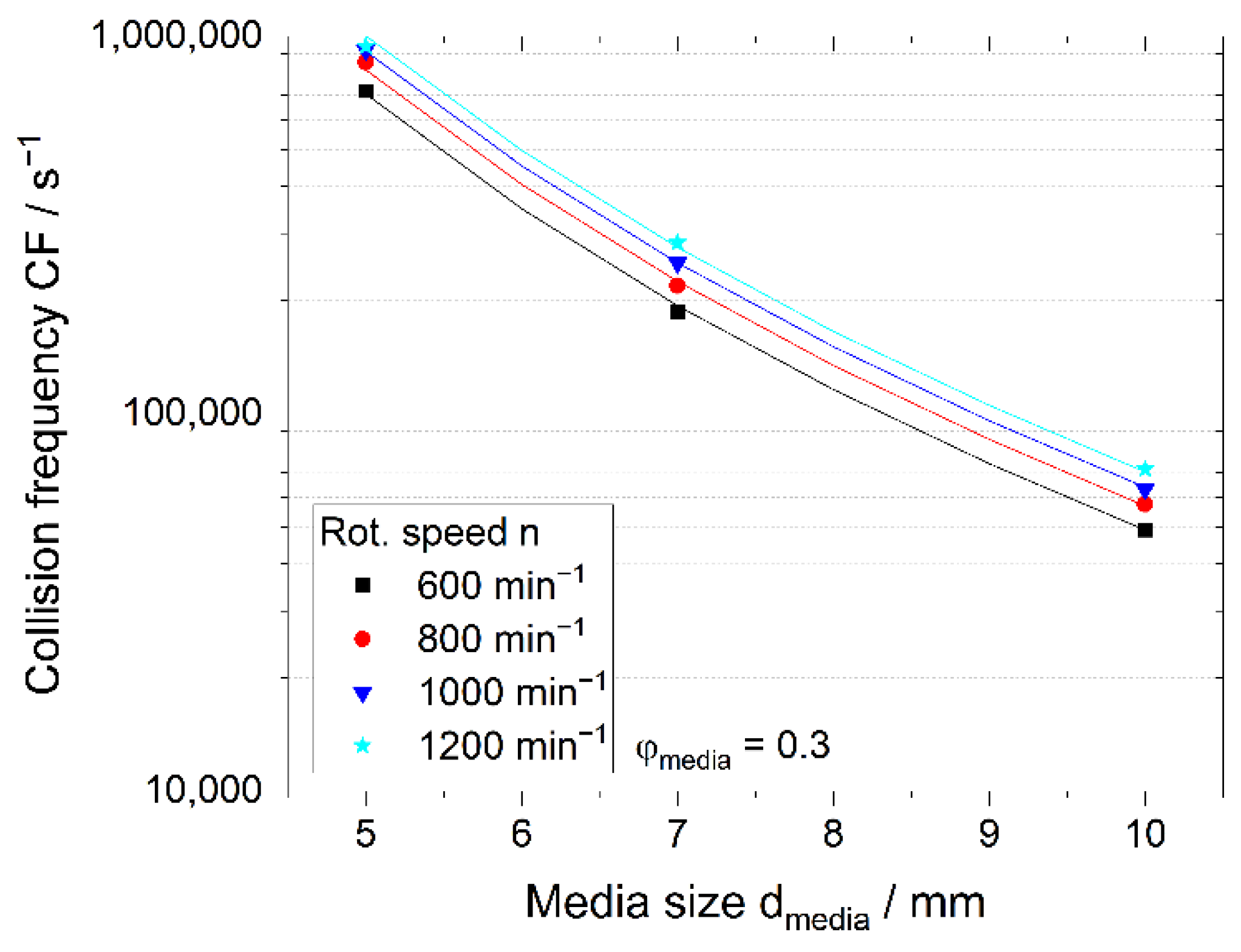
3.2. Effect of Media Size and Rotational Speed
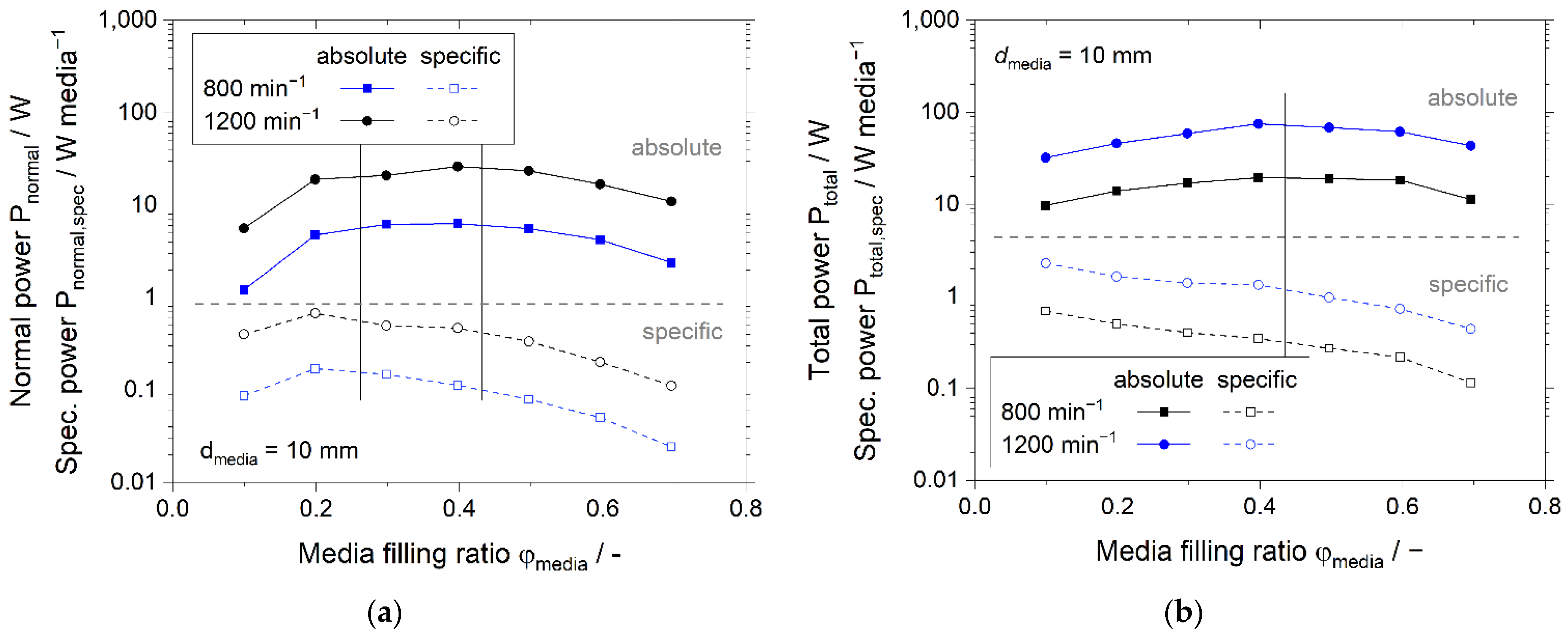
3.3. Effect of Media Filling Ratio
3.4. Discussion on Application of Mechanistic Model Equations
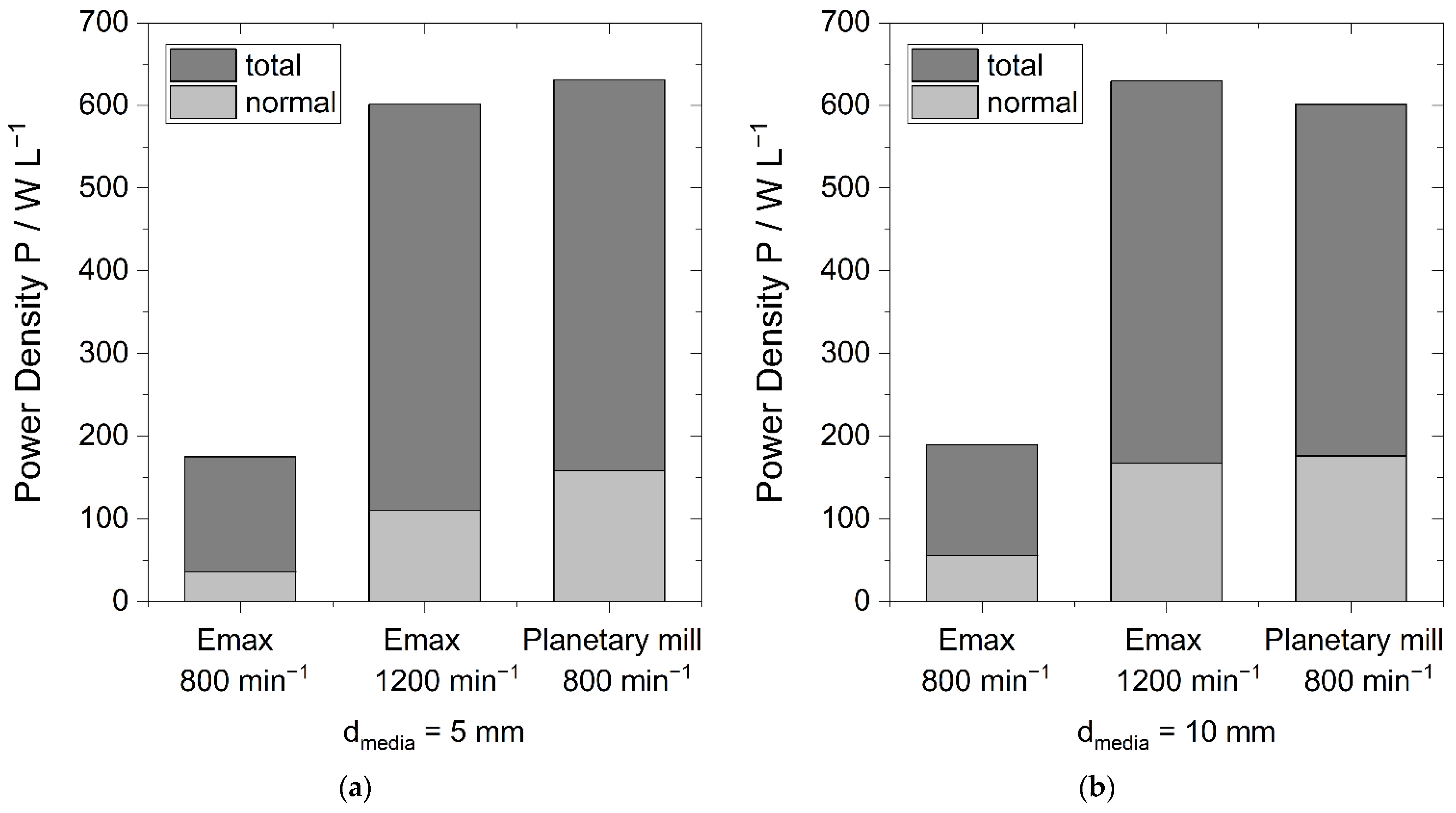
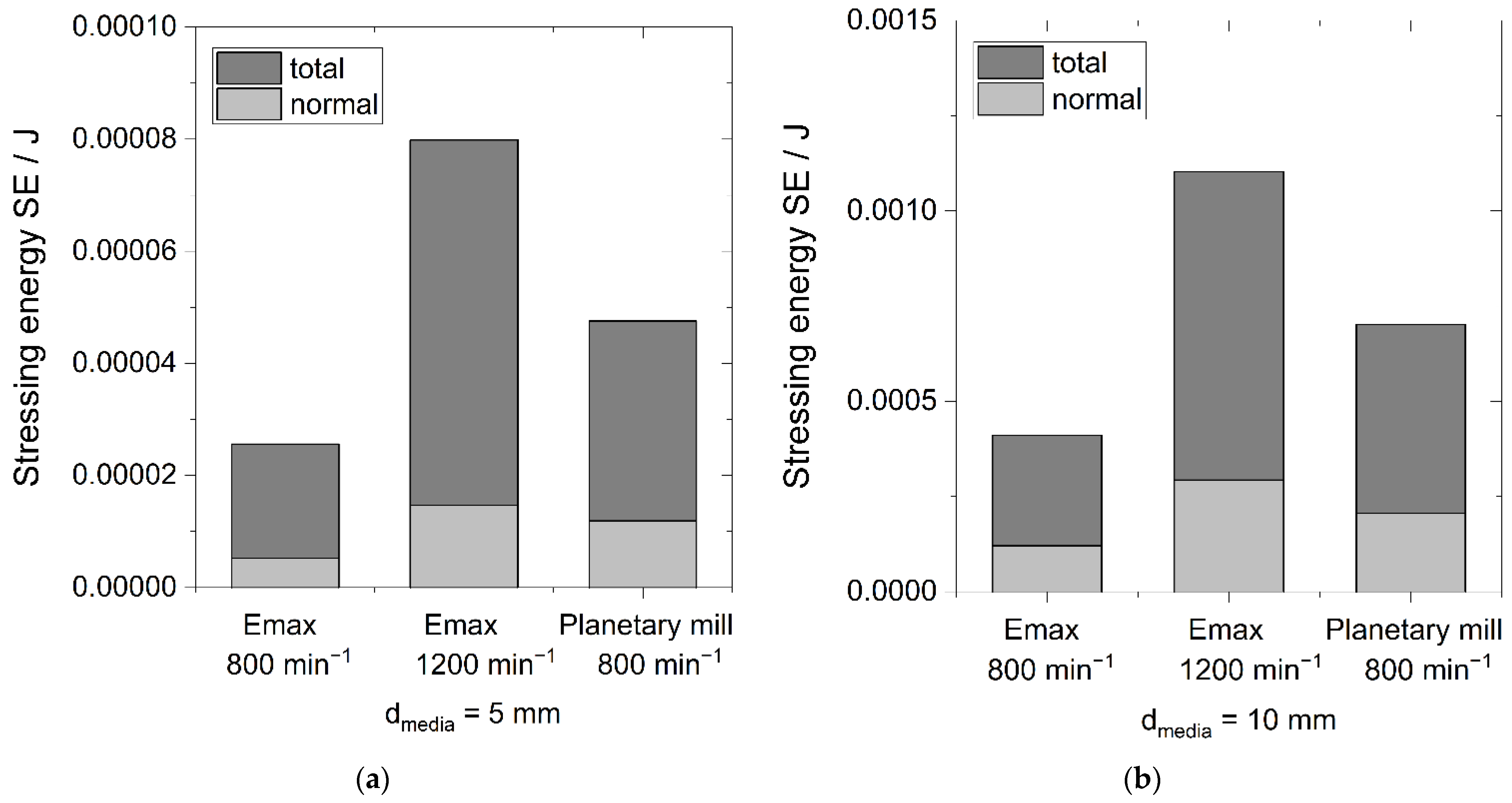
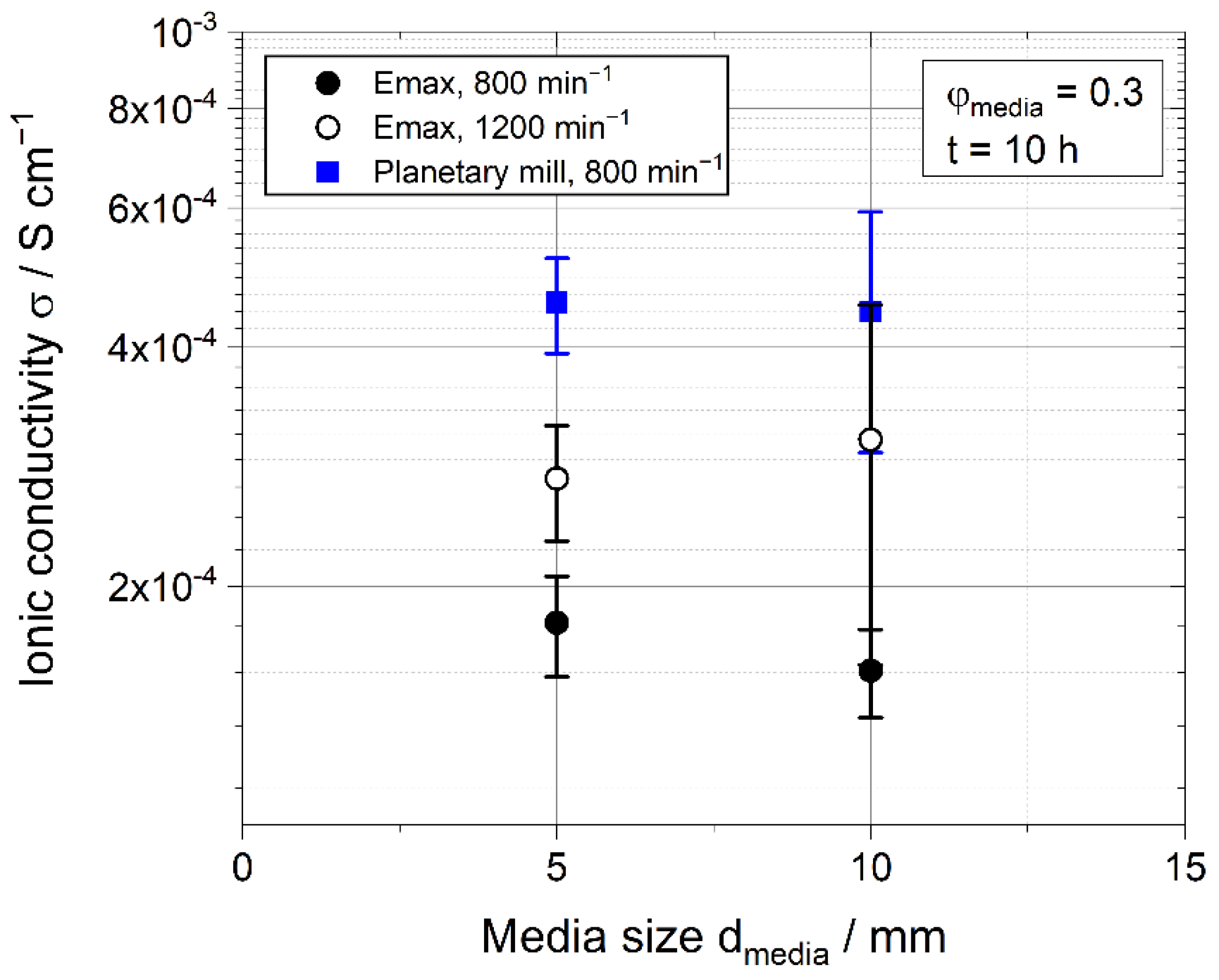
3.5. Comparison to a Planetary Ball Mill
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Schlem, R.; Burmeister, C.F.; Michalowski, P.; Ohno, S.; Dewald, G.F.; Kwade, A.; Zeier, W.G. Energy Storage Materials for Solid-State Batteries: Design by Mechanochemistry. Adv. Energy Mater. 2021, 11, 2101022. [Google Scholar] [CrossRef]
- Ghidiu, M.; Ruhl, J.; Culver, S.P.; Zeier, W.G. Solution-based synthesis of lithium thiophosphate superionic conductors for solid-state batteries: A chemistry perspective. J. Mater. Chem. A 2019, 7, 17735–17753. [Google Scholar] [CrossRef]
- Zhou, L.; Park, K.-H.; Sun, X.; Lalère, F.; Adermann, T.; Hartmann, P.; Nazar, L.F. Solvent-Engineered Design of Argyrodite Li6PS5X (X = Cl, Br, I) Solid Electrolytes with High Ionic Conductivity. ACS Energy Lett. 2019, 4, 265–270. [Google Scholar] [CrossRef]
- Tan, D.H.S.; Banerjee, A.; Deng, Z.; Wu, E.A.; Nguyen, H.; Doux, J.-M.; Wang, X.; Cheng, J.-H.; Ong, S.P.; Meng, Y.S.; et al. Enabling Thin and Flexible Solid-State Composite Electrolytes by the Scalable Solution Process. ACS Appl. Energy Mater. 2019, 2, 6542–6550. [Google Scholar] [CrossRef]
- Yan, X.; Li, Z.; Wen, Z.; Han, W. Li/Li7La3Zr2O12/LiFePO4 All-Solid-State Battery with Ultrathin Nanoscale Solid Electrolyte. J. Phys. Chem. C 2017, 121, 1431–1435. [Google Scholar] [CrossRef]
- Wang, Y.; Song, S.; Xu, C.; Hu, N.; Molenda, J.; Lu, L. Development of solid-state electrolytes for sodium-ion battery–A short review. Nano Mater. Sci. 2019, 1, 91–100. [Google Scholar] [CrossRef]
- Burgio, N.; Iasonna, A.; Magini, M.; Martelli, S.; Padella, F. Mechanical alloying of the Fe−Zr system. Correlation between input energy and end products. Il Nuovo Cim. D 1991, 13, 459–476. [Google Scholar] [CrossRef]
- Kessler, M.; Woodward, R.T.; Wong, N.; Rinaldi, R. Kinematic Modeling of Mechanocatalytic Depolymerization of α-Cellulose and Beechwood. ChemSusChem 2018, 11, 552–561. [Google Scholar] [CrossRef] [Green Version]
- Burmeister, C.F. Materialbeanspruchung und Mechanische Aktivierung in Planetenkugelmühlen, Auflage; Sierke VERLAG-Internationaler Wissenschaftsverlag: Göttingen, Germany, 2020; ISBN 9783965480759. [Google Scholar]
- Rosenkranz, S.; Breitung-Faes, S.; Kwade, A. Experimental investigations and modelling of the ball motion in planetary ball mills. Powder Technol. 2011, 212, 224–230. [Google Scholar] [CrossRef]
- Beinert, S.; Fragnière, G.; Schilde, C.; Kwade, A. Analysis and modelling of bead contacts in wet-operating stirred media and planetary ball mills with CFD–DEM simulations. Chem. Eng. Sci. 2015, 134, 648–662. [Google Scholar] [CrossRef]
- Burmeister, C.; Titscher, L.; Breitung-Faes, S.; Kwade, A. Dry grinding in planetary ball mills: Evaluation of a stressing model. Adv. Powder Technol. 2018, 29, 191–201. [Google Scholar] [CrossRef]
- Kwade, A. A Stressing Model for the Description and Optimization of Grinding Processes. Chem. Eng. Technol. 2003, 26, 199–205. [Google Scholar] [CrossRef]
- Schönert, K. Advances in comminution fundamentals and impacts on technology. Aufbereit.-Tech. 1991, 32, 487–494. [Google Scholar]
- Prziwara, P.; Hamilton, L.D.; Breitung-Faes, S.; Kwade, A. Evaluation of the capturing of dry fine particles between grinding media by drop-weight tests. Powder Technol. 2020, 363, 326–336. [Google Scholar] [CrossRef]
- Burmeister, C.F.; Schmidt, R.; Jacob, K.; Breitung-Faes, S.; Stolle, A.; Kwade, A. Effect of stressing conditions on mechanochemical Knoevenagel synthesis. Chem. Eng. J. 2020, 396, 124578. [Google Scholar] [CrossRef]
- de Carvalho, R.M.; Tavares, L.M. Predicting the effect of operating and design variables on breakage rates using the mechanistic ball mill model. Miner. Eng. 2013, 43–44, 91–101. [Google Scholar] [CrossRef]
- Tavares, L.M.; de Carvalho, R.M. Modeling breakage rates of coarse particles in ball mills. Miner. Eng. 2009, 22, 650–659. [Google Scholar] [CrossRef]
- Beinert, S.; Fragnière, G.; Schilde, C.; Kwade, A. Multiscale simulation of fine grinding and dispersing processes: Stressing probability, stressing energy and resultant breakage rate. Adv. Powder Technol. 2018, 29, 573–583. [Google Scholar] [CrossRef]
- Brinek, M.; Hiebl, C.; Wilkening, H.M.R. Understanding the Origin of Enhanced Li-Ion Transport in Nanocrystalline Argyrodite-Type Li6PS5I. Chem. Mater. 2020, 32, 4754–4766. [Google Scholar] [CrossRef] [PubMed]
- Krauskopf, T.; Culver, S.P.; Zeier, W.G. Local Tetragonal Structure of the Cubic Superionic Conductor Na3PS4. Inorg. Chem. 2018, 57, 4739–4744. [Google Scholar] [CrossRef] [PubMed]
- Ohno, S.; Rosenbach, C.; Dewald, G.F.; Janek, J.; Zeier, W.G. Linking Solid Electrolyte Degradation to Charge Carrier Transport in the Thiophosphate-Based Composite Cathode toward Solid-State Lithium-Sulfur Batteries. Adv. Funct. Mater. 2021, 31, 2010620. [Google Scholar] [CrossRef]
- Rayavarapu, P.R.; Sharma, N.; Peterson, V.K.; Adams, S. Variation in structure and Li+-ion migration in argyrodite-type Li6PS5X (X = Cl, Br, I) solid electrolytes. J. Solid State Electrochem. 2012, 16, 1807–1813. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Hertz, H. Ueber die Berührung fester elastischer Körper. In Journal Für Die Reine und Angewandte Mathematik Band 92; Crelle, A.L., Borchardt, C.W., Schellbach, Eds.; De Gruyter: Berlin, Germany, 1882; pp. 156–171. ISBN 9783112342404. [Google Scholar]
- Mindlin, R.D. Compliance of Elastic Bodies in Contact. J. Appl. Mech. 1949, 16, 259–268. [Google Scholar] [CrossRef]
- Burmeister, C.F.; Stolle, A.; Schmidt, R.; Jacob, K.; Breitung-Faes, S.; Kwade, A. Experimental and Computational Investigation of Knoevenagel Condensation in Planetary Ball Mills. Chem. Eng. Technol. 2014, 37, 857–864. [Google Scholar] [CrossRef]
- Santhanam, P.R.; Dreizin, E.L. Predicting conditions for scaled-up manufacturing of materials prepared by ball milling. Powder Technol. 2012, 221, 403–411. [Google Scholar] [CrossRef]
- Weiler, R.; Ripp, M.; Dau, G.; Ripperger, S. Anwendung der Diskrete-Elemente-Methode zur Simulation des Verhaltens von Schüttgütern. Chem. Ing. Tech. 2009, 81, 749–757. [Google Scholar] [CrossRef]
- Venkataraman, K.S.; Narayanan, K.S. Energetics of collision between grinding media in ball mills and mechanochemical effects. Powder Technol. 1998, 96, 190–201. [Google Scholar] [CrossRef]
- Eller, C. Stoß. In Holzmann/Meyer/Schumpich Technische Mechanik Kinematik und Kinetik; Eller, C., Ed.; Springer Fachmedien: Wiesbaden, Germany, 2019; pp. 260–278. ISBN 9783658255862. [Google Scholar]
- Chabay, R.W.; Sherwood, B.A. Matter & Interactions; John Wiley & Sons: Hoboken, NJ, USA, 2015; ISBN 9781118875865. [Google Scholar]
- Breitung-Faes, S.; Kwade, A. Prediction of energy effective grinding conditions. Miner. Eng. 2013, 43–44, 36–43. [Google Scholar] [CrossRef]
- Kwade, A.; Schwedes, J. Breaking characteristics of different materials and their effect on stress intensity and stress number in stirred media mills. Powder Technol. 2002, 122, 109–121. [Google Scholar] [CrossRef]
- Breitung-Faes, S.; Kwade, A. Use of an Enhanced Stress Model for the Optimization of Wet Stirred Media Milling Processes. Chem. Eng. Technol. 2014, 37, 819–826. [Google Scholar] [CrossRef]
- Restrepo, A.H.; Ríos, J.M.; Arango, F.; Correa, E.; Zuleta, A.A.; Valencia-Escobar, A.; Bolivar, F.J.; Castaño, J.G.; Echeverría, F.E. Characterization of titanium powders processed in n-hexane by high-energy ball milling. Int. J. Adv. Manuf. Technol. 2020, 110, 1681–1690. [Google Scholar] [CrossRef]
- Kaupp, G. Mechanochemistry: The varied applications of mechanical bond-breaking. CrystEngComm 2009, 11, 388–403. [Google Scholar] [CrossRef]
- Takacs, L. Combustion Phenomena Induced by Ball Milling. Mater. Sci. Forum 1998, 269–272, 513–522. [Google Scholar] [CrossRef]



| Model Parameter | Calibrated Input Value |
|---|---|
| Coefficient of Rolling Friction μR | 0.05 |
| Coefficient of Static Friction μS | 0.58 |
| Coefficient of Restitution COR | 0.47 |
| Parameter | Input Value |
|---|---|
| Shear modulus G | 8 · 1010 Pa |
| Poisson’s ratio ν | 0.3 |
| Density ρ |
| Media Filling Ratio φmedia | Media Number Nmedia | ||
|---|---|---|---|
| 5 mm | 7 mm | 10 mm | |
| 0.1 | - | - | 14 |
| 0.2 | - | - | 28 |
| 0.3 | 332 | 123 | 42 |
| 0.4 | 451 | 164 | 56 |
| 0.5 | - | - | 70 |
| 0.6 | - | - | 84 |
| 0.7 | - | - | 98 |
| Mill | Chamber Volume/mL | Rotational Speed n/min−1 | Media Size dmedia/mm | Media Number Nmedia/− | Mass of Educts/g |
|---|---|---|---|---|---|
| Emax | 125 | 800 | 5 | 332 | 8 |
| Emax | 125 | 800 | 10 | 42 | 8 |
| Emax | 125 | 1200 | 5 | 332 | 8 |
| Emax | 125 | 1200 | 10 | 42 | 8 |
| Planetary mill | 80 | 800 | 5 | 216 | 5 |
| Planetary mill | 80 | 800 | 10 | 27 | 5 |
| Filling Ratio φmedia/− | Coefficient kP,t/− | Exponent aP,t/− |
|---|---|---|
| 0.3 | 1.06 × 10−7 | 2.84 |
| 0.4 | 1.06 × 10−7 | 2.86 |
| Filling Ratio φmedia/− | Coefficient kP,n/− | Exponent aP,n/− | Exponent bP,n/− |
|---|---|---|---|
| 0.3 | 6.75 × 10−9 | 2.91 | 0.50 |
| 0.4 | 6.75 × 10−9 | 2.96 | 0.44 |
| Filling Ratio φmedia/− | Coefficient kt/− | Exponent of Rotational Speed at/− | Exponent of Media Size bt/− |
|---|---|---|---|
| 0.3 | 1.00 × 10−15 | 2.29 | 4.41 |
| 0.4 | 7.00 × 10−16 | 2.29 | 4.39 |
| Filling Ratio φmedia/− | Coefficient kt/− | Exponent of Rotational Speed at/− | Exponent of Media Size bt/− |
|---|---|---|---|
| 0.3 | 6.90 × 10−15 | 2.37 | 3.76 |
| 0.4 | 4.90 × 10−15 | 2.32 | 3.91 |
| Filling Ratio φmedia/− | Coefficient kCF/− | Exponent of Rotational Speed aCF/− | Exponent of Media Size bCF/− |
|---|---|---|---|
| 0.3 | 1.28 × 107 | 0.51 | 3.84 |
| 0.4 | 2.59 × 107 | 0.53 | 3.99 |
| Rotational Speed n /min−1 | Coefficient kfilling,n/− | Exponent of Filling Ratio fn/− |
|---|---|---|
| 800 | 1.08 × 10−5 | 1.95 |
| 1200 | 3.16 × 10−5 | 1.84 |
| Rotational Speed n /min−1 | Coefficient kfilling,t/− | Exponent of Filling Ratio ft/− |
|---|---|---|
| 800 | 3.08 × 10−4 | 1.00 |
| 1200 | 2.80 × 10−4 | 0.87 |
| Rotational Speed n /min−1 | Coefficient kfilling,CF/− | Exponent of Filling Ratio fCF/− |
|---|---|---|
| 800 | 3.22 × 103 | 0.69 |
| 1200 | 3.68 × 103 | 0.59 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Burmeister, C.F.; Hofer, M.; Molaiyan, P.; Michalowski, P.; Kwade, A. Characterization of Stressing Conditions in a High Energy Ball Mill by Discrete Element Simulations. Processes 2022, 10, 692. https://doi.org/10.3390/pr10040692
Burmeister CF, Hofer M, Molaiyan P, Michalowski P, Kwade A. Characterization of Stressing Conditions in a High Energy Ball Mill by Discrete Element Simulations. Processes. 2022; 10(4):692. https://doi.org/10.3390/pr10040692
Chicago/Turabian StyleBurmeister, Christine Friederike, Moritz Hofer, Palanivel Molaiyan, Peter Michalowski, and Arno Kwade. 2022. "Characterization of Stressing Conditions in a High Energy Ball Mill by Discrete Element Simulations" Processes 10, no. 4: 692. https://doi.org/10.3390/pr10040692
APA StyleBurmeister, C. F., Hofer, M., Molaiyan, P., Michalowski, P., & Kwade, A. (2022). Characterization of Stressing Conditions in a High Energy Ball Mill by Discrete Element Simulations. Processes, 10(4), 692. https://doi.org/10.3390/pr10040692








