Optimization Design and Performance Evaluation of a Hybrid Excitation Claw Pole Machine
Abstract
:1. Introduction
2. Machine Configuration and Flux Path
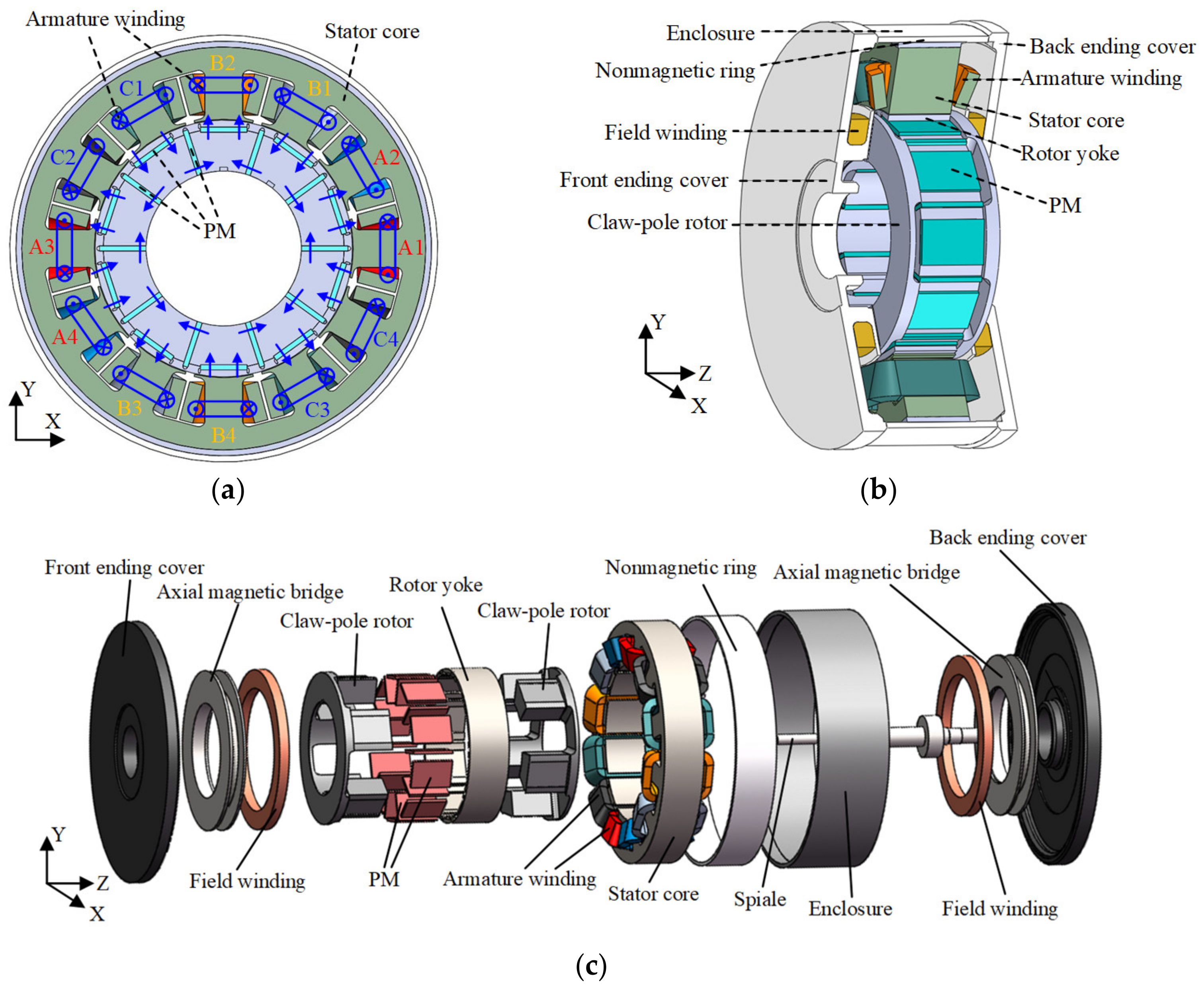
2.1. Machine Configuration
- (1)
- The size of the slot formed by the two claw-pole rotors exactly matches the size of PM. Therefore, no glue is needed when assembling the rotor, which is more environmentally friendly. The noise when the rotor moves is also reduced.
- (2)
- The field winding is placed at the end cover of the proposed HE-CPM. Compared with the hybrid excitation machine with the field winding placed on the stator, placing the field winding at the end cover can reduce the complexity of machine configuration.
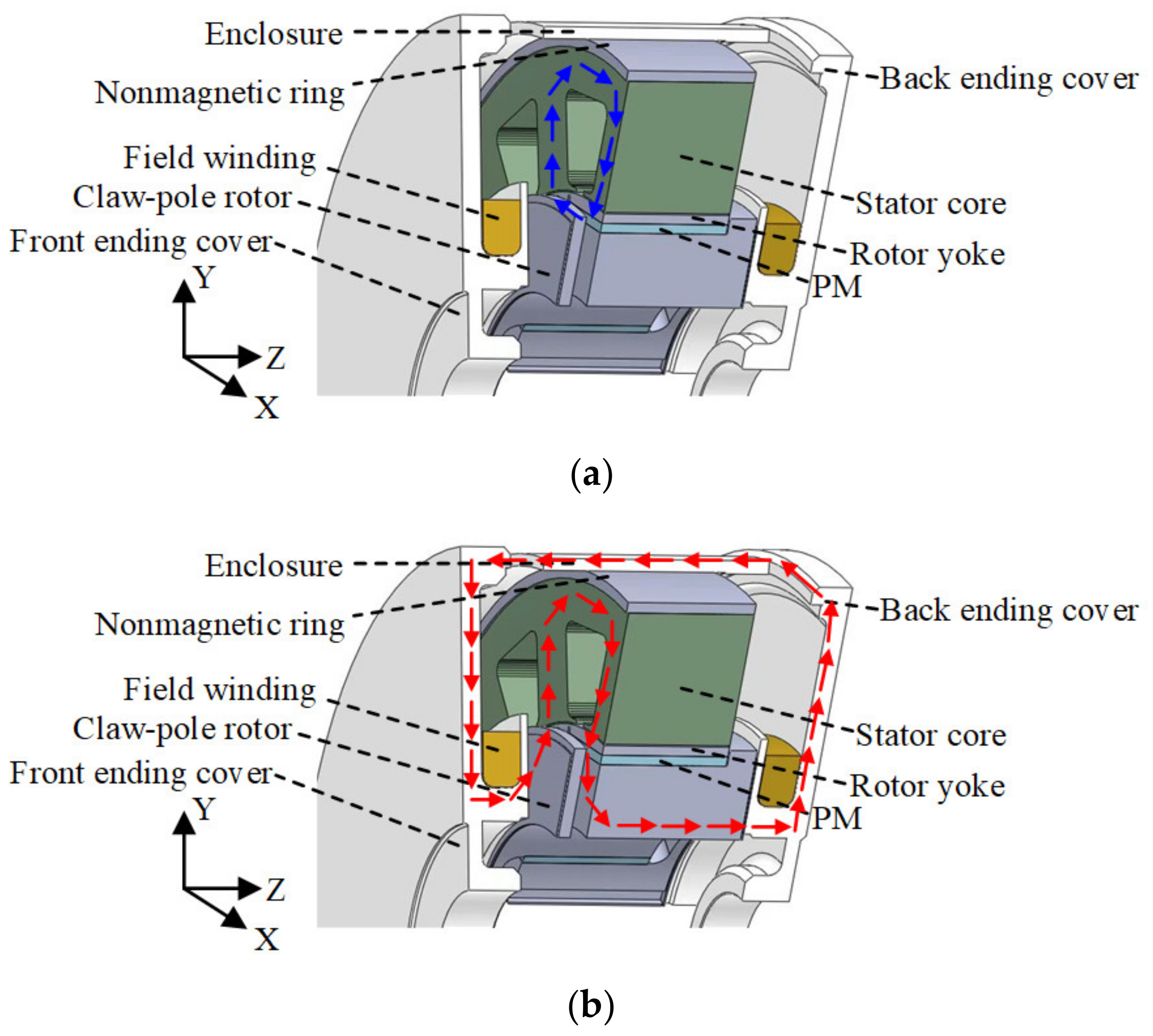
2.2. Hybrid Flux Path
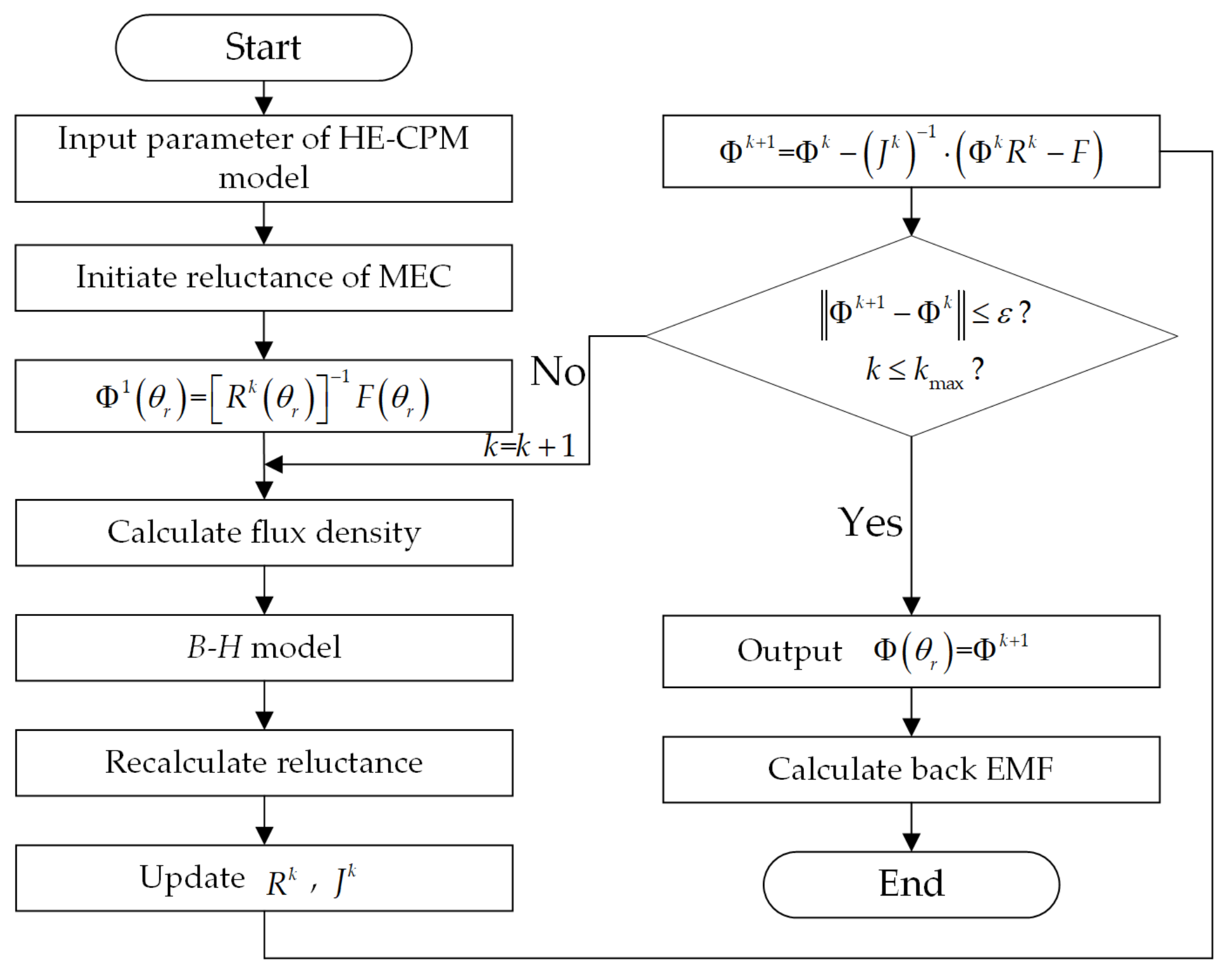
3. MEC Model
4. Optimization of Dimension Parameters
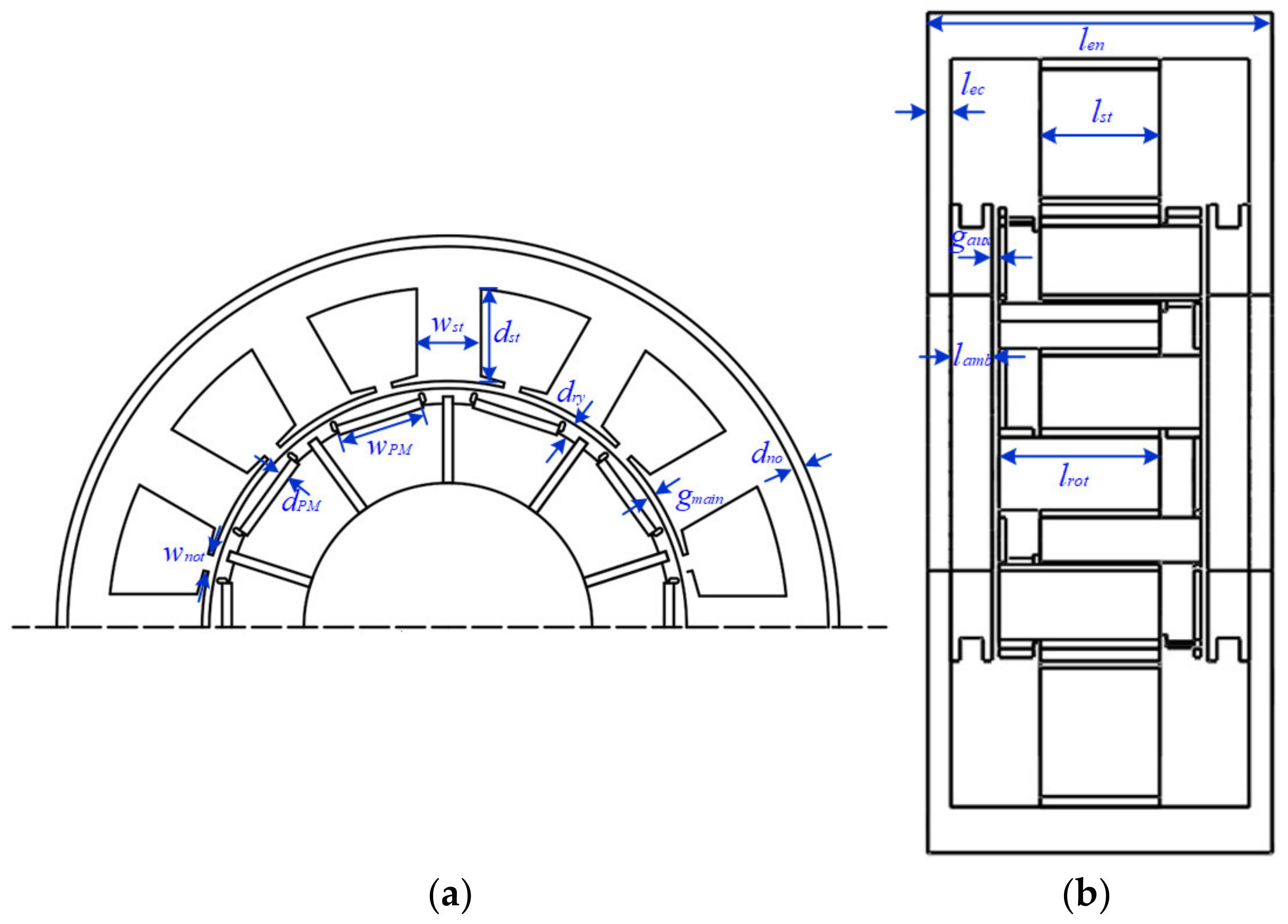
4.1. Machine Parameters Definition and Selection
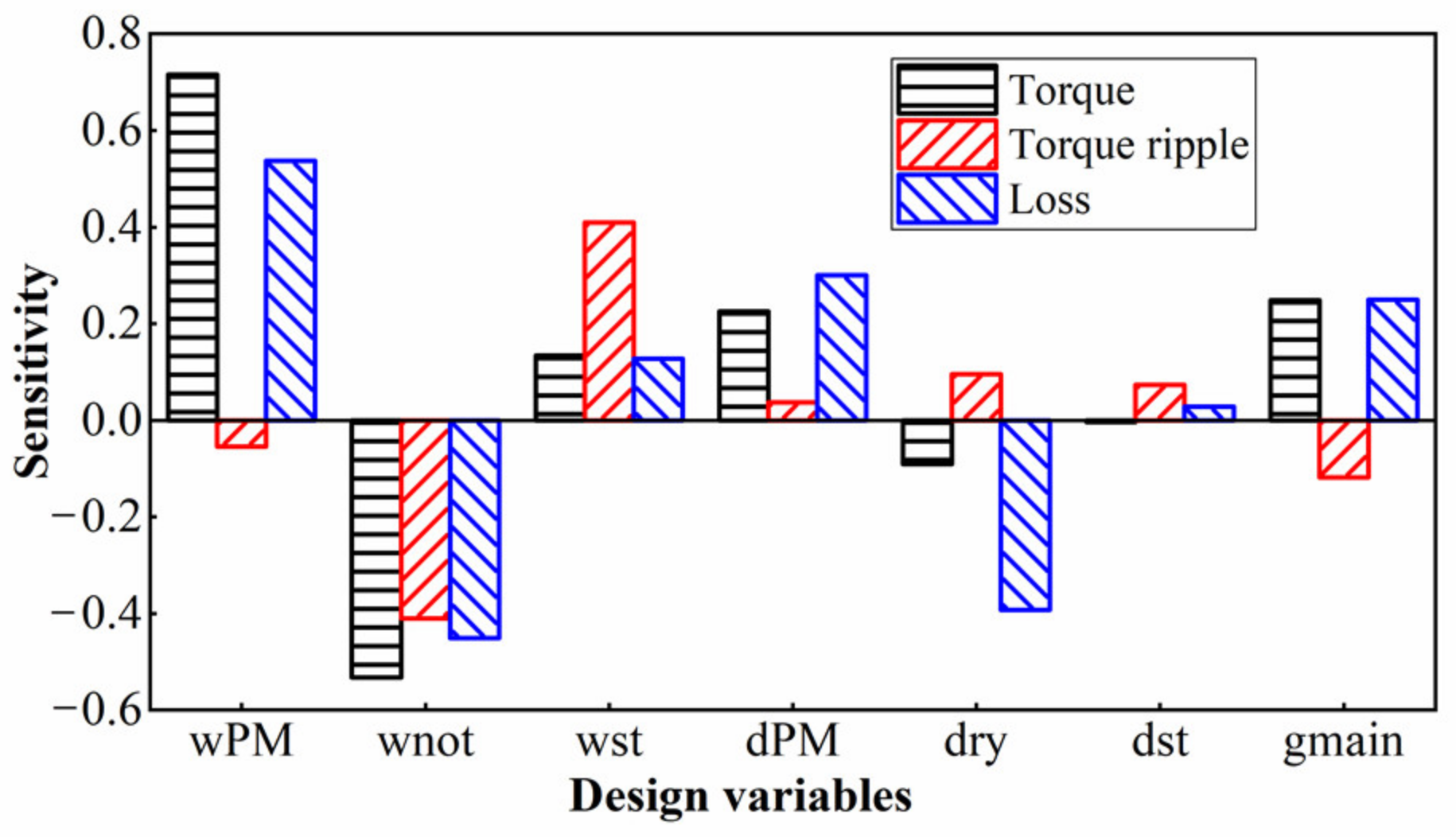
4.2. Machine Parameters Optimization
5. Machine Performance Evaluation
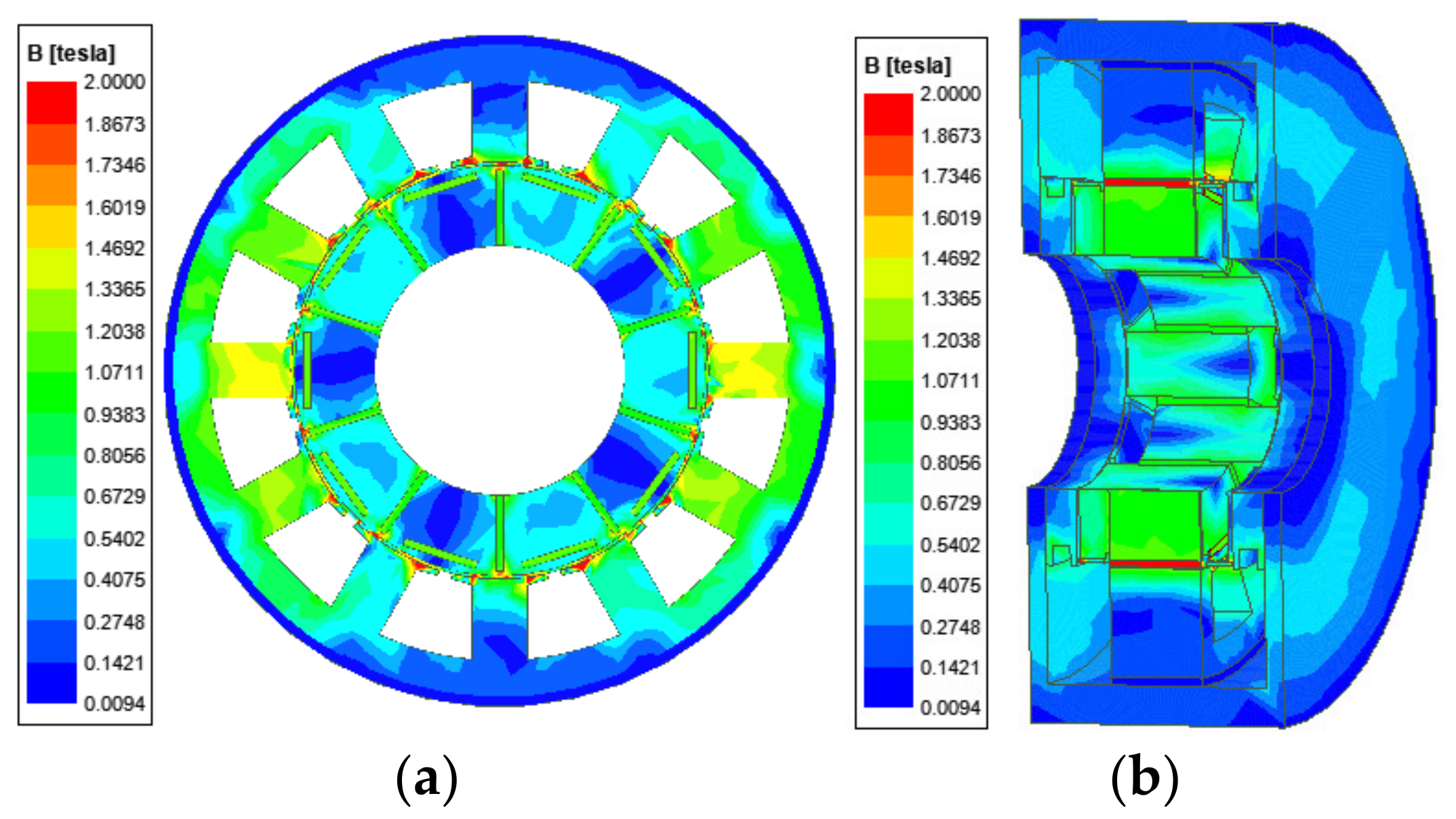
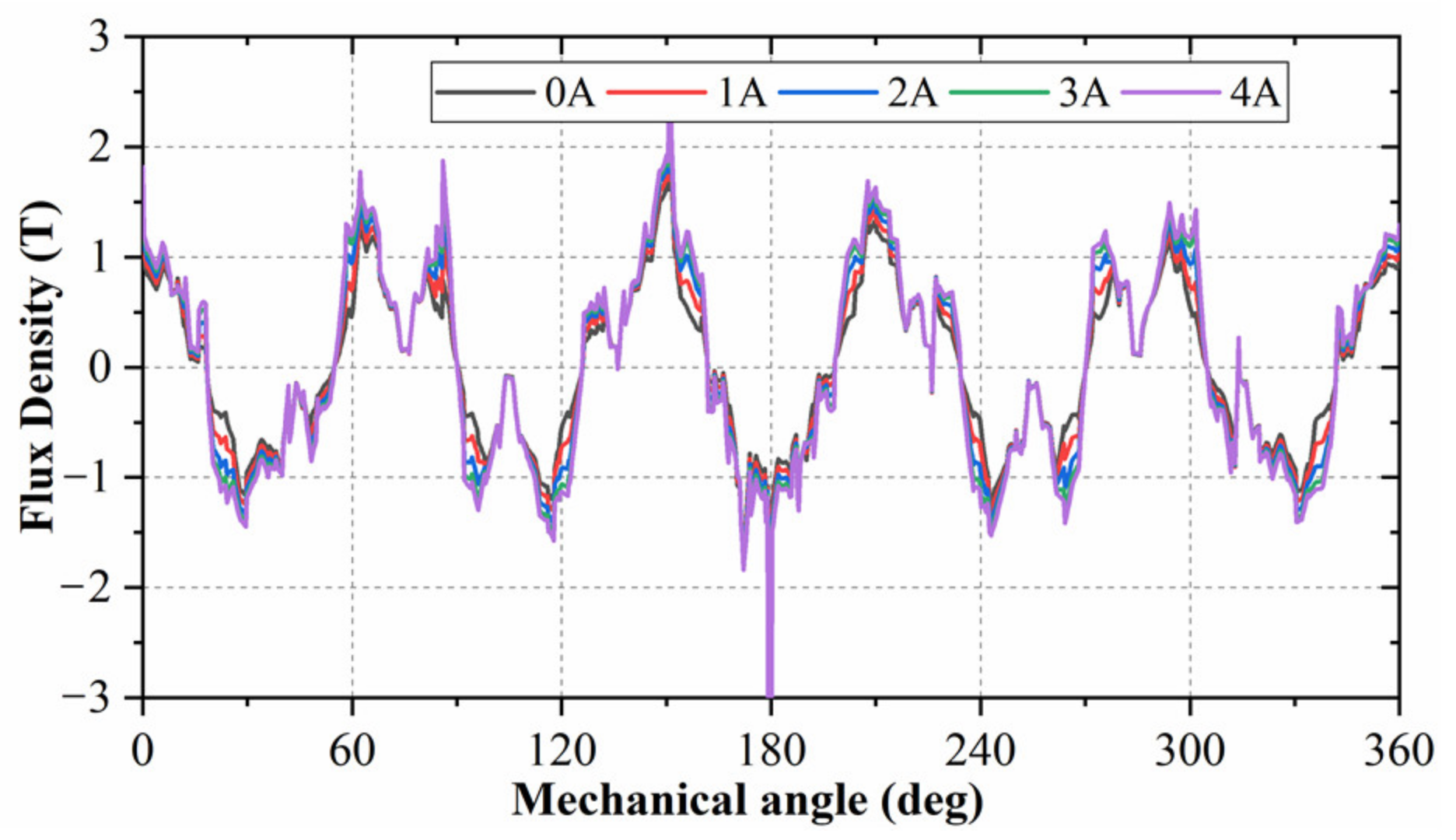
5.1. Flux Density Distribution
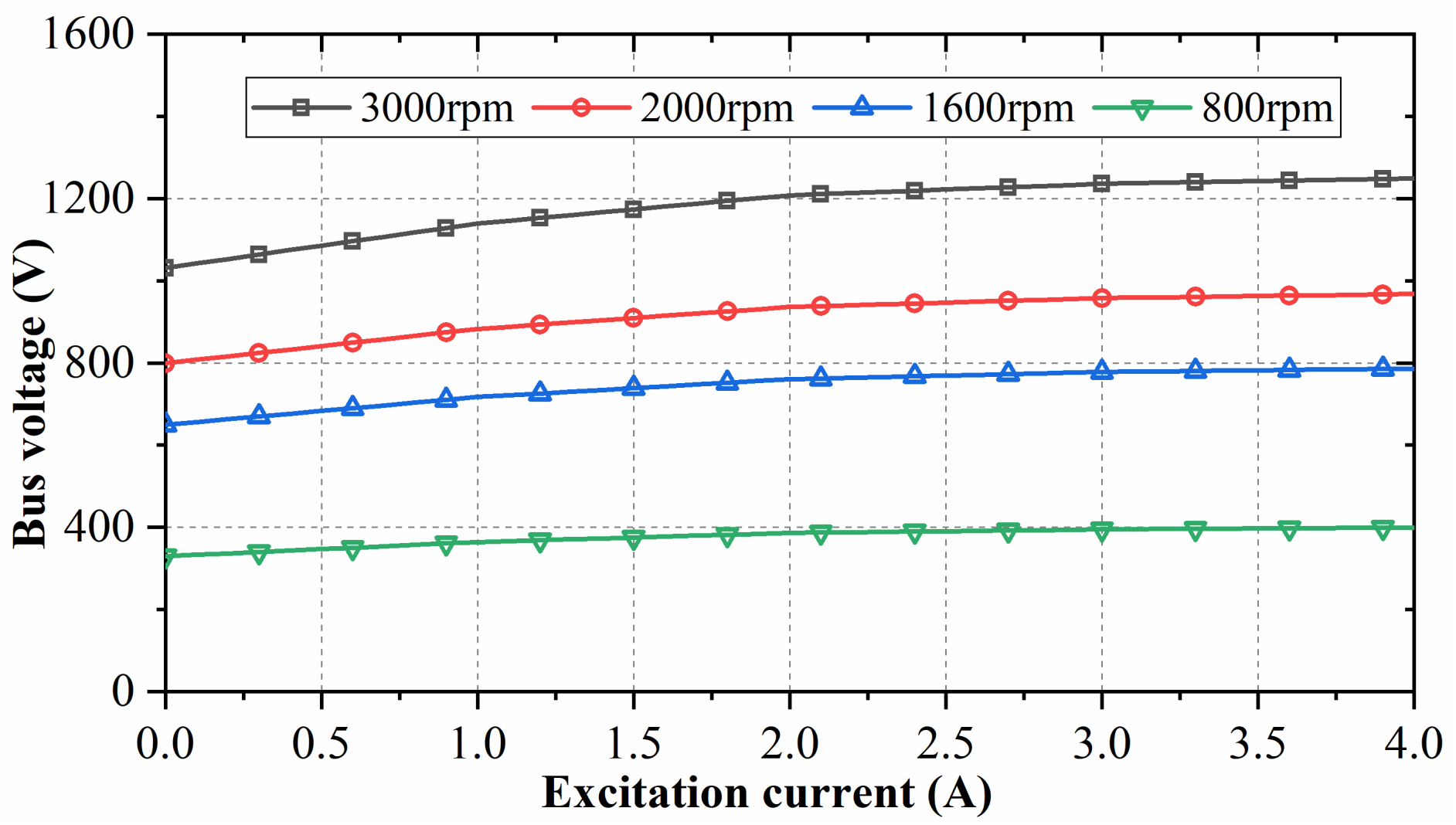
5.2. Electromagnetic Characteristics
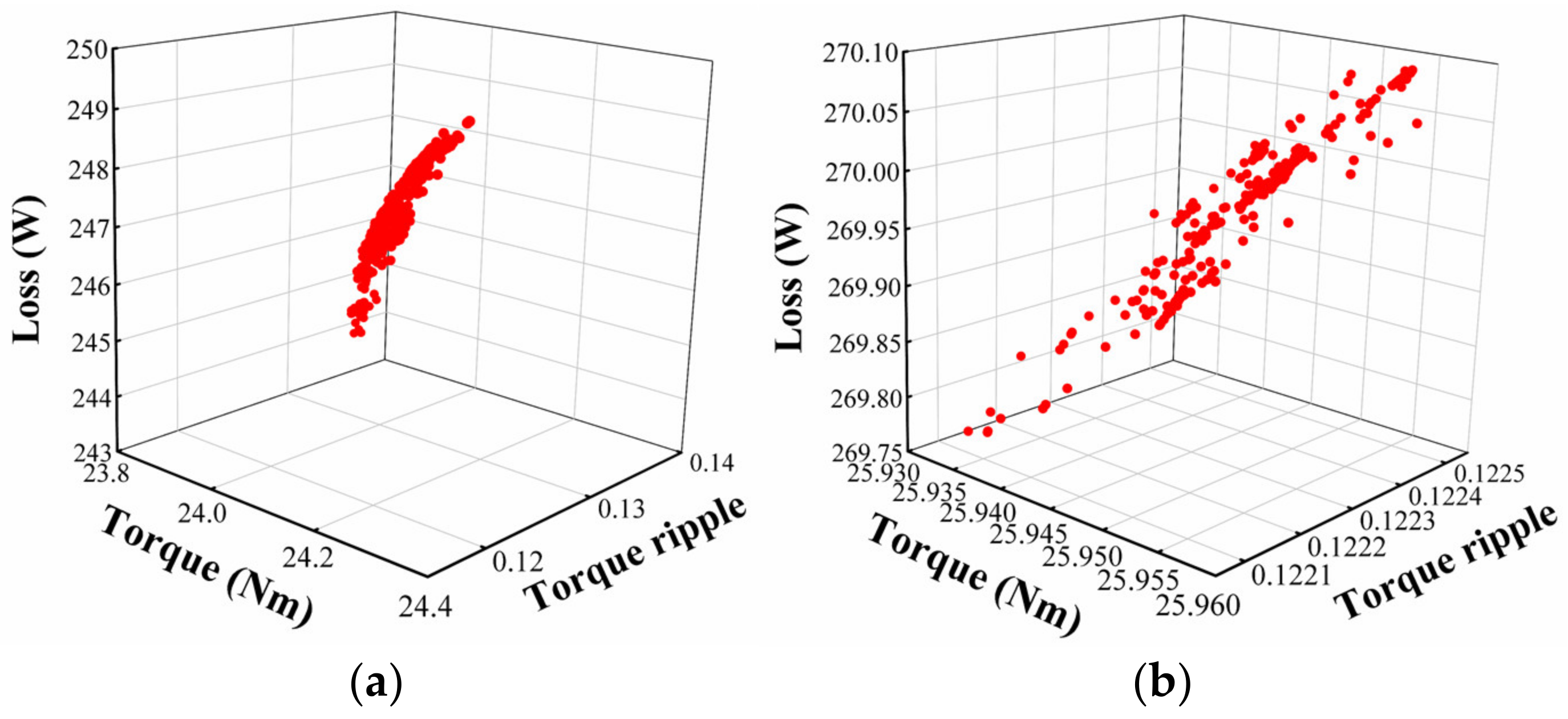
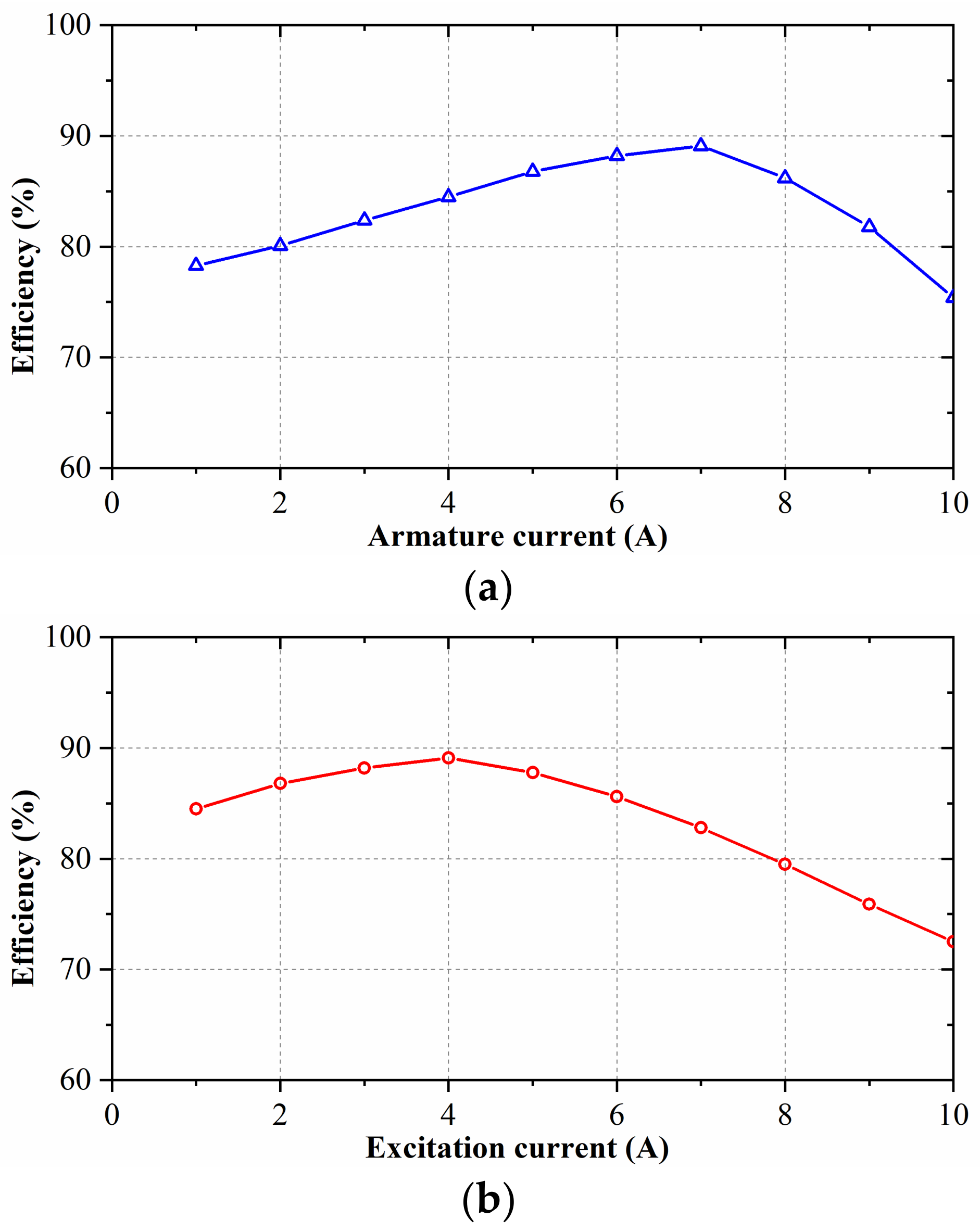
5.3. Loss and Efficiency
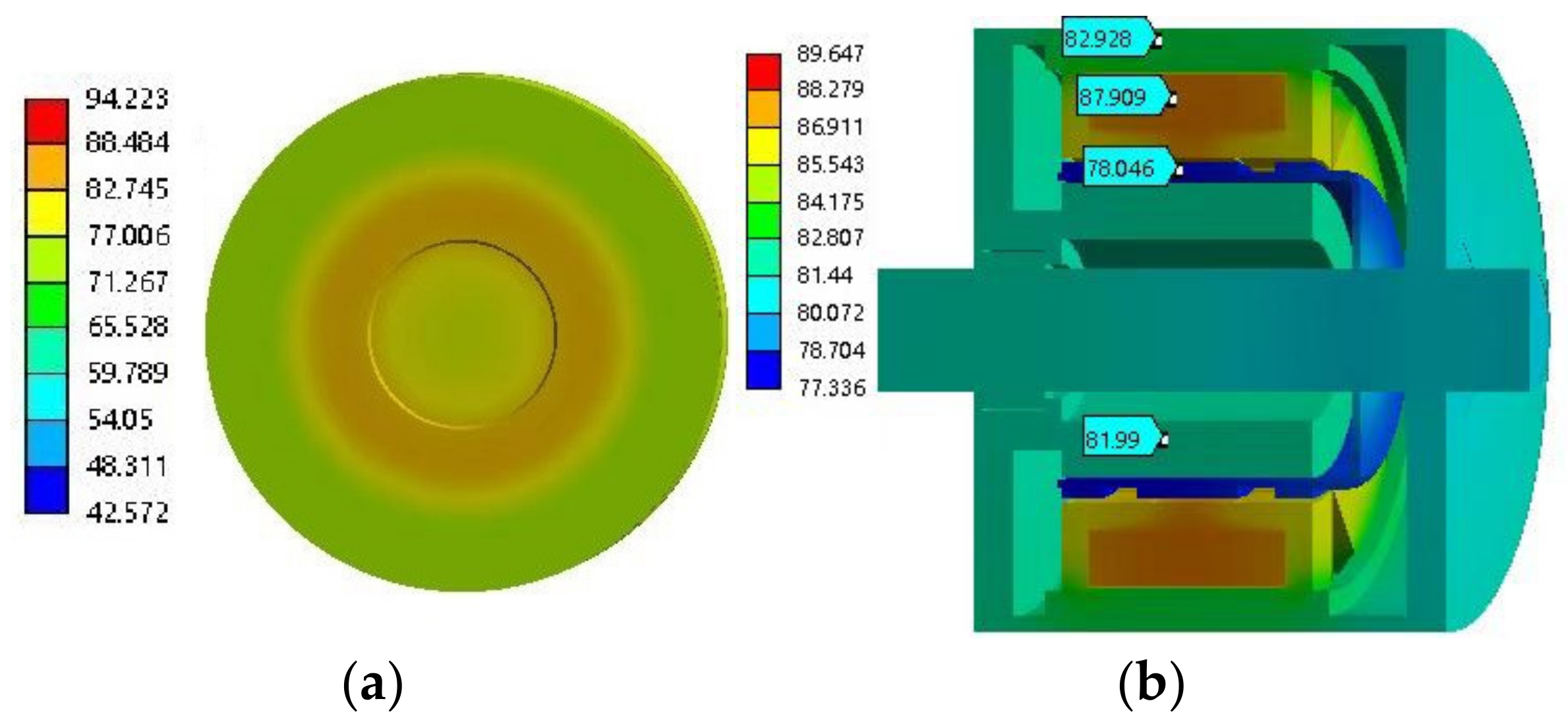
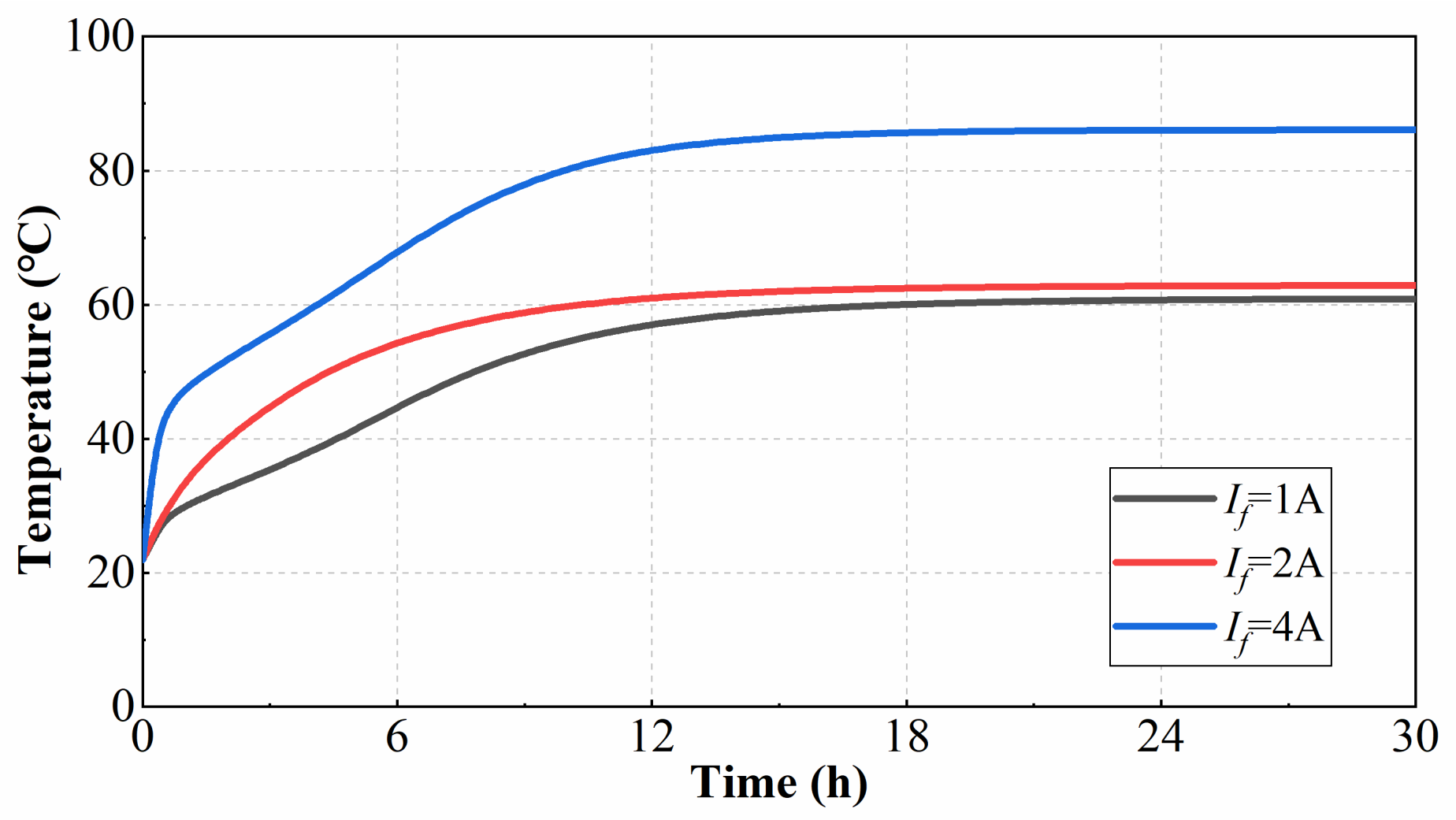
5.4. Temperature Field Simulation
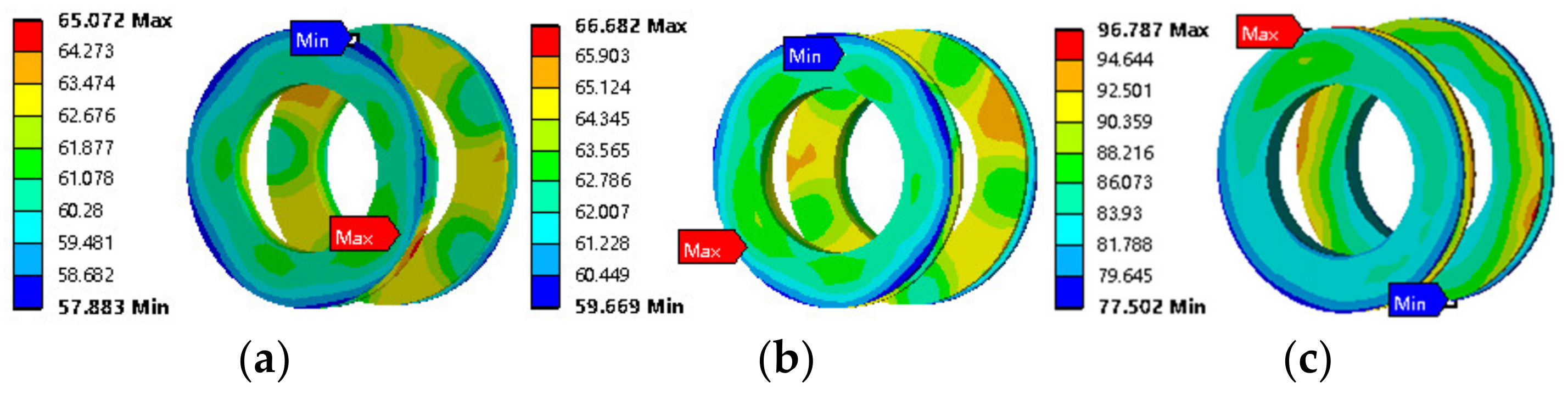
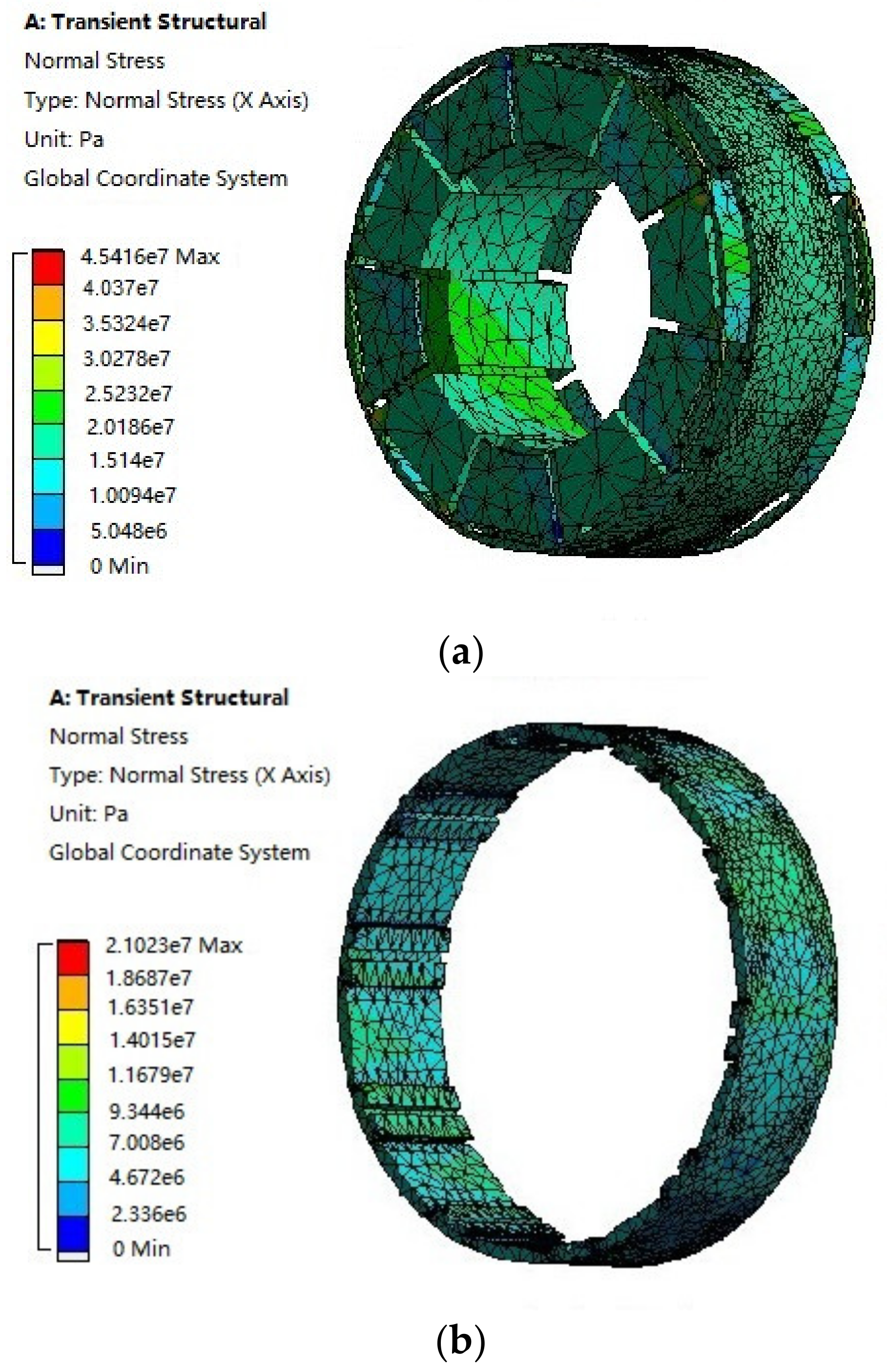
5.5. Mechanical Stress
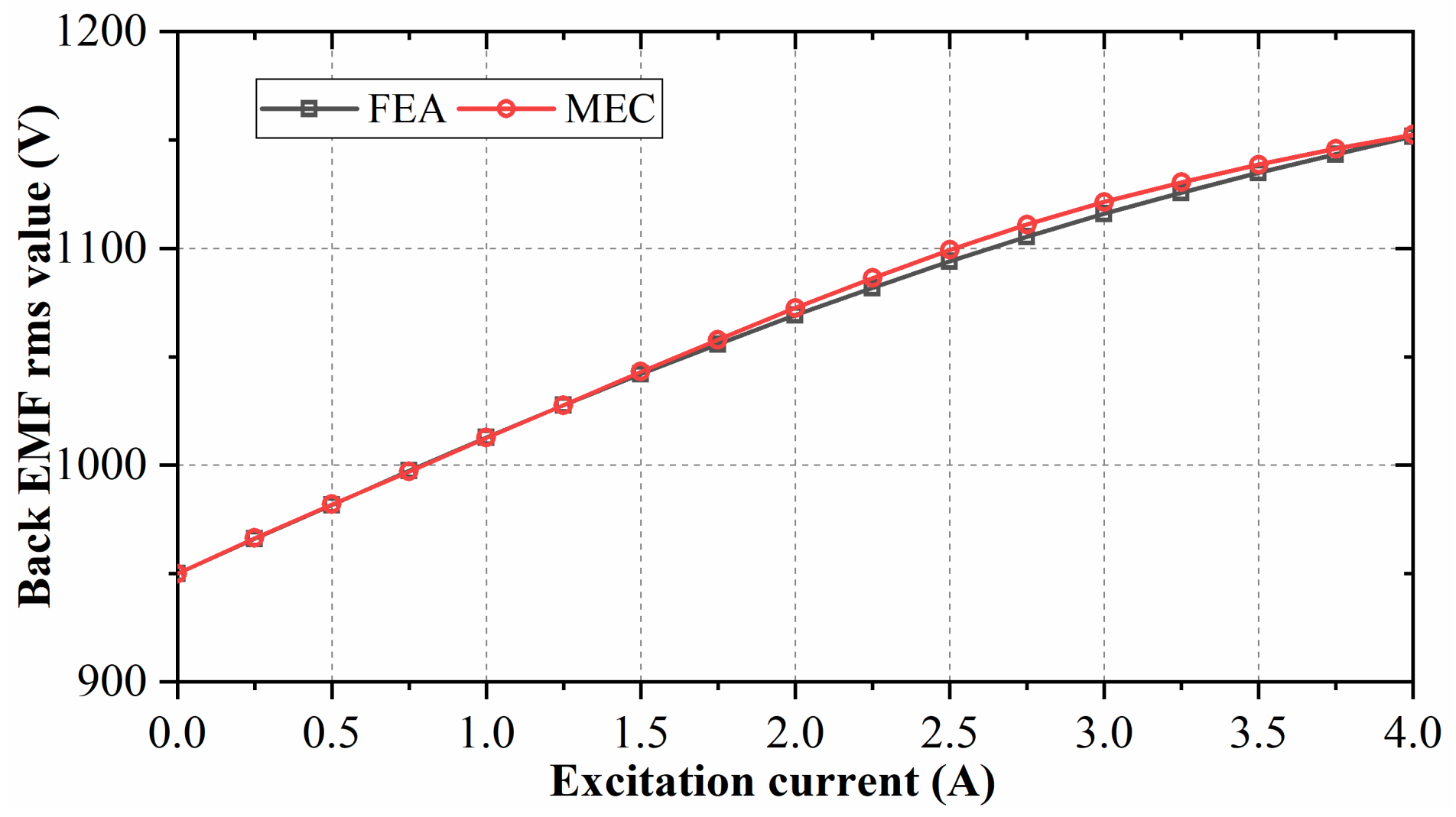
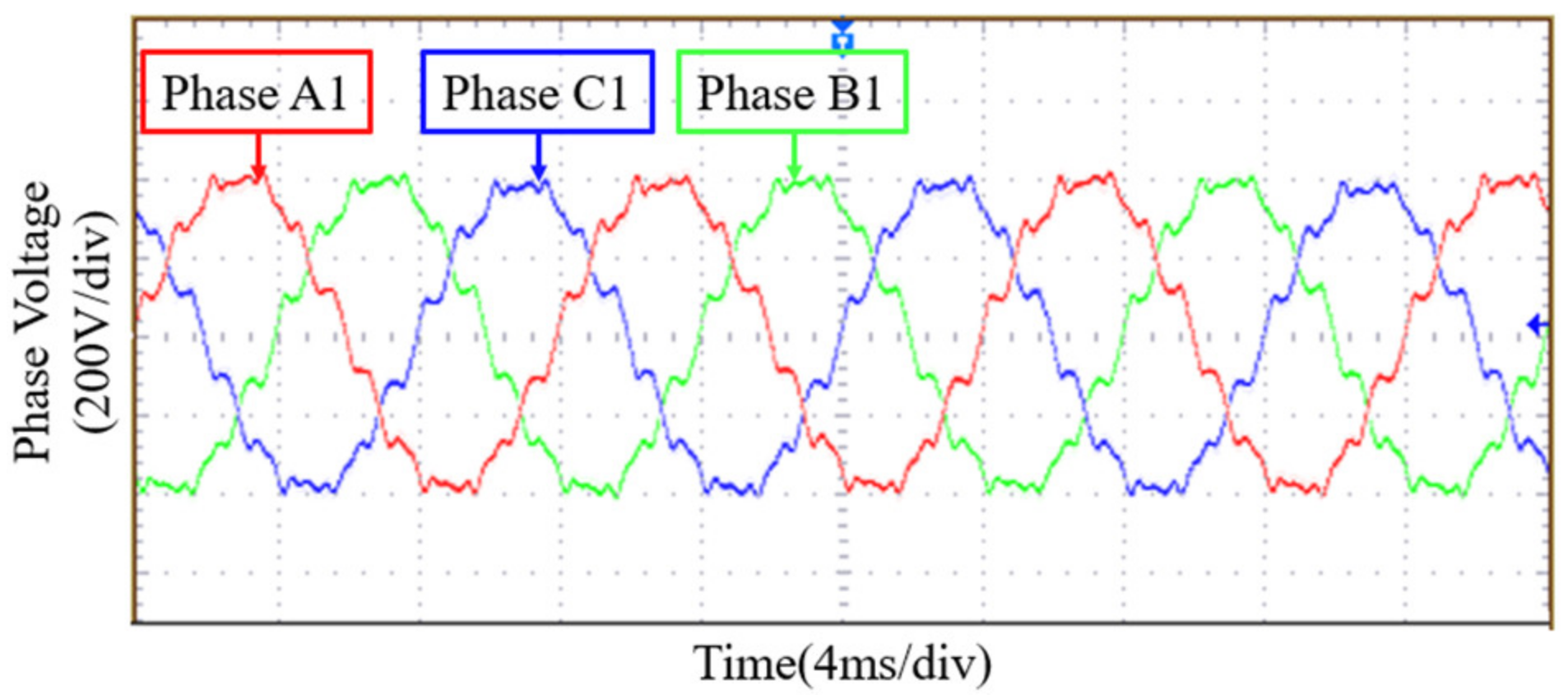
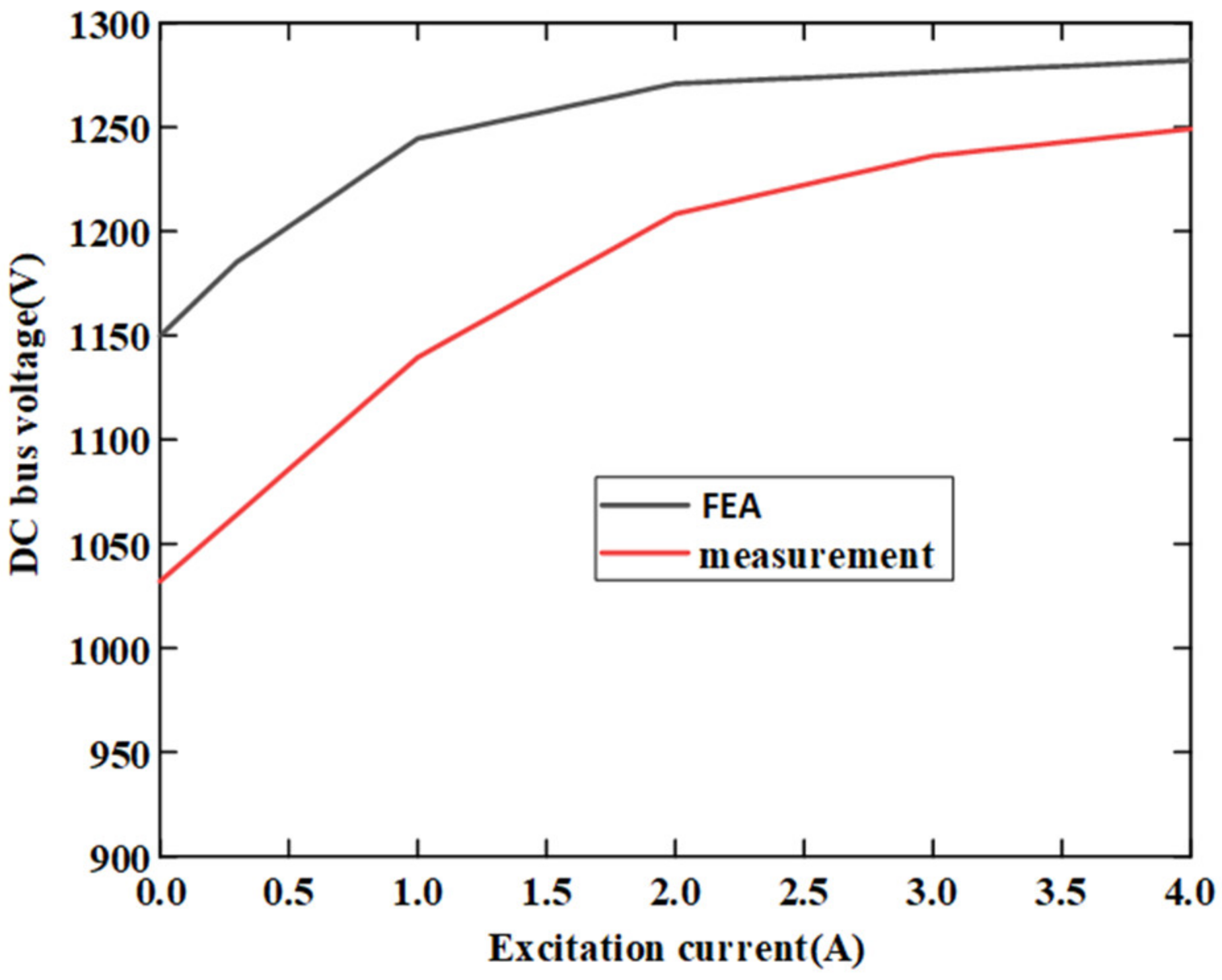
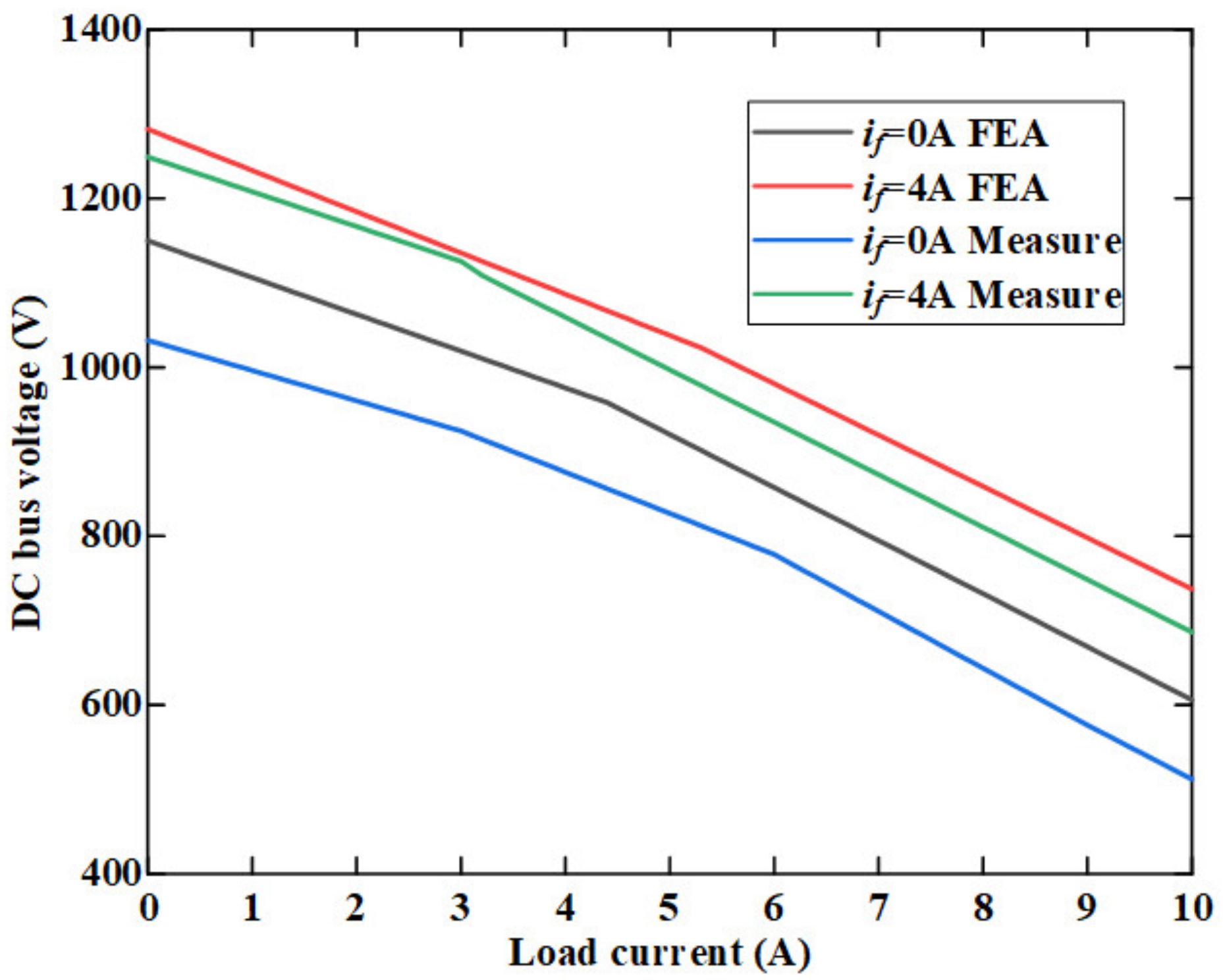
6. Experimental Validation
7. Discussion
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Zhu, Z.Q.; Cai, S. Overview of Hybrid Excited Machines for Electric Vehicles. In Proceedings of the Fourteenth International Conference on Ecological Vehicles and Renewable Energies (EVER), Monte Carlo, Monaco, 9–10 May 2019; pp. 1–14. [Google Scholar]
- Wardach, M.; Palka, R.; Paplicki, P.; Prajzendanc, P.; Zarebski, T. Modern Hybrid Excited Electric Machines. Energies 2020, 13, 5910. [Google Scholar] [CrossRef]
- Li, Y.; Yu, Z.; Meng, H.; Wang, J.; Jing, Y. Design and Optimization of Hybrid-Excited Claw-Pole Machine for Vehicle. IEEE Trans. Appl. Supercond. 2021, 31, 1–4. [Google Scholar] [CrossRef]
- Omri, R.; Ibala, A.; Masmoudi, A. Hybrid Excited Claw-Pole Machines: Comparison between Different Topologies. In Proceedings of the 16th International Multi-Conference on Systems, Signals & Devices (SSD), Istanbul, Turkey, 21–24 March 2019; pp. 423–428. [Google Scholar] [CrossRef]
- Liu, C.; Lu, J.; Wang, Y.; Lei, G.; Zhu, J.; Guo, Y. Design Issues for Claw Pole Machines with Soft Magnetic Composite Cores. Energies 2018, 11, 1998. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Zhang, Z.; Zhang, X. Design and Optimization of Hybrid Excitation Synchronous Machines with Magnetic Shunting Rotor for Electric Vehicle Traction Applications. IEEE Trans. Ind. Appl. 2017, 53, 5252–5261. [Google Scholar] [CrossRef]
- Rebhi, R.; Ibala, A.; Masmoudi, A. Hybrid excited claw pole alternators: Attempt to satisfy the increasing power need on board. In Proceedings of the 17th International Conference on Electrical Machines and Systems (ICEMS), Hangzhou, China, 22–25 October 2014; pp. 3510–3514. [Google Scholar] [CrossRef]
- Rebhi, R.; Ibala, A.; Masmoudi, A. MEC-Based Sizing of a Hybrid-Excited Claw Pole Alternator. IEEE Trans. Ind. Appl. 2014, 51, 211–223. [Google Scholar] [CrossRef]
- Omri, R.; Ibala, A.; Masmoudi, A. 3D-FEA based-comparison of different topologies of claw-pole alternators with a dual excitation. In Proceedings of the Thirteenth International Conference on Ecological Vehicles and Renewable Energies (EVER), Monte Carlo, Monaco, 10–12 April 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Yu, J.; Cao, Y.; Zhu, S.; Liu, C. Comparison Research of Hybrid Excitation Synchronous Generator between Uniform and Nonuniform Rotor Structure. In Proceedings of the IECON 2019-45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 14–17 October 2019; pp. 951–956. [Google Scholar] [CrossRef]
- Zhao, X.; Niu, S.; Ching, T.W. Design and Analysis of a New Brushless Electrically Excited Claw-Pole Generator for Hybrid Electric Vehicle. IEEE Trans. Magn. 2018, 54, 1–5. [Google Scholar] [CrossRef]
- Wang, Q.; Niu, S. A Novel DC-Coil-Free Hybrid-Excited Machine with Consequent-Pole PM Rotor. Energies 2018, 11, 700. [Google Scholar] [CrossRef] [Green Version]
- Wardach, M. Design of hybrid excited claw pole machine with laminated rotor structure. In Proceedings of the 2018 Innovative Materials and Technologies in Electrical Engineering (i-MITEL), Sulecin, Poland, 18–20 April 2018; pp. 1–4. [Google Scholar]
- Zhang, X.; Zhao, X.; Niu, S. A Novel Dual-Structure Parallel Hybrid Excitation Machine for Electric Vehicle Propulsion. Energies 2019, 12, 338. [Google Scholar] [CrossRef] [Green Version]
- Geng, H.; Zhang, X.; Zhang, Y.; Hu, W.; Lei, Y.; Xu, X.; Wang, A.; Wang, S.; Shi, L. Development of Brushless Claw Pole Electrical Excitation and Combined Permanent Magnet Hybrid Excitation Generator for Vehicles. Energies 2020, 13, 4723. [Google Scholar] [CrossRef]
- Yang, C.; Lin, H.; Guo, J.; Zhu, Z. Design and Analysis of a Novel Hybrid Excitation Synchronous Machine with Asymmetrically Stagger Permanent Magnet. IEEE Trans. Magn. 2008, 44, 4353–4356. [Google Scholar] [CrossRef]
- Melcescu, L.M.; Cistelecan, M.V.; Popescu, M.; Craiu, O. Design and development of a hybrid excited claw pole synchronous machine. In Proceedings of the International Aegean Conference on Electrical Machines and Power Electronics and Electromotion, Joint Conference, Istanbul, Turkey, 8–10 September 2011; pp. 799–804. [Google Scholar]
- Derbas, H.W.; Williams, J.M.; Koenig, A.C.; Pekarek, S.D. A Comparison of Nodal- and Mesh-Based Magnetic Equivalent Circuit Models. IEEE Trans. Energy Convers. 2009, 24, 388–396. [Google Scholar] [CrossRef] [Green Version]
- Elloumi, D.; Ibala, A.; Rebhi, R.; Masmoudi, A. 3D MEC modeling of a hybrid-excited claw pole alternator incorporating the rotor motion. In Proceedings of the 2015 International Conference on Sustainable Mobility Applications, Renewables and Technology (SMART), Kuwait City, Kuwait, 23–25 November 2015; pp. 1–7. [Google Scholar] [CrossRef]
- Elloumi, D.; Ibala, A.; Rebhi, R.; Masmoudi, A. Lumped Circuit Accounting for the Rotor Motion Dedicated to the Investigation of the Time-Varying Features of Claw Pole Topologies. IEEE Trans. Magn. 2015, 51, 1–8. [Google Scholar] [CrossRef]
- Asfirane, S.; Hlioui, S.; Amara, Y.; Gabsi, M. Study of a Hybrid Excitation Synchronous Machine: Modeling and Experimental Validation. Math. Comput. Appl. 2019, 24, 34. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.H.; Kim, J.; Song, J.; Kim, D.; Kim, Y.; Jung, S. Distance-Based Intelligent Particle Swarm Optimization for Optimal Design of Permanent Magnet Synchronous Machine. IEEE Trans. Magn. 2017, 53, 1–4. [Google Scholar] [CrossRef]
- Wrobel, R.; Griffo, A.; Mellor, P.H. Scaling of AC copper loss in thermal modeling of electrical machines. In Proceedings of the 2012 XXth International Conference on Electrical Machines, Marseille, France, 2–5 September 2012; pp. 1424–1429. [Google Scholar] [CrossRef]
- Ding, H.C.; Xiao, L.J.; Zhang, H.Y.; Sun, C.Y. Interference Fit Calculation and Stress Analysis for Rotor Sleeve of High-speed Permanent Magnet Electric Machine. Mach. Des. Res. 2011. [Google Scholar]
- Wardach, M. Hybrid excited claw pole electric machine. In Proceedings of the 21st International Conference on Methods and Models in Automation and Robotics (MMAR), Miedzyzdroje, Poland, 4–5 October 2016; pp. 152–156. [Google Scholar]
- Chao-Hui, Z.; Huanqiu, G.; Xin-Wei, W. The Study of Structure and Characteristic of a New Type HECPSG. In Proceedings of the IEEE International Symposium on Industrial Electronics, Vigo, Spain, 4–7 June 2007; pp. 1097–1100. [Google Scholar] [CrossRef]
- Hagstedt, D.; Reinap, A.; Ottosson, J.; Alakula, M. Design and experimental evaluation of a compact hybrid excitation claw-pole rotor. In Proceedings of the 2012 XXth International Conference on Electrical Machines, Marseille, France, 2–5 September 2012; pp. 2896–2901. [Google Scholar] [CrossRef]
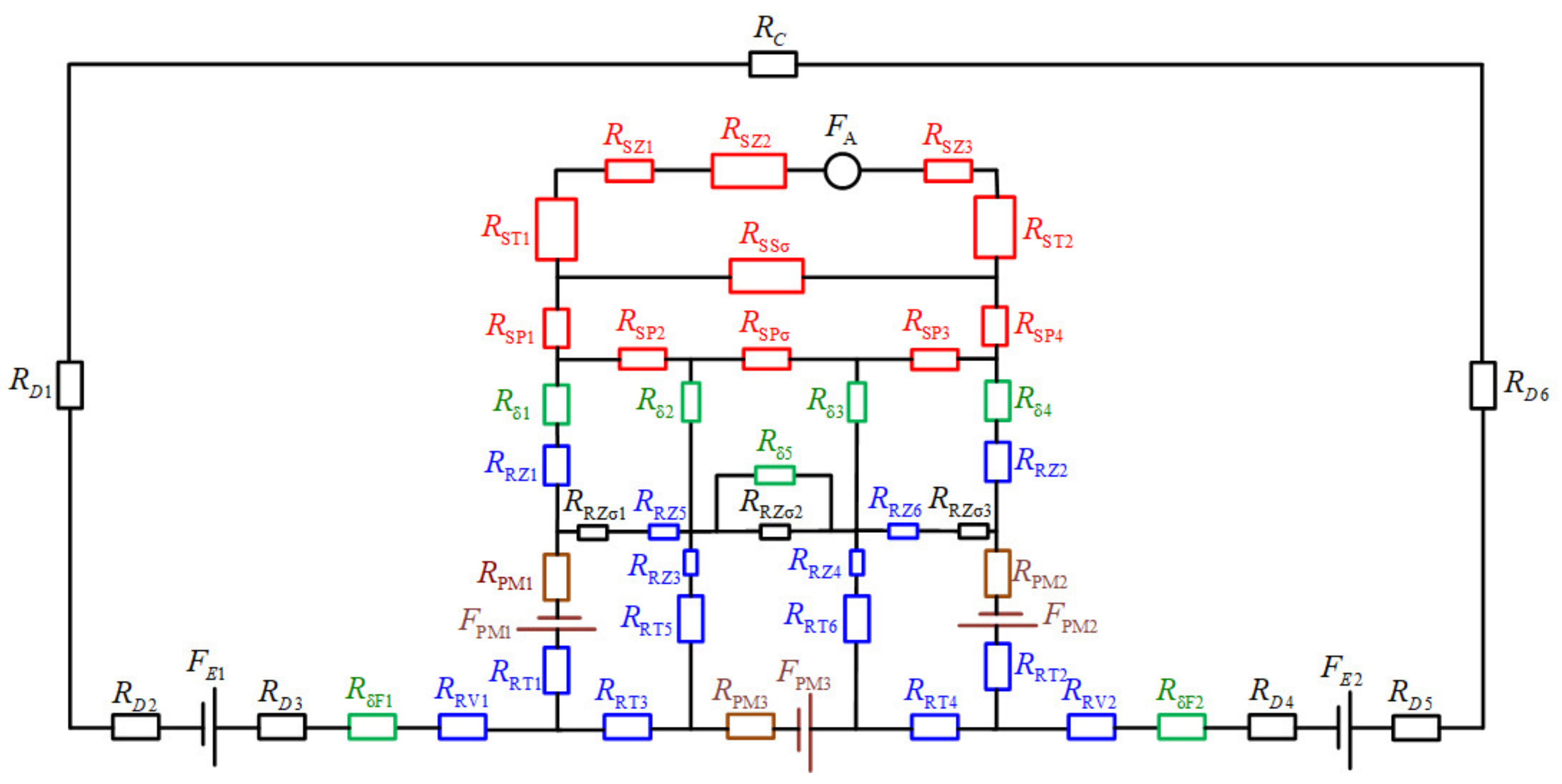






| Item | Symbol |
|---|---|
| Equivalent reluctance of stator yoke | |
| Equivalent reluctance of stator tooth | |
| Equivalent reluctance of stator shoe | |
| Equivalent reluctance of rotor yoke | |
| Equivalent reluctance of axial magnetic bridge | |
| Equivalent reluctance of claw-pole rotor finger | |
| Equivalent reluctance of enclosure | |
| Equivalent reluctance of front and back ending cover | |
| Equivalent reluctance of claw-pole rotor finger yoke | |
| PM equivalent internal reluctance | |
| Main air gap reluctance | |
| Auxiliary air gap reluctance | |
| Flux leakage reluctance in stator slot | |
| Flux leakage reluctance between adjacent stator shoes | |
| Phase A armature reactive MMF | |
| PM equivalent MMF source | |
| Field excitation equivalent MMF source |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| PM width | wPM | Main air gap thickness | gmain |
| Stator notch width | wnot | Auxiliary air gap thickness | gaux |
| Stator tooth width | wst | Stator length | lst |
| PM thickness | dPM | Enclosure length | len |
| Rotor yoke thickness | dry | Rotor length | lrot |
| Stator tooth height | dst | Ending cover length | lec |
| Nonmagnetic ring thickness | dno | Axial magnetic bridge length | lamb |
| Design Variable | ||||
|---|---|---|---|---|
| wPM | 0.716 | −0.054 | 0.537 | 0.512 |
| wnot | −0.533 | −0.41 | −0.451 | 0.4174 |
| wst | 0.134 | 0.409 | 0.127 | 0.1862 |
| dPM | 0.226 | 0.037 | 0.3 | 0.2178 |
| dry | −0.091 | 0.096 | −0.393 | 0.2128 |
| dst | −0.004 | 0.074 | 0.028 | 0.0276 |
| gmain | 0.249 | −0.119 | 0.25 | 0.2234 |
| Design Variable | Initial Value | Optimized Value |
|---|---|---|
| wPM | 22 | 23.1 |
| wnot | 26 | 28.6 |
| gmain | 1 | 0.6 |
| dPM | 3.2 | 4.4 |
| dry | 6 | 6.4 |
| Before Optimization | After Optimization | |
|---|---|---|
| Maximum value | 29.8 Nm | 31.5 Nm |
| Minimum value | 22.4 Nm | 25.1 Nm |
| Average value | 26.1 Nm | 28.3 Nm |
| Torque ripple | 28.4% | 22.6% |
| Elastic Modulus | Density | Poisson’s Ratio v | Allowable Stress |
|---|---|---|---|
| 2.06 × 1011 | 7850 | 0.31 | 800 |
| Parameters | Value |
|---|---|
| Stator outer diameter | 312 mm |
| Stator inner diameter | 200 mm |
| Effective core length | 52 mm |
| Rotor outer diameter | 198.8 mm |
| Rotor inner diameter | 120 mm |
| Winding factor | 0.966 |
| Number of slots | 12 |
| Stacking factor | 0.9 |
| Armature winding turns | 210 |
| Stator yoke width | 17 mm |
| Stator tooth width | 28.28 mm |
| PM length | 53 mm |
| Rated Power | Rated Torque | Rated Voltage | Rated Speed |
|---|---|---|---|
| 10.28 kW | 32.72 Nm | 543.1 V | 3000 rpm |
| Proposed HE-CPM | Electrically Excited Claw Pole Generator Reported in [11] | Hybrid Excited Claw Pole Synchronous Machine Reported in [17] | Hybrid Excited Claw Pole Electric Machine Reported in [25] | Hybrid Excitation Claw Pole Synchronous Generator Reported in [26] | Hybrid Excitation Claw Pole Machine Reported in [27] | |
|---|---|---|---|---|---|---|
| Rated power | 10.28 kW | 7.2 kW | 0.73 kW | - | 0.65 kW | 5 kW |
| Rated voltage | 543.1 V | 48 V | 120 V | 14 V | 135.5 V | 108 V |
| Rated speed | 3000 rpm | 900 rpm | 1200 rpm | 1300 rpm | 1500 rpm | 3000 rpm |
| Efficiency | 89% | 92% | - | 81% | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, Y.; Zhu, S.; Yu, J.; Liu, C. Optimization Design and Performance Evaluation of a Hybrid Excitation Claw Pole Machine. Processes 2022, 10, 541. https://doi.org/10.3390/pr10030541
Cao Y, Zhu S, Yu J, Liu C. Optimization Design and Performance Evaluation of a Hybrid Excitation Claw Pole Machine. Processes. 2022; 10(3):541. https://doi.org/10.3390/pr10030541
Chicago/Turabian StyleCao, Yu, Shushu Zhu, Junyue Yu, and Chuang Liu. 2022. "Optimization Design and Performance Evaluation of a Hybrid Excitation Claw Pole Machine" Processes 10, no. 3: 541. https://doi.org/10.3390/pr10030541
APA StyleCao, Y., Zhu, S., Yu, J., & Liu, C. (2022). Optimization Design and Performance Evaluation of a Hybrid Excitation Claw Pole Machine. Processes, 10(3), 541. https://doi.org/10.3390/pr10030541







