The Study of the Pore Structure Properties of Rocks Based on Complex Network Theory: Taking an Example of the Sandstone in the Tongnan Area in China
Abstract
:1. Introduction
2. Basic Characteristics of a Sandstone Pore Network
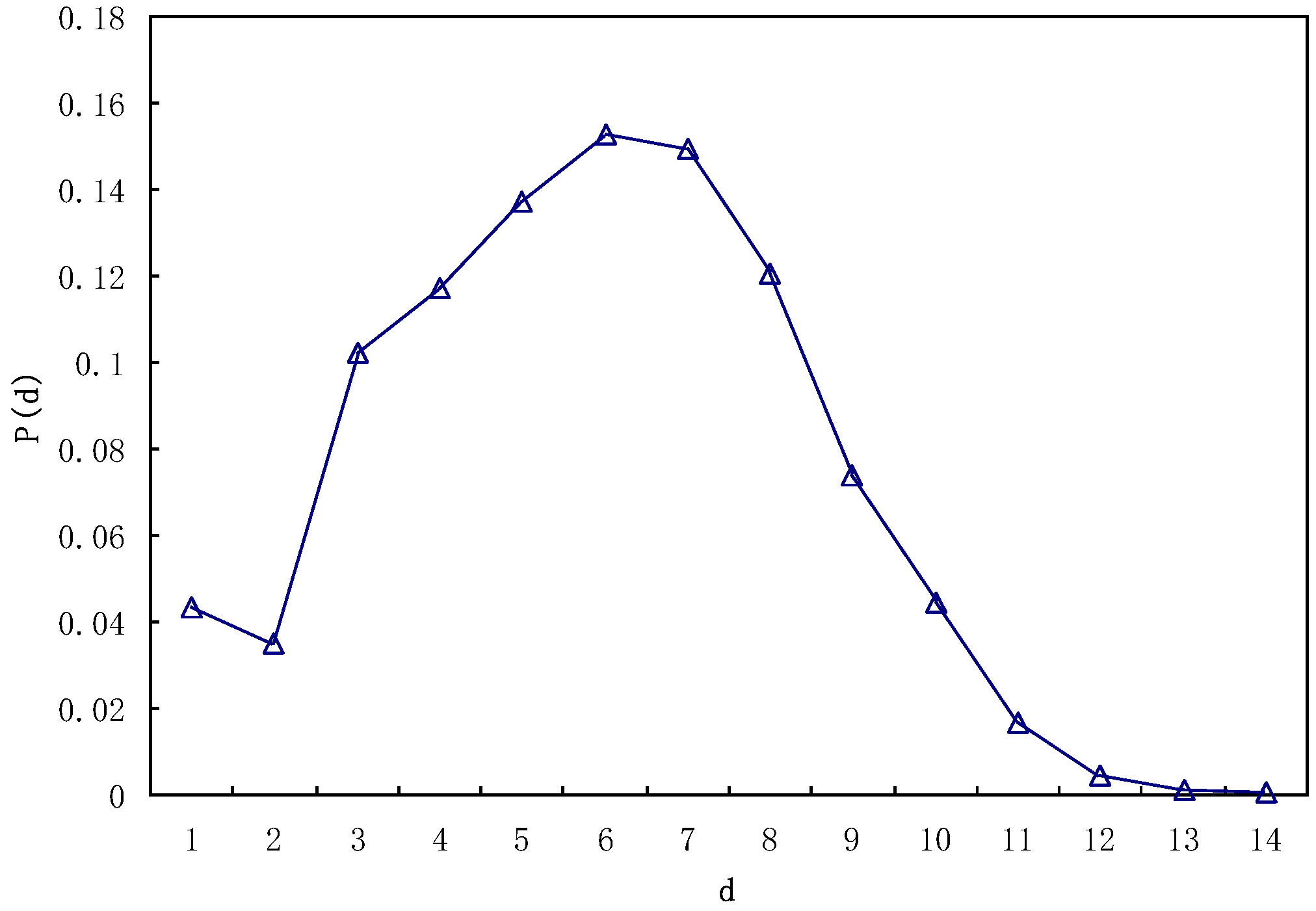
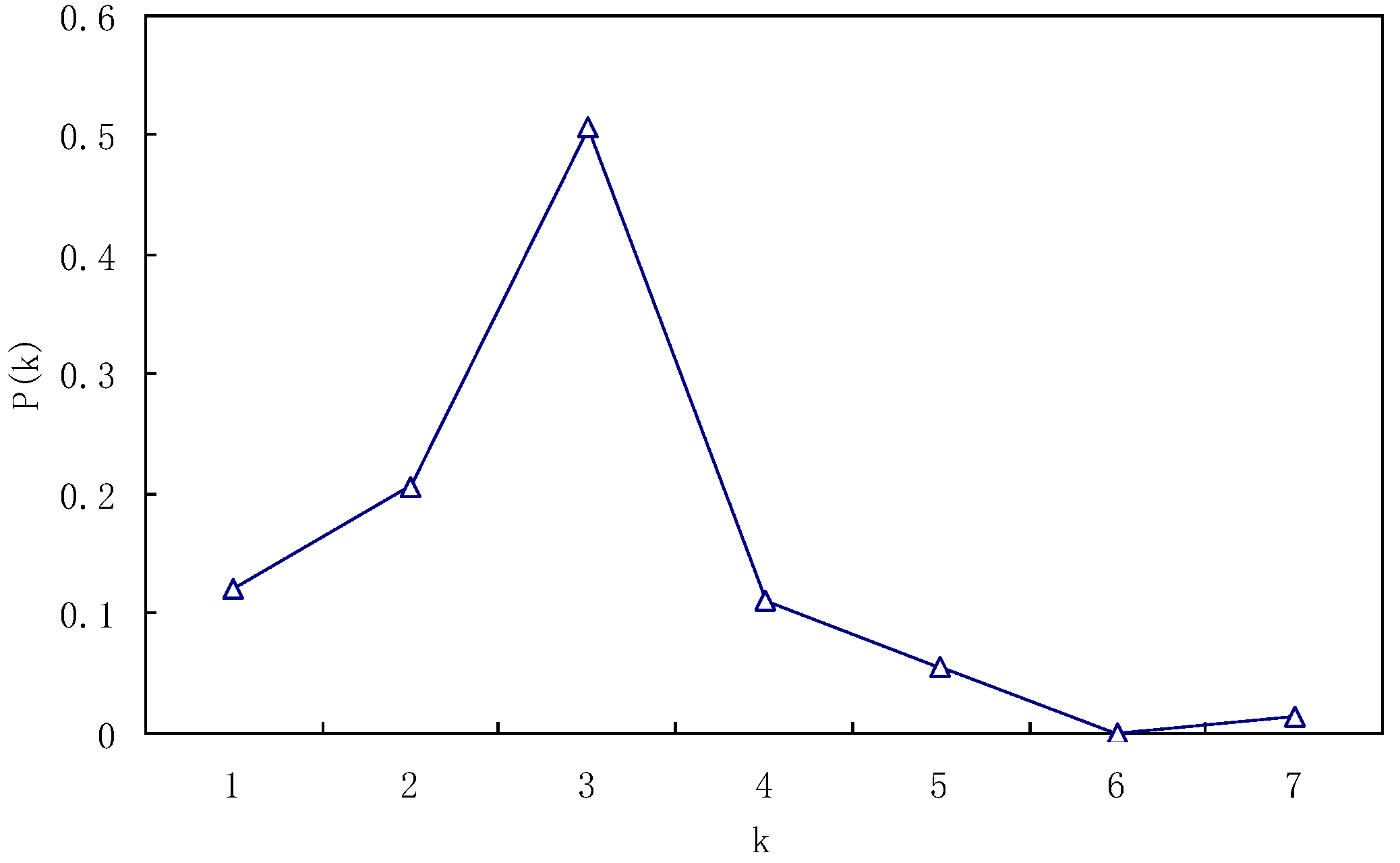
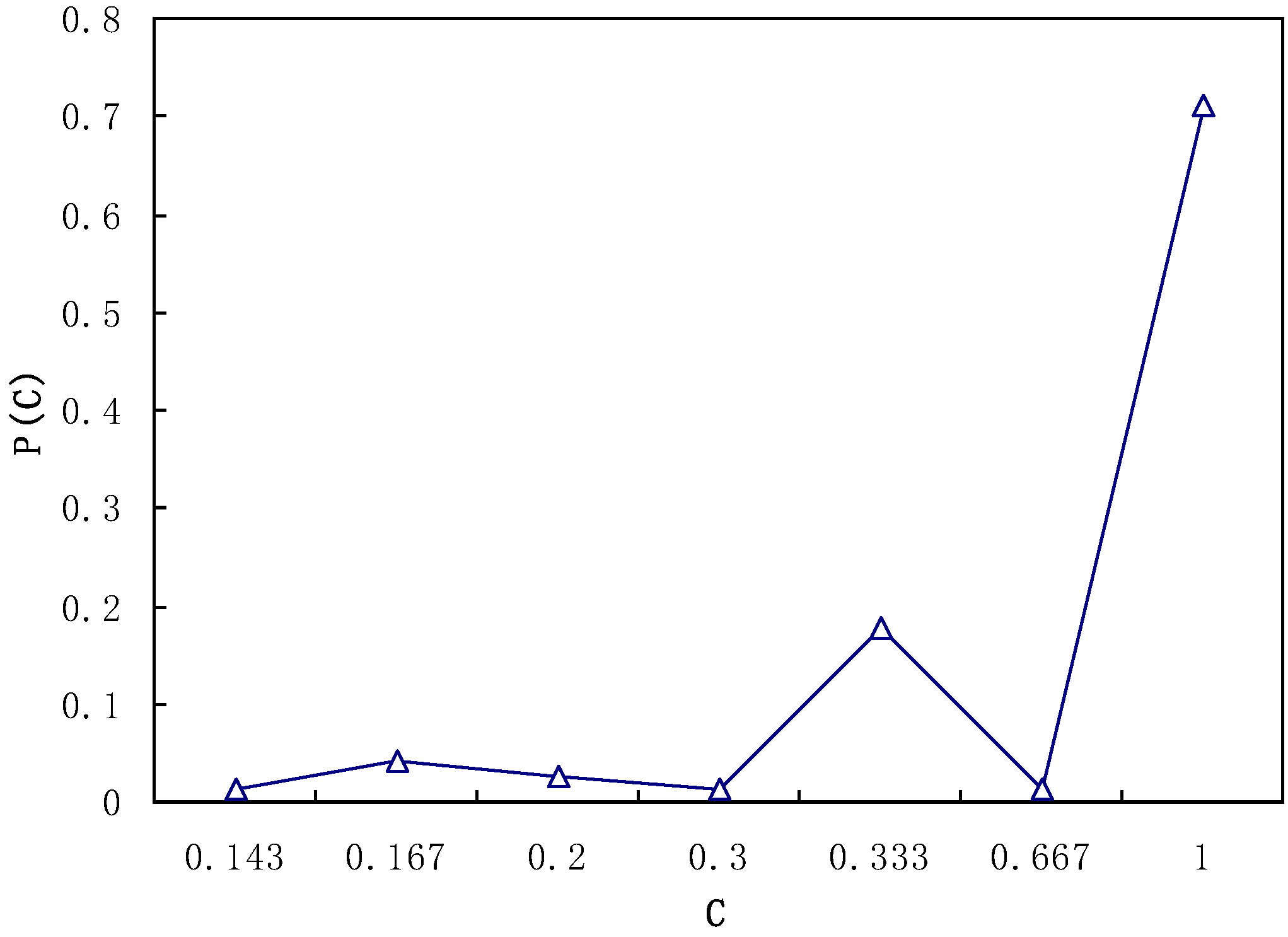
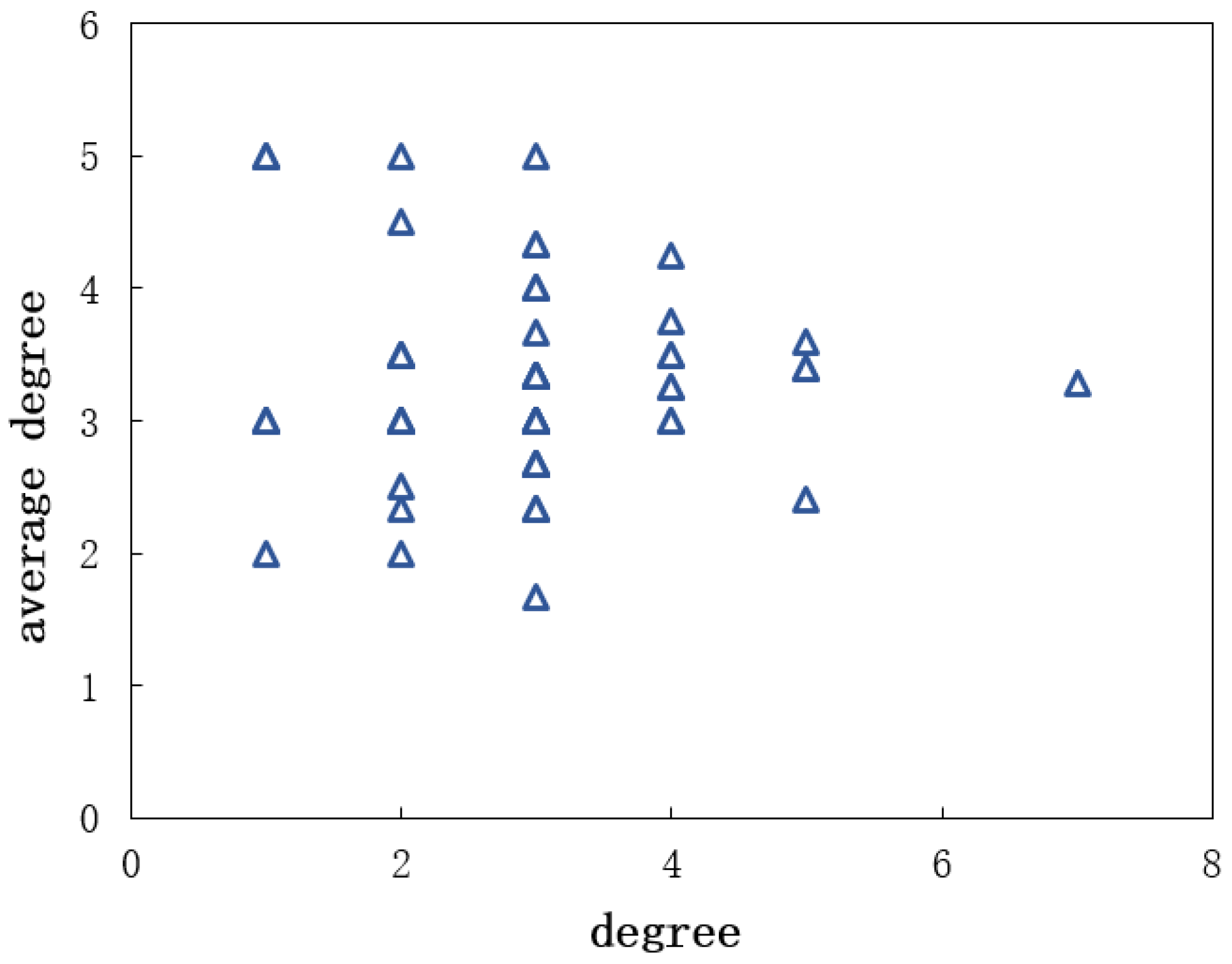
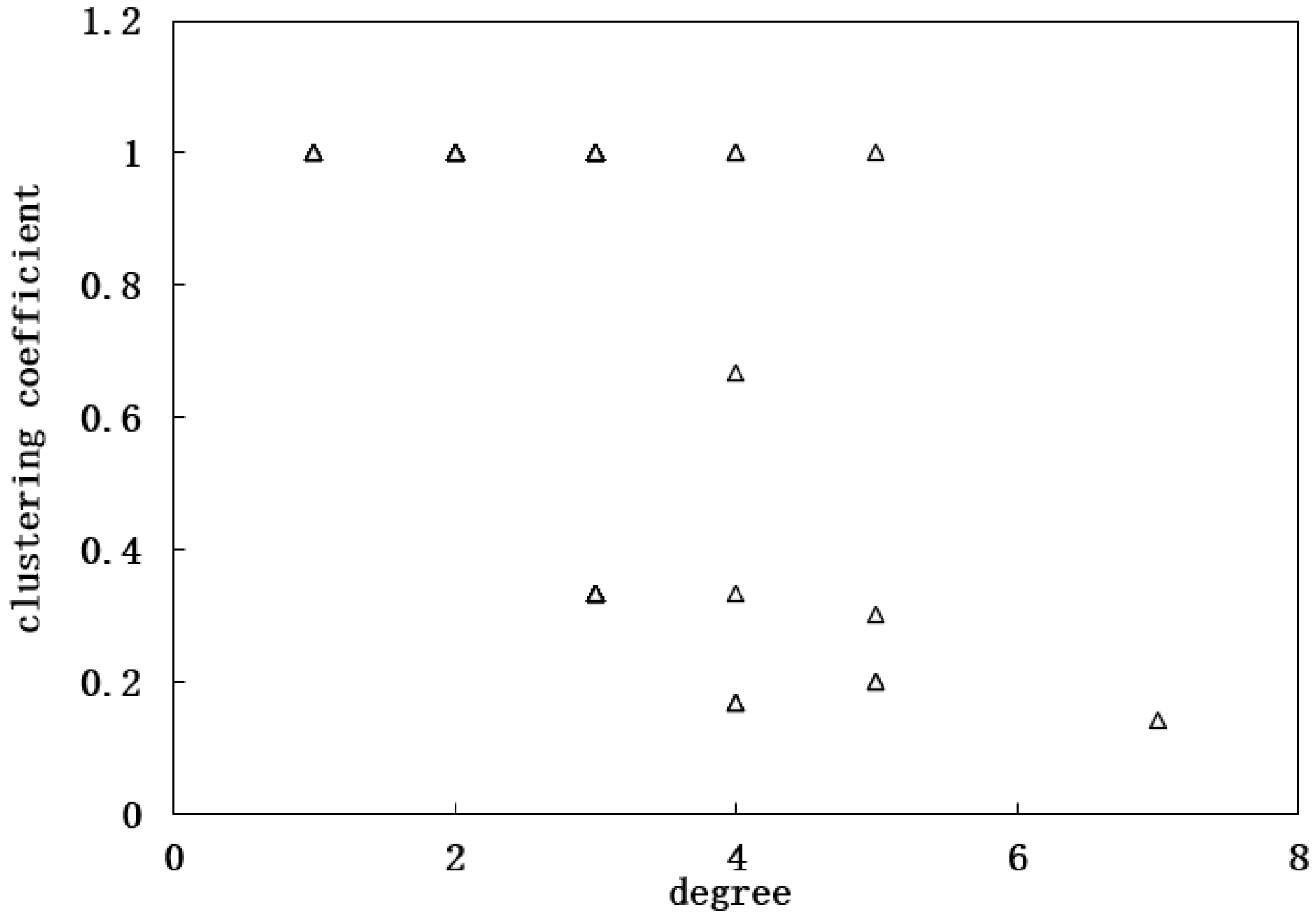
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jimenez-Hornero, F.J.; Ariza-Villaverde, A.B.; de Ravé, E.G. Multifractal Description of simulated flow velocity in idealised porous media by using the sandbox method. Fractals 2013, 21, 157–169. [Google Scholar] [CrossRef]
- Mohammadpour, R.; Ghani, A.A.; Azamathulla, H.M. Numerical modeling of 3-D flow on porous broad crested weirs. Appl. Math. Model. 2013, 37, 9324–9337. [Google Scholar] [CrossRef]
- Hajizadeh, A.; Safekordi, A.; Farhadpour, F.A. A multiple-point statistics algorithm for 3D pore space reconstruction from 2D images. Adv. Water Resour. 2011, 34, 1256–1267. [Google Scholar] [CrossRef]
- Civan, F.; Rai, C.S.; Sondergeld, C.H. Shale-gas permeability and diffusivity inferred by improved formulation of relevant retention and transport mechanisms. Transp. Porous Media 2011, 86, 925–944. [Google Scholar] [CrossRef]
- Zhang, T.Y.; Li, D.L.; Yang, J.Q. A study of the effect of pore characteristic on permeability with a pore network model. Pet. Sci. Technol. 2013, 31, 1790–1796. [Google Scholar] [CrossRef]
- Yang, J.; Jiangtao, Z.; Marcelo, E. 3D numerical reconstruction of well-connected porous structure of rock using fractal algorithms. Comput. Methods Appl. Mech. Eng. 2014, 279, 212–226. [Google Scholar]
- Shaina, K.; Hesham, E.; Carlos, T. Assessing the utility of FIB-SEM images for shale digital rock physics. Adv. Water Resour. 2015, 18, 1350006. [Google Scholar]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef]
- Barabási, A.L.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, H.; Yuan, L. A Kind of Deterministic Small-World Network Derived from Polygonal Nesting. Appl. Mech. Mater. 2014, 614, 543–549. [Google Scholar] [CrossRef]
- Amartya, S.; Bryan, R.L.; Gaurav, J. The long-range interaction landscape of gene promoters. Nature 2012, 389, 109–113. [Google Scholar]
- Jiang, Z.Y.; Liang, M.G.; Li, Q. Optimal dynamic bandwidth allocation for complex networks. Phys. A Stat. Mech. Its Appl. 2013, 392, 1256–1262. [Google Scholar] [CrossRef]
- Huang, D.Z. Research on Reservoir Parameters and Characterization of Continental Tight Sandstone. Ph.D. Thesis, Chengdu University of Technology, Chengdu, China, 2009. [Google Scholar]
- Strogatz, S.H. Exploring complex networks. Nature 2001, 410, 268–276. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Quezada, G.R.; Toledo, P.G.; Saavedra, J.H.; Rozas, R.E. Generation of Spatially Correlated Network Models of Porous Media. Transp. Porous Media 2015, 111, 499–515. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Y.; Gu, J.; Liu, H.; Zhu, J.; Ye, D.; Liu, G.; Jin, Q. The Study of the Pore Structure Properties of Rocks Based on Complex Network Theory: Taking an Example of the Sandstone in the Tongnan Area in China. Processes 2022, 10, 211. https://doi.org/10.3390/pr10020211
Hu Y, Gu J, Liu H, Zhu J, Ye D, Liu G, Jin Q. The Study of the Pore Structure Properties of Rocks Based on Complex Network Theory: Taking an Example of the Sandstone in the Tongnan Area in China. Processes. 2022; 10(2):211. https://doi.org/10.3390/pr10020211
Chicago/Turabian StyleHu, Yuhao, Jiayi Gu, Hu Liu, Jingyun Zhu, Dayu Ye, Guannan Liu, and Qing Jin. 2022. "The Study of the Pore Structure Properties of Rocks Based on Complex Network Theory: Taking an Example of the Sandstone in the Tongnan Area in China" Processes 10, no. 2: 211. https://doi.org/10.3390/pr10020211
APA StyleHu, Y., Gu, J., Liu, H., Zhu, J., Ye, D., Liu, G., & Jin, Q. (2022). The Study of the Pore Structure Properties of Rocks Based on Complex Network Theory: Taking an Example of the Sandstone in the Tongnan Area in China. Processes, 10(2), 211. https://doi.org/10.3390/pr10020211





