Optimal DGs Siting and Sizing Considering Hybrid Static and Dynamic Loads, and Overloading Conditions
Abstract
:1. Introduction
- -
- Reducing the transmission lines’ losses;
- -
- Improving the voltage profile on the system;
- -
- Reducing the emissions from centralized plants;
- -
- Low operating costs due to peak shaving;
- -
- Reduced or postponed investment in upgrading generation, transmission, transformers, and distribution infrastructure because of transmission and distribution congestion relief.
- -
- Investigating the power system performance against different load types, including static, dynamic and a composite of static and dynamic loads, as well as overloading conditions;
- -
- Optimally sizing and allocating DGs using the HSA algorithm, and two analytical techniques, respectively.
2. System Modeling
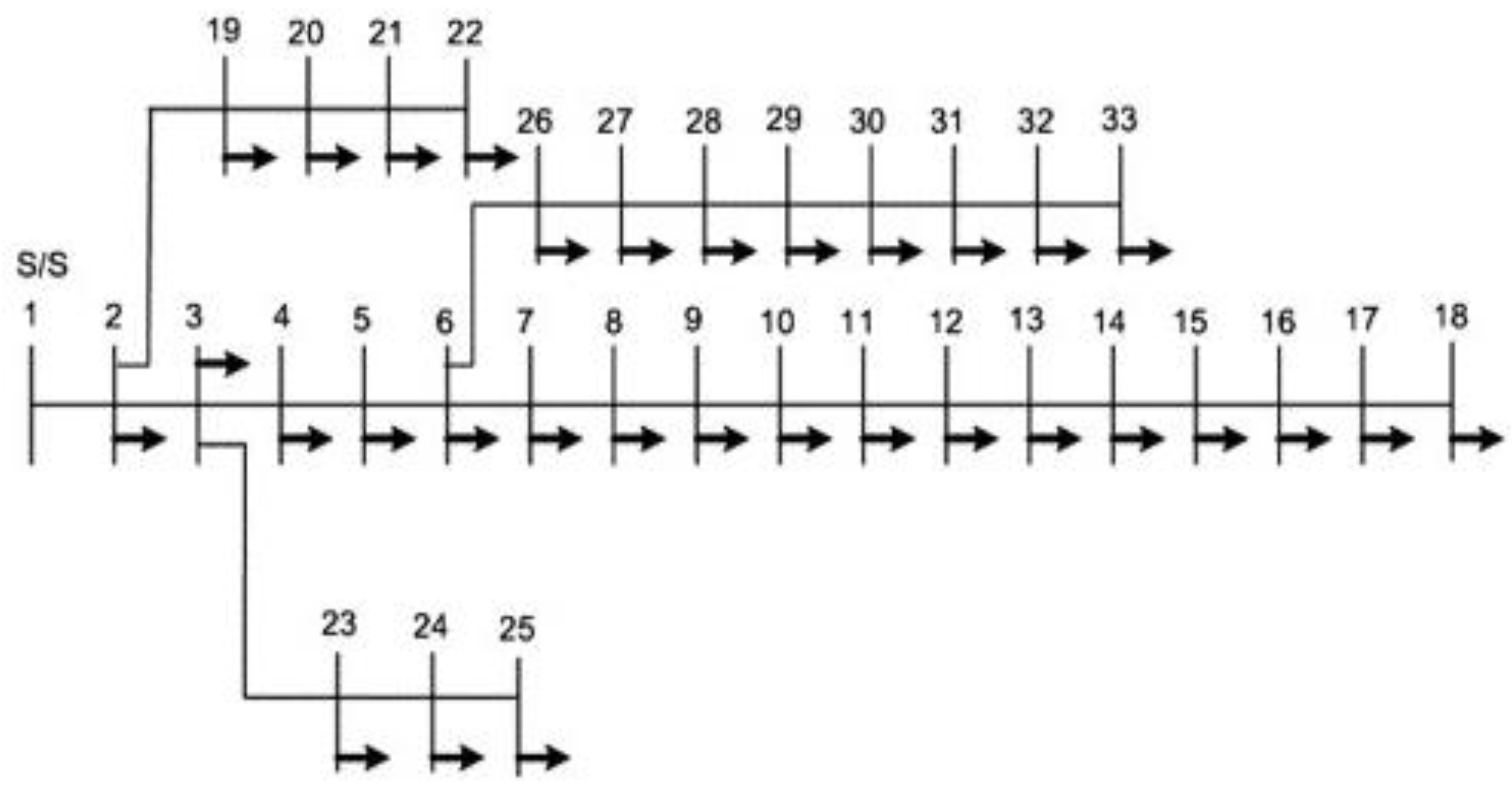
2.1. IEEE 33-Bus System
2.2. Backward/Forward Sweep Method

2.3. Type of DG Used in This Work
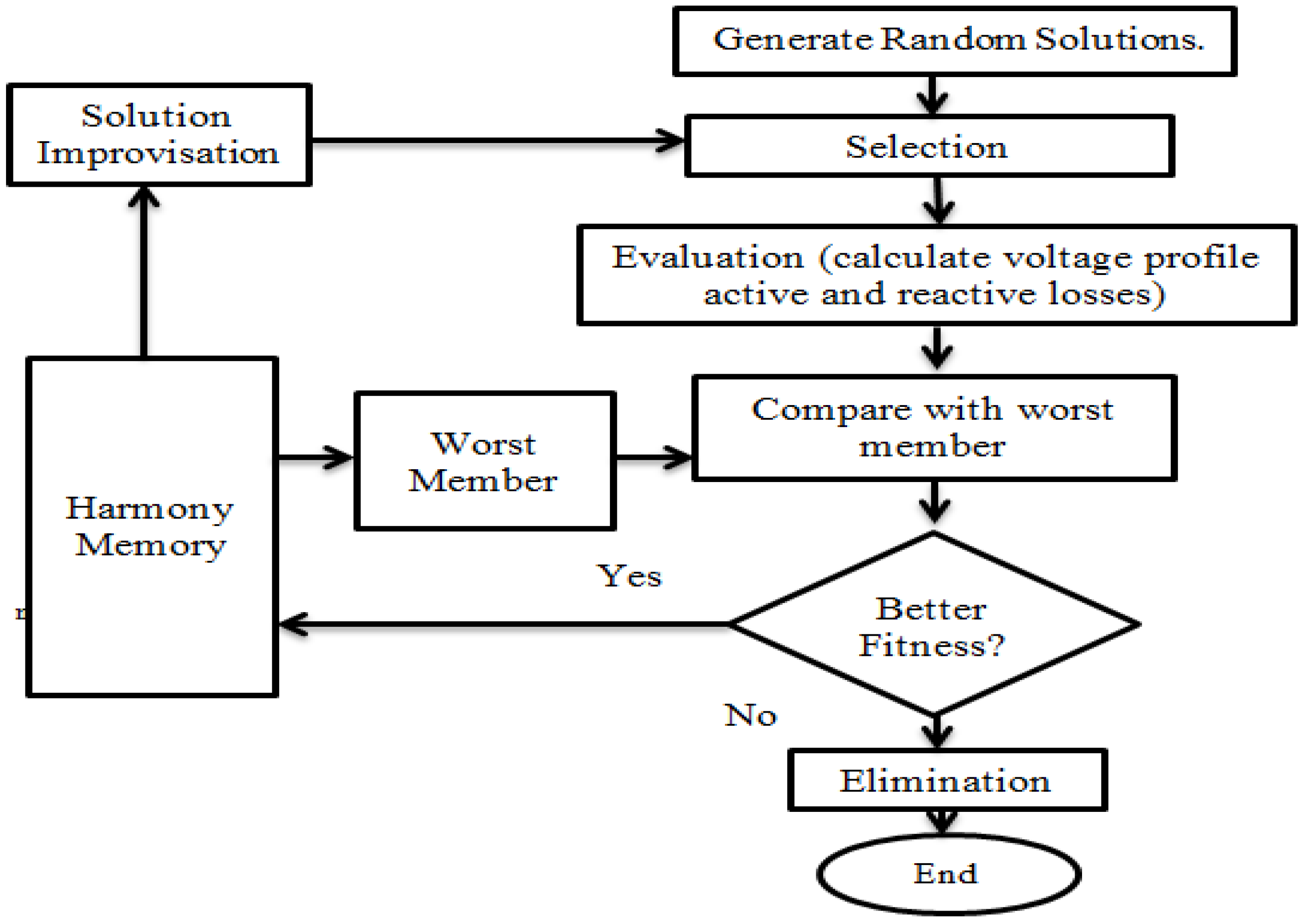
2.4. Harmony Search Algorithm (HSA)
2.5. Types of Loads
2.5.1. Static Loads
- -
- Constant current: In this load type, the change in load occurs according to the change in voltage, and can be represented as:
- -
- Constant power: The active and reactive powers are independent of change or vibration in voltage magnitude, and can be represented as:
- -
- Constant impedance: The active and reactive powers of the load change with the square of the voltage magnitude. This model will be used in this paper as a static type, and can be represented as:
- -
- Polynomial: This is a non-linear model where the active and reactive powers change according to the voltage magnitude and it is usually a combination of the previous types, as modelled below:
- -
- Exponential: This type of load has a non-linear relationship, where the absorbing of power variation is according to the exponential parameter of the load as shown below:
2.5.2. Dynamic Loads
3. Results
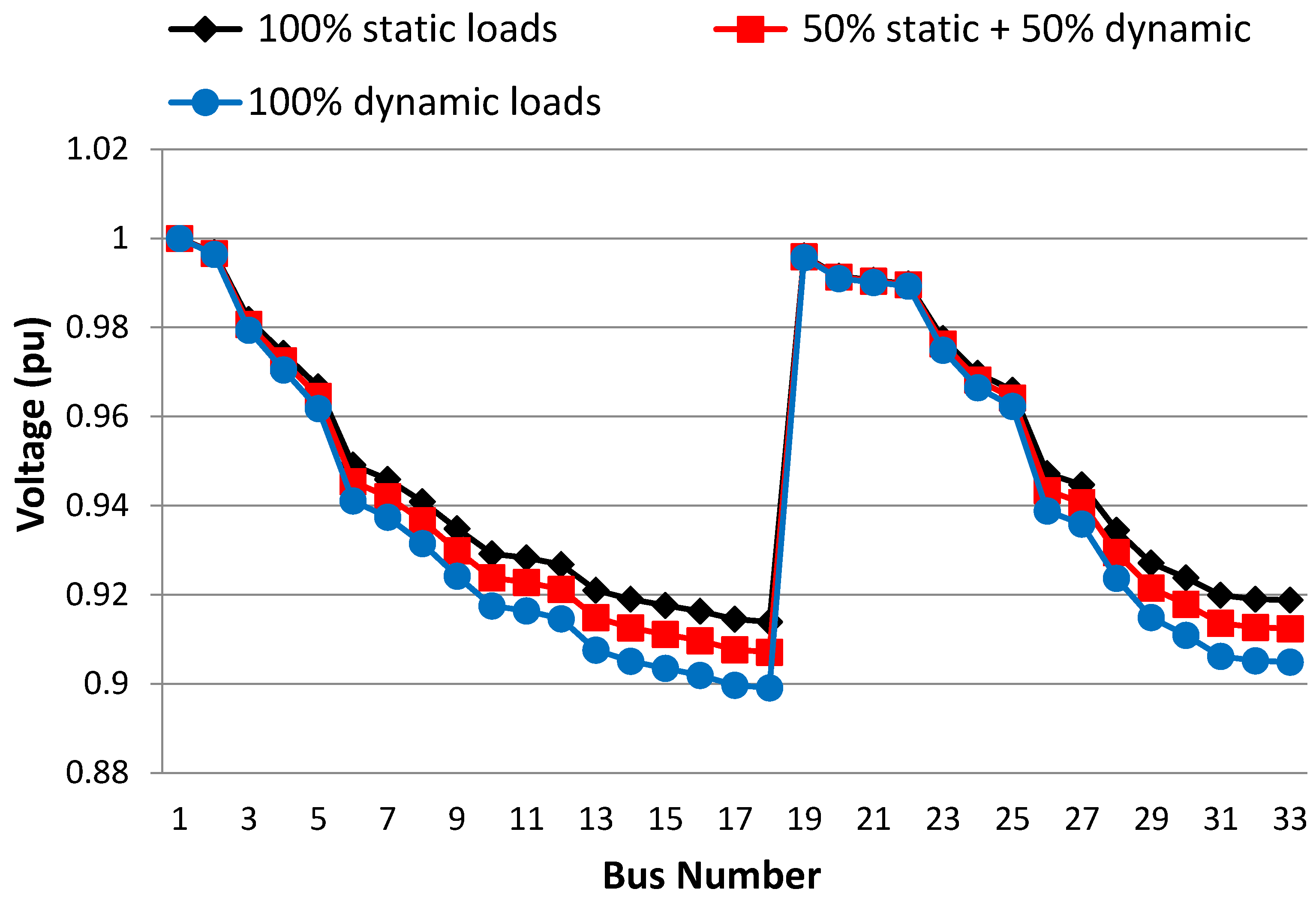
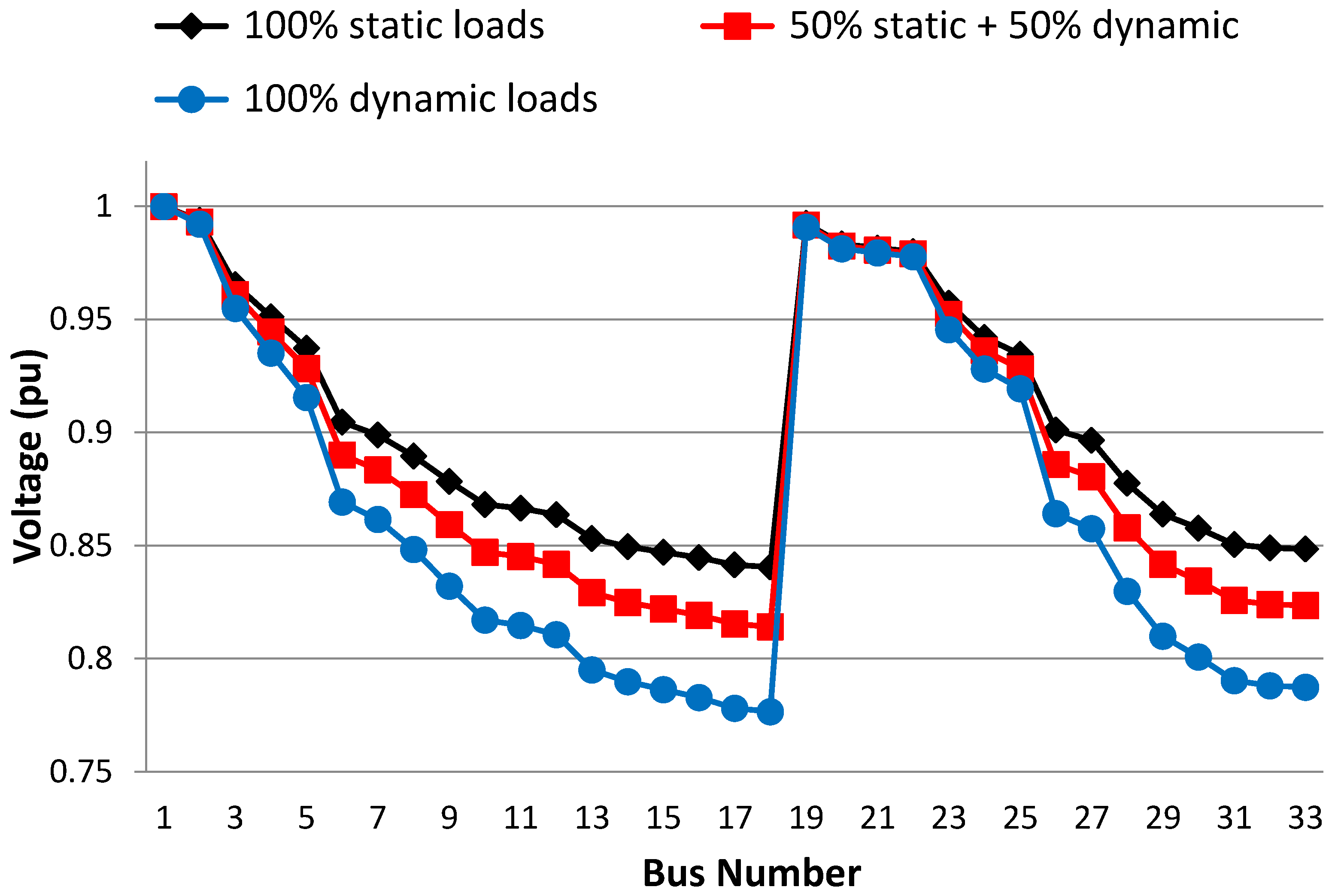
3.1. Selection of Load Type
3.2. Siting and Sizing of DGs
- ○
- DGs are connected to the nodes that are connected to three branches, called interconnection nodes;
- ○
- DGs are connected to the fifth minimum node voltage in the main or lateral feeder.
- -
- Total system losses = (211.01 + j140.17) kVA
- -
- Lowest bus voltage = 0.899 pu (bus number 18)
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Symbol | Description |
| CHP | Combined Heat and Power |
| HM | Harmony Memory |
| LSF | Loss Sensitivity Factor |
| NIC | Nature-Inspired Computing Algorithms |
| PAR | Pitch-Adjusting Rate |
| WK | Weak Bus |
| bw | Band Width |
| DER | Distributed Energy Resources |
| DFIG | Doubly Fed Induction Generation |
| DG | Distributed Generation |
| HMCR | Harmony Memory Consider Rate |
| HSA | Harmony Search Algorithm |
| IA | Improved Analytical |
| LL | Lower Limit |
| N | Population Size |
| Pk | Real Power Flowing Out of Bus. |
| Pk+1 | Real Load Power at Bus k + 1. |
| Ploss(k,k+1) | Real Power Loss in the Line Section Connecting Buses k and k + 1. |
| PT,loss(k,k+1) | Total Real Power Loss in the Line Section. |
| PSO | Particle Swarm Optimization |
| PV | Photovoltaic |
| Qk | Reactive Power Flowing Out of Bus. |
| Qk+1 | Reactive Load Power at Bus k + 1. |
| Qloss(k,k+1) | Reactive Power Loss in The Line Section Connecting Buses k and k + 1. |
| QT,loss(k,k+1) | Total Reactive Power Loss in the Line Section |
| SQP | Sequential Quadratic Programming |
| tmax | Maximum Number of Iterations |
| UL | Upper Limit |
| xi | Current Position |
| xi,new | New Position |
Appendix A
| Branch | Impedance of Lines | Branch | Impedance of Lines | ||||
|---|---|---|---|---|---|---|---|
| From Bus | To Bus | Resistance | Reactance | From Bus | To Bus | Resistance | Reactance |
| 1 | 2 | 0.0922 | 0.047 | 17 | 18 | 0.732 | 0.574 |
| 2 | 3 | 0.493 | 0.2511 | 2 | 19 | 0.164 | 0.1565 |
| 3 | 4 | 0.366 | 0.1864 | 19 | 20 | 1.5042 | 1.3554 |
| 4 | 5 | 0.3811 | 0.1941 | 20 | 21 | 0.4095 | 0.4784 |
| 5 | 6 | 0.819 | 0.707 | 21 | 22 | 0.7089 | 0.9373 |
| 6 | 7 | 0.1872 | 0.6188 | 3 | 23 | 0.4512 | 0.3083 |
| 7 | 8 | 0.7114 | 0.2351 | 23 | 24 | 0.898 | 0.7091 |
| 8 | 9 | 1.03 | 0.74 | 24 | 25 | 0.896 | 0.7011 |
| 9 | 10 | 1.044 | 0.74 | 6 | 26 | 0.203 | 0.1034 |
| 10 | 11 | 0.1966 | 0.065 | 26 | 27 | 0.2842 | 0.1447 |
| 11 | 12 | 0.3744 | 0.1238 | 27 | 28 | 1.059 | 0.9337 |
| 12 | 13 | 1.468 | 1.155 | 28 | 29 | 0.8042 | 0.7006 |
| 13 | 14 | 0.5416 | 0.7129 | 29 | 30 | 0.5075 | 0.2585 |
| 14 | 15 | 0.591 | 0.526 | 30 | 31 | 0.9744 | 0.963 |
| 15 | 16 | 0.7463 | 0.545 | 31 | 32 | 0.3105 | 0.3619 |
| 16 | 17 | 1.289 | 1.721 | 32 | 33 | 0.341 | 0.5302 |
| Bus No. | The Load Is Connected at 100% | Bus No. | The Load Is Connected at 100% | ||
|---|---|---|---|---|---|
| Active Power | Reactive Power | Active Power | Reactive Power | ||
| 1 | 0 | 0 | 18 | 82.8039 | 27.7415 |
| 2 | 99.724 | 59.2761 | 19 | 89.5248 | 39.526 |
| 3 | 88.5914 | 37.323 | 20 | 89.0369 | 39.0426 |
| 4 | 117.2925 | 72.3716 | 21 | 88.9421 | 38.9491 |
| 5 | 58.2424 | 26.3281 | 22 | 88.8609 | 38.8691 |
| 6 | 57.2233 | 16.2429 | 23 | 87.2152 | 46.5837 |
| 7 | 190.0976 | 80.0123 | 24 | 402.8074 | 182.0364 |
| 8 | 189.2103 | 78.3852 | 25 | 400.7457 | 179.9452 |
| 9 | 56.4135 | 15.2575 | 26 | 59.4249 | 18.1349 |
| 10 | 56.0916 | 14.8788 | 27 | 59.3955 | 17.8385 |
| 11 | 42.0354 | 22.2407 | 28 | 59.266 | 13.2688 |
| 12 | 55.9639 | 25.7786 | 29 | 118.3439 | 44.0473 |
| 13 | 55.625 | 25.1002 | 30 | 197.1054 | 369.0642 |
| 14 | 110.9944 | 56.7952 | 31 | 147.7076 | 41.8942 |
| 15 | 55.4194 | 7.0558 | 32 | 206.7542 | 59.4977 |
| 16 | 55.3471 | 14.031 | 33 | 59.0691 | 23.7524 |
| 17 | 55.2359 | 13.9076 | |||
References
- Stecanella, P.A.J.; Camargos, R.S.C.; Vieira, D.; Domingues, E.G.; Filho, A.d.L.F. A methodology for determining the incentive policy for photovoltaic distributed generation that leverages its technical benefits in the distribution system. Renew. Energy 2022, 199, 474–485. [Google Scholar] [CrossRef]
- Elmitwally, A.; Kotb, M.F.; Gouda, E.; Elgamal, M. A Coordination Scheme for a Combined Protection System Considering Dynamic Behavior and Wind DGs Fault Ride-Through Constraints. Electr. Power Syst. Res. 2022, 213, 108720. [Google Scholar] [CrossRef]
- Kumar, M.; Soomro, A.M.; Uddin, W.; Kumar, L. Optimal Multi-Objective Placement and Sizing of Distributed Generation in Distribution System: A Comprehensive Review. Energies 2022, 15, 7850. [Google Scholar] [CrossRef]
- Khan, M.H.; Ulasyar, A.; Khattak, A.; Zad, H.S.; Alsharef, M.; Alahmadi, A.A.; Ullah, N. Optimal Sizing and Allocation of Distributed Generation in the Radial Power Distribution System Using Honey Badger Algorithm. Energies 2022, 15, 5891. [Google Scholar] [CrossRef]
- Bizhani, H.; Noroozian, R.; Muyeen, S.M.; Techato, K.; Blaabjerg, F. A grid-connected smart extendable structure for hybrid integration of distributed generations. IEEE Access 2019, 7, 105235–105246. [Google Scholar] [CrossRef]
- Zimran, R.; Khalid, H.M.; Muyeen, S.M. Communication systems in distributed generation: A bibliographical review and frameworks. IEEE Access 2020, 8, 207226–207239. [Google Scholar]
- Prashant; Siddiqui, A.S.; Sarwar, M.; Althobaiti, A.; Ghoneim, S.S.M. Optimal Location and Sizing of Distributed Generators in Power System Network with Power Quality Enhancement Using Fuzzy Logic Controlled D-STATCOM. Sustainability 2022, 14, 3305. [Google Scholar] [CrossRef]
- Agajie, T.F.; Khan, B.; Alhelou, H.H.; Mahela, O.P. Optimal expansion planning of distribution system using grid-based multi-objective harmony search algorithm. Comput. Electr. Eng. 2020, 87, 106823. [Google Scholar] [CrossRef]
- Bhatt, N.; Chandel, A.K. An intelligent water drop approach for simultaneous reconfiguration and DG integration in distribution system. Energy Syst. 2022, 13, 1–24. [Google Scholar] [CrossRef]
- Zimran, R.; Khalid, H.M.; Muyeen, S.M.; Kamwa, I. Bibliographic review on power system oscillations damping: An era of conventional grids and renewable energy integration. Int. J. Electr. Power Energy Syst. 2022, 136, 107556. [Google Scholar]
- Hatata, A.Y.; Ebeid, A.S.; El-Saadawi, M.M. Optimal restoration of directional overcurrent protection coordination for meshed distribution system integrated with DGs based on FCLs and adaptive relays. Electr. Power Syst. Res. 2022, 205, 107738. [Google Scholar] [CrossRef]
- Aquino-Lugo, A.A.; Klump, R.; Overbye, T.J. A Control Framework for The Smart Grid For Voltage Support Using Agent-Based Technologies. IEEE Trans. Smart Grid 2011, 2, 161–168. [Google Scholar] [CrossRef]
- Chiradeja, P.; Ramakumar, R. An Approach to Quantify the Technical Benefits of Distributed Generation. IEEE Trans. Energy Convers. 2004, 19, 1686–1693. [Google Scholar] [CrossRef]
- Aloukili, A.A.; El-Sharkawy, M.A.; Attia, M.A. Optimum Sizing and Siting for DG Unitsusing Hybrid 2/3 Rule and Harmony Search Algorithm. Int. J. Eng. Work. 2018, 5, 1–9. [Google Scholar] [CrossRef]
- Ambika, R.; Rajeswari, R. Optimal Siting and Sizing of Multiple DG Units for the Enhancement of Voltage Profile and Loss Minimization in Transmission Systems Using Nature Inspired Algorithms. Sci. World J. 2016, 2016, 6579. [Google Scholar]
- Zhu, D.; Broadwater, R.P.; Tam, K.-S.; Seguin, R.; Asgeirsson, H. Impact of DG Placement on Reliability and Efficiency with Time-Varying Loads. IEEE Trans. Power Syst. 2006, 21, 419–427. [Google Scholar] [CrossRef]
- Keane, A.; O’Malley, M. Optimal Allocation of Embedded Generation on Distribution Networks. IEEE Trans. Power Syst. 2005, 20, 1640–1646. [Google Scholar] [CrossRef]
- EI-Zonkoly, A.M. Optimal Placement of Multi-distributed Generation Units Including Different Load models using Particle Swarm Optimization. IET Gener. Transm. Distrib. 2011, 5, 760–771. [Google Scholar] [CrossRef]
- Shaaban, M.; Petinrin, J.O. Sizing and Sitting of DG in Distribution System for Voltage Profile Improvement and Loss Reduction. Int. J. Smart Grid Clean Energy 2013, 8, 1–7. [Google Scholar]
- Le, A.D.T.; Kashem, M.A.; Negnevitsky, M.; Ledwich, G. Optimal Distribution Generation Parameters for Reducing Losses with Economic Consideration. In Proceedings of the 2007 IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007; pp. 1–8. [Google Scholar]
- Mohamad, A.; Kandelousi, S.M.; Moghadasian, M. Distribution Feeder Reconfiguration Considering Distributed Generators using Cuckoo Optimization Algorithm. In Proceedings of the 2nd International Conference on Research in Science, Engineering and Technology (ICRSET’2014), Dubai, United Arab Emirates, 21–22 March 2014. [Google Scholar]
- Wang, L.; Singh, C. Reliability-constrained Optimum Placement of Reclosers and Distributed Generators in Distribution Networks using an ant Colony System Algorithm. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2008, 38, 757–764. [Google Scholar] [CrossRef]
- Rao, R.S.; Ravindra, K.; Satish, K.; Narasimham, S.V.L. Power Loss minimization in Distribution System using Network Reconfiguration in the Presence of Distributed Generation. IEEE Trans. Power Syst. 2013, 28, 317–325. [Google Scholar] [CrossRef]
- Hemdan, N.G.A.; Kurrat, M. Efficient Integration of Distributed Generation for Meeting the Increased Load Demand. Int. J. Electr. Power Energy Syst. 2011, 33, 1572–1583. [Google Scholar] [CrossRef]
- Kumar, T.R.; Rao, G.K. Analysis of IA and PSO Algorithms for Siting and sizing of DG in Primary Distribution Networks. Int. J. Control. Theory Appl. 2017, 10, 341–350. [Google Scholar]
- Kim, J.O.; Nam, S.W.; Park, S.K.; Singh, C. Dispersed Generation Planning using Improved Hereford Ranch Algorithm. Elect. Power Syst. Res. 1998, 47, 47–55. [Google Scholar] [CrossRef]
- Adewumi, O.B.; Fotis, G.; Vita, V.; Nankoo, D.; Ekonomou, L. The impact of distributed energy storage on distribution and transmission networks’ power quality. Appl. Sci. 2022, 12, 6466. [Google Scholar] [CrossRef]
- Caballero-Peña, J.; Cadena-Zarate, C.; Parrado-Duque, A.; Osma-Pinto, G. Distributed energy resources on distribution networks: A systematic review of modelling, simulation, metrics, and impacts. Int. J. Electr. Power Energy Syst. 2022, 138, 107900. [Google Scholar] [CrossRef]
- Pereira, L.D.L.; Yahyaoui, I.; Fiorotti, R.; de Menezes, L.S.; Fardin, J.F.; Rocha, H.R.O.; Tadeo, F. Optimal allocation of distributed generation and capacitor banks using probabilistic generation models with correlations. Appl. Energy 2022, 307, 118097. [Google Scholar] [CrossRef]
- Ayalew, M.; Khan, B.; Giday, I.; Mahela, O.P.; Khosravy, M.; Gupta, N.; Senjyu, T. Integration of Renewable Based Distributed Generation for Distribution Network Expansion Planning. Energies 2022, 15, 1378. [Google Scholar] [CrossRef]
- Wazir, A.; Naeem Arbab, D.G. Analysis and Optimization of IEEE 33 Bus Radial Distributed System Using Optimization Algorithm. J. Emerg. Trends Appl. Eng. 2016, 1, 17–21. [Google Scholar]
- Chang, G.W.; Chu, S.Y.; Wang, H.L. An Improved Backward/Forward Sweep Load Flow Algorithm for Radial Distribution Systems. IEEE Trans. Power Syst. 2007, 22, 882–884. [Google Scholar] [CrossRef]
- Geem, Z.W.; Kim, J.H.; Loganathan, G.V. A new heuristic optimization algorithm: Harmony search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Wang, X.; Gao, X.-Z.; Zenger, K. An Introduction to Harmony Search Optimization Method; Springer Briefs in Computational Intelligence; Springer International Publishing: New York, NY, USA, 2015. [Google Scholar] [CrossRef]
- Lindén, K.; Segerqvist, I. Modelling of Load Devices and Studying Load/System Characteristics School of Electrical and Computer Engineering. Chalmers University of Technology: Göteborg, Sweden, 1992. [Google Scholar]





| Case Study at 100% Loading | Min Voltage (pu) | Max Voltage (pu) | Active Power Loss (kW) | Reactive Power Loss (kVAr) |
|---|---|---|---|---|
| 100% static | 0.914 | 1 | 158.10 | 104.53 |
| 50% dynamic + 50% static | 0.907 | 1 | 181.48 | 120.26 |
| 100% dynamic | 0.899 | 1 | 211.01 | 140.17 |
| Case Study 150% Loading | Minimum Voltage (pu) | Max Voltage (pu) | Active Power Loss (KW) | Reactive Power Loss (KVAr) |
|---|---|---|---|---|
| 100% static | 0.876 | 1 | 334.13 | 220.70 |
| 50% dynamic + 50% static | 0.861 | 1 | 411.30 | 272.62 |
| 100% dynamic | 0.841 | 1 | 522.97 | 348.00 |
| Case Study 200% Loading | Minimum Voltage (pu) | Max Voltage (pu) | Active Power Loss (kW) | Reactive Power Loss (kVAr) |
|---|---|---|---|---|
| 100% static | 0.841 | 1 | 559.30 | 369.07 |
| 50% dynamic + 50% static | 0.814 | 1 | 739.37 | 490.23 |
| 100% dynamic | 0.777 | 1 | 1.0446 × 103 | 696.57 |
| Case Study 250% Loading | Min Voltage (pu) | Max Voltage | Active Power Loss (kW) | Reactive Power Loss (kVAr) |
|---|---|---|---|---|
| 100% static | 0.808 | 1 | 824.7027 | 543.7000 |
| 50% dynamic + 50% static | 0.768 | 1 | 1.1735 × 103 | 778.4279 |
| 100% dynamic | 0.704 | 1 | 1.8893 × 103 | 1.2632 × 103 |
| Branch | Active Power Losses (kW) | Reactive Power Losses (kVAr) | Bus | ||
|---|---|---|---|---|---|
| From Bus | To Bus | no. | Voltage (pu) | ||
| 1 | 2 | 13.64 | 6.95 | 1 | 1.000 |
| 2 | 3 | 56.46 | 28.76 | 2 | 0.997 |
| 3 | 4 | 20.60 | 10.49 | 3 | 0.979 |
| 4 | 5 | 19.19 | 9.76 | 4 | 0.971 |
| 5 | 6 | 39.06 | 33.71 | 5 | 0.962 |
| 6 | 7 | 2.12 | 7.01 | 6 | 0.941 |
| 7 | 8 | 5.32 | 1.76 | 7 | 0.937 |
| 8 | 9 | 4.56 | 3.27 | 8 | 0.931 |
| 9 | 10 | 3.86 | 2.73 | 9 | 0.924 |
| 10 | 11 | 0.60 | 0.20 | 10 | 0.916 |
| 11 | 12 | 0.95 | 0.31 | 11 | 0.916 |
| 12 | 13 | 2.88 | 2.26 | 12 | 0.915 |
| 13 | 14 | 0.79 | 1.04 | 13 | 0.908 |
| 14 | 15 | 0.40 | 0.35 | 14 | 0.905 |
| 15 | 16 | 0.31 | 0.23 | 15 | 0.904 |
| 16 | 17 | 0.27 | 0.37 | 16 | 0.902 |
| 17 | 18 | 0.06 | 0.045 | 17 | 0.900 |
| 2 | 19 | 0.21 | 0.20 | 18 | 0.899 |
| 19 | 20 | 1.07 | 0.97 | 19 | 0.996 |
| 20 | 21 | 0.13 | 0.15 | 20 | 0.991 |
| 21 | 22 | 0.06 | 0.07 | 21 | 0.990 |
| 3 | 23 | 3.84 | 2.63 | 22 | 0.989 |
| 23 | 24 | 6.20 | 4.89 | 23 | 0.975 |
| 24 | 25 | 1.54 | 1.21 | 24 | 0.967 |
| 6 | 26 | 2.35 | 1.198 | 25 | 0.962 |
| 26 | 27 | 2.95 | 1.50 | 26 | 0.939 |
| 27 | 28 | 9.78 | 8.62 | 27 | 0.936 |
| 28 | 29 | 6.60 | 5.75 | 28 | 0.924 |
| 29 | 30 | 3.14 | 1.60 | 29 | 0.915 |
| 30 | 31 | 1.83 | 1.82 | 30 | 0.911 |
| 31 | 32 | 0.24 | 0.284 | 31 | 0.906 |
| 32 | 33 | 0.01 | 0.021 | 32 | 0.905 |
| 33 | 0.905 | ||||
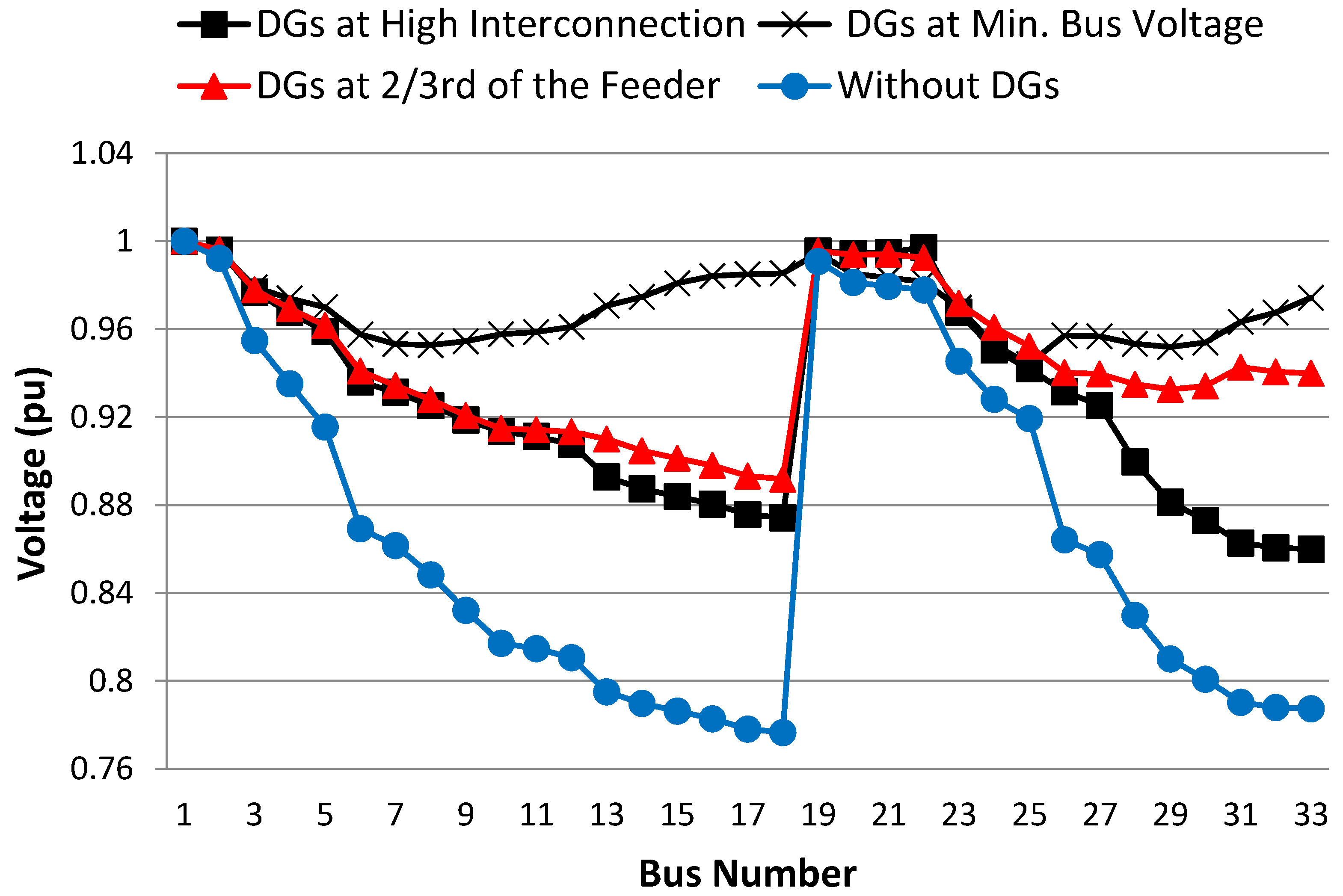
| DG Rating | Min. Voltage | Active Power Losses | Reactive Power Losses | |
|---|---|---|---|---|
| DGs at high interconnection | 3000 kW | 0.925 pu | 109.26 kW | 78.86 kVAr |
| DGs at minimum bus voltage | 1686 kW | 0.970 pu | 72.45 kW | 51.55 kVAr |
| DGs at 2/3rd of the feeder [14] | 1685 kW | 0.953 pu | 72.273 kW | 47.71 kVAr |
| Without DGs | ---- | 0.899 pu | 211.01 kW | 140.18 kVAr |
| DG Rating | Min. Voltage | Active Power Losses | Reactive Power Losses | |
|---|---|---|---|---|
| DGs at high interconnection | 3890 kW | 0.883 | 270.678 kW | 194.078 kVAr |
| DGs at minimum bus voltage | 2491 kW | 0.950 | 169.77 kW | 119.46 kVAr |
| DGs at 2/3rd of the feeder [14] | 2996 kW | 0.938 | 150.43 kW | 100.08 kVAr |
| Without DGs | ---- | 0.841 | 522.97 kW | 348.00 kVAr |
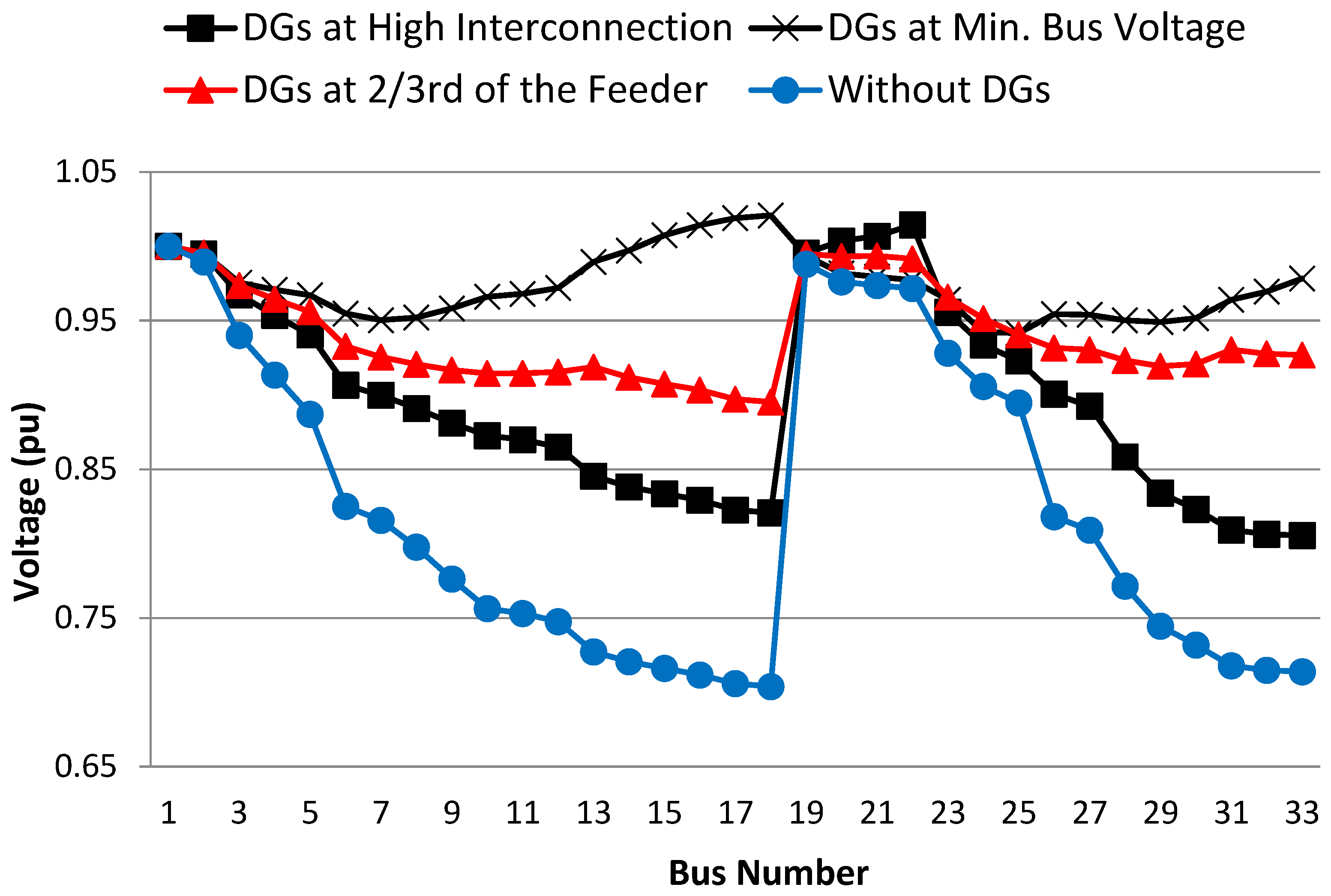
| DG Rating | Min. Voltage | Active Power Losses | Reactive Power Losses | |
|---|---|---|---|---|
| DGs at high interconnection | 5033 kW | 0.831 | 543.38 kW | 387.51 kVAr |
| DGs at minimum bus voltage | 3708 kW | 0.953 | 297.15 kW | 217.72 kVAr |
| DGs at 2/3rd of the feeder [14] | 4075 kW | 0.892 | 280.61 kW | 193.40 kVAr |
| Without DGs | ---- | 0.777 | 1045 kW | 696.57 kVAr |
| DG Rating | Min. Voltage | Active Power Losses | Reactive Power Losses | |
|---|---|---|---|---|
| DGs at high interconnection | 6290 kW | 0.777 | 942.23 kW | 672.65 kVAr |
| DGs at minimum bus voltage | 4711 kW | 0.942 | 485.07 kW | 360.92 kVAr |
| DGs at 2/3rd of the feeder [14] | 5302 kW | 0.896 | 403.33 kW | 274.78 kVAr |
| Without DGs | ---- | 0.704 | 1890 kW | 1260 kVAr |
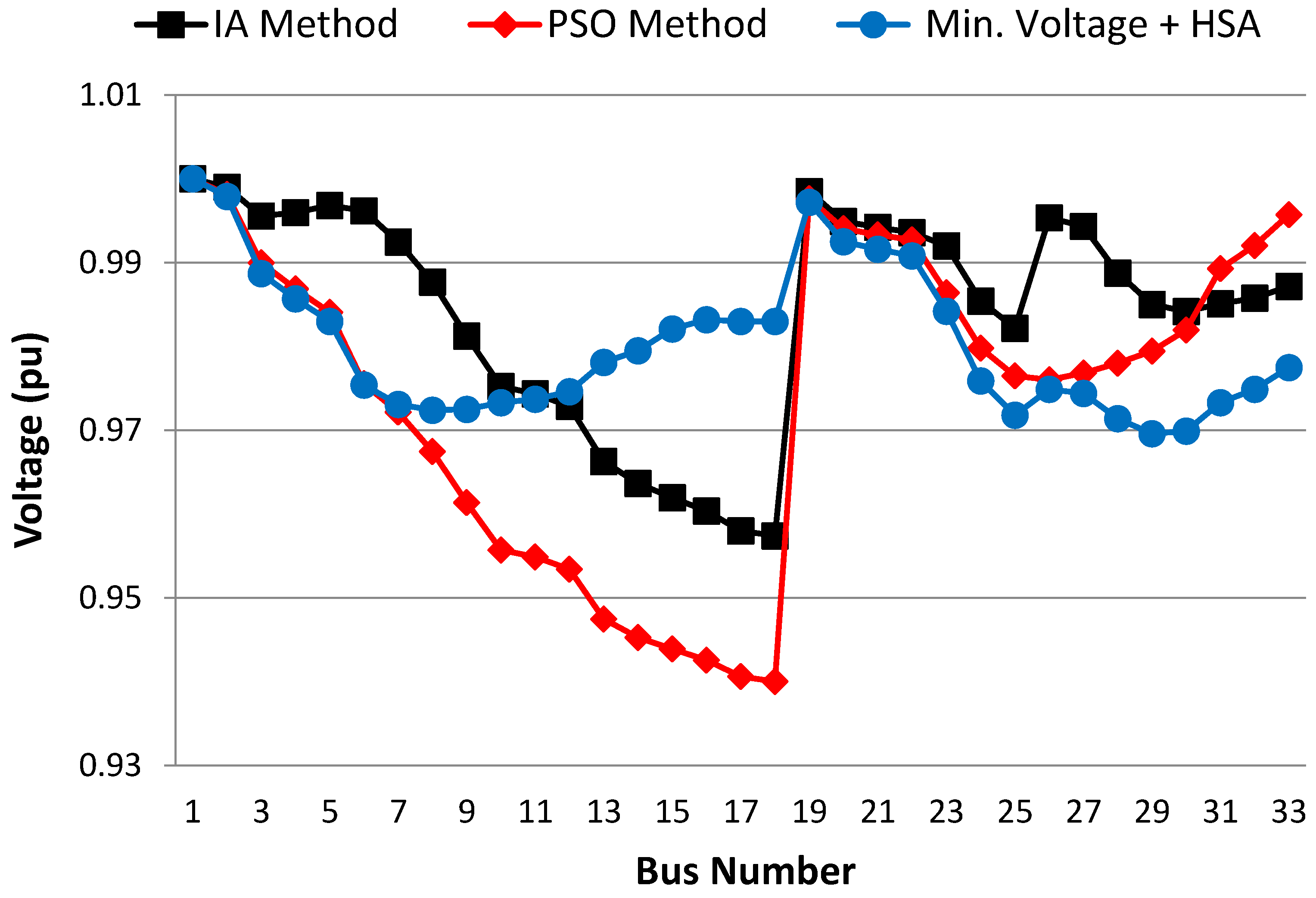
| DG Rating | Min. Voltage | Active Power Losses | Reactive Power Losses | |
|---|---|---|---|---|
| Improved Analytical IA method [25] | 2560.23 kW | 0.9574 | 110.15 kW | ---- |
| PSO method [25] | 1857.5 kW | 0.9400 | 92.44 kW | ---- |
| Minimum bus voltage and HSA | 1686 kW | 0.970 | 72.45 kW | 51.55 kVAr |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sameh, M.A.; Aloukili, A.A.; El-Sharkawy, M.A.; Attia, M.A.; Badr, A.O. Optimal DGs Siting and Sizing Considering Hybrid Static and Dynamic Loads, and Overloading Conditions. Processes 2022, 10, 2713. https://doi.org/10.3390/pr10122713
Sameh MA, Aloukili AA, El-Sharkawy MA, Attia MA, Badr AO. Optimal DGs Siting and Sizing Considering Hybrid Static and Dynamic Loads, and Overloading Conditions. Processes. 2022; 10(12):2713. https://doi.org/10.3390/pr10122713
Chicago/Turabian StyleSameh, Mariam A., Abdulsalam A. Aloukili, Metwally A. El-Sharkawy, Mahmoud A. Attia, and Ahmed O. Badr. 2022. "Optimal DGs Siting and Sizing Considering Hybrid Static and Dynamic Loads, and Overloading Conditions" Processes 10, no. 12: 2713. https://doi.org/10.3390/pr10122713
APA StyleSameh, M. A., Aloukili, A. A., El-Sharkawy, M. A., Attia, M. A., & Badr, A. O. (2022). Optimal DGs Siting and Sizing Considering Hybrid Static and Dynamic Loads, and Overloading Conditions. Processes, 10(12), 2713. https://doi.org/10.3390/pr10122713








