Novel Fuzzy Measurement Alternatives and Ranking according to the Compromise Solution-Based Green Machining Optimization
Abstract
1. Introduction
- A newly developed MCDM technique Measurement Alternatives and Ranking according to the COmpromise Solution (MARCOS) in conjunction with fuzzy theory is used to obtain the optimum combination of green milling parameters for machining of SS 304 and AISI 1045 steel. To the best of the authors’ knowledge, Fuzzy-MARCOS has so far not been used for machining process optimization.
- A linguistic scale is developed using Triangular Fuzzy Numbers (TFNs) to consider different expectations of the product by different users.
- The proposed Fuzzy MARCOS utilizes fuzzy ideal and anti-ideal solutions for referencing, it also provides a more precise utility degree, and a large set of alternatives and criteria is considered for the analysis as well as makes the problem more realistic by defining the linguistic scale based on TFNs.
- This article considers cutting speed (), depth of cut (), feed rate (), and nose radius () as the input variables to optimize the ratio of active to apparent power consumption (PF), active cutting energy (ACE), and surface roughness (Ra) as the response variables.
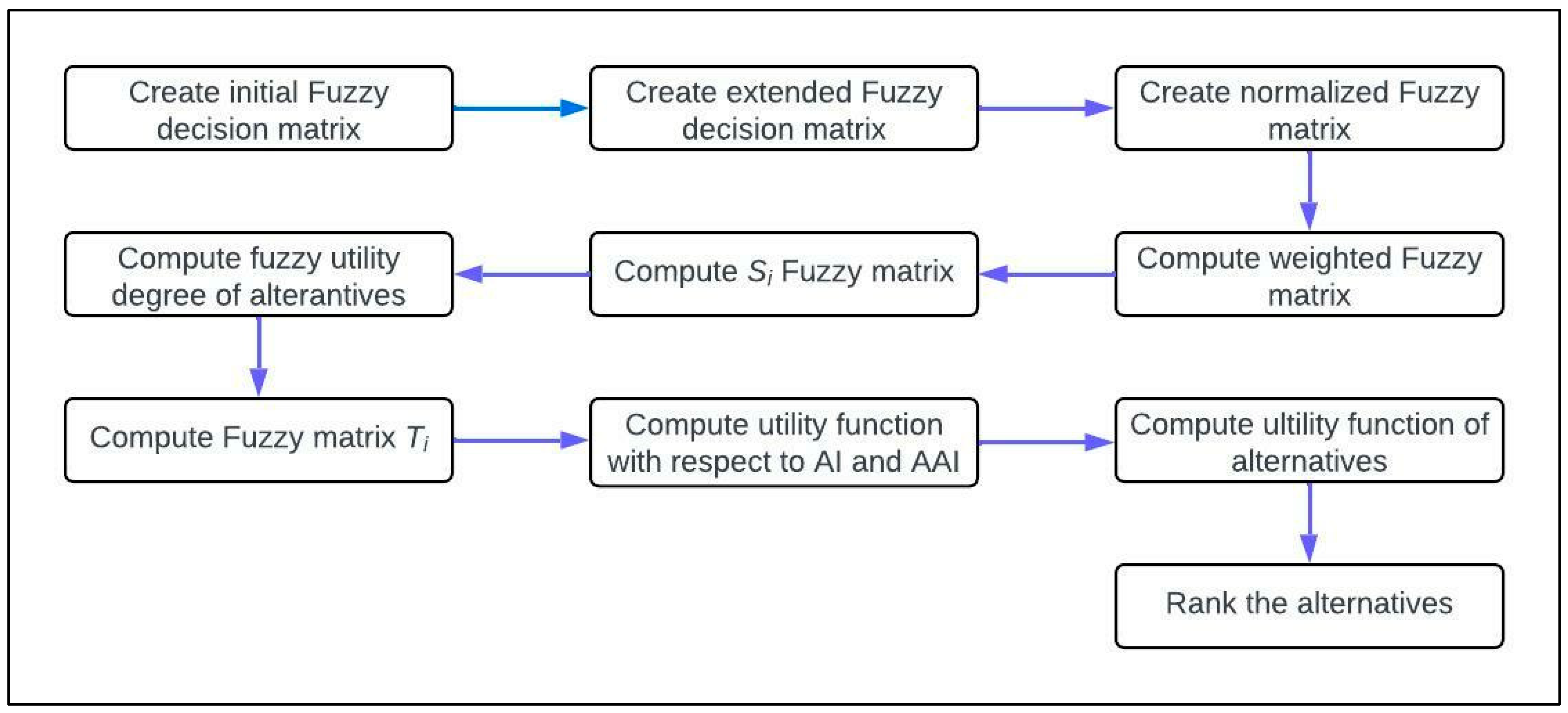
2. Methodology
2.1. Fuzzification
2.2. MARCOS
2.3. Fuzzy MARCOS
3. Case Study 1: Green Dry Milling of SS 304 Steel
3.1. Problem Description
3.2. Discussion
4. Case Study 2: Green Face Milling of AISI 1045 Steel
4.1. Problem Description
4.2. Discussion
5. Conclusions
- The application of the Fuzzy MARCOS method does not follow a rigid weight allocation. The inclusion of fuzzy provides a linguistic scale to provide the weight for the criterion based on different fuzzy numbers; here we used triangular fuzzy numbers, which divided the scale into 9 parts. This allowed us to analyze the problem more practically.
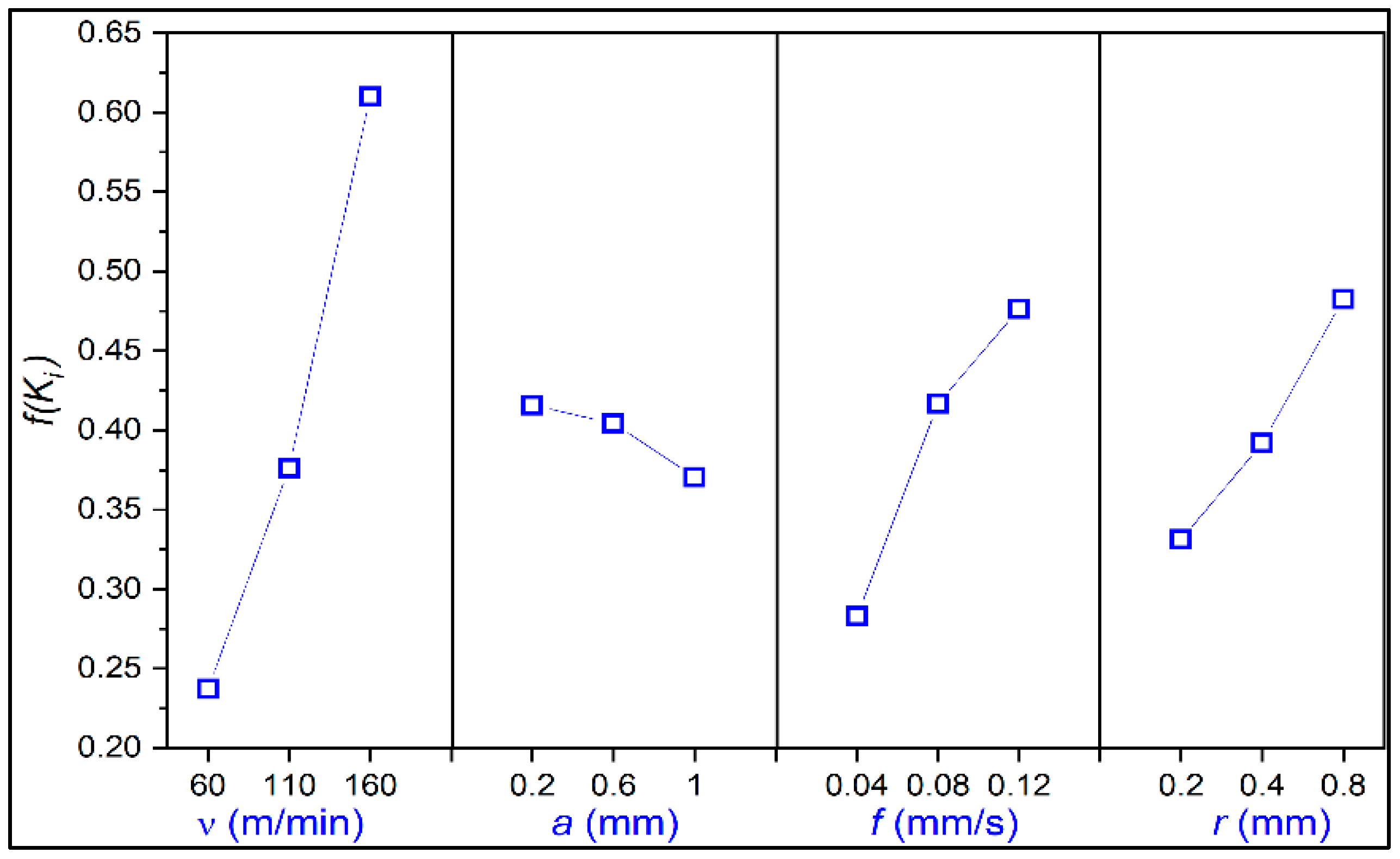
- From the analysis, it is found that for the machining of SS 304 in case study 1 alternative 22 was the best alternative for the experiments. This suggests that a cutting speed of 160 m/min, 0.6 mm depth of cut, 0.08 mm/s feed, and nose radius of 0.8 mm was the best combination for the operation. This combination has a power factor (PF) of 0.862, 26.68 kJ of utilization of electrical energy, and produces a surface roughness of 0.36 .
- If we consider the worst alternative for the 1st case study, alternative 17 was given the lowest rank by the complete analysis. From the analysis, we can say that a combination of = 60 m/min, = 0.6 mm, = 0.04 mm/s, and r = 0.4 mm which have a PF ratio of 0.529, consumes 94.95 kJ of electrical energy, and produces 0.82 surface roughness.
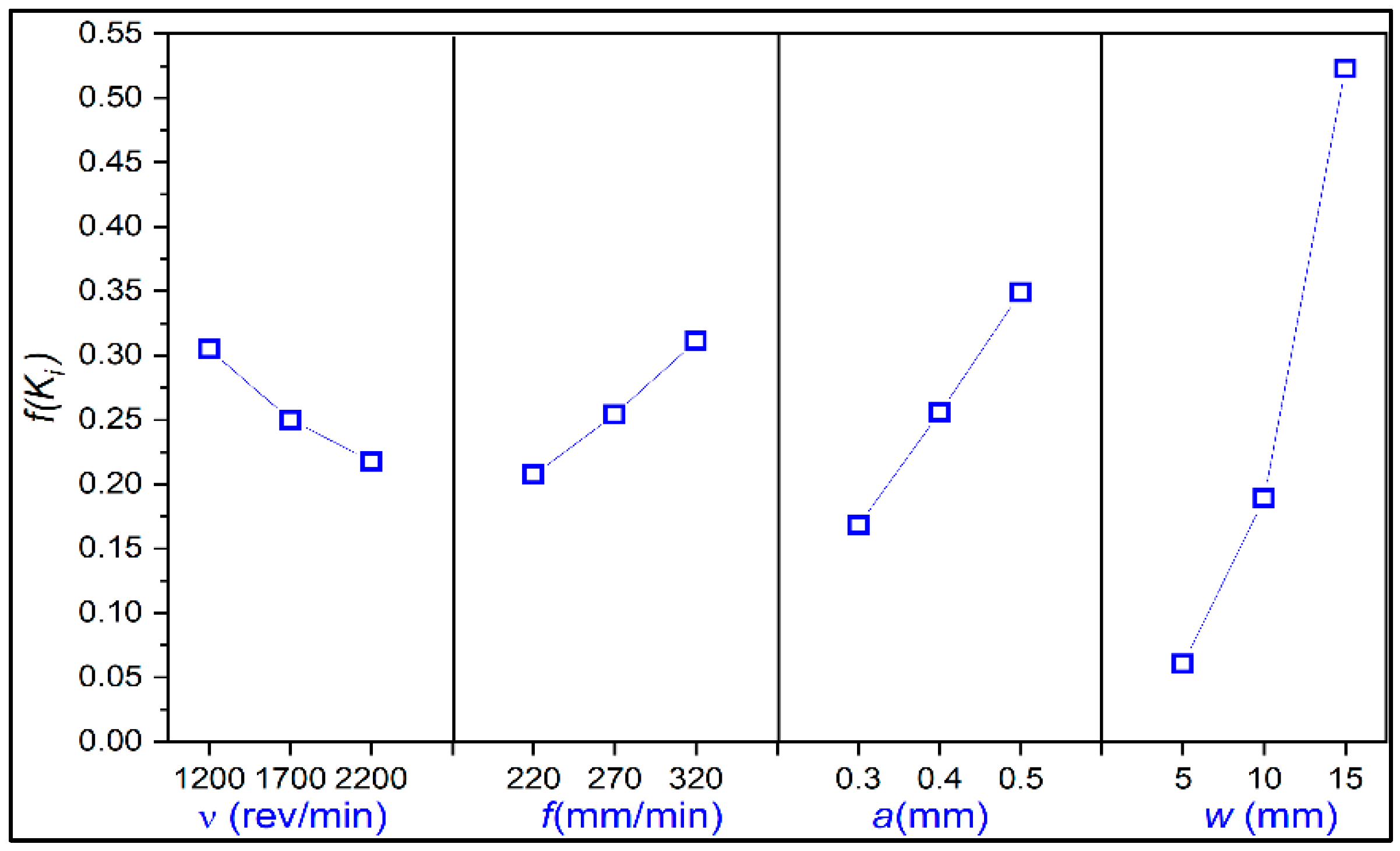
- In the case of the second case study for the green machining of AISI 1045, alternative 9 was the best alternative for the experiments. This suggests that a cutting speed () of 1200 rev/min, 0.5 mm depth of cut (), 320 mm/min feed rate (), and width of cut () of 15 mm was the best combination for the operation. This combination has MRR of 2400 , produces the surface roughness (Ra) of 2.29 , and utilizes 53.988 kJ active cutting energy (ACE).
- Alternative 1 was provided with the lowest rank by the complete analysis for the green machining of AISI 1045. From the analysis, we can say that combination of = 1200 rev/min, = 0.3 mm, = 220 mm/min, and = 5 mm has a MRR of 330 , consumes 535.802 kJ of active cutting energy (ACE), and produces 3.3 surface roughness (Ra).
- Thus, Fuzzy MARCOS is seen to be a powerful technique that combines the uncertainty analysis component and group decision-making ability of fuzzification with the superb selection capability of MARCOS. The method is however limited by its complexity as compared to vanilla MARCOS. Moreover, the fuzzy MARCOS needs several additional calculations which makes it relatively more time intensive. Nevertheless, it is expected that fuzzy MARCOS will become a preferred tool among MCDM specialists, especially due to the remarkable success vanilla MARCOS has had in recent times. This study can be further extended to incorporate various other fuzzy numbers and theories such as interval fuzzy, intuitionistic fuzzy, etc.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Krolczyk, G.M.; Maruda, R.W.; Krolczyk, J.B.; Wojciechowski, S.; Mia, M.; Nieslony, P.; Budzik, G. Ecological Trends in Machining as a Key Factor in Sustainable Production—A Review. J. Clean. Prod. 2019, 218, 601–615. [Google Scholar] [CrossRef]
- Khanna, N.; Shah, P.; Sarikaya, M.; Pusavec, F. Energy Consumption and Ecological Analysis of Sustainable and Conventional Cutting Fluid Strategies in Machining 15–5 PHSS. Sustain. Mater. Technol. 2022, 32, e00416. [Google Scholar] [CrossRef]
- Nouioua, M.; Laouissi, A.; Brahami, R.; Blaoui, M.M.; Hammoudi, A.; Yallese, M.A. Evaluation Of: MOSSA, MOALO, MOVO and MOGWO Algorithms in Green Machining to Enhance the Turning Performances of X210Cr12 Steel. Int. J. Adv. Manuf. Technol. 2022, 120, 2135–2150. [Google Scholar] [CrossRef]
- Kadam, G.S.; Pawade, R.S. Comparative Assessment of Machining Induced Hardening in HSM of Inconel 718 with Aid of Eco-Friendly Cutting Fluids. Mater. Today: Proc. 2022, 62, 7528–7533. [Google Scholar] [CrossRef]
- Bibin, C.; Devarajan, Y.; Bharadwaj, A.; Patil, P.Y. Detailed Analysis on Nonedible Waste Feedstock as a Renewable Cutting Fluid for a Sustainable Machining Process. Biomass Convers. Biorefinery 2022, 1–9. [Google Scholar] [CrossRef]
- Baroi, B.K.; Jagadish; Patowari, P.K. A Review on Sustainability, Health, and Safety Issues of Electrical Discharge Machining. J. Braz. Soc. Mech. Sci. Eng. 2022, 44, 59. [Google Scholar] [CrossRef]
- Sanmotra, H.; Mishra, V.; Gangwar, S.; Singh, G.; Singh, R.; Garg, H.; Karar, V. Feasibility Study on Machining of Niobium to Achieve Nanometric Surface Finish. Lecture Notes in Mechanical Engineering; In Advances in Materials Processing; Springer: Singapore, Singapore, 2020; pp. 301–311. [Google Scholar] [CrossRef]
- Airao, J.; Nirala, C.K.; Bertolini, R.; Krolczyk, G.M.; Khanna, N. Sustainable Cooling Strategies to Reduce Tool Wear, Power Consumption and Surface Roughness during Ultrasonic Assisted Turning of Ti-6Al-4V. Tribol. Int. 2022, 169, 107494. [Google Scholar] [CrossRef]
- Kulisz, M.; Zagórski, I.; Weremczuk, A.; Rusinek, R.; Korpysa, J. Analysis and Prediction of the Impact of Technological Parameters on Cutting Force Components in Rough Milling of AZ31 Magnesium Alloy. Arch. Civ. Mech. Eng. 2021, 22, 1. [Google Scholar] [CrossRef]
- Liu, X.; Han, L.; Wu, S.; Meng, Y.; Yue, C.; Liang, S.Y. Influence of Blade Curvature Characteristics on Energy Consumption in Machining Process. Int. J. Adv. Manuf. Technol. 2022, 121, 1867–1885. [Google Scholar] [CrossRef]
- Wu, P.; He, Y.; Li, Y.; He, J.; Liu, X.; Wang, Y. Multi-Objective Optimisation of Machining Process Parameters Using Deep Learning-Based Data-Driven Genetic Algorithm and TOPSIS. J. Manuf. Syst. 2022, 64, 40–52. [Google Scholar] [CrossRef]
- EKİCİ, E.; UZUN, G. Effects on Machinability of Cryogenic Treatment Applied to Carbide Tools in the Milling of Ti6AI4V with Optimization via the Taguchi Method and Grey Relational Analysis. J. Braz. Soc. Mech. Sci. Eng. 2022, 44, 270. [Google Scholar] [CrossRef]
- Kumar, R.; Katyal, P.; Kumar, K.; Singh, V. Multiresponse Optimization of End Milling Process Parameters on ZE41A Mg Alloy Using Taguchi and TOPSIS Approach. Mater. Today Proc. 2021, 56, 2497–2504. [Google Scholar] [CrossRef]
- Safi, K.; Yallese, M.A.; Belhadi, S.; Mabrouki, T.; Laouissi, A. Tool Wear, 3D Surface Topography, and Comparative Analysis of GRA, MOORA, DEAR, and WASPAS Optimization Techniques in Turning of Cold Work Tool Steel. Int. J. Adv. Manuf. Technol. 2022, 121, 701–721. [Google Scholar] [CrossRef]
- Singh, T.; Sharma, V.K.; Rana, M.; Singh, K.; Saini, A. GRA Based Optimization of Tool Vibration and Surface Roughness in Face Milling of Hardened Steel Alloy. Mater. Today Proc. 2022, 50, 2288–2293. [Google Scholar] [CrossRef]
- Zheng, Q.; Chen, G.; Jiao, A. Chatter Detection in Milling Process Based on the Combination of Wavelet Packet Transform and PSO-SVM. Int. J. Adv. Manuf. Technol. 2022, 120, 1237–1251. [Google Scholar] [CrossRef]
- Stanković, M.; Stević, Ž.; Das, D.K.; Subotić, M.; Pamučar, D. A New Fuzzy MARCOS Method for Road Traffic Risk Analysis. Mathematics 2020, 8, 457. [Google Scholar] [CrossRef]
- Taş, M.A.; Çakır, E.; Ulukan, Z. Spherical Fuzzy SWARA-MARCOS Approach for Green Supplier Selection. 3C Tecnol. Glosas Innovación Apl. Pyme 2021, 10, 115–133. [Google Scholar] [CrossRef]
- Ali, J. A Q-Rung Orthopair Fuzzy MARCOS Method Using Novel Score Function and Its Application to Solid Waste Management. Appl. Intell. 2021, 52, 8770–8792. [Google Scholar] [CrossRef]
- Bakır, M.; Atalık, Ö. Application of Fuzzy AHP and Fuzzy MARCOS Approach for the Evaluation of E-Service Quality in the Airline Industry. Decis. Mak. Appl. Manag. Eng. 2021, 4, 127–152. [Google Scholar] [CrossRef]
- Kovač, M.; Tadić, S.; Krstić, M.; Bouraima, M.B. Novel Spherical Fuzzy MARCOS Method for Assessment of Drone-Based City Logistics Concepts. Complexity 2021, 2021, 2374955. [Google Scholar] [CrossRef]
- Nguyen, T.-T.; Nguyen, T.-A.; Trinh, Q.-H. Optimization of Milling Parameters for Energy Savings and Surface Quality. Arab. J. Sci. Eng. 2020, 45, 9111–9125. [Google Scholar] [CrossRef]
- Das, P.P.; Chakraborty, S. SWARA-CoCoSo Method-Based Parametric Optimization of Green Dry Milling Processes. J. Eng. Appl. Sci. 2022, 69, 35. [Google Scholar] [CrossRef]
- Khan, A.; Jamil, M.; Salonitis, K.; Sarfraz, S.; Zhao, W.; He, N.; Mia, M.; Zhao, G. Multi-Objective Optimization of Energy Consumption and Surface Quality in Nanofluid SQCL Assisted Face Milling. Energies 2019, 12, 710. [Google Scholar] [CrossRef]
| Linguistic Term for Importance of Criteria | Symbol | Triangular Fuzzy Number |
|---|---|---|
| Extremely Poor | EP | (1,1,1) |
| Very Poor | VP | (1,1,3) |
| Poor | P | (1,3,3) |
| Medium Poor | MP | (3,3,5) |
| Medium | M | (3,5,5) |
| Medium Good | MG | (5,5,7) |
| Good | G | (5,7,7) |
| Very Good | VG | (7,7,9) |
| Extremely Good | EG | (7,9,9) |
| Exp.no. | PF | EC (kJ) | |||||
|---|---|---|---|---|---|---|---|
| 1 | 110 | 0.2 | 0.04 | 0.4 | 0.518 | 50.33 | 0.45 |
| 2 | 110 | 0.6 | 0.12 | 0.8 | 0.867 | 25.46 | 1.08 |
| 3 | 110 | 0.6 | 0.08 | 0.4 | 0.652 | 31.56 | 0.85 |
| 4 | 60 | 0.6 | 0.08 | 0.2 | 0.611 | 53.66 | 1.34 |
| 5 | 160 | 0.6 | 0.12 | 0.4 | 0.851 | 18.42 | 0.95 |
| 6 | 60 | 0.6 | 0.12 | 0.4 | 0.736 | 42.6 | 1.47 |
| 7 | 110 | 0.2 | 0.12 | 0.4 | 0.69 | 21.99 | 1.14 |
| 8 | 60 | 0.6 | 0.08 | 0.8 | 0.685 | 59.13 | 0.78 |
| 9 | 60 | 1 | 0.08 | 0.4 | 0.703 | 61.68 | 1.31 |
| 10 | 110 | 1 | 0.12 | 0.4 | 0.868 | 26.72 | 1.49 |
| 11 | 110 | 1 | 0.08 | 0.2 | 0.732 | 35.41 | 1.42 |
| 12 | 160 | 0.6 | 0.08 | 0.2 | 0.719 | 22.84 | 0.89 |
| 13 | 160 | 1 | 0.08 | 0.4 | 0.835 | 27.26 | 0.79 |
| 14 | 60 | 0.2 | 0.08 | 0.4 | 0.547 | 48.96 | 0.82 |
| 15 | 160 | 0.6 | 0.04 | 0.4 | 0.69 | 44.62 | 0.47 |
| 16 | 110 | 0.6 | 0.04 | 0.2 | 0.566 | 54.03 | 0.98 |
| 17 | 60 | 0.6 | 0.04 | 0.4 | 0.529 | 94.95 | 0.82 |
| 18 | 110 | 1 | 0.04 | 0.4 | 0.659 | 63.82 | 1.06 |
| 19 | 160 | 0.2 | 0.08 | 0.4 | 0.671 | 22.07 | 0.41 |
| 20 | 110 | 0.6 | 0.12 | 0.2 | 0.752 | 23.74 | 1.55 |
| 21 | 110 | 0.6 | 0.04 | 0.8 | 0.648 | 62.35 | 0.52 |
| 22 | 160 | 0.6 | 0.08 | 0.8 | 0.862 | 26.68 | 0.36 |
| 23 | 110 | 0.2 | 0.08 | 0.2 | 0.576 | 28.23 | 0.91 |
| 24 | 110 | 0.2 | 0.08 | 0.8 | 0.681 | 32.95 | 0.48 |
| 25 | 110 | 1 | 0.08 | 0.8 | 0.843 | 39.02 | 0.89 |
| Decision Maker | Linguistic Term | Triangular Fuzzy Number | ||||
|---|---|---|---|---|---|---|
| PF | EC (kJ) | PF | EC (kJ) | |||
| Expert 1 | VG | M | G | (7,7,9) | (3,5,5) | (5,7,7) |
| Expert 2 | MG | G | M | (5,5,7) | (5,7,7) | (3,5,5) |
| Expert 3 | G | MG | P | (5,7,7) | (5,5,7) | (1,3,3) |
| Expert 4 | VG | MP | MP | (7,7,9) | (3,3,5) | (3,3,5) |
| Alternative | PF | EC (kJ) | ||
|---|---|---|---|---|
| AAI | (3.5806, 3.879, 4.7742) | (0.776, 0.97, 1.164) | (0.6968, 1.0452, 1.1613) | (5.0534, 5.8942, 7.0995) |
| A1 | (3.5806, 3.879, 4.7742) | (1.4639, 1.8299, 2.1959) | (2.4, 3.6, 4) | (7.4446, 9.309, 10.9701) |
| A2 | (5.9931, 6.4925, 7.9908) | (2.894, 3.6174, 4.3409) | (1, 1.5, 1.6667) | (9.887, 11.61, 13.9984) |
| A3 | (4.5069, 4.8825, 6.0092) | (2.3346, 2.9183, 3.5019) | (1.2706, 1.9059, 2.1176) | (8.1121, 9.7066, 11.6288) |
| A4 | (4.2235, 4.5755, 5.6313) | (1.3731, 1.7164, 2.0596) | (0.806, 1.209, 1.3433) | (6.4026, 7.5008, 9.0343) |
| A5 | (5.8825, 6.3727, 7.8433) | (4, 5, 6) | (1.1368, 1.7053, 1.8947) | (11.0193, 13.078, 15.7381) |
| A6 | (5.0876, 5.5115, 6.7834) | (1.7296, 2.162, 2.5944) | (0.7347, 1.102, 1.2245) | (7.5518, 8.7755, 10.6023) |
| A7 | (4.7696, 5.1671, 6.3594) | (3.3506, 4.1883, 5.0259) | (0.9474, 1.4211, 1.5789) | (9.0676, 10.7764, 12.9643) |
| A8 | (4.735, 5.1296, 6.3134) | (1.2461, 1.5576, 1.8691) | (1.3846, 2.0769, 2.3077) | (7.3657, 8.7641, 10.4902) |
| A9 | (4.8594, 5.2644, 6.4793) | (1.1946, 1.4932, 1.7918) | (0.8244, 1.2366, 1.374) | (6.8784, 7.9942, 9.6451) |
| A10 | (6, 6.5, 8) | (2.7575, 3.4469, 4.1362) | (0.7248, 1.0872, 1.2081) | (9.4823, 11.0341, 13.3443) |
| A11 | (5.0599, 5.4816, 6.7465) | (2.0808, 2.601, 3.1212) | (0.7606, 1.1408, 1.2676) | (7.9012, 9.2234, 11.1353) |
| A12 | (4.97, 5.3842, 6.6267) | (3.2259, 4.0324, 4.8389) | (1.2135, 1.8202, 2.0225) | (9.4094, 11.2368, 13.4881) |
| A13 | (5.7719, 6.2529, 7.6959) | (2.7029, 3.3786, 4.0543) | (1.3671, 2.0506, 2.2785) | (9.8418, 11.6821, 14.0286) |
| A14 | (3.7811, 4.0962, 5.0415) | (1.5049, 1.8811, 2.2574) | (1.3171, 1.9756, 2.1951) | (6.6031, 7.9529, 9.4939) |
| A15 | (4.7696, 5.1671, 6.3594) | (1.6513, 2.0641, 2.4769) | (2.2979, 3.4468, 3.8298) | (8.7187, 10.678, 12.6662) |
| A16 | (3.9124, 4.2385, 5.2166) | (1.3637, 1.7046, 2.0455) | (1.102, 1.6531, 1.8367) | (6.3782, 7.5961, 9.0989) |
| A17 | (3.6567, 3.9614, 4.8756) | (0.776, 0.97, 1.164) | (1.3171, 1.9756, 2.1951) | (5.7497, 6.907, 8.2347) |
| A18 | (4.5553, 4.9349, 6.0737) | (1.1545, 1.4431, 1.7317) | (1.0189, 1.5283, 1.6981) | (6.7287, 7.9063, 9.5036) |
| A19 | (4.6382, 5.0248, 6.1843) | (3.3385, 4.1731, 5.0077) | (2.6341, 3.9512, 4.3902) | (10.6109, 13.1491, 15.5823) |
| A20 | (5.1982, 5.6313, 6.9309) | (3.1036, 3.8795, 4.6554) | (0.6968, 1.0452, 1.1613) | (8.9986, 10.556, 12.7476) |
| A21 | (4.4793, 4.8525, 5.9724) | (1.1817, 1.4771, 1.7726) | (2.0769, 3.1154, 3.4615) | (7.7379, 9.4451, 11.2065) |
| A22 | (5.9585, 6.4551, 7.9447) | (2.7616, 3.452, 4.1424) | (3, 4.5, 5) | (11.7201, 14.4071, 17.0871) |
| A23 | (3.9816, 4.3134, 5.3088) | (2.61, 3.2625, 3.915) | (1.1868, 1.7802, 1.978) | (7.7784, 9.3561, 11.2018) |
| A24 | (4.7074, 5.0997, 6.2765) | (2.2361, 2.7951, 3.3542) | (2.25, 3.375, 3.75) | (9.1935, 11.2698, 13.3807) |
| A25 | (5.8272, 6.3128, 7.7696) | (1.8883, 2.3603, 2.8324) | (1.2135, 1.8202, 2.0225) | (8.9289, 10.4933, 12.6245) |
| AI | (6, 6.5, 8) | (4, 5, 6) | (3, 4.5, 5) | (13, 16, 19) |
| Alternative | Utility Degree | Utility Functions | ||
|---|---|---|---|---|
| A1 | (1.0486, 1.5793, 2.1708) | (0.3918, 0.5818, 0.8439) | (0.1156, 0.1716, 0.2489) | (0.3093, 0.4658, 0.6403) |
| A2 | (1.3926, 1.9697, 2.7701) | (0.5204, 0.7256, 1.0768) | (0.1535, 0.214, 0.3176) | (0.4108, 0.581, 0.817) |
| A3 | (1.1426, 1.6468, 2.3012) | (0.427, 0.6067, 0.8945) | (0.1259, 0.1789, 0.2638) | (0.337, 0.4857, 0.6787) |
| A4 | (0.9018, 1.2726, 1.7878) | (0.337, 0.4688, 0.6949) | (0.0994, 0.1383, 0.205) | (0.266, 0.3753, 0.5273) |
| A5 | (1.5521, 2.2188, 3.1143) | (0.58, 0.8174, 1.2106) | (0.1711, 0.2411, 0.3571) | (0.4578, 0.6544, 0.9186) |
| A6 | (1.0637, 1.4888, 2.098) | (0.3975, 0.5485, 0.8156) | (0.1172, 0.1618, 0.2406) | (0.3137, 0.4391, 0.6188) |
| A7 | (1.2772, 1.8283, 2.5655) | (0.4772, 0.6735, 0.9973) | (0.1408, 0.1987, 0.2941) | (0.3767, 0.5393, 0.7567) |
| A8 | (1.0375, 1.4869, 2.0759) | (0.3877, 0.5478, 0.8069) | (0.1143, 0.1616, 0.238) | (0.306, 0.4386, 0.6123) |
| A9 | (0.9689, 1.3563, 1.9086) | (0.362, 0.4996, 0.7419) | (0.1068, 0.1474, 0.2188) | (0.2858, 0.4, 0.563) |
| A10 | (1.3356, 1.872, 2.6407) | (0.4991, 0.6896, 1.0265) | (0.1472, 0.2034, 0.3028) | (0.3939, 0.5522, 0.7789) |
| A11 | (1.1129, 1.5648, 2.2035) | (0.4159, 0.5765, 0.8566) | (0.1227, 0.17, 0.2526) | (0.3283, 0.4615, 0.6499) |
| A12 | (1.3254, 1.9064, 2.6691) | (0.4952, 0.7023, 1.0375) | (0.1461, 0.2071, 0.306) | (0.3909, 0.5623, 0.7873) |
| A13 | (1.3863, 1.982, 2.7761) | (0.518, 0.7301, 1.0791) | (0.1528, 0.2154, 0.3183) | (0.4089, 0.5846, 0.8188) |
| A14 | (0.9301, 1.3493, 1.8787) | (0.3475, 0.4971, 0.7303) | (0.1025, 0.1466, 0.2154) | (0.2743, 0.398, 0.5541) |
| A15 | (1.2281, 1.8116, 2.5065) | (0.4589, 0.6674, 0.9743) | (0.1353, 0.1968, 0.2874) | (0.3622, 0.5343, 0.7393) |
| A16 | (0.8984, 1.2888, 1.8005) | (0.3357, 0.4748, 0.6999) | (0.099, 0.14, 0.2064) | (0.265, 0.3801, 0.5311) |
| A17 | (0.8099, 1.1718, 1.6295) | (0.3026, 0.4317, 0.6334) | (0.0893, 0.1273, 0.1868) | (0.2389, 0.3456, 0.4806) |
| A18 | (0.9478, 1.3414, 1.8806) | (0.3541, 0.4941, 0.731) | (0.1045, 0.1457, 0.2156) | (0.2795, 0.3956, 0.5547) |
| A19 | (1.4946, 2.2309, 3.0835) | (0.5585, 0.8218, 1.1986) | (0.1647, 0.2424, 0.3535) | (0.4408, 0.658, 0.9095) |
| A20 | (1.2675, 1.7909, 2.5226) | (0.4736, 0.6598, 0.9806) | (0.1397, 0.1946, 0.2892) | (0.3738, 0.5282, 0.744) |
| A21 | (1.0899, 1.6024, 2.2176) | (0.4073, 0.5903, 0.862) | (0.1201, 0.1741, 0.2543) | (0.3215, 0.4726, 0.6541) |
| A22 | (1.6508, 2.4443, 3.3813) | (0.6168, 0.9004, 1.3144) | (0.1819, 0.2656, 0.3877) | (0.4869, 0.7209, 0.9973) |
| A23 | (1.0956, 1.5873, 2.2167) | (0.4094, 0.5848, 0.8617) | (0.1207, 0.1725, 0.2542) | (0.3232, 0.4682, 0.6538) |
| A24 | (1.295, 1.912, 2.6479) | (0.4839, 0.7044, 1.0293) | (0.1427, 0.2078, 0.3036) | (0.3819, 0.564, 0.781) |
| A25 | (1.2577, 1.7803, 2.4982) | (0.4699, 0.6558, 0.9711) | (0.1386, 0.1934, 0.2864) | (0.371, 0.5251, 0.7368) |
| Alternative | Rank | |||||||
|---|---|---|---|---|---|---|---|---|
| A1 | 1.5895 | 0.5938 | 0.1751 | 0.4688 | 4.7095 | 1.1330 | 0.3191 | 17 |
| A2 | 2.0069 | 0.7499 | 0.2212 | 0.5920 | 3.5209 | 0.6893 | 0.5291 | 5 |
| A3 | 1.6718 | 0.6247 | 0.1843 | 0.4931 | 4.4273 | 1.0279 | 0.3558 | 13 |
| A4 | 1.2966 | 0.4845 | 0.1429 | 0.3824 | 5.9974 | 1.6147 | 0.2068 | 24 |
| A5 | 2.2569 | 0.8433 | 0.2487 | 0.6657 | 3.0202 | 0.5022 | 0.6855 | 2 |
| A6 | 1.5195 | 0.5678 | 0.1675 | 0.4482 | 4.9709 | 1.2312 | 0.2898 | 18 |
| A7 | 1.8593 | 0.6948 | 0.2049 | 0.5484 | 3.8799 | 0.8235 | 0.4478 | 9 |
| A8 | 1.5102 | 0.5643 | 0.1664 | 0.4454 | 5.0084 | 1.2450 | 0.2860 | 19 |
| A9 | 1.3838 | 0.5171 | 0.1525 | 0.4081 | 5.5567 | 1.4501 | 0.2374 | 20 |
| A10 | 1.9107 | 0.7140 | 0.2106 | 0.5636 | 3.7484 | 0.7744 | 0.4753 | 8 |
| A11 | 1.5960 | 0.5964 | 0.1759 | 0.4707 | 4.6850 | 1.1244 | 0.3220 | 16 |
| A12 | 1.9367 | 0.7237 | 0.2134 | 0.5712 | 3.6850 | 0.7506 | 0.4894 | 6 |
| A13 | 2.0150 | 0.7529 | 0.2221 | 0.5943 | 3.5029 | 0.6825 | 0.5338 | 4 |
| A14 | 1.3677 | 0.5110 | 0.1507 | 0.4034 | 5.6347 | 1.4790 | 0.2315 | 21 |
| A15 | 1.8302 | 0.6838 | 0.2017 | 0.5398 | 3.9583 | 0.8525 | 0.4326 | 10 |
| A16 | 1.3090 | 0.4891 | 0.1443 | 0.3861 | 5.9318 | 1.5901 | 0.2110 | 23 |
| A17 | 1.1878 | 0.4438 | 0.1309 | 0.3503 | 6.6394 | 1.8544 | 0.1719 | 25 |
| A18 | 1.3657 | 0.5103 | 0.1505 | 0.4028 | 5.6440 | 1.4826 | 0.2308 | 22 |
| A19 | 2.2503 | 0.8407 | 0.2480 | 0.6637 | 3.0327 | 0.5067 | 0.6809 | 3 |
| A20 | 1.8256 | 0.6822 | 0.2012 | 0.5385 | 3.9698 | 0.8571 | 0.4304 | 11 |
| A21 | 1.6195 | 0.6051 | 0.1785 | 0.4777 | 4.6031 | 1.0934 | 0.3322 | 14 |
| A22 | 2.4682 | 0.9222 | 0.2720 | 0.7280 | 2.6765 | 0.3736 | 0.8371 | 1 |
| A23 | 1.6103 | 0.6017 | 0.1775 | 0.4750 | 4.6349 | 1.1055 | 0.3282 | 15 |
| A24 | 1.9318 | 0.7218 | 0.2129 | 0.5698 | 3.6974 | 0.7550 | 0.4867 | 7 |
| A25 | 1.8128 | 0.6774 | 0.1998 | 0.5347 | 4.0050 | 0.8702 | 0.4239 | 12 |
| Source | PF | EC (kJ) | Average | |||||
|---|---|---|---|---|---|---|---|---|
| Current | 160 | 0.2 | 0.12 | 0.8 | 0.9908 | 23.2264 | 0.2949 | - |
| Nguyen et al. [22] | 160 | 0.42 | 0.09 | 0.8 | 0.8360 | 20.6300 | 0.3500 | - |
| % Improvement | - | - | - | - | 18.52% | −12.59% | 15.74% | 7.22% |
| Das and Chakraborty [23] | 160 | 1 | 0.08 | 0.8 | 0.9830 | 19.9288 | 0.3921 | - |
| % Improvement | - | - | - | - | 0.79% | −16.55% | 24.79% | 3.01% |
| Das and Chakraborty [23] | 160 | 0.2 | 0.08 | 0.8 | 0.8695 | 19.9288 | 0.2947 | - |
| % Improvement | - | - | - | - | 13.95% | −16.55% | −0.07% | −0.89% |
| Exp.no. | ACE (kJ) | ||||||
|---|---|---|---|---|---|---|---|
| 1 | 1200 | 220 | 0.3 | 5 | 330 | 3.3 | 535.802 |
| 2 | 1200 | 220 | 0.4 | 10 | 880 | 2.95 | 184.929 |
| 3 | 1200 | 220 | 0.5 | 15 | 1650 | 1.41 | 88.519 |
| 4 | 1200 | 270 | 0.3 | 5 | 405 | 3.83 | 426.109 |
| 5 | 1200 | 270 | 0.4 | 10 | 1080 | 3.87 | 146.05 |
| 6 | 1200 | 270 | 0.5 | 15 | 2025 | 1.68 | 69.823 |
| 7 | 1200 | 320 | 0.3 | 5 | 480 | 3.97 | 361.832 |
| 8 | 1200 | 320 | 0.4 | 10 | 1280 | 3.53 | 122.976 |
| 9 | 1200 | 320 | 0.5 | 15 | 2400 | 2.29 | 53.988 |
| 10 | 1700 | 220 | 0.3 | 10 | 660 | 1.81 | 337.042 |
| 11 | 1700 | 220 | 0.4 | 15 | 1320 | 1.13 | 142.727 |
| 12 | 1700 | 220 | 0.5 | 5 | 550 | 3.47 | 299.031 |
| 13 | 1700 | 270 | 0.3 | 10 | 810 | 2.85 | 269.604 |
| 14 | 1700 | 270 | 0.4 | 15 | 1620 | 1.41 | 113.648 |
| 15 | 1700 | 270 | 0.5 | 5 | 675 | 3.91 | 238.476 |
| 16 | 1700 | 320 | 0.3 | 10 | 960 | 2.55 | 213.559 |
| 17 | 1700 | 320 | 0.4 | 15 | 1920 | 1.39 | 92.551 |
| 18 | 1700 | 320 | 0.5 | 5 | 800 | 4.12 | 193.109 |
| 19 | 2200 | 220 | 0.3 | 15 | 990 | 1.76 | 244.303 |
| 20 | 2200 | 220 | 0.4 | 5 | 440 | 3.33 | 425.797 |
| 21 | 2200 | 220 | 0.5 | 10 | 1100 | 2.36 | 165.62 |
| 22 | 2200 | 270 | 0.3 | 15 | 1215 | 1.17 | 193.939 |
| 23 | 2200 | 270 | 0.4 | 5 | 540 | 3.72 | 338.579 |
| 24 | 2200 | 270 | 0.5 | 10 | 1350 | 2.58 | 131.343 |
| 25 | 2200 | 320 | 0.3 | 15 | 1440 | 1.41 | 160.886 |
| 26 | 2200 | 320 | 0.4 | 5 | 640 | 3.86 | 286.85 |
| 27 | 2200 | 320 | 0.5 | 10 | 1600 | 2.76 | 108.147 |
| Decision Maker | Linguistic Term | Triangular Fuzzy Number | ||||
|---|---|---|---|---|---|---|
| ACE (kJ) | ACE (kJ) | |||||
| Expert 1 | EG | MP | MP | (7,9,9) | (3,3,5) | (3,3,5) |
| Expert 2 | VG | G | MG | (7,7,9) | (5,7,7) | (5,5,7) |
| Expert 3 | G | MG | G | (5,7,7) | (5,5,7) | (5,7,7) |
| Expert 4 | G | MG | P | (5,7,7) | (5,5,7) | (1,3,3) |
| Alternative | ||||||||
|---|---|---|---|---|---|---|---|---|
| A1 | 1.1462 | 0.1942 | 0.0326 | 0.1922 | 29.7081 | 4.2033 | 0.0384 | 27 |
| A2 | 2.1212 | 0.3594 | 0.0603 | 0.3557 | 15.5956 | 1.8116 | 0.1348 | 16 |
| A3 | 4.2299 | 0.7166 | 0.1202 | 0.7093 | 7.3221 | 0.4099 | 0.5665 | 4 |
| A4 | 1.1818 | 0.2002 | 0.0336 | 0.1982 | 28.7837 | 4.0463 | 0.0409 | 26 |
| A5 | 2.2947 | 0.3887 | 0.0652 | 0.3848 | 14.3419 | 1.5990 | 0.1584 | 14 |
| A6 | 4.6603 | 0.7895 | 0.1324 | 0.7814 | 6.5540 | 0.2797 | 0.6957 | 2 |
| A7 | 1.2798 | 0.2168 | 0.0364 | 0.2146 | 26.5041 | 3.6599 | 0.0480 | 25 |
| A8 | 2.6735 | 0.4529 | 0.0759 | 0.4483 | 12.1684 | 1.2307 | 0.2171 | 11 |
| A9 | 5.0999 | 0.8639 | 0.1449 | 0.8551 | 5.9032 | 0.1694 | 0.8432 | 1 |
| A10 | 2.1151 | 0.3584 | 0.0601 | 0.3547 | 15.6407 | 1.8196 | 0.1340 | 17 |
| A11 | 3.8667 | 0.6552 | 0.1099 | 0.6484 | 8.1028 | 0.5423 | 0.4688 | 6 |
| A12 | 1.4809 | 0.2509 | 0.0421 | 0.2483 | 22.7699 | 3.0272 | 0.0646 | 22 |
| A13 | 1.9234 | 0.3259 | 0.0546 | 0.3225 | 17.3014 | 2.1006 | 0.1102 | 18 |
| A14 | 3.9816 | 0.6746 | 0.1131 | 0.6676 | 7.8409 | 0.4978 | 0.4986 | 5 |
| A15 | 1.6221 | 0.2748 | 0.0461 | 0.2720 | 20.7012 | 2.6765 | 0.0778 | 20 |
| A16 | 2.2552 | 0.3821 | 0.0641 | 0.3782 | 14.6088 | 1.6444 | 0.1529 | 15 |
| A17 | 4.5004 | 0.7624 | 0.1278 | 0.7546 | 6.8221 | 0.3252 | 0.6460 | 3 |
| A18 | 1.8153 | 0.3075 | 0.0516 | 0.3044 | 18.3922 | 2.2852 | 0.0979 | 19 |
| A19 | 2.6017 | 0.4408 | 0.0739 | 0.4362 | 12.5296 | 1.2923 | 0.2053 | 12 |
| A20 | 1.3011 | 0.2204 | 0.0370 | 0.2182 | 26.0535 | 3.5838 | 0.0497 | 24 |
| A21 | 2.5891 | 0.4386 | 0.0736 | 0.4341 | 12.5961 | 1.3034 | 0.2032 | 13 |
| A22 | 3.5307 | 0.5982 | 0.1003 | 0.5920 | 8.9692 | 0.6891 | 0.3874 | 8 |
| A23 | 1.3962 | 0.2365 | 0.0397 | 0.2341 | 24.2122 | 3.2716 | 0.0573 | 23 |
| A24 | 2.9206 | 0.4948 | 0.0830 | 0.4897 | 11.0536 | 1.0420 | 0.2608 | 10 |
| A25 | 3.5638 | 0.6038 | 0.1012 | 0.5976 | 8.8771 | 0.6734 | 0.3950 | 7 |
| A26 | 1.5301 | 0.2592 | 0.0435 | 0.2566 | 22.0067 | 2.8977 | 0.0691 | 21 |
| A27 | 3.2795 | 0.5556 | 0.0932 | 0.5499 | 9.7348 | 0.8185 | 0.3320 | 9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shanmugasundar, G.; Mahanta, T.K.; Čep, R.; Kalita, K. Novel Fuzzy Measurement Alternatives and Ranking according to the Compromise Solution-Based Green Machining Optimization. Processes 2022, 10, 2645. https://doi.org/10.3390/pr10122645
Shanmugasundar G, Mahanta TK, Čep R, Kalita K. Novel Fuzzy Measurement Alternatives and Ranking according to the Compromise Solution-Based Green Machining Optimization. Processes. 2022; 10(12):2645. https://doi.org/10.3390/pr10122645
Chicago/Turabian StyleShanmugasundar, G., Tapan K. Mahanta, Robert Čep, and Kanak Kalita. 2022. "Novel Fuzzy Measurement Alternatives and Ranking according to the Compromise Solution-Based Green Machining Optimization" Processes 10, no. 12: 2645. https://doi.org/10.3390/pr10122645
APA StyleShanmugasundar, G., Mahanta, T. K., Čep, R., & Kalita, K. (2022). Novel Fuzzy Measurement Alternatives and Ranking according to the Compromise Solution-Based Green Machining Optimization. Processes, 10(12), 2645. https://doi.org/10.3390/pr10122645








