Abstract
To solve the anti-disturbance control problem of dissolved oxygen concentration in the wastewater treatment plant (WWTP), an anti-disturbance control scheme based on reinforcement learning (RL) is proposed. An extended state observer (ESO) based on the Takagi–Sugeno (T-S) fuzzy model is first designed to estimate the the system state and total disturbance. The anti-disturbance controller compensates for the total disturbance based on the output of the observer in real time, online searches the optimal control policy using a neural-network-based adaptive dynamic programming (ADP) controller. For reducing the computational complexity and avoiding local optimal solutions, the echo state network (ESN) is used to approximate the optimal control policy and optimal value function in the ADP controller. Further analysis demonstrates the observer estimation errors for system state and total disturbance are bounded, and the weights of ESNs in the ADP controller are convergent. Finally, the effectiveness of the proposed ESO-based ADP control scheme is evaluated on a benchmark simulation model of the WWTP.
1. Introduction
The aim of a wastewater treatment plant (WWTP) is to degrade the organic matter in the wastewater to meet the various discharge performance requirements [1]. In municipal wastewater treatment plants, the activated sludge process (ASP) is widely used to remove pollutants. The dissolved oxygen (DO) concentration in the ASP is an important indicator for survival and growth of aerobic microorganisms [2]. If the DO concentration is too high, it will increase the aeration energy consumption, affect the ammonia nitrogen conversion efficiency and deteriorate the sludge quality. If the concentration is too low, it will affect the activity of microorganisms, thereby reducing the efficiency of organic matter degradation, resulting in sludge expansion [3]. Moreover, due to the complexity of the physical, chemical, and biological phenomena in the wastewater treatment process, as well as the variability of the influent flow, the WWTPs are difficult to be controlled [2,4].
In the past few decades, proportional-integral-derivative (PID) control has been the most widely used method in WWTPs [5]. However, it is often difficult to obtain satisfactory performance through PID controllers to control complex nonlinear systems. Model Predictive Control (MPC) uses predictive models of the systems to optimize future behavior and has received a lot of attention from WWTPs [6,7,8,9,10]. For example, the MPC was proposed for adjusting the DO concentration of aerobic ponds in WWTPs. It solved the control problem of the activated sludge process [6]. Vrečko et al. designed an MPC controller for the ammonia nitrogen and evaluated it in the actual activated sludge process [7]. In addition, neural networks and fuzzy models were also used in MPC to obtain more accurate predictive models, thus to improve the accuracy of MPC [8,9]. Zeng et al. used a neural-network-based model in MPC and obtained better prediction and control performance [10]. Nevertheless, it is difficult to establish a reasonable prediction model due to the nonlinear, time-varying and strong uncertainty of WWTPs, and MPC cannot satisfactorily control WWTPs in industrial practice [11].
In recent years, reinforcement learning (RL) has been widely used in control systems due to its excellent learning ability, which is closely related to traditional optimal control and adaptive control [12]. For the nonlinear systems, the optimal control policy is determined by the solution of Hamilton–Jacobi–Bellman (HJB) equation [13]. However, the traditional dynamic programming(DP) is difficult to obtain the optimal control policy because of the famous “curse of dimensionality” [14], and the RL-based controller can solve this problem well. The RL controller can obtain the approximate solution of the HJB equation through a learning approach. For instance, an important progress was reported in [15]. It investigated a data-driven iterative adaptive critic strategy for the WWTPs control. In [16], an online adaptive dynamic programming (ADP) scheme based on echo state networks (ESN) was proposed to solve the DO control problem. A direct heuristic dynamic programming (dHDP) controller was designed to solve the multivariate tracking control problem for dissolved oxygen and nitrate concentrations [17]. Notably, the disturbance in the WWTP control problem is rarely considered in these studies.
There are many large disturbances during the operation of WWTPs, such as perturbations in influent flow and pollutant loads, changes in kinetic parameter values under the influence of internal biochemical and external environmental factors, etc. [18]. Although ADP has been widely used in optimal control of WWTPs [15,16,17], to the best of our knowledge, very little literature has considered time-varying disturbances. In [19], Jiang et al. combined robust redesign, backpropagation techniques and nonlinear small gain theorems with ADP theory, to design robust optimal control for a class of uncertain nonlinear systems. Aside from robust control [20], another effective method to reduce the effects of disturbances is sliding mode control (SMC). Muñoz et al. [21] developed an SMC controller to adjust the DO concentration. Yang et al. [22] designed a nonlinear disturbance observer (DOB) to estimate disturbances, and proposed a novel SMC method to counteract the mismatch disturbances of a class of second-order systems. However, the SMC and the DOB require the complete nonlinear dynamics of the systems, which makes it very difficult to design the sliding surface [23], not to mention learning the optimal control policy online.
To address the DO concentration anti-disturbance control problem, the active disturbance rejection control (ADRC) proposed by Han [24] is an effective method, and some related works for WWTPs have been reported [25,26,27]. The core ideas of ADRC are (1) using the extended state observer (ESO), all uncertainties acting on the system (including internal unmodeled dynamics and external disturbances) are equated into a total disturbance, (2) then the system is compensated in real time according to the total disturbance [28]. The existing research on ADRC has mainly emphasized its industrial process applications and theoretical validation of different types of uncertainty systems, while the design of nominal controllers is rarely mentioned since the compensated systems are usually reduced to multiple integrators connected in series [29].
All the above mentioned works have made some progress in the DO control problem for WWTPs, but the anti-disturbance optimal control problem is still challenging. For nonlinear WWTPs subject to complex influent conditions, there are three major challenges to be solved:
- (1)
- How to ensure the stable tracking performance of DO concentration in the case of complex influent conditions and different operation conditions.
- (2)
- How to design a disturbance estimation strategy for the unknown nonlinear WWTPs.
- (3)
- How to design the stable reinforcement learning controller in the system with disturbance compensation.
Motivated by the above, this paper investigates the disturbance-rejection optimal tracking control problem for WWTPs with complex external disturbances. The main advantages of the proposed control scheme are highlighted as follows:
- (1)
- An RL-based anti-disturbance control framework is designed for WWTPs to obtain acceptable and stable DO tracking performance. Compared with the previous results of WWTPs [15,16,17,25,26,27], the adopted disturbance estimation and compensation techniques provide WWTPs with stronger adaptability to the environment disturbance and the adopted RL control technology provides convenience for unattended operation.
- (2)
- Since the unknown complex dynamics of WWTPs is not available, a T-S fuzzy model is designed to simulate the nonlinear properties, based on which an ESO with boundary constraints is designed, which not only facilitates the estimation of disturbances but also deals with the observer transient peaking problem [18,30]. The observer simultaneously provides estimates of the state vector, unknown parameter variations and unknown disturbances (total disturbance), which is then used by the compensation controller in order to provide appropriate compensation signals.
- (3)
- The designed neural-network-based ADP controller can accomplish the optimal tracking control of the compensated system. To simplify the training of the traditional artificial neural network (ANN) [15,17], ESN is considered to approximate the actor and the critic of ADP. The detailed proof shows the proposed ESO-based ADP controller can guarantee the stability of the considered system.
The remainder of this paper is organized as follows. Section 2 presents some preliminary ideas and formulation descriptions. Section 3 describes the design the fuzzy ESO. In Section 4, the details of ADP are presented. Section 5 presents the convergence analysis. The simulation results demonstrate the effectiveness of ESO-ADP in Section 6, and conclusions are given in Section 7.
2. Problem Formulation
Consider the following single-input-single-output unknown discrete-time nonlinear system with disturbance
where is the system state at time step k, is the control input, is the unknown time-varying disturbance, , are unknown and bounded nonlinear smooth functions, is the system output factor. For system (1), the following assumption is given
Assumption 1.
The disturbance variable and its first-order difference are bounded.
Inspired by ADRC [24], we consider the unknown total external disturbance in the system as an extended state, denoted as
under the assumption that is non-singular and the extended state of the system can be used for feedback, we can design the controller as follows
where is the disturbance compensation factor. The second term is the compensation term for the system total disturbance, denoted as , and is the optimal control strategy for the compensated system
For calculating , we consider the optimal control problem for system (4) in infinite-horizon and expected to find a feedback control law to minimize the cost function
where is the discount factor and is the one-step cost function generated by the control at time step k, and is the admissible control set.
According to the optimality principle, the optimal cost function defined as
satisfies the discrete-time HJB equation
for simplicity, denote , as , , respectively. Then the HJB equation can be represented by
The optimal control problem is to solve the control policy from (7), and the optimal control policy need to satisfy the Bellman optimality principle
In controller (3), the optimal control is usually not analytically feasible because the HJB equation is hard to be solved with the traditional manners and the extended state is not directly available. Therefore, this paper is dedicated to developing an ESO-based RL control scheme, where the ESO is used to estimate the total disturbance for the compensation term and the ADP controller is designed to approximate the optimal control policy for the compensated system.
3. Observer Design
First, to estimate the system total disturbance, we design the nonlinear ESO for system (1). Considering the process dynamics are unknown and unavailable, the primary system without influent disturbance can be described as a T-S fuzzy form, the state space form of the T-S fuzzy system can be expressed as
where is the premise variables to be selected, s is the number of premise variables, which can be determined according to the source of nonlinearity of the system, is the normalized weight of the sub-model, r denotes the number of sub-models, and is the affiliation function of the premise variables to each sub-model, that is, the weight of the sub-model. are the parameters of each sub-model, and the sub-model coefficients are denoted as , , then the system (10) can be simplified as
Consider system (11) with unknown time-varying disturbance:
then system (1) is described as system (12) and the observer of system (12) can be designed as
where is the state vector of ESO representing the estimations of the system state and disturbance, is the state estimation error, is the appropriate observer gain vector and is the nonlinear function to be designed and . Therefore, the control policy described by Equation (3) can be represented by
In order to counteract the peaking phenomenon generated during the transitions of ESO [28,31], we constrain the output of the observer within a compact set by using saturation techniques [32].
where is the constraint boundary value to be selected, and the above constraint ensures that the peak value of the observer transition process will not be transmitted to the system. The constraint function is defined as follows
where is a small positive constant. This constraint function can achieve a smooth transition from the unsaturated state to the saturated state, and reduce the influence of the unstable factors of the observer on the system.
Remark 1.
The ESO is designed by rewriting the system as the T-S multi-model form of the state space, rather than the system dynamic equation(which is usually unknown in actual WWTPs). This means the T-S fuzzy model can be obtained by identification, which eliminates the reliance on the priori knowledge [18,33,34], while simplifying the structure of the control system and improving the versatility of the observer.
4. Online ADP Controller Design
When the observer (13) is capable of unbiased estimation of the total system disturbance and the system is real-time compensated, the optimal control policy of the compensated system (4) can be learned online by ADP.
4.1. Structure of ESO-ADP
The main idea of ADP is to obtain the optimal cost function and optimal control law by function approximation to satisfy the optimality principle and the HJB equation. To simplify the training of the traditional ANN, the ESN is used in the ADP controller. The principle of ADP with disturbance compensation control policy is shown in Figure 1, which contains three ESN modules, Actor ESN, Critic ESN and Model ESN. The Actor ESN represents the mapping between the system state variables to the control variables and is used to approximate the optimal control policy; Critic ESN takes the state variables as input and its output is the estimation of the optimal cost function; the Model ESN is used to describe the unknown nonlinear system to generate forward time difference for updating the Actor ESN. The Utility module serves to calculate the cost incurred by the one-step control.
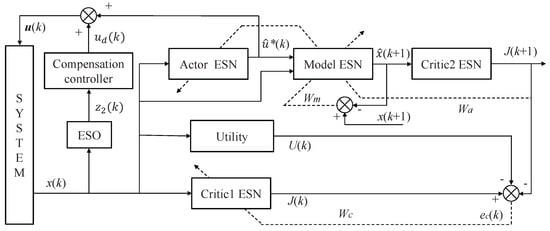
Figure 1.
ADP control schematic with disturbance compensation.
The DO concentration in the WWTP is set as the state variable, which can be directly measured by the DO sensor. In other words, the system state is directly available and thus we use the measured state for feedback instead of the estimated value of the ESO. Assume the adjustable parameter of the critic network, actor network and model network are , and , respectively, then the workflow of the ESO-ADP controller with disturbance compensation is as follows
- Step 1.
- Let , select simulation step N, randomly initialize , and .
- Step 2.
- The actor ESN generates based on at time step k.
- Step 3.
- The Critic1 ESN evaluates the current state and outputs .
- Step 4.
- The Utility module calculates .
- Step 5.
- The Model ESN predicts the state at next time step .
- Step 6.
- The Critic2 ESN evaluates and outputs .
- Step 7.
- ESO estimates the system disturbance and outputs , and the compensation controller gives the compensation control policy .
- Step 8.
- Apply the control policy to the system, thus is obtained.
- Step 9.
- Calculate the weight increment for each network, update the parameters as below
- Step 10.
- When , let , go back to 2 and continue.
As the simulation time step k increases, the ADP controller will gradually approach the optimal control policy and the optimal cost function, while the total disturbance of the system is compensated.
4.2. Echo State Network Approximation
The principle of ESN used in ADP is shown in Figure 2. Proposed by Jaeger [35], the ESN consists of the input layer, the dynamic reservoir and the readout layer. The dynamic reservoir contains a large number of neurons, which are connected with a random sparse matrix, and the output of the hidden layer of the ESN can be expressed as
where is the input vector at time step k and is the internal state at time step k, that is, the output of ESN dynamic reservoir neurons. is the weight matrix of input layer and is the internal connection matrix. is the activation function of the hidden layer neurons, K denotes the input dimension, and N denotes the number of reservoir internal neurons. The ESN output can be described by
where is the output vector at time step k, L denotes the dimensionality of the output vector, and is the readout layer weight. Only is trained, and are randomly determined when the network is initialized and fixed during the training process [35].
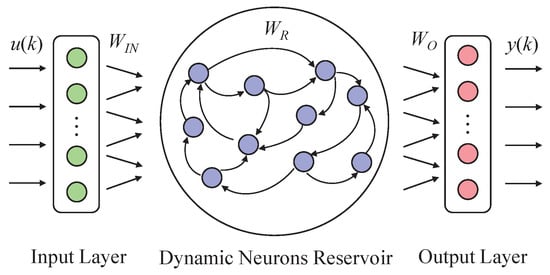
Figure 2.
The principle of ESN.
4.3. Online Learning of the ADP Controller
The learning of the ADP controller is actually the parameter update of the ESNs. The weight-adjustment rules for each ESN are as follows.
4.3.1. Critic ESN
The aim of Critic ESN weight adjustment is to approximate the optimal cost function described by (6). The output weights of the Critic ESN are denoted as , and the loss function is defined as
where is defined as
The weights of Critic ESN are updated as follows
the increment of the weights of the Critic ESN by gradient descent is
where is the learning rate of the Critic ESN, (22) can be further simplified as
where is the internal state of Critic ESN.
4.3.2. Actor ESN
The aim of the Actor ESN weight adjustment is to generate control decisions to minimize the cost function, and the adjustable weight of actor ESN is denoted as , then the loss function for weight update is defined as [16,36]
The necessary condition for the Actor ESN weight to be optimal is that (24) is equal to 0, so the increment of the actor ESN weight can be expressed as
where is the learning rate of the Actor ESN, based on (24) and the chain derivative rule, (25) can be written as
mark the middle part as
then (26) can be written as
where is the internal state of Actor ESN.
From (28), the increment of the weights of the Actor ESN can be calculated by simply calculating from (27). is a one-step cost function defined according to the actual problem and is easy to be obtained, then the second term of (27) can be calculated by
According to (17), (18) and Figure 1, we can obtain
where is the derivative of the activation function of the dynamic reservoir neuron, and are the input of the dynamic reservoir neuron of Critic ESN and Model ESN, respectively. and are the output weight matrices of the Critic ESN and Model ESN, respectively. is the input weight vector of the Critic ESN2, and is the component of the input weight vector associated with u of the Model ESN.
4.3.3. Model ESN
For the Model ESN, the output weights are denoted as , and the loss function of the model network is defined as
where , is the predicted output of the Model ESN and is the actual measured of the system output. is updated by
where is the learning rate and is the internal state of Model ESN.
5. Stability Analysis
In this section, the proof will be divided into two steps. In the first step the boundedness of the states and disturbance estimation errors of ESO is proved to ensure the availability of the observer. Then, in the second step, the convergence of the ESN weights in the ADP controller is given for the effectiveness of the neural network.
Step (1): The boundedness of the ESO estimation errors is shown as follows.
For the observer (13), we make the following assumption
Assumption 2.
The nonlinear function to be selected is global Lipschitz, that is, for any and , there exists a constant , so that holds.
Defining the estimation errors of the system state and the total disturbance as , , respectively, the dynamics of and can be obtained as
Denote , then the above two equations are combined to obtain
where , .
Theorem 1.
Given a discrete T-S fuzzy system (12) with time-dependent non-repetitive disturbance, the following equation holds if there exists a positive definite symmetric matrix and a positive number :
where “*” denotes the transpose of the symmetric part of the matrix, then the estimation errors of the ESO is bounded.
Proof of Theorem 1.
Take the following Lyapunov function
with Assumption 2 and the condition , there is
then, based on , it is further deduced that
adding (41) to the right of (39) yields
the can be equated to
according to Schur’s Compliment theorem, (43) can be equated as
multiplying left and right by , there is
The above equation shows that the estimation errors and are bounded when , that is, the observation error dynamic (36) is stable. □
Step (2): The convergence of the ESN weights is shown as follows.
Define the Lyapunov function as
where is the error function defined in the ESN learning process, let , then
Theorem 2.
If satisfies the following condition, the weight of Critic ESN is convergent.
Proof of Theorem 2.
Definition , according to (20), there is
according to the full differentiation theorem, one has
substituting (23), (49) into (50) yields
substituting (51) into (47) yields
therefore, as long as
then , solving equation (53) yields equation (48), and according to the Lyapunov theory of discrete systems, the Critic ESN weight learning process is convergent when (48) holds. □
Theorem 3.
If satisfies the following condition, the weight of Actor ESN is convergent.
Proof of Theorem 3.
Let , then
according to (24)–(28) and (55), there is
according to the full differentiation theorem, one has
substituting (56) and (28) into (57) yields
substituting (58) into (47) yields
When the following inequality holds
that is
then , the Actor ESN weight is convergent. The proof is over. □
It is worth noting that the Critic ESN may not converge to zero, it is equivalent to . As the learning process proceeds, the Critic ESN will gradually approach the optimal cost function described by (6), and the total cost value decreases as the policy improvement proceeds, finally converging to an constant value.
Remark 2.
Based on the above discussion, unlike typical iterative adaptive critic control [15], the proposed ESO-ADP is learned online using on-policy, which retains the advantages of ESNs relative to single hidden layer feedforward neural networks. In general, this reinforcement learning method for neural network approximation can be widely used in practical applications. Meanwhile, based on the state estimation results of T-S fuzzy ESO, the proposed compensation controller can effectively suppress perturbations, so that the reinforcement learning method can take effective measures to make DO concentration recover quickly and keep it stable.
6. Simulation Studies
This section presents the simulation experiment to illustrate the effectiveness of ESO-ADP.
6.1. Parameter Initialization
The simulation experiments in this paper are conducted on the Benchmark Simulation Model No.1 (BSM1) developed by the International Water Quality Association and the European Union Scientific and Technical Cooperation [37], which aims to provide a standardized platform to compare different control strategies. The plant layout of BSM1 is a bioreactor and a secondary sedimentation tank, as shown in Figure 3.
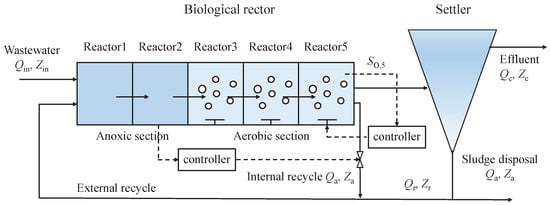
Figure 3.
BSM1 layout.
BSM1 contains two main control loops, nitrate concentration and DO concentration , which are controlled by two single-loop controllers in this paper. For , PID control is used in all simulation experiments and the parameters are P = 10,000, , . The DO concentration is the mainly concerned variable in this paper, so the ESO-ADP controller is used in DO control loop. The manipulated variable of the is the oxygen transfer coefficient of the fifth reactor, which operates in the range of 0–360/d; the manipulated variable of the nitrate control loop is the flow rate , which ranges from 0–92,230 m/d. BSM1 provides the influent data under three different weather. They are dry weather, rain weather, and storm weather. This work evaluates the control performance of the proposed ESO-ADP controller under dry weather, then rain weather are also used to evaluate the anti-interference performance of ESO-ADP and the tracking ability.
is the state variable and output of the control system and is the control input, while the second-order ESO for the DO control system described in (13) is designed as
this means in (13) is defined as . The T-S fuzzy model under constant influent conditions is described as
where the premise variable is the normalized , is the normalized sub-model weight, is the affiliation function, and is expressed as
where is the center of the second affiliation function, which is determined by identification. In addition, the parameters of the three sub-models in (39) are shown in Table 1.

Table 1.
Sub-model parameters.
Remark 3.
The nonlinearity of the activated sludge system mainly comes from its structure, the growth characteristics of microorganisms and the settling law of sludge. Theoretically the premise variable should be selected as the state variable, but the unmeasurability of the premise variable is not conducive to parameter estimation. Considering the correlation between the state and the output, the premise variable is selected as DO concentration in this paper.
In the simulation, the observer parameter is set to , and , and the saturation bounds of the observer output and are set to , .
Table 2 lists the inputs and outputs of each module of the ADP controller, where is ESN learning rate and is the set value of DO. The parameter n denotes the number of neurons in the ESN dynamic reservoir, and is the sparsity, which indicates the percentage of the number of not interconnected neurons. is the spectral radius of the internal connection matrix, denoted by

Table 2.
ADP controller module inputs and outputs and parameters.
Taking as the activation function of ESN, and the sampling time is set to T = 60 s. The compensation coefficient is set to . The utility is defined as
6.2. Results and Analysis
Three sub-sections will be given to illustrate the advantages of the proposed ESO-ADP. Furthermore, the proportional-integral-derivative controller (PID), the improved active disturbance rejection controller (ADRC) [27], and online adaptive dynamic programming controller (ADP) [16] applied in WWTPs are introduced to evaluate the proposed ESO-ADP performance, where the PID control parameters are , , , and the other two controllers are configured with default values from the work [16,27].
6.2.1. Constant Value Control
The simulation results of DO regulation under dry and rainy weather conditions manipulated by the designed control algorithm are shown in Figure 4 and Figure 5. The first several days are the controller’s online learning period, so the results of 7–14 days are used for evaluation. The results in Figure 4 show that the proposed ESO-ADP ensures that the DO concentration can track the reference trajectory, and the control performance is better than PID, ADRC and ADP. The DO tracking error shown in Figure 5 demonstrates the accuracy of the ESO-ADP controller which is higher than other controllers. Figure 6 demonstrates the effectiveness of ESO. From Figure 6a, the system state fluctuates greatly in the initial moments and the estimation error of ESO is relatively large. The ESO estimation error can be kept near 0 when reaching stability (see Figure 6b), thus to provide reasonable estimation of the system state and total disturbance. In addition, the output constraint of the observer limits the estimation value to the target compact set.
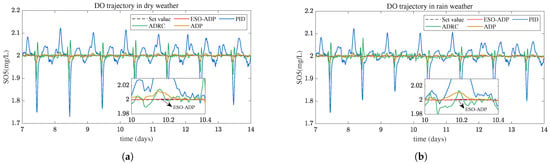
Figure 4.
Dissolved oxygen concentration control effects. (a) Dissolved oxygen concentration control curve in dry weather. (b) Dissolved oxygen concentration control curve in rain weather.
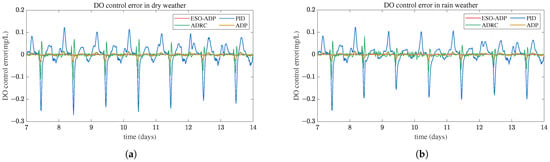
Figure 5.
Dissolved oxygen concentration control error. (a) Dissolved oxygen concentration control error in dry weather. (b) Dissolved oxygen concentration control error in rain weather.
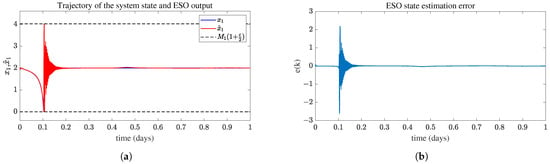
Figure 6.
The performance of ESO. (a) System State and ESO Output. (b) ESO state estimation error.
Some performance indicators defined in BSM1 for controller assessment are given in Table 3, and the performance improvement of ESO-ADP relative to the other three controllers is shown in Table 4. As can be seen, the ESO-ADP controller significantly reduces the values of three performance indicators compared with the three other controllers, which indicates the proposed ESO-ADP controller can obtain better stability performance.

Table 3.
Performance index of different control strategies in dry weather.

Table 4.
The improvement of ESO-ADP performance index.
To evaluate the anti-interference performance of the ESO-ADP controller, the rain-weather influent data are considered. Figure 4b and Figure 5b present the results of the ESO-ADP controller under rainy weather. The DO concentrations under PID control fluctuate greatly, with a peak value 2.12 mg/L and a minimum level 1.75 mg/L. The proposed ESO-ADP has the minimal fluctuation and tracking error even though ADRC and ADP controllers greatly improve performance compared to PID. The control curves of the ESO-ADP controller in the dry and rain weather are very smooth, and the DO concentration is stable around the set value. Table 5 shows the ESO-ADP controller performance in dry and rain weather. The results show that the ESO-ADP controller has excellent control accuracy and adaptability to disturbances.

Table 5.
Control performance of ESO-ADP controller under different weather.
Remark 4.
It is worth noting that the three controllers (PID, ADRC, and ADP) without fuzzy ESO produced poor tracking performance and large error fluctuations in the above control results. In addition, Table 4 quantitatively shows the advantages of the proposed ESO-ADP controller. Therefore, the disturbance estimation technique introduced in this paper is beneficial to achieve active disturbance suppression and high tracking accuracy.
6.2.2. Online Learning of ESO-ADP Controller
The ESO-ADP controller is completely unknown to the system in the initial stage, while the weights are updated online by interacting with the environment. Similarly, the ESO’s estimation error requires a transition process to reach convergence. The DO concentration in the first four days is shown in Figure 7. The ESO-ADP controller reaches convergence at approximately 0.2 days. The process before 0.2 days is defined as the learning process of the controller. From Figure 7a, The deviation of DO concentration from the reference value is relatively large and fluctuates widely during learning process, and the control input under the ESO-ADP controller also fluctuates greatly as shown in Figure 7b, furthermore, when stabilization is reached the proposed ESO-ADP controller is able to generate more accurate control input. Figure 8 presents the weight-adjustment process of the ESNs in the ESO-ADP controller, obviously, the weights finally achieve convergence. Figure 8b,c indicate that the weights of Critic ESN and Model ESN are fine-tuned in a small range with the fluctuation of influent flow to continuously adapt to the influence of system disturbance and thus improve the anti-interference capability of the controller. Based on the above descriptions, it can be summarized that the proposed ESO-ADP has good convergence and stability.
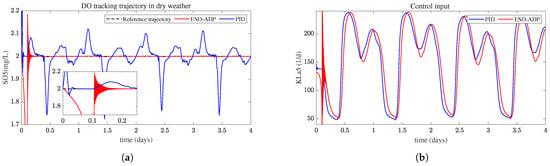
Figure 7.
The learning process of ESO-ADP. (a) Dissolved oxygen concentration during learning process. (b) Control input during learning process.
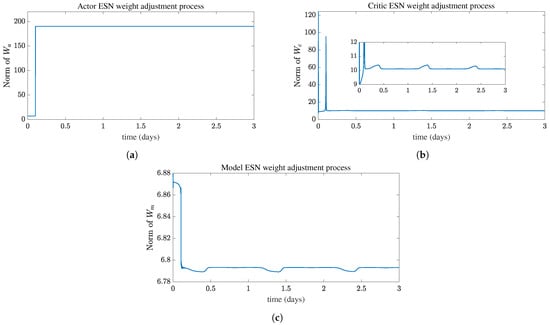
Figure 8.
The neural network weights learning process of ESO-ADP controller. (a) Actor ESN weight learning process. (b) Critic ESN weight learning process. (c) Model ESN weight learning process.
6.2.3. Time-Varying Reference Trajectory Control
The performance of ESO-ADP controller in the case of time-varying reference trajectory is evaluated with the reference trajectory: 2 mg/L from day 7 to day 9, 1.9 mg/L from day 9 to day 11, 2.1 mg/L from day 11 to day 13, and 2 mg/L from day 13 to day 14. Figure 9 presents the results in dry and rain weather. The DO concentration under ESO-ADP controller tracked the reference trajectory quickly when the set value has a step change, but a large overshoot occurred. Whatever, the tracking performance of the ESO-ADP controller for the time-varying reference trajectory is still satisfactory, and the proposed ESO-ADP has better tracking performance than other controllers. The DO tracking error is shown in Figure 10. It can be seen that the system stability and control accuracy under ESO-ADP are better than PID, ADRC and ADP.
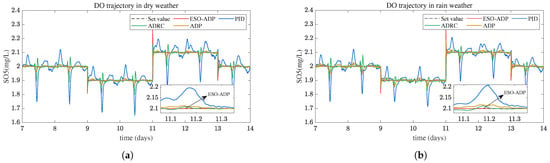
Figure 9.
Dissolved oxygen concentration control effects. (a) Dissolved oxygen concentration control curve in dry weather. (b) Dissolved oxygen concentration control curve in rain weather.
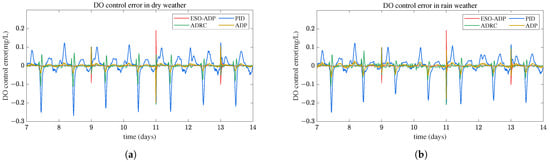
Figure 10.
Dissolved oxygen concentration control error. (a) Dissolved oxygen concentration control error in dry weather. (b) Dissolved oxygen concentration control error in rain weather.
7. Conclusions
For DO concentration control in BSM1, a fuzzy ESO-based ADP controller and disturbance rejection control scheme are designed and investigated. The ESN is used to approximate the optimal control policy of the system online while compensating the total disturbance of the system. The fuzzy-model-based ESO is designed to estimate the disturbances that cannot be measured in the system using the pre-identified T-S fuzzy model, and the experiments show that the proposed method has high control accuracy and strong anti-interference ability.
The proposed fuzzy ESO is suitable for state and disturbance estimation in the BSM1 DO concentration control system, and can be combined with the existing ADP controller design methods to achieve disturbance rejection control. Theoretical analysis and experimental results show that the proposed reinforcement learning anti-disturbance control system is convergent and stable. The disturbance compensation controller enables the system to have a certain suppression capability for the system disturbance. Moreover, the online learning of the ESO-ADP controller makes it adaptive and able to adapt well to the changes in the operating environment. Therefore, the controller design method used in this paper and the disturbance suppression scheme are suitable for the control problem of unknown complex nonlinear systems with unknown disturbance. The univariate control of DO concentration is considered in this paper, and the future work will take DO concentration and nitrate level into consideration, design controllers for multiple-input-multiple-output (MIMO) systems to improve the policy search and disturbance rejection capability.
Author Contributions
Formal analysis, X.C. and P.D.; Funding acquisition, W.Z.; Investigation, Z.L.; Methodology, X.P. and Z.L.; Project administration, W.Z.; Resources, X.P.; Software, X.C. Supervision, W.Z., X.P. and Z.L.; Validation, X.C.; Writing—original draft, X.C.; Writing—review & editing, X.P. and P.D. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (61890930-3), National Natural Science Fund for Distinguished Young Scholars (61925305), National Natural Science Foundation of China (62173145), Shanghai Pujiang Program (21PJ1402200) and Shanghai AI Lab.
Data Availability Statement
The data presented in this study are available in the manuscript.
Conflicts of Interest
The authors have already confirmed that this manuscript has been approved by all authors for publication and no conflict of interest is declared in this manuscript.
References
- Hamitlon, R.; Braun, B.; Dare, R.; Koopman, B.; Svoronos, S.A. Control issues and challenges in wastewater treatment plants. IEEE Control Syst. Mag. 2006, 26, 63–69. [Google Scholar]
- Han, H.; Zhen, B.; Qiao, J. Dynamic structure optimization neural network and its applications to dissolved oxygenic (DO) control. Inf. Control 2010, 39, 354–360. [Google Scholar]
- Fu, W.T.; Qiao, J.F.; Han, G.T. Dissolved oxygen control system based on the TS fuzzy neural network. In Proceedings of the 2015 International Joint Conference on Neural Networks (IJCNN), Killarney, Ireland, 12–17 July 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1–7. [Google Scholar]
- Santín, I.; Pedret, C.; Vilanova, R. Applying variable dissolved oxygen set point in a two level hierarchical control structure to a wastewater treatment process. J. Process Control 2015, 28, 40–55. [Google Scholar] [CrossRef]
- Qiao, X.; Luo, F.; Xu, Y. Robust PID controller design using genetic algorithm for wastewater treatment process. In Proceedings of the 2016 IEEE Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Xi’an, China, 3–5 October 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1081–1086. [Google Scholar]
- Holenda, B.; Domokos, E.; Redey, A.; Fazakas, J. Dissolved oxygen control of the activated sludge wastewater treatment process using model predictive control. Comput. Chem. Eng. 2008, 32, 1270–1278. [Google Scholar] [CrossRef]
- Vrečko, D.; Hvala, N.; Stražar, M. The application of model predictive control of ammonia nitrogen in an activated sludge process. Water Sci. Technol. 2011, 64, 1115–1121. [Google Scholar] [CrossRef]
- Han, H.; Liu, Z.; Hou, Y.; Qiao, J. Data-driven multiobjective predictive control for wastewater treatment process. IEEE Trans. Ind. Inform. 2019, 16, 2767–2775. [Google Scholar] [CrossRef]
- Li, M.; Hu, S.; Xia, J.; Wang, J.; Song, X.; Shen, H. Dissolved oxygen model predictive control for activated sludge process model based on the fuzzy C-means cluster algorithm. Int. J. Control Autom. Syst. 2020, 18, 2435–2444. [Google Scholar] [CrossRef]
- Zeng, G.; Qin, X.; He, L.; Huang, G.; Liu, H.; Lin, Y. A neural network predictive control system for paper mill wastewater treatment. Eng. Appl. Artif. Intell. 2003, 16, 121–129. [Google Scholar] [CrossRef]
- Han, H.; Qiao, J. Nonlinear model-predictive control for industrial processes: An application to wastewater treatment process. IEEE Trans. Ind. Electron. 2013, 61, 1970–1982. [Google Scholar] [CrossRef]
- Lewis, F.L.; Vrabie, D. Reinforcement learning and adaptive dynamic programming for feedback control. IEEE Circuits Syst. Mag. 2009, 9, 32–50. [Google Scholar] [CrossRef]
- Wang, F.Y.; Zhang, H.; Liu, D. Adaptive dynamic programming: An introduction. IEEE Comput. Intell. Mag. 2009, 4, 39–47. [Google Scholar] [CrossRef]
- Song, R.-Z.; Xiao, W.-D.; Sun, C.-Y.; Wei, Q.-L. Approximation-error-ADP-based optimal tracking control for chaotic systems with convergence proof. Chin. Phys. B 2013, 22, 090502. [Google Scholar]
- Wang, D.; Ha, M.; Qiao, J. Data-driven iterative adaptive critic control toward an urban wastewater treatment plant. IEEE Trans. Ind. Electron. 2020, 68, 7362–7369. [Google Scholar] [CrossRef]
- Bo, Y.C.; Zhang, X. Online adaptive dynamic programming based on echo state networks for dissolved oxygen control. Appl. Soft Comput. 2018, 62, 830–839. [Google Scholar] [CrossRef]
- Yang, Q.; Cao, W.; Meng, W.; Si, J. Reinforcement-Learning-Based Tracking Control of Waste Water Treatment Process Under Realistic System Conditions and Control Performance Requirements. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 5284–5294. [Google Scholar] [CrossRef]
- Lin, M.J.; Luo, F. Adaptive neural control of the dissolved oxygen concentration in WWTPs based on disturbance observer. Neurocomputing 2016, 185, 133–141. [Google Scholar] [CrossRef]
- Jiang, Y.; Jiang, Z.P. Robust adaptive dynamic programming and feedback stabilization of nonlinear systems. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 882–893. [Google Scholar] [CrossRef]
- Du, P.; Peng, X.; Li, Z.; Li, L.; Zhong, W. Performance-guaranteed adaptive self-healing control for wastewater treatment processes. J. Process Control 2022, 116, 147–158. [Google Scholar] [CrossRef]
- Muñoz, C.; Young, H.; Antileo, C.; Bornhardt, C. Sliding mode control of dissolved oxygen in an integrated nitrogen removal process in a sequencing batch reactor (SBR). Water Sci. Technol. 2009, 60, 2545–2553. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Li, S.; Yu, X. Sliding-mode control for systems with mismatched uncertainties via a disturbance observer. IEEE Trans. Ind. Electron. 2012, 60, 160–169. [Google Scholar] [CrossRef]
- Fan, Q.Y.; Yang, G.H. Adaptive actor–critic design-based integral sliding-mode control for partially unknown nonlinear systems with input disturbances. IEEE Trans. Neural Netw. Learn. Syst. 2015, 27, 165–177. [Google Scholar] [CrossRef] [PubMed]
- Han, J. From PID to active disturbance rejection control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Wei, W.; Chen, N.; Zhang, Z.; Liu, Z.; Zuo, M. U-model-based active disturbance rejection control for the dissolved oxygen in a wastewater treatment process. Math. Probl. Eng. 2020, 2020, 3507910. [Google Scholar] [CrossRef]
- Wei, W.; Chen, N.; Zuo, M.; Liu, Z.W. Disturbance rejection control for the dissolved oxygen in a wastewater treatment process. Meas. Control 2020, 53, 899–907. [Google Scholar] [CrossRef]
- Zhang, Y.; Wei, W. Finite-Time Extended State Observer-based PI Control for Dissolved Oxygen. In Proceedings of the 2019 19th International Conference on Control, Automation and Systems (ICCAS), Jeju, Republic of Korea, 15–18 October 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 40–43. [Google Scholar]
- Ran, M.; Li, J.; Xie, L. Reinforcement-Learning-Based Disturbance Rejection Control for Uncertain Nonlinear Systems. IEEE Trans. Cybern. 2022, 52, 9621–9633. [Google Scholar] [CrossRef] [PubMed]
- Ran, M.; Wang, Q.; Dong, C. Active disturbance rejection control for uncertain nonaffine-in-control nonlinear systems. IEEE Trans. Autom. Control 2016, 62, 5830–5836. [Google Scholar] [CrossRef]
- Nagy-Kiss, A.M.; Ichalal, D.; Schutz, G.; Ragot, J. Fault tolerant control for uncertain descriptor multi-models with application to wastewater treatment plant. In Proceedings of the 2015 American Control Conference (ACC), Chicago, IL, USA, 1–3 July 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 5718–5725. [Google Scholar]
- Guo, B.Z.; Zhao, Z.L. On convergence of the nonlinear active disturbance rejection control for MIMO systems. SIAM J. Control Optim. 2013, 51, 1727–1757. [Google Scholar] [CrossRef]
- Freidovich, L.B.; Khalil, H.K. Performance recovery of feedback-linearization-based designs. IEEE Trans. Autom. Control 2008, 53, 2324–2334. [Google Scholar] [CrossRef]
- Wei, W.; Chen, N.; Zhang, Z.; Liu, Z.; Zuo, M.; Liu, K.; Xia, Y. A scalable-bandwidth extended state observer-based adaptive sliding-mode control for the dissolved oxygen in a wastewater treatment process. IEEE Trans. Cybern. 2022, 52, 13448–13457. [Google Scholar] [CrossRef]
- Fan, Z.X.; Adhikary, A.C.; Li, S.; Liu, R. Disturbance observer based inverse optimal control for a class of nonlinear systems. Neurocomputing 2022, 500, 821–831. [Google Scholar] [CrossRef]
- Jaeger, H.; Haas, H. Harnessing nonlinearity: Predicting chaotic systems and saving energy in wireless communication. science 2004, 304, 78–80. [Google Scholar] [CrossRef] [PubMed]
- Prokhorov, D.V.; Wunsch, D.C. Adaptive critic designs. IEEE Trans. Neural Netw. 1997, 8, 997–1007. [Google Scholar] [CrossRef] [PubMed]
- Jeppsson, U.; Pons, M.N. The COST benchmark simulation model—Current state and future perspective. Control Eng. Pract. 2004, 12, 299–304. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).