4.1. Effect of the Deflagration Position
A numerical model of single-point deflagration was established in this study. Near-wellbore deflagration, middle deflagration, and toe deflagration were simulated, respectively, by setting the deflagration position at the left end (0, −5, 0), the midpoint (0, 0, 0), and the right end (0, 6, 0), as shown in
Figure 3. It is interesting to note that, in a short time, the deflagration of the explosive materials started and extended preferentially along the wellbore until all the explosives were ignited, and then the energy was rapidly radiated as a spherical form and transmitted to the reservoir, as shown in
Figure 4.
To obtain the real fracture morphology, the XOY and YOZ sections and the cohesive units corresponding to the deflagration points (as shown in
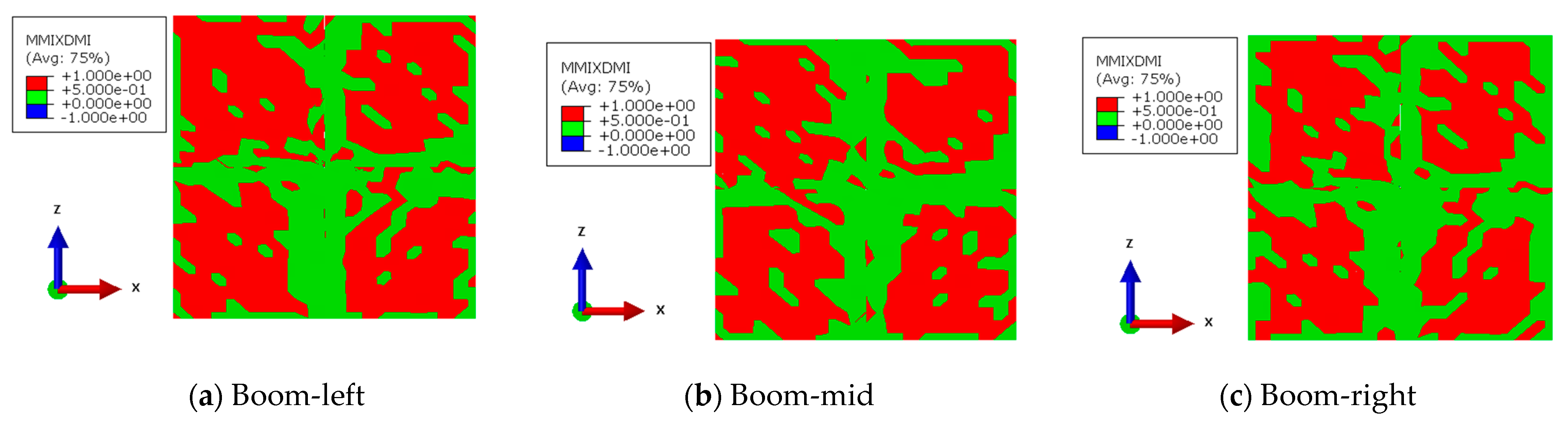
Figure 5) were extracted, and the fracture propagation pattern across the radial well was analyzed. In the cohesive units, three basic fracture morphologies are simulated: type I—open fracture, type II—slip fracture, and type III—rip fracture. The MMIXDMI parameter represents the field output in cases of tensile and shear failure. When the value is between −1~0, rock failure does not occur (blue area); when the value is 0~0.5, tensile failure is dominant (green area); and when the value is 0.5~1, shear failure is dominant (red area). Moreover, the area of the cohesive fracture surface is calculated by post-processing in the Python language, which facilitates the quantitative analysis of the data.
During deflagration, under three deflagration points, part of the reservoir in the area around the radial well (XOY and YOZ planes) in the direction of the horizontal minimum principal stress is fractured completely, and tensile failure is dominant, accompanied by some shear failure. Tensile failure occurs mainly in the area parallel to the direction of the horizontal maximum principal stress (XOZ plane), and almost no shear failure occurs. The fracture propagation mechanism is analyzed quantitatively in five typical interfaces.
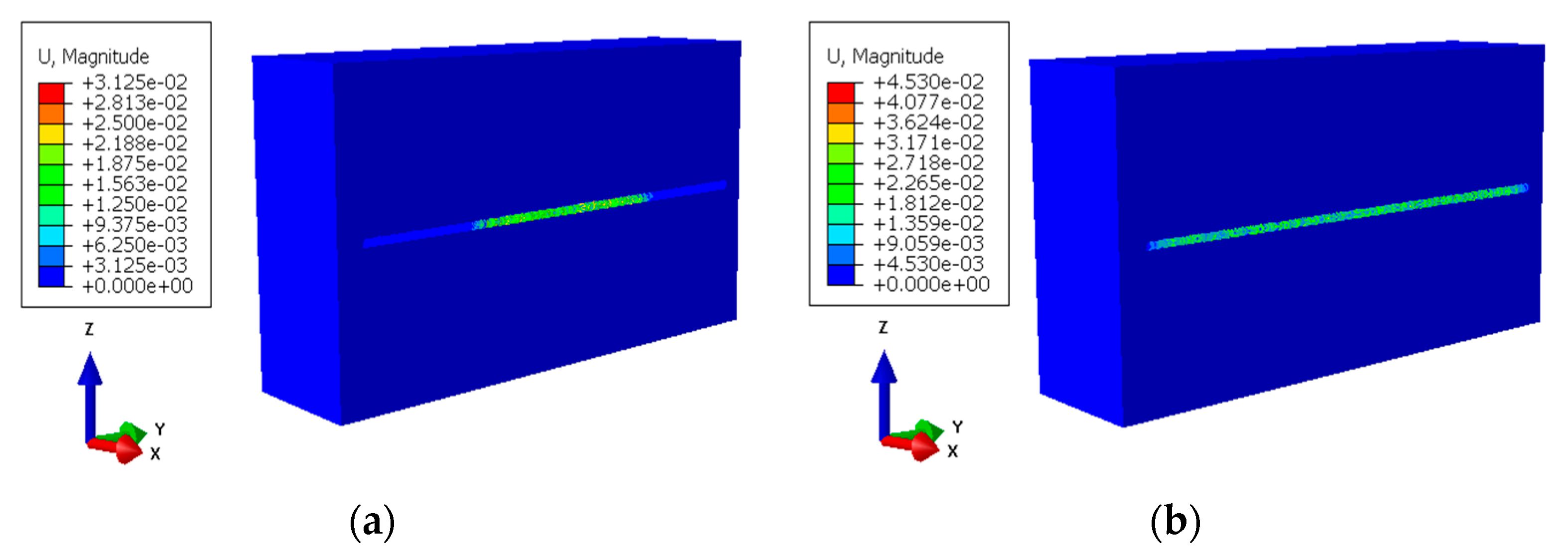
The simulation shows that when deflagration occurs in the middle of the radial well, a higher deflagration pressure and larger fracture area are generated in the middle area, and a smaller fracture area is generated at both ends (
Figure 6). The fracture is analyzed at the cross-section of the radial well. Around the deflagration point, tensile failure leads to the fracture area of 41.58 m
2, and the fracture extends in a cross-shape from the deflagration point (green area). Shear failure leads to the fracture area of 58.37 m
2 (red area) around the tensile fracture. Comparatively, the reservoir stimulation near the deflagration point is dominated by shear failure. As the distance from the deflagration point increases, the shear failure decreases, the total fracture area decreases, and the reservoir stimulation efficiency decreases, as shown in
Table 4. In the sections that are 5 m and 6 m away from the deflagration point, the shear fracture areas of 17.26 m
2 and 13.47 m
2 and the tensile fracture areas of 50.13 m
2 and 47.75 m
2 are generated, respectively. The reservoir stimulation areas are reduced by 32.58% and 38.75%, respectively, compared with those at the deflagration point.
When deflagration occurs at the radial well ends, the fracture is also initiated in the same way as the abovementioned mechanism. This indicates that the deflagration point directly affects the fracture propagation pattern. A larger deflagration pressure wave and larger fracture area are generated at the position closer to the deflagration point, and this is favorable for local reservoir stimulation. With the increase in the distance from the deflagration point, the reservoir stimulation efficiency is reduced significantly, and this indicates the characteristics of deflagration fracturing, in which a greater reservoir stimulation area is generated near the radial well, and a lower stimulation volume is generated far from the deflagration point.
4.2. Effect of the Radial Well Azimuth
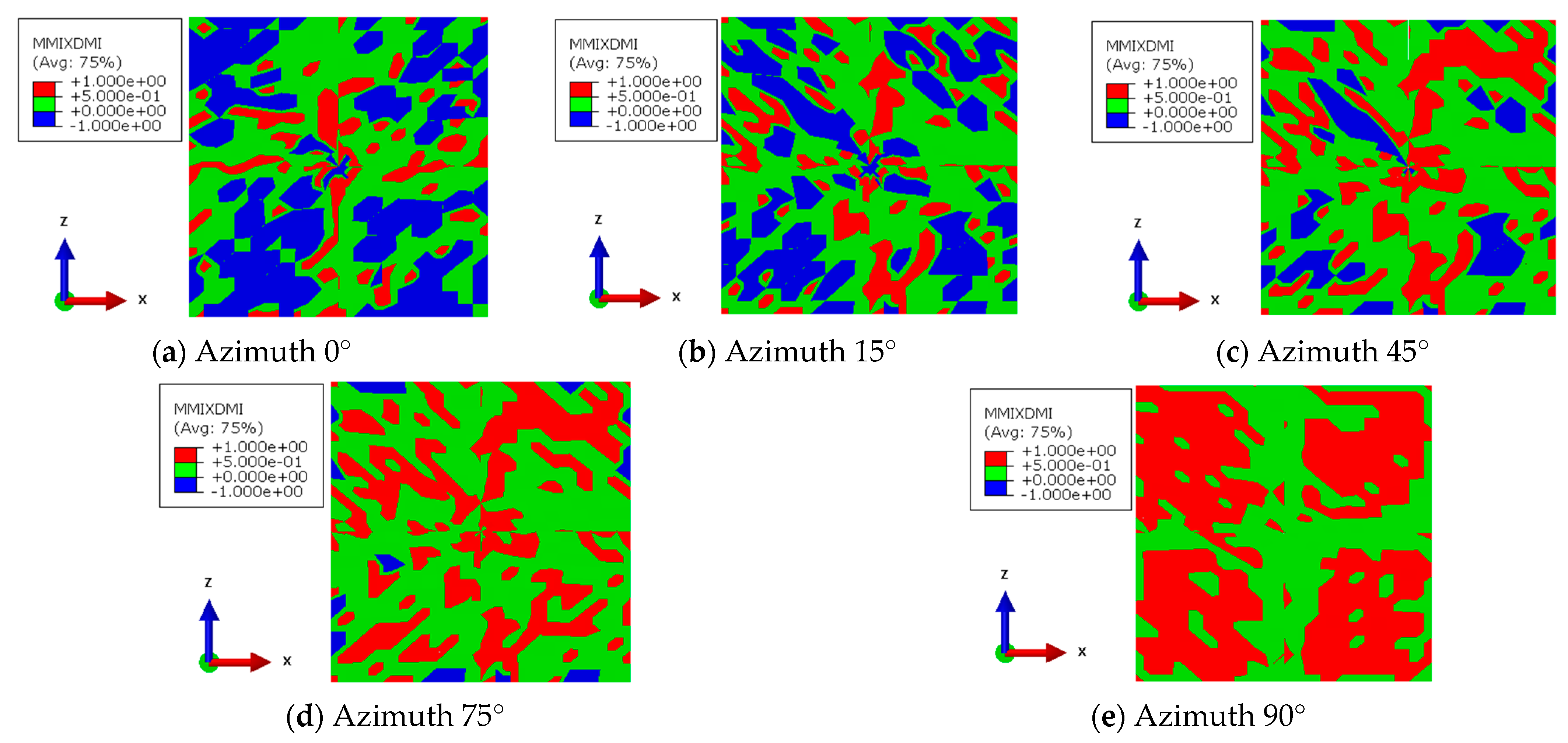
Assuming that deflagration occurs in the middle of the radial well and that the abovementioned rock mechanic parameters are unchanged, the effect of the radial well azimuth on the deflagration fracturing was simulated by setting the radial well azimuth α (the angle between the radial well axis and the horizontal maximum principal stress) as 0°, 15°, 45°, 75°, and 90°.
The results show that with the increase in the radial well azimuth, the fracture area at the deflagration point increases from 60.09 m
2 to 99.95 m
2, with an increment of 66.33%. As the radial well azimuth changes, the stress distribution on the borehole wall and deflagration stress field change accordingly, which affects the fracture propagation pattern. The larger radial well azimuth indicates lower horizontal stress on the section across the wellbore, and the fractures are prone to initiation and propagation, resulting in a larger stimulation area. Moreover, with the increase in the radial azimuth, the shear fracture area increases gradually, as shown in
Figure 7. The tensile fracture area reaches a maximum of 61.15 m
2 when α = 75° and decreases to 41.58 m
2 when α = 90°. With the increase in the radial well azimuth (α > 75°), the stress in the rock changes, and the fracture mechanism changes from tensile failure to shear failure, as shown in
Table 5. This provides a reference for understanding the fracture mechanism of deflagration fracturing.
4.3. Effect of the Horizontal Stress Difference
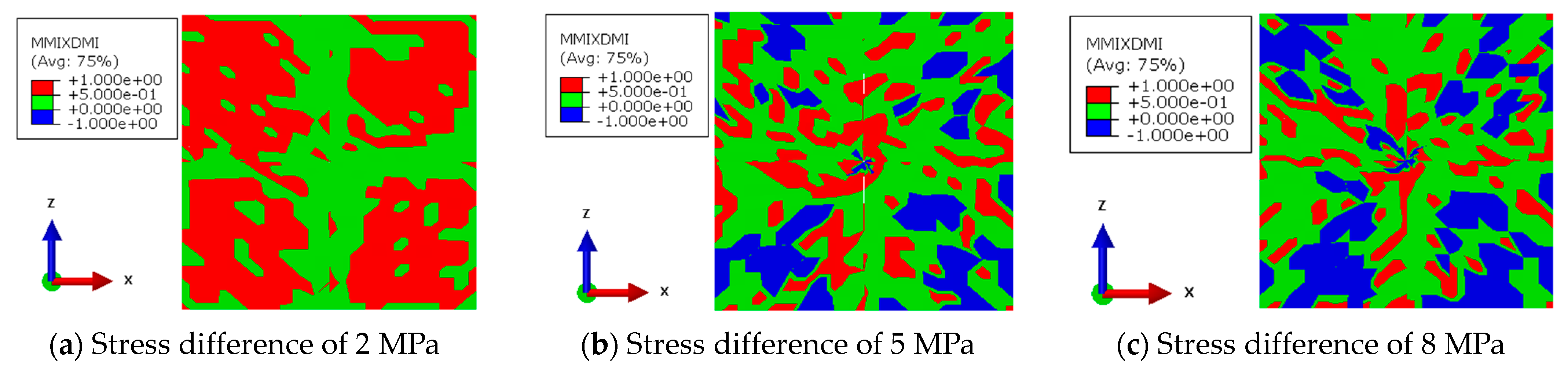
Assuming that deflagration occurs in the middle of the radial well, the abovementioned rock mechanic parameters are unchanged, and the horizontal minimum principal stress is 28 MPa, the effect of the horizontal stress difference on the fracture morphology was simulated by setting the horizontal maximum principal stress as 33 MPa and 36 MPa (
Figure 8). When the horizontal stress difference increased from 2 MPa to 8 MPa, the fracture area decreased from 99.95 m
2 to 71.33 m
2, with a reduction of 28.63%. The large stress difference had a significant negative effect on the fracture initiation and propagation, as shown in
Table 6. However, in deflagration fracturing, there is still a good capacity for fracture initiation in the rock. With the increase in the horizontal stress difference, the shear failure area decreased rapidly, and the tensile failure area increased to a certain extent. A larger stress difference is conductive to tensile failure.
It should be noticed that with the increase in the horizontal maximum principal stress, the difference between the horizontal maximum principal stress and the vertical stress decreased. The horizontal maximum principal stress of 36 MPa is greater than the vertical stress. According to the theory of solid mechanics, variation in the maximum stress directions of the
X,
Y, and
Z axis leads to variation in the fracture morphology in deflagration fracturing. Thus, further study of fracture initiation and propagation in the cohesive plane is needed. An example in a cohesive unit on the
X-
Y plane was analyzed here, as shown in
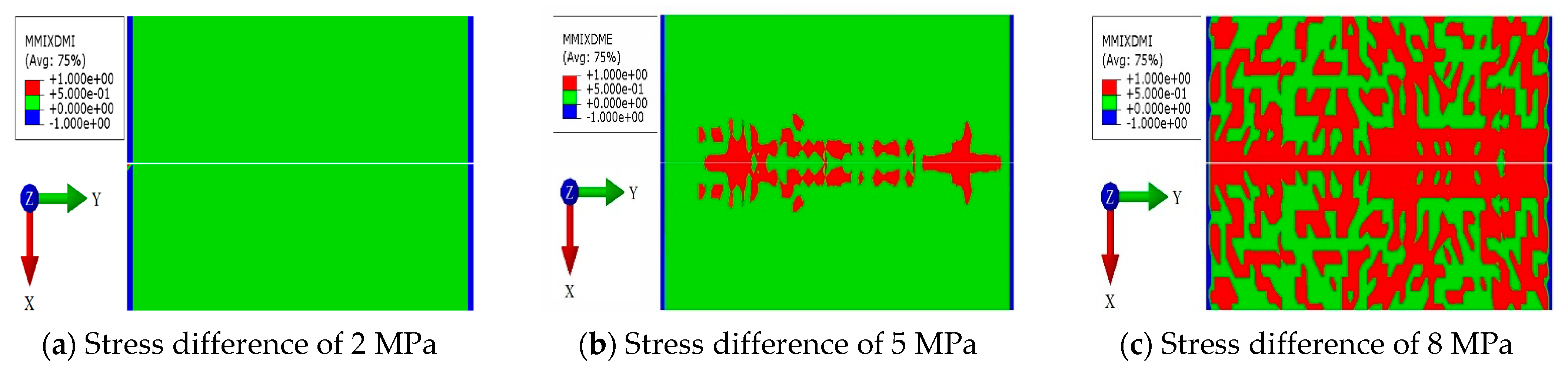
Figure 9.
The numerical simulation shows that when the horizontal maximum principal stress is lower than the vertical stress, the fractures on the
X-
Y plane are dominated by tensile failure. When the horizontal maximum principal stress increases to 33 MPa, a small number of shear fractures occur on the
X-
Y plane, with the shear fracture proportion of 9.61%. When the horizontal maximum principal stress is larger than the vertical stress, shear failure occurs obviously on the
X-
Y plane, with the shear fracture proportion of up to 56.2%, as shown in
Table 7. It is confirmed that in all the stress distributions, the deflagration horizontal fracture occurs on the plane of the radial well axis, indicating that the stress distribution has little effect on the horizontal fractures, and fracture initiation and propagation in deflagration fracturing are mainly affected by the stress wave generated by deflagration. The stress distribution has an obvious effect on the rock failure type. When the horizontal maximum principal stress and the vertical stress are reversed, fracture initiation in the horizontal direction is more likely to be subject to shear failure.