New Multi-Leg Converter for DC Microgrid with Two Duty Cycles
Abstract
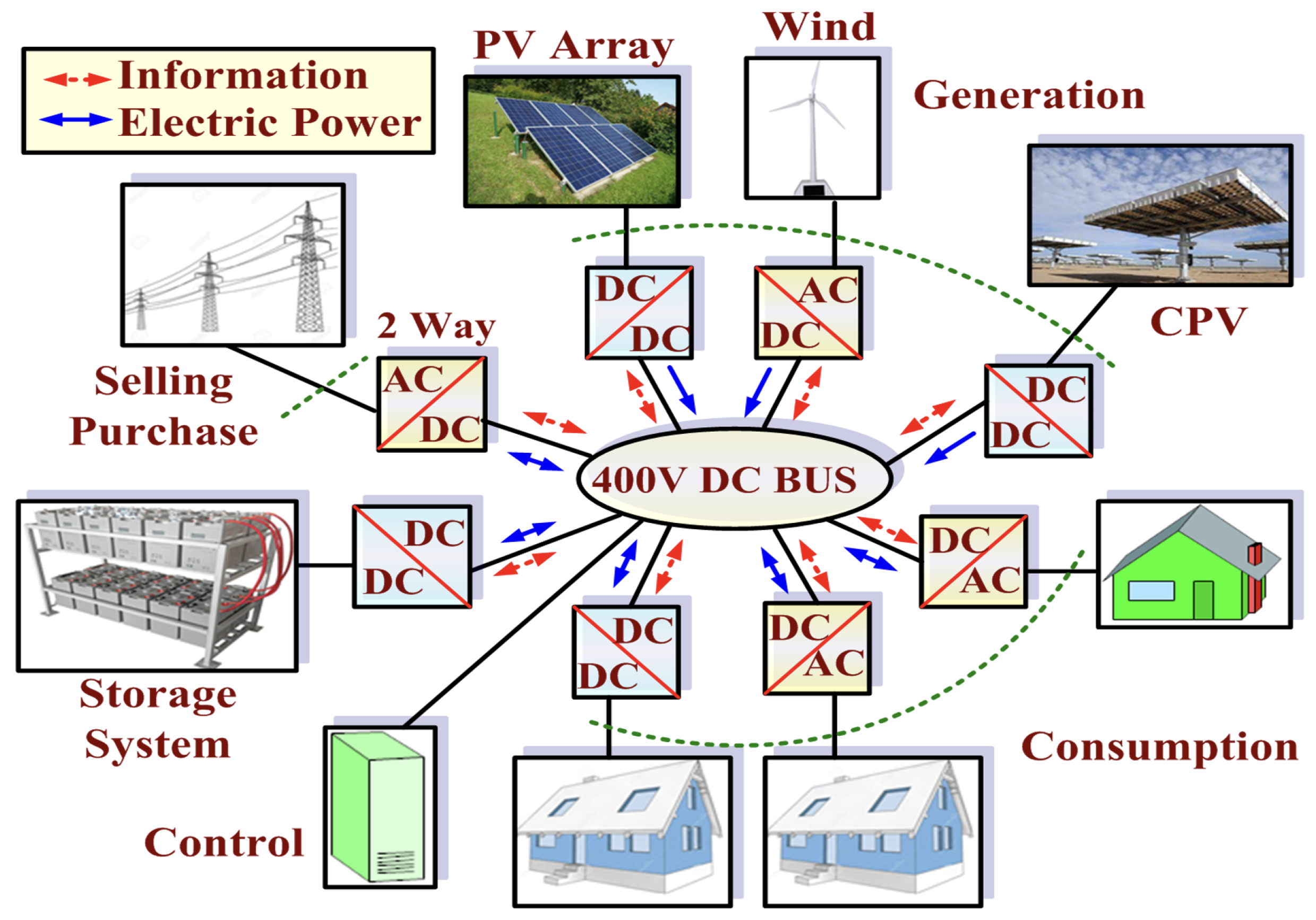
1. Introduction
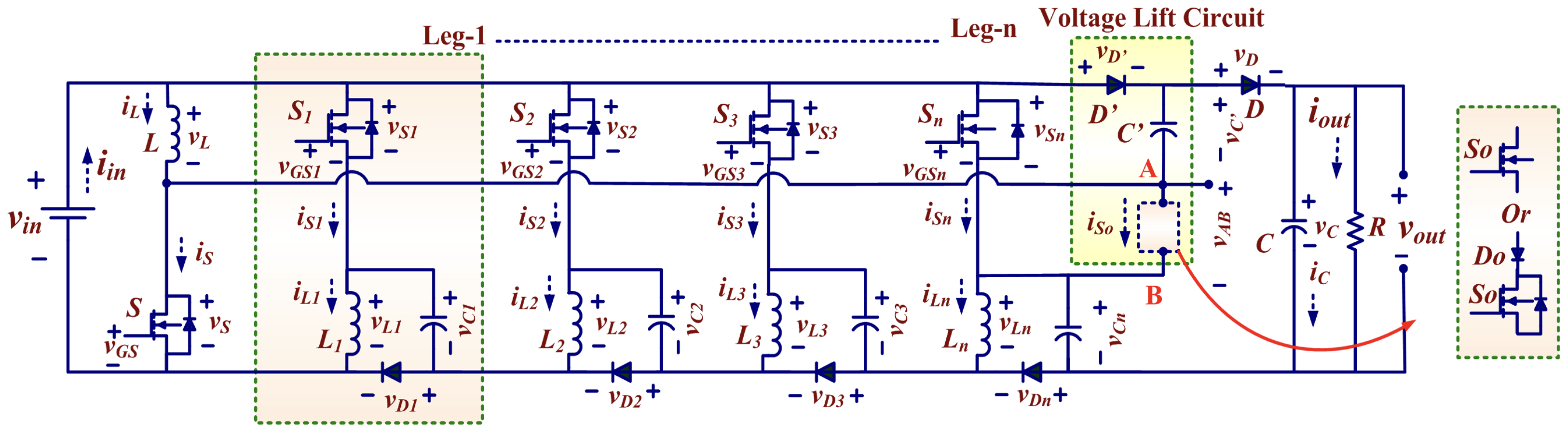
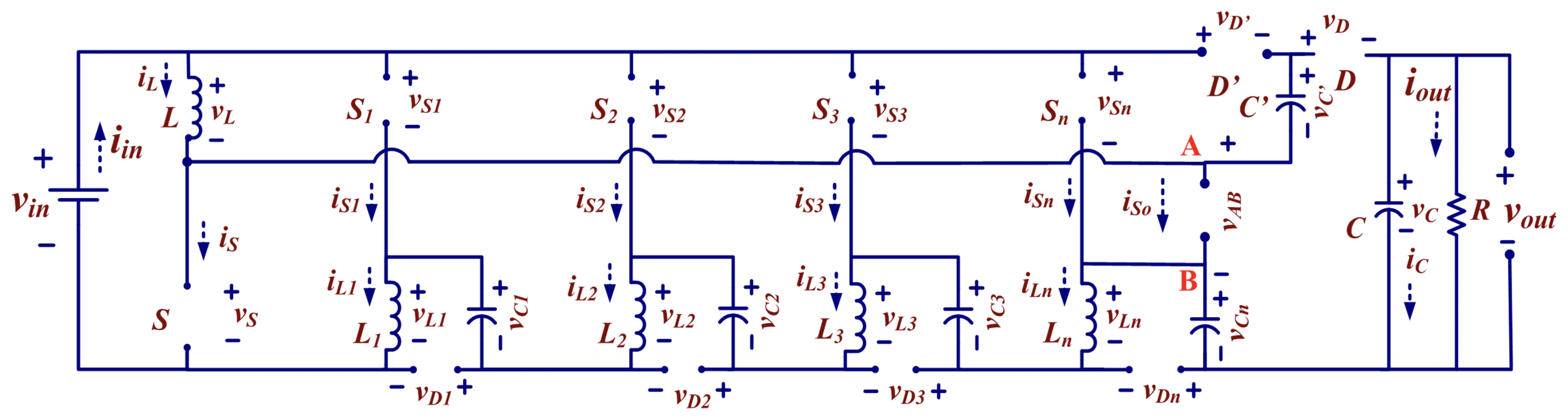
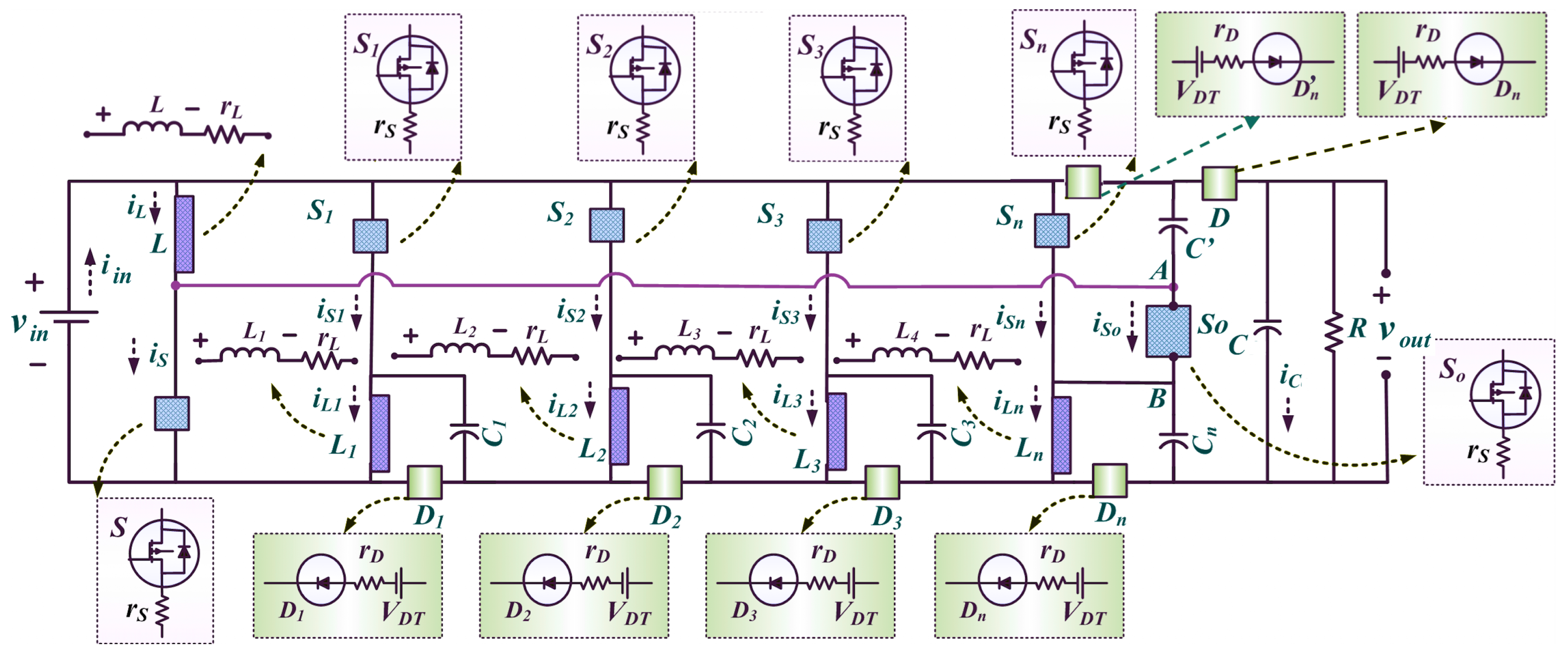
2. Multi-Leg (ML) Converter
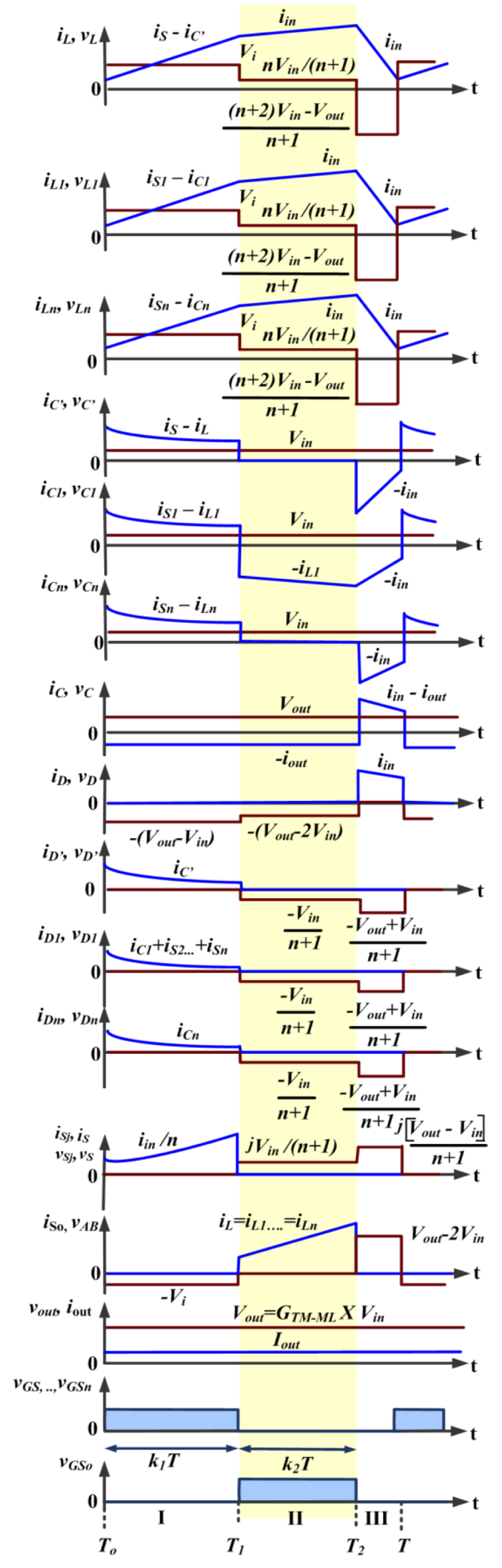
3. Continuous Conduction Mode
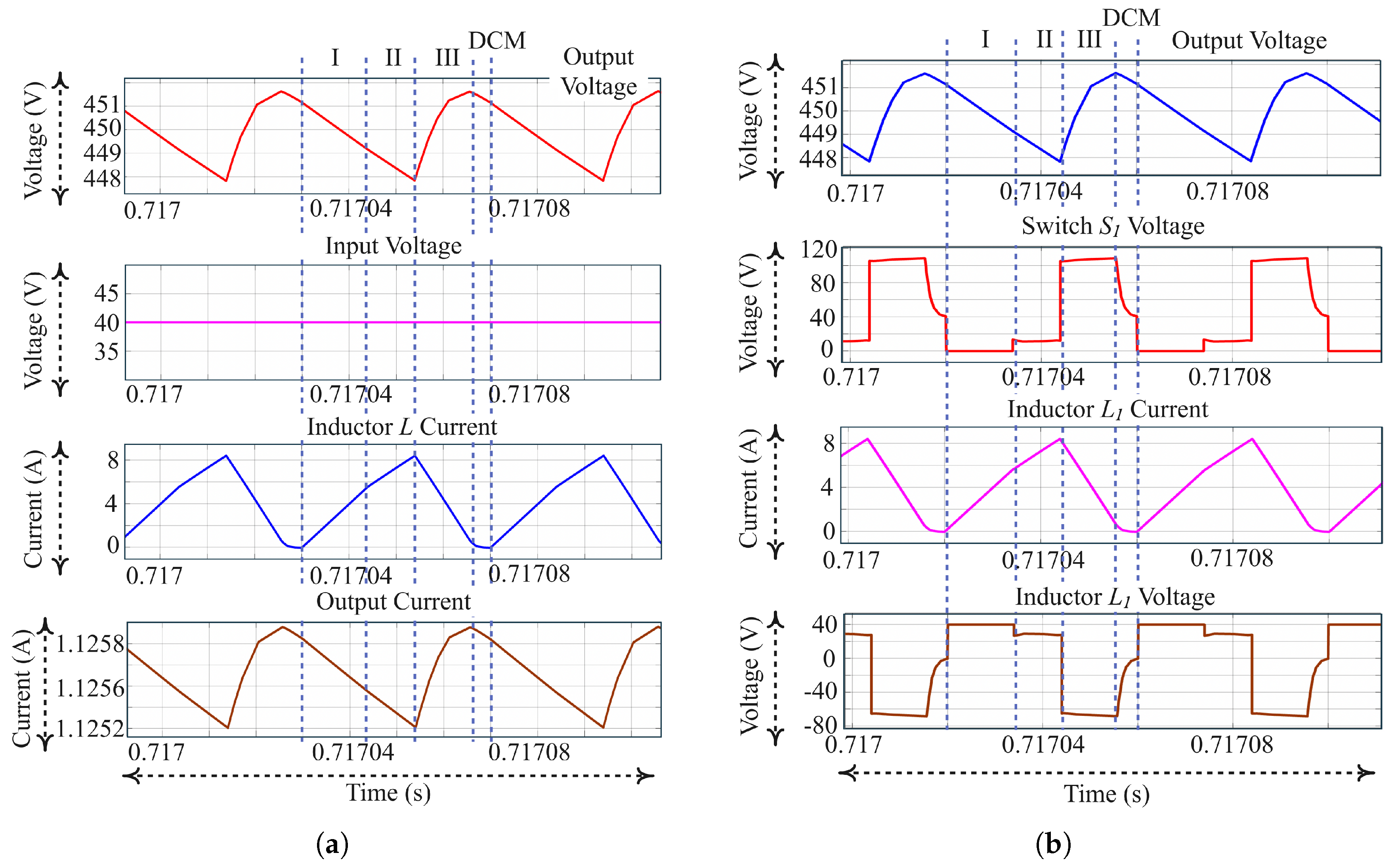
3.1. MODE-I ( to )
3.2. MODE-II ( to )
3.3. MODE-III ( to )
4. Discontinuous Conduction Mode
4.1. MODE-I ( to )
4.2. MODE-II ( to )
4.3. MODE-III ( to )
4.4. MODE-IV ( to )
5. Non-Ideal Model and Efficiency Analysis of ML Converter
5.1. MODE-I []
5.2. MODE-II []
5.3. State-III []
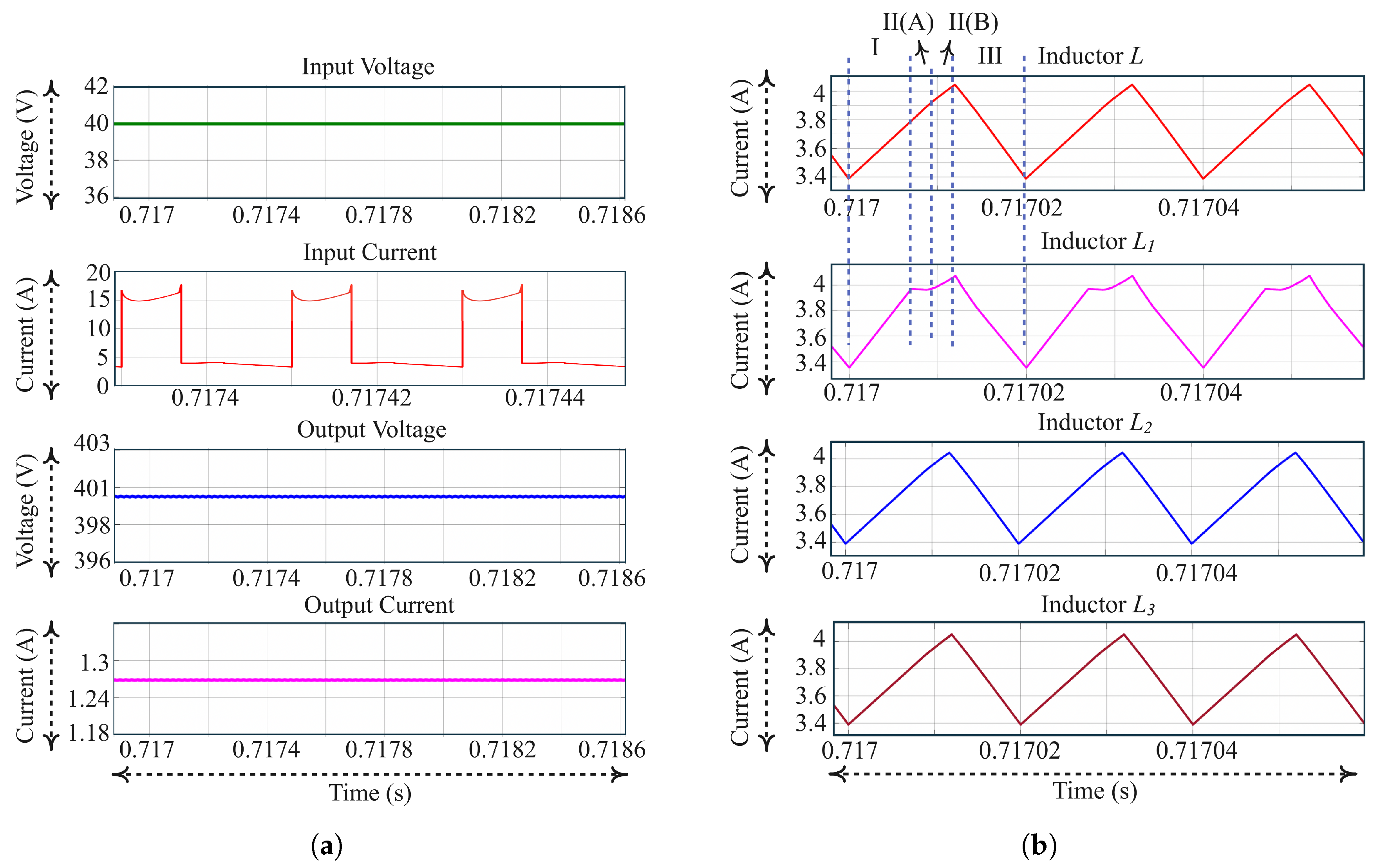
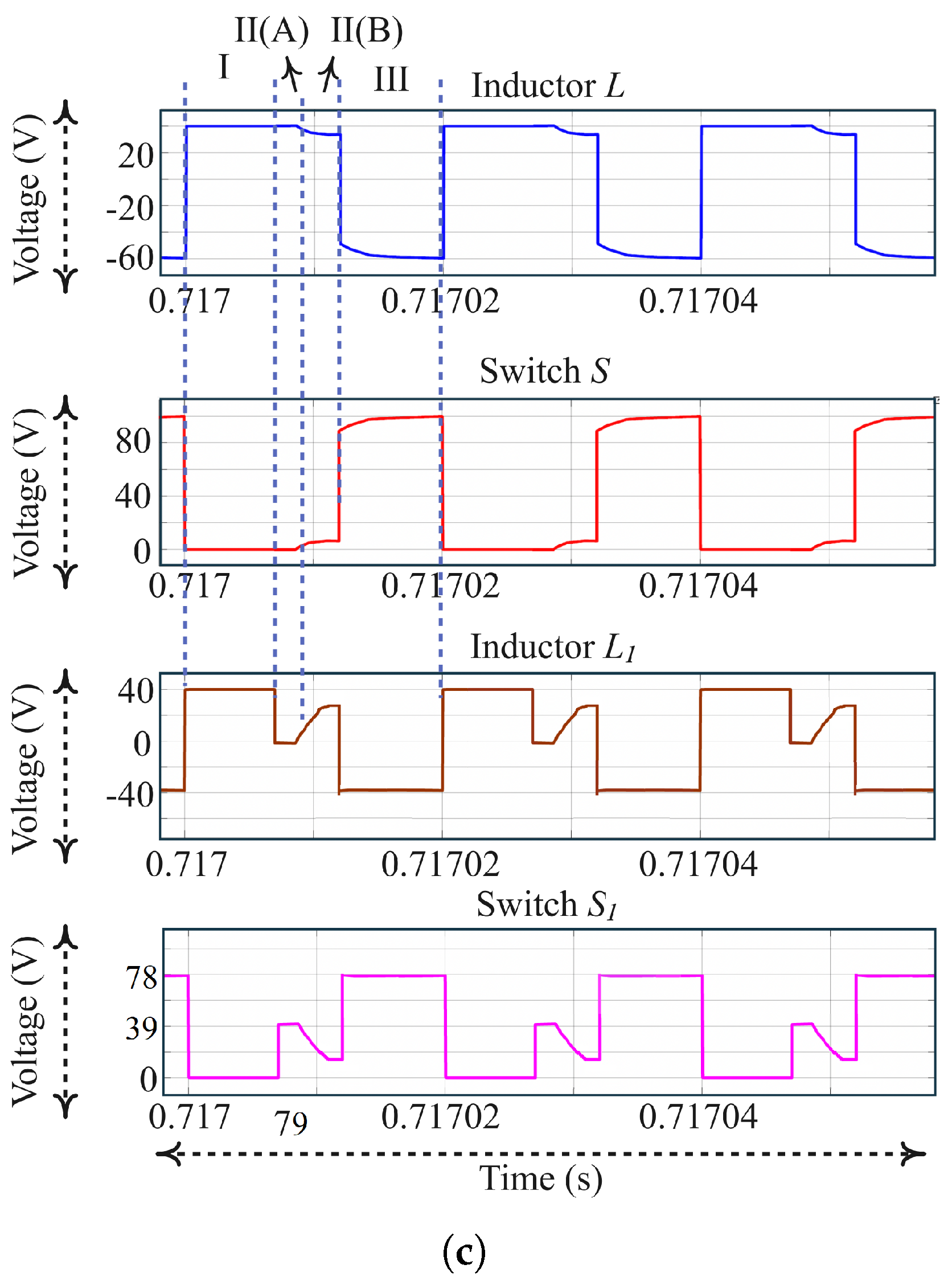
6. ML Converter with the Discrepancy in Inductors
6.1. MODE-I []
6.2. MODE-II(A) []
6.3. MODE-II(B) []
6.4. MODE-III []
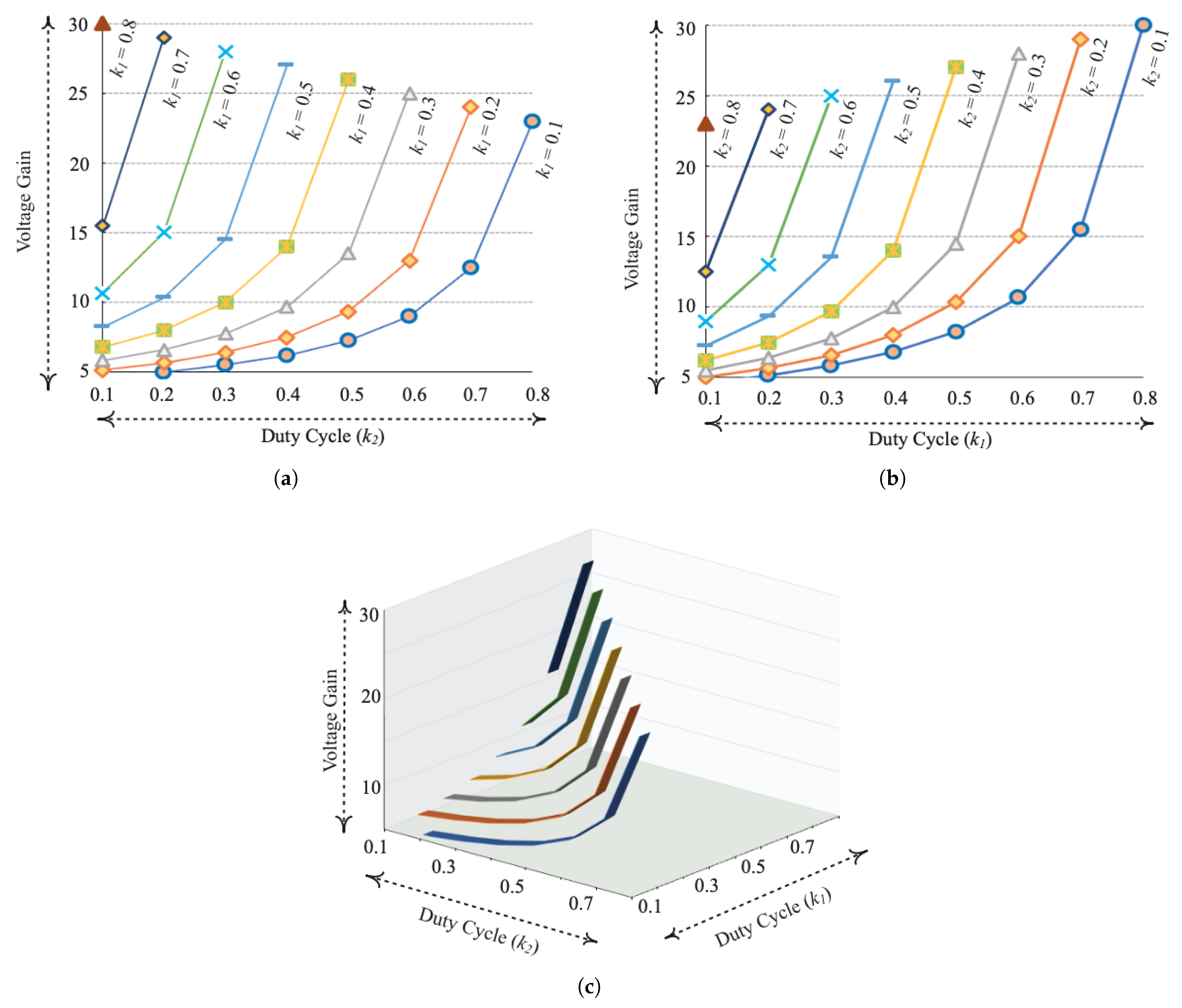
7. Design of ML Converter
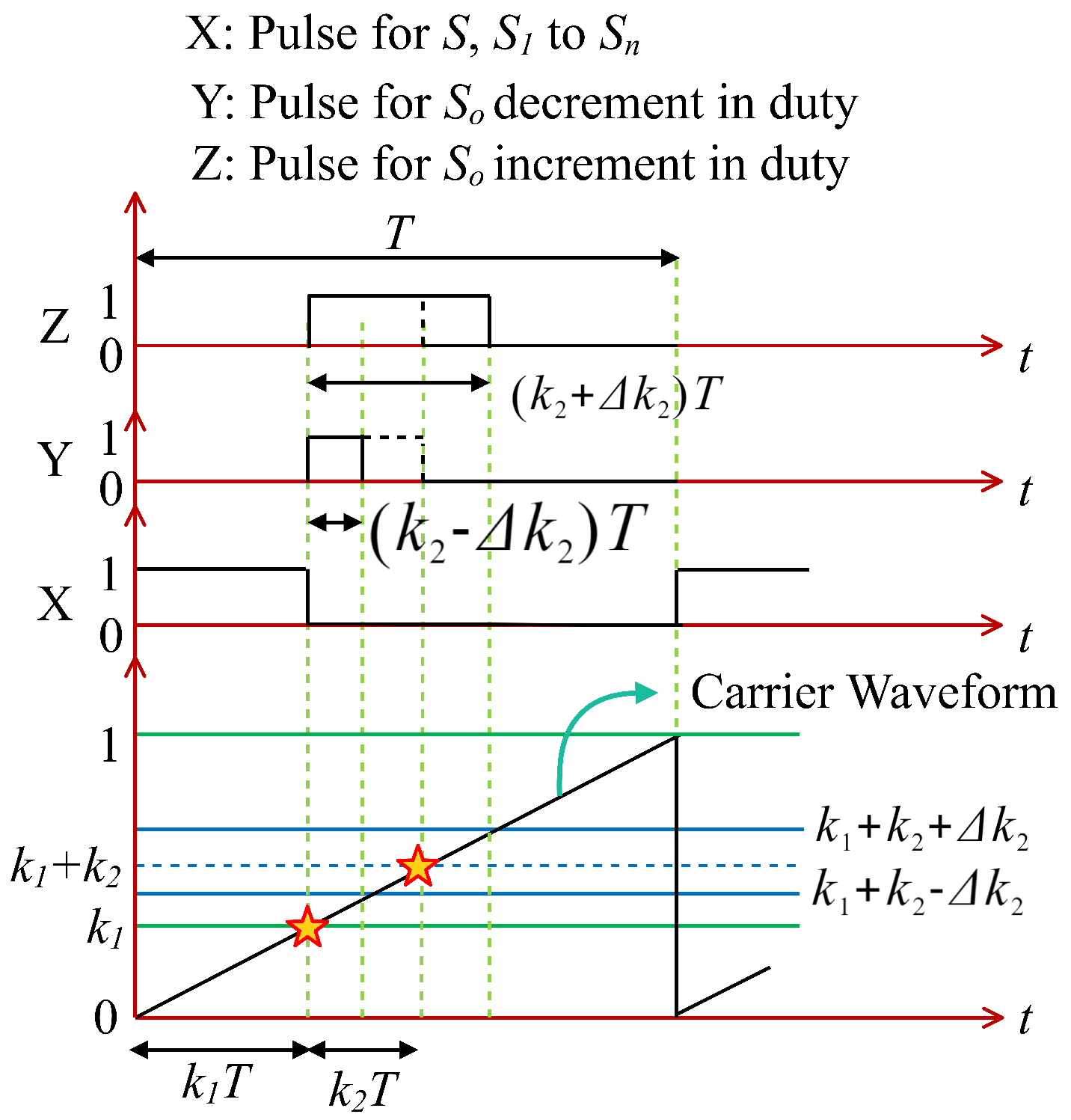
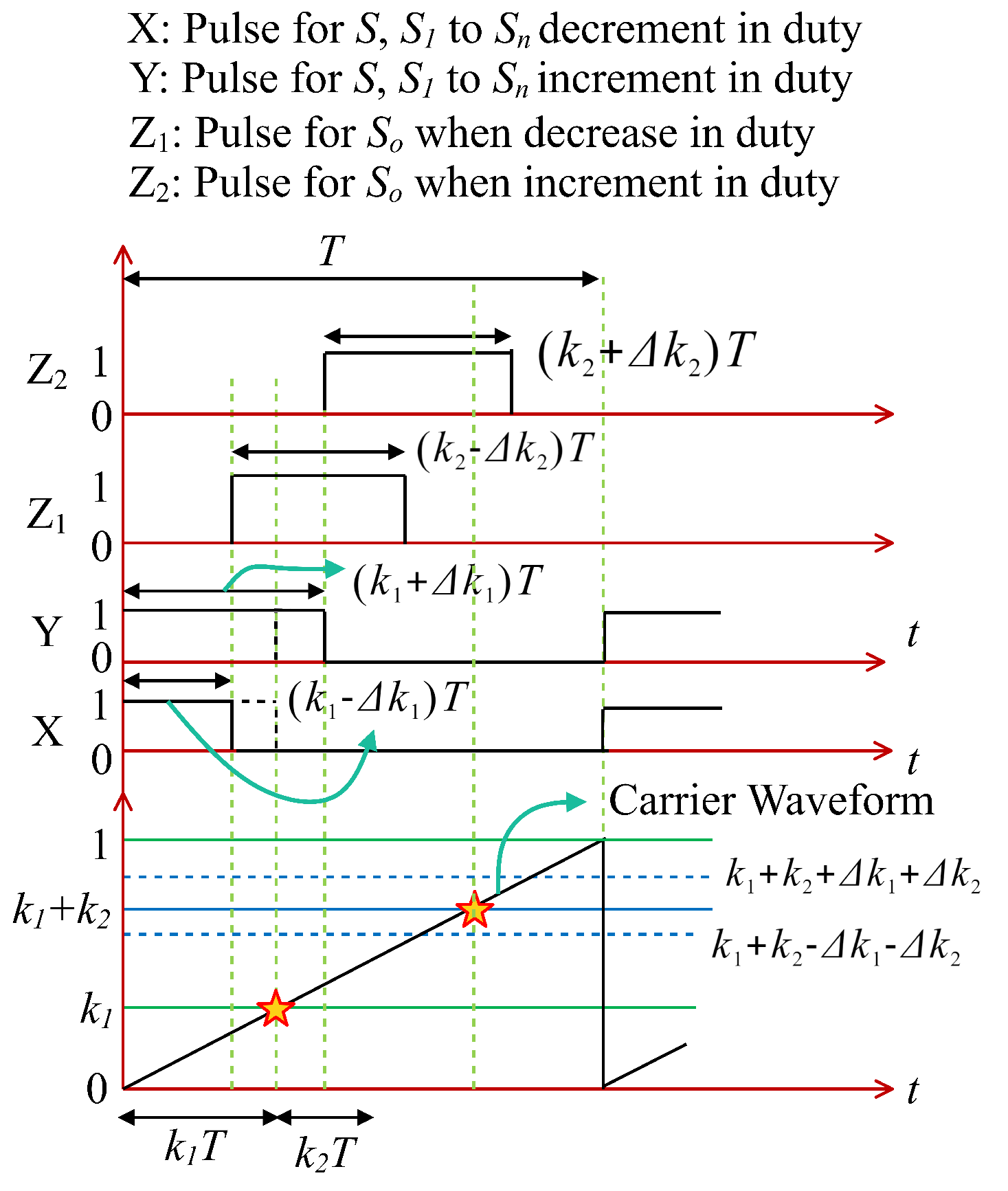
8. Possible Control Schemes for the ML Converter
- Scheme-1: Fixed duty ratio and a adjust duty ratio ,
- Scheme-2: Fixed duty ratio and a adjust duty ratio ,
- Scheme-3: Adjust both duty ratios and .
8.1. Control Scheme-1
8.2. Control Scheme-2
8.3. Control Scheme-3
9. Comparison of ML and Recent Converters
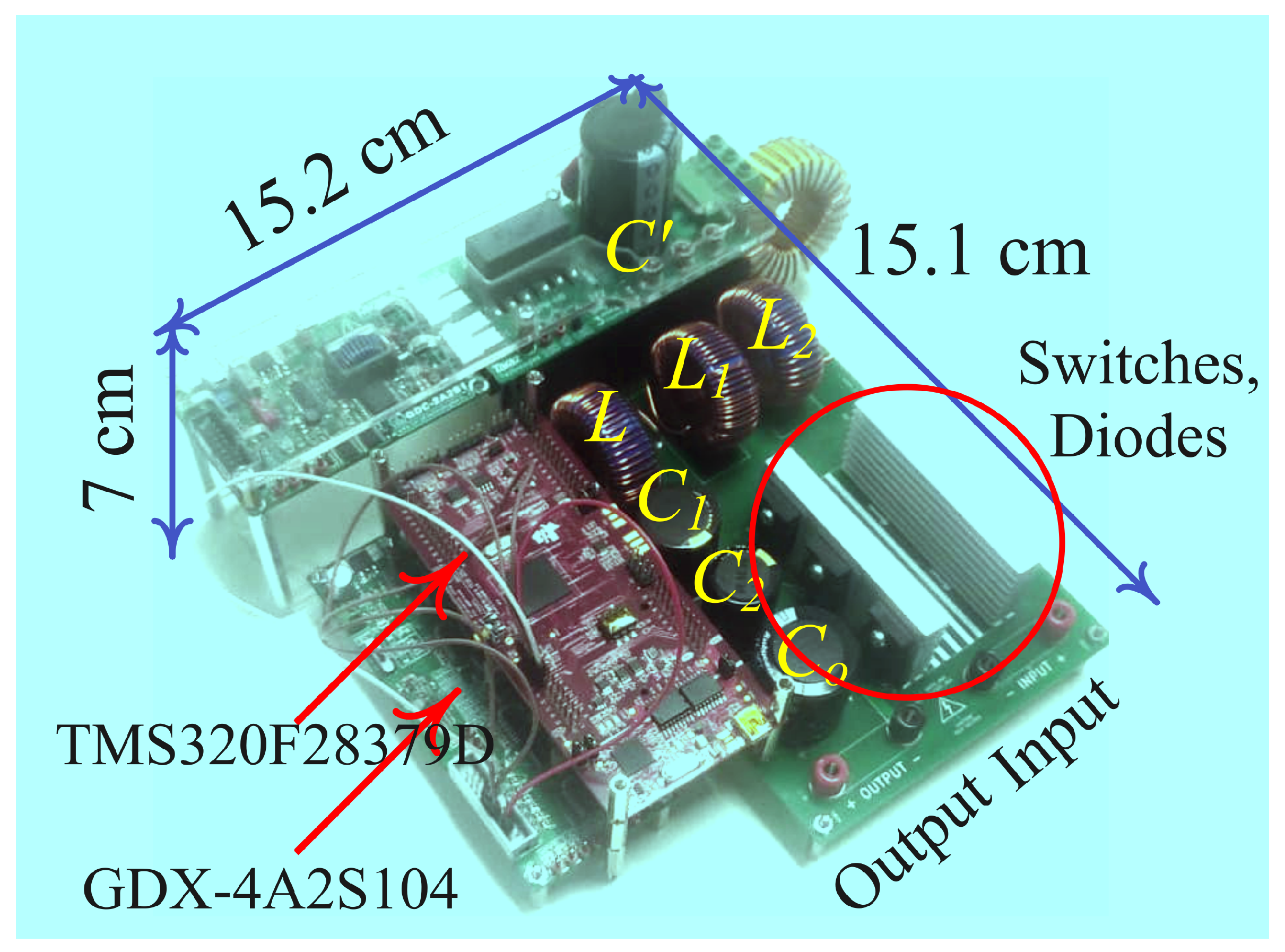
10. Validation of the ML Converter
10.1. Equal Case of Inductances: Experimental Findings
10.2. Discontinuous Conduction Mode Validation-Simulation Results
10.3. Unequal Case of Inductances-Simulation Results
11. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Qazi, A.; Hussain, F.; Rahim, N.A.; Hardaker, G.; Alghazzawi, D.; Shaban, K.; Haruna, K. Towards sustainable energy: A systematic review of renewable energy sources, technologies, and public opinions. IEEE Access 2019, 7, 63837–63851. [Google Scholar] [CrossRef]
- de Aguiar, C.R.; Fuzato, G.H.F.; Machado, R.Q.; Guerrero, J.M. An adaptive power sharing control for management of DC microgrids powered by fuel cell and storage system. IEEE Trans. Ind. Electron. 2019, 67, 3726–3735. [Google Scholar] [CrossRef]
- Hassan, W.; Lu, Y.; Farhangi, M.; Lu, D.D.C.; Xiao, W. Design, analysis and experimental verification of a high voltage gain and high-efficiency DC–DC converter for photovoltaic applications. IET Renew. Power Gener. 2020, 14, 1699–1709. [Google Scholar] [CrossRef]
- Xue, F.; Yu, R.; Huang, A.Q. A 98.3% efficient GaN isolated bidirectional DC–DC converter for DC microgrid energy storage system applications. IEEE Trans. Ind. Electron. 2017, 64, 9094–9103. [Google Scholar] [CrossRef]
- Afkar, M.; Gavagsaz-Ghoachani, R.; Phattanasak, M.; Martin, J.P.; Pierfederici, S. Proposed system based on a three-level boost converter to mitigate voltage imbalance in photovoltaic power generation systems. IEEE Trans. Power Electron. 2021, 37, 2264–2282. [Google Scholar] [CrossRef]
- Srinivasan, S.; Tiwari, R.; Krishnamoorthy, M.; Lalitha, M.P.; Raj, K.K. Neural network based MPPT control with reconfigured quadratic boost converter for fuel cell application. Int. J. Hydrog. Energy 2021, 46, 6709–6719. [Google Scholar] [CrossRef]
- Khan, S.; Mahmood, A.; Tariq, M.; Zaid, M.; Khan, I.; Rahman, S. Improved dual switch non-isolated high gain boost converter for DC microgrid application. In Proceedings of the 2021 IEEE Texas Power and Energy Conference (TPEC), College Station, TX, USA, 2–5 February 2021; pp. 1–6. [Google Scholar]
- Ramanathan, G.G.; Urasaki, N. Non-Isolated Interleaved Hybrid Boost Converter for Renewable Energy Applications. Energies 2022, 15, 610. [Google Scholar] [CrossRef]
- Salim, K.; Asif, M.; Ali, F.; Armghan, A.; Ullah, N.; Mohammad, A.S.; Al Ahmadi, A.A. Low-stress and optimum design of boost converter for renewable energy systems. Micromachines 2022, 13, 1085. [Google Scholar] [CrossRef] [PubMed]
- Zeng, Y.; Li, H.; Wang, W.; Zhang, B.; Zheng, T.Q. Cost-effective clamping capacitor boost converter with high voltage gain. IET Power Electron. 2020, 13, 1775–1786. [Google Scholar] [CrossRef]
- Yari, K.; Shahalami, S.H.; Mojallali, H. A novel nonisolated buck–boost converter with continuous input current and semiquadratic voltage gain. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 6124–6138. [Google Scholar] [CrossRef]
- Ahmed, H.Y.; Abdel-Rahim, O.; Ali, Z.M. New High-Gain Transformerless DC/DC Boost Converter System. Electronics 2022, 11, 734. [Google Scholar] [CrossRef]
- Jou, H.L.; Huang, J.J.; Wu, J.C.; Wu, K.D. Novel isolated multilevel DC–DC power converter. IEEE Trans. Power Electron. 2015, 31, 2690–2694. [Google Scholar] [CrossRef]
- Eskandarpour Azizkandi, M.; Sedaghati, F.; Shayeghi, H.; Blaabjerg, F. Two-and three-winding coupled-inductor-based high step-up DC–DC converters for sustainable energy applications. IET Power Electron. 2020, 13, 144–156. [Google Scholar] [CrossRef]
- Meng, T.; Yu, S.; Ben, H.; Wei, G. A family of multilevel passive clamp circuits with coupled inductor suitable for single-phase isolated full-bridge boost PFC converter. IEEE Trans. Power Electron. 2014, 29, 4348–4356. [Google Scholar] [CrossRef]
- Ragonese, E.; Spina, N.; Parisi, A.; Palmisano, G. An experimental comparison of galvanically isolated DC-DC converters: Isolation technology and integration approach. Electronics 2021, 10, 1186. [Google Scholar] [CrossRef]
- Zhao, Q.; Lee, F. High-efficiency, high step-up DC-DC converters. IEEE Trans. Power Electron. 2003, 18, 65–73. [Google Scholar] [CrossRef]
- Wu, T.; Lai, Y.; Hung, J.; Chen, Y. Boost converter with coupled inductors and buck–boost type of active clamp. IEEE Trans. Ind. Electron. 2008, 55, 154–162. [Google Scholar] [CrossRef]
- Wai, R.; Duan, R. High step-up converter with coupled-inductor. IEEE Trans. Power Electron. 2005, 20, 1025–1035. [Google Scholar] [CrossRef]
- Forouzesh, M.; Siwakoti, Y.; Gorji, S.; Blaabjerg, F.; Lehman, B. Step-up DC–DC converters: A comprehensive review of voltage-boosting techniques, topologies, and applications. IEEE Trans. Power Electron. 2017, 32, 9143–9178. [Google Scholar] [CrossRef]
- Guo, Z.; Li, H.; Liu, C.; Zhao, Y.; Su, W. Stability-improvement method of cascaded DC-DC converters with additional voltage-error mutual feedback control. Chin. J. Electr. Eng. 2019, 5, 63–71. [Google Scholar] [CrossRef]
- Mukherjee, N.; Strickland, D. Control of cascaded DC–DC converter-based hybrid battery energy storage systems—Part I: Stability issue. IEEE Trans. Ind. Electron. 2015, 63, 2340–2349. [Google Scholar] [CrossRef]
- Rosas-Caro, J.C.; Ramirez, J.M.; Peng, F.Z.; Valderrabano, A. A DC–DC multilevel boost converter. IET Power Electron. 2010, 3, 129–137. [Google Scholar] [CrossRef]
- Rajaei, A.; Shahparasti, M.; Nabinejad, A.; Niazi, Y.; Guerrero, J.M. Switching Strategy Development, Dynamic Model, and Small Signal Analysis of Current-Fed Cockcroft-Walton Voltage Multiplier. IEEE Open J. Power Electron. 2021, 2, 591–602. [Google Scholar] [CrossRef]
- Lei, Y.; Pilawa-Podgurski, R.C. Soft-charging operation of switched-capacitor DC-DC converters with an inductive load. In Proceedings of the 2014 IEEE Applied Power Electronics Conference and Exposition-APEC 2014, Fort Worth, TX, USA, 16–20 March 2014; pp. 2112–2119. [Google Scholar]
- Farswan, R.S.; Datta, A.; Kamble, G.; Fernandes, B. A low leakage transformer-less 3-level DC-DC boost converter for transformer-less PV inverters. In Proceedings of the 2015 17th European Conference on Power Electronics and Applications (EPE’15 ECCE-Europe), Geneva, Switzerland, 8–10 September 2015; pp. 1–10. [Google Scholar]
- Mayo-Maldonado, J.C.; Valdez-Resendiz, J.E.; Sanchez, V.M.; Rosas-Caro, J.C.; Claudio-Sanchez, A.; Puc, F.C. A novel PEMFC power conditioning system based on the interleaved high gain boost converter. Int. J. Hydrog. Energy 2019, 44, 12508–12514. [Google Scholar] [CrossRef]
- Baddipadiga, B.P.; Ferdowsi, M. A high-voltage-gain dc-dc converter based on modified dickson charge pump voltage multiplier. IEEE Trans. Power Electron. 2016, 32, 7707–7715. [Google Scholar] [CrossRef]
- Tewari, N.; Thazhathu, S.V. Family of modular, extendable and high gain dc–dc converter with switched inductor and switched capacitor cells. IET Power Electron. 2020, 13, 1321–1331. [Google Scholar] [CrossRef]
- Sadaf, S.; Bhaskar, M.S.; Meraj, M.; Iqbal, A.; Al-Emadi, N. A novel modified switched inductor boost converter with reduced switch voltage stress. IEEE Trans. Ind. Electron. 2020, 68, 1275–1289. [Google Scholar] [CrossRef]
- Yang, L.S.; Liang, T.J.; Chen, J.F. Transformerless DC–DC converters with high step-up voltage gain. IEEE Trans. Ind. Electron. 2009, 56, 3144–3152. [Google Scholar] [CrossRef]
- Bhaskar, M.S.; Alammari, R.; Meraj, M.; Padmanaban, S.; Iqbal, A. A new triple-switch-triple-mode high step-up converter with wide range of duty cycle for DC microgrid applications. IEEE Trans. Ind. Appl. 2019, 55, 7425–7441. [Google Scholar] [CrossRef]
- Lakshmi, M.; Hemamalini, S. Nonisolated high gain DC–DC converter for DC microgrids. IEEE Trans. Ind. Electron. 2017, 65, 1205–1212. [Google Scholar] [CrossRef]
- Maheri, H.M.; Babaei, E.; Sabahi, M.; Hosseini, S.H. High step-up DC–DC converter with minimum output voltage ripple. IEEE Trans. Ind. Electron. 2017, 64, 3568–3575. [Google Scholar] [CrossRef]
- Babaei, E.; Maheri, H.M.; Sabahi, M.; Hosseini, S.H. Extendable nonisolated high gain DC–DC converter based on active–passive inductor cells. IEEE Trans. Ind. Electron. 2018, 65, 9478–9487. [Google Scholar] [CrossRef]
- Hauke, B. Basic Calculation of a Boost Converter’s Power Stage; Application Report November; Texas Instruments: Dallas, TX, USA, 2009; pp. 1–9. [Google Scholar]









| Para. | CB | [31] | [33] | [34] | [35] | ML Converter | ||
|---|---|---|---|---|---|---|---|---|
| I | II | III | ||||||
| 1 | 2 | 2 | 3 | 3 | n + 1 | n + 2 | n + 2 | |
| 1 | 2 | 2 | 2 | 2 | n + 2 | + 4 | n + 1 | |
| 1 | 1 | 2 | 3 | 1 | 1 | 1 | n + 1 | |
| 1 | 1 | 2 | 3 | 2 | + 1 | + 6 | n + 2 | |
| 1 | ||||||||
| - | - | |||||||
| TDC: | No | No | No | No | Yes | No | No | Yes |
| Parameters | Value /Model |
|---|---|
| 32–40 V | |
| 400 V | |
| n | 2 |
| f | 50 kHz |
| L, , | 400 H/10 A |
| , , | 100 F/50 V |
| C | 220 F/450 V |
| S, , | STW46NF30 |
| IRFP360PBF | |
| , , | STTH3002W |
| D | STTH6004W |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sagar Bhaskar, M.; Almakhles, D. New Multi-Leg Converter for DC Microgrid with Two Duty Cycles. Processes 2022, 10, 2520. https://doi.org/10.3390/pr10122520
Sagar Bhaskar M, Almakhles D. New Multi-Leg Converter for DC Microgrid with Two Duty Cycles. Processes. 2022; 10(12):2520. https://doi.org/10.3390/pr10122520
Chicago/Turabian StyleSagar Bhaskar, Mahajan, and Dhafer Almakhles. 2022. "New Multi-Leg Converter for DC Microgrid with Two Duty Cycles" Processes 10, no. 12: 2520. https://doi.org/10.3390/pr10122520
APA StyleSagar Bhaskar, M., & Almakhles, D. (2022). New Multi-Leg Converter for DC Microgrid with Two Duty Cycles. Processes, 10(12), 2520. https://doi.org/10.3390/pr10122520







