Effect of Dynamic Biaxial Loading of Car Seats
Abstract
1. Introduction
2. Materials and Methods
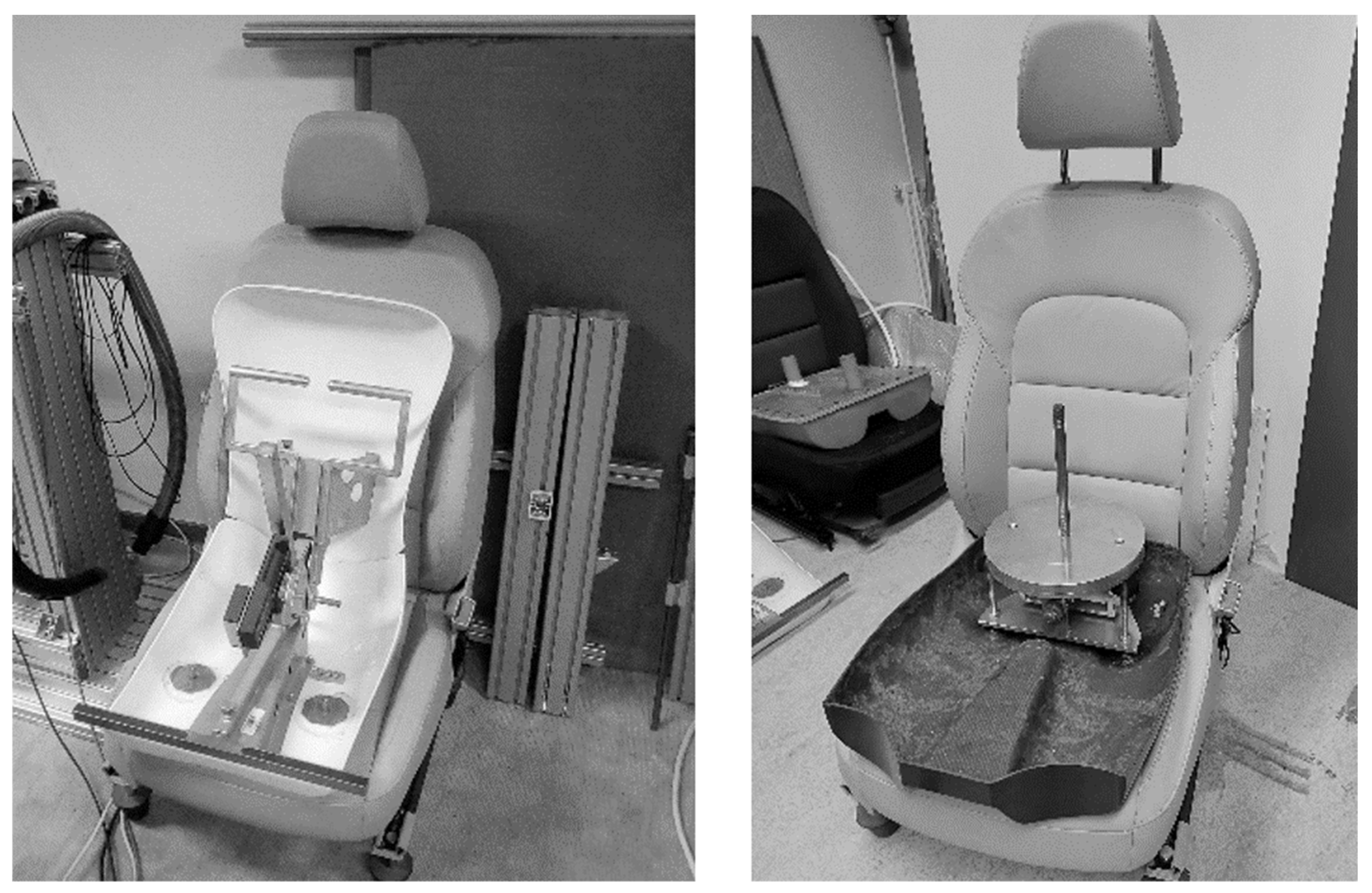
2.1. Testing Device
2.2. Testing Loading
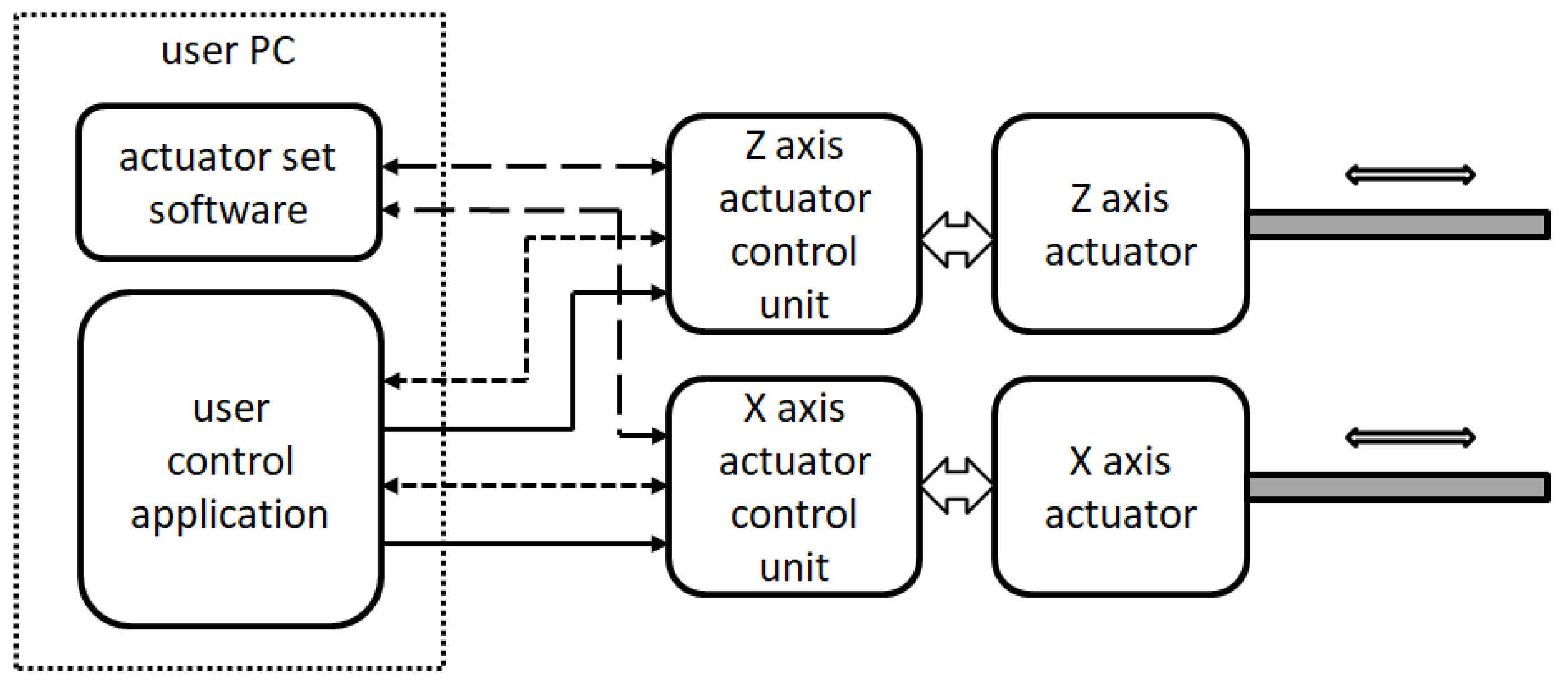
2.3. Principles of Control
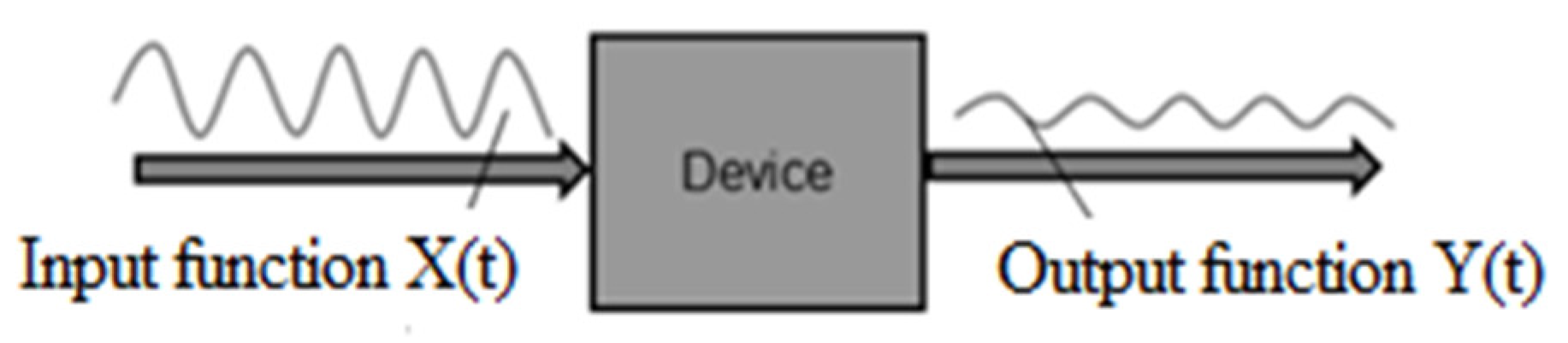
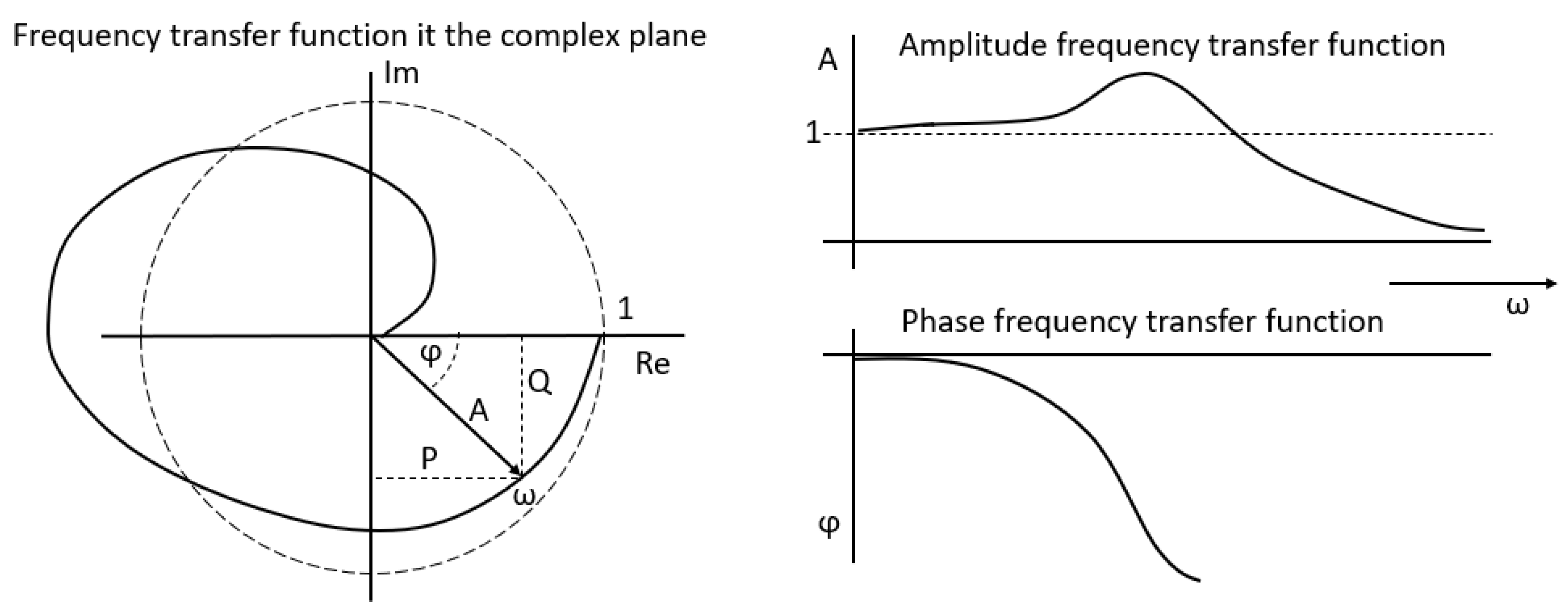
2.4. The Theoretical Basis of the Transfer Function Measurement
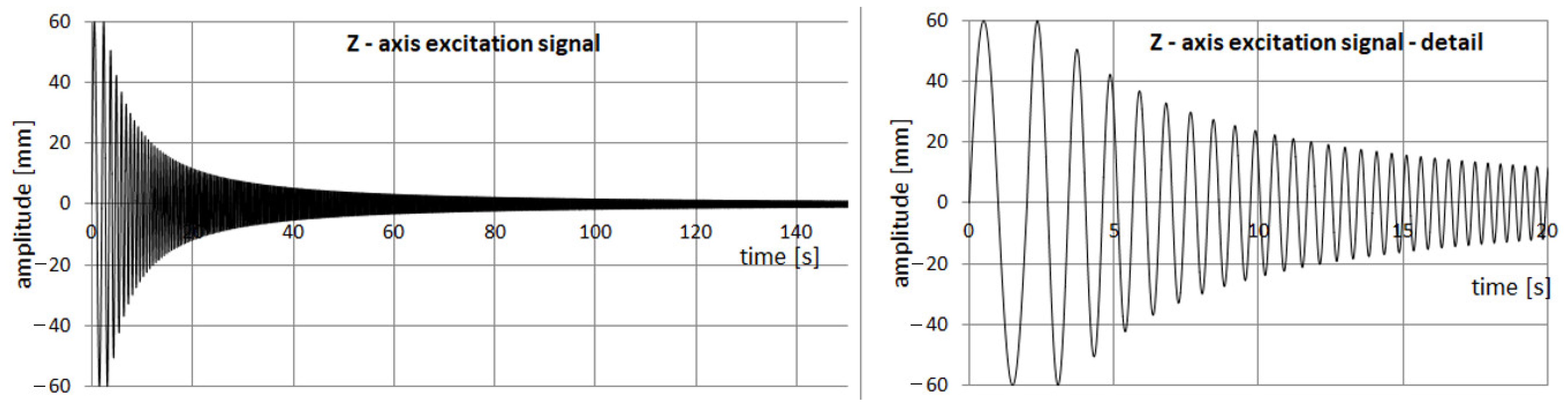
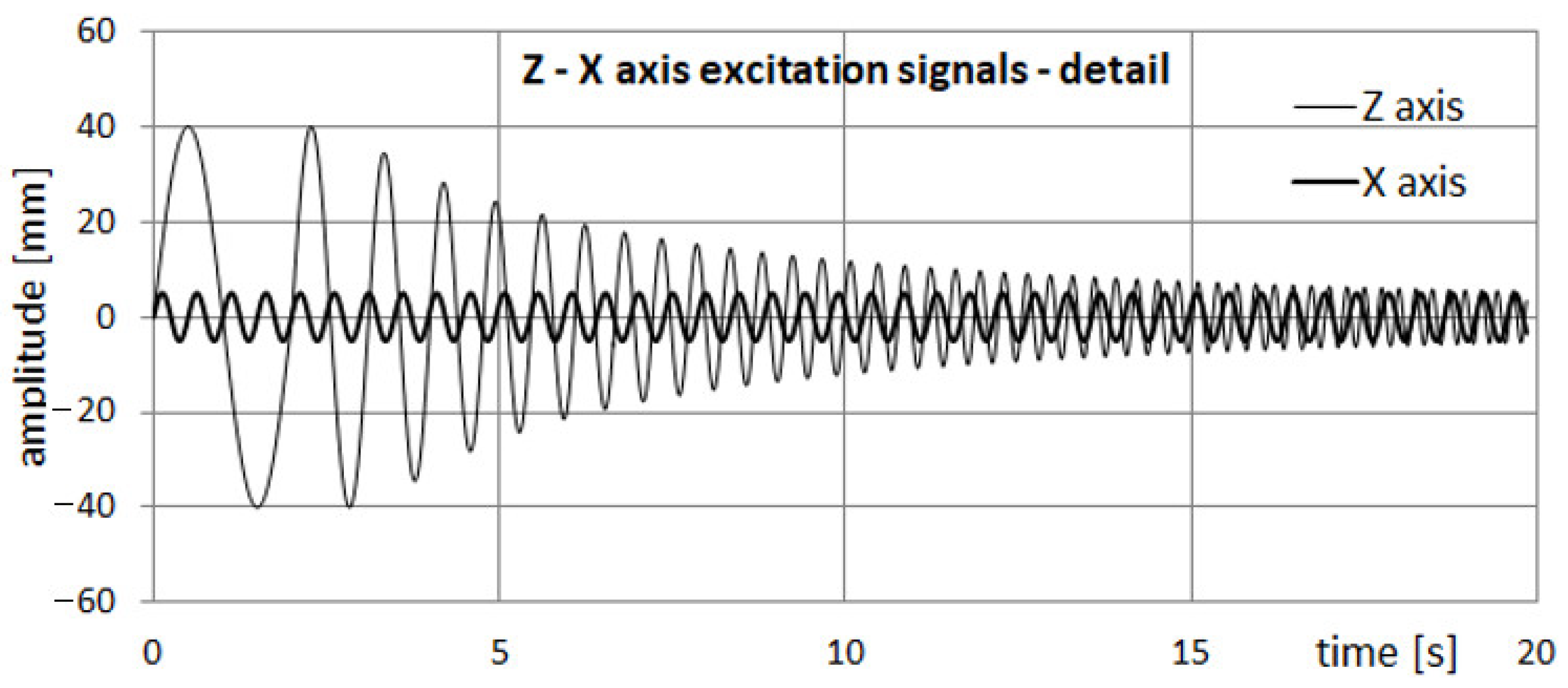
2.5. Test Signals and Measurement
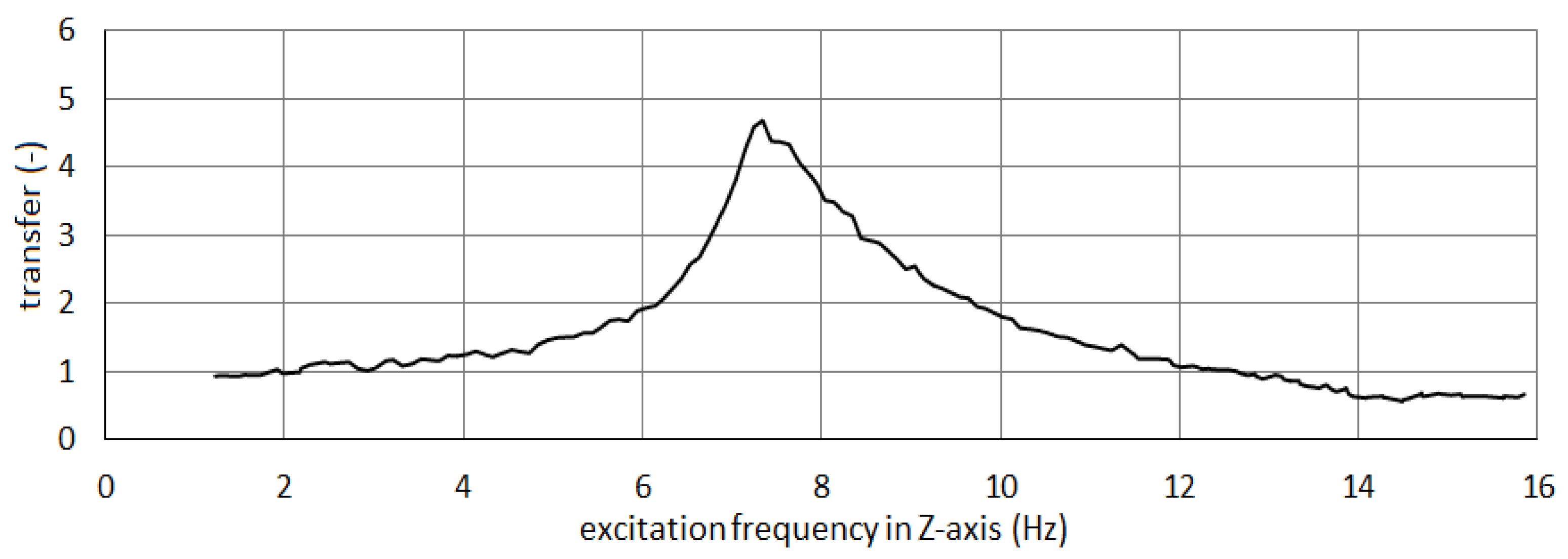
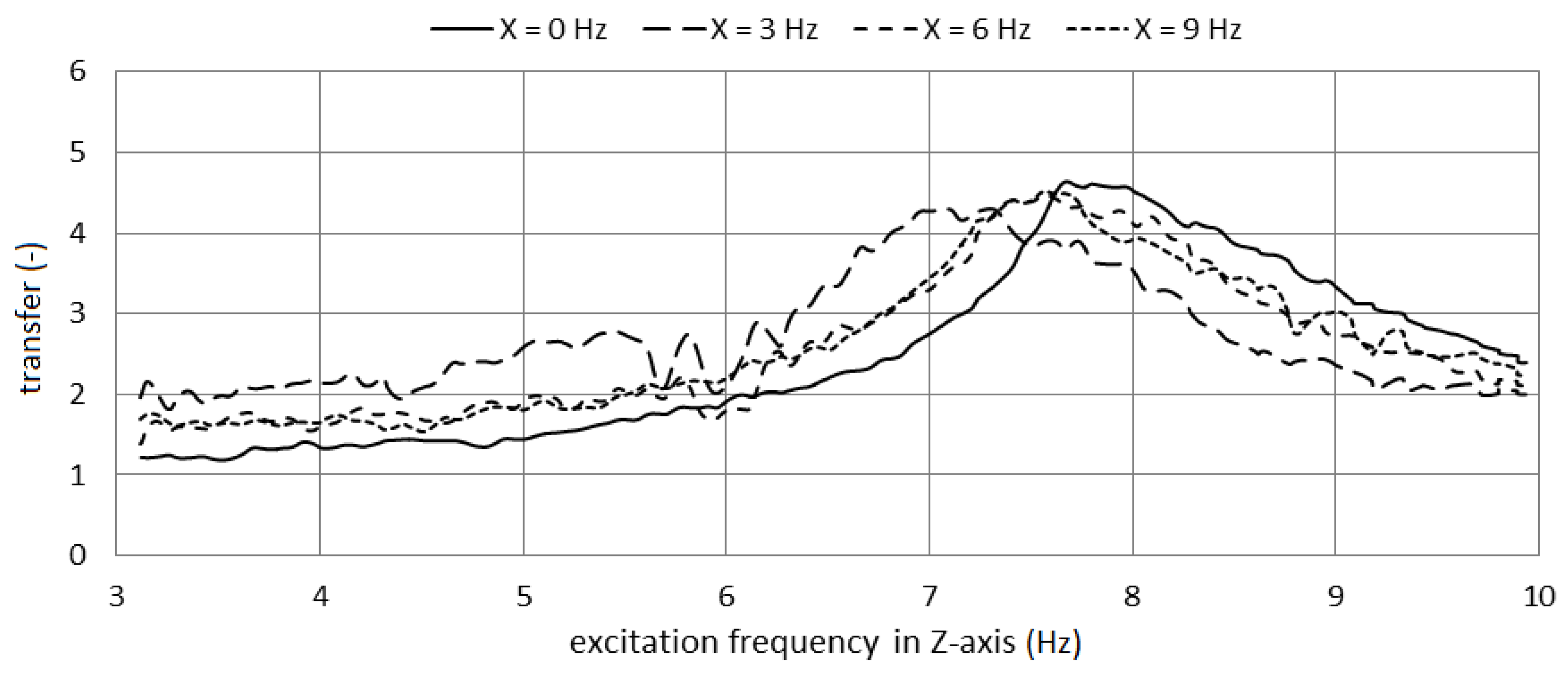
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- ASTM D3574-11; Standard Test Methods for Flexible Cellular Materials—Slab, Bonded, and Moulded Urethane Fo-Ams. ASTM International (ASTM): West Conshohocken, PA, USA, 2017. Available online: https://www.astm.org/d3574-17.html (accessed on 2 October 2022).
- JASO B407-87; Test Code of Seating Comfort for Automobile Seats. Society of Automotive Engineers of Japan (JSAE): Tokyo, Japan, 1987. Available online: https://standards.globalspec.com/std/741387/JASO%20B407 (accessed on 2 October 2022).
- DIN EN ISO 3385; Flexible Cellular Polymeric Materials—Determinati-on of Fatigue by Constant-Load Pounding. Deutsches Institut fur Normung E.V. (DIN): Berlin, Germany, 2014. Available online: https://www.din.de/en/getting-involved/standards-committees/nmp/publications/wdc-beuth:din21:200767482?destinationLanguage=&sourceLanguage= (accessed on 3 October 2022).
- Martonka, R.; Fliegel, V. Analysis and Construction of Measurement Device. In Proceedings of the EAN 2016—54th International Conference on Experimental Stress Analysis, Srni, Czech Republic, 30 May–2 June 2016; Czech Society for Mechanics: Srni, Czech Republic, 2016; pp. 242–248. Available online: http://toc.proceedings.com/31161webtoc.pdf (accessed on 6 October 2022).
- Lepsik, P.; Fliegel, V.; Lufinka, A. Innovation of Car Seat Testing Device with Three Axes of Loading. AD ALTA J. Interdiscip. Res. 2021, 11, 331–335. Available online: http://www.magnanimitas.cz/ADALTA/1102/papers/J_lepsik.pdf (accessed on 18 October 2022).
- Zhang, X. Measurement and Modelling of Seating Dynamics to Predict Seat Transmissibility. Ph.D. Thesis, University of Southampton, Engineering and the Environment, Southampton, UK, 2014. Available online: http://eprints.soton.ac.uk/id/eprint/370542 (accessed on 15 October 2022).
- Abdul Jalil, N.A.; Griffin, M.J. Fore-and-Aft Transmissibility of Backrests: Variation with Height above the Seat Surface and Non-Linearity. J. Sound Vib. 2007, 299, 109–122. [Google Scholar] [CrossRef]
- Han, S.H.; Lu, Z.H.; Liu, Y.J. Study on Multi-Axial Mechanical Properties of a Polyurethane Foam and Experimental Verification. AMR 2011, 311–313, 301–308. [Google Scholar] [CrossRef]
- Daniel, I.M.; Fenner, J.S.; Werner, B.T.; Cho, J.-M. Characterization and Modeling of Polymeric Foam Under Multi-Axial Static and Dynamic Loading. In Experimental and Applied Mechanics, Volume 4; Conference Proceedings of the Society for Experimental Mechanics Series; Zhu, Y., Zehnder, A.T., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 123–134. [Google Scholar] [CrossRef]
- Yang, L.; Li, X.; Zi, F.; Yang, S.; Zhang, Z.; Qu, J.; Dong, Y.; Wu, L. Dynamic Response of Graded PVC Foam Sandwich Panel under Air Blast Loads. Mech. Adv. Mater. Struct. 2021, 29, 3694–3708. [Google Scholar] [CrossRef]
- Toward, M.G.R.; Griffin, M.J. The Transmission of Vertical Vibration through Seats: Influence of the Characteristics of the Human Body. J. Sound Vib. 2011, 330, 6526–6543. [Google Scholar] [CrossRef]
- Werner, B.T.; Daniel, I.M. Characterization and Modeling of Polymeric Matrix under Multi-Axial Static and Dynamic Loading. Compos. Sci. Technol. 2014, 102, 113–119. [Google Scholar] [CrossRef]
- Mosleh, Y.; Vanden Bosche, K.; Depreitere, B.; Vander Sloten, J.; Verpoest, I.; Ivens, J. Effect of Polymer Foam Anisotropy on Energy Absorption during Combined Shear-Compression Loading. J. Cell. Plast. 2018, 54, 597–613. [Google Scholar] [CrossRef]
- Kia, K.; Johnson, P.W.; Kim, J.H. The Effects of Different Seat Suspension Types on Occupants’ Physiologic Responses and Task Performance: Implications for Autonomous and Conventional Vehicles. Appl. Ergon. 2021, 93, 103380. [Google Scholar] [CrossRef] [PubMed]
- Mondal, P.; Arunachalam, S. Vibration Study in Human-Car Seat System: Overview and a Novel Simulation Technique. J. Mater. Sci. Eng. 2018, 7, 421. [Google Scholar] [CrossRef]
- Fliegel, V.; Martonka, R. Characteristics of PU Foam at Long Term Static and Dynamic Loading. AMM 2015, 732, 149–152. [Google Scholar] [CrossRef]
- Martonka, R.; Fliegel, V. Live Tests of Car Seats. Vibroeng. Procedia 2016, 7, 138–141. Available online: https://www.extrica.com/article/17472 (accessed on 8 October 2022).
- Zhang, X.; Qiu, Y.; Griffin, M.J. Developing a Simplified Finite Element Model of a Car Seat with Occupant for Predicting Vibration Transmissibility in the Vertical Direction. Ergonomics 2015, 58, 1220–1231. [Google Scholar] [CrossRef]
- Rahmatalla, S.; DeShaw, J. Effective Seat-to-Head Transmissibility in Whole-Body Vibration: Effects of Posture and Arm Position. J. Sound Vib. 2011, 330, 6277–6286. [Google Scholar] [CrossRef]
- Van Niekerk, J.L.; Pielemeier, W.J.; Greenberg, J.A. The Use of Seat Effective Amplitude Transmissibility (SEAT) Values to Predict Dynamic Seat Comfort. J. Sound Vib. 2003, 260, 867–888. [Google Scholar] [CrossRef]
- Martonka, R.; Fliegel, V.; Lufinka, A. Measurement of Mechanical Vibration on Hexapod on Car Seat—Verification of Measurements Whole-Body Human and 3DH Dummy and 2H Dummy, Vibration Assessment. Vib. Assess. Vibroeng. Procedia 2015, 6, 292–295. Available online: https://www.extrica.com/article/16188/pdf (accessed on 9 October 2022).
- Fliegel, V.; Lepšík, P.; Martonka, R. Innovation Measurement Device of Car Seats. In Proceedings of the 7th International Conference on Trends in Agricultural Engineering 2019, Prague, Czech Republic, 17–20 September 2019; Volume 7, pp. 127–132. Available online: https://proceedings.tae-conference.cz/2019/ (accessed on 11 October 2022).
- Liu, Y. A Kind of Multifunctional Car Seat Impact Test Detection Device. CN109540541A, 29 March 2019. Available online: https://patents.google.com/patent/CN109540541A/en (accessed on 14 October 2022).
- Fang, G.; Li, S.; Ren, C.; Wang, Y.; Zhang, Y. Fixing Device for Automobile Seat Test. CN211652086U, 9 October 2020. Available online: https://patents.google.com/patent/CN211652086U/en (accessed on 14 October 2022).
- Feng, J.; Ge, F.; Li, B.; Mo, B.; Zhang, G. Durable Testing Arrangement of Car Seat Headrest Governing System. CN211576561U, 25 September 2019. Available online: https://patents.google.com/patent/CN211576561U/en (accessed on 15 October 2022).
- Feng, X.; Liu, B.; Song, C.; Xia, L.; Zhou, H. Impact Test Device for Automobile Seat Guard Plate. CN210638877U, 29 May 2020. Available online: https://patents.google.com/patent/CN210638877U/en (accessed on 15 October 2022).
- Ge, J.; Sun, W.; Yang, B.; Yu, F. Handheld Automobile Seat Durability Testing Device. CN211347359U, 25 August 2020. Available online: https://patents.google.com/patent/CN211347359U/en (accessed on 16 October 2022).
- Ji, B.; Li, G.; Yang, Y. Multifunctional Fatigue Durability Testing Device for Automobile Seat. CN211824999U, 30 October 2020. Available online: https://patents.google.com/patent/CN211824999U/en (accessed on 16 October 2022).
- Wang, H. Automobile Seat Heightening Durability Testing Device. CN211527833U, 18 September 2020. Available online: https://patents.google.com/patent/CN211527833U/en (accessed on 18 October 2022).
- Zhu, H. Car Seat Testing Arrangement with Regulatory Function. CN210571729U, 19 May 2020. Available online: https://patents.google.com/patent/CN210571729U/en (accessed on 18 October 2022).




| Excitation X (Hz) | Transfer (-) | Transfer Drop (%) | Resonance Frequency in Z (Hz) |
|---|---|---|---|
| 0.0 | 4.7 | 0 | 7.8 |
| 3.0 | 4.1 | 22.8 | 7.1 |
| 6.0 | 4.3 | 8.5 | 7.5 |
| 9.0 | 4.6 | 2.1 | 7.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lepsik, P.; Fliegel, V.; Lufinka, A. Effect of Dynamic Biaxial Loading of Car Seats. Processes 2022, 10, 2483. https://doi.org/10.3390/pr10122483
Lepsik P, Fliegel V, Lufinka A. Effect of Dynamic Biaxial Loading of Car Seats. Processes. 2022; 10(12):2483. https://doi.org/10.3390/pr10122483
Chicago/Turabian StyleLepsik, Petr, Vitezslav Fliegel, and Ales Lufinka. 2022. "Effect of Dynamic Biaxial Loading of Car Seats" Processes 10, no. 12: 2483. https://doi.org/10.3390/pr10122483
APA StyleLepsik, P., Fliegel, V., & Lufinka, A. (2022). Effect of Dynamic Biaxial Loading of Car Seats. Processes, 10(12), 2483. https://doi.org/10.3390/pr10122483






