Systematic Parameter Estimation and Dynamic Simulation of Cold Contact Fermentation for Alcohol-Free Beer Production
Abstract
1. Introduction
1.1. Low-Alcohol Beer (LAB) and Alcohol-Free Beer (AFB)
1.2. Beer Manufacturing
1.3. Organoleptic Constituents and Sensory Characteristics
1.4. Metabolic and Non-Metabolic Pathways
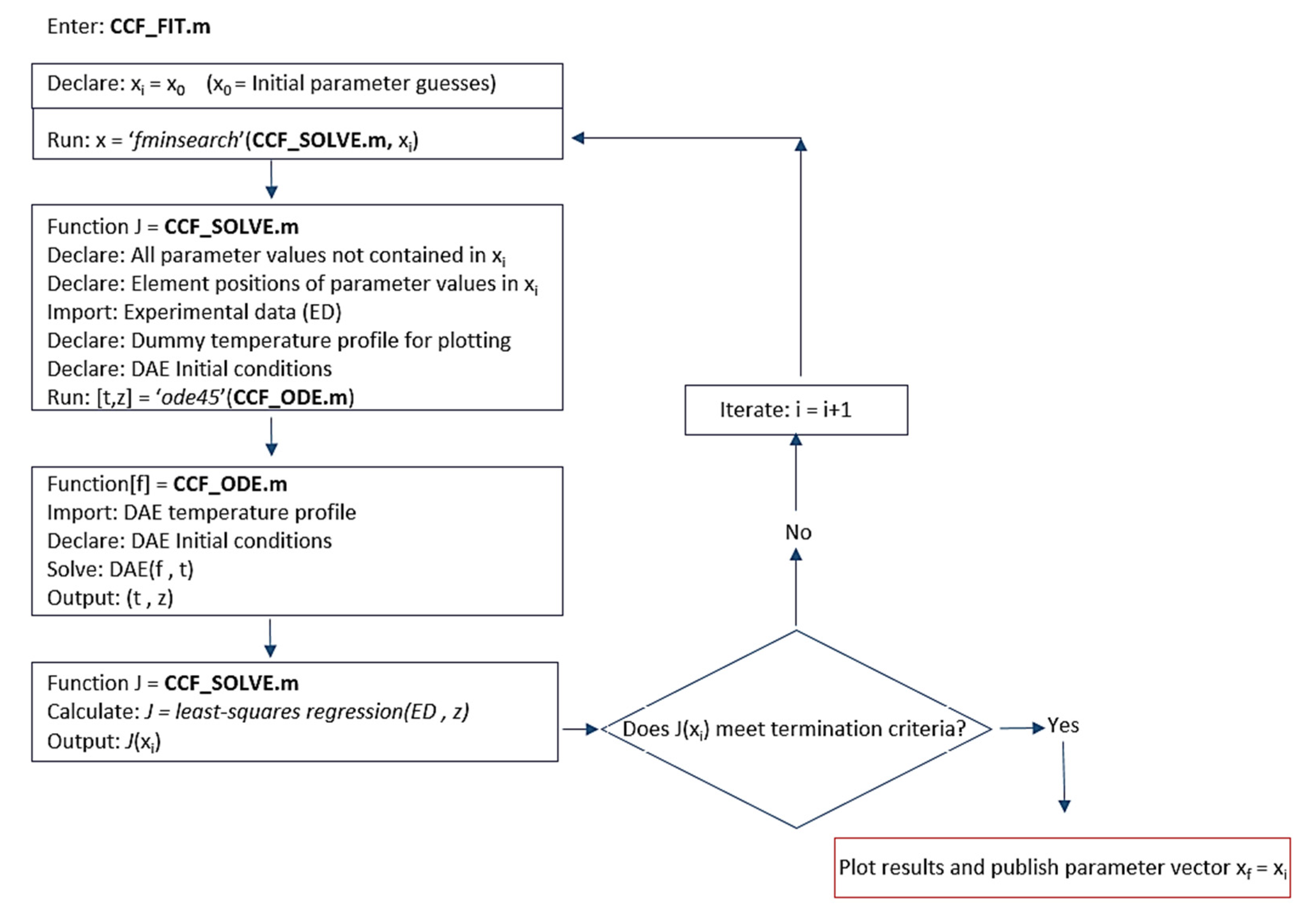
2. Methodology
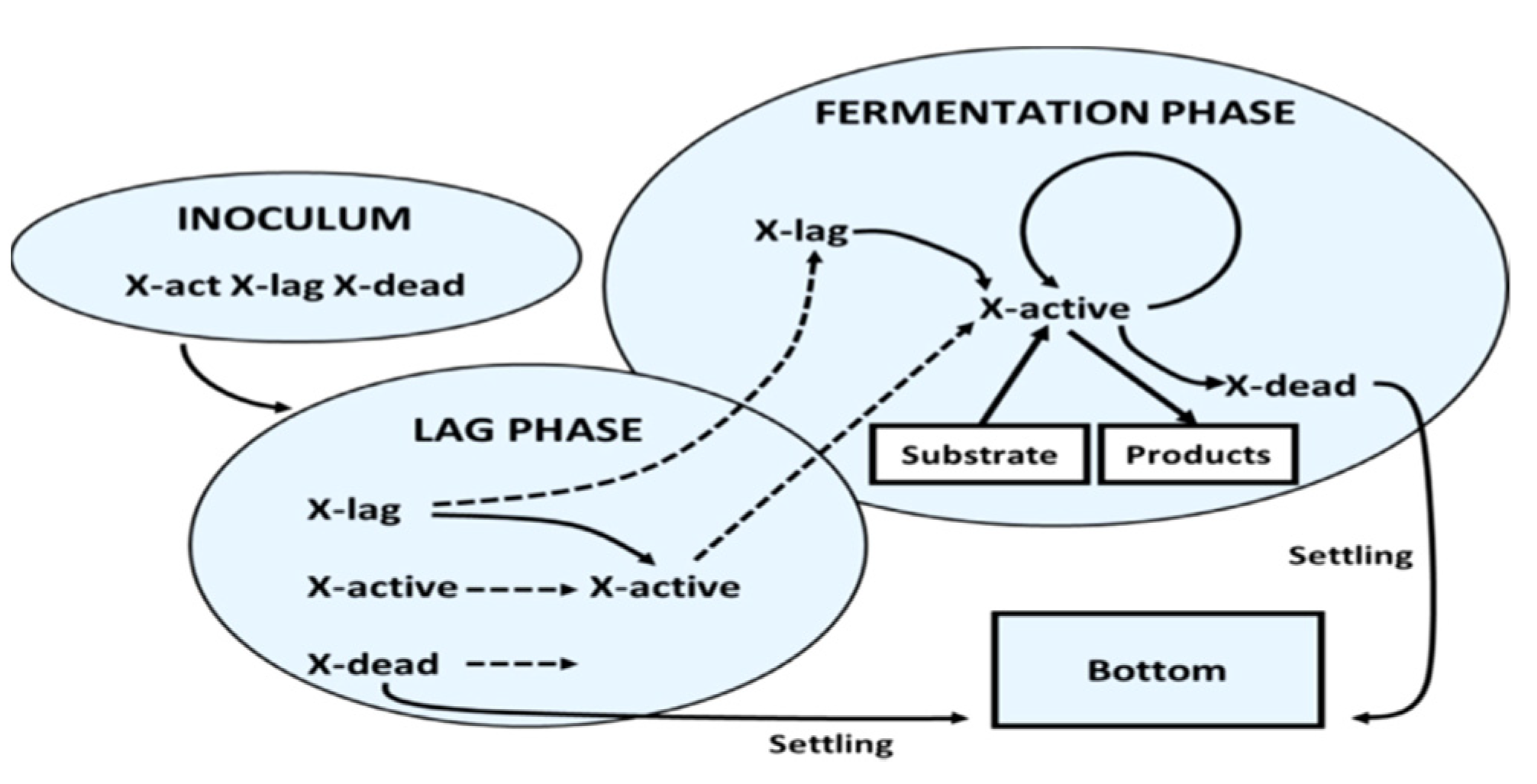
2.1. Mathematical Modeling of Fermentation
2.2. Model Description
2.3. Numerical Integration
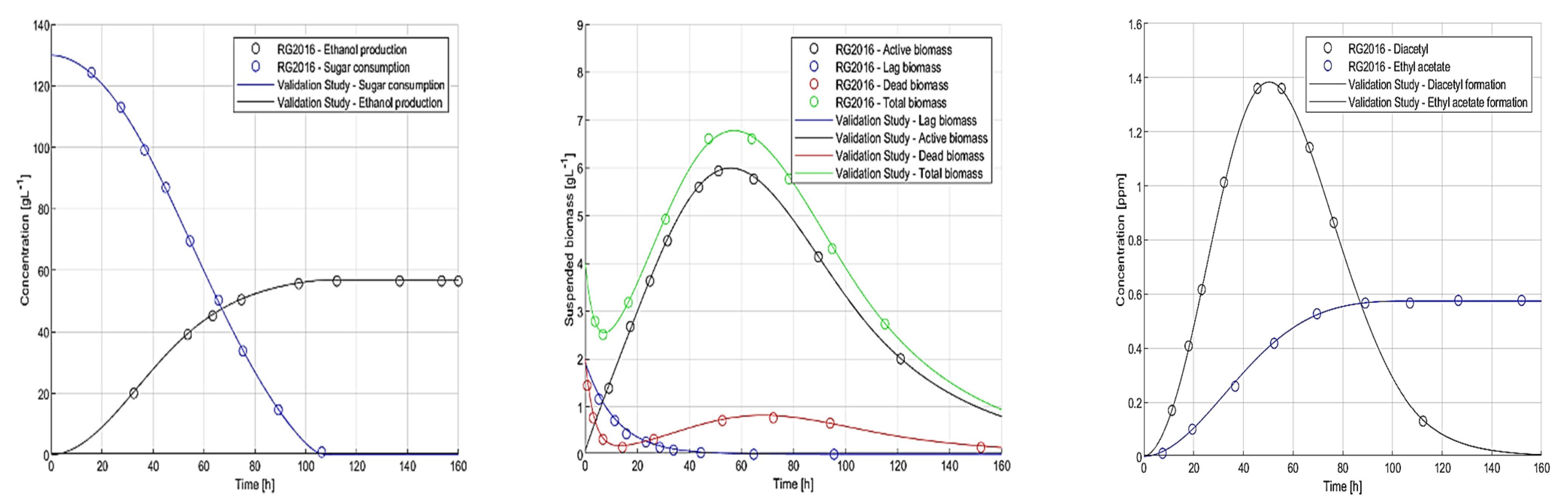
2.4. Dynamic Simulation of Warm Fermentation for Code Validation
3. Industrial Processing and Experimental Results
3.1. Process Description
3.2. Flavor Considerations
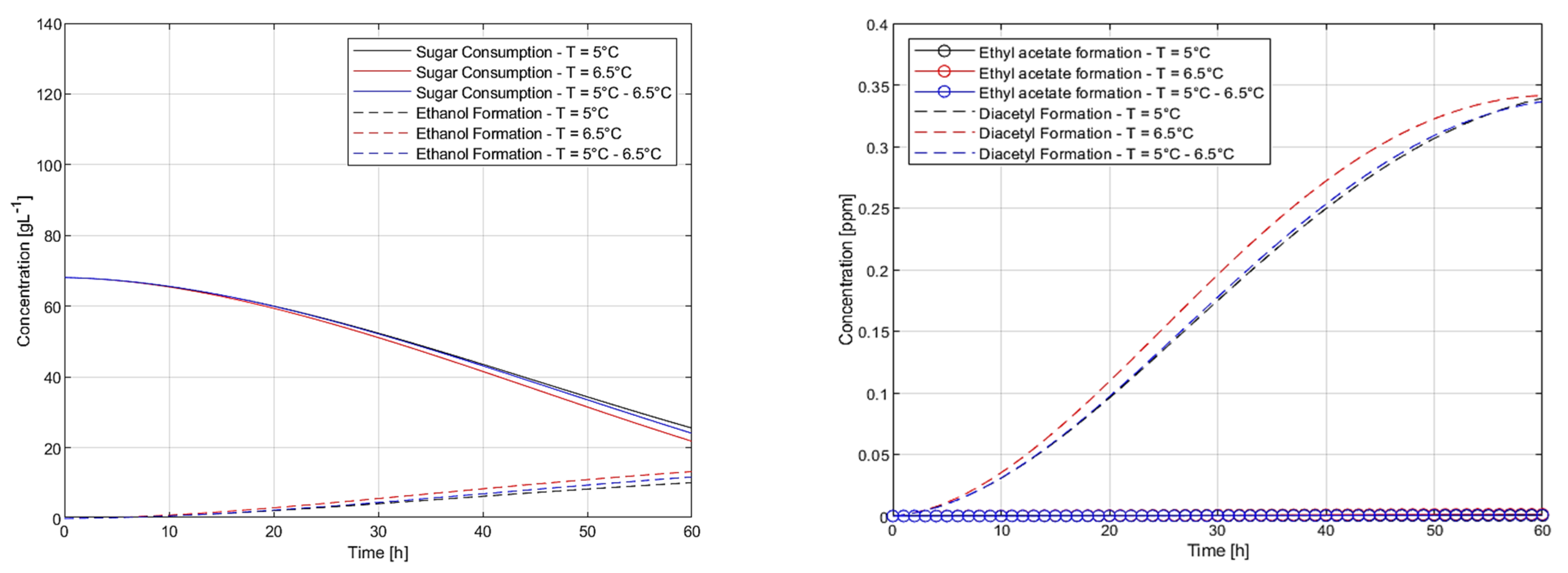
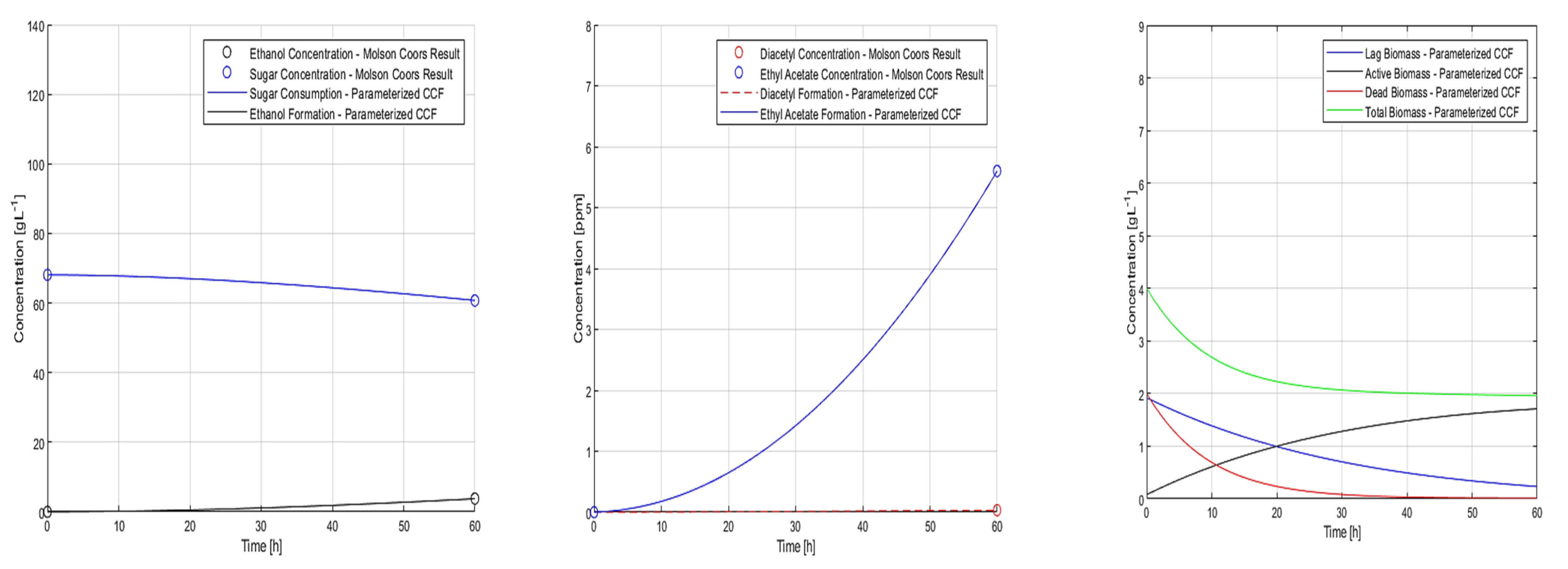
4. Fermentation Response Comparisons
4.1. Initial Condition Considerations
4.2. Comparative Analysis
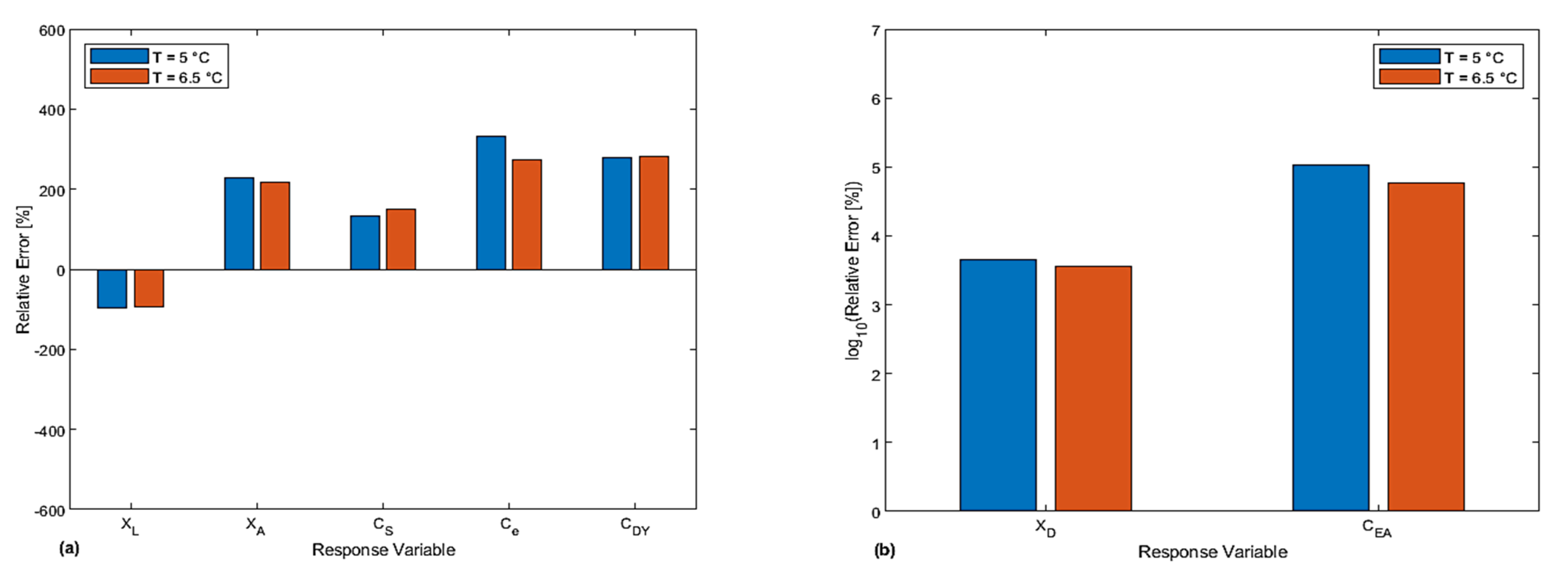
5. Parameter Estimation
5.1. Background
5.2. Model Reparameterization Trials
5.3. Summary
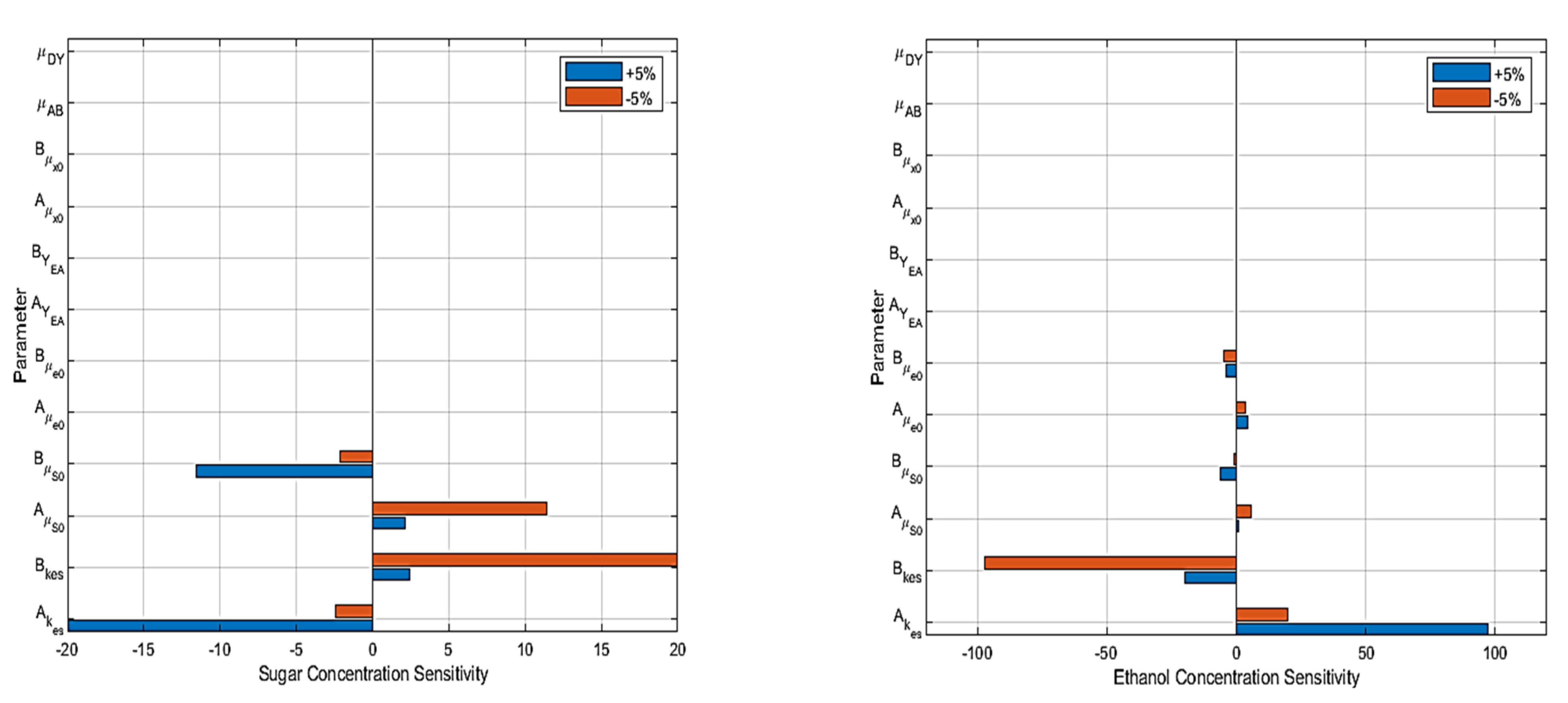
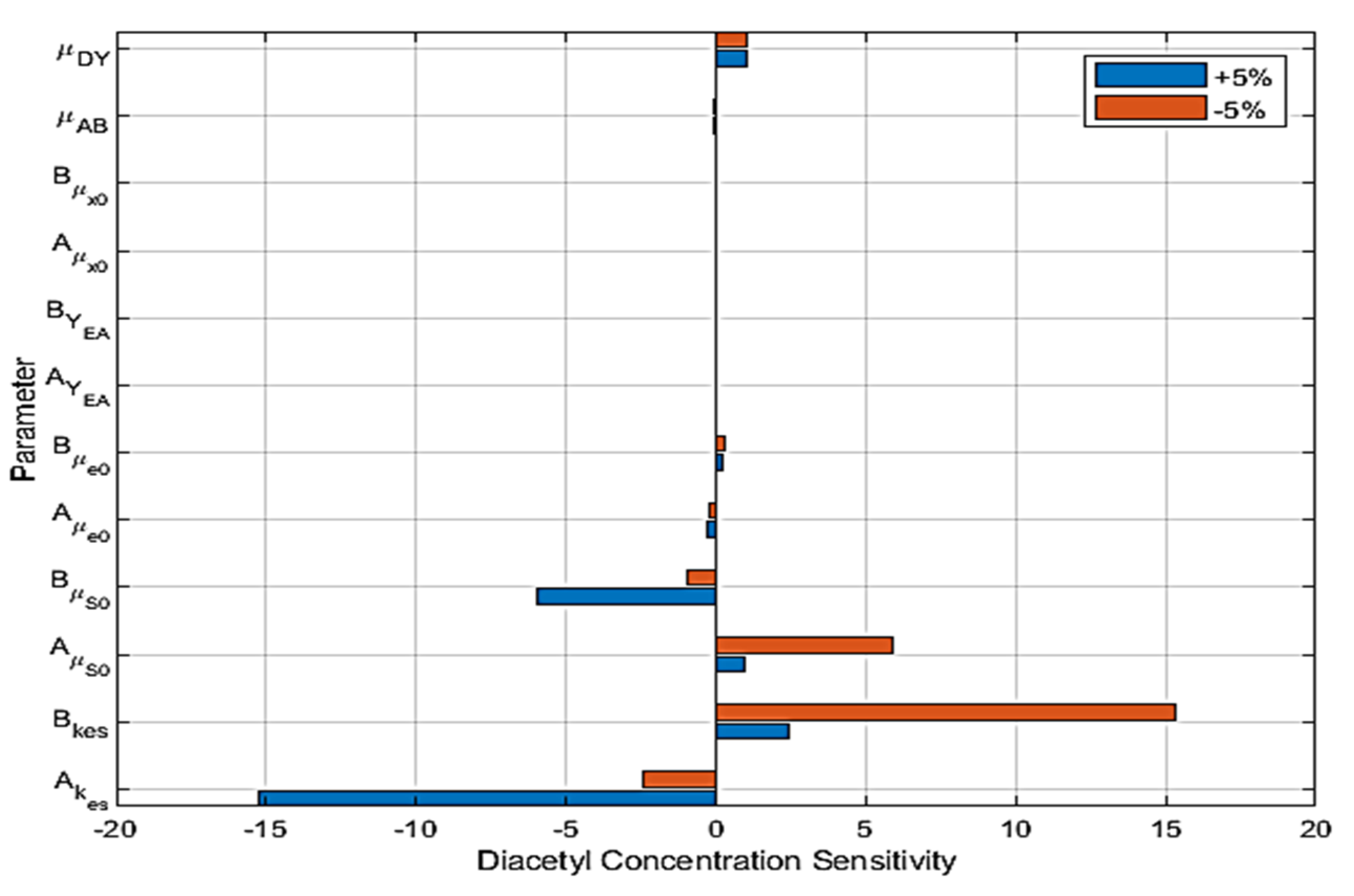
6. Sensitivity Analysis
7. Coarse Grid Enumeration of Plausible Temperature Manipulation Profiles
7.1. Heuristics for Plausible Temperature Manipulation Profiles
7.2. Effect of Total Theoretical Heat Input on Final-Time CCF Concentrations
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Southby, E.R. A Systematic Handbook of Practical Brewing; Franklin Classics: Oxford, UK, 1885. [Google Scholar]
- Boulton, C.; Quain, D. Brewing Yeast and Fermentation; Elsevier: Amsterdam, The Netherlands, 2001. [Google Scholar]
- Liguori, L.; Russo, P.; Albanese, D.; Di Matteo, M. Production of low-alcohol beverages: Current status and perspectives. In Food Processing for Increased Quality and Consumption; Elsevier: Amsterdam, The Netherlands, 2018; pp. 347–382. [Google Scholar]
- STATISTA. Beer Production Worldwide (1998–2018). Available online: Statista.com/statistics/270275 (accessed on 1 May 2019).
- Wunderlich, S.; Back, W. Overview of manufacturing beer: Ingredients, processes and quality criteria. In Beer in Health & Disease Prevention; Elsevier: Amsterdam, The Netherlands, 2009; pp. 3–16. [Google Scholar]
- Pavsler, A.; Buiatti, S. Non-lager & Lager beer. In Beer in Health & Disease Prevention; Elsevier: Amsterdam, The Netherlands, 2009; pp. 17–43. [Google Scholar]
- Shopska, V.; Denkova-Kostova, R.; Kostov, G. Modeling in brewing—A review. Processes 2022, 10, 267. [Google Scholar] [CrossRef]
- Montanari, L.; Marconi, O.; Mayer, H.; Fantozzi, P. Production of alcohol-free beer. In Beer in Health & Disease Prevention; Elsevier: Amsterdam, The Netherlands, 2009; pp. 61–75. [Google Scholar]
- Brányik, T.; Silva, D.P.; Baszczyňski, M.; Lehnert, R.; e Silva, J.B.A. A review of methods of low alcohol and alcohol-free beer production. J. Food Eng. 2012, 108, 493–506. [Google Scholar] [CrossRef]
- Liguori, L.; De Francesco, G.; Russo, P.; Perretti, G.; Albanese, D.; Di Matteo, M. Production and characterization of alcohol-free beer by membrane process. Food Bioprod. Process. 2015, 94, 158–168. [Google Scholar] [CrossRef]
- Kyselová, L.; Brányik, T. Quality improvement and fermentation control in beer. In Advances in Fermented Foods and Beverages; Elsevier: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Blanco, C.A.; Caballero, I.; Barrios, R.; Rojas, A. Innovations in the brewing industry: Light beer. Int. J. Food Sci. Nutr. 2004, 65, 655–660. [Google Scholar] [CrossRef] [PubMed]
- Catarino, M.D. Production of Non-Alcoholic Beer with Reincorporation of Original Compounds. Ph.D. Thesis, University of Porto, Porto, Portugal, 2010. [Google Scholar]
- Sohrabvandi, S.; Mousavi, S.M.; Razavi, S.H.; Mortazavian, A.M.; Rezaei, K. Alcohol-free beer: Methods of production, sensorial defects, and healthful effects. Food Rev. Int. 2010, 26, 335–352. [Google Scholar] [CrossRef]
- De Francesco, G.; Turchetti, B.; Sileoni, V.; Marconi, O.; Perretti, G. Screening of new strains of Saccharomycodes ludwigii and Zygosaccharomyces rouxii to produce low-alcohol beer. J. Inst. Brew. 2015, 121, 113–121. [Google Scholar] [CrossRef]
- Schur, F. Ein neues verfharen herstellung von alkoholfreien bier. In Proceedings of the 19th European Brewery Convention Congress; IRL Press: Oxford, UK, 1983; pp. 353–360. [Google Scholar]
- Perpète, P.; Collin, S. Fate of the worty flavours in cold contact fermentation. Food Chem. 1999, 66, 359–363. [Google Scholar] [CrossRef]
- Perpète, P.; Collin, S. How to improve the enzymatic worty flavour reduction in a cold contact fermentation. Food Chem. 2000, 70, 457–462. [Google Scholar] [CrossRef]
- Mota, A.; Novák, P.; Macieira, F.; Vicente, A.A.; Teixeira, J.A.; Šmogrovičová, D.; Brányik, T. Formation of flavor-active compounds during continuous alcohol-free beer production. J. Am. Soc. Brew. Chem. 2010, 69, 1–7. [Google Scholar]
- Rodman, A.D.; Gerogiorgis, D.I. Multi-objective process optimisation of beer fermentation via dynamic simulation. Food Bioprod. Process. 2016, 100, 255–274. [Google Scholar] [CrossRef]
- Rodman, A.D.; Gerogiorgis, D.I. Dynamic optimization of beer fermentation: Sensitivity analysis of attainable performance vs. product flavour constraints. Comput. Chem. Eng. 2017, 106, 582–595. [Google Scholar] [CrossRef]
- Rodman, A.D.; Fraga, E.S.; Gerogiorgis, D. On the application of a nature-inspired stochastic evolutionary algorithm to constrained multi-objective beer fermentation optimisation. Comput. Chem. Eng. 2018, 108, 448–459. [Google Scholar] [CrossRef]
- Rodman, A.D.; Weaser, M.; Griffiths, L.; Gerogiorgis, D. I. Dynamic optimisation and visualisation of industrial beer fermentation with explicit heat transfer dynamics. Comput. Aid. Chem. Eng. 2019, 46, 1459–1464. [Google Scholar]
- Rodman, A.D.; Gerogiorgis, D.I. Parameter estimation and sensitivity analysis for dynamic modelling and simulation of beer fermentation. Comput. Chem. Eng. 2020, 136, 106665. [Google Scholar] [CrossRef]
- Parker, D.K. Beer: Production, sensory characteristics and sensory analysis. In Alcoholic Beverages: Sensory Evaluation and Consumer Research; Woodhead Publishing Limited: Thorston, UK, 2012. [Google Scholar]
- Vanderhaegen, B.; Neven, H.; Verachtert, H.; Derdelinckx, G. The chemistry of beer aging–a critical review. Food Chem. 2006, 95, 357–381. [Google Scholar] [CrossRef]
- Evellin, F.; Perpète, P.; Collin, S. Yeast ADHI disruption: A way to promote carbonyl compounds reduction in alcohol-free beer production. J. Am. Soc. Brew. Chem. 1999, 57, 109–113. [Google Scholar]
- Purificación Hernández-Artiga, M.; Bellido-Milla, D. The evaluation of beer aging. In Beer in Health & Disease Prevention; Elsevier: Amsterdam, The Netherlands, 2009; pp. 913–922. [Google Scholar]
- Baert, J.J.; De Clippeleer, J.; Hughes, P.S.; De Cooman, L.; Aerts, G. On the origin of free and bound staling aldehydes in beer. J. Agric. Food Chem. 2012, 60, 11449–11472. [Google Scholar] [CrossRef]
- Strejc, J.; Siříšťová, L.; Karabín, M.; Almeida e Silva, J.B.; Brányik, T. Production of alcohol-free beer with elevated amounts of flavouring compounds using lager yeast mutants. J. Inst. Brew. 2013, 119, 149–155. [Google Scholar]
- Gee, D.A.; Ramirez, W.F. A flavour model for beer fermentation. J. Inst. Brew. 1994, 100, 321–329. [Google Scholar] [CrossRef]
- Perpète, P.; Collin, S. Contribution of 3-methylthiopropionaldehyde to the worty flavor of alcohol-free beers. J. Agric. Food Chem. 1999, 47, 2374–2378. [Google Scholar] [CrossRef]
- Verstrepen, K.J.; Derdelinckx, G.; Dufour, J.P.; Winderickx, J.; Thevelein, J.M.; Pretorius, I.S.; Delvaux, F.R. Flavor-active esters: Adding fruitiness to beer. J. Biosci. Bioeng. 2003, 96, 110–188. [Google Scholar] [CrossRef]
- Hellborg, L.; Piskur, J. Yeast diversity in the brewing industry. In Beer in Health & Disease; Elsevier: Amsterdam, The Netherlands, 2009; pp. 77–88. [Google Scholar]
- Bokulich, N.A.; Bamforth, C.W. The microbiology of malting and brewing. Microbiol. Mol. Biol. Rev. 2013, 77, 157–172. [Google Scholar] [CrossRef] [PubMed]
- Van Iersel, M.; Van Dieren, B.; Rombouts, F.; Abee, T. Flavor formation and cell physiology during the production of alcohol-free beer with immobilized Saccharomyces cerevisiae. Enzyme Microb. Technol. 1999, 24, 407–411. [Google Scholar] [CrossRef]
- Van Iersel, M.F.M.; Brouwer-Post, E.; Rombouts, F.; Abee, T. Influence of yeast immobilization on fermentation and aldehyde reduction during the production of alcohol-free beer. Enzyme Microb. Technol. 2000, 26, 602–607. [Google Scholar] [CrossRef]
- Engasser, J.M.; Marc, I.; Moll, M; Duteurtre, B. Kinetic modeling of beer fermentation. Congr. Eur. Brew. Conv. 1981, 18, 579–586. [Google Scholar]
- García, A.I.; García, L.A.; Díaz, M. Modeling of diacetyl production during beer fermentation. J. Inst. Brew. 1994, 100, 179–183. [Google Scholar] [CrossRef]
- Pilarski, D.W.; Gerogiorgis, D.I. Progress and modelling of cold contact fermentation for alcohol-free beer production: A review. J. Food. Eng. 2020, 273, 109804. [Google Scholar] [CrossRef]
- de Andrés-Toro, B.; Giron-Sierra, J.M.; Lopez-Orozco, J.A.; Fernandez-Conde, C.; Peinado, J. M.; García-Ochoa, F. A kinetic model for beer production under industrial operational conditions. Math. Comput. Simul. 1998, 48, 65–74. [Google Scholar] [CrossRef]
- de Andrés-Toro, B.; Giron-Sierra, J.M.; Lopez-Orozco, J.A.; Fernandez-Conde, C.; Peinado, J. M.; García-Ochoa, F. Multiobjective optimization and multivariable control of the beer fermentation process with the use of evolutionary algorithms. J. Zheijang Univ. Sci. 2004, 5, 378–389. [Google Scholar] [CrossRef]
- Carrillo-Ureta, G.E.; Roberts, P.D.; Becerra, V.M. Genetic algorithms for optimal control of beer fermentation. In Proceedings of the 2001 IEEE International Symposium on Intelligent Control (ISIC’01), Mexico City, Mexico, 5–7 September 2001. [Google Scholar]
- Saison, D. Effect of fermentation conditions on staling indicators in beer. J. Am. Soc. Brew. Chem. 2009, 67, 222–228. [Google Scholar] [CrossRef]
- Buiatti, S. Beer composition: An overview. In Beer in Health & Disease Prevention; Elsevier: Amsterdam, The Netherlands, 2009; pp. 213–225. [Google Scholar]
- Pires, E.J.; Teixeira, J.A.; Brányik, T. Yeast: The soul of beer’s aroma—A review of flavour-active esters and higher alcohols produced by the brewing yeast. Appl. Microbiol. Biotechnol. 2014, 98, 1937–1949. [Google Scholar] [CrossRef] [PubMed]
- Nelder, J.A.; Mead, R. A simplex method for function minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Angelopoulos, P.M.; Gerogiorgis, D.I.; Paspaliaris, I. Model-based sensitivity analysis and experimental investigation of perlite grain expansion in a vertical electrical furnace. Ind. Eng. Chem. Res. 2013, 52, 17953–17975. [Google Scholar] [CrossRef]
- Biegler, L.T. Nonlinear Programming: Theory, Algorithms, and Applications; SIAM: Philadelphia, PA, USA, 2010. [Google Scholar]
- NIST/SEMATECH. e-Handbook of Statistical Methods. Available online: http://www.itl.nist.gov/div898/handbook/ (accessed on 1 May 2019).
- Ivanov, K.; Petelkov, I.; Shopska, V.; Denkova, R.; Gochev, V.; Kostov, G. Investigation of mashing regimes for low-alcohol beer production. J. Inst. Brew. 2016, 122, 508–516. [Google Scholar] [CrossRef]






| Rates + Factors | Description | Ai | Bi |
|---|---|---|---|
| μSD0 | Maximum dead cell settling rate | 33.82 | −10,033.28 |
| μX0 | Maximum cell growth rate | 108.31 | −31,934.09 |
| μS0 | Maximum sugar consumption rate | −41.92 | 11,654.64 |
| μe0 | Maximum ethanol production rate | 3.27 | −1267.24 |
| μDT | Specific cell death rate | 130.16 | −38,313.00 |
| μL | Specific cell activation rate | 30.72 | −9501.54 |
| ke = kS | Affinity constant for sugar and ethanol | −119.63 | 34,203.95 |
| YEA | Stoichiometric factor—EA production | 89.92 | −26,589.00 |
| Rates | Description | Value | Units |
|---|---|---|---|
| μDY | Rate of diacetyl production | 1.27672·10−4 | g−1 h−1 L |
| μAB | Rate of diacetyl consumption | 1.13864·10−3 | g−1 h−1 L |
| Variable | Initial Condition (t = 0) | Units | Literature Reference/Calculation |
|---|---|---|---|
| XL | 1.92 | g·L−1 | |
| XA | 0.08 | g·L−1 | |
| XD | 2.00 | g·L−1 | |
| XS | 4.00 | g·L−1 | [41] |
| CS | 130.00 | g·L−1 | [41] |
| CE | 0 | g·L−1 | [41] |
| CEA | 0 | ppm | [41] |
| CDY | 0 | ppm | [41] |
| T | 286.15 | K | Interpolation of temperature profile from [20] |
| Time (h) | Specific Gravity (SG) | Acetaldehyde Concentration (ppm) | pH |
|---|---|---|---|
| 0 | 1.027 | 0 | 4.09 |
| 12 | 1.027 | (–) | (–) |
| 24 | 1.026 | (–) | (–) |
| 36 | 1.025 | (–) | (–) |
| 48 | 1.025 | (–) | (–) |
| 60 | 1.024 | (–) | 4.07 |
| post-dilution | 1.015–1.016 | 24.50 | (–) |
| Time (h) | CEA (ppm) | CDY (ppm) | CΕ (g L–1) | ABV (% v/v) | XS (cells·mL−1) | CS (g·L−1) |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 3·107 | 68.1 |
| 12 | (–) | (–) | (–) | (–) | (–) | (–) |
| 24 | (–) | (–) | (–) | (–) | (–) | (–) |
| 36 | (–) | (–) | (–) | (–) | (–) | (–) |
| 48 | (–) | (–) | (–) | (–) | (–) | (–) |
| 60 | 5.60 | 0.032 | 3.80 | 0.48 | (–) | 60.7 |
| Post-dilution | 3.50 | 0.020 | 2.37 | 0.30 | (–) | 38.2–40.8 |
| Chemical Name | Final Pack Concentration (ppm) | Flavor Threshold (ppm) | Ref. | Flavor Association |
|---|---|---|---|---|
| Aldehydes (Non-VDK) | ||||
| 2-methylbutanal | 4.96·10−3 | 1.00·10−3 | [32] | Almond, apple-like, malty, wort |
| 3-methylbutanal | 1.98·10−2 | 5.60·10−2 | [29] | Malty, chocolate, cherry, wort |
| Furfural | 1.12·10−2 | 1.50·101 | [44] | Caramel, bread, cooked meat |
| Trans-2-nonenal | 4.00·10−4 | 3.00·10−5 | [29] | Cardboard, papery, cucumber |
| Acetaldehyde | 2.82·10−3 | 1.10 | [29] | Green apple, fruity |
| VDKs | ||||
| Diacetyl | 2.00·10−2 | 1.50·101 | [45] | Buttery, butterscotch |
| Pentane-2,3-dione | 1.00·10−2 | 9.00·101 | [45] | Buttery |
| Fusel alcohols | ||||
| Propanol | 1.70 | 6.00·102 | [46] | Solvent-like |
| Isobutanol | 1.80 | 1.00·102 | [46] | Solvent-like |
| Esters | ||||
| Ethyl hexanoate | 1.00·10−2 | 2.00·10−1 | [23] | Apple, pineapple |
| Isoamyl acetate | 5.00·10−2 | 5.00·10−1 | [44] | Banana, pear |
| Ethyl acetate | 9.00·10−1 | 2.10·101 | [33] | Fruity, solvent-like |
| Trial | Aμe0 | Bμe0 | AμS0 | BμS0 | Akes | Bkes | AμX0 | BμX0 | AYEA | BYEA | μAB | μDY | Result |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | Severe Non-Convergence |
| 2 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | (–) | ✓ | Severe Non-Convergence |
| 3 | (–) | (–) | (–) | (–) | ✓ | (–) | ✓ | (–) | (–) | (–) | (–) | ✓ | Slight Non-Convergence |
| 4 | (–) | (–) | (–) | (–) | ✓ | (–) | ✓ | ✓ | (–) | (–) | (–) | ✓ | Slight Non-Convergence |
| 5 | (–) | (–) | (–) | ✓ | ✓ | (–) | ✓ | (–) | (–) | (–) | (–) | ✓ | Convergence |
| 6 | (–) | ✓ | (–) | ✓ | ✓ | (–) | ✓ | (–) | (–) | (–) | (–) | ✓ | Slight Non-Convergence |
| 7 | (–) | ✓ | (–) | ✓ | ✓ | (–) | ✓ | (–) | ✓ | (–) | ✓ | (–) | Slight Non-Convergence |
| 8 | (–) | ✓ | (–) | ✓ | ✓ | (–) | ✓ | (–) | (–) | ✓ | ✓ | (–) | Slight Non-Convergence |
| 9 | (–) | ✓ | (–) | ✓ | ✓ | (–) | (–) | ✓ | ✓ | (–) | (–) | ✓ | Convergence |
| 10 | (–) | ✓ | ✓ | (–) | (–) | ✓ | ✓ | (–) | ✓ | (–) | (–) | ✓ | Convergence |
| 11 | (–) | ✓ | (–) | ✓ | (–) | ✓ | ✓ | (–) | ✓ | (–) | (–) | ✓ | Convergence |
| 12 | ✓ | (–) | (–) | ✓ | (–) | ✓ | ✓ | (–) | ✓ | (–) | (–) | ✓ | Convergence |
| 13 | (–) | ✓ | (–) | ✓ | (–) | ✓ | ✓ | (–) | ✓ | (–) | ✓ | ✓ | Convergence |
| 14 | ✓ | (–) | (–) | ✓ | (–) | ✓ | (–) | ✓ | (–) | ✓ | ✓ | ✓ | Convergence |
| 15 | ✕ | (–) | (–) | ✓ | (–) | ✓ | (–) | ✓ | (–) | ✓ | (–) | ✓ | Severe Non-Convergence |
| 16 | (–) | ✓ | ✓ | (–) | ✓ | (–) | ✓ | (–) | ✓ | (–) | (–) | ✓ | Severe Non-Convergence |
| 17 | (–) | ✓ | ✓ | (–) | ✓ | (–) | ✓ | (–) | ✓ | (–) | ✓ | ✓ | Convergence |
| Symbol | CCF (T = 5 °C) | RPE (T = 5 °C) | CCF (T = 6.5 °C) | RPE (T = 6.5 °C) | CCF (T = 5–6.5 °C) | RPE (T = 5–6.5 °C) |
|---|---|---|---|---|---|---|
| μAB | (–) | (–) | (–) | (–) | (–) | (–) |
| μDY | 7.80·10−6 | −93.890 | 7.27·10−6 | −94.308 | 7.59·10−6 | −94.054 |
| BYEA | (–) | (–) | (–) | (–) | (–) | (–) |
| AYEA | 123.040 | 36.832 | 136.724 | 52.051 | 169.130 | 88.090 |
| Bμe0 | (–) | (–) | (–) | (–) | (–) | (–) |
| Aμe0 | 2.903 | −11.206 | 4.733 | 44.744 | 4.125 | 26.148 |
| Akes | (–) | (–) | (–) | (–) | (–) | (–) |
| Bkes | 34,658.614 | 1.329 | 35,474.587 | 3.714 | 35,203.709 | 2.922 |
| Aμx0 | 84.280 | −22.185 | 69.395 | −35.929 | 37.450 | −65.423 |
| Bμx0 | (–) | (–) | (–) | (–) | (–) | (–) |
| AμS0 | (–) | (–) | (–) | (–) | (–) | (–) |
| BμS0 | 11,370.511 | −2.437 | 11,950.314 | 2.536 | 11,754.776 | 0.859 |
| AμSD0 | (–) | (–) | (–) | (–) | (–) | (–) |
| BμSD0 | (–) | (–) | (–) | (–) | (–) | (–) |
| AμDT | (–) | (–) | (–) | (–) | (–) | (–) |
| BμDT | (–) | (–) | (–) | (–) | (–) | (–) |
| AμL | (–) | (–) | (–) | (–) | (–) | (–) |
| BμL | (–) | (–) | (–) | (–) | (–) | (–) |
| Rates and Factors | Description | Ai | Bi |
|---|---|---|---|
| μSD0 | Maximum dead cell settling rate | 33.820 | −10,033.280 |
| μx0 | Maximum cell growth rate | 37.450 | −31,934.090 |
| μS0 | Maximum sugar consumption rate | −41.920 | 11,754.776 |
| μe0 | Maximum ethanol production rate | 4.125 | −1267.240 |
| μDT | Specific cell death rate | 130.160 | −38,313.000 |
| μL | Specific cell activation rate | 30.720 | −9501.540 |
| ke = kS | Affinity constant for sugar and ethanol | −119.630 | 35,203.709 |
| YEA | Stoichiometric factor, ethyl acetate production | 169.130 | −26,589.000 |
| μDY | Rate of diacetyl production | 7.590·10−6 | |
| μAB | Rate of diacetyl consumption | 1.138·10−3 | |
| T(t) Trial | T(t = 0) | T(t = 10) | T(t = 20) | T(t = 30) | T(t = 40) | T(t = 50) | T(t = 60) | Type |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | a |
| 2 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | c |
| 3 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | a |
| 4 | 1 | 2 | 3 | 3 | 3 | 3 | 3 | d |
| 5 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | c |
| 6 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | a |
| 7 | 1 | 2 | 3 | 4 | 4 | 4 | 4 | d |
| 8 | 1 | 2 | 3 | 4 | 5 | 5 | 5 | d |
| 9 | 2 | 3 | 4 | 4 | 4 | 4 | 4 | d |
| 10 | 3 | 4 | 4 | 4 | 4 | 4 | 4 | c |
| 11 | 1 | 2 | 3 | 4 | 5 | 6 | 6 | d |
| 12 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | a |
| 13 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | b |
| 14 | 2 | 3 | 4 | 5 | 5 | 5 | 5 | d |
| 15 | 2 | 3 | 4 | 5 | 6 | 6 | 6 | d |
| 16 | 3 | 4 | 5 | 5 | 5 | 5 | 5 | d |
| 17 | 4 | 5 | 5 | 5 | 5 | 5 | 5 | c |
| 18 | 2 | 3 | 4 | 5 | 6 | 7 | 7 | d |
| 19 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | a |
| 20 | 3 | 4 | 5 | 6 | 6 | 6 | 6 | d |
| 21 | 3 | 4 | 5 | 6 | 7 | 7 | 7 | d |
| 22 | 4 | 5 | 6 | 6 | 6 | 6 | 6 | d |
| 23 | 5 | 5.25 | 5.5 | 5.75 | 6 | 6.25 | 6.5 | (–) |
| 24 | 5 | 6 | 6 | 6 | 6 | 6 | 6 | c |
| 25 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | a |
| 26 | 4 | 5 | 6 | 7 | 7 | 7 | 7 | d |
| 27 | 5 | 6 | 7 | 7 | 7 | 7 | 7 | d |
| 28 | 6 | 7 | 7 | 7 | 7 | 7 | 7 | c |
| 29 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | a |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pilarski, D.W.; Gerogiorgis, D.I. Systematic Parameter Estimation and Dynamic Simulation of Cold Contact Fermentation for Alcohol-Free Beer Production. Processes 2022, 10, 2400. https://doi.org/10.3390/pr10112400
Pilarski DW, Gerogiorgis DI. Systematic Parameter Estimation and Dynamic Simulation of Cold Contact Fermentation for Alcohol-Free Beer Production. Processes. 2022; 10(11):2400. https://doi.org/10.3390/pr10112400
Chicago/Turabian StylePilarski, Dylan W., and Dimitrios I. Gerogiorgis. 2022. "Systematic Parameter Estimation and Dynamic Simulation of Cold Contact Fermentation for Alcohol-Free Beer Production" Processes 10, no. 11: 2400. https://doi.org/10.3390/pr10112400
APA StylePilarski, D. W., & Gerogiorgis, D. I. (2022). Systematic Parameter Estimation and Dynamic Simulation of Cold Contact Fermentation for Alcohol-Free Beer Production. Processes, 10(11), 2400. https://doi.org/10.3390/pr10112400







