Abstract
There are many petrochemical industries that need adequate knowledge of multiphase flow phenomena inside pipes. In such industries, measuring the void fraction is considered to be a very challenging task. Thus, various techniques have been used for void fraction measurements. For determining more accurate multiphase flow measurements, this study employed dual non-intrusive techniques, gamma-ray and electrical capacitance sensors. The techniques using such sensors are considered non-intrusive as they do not cause any perturbation of the local structure of the phases’ flow. The first aim of this paper is to analyze both techniques separately for the void fraction data obtained from practical experiments. The second aim is to use both techniques’ data in a neural network model to analyze measurements more efficiently. Accordingly, a new system is configured to combine the two techniques’ data to obtain more precise results than they can individually. The simulations and analyzing procedures were performed using MATLAB. The model shows that using gamma-ray and capacitance-based sensors gives Mean Absolute Errors (MAE) of 3.8% and 2.6%, respectively, while using both techniques gives a lower MAE that is nearly 1%. Consequently, measurements using two techniques have the ability to enhance the multiphase flows’ observation with more accurate features. Such a hybrid measurement system is proposed to be a forward step toward an adaptive observation system within related applications of multiphase flows.
Keywords:
void fraction; capacitance; gamma-ray; sensors; ANN; multiphase flow; flow measurement; neural networks; flow regimes 1. Introduction
The term multiphase flow refers to the flow of a mixture of solid, liquid or vapor states (phases). Such phenomena often affect industrial production and happen in applications of power, chemical industry, oil, nuclear energy and metallurgical engineering. For the study of multiphase flow measurements, there is a very significant factor called void fraction. Generally, any flow characteristics may be affected by void fraction such as the heat transfer coefficient, pressure drop and flow pattern. The term can be defined as a dimensionless parameter from the ratio between the gas phase area and the total flow area in a cross-sectional evaluation. Additionally, that ratio is useful for the determination of the average density. The industries can see that it is very necessary to describe the phases’ flows in terms of some fluids’/gases’ characteristics. Fortunately, these properties can be determined using different types of techniques that are available for such tasks nowadays. Specific sensors exist in various methods for flow measurement. In addition, some computing methods, e.g., neural network models, are needed for analytical tasks in order to show more precise and valuable characteristics of phases inside pipes.
In regard to the measuring process, particular steps are required to be taken at the exact time, and also accurately, depending on the most appropriate technology. For a given application, and according to industry standards, picking the best measuring tool is as significant a point as demonstrating the required features [1]. The flows’ complexity comes from the characteristics of the interfaces; the flow direction; the pipe geometry; the nature of one phase among others; the situation of the measuring procedures; and into which flow regime it happens. The major flow regimes in multiphase flows are slug, bubbly, annular and stratified. Materials in their three statuses (liquid, gas and solid) have various electrical characteristics. The most distinguishable ones are the permittivity and conductivity properties, which vary in multiphase flows. Therefore, well-known measuring techniques consider these properties to understand the flows’ behavior and quantities.
In the 1980s, capacitance-based sensors were used in multiphase flow measurements with different configurations [2]. In the 1990s, researchers used helical and concave configurations of capacitance-based sensors much more widely than other types. They considered 9.53-mm vertical pipes by Elkow et al. [3] and 45-mm vertical pipes by Keska et al. [4], focused on two-phase flow measurements with different flow patterns. However, Tollefsan et al. [5] observed oil–gas and glycerol–air flows and Belo et al. used concave only for static flow measurement [6]. In later decades, concave capacitance-based sensors have been more frequently used, particularly with water–air flows in horizontal pipes [7]. For measuring systems that are based on capacitance sensors, a design step of electrode configuration was performed related to exciting frequency and electrode structure [8]. A varying sensitivity factor was determined depending on the electrode shape [9]; thus, a sensor of twin rectangular fork-like capacitance (TRFLC) was proposed for recognizing flow patterns in a horizontal pipe [10]. Since the data of void fractions were obtained, artificial neural models were designed to analyze the void fraction data according to specific criteria [11,12].
On the other side, the high capability of the gamma-ray technique comes from its high penetration property. That benefit made the radioisotope gauges become preferred over other measuring principles according to many work–environmental requirements [13]. Thus, and since the 1950s, gamma-ray technology has been included for void fraction measurements [14], and it appeared in the analysis of volume fractions for a biphasic stratified flow regime [15]. Most measurements utilized the gamma-ray technique for two-phase flows in particular. Cook and Rhodes simulated a gamma-ray sensor for vertical pipes and observed a high error when the channel size increased [16]. One-shot and traversing methods were included for two-phase flows in horizontal and vertical pipes [17,18]. Bishop and James applied a multiple beam gamma-ray in a three-phase flow to determine phase fraction [19]. They involved those techniques with artificial neural network (ANN) models to be used in multiphase flow measurements. Nuclear radiation attenuation methods have been employed for the measurement of void fractions. Measurements using multibeam gamma-ray attenuation, over single beam, have been enhanced for measuring void fractions. As an example of oil–water–gas flow measurement, various principles of a multibeam gamma-ray densitometer have been applied and improved to provide adequate information about flows [20,21]. The high resolution property of a multibeam gamma-ray densitometer was introduced in multiphase flow applications by Hampel et al. [22].
ANN techniques offer powerful approaches in regard to analyzing data from a varying range of measurement techniques. There are many researchers who have designed a wide range of neural networks for predicting flow patterns [23]. In order to determine the fractions of oil, water and gas in pipelines, the phases’ fractions and configuration were determined using an ANN model with gamma densitometers [19]. Ozbayoglu et al. included a model of a computational intelligence method for estimating the main properties of a multiphase flow [24]. Using a model of ANN, void fraction measurement were analyzed with liquid densities by Nazemi et al. [25], and with flow regime by Roshani et al. [26]. Omid and Hussein in [27], applied a Multilayer Perceptron (MLP) network with a three-detector gamma ray for void fraction with water–liquid ratio estimation. Furthermore, neural networks have been included for flow regime identification in multiphase flows [28] and for the estimation of bubble formation in bubble columns [29]. This paper explains both mentioned techniques with their functionalities, and then evaluates their analysis in MATLAB through a neural network model for void fraction measurements. With the help of the previous studies that have been conducted in this field, in this study, an attempt is made to provide a void fraction diagnostic system with high precision. For this purpose, a two-phase flow regime in different void fractions was simulated using MCNP and COMSOL. By considering both the capacitance-based sensor and the gamma ray-based sensor with the two-phase flow and applying their outputs to an MLP neural network, an attempt is made to predict void percentages with high precision. In fact, improving the detecting system’s precision and the combination of two different sensors with different operational aspects are the main contributions of the present research.
2. Void Fraction Measurement Techniques
Within a flow, and from an experimental point of view, the characteristics of momentum, mass and energy transfer rates may be sensitive to the components’ geometric distribution. Moreover, within each component or phase, the flow will depend on the flow pattern, which is considered as a type of the component’s geometric distribution [30]. Due to the high demand of accurate measurement results through non-intrusive and non-invasive techniques, gamma-ray and electrical capacitance-based sensors were used in this project. Their data were then sent to a neural model to analyze the characteristics of gas–water–oil flows efficiently. Generally speaking, at least two different measuring techniques are often utilized in multiphase flow industries. Thus, the point here is to obtain adequate and accurate information from dual measuring techniques and for a multiphase application.
The dimensionless quantity of void fraction is considered as the most important aspect in multiphase flow. Although its first use started in the 1940s, void fraction still has a valuable role nowadays. This quantity refers to the fraction of a geometric domain occupied by another phase, as shown in Figure 1, which illustrates void fraction-related terms used in multiphase flow. Estimating the values of void fraction has been reviewed by many works such as Rosehart et al., for void fraction characteristics [28]; Smith SL., for void fraction in two-phase flows [29]; Owen et al., for void fraction fluctuation [30]; Tandon et al., for void fraction prediction [31]; Usui et al., for void fraction among basic regimes [32].
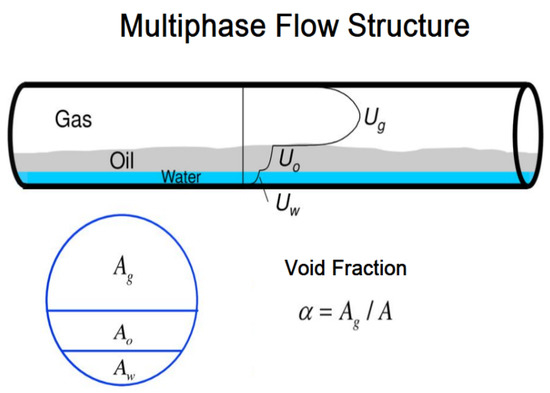
Figure 1.
Multiphase flow structure.
The non-intrusive property adds extra capability to the dual techniques in flow measurement processes. Therefore, this study considers two measurement tasks depending on the data resulting from each technology. The first task was performed for both the capacitance-based sensor and gamma-ray attenuation technique individually. The second one involved both techniques together in one measuring system.
3. Sensor Simulations
The gas and liquid phases were represented, respectively, as air and gasoil (C12H23, 0.826 g/cm3 and 2.1 relative permittivity). MATLAB, COMSOL and MCNP packages were used in the simulation of this study. For polyphasic flows, the gamma-ray and capacitance-based sensors were simulated using MCNP and COMSOL packages. Those methods were implemented in references [26] and [31], whose study only compared the techniques separately. With the MCNP5 code, that technology was presented by Mosorov and his coworkers in [32]. Moreover, Salgado’s group used the MCNP6 code with the gamma-ray technique to calculate the volume fraction on a stratified flow regime [33].
It should be noted that the studies were conducted for air–oil flow and particularly on the flow pattern of the annular regime. The MCNP code was used for simulating the gamma-ray attenuation sensor in two-phase flow (air–oil), while the capacitance-based sensor was simulated in the COMSOL Multiphysics package for the same air–oil phases flow. On the other side, the MATLAB package was used to run the MLP model in a neural network that was applied to analyze the data of both sensors. The MLP neural network was run to perform both simulated sensors’ data, but with a wider range of void fraction values of air–oil two-phase flow measurements.
3.1. Capacitance-Based Sensor Using COMSOL
Since the last century, electrical capacitance-based technology has used the sensitivity of various electrical characteristics in multiphase flow measurements. Its physical understanding describes those different mediums that have various electrical features such as magnetic permeability, conductivity, dielectric coefficient and complex admittance. Thus, the distribution status of a medium can be known by inferring the distribution of its electrical properties. Inside the pipes, the value of capacitance between the measuring and exciting electrodes can be calculated using electromagnetic theory. Thus, in the case of a three-dimensional electrostatic field, the potential distribution is given as
where ρ(x,y,z), ε(x,y,z) and V(x,y,z) represent, respectively, the charge distribution, the medium permittivity between electrodes and the electric potential allocation.
Regarding the design parameters of the capacitance-based sensor, the COMSOL package was used to model the sensor from soft copper material with a thickness of 10 mm and length of 120 mm. The electrodes were separated with a 10 mm distance. The simulated structure for the validation of the COMSOL simulation is depicted in Figure 2a that illustrates the sensor design and its boundaries, while Figure 2b shows the sensor’s electric potential distribution. The result of this simulation was verified using obtained results in [31]. Using verified simulation, other required simulations in this study were performed.
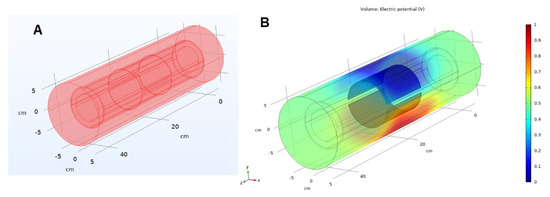
Figure 2.
(A) The structure schematic used for validating the COMSOL simulation. (B) Electric potential distribution of simulated structure of capacitance sensor [31].
3.2. Gamma-Ray Attenuation-Based Sensor by MCNP
The gamma-rays attenuation technique is very useful and powerful in measurements due to its advantages such as its non-intrusive property, and it being inexpensive, reliable, portable and applicable in two/three-phase flow measurements. The method is essentially based on allowing a beam of radiation gamma-rays to traverse the cross-section of the pipe where it is detected. Figure 3a describes the basic principles of the gamma-ray attenuation measuring system. The object is located between a source and a detector, which are placed oppositely. Typically, the detector measures the radiation that is scattered from the related interactions of the incident beam, while the collimator aligns the beams along the pipe diameter. Further information regarding the layout of sources, detectors and tubes is shown in the same figure.
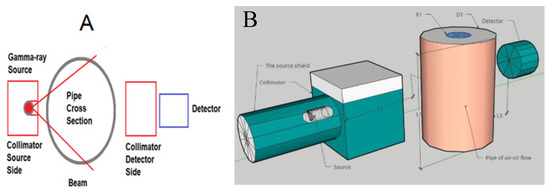
Figure 3.
(A) Gamma-ray technique for multiphase flow measurements. (B) Simulation of gamma-ray attenuation sensor.
A few detectors with one source and mechanical scanning are used so that multiple projections can be obtained to observe a dynamic process with time constants in the region of interest of multiphase flow. In regards to measurements, and in the case of a vacuum inside the pipe, Equation (2) expresses the measured value of the detector when the pipe is filled up with air. Thus, the recorded value in the detector is I0.
Initially, I0 is considered as the calibration value of the pipe. Since the air has low density property, very weak attenuation occurs. Consequently, I0 and Ia can be assumed to be equal. However, despite the landing photon energy, the air attenuation coefficient is equal to zero. In a multiphase flow, Ia is recorded as the maximum value that the detector may sense. When a pipe is filled with liquid, the value of a single energy beam is recorded by the detector
The minimum threshold for a multiphase system is the value Il (counting per pipe full of liquid). By obtaining the maximum and minimum calibration values, it is possible to calculate the difference between the linear attenuation coefficients of both phases, air and liquid, from the equation below
The predefined parameters of the gamma-ray sensor were already set according to the simulation of two-phase flow with the sensor configuration as the following. The MCNP code was run to simulate a gamma-ray attenuation-based sensor with a source of 2 mCi Cs-137 placed 30 cm away from the pipe. Moreover, the MCNP code simulated the NaI detector of 1 × 1 inches placed 20 cm away from the pipe, as referred to in Figure 3b. Table 1 represents the data set of the void fractions obtained showing the picofarad values of the capacitance-based sensor and the counts per 100 source particles of the gamma-ray attenuation-based sensor. According to the main structure, the pipe of Pyrex–glass has a length of 400 mm, an inner radius of 47.5 mm and a wall thickness of 250 mm, and the main pipe’s relative permittivity is 4.7. Using Pulse Height Tally F8, the registered counts in the detector were determined for each source particle in the MCNP-X algorithm.

Table 1.
Results of capacitance and gamma-ray attenuation-based sensors for void fractions.
3.3. ANN Models in Multiphase Flows Measurements
Neural networks have better learning ability and higher performance compared with conventional statistical methods. There are many engineering fields that use ANN modeling tools. Recently, computational and numerical calculations, including Digital Signal Processing (DSP) and especially the artificial neural network (ANN), as a very powerful mathematical tool, have shown a wide application in their use in different aspects of electrical engineering [34,35], instrumentation and control engineering [36,37,38], etc.
Figure 4 refers to Multilayer Perceptrons (MLPs) that have the ability to mimic non-linear systems of a dependent output variable Y and an input vector X by consuming the information in a set of training samples of the known values of input and output. Equation (5) represents the fitting function of a parameterized neural network with a single output
where w refers to the parameters called weights and I is the dimensionality of the input vector. The J activation function in the first layer σj(1) and the single one in the output layer σ(2) are sigmoid functions, whereas the I + 1 component includes the feature vector, XI + 1, and the J + 1 activation function.
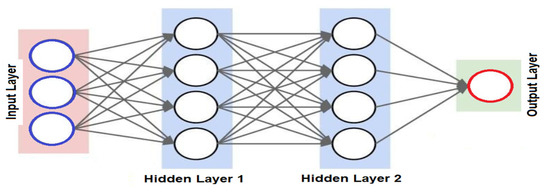
Figure 4.
A Multilayer Neural Network.
It is worth noting for the neural network model, that the number of the input layer’s neurons is taken as one neuron according to each technique individually, and as two neurons for both techniques because it needs two inputs. Several neural networks with a variant number of hidden layers and a different number of neurons in hidden layers were implemented and tested in order to find the optimum structure with minimum error. This algorithm was performed using several nested loops in written code in MATLAB software.
In this article we have tried to show the function of an MLP neural network to predict the void fraction of a two-phase flow using the combination of two different sensors. The use of other neural networks such as RBF, GMDH, etc., can be the subject of future research.
4. Results and Discussion
The performance of the neural network model was already conducted through the testing data. As shown in Table 1, 21 samples were obtained from both the capacitance-based sensor and gamma-ray attenuation-based sensor. For this study, the ratio of 70% of the data (14 samples) was involved to train the neural network, while 30% (7 samples) was used for testing the network. The proposed step was analyzed using MATLAB, which has shown more precise measurements from using the dual-techniques measurement. The sensitivity factor is higher in the gamma-ray attenuation-based sensor than in the capacitance-based sensor as determined in [31]. This property necessitates us to pick the most suitable technique for measuring void fraction and for which flow pattern of the two-phase flow it might be used. The neural network model, from Table 2 and Figure 5, shows that using gamma-ray and capacitance-based sensors gives an MAE of 3.8% and 2.6%, respectively, although a similar structure with both techniques gives a lower MAE, which is exactly 0.56%. Furthermore, the value of the MSE using the dual measurement technique is much better than the MSE values from the same techniques individually. In order to combat over-fitting and under-fitting, the accessible data are separated into two categories: training data and test data. The training data includes the information seen by the neural network and used to create the model. After the neural network is trained, its performance may be assessed using test data. As long as the neural network responds appropriately to these two data sets, the proposed network will be safe from over-fitting and under-fitting problems.

Table 2.
ANN relative-error criterion of three techniques.
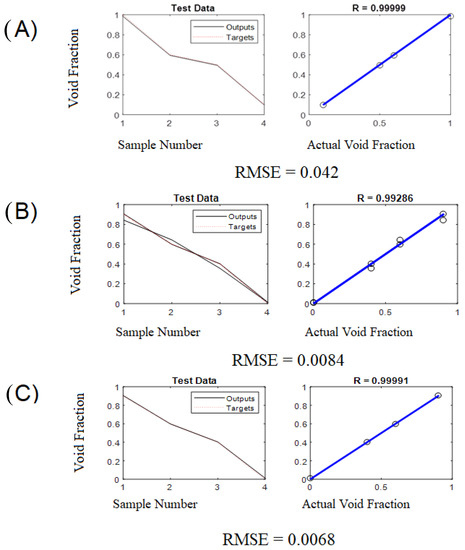
Figure 5.
Neural network performance for (A) gamma-ray, (B) capacitance, (C) capacitance and gamma-ray in annular flow regime.
5. Conclusions
In this study, dual non-intrusive techniques (capacitance-based and gamma-ray attenuation-based sensors with ANN model) were simulated for void fraction measurements. A Monte Carlo code (MCNP-X) and Finite Element (FE) package were used to design both sensors depending on predefined features of the sensors and flow regime. The phases were of two-phase flow (air–oil) and in an annular flow pattern. In a MATLAB environment, the obtained results with relative low errors determined the high accuracy of using the dual measurement techniques in multiphase flow measurements. In addition, the MLP neural network, using data from the capacitance-based and gamma-ray attenuation-based sensors, performed more accurate void fraction observations than using the techniques separately. The MAE of less than 0.006 shows the precision of the presented novel metering system. For future works, investigations of this metering system in other two-phase or three-phase flow regimes are proposed.
Author Contributions
Conceptualization, S.M., L.A., G.H.R., E.E.-Z. and E.H.; methodology, S.M., L.A. and G.H.R.; software, S.M.; data curation, S.M.; writing—original draft preparation, S.M. and E.E.-Z.; writing—review and editing, S.M.; investigation, S.M.; visualization, S.M.; supervision, L.A., G.H.R. and E.H.; resource, S.M.; validation, S.M.; funding acquisition, L.A., G.H.R. and E.E.-Z. All authors have read and agreed to the published version of the manuscript.
Funding
The authors acknowledge the support from the University of Zakho, College of Engineering, Multiphase Flow Laboratory. The authors also acknowledge the support from the German Research Foundation and the Open Access Publication Fund of the Thueringer Universitaets-und Landesbibliothek Jena Projekt-Nr. 433052568.
Institutional Review Board Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Upp, E.L.; Edmund, L.; LaNasa, P.J. Fluid Flow Measurement: A Practical Guide to Accurate Flow Measurement; Gulf Professional Pub: Houston, TX, USA, 2002; ISBN 9780884157588. [Google Scholar]
- Abouelwafa, M.S.A.; Kendall, E.J.M. The Use of Capacitance Sensors for Phase Multiphase Pipelines. IEEE Trans. Instrum. Meas. 1980, 29, 24–27. [Google Scholar] [CrossRef]
- Elkow, K.J.; Rezkallah, K.S. Void fraction measurements in gas-liquid flows using capacitance sensors. Meas. Sci. Technol. 1996, 7, 1153. [Google Scholar] [CrossRef]
- Keska, J.K.; Williams, B.E. Experimental comparison of flow pattern detection techniques for air–water mixture flow. Exp. Therm. Fluid Sci. 1999, 19, 1–12. [Google Scholar] [CrossRef]
- Tollefsen, J.; Hammer, E.A. Capacitance sensor design for reducing errors in phase concentration measurements. Flow Meas. Instrum. 1998, 9, 25–32. [Google Scholar] [CrossRef]
- Belo, F.A.; Mendes De Moura, L.F. A high frequency electronic transducer for multiphase flow measurements. J. Brazilian Soc. Mech. Sci. 1999, 21, 611–621. [Google Scholar] [CrossRef]
- Pal, A.; Vasuki, B. Void fraction measurement using concave capacitor based sensor—Analytical and experimental evaluation. Measurement 2018, 124, 81–90. [Google Scholar] [CrossRef]
- Salehi, S.M.; Karimi, H.; Dastranj, A.A. A Capacitance Sensor for Gas/Oil Two-Phase Flow Measurement: Exciting Frequency Analysis and Static Experiment. IEEE Sens. J. 2017, 17, 679–686. [Google Scholar] [CrossRef]
- Salehi, S.M.; Karimi, H.; Moosavi, R.; Dastranj, A.A. Different configurations of capacitance sensor for gas/oil two phase flow measurement: An experimental and numerical study. Exp. Therm. Fluid Sci. 2017, 82, 349–358. [Google Scholar] [CrossRef]
- Salehi, S.M.; Karimi, H.; Dastranj, A.A.; Moosavi, R. Twin rectangular fork-like capacitance sensor to flow regime identification in horizontal co-current gas-liquid two-phase flow. IEEE Sens. J. 2017, 17, 4834–4842. [Google Scholar] [CrossRef]
- Salgado, C.M.; Pereira, C.M.N.A.; Schirru, R.; Brandão, L.E.B. Flow regime identification and volume fraction prediction in multiphase flows by means of gamma-ray attenuation and artificial neural networks. Prog. Nucl. Energy 2010, 52, 555–562. [Google Scholar] [CrossRef]
- Osman, E.S.A. Artificial Neural Network Models for Identifying Flow Regimes and Predicting Liquid Holdup in Horizontal Multiphase Flow. SPE Prod. Facil. 2004, 19, 33–40. [Google Scholar] [CrossRef]
- Johansen, G.A.; Jackson, P. Radioisotope Gauges for; John Wiley & Sons: New York, NY, USA, 2004; ISBN 0471489999. [Google Scholar]
- Hooker, H.H.; Popper, G.F. A Gamma-Ray Attenuation Method for Void Fraction Determinations in Experimental Boiling Heat Transfer Test Facilities; No. ANL-5766; Argonne National Lab: Lemont, IL, USA, November 1958. [Google Scholar] [CrossRef]
- Salgado, W.L.; Brandão, L.E.B. Study of volume fractions on biphasic stratified regime using gamma ray. Braz. J. Radiat. Sci. 2019, 7, 1–14. [Google Scholar] [CrossRef]
- Cook, W.H.; Rhode, R.R. Effect of Preferred Void Distribution on Void Measurements; Argonne National Lab: Lemont, IL, USA, 1955. [Google Scholar]
- Richardson, B.L. Some Problems in Horizontal Two-Phase Tow-Component Flow (Thesis); Technical Report; Argonne National Lab.: Lemont, IL, USA, December 1958. [Google Scholar] [CrossRef]
- Petrick, M.; Swanson, B.S. Radiation Attenuation Method of Measuring Density of a Two-Phase Fluid. Rev. Sci. Instrum. 2004, 29, 1079. [Google Scholar] [CrossRef]
- Bishop, C.M.; James, G.D. Analysis of multiphase flows using dual-energy gamma densitometry and neural networks. Nucl. Instrum. Methods Phys. Res. 1993, 327, 580–593. [Google Scholar] [CrossRef]
- Åbro, E.; Johansen, G.A. Improved void fraction determination by means of multibeam gamma-ray attenuation measurements. Flow Meas. Instrum. 1999, 10, 99–108. [Google Scholar] [CrossRef]
- Tjugum, S.A.; Hjertake, B.T.; Johansen, G.A. Multiphase flow regime identification by multibeam gamma-ray densitometry. Meas. Sci. Technol. 2002, 13, 1319–1326. [Google Scholar] [CrossRef]
- Hampel, U.; Bieberle, A.; Schleicher, E.; Hoppe, D.; Zippe, C. High Resolution Gamma Ray Tomography and its Application to Multiphase Flow Measurement. In AIP Conference Proceedings; American Institute of Physics: College Park, MD, USA, 2008. [Google Scholar]
- Sun, Z.; Zhang, H. Neural networks approach for prediction of gas–liquid two-phase flow pattern based on frequency domain analysis of vortex flowmeter signals. Meas. Sci. Technol. 2007, 19, 015401. [Google Scholar] [CrossRef]
- Ozbayoglu, A.M.; Yuksel, H.E. Estimation of multiphase flow properties using computational intelligence models. In Procedia Computer Science; Elsevier: Amsterdam, The Netherlands, 2011; Volume 6, pp. 493–498. [Google Scholar]
- Nazemi, E.; Feghhi, S.A.H.; Roshani, G.H. Void fraction prediction in two-phase flows independent of the liquid phase density changes. Radiat. Meas. 2014, 68, 49–54. [Google Scholar] [CrossRef]
- Roshani, G.H.; Nazemi, E.; Feghhi, S.A.H.; Setayeshi, S. Flow regime identification and void fraction prediction in two-phase flows based on gamma ray attenuation. Meas. J. Int. Meas. Confed. 2015, 62, 25–32. [Google Scholar] [CrossRef]
- Khayat, O.; Afarideh, H. Design and simulation of a multienergy gamma ray absorptiometry system for multiphase flow metering with accurate void fraction and water-liquid ratio approximation. Nukleonika 2019, 64, 19–29. [Google Scholar] [CrossRef]
- Barbosa, P.R.; Crivelaro, K.C.O.; Seleghim, P. On the application of self-organizing neural networks in gas-liquid and gas-solid flow regime identification. J. Braz. Soc. Mech. Sci. Eng. 2010, 32, 15–20. [Google Scholar] [CrossRef][Green Version]
- Jamialahmadi, M.; Zehtaban, M.R.; Müller-Steinhagen, H.; Sarrafi, A.; Smith, J.M. Study of Bubble Formation Under Constant Flow Conditions. Chem. Eng. Res. Des. 2001, 79, 523–532. [Google Scholar] [CrossRef]
- Brennen, C.E.; Christopher, E. Fundamentals of Multiphase Flow; Cambridge University Press: Cambridge, UK, 2005; ISBN 0521848040. [Google Scholar]
- Roshani, M.; Phan, G.T.T.; Nazemi, E.; Eftekhari-Zadeh, E.; Phan, N.-H.; Corniani, E.; Tran, H.-N.; Duong, V.H.; Roshani, G.H. Performance comparison of capacitance-based flowmeter with gamma-ray attenuation-based two-phase flowmeter for determining volume fractions in an annular flow regime’s components. Eur. Phys. J. Plus 2021, 136, 176. [Google Scholar] [CrossRef]
- Mosorov, V.; Zych, M.; Hanus, R.; Petryka, L. Modelling of dynamic experiments in MCNP5 environment. Appl. Radiat. Isot. 2016, 112, 136–140. [Google Scholar] [CrossRef]
- Salgado, W.L.; de Freitas Dam, R.S.; Miranda, R.O.; Salgado, C.M.; da Silva Xavier, A. Volume fractions calculation of a biphasic system on cylindrical tube using gamma ray and MCNP6 code. Braz. J. Radiat. Sci. 2021, 9, 1–20. [Google Scholar] [CrossRef]
- Roshani, S.; Jamshidi, M.B.; Mohebi, F.; Roshani, S. Design and modeling of a compact power divider with squared resonators using artificial intelligence. Wirel. Pers. Commun. 2021, 117, 2085–2096. [Google Scholar] [CrossRef]
- Roshani, S.; Azizian, J.; Roshani, S.; Jamshidi, M.B.; Parandin, F. Design of a miniaturized branch line microstrip coupler with a simple structure using artificial neural network. Frequenz 2022, 76, 255–263. [Google Scholar] [CrossRef]
- Zych, M.; Petryka, L.; Kępński, J.; Hanus, R.; Bujak, T.; Puskarczyk, E. Radioisotope investigations of compound two-phase flows in an ope channel. Flow Meas. Instrum. 2014, 35, 11–15. [Google Scholar] [CrossRef]
- Zych, M.; Hanus, R.; Wilk, B.; Petryka, L.; Świsulski, D. Comparison of noise reduction methods in radiometric correlation measurements of two-phase liquid-gas flows. Measurement 2018, 129, 288–295. [Google Scholar] [CrossRef]
- Alanazi, A.K.; Alizadeh, S.M.; Nurgalieva, K.S.; Nesic, S.; Grimaldo Guerrero, J.W.; Abo-Dief, H.M.; Eftekhari-Zadeh, E.; Nazemi, E.; Narozhnyy, I.M. Application of Neural Network and Time-Domain Feature Extraction Techniques for Determining Volumetric Percentages and the Type of Two Phase Flow Regimes Independent of Scale Layer Thickness. Appl. Sci. 2022, 12, 1336. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).