A Review of the Hydraulic Fracturing in Ductile Reservoirs: Theory, Simulation, and Experiment
Abstract
1. Introduction
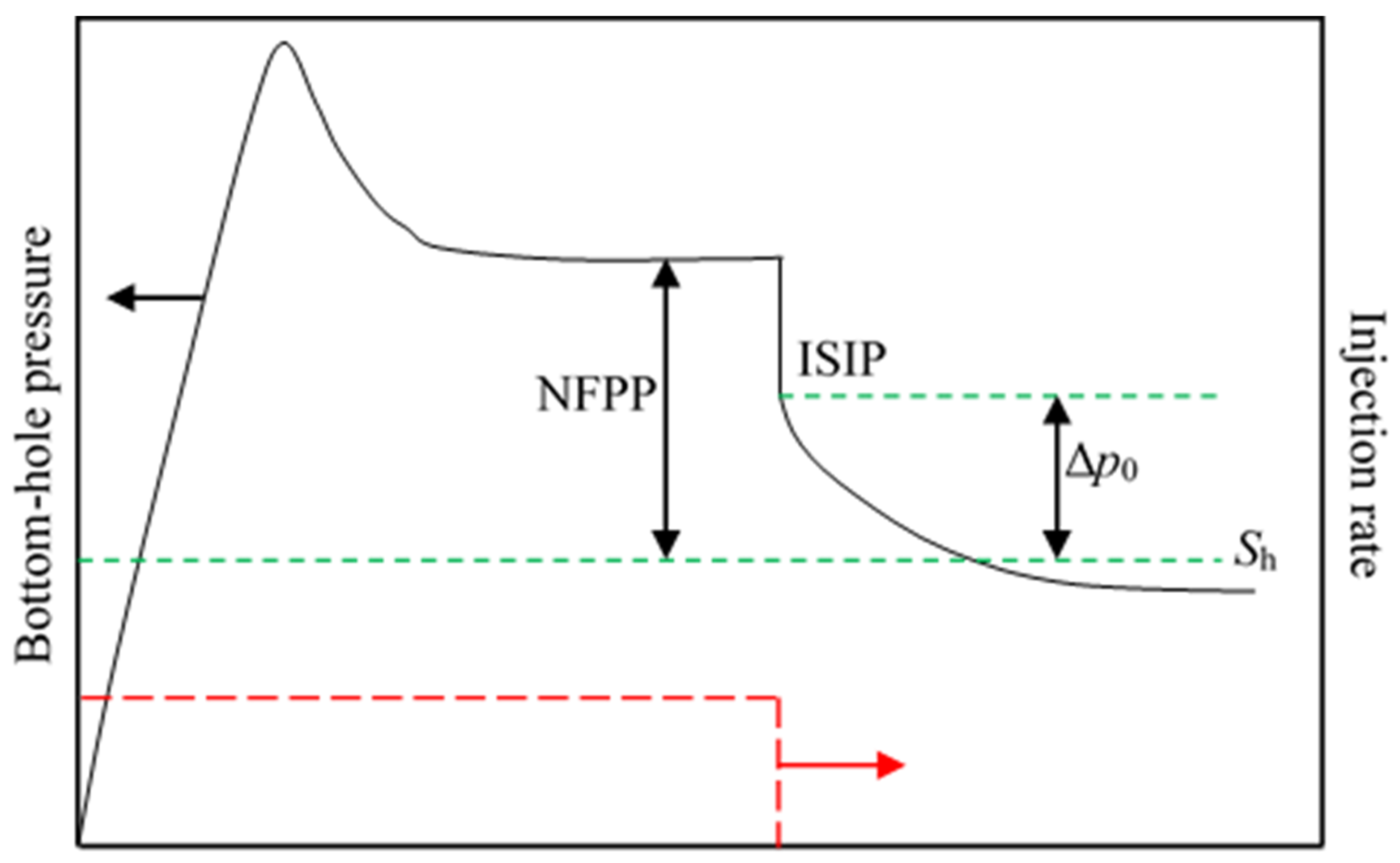
2. Phenomenon and Explanation
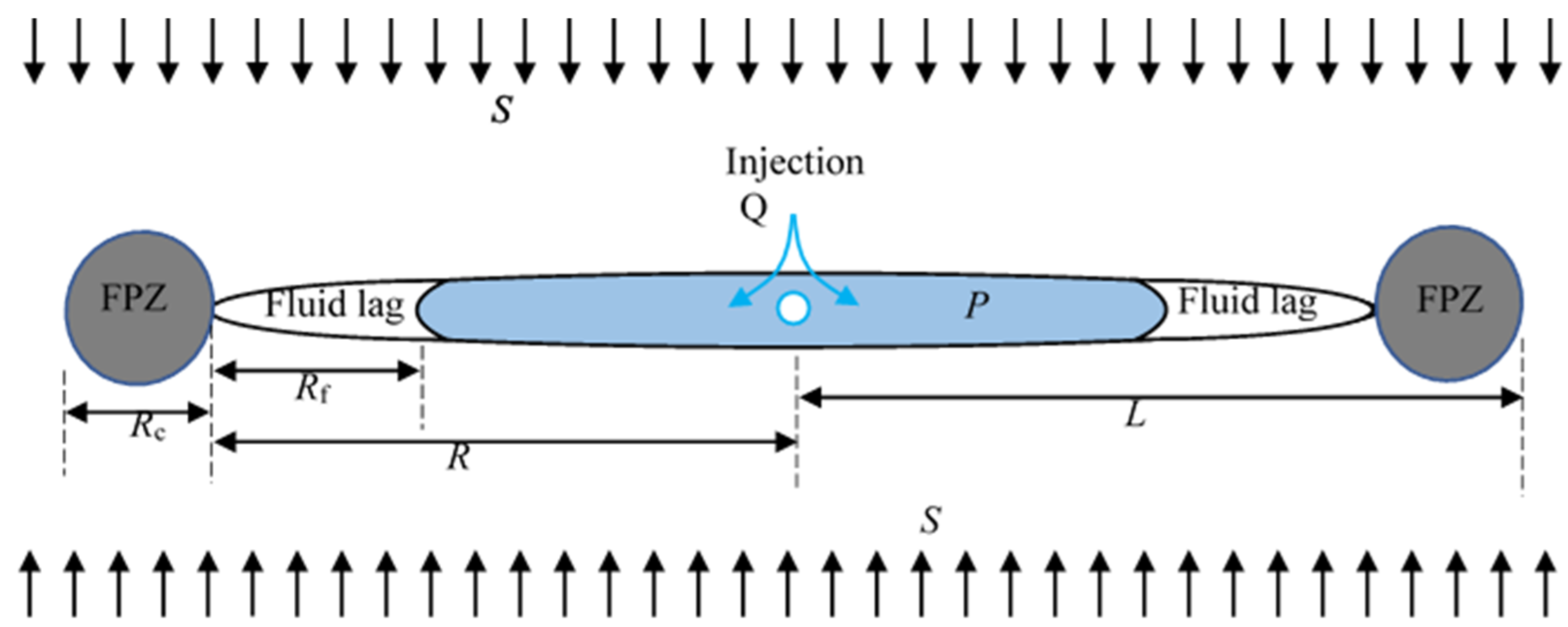
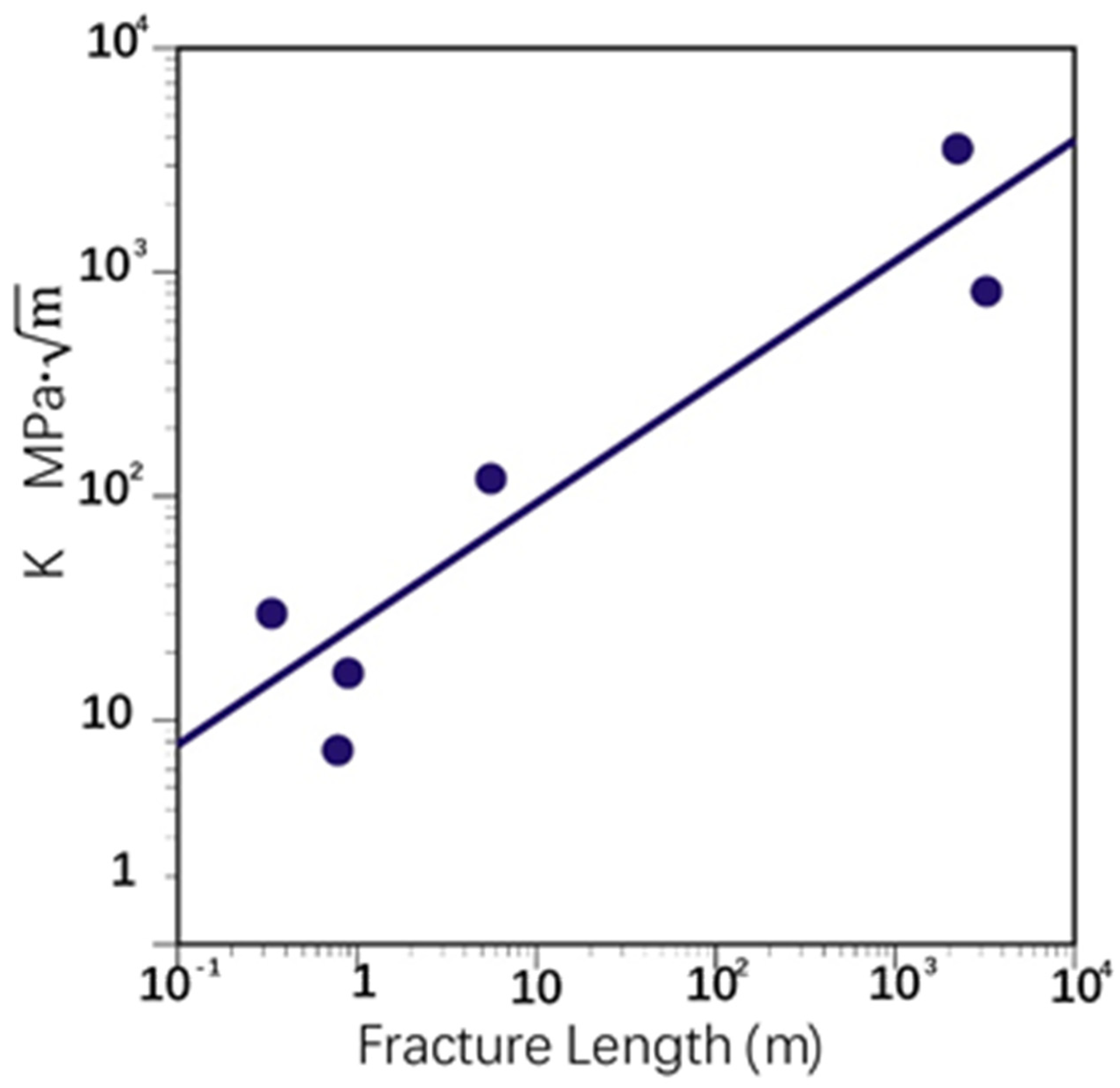
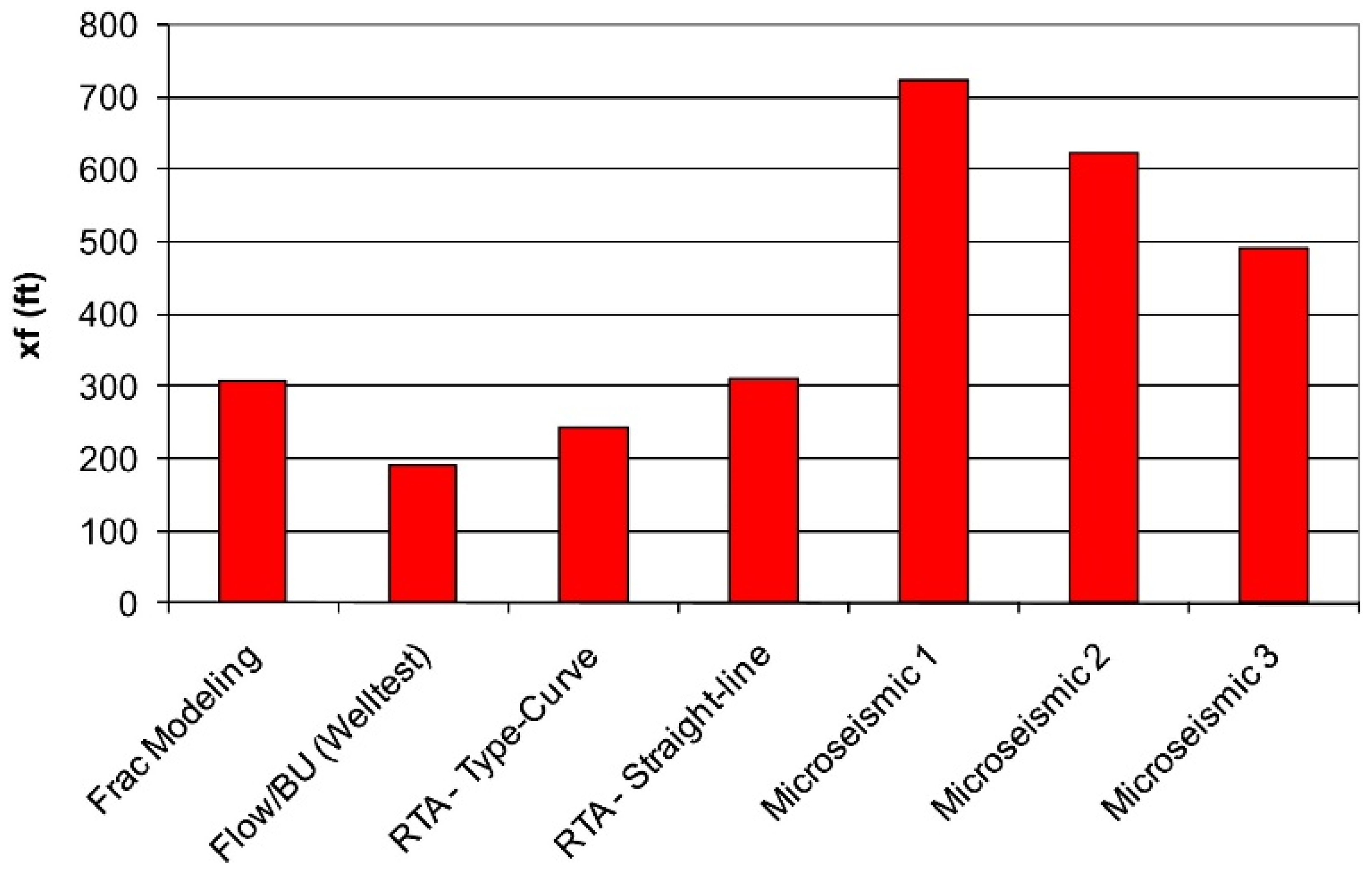
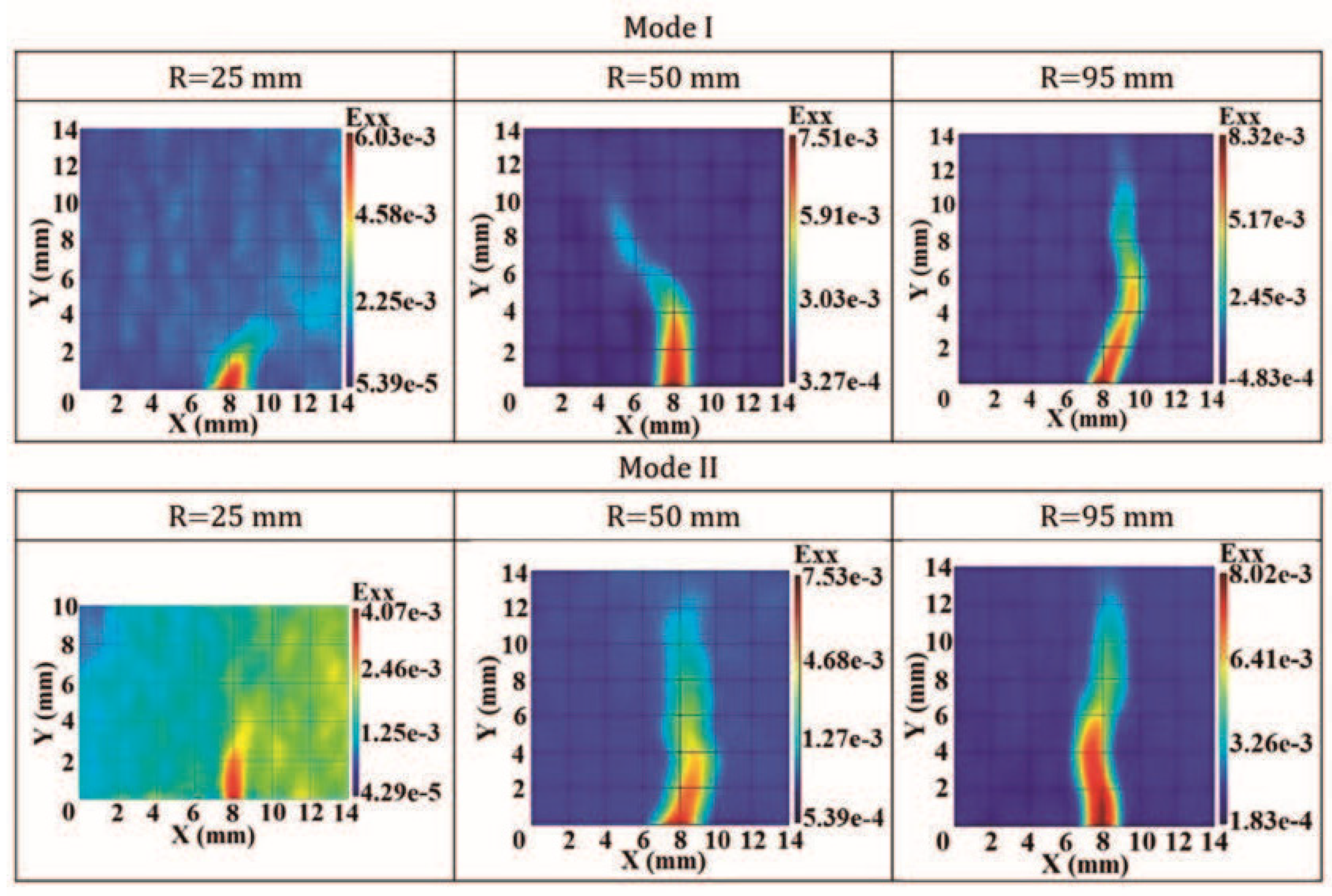
3. Fracture Process Zone
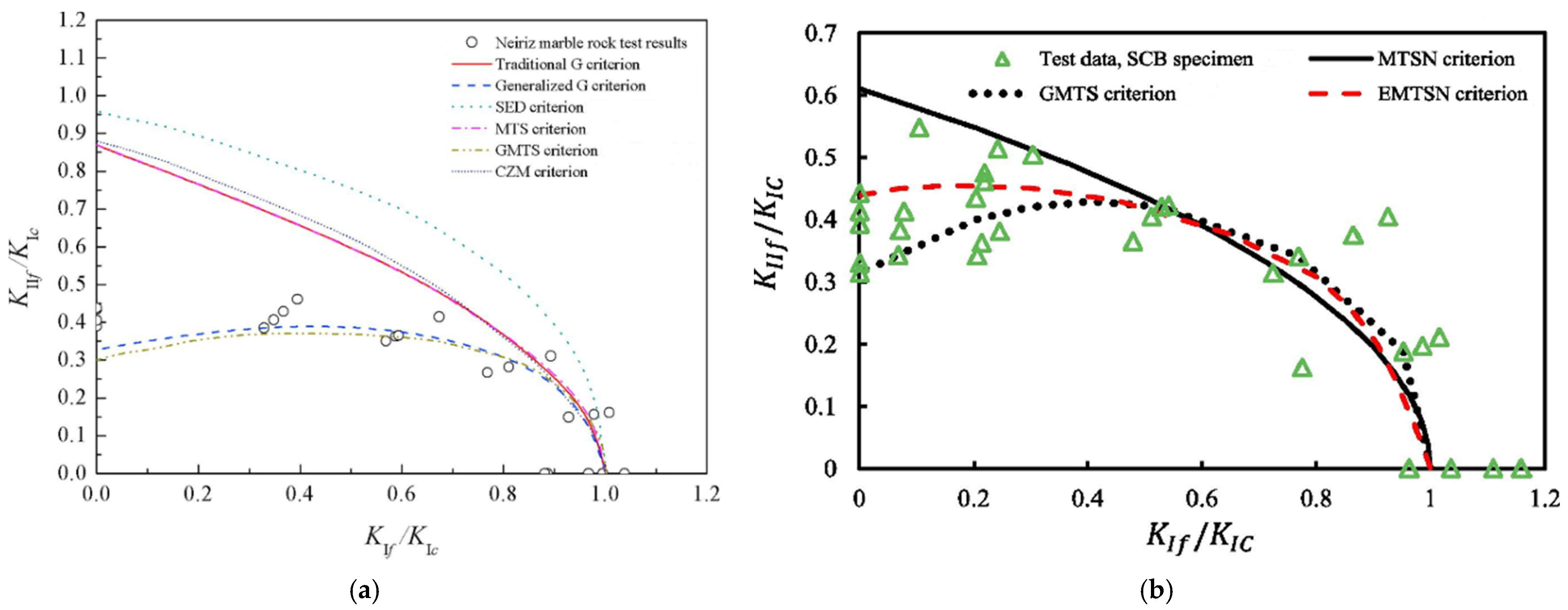
4. Fracture Propagation Criterion for Ductile Rocks
5. Hydraulic Fracturing Simulation Method Considering Rock Plastic Deformation
6. Conclusions and Prospects
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- King, G.E. Thirty Years of Gas Shale Fracturing: What Have We Learned? In Proceedings of the SPE Annual Technical Conference and Exhibition, Florence, Italy, 19–22 September 2010. [Google Scholar]
- Feng, Q.; Xu, S.; Xing, X.; Zhang, W.; Wang, S. Advances and challenges in shale oil development: A critical review. Adv. Geo-Energy Res. 2020, 4, 406–418. [Google Scholar] [CrossRef]
- Han, G.; Liu, Y.; Nawnit, K.; Zhou, Y. Discussion on seepage governing equations for low permeability reservoirs with a threshold pressure gradient. Adv. Geo-Energy Res. 2018, 2, 245–259. [Google Scholar] [CrossRef]
- Zhao, J.; Ren, L.; Jiang, T.; Hu, D.; Wu, L.; Wu, J.; Yin, C.; Li, Y.; Hu, Y.; Lin, R.; et al. Ten years of gas shale fracturing in China: Review and prospect. Nat. Gas Ind. B 2022, 9, 158–175. [Google Scholar] [CrossRef]
- Wu, Z.; Cui, C.; Jia, P.; Wang, Z.; Sui, Y. Advances and challenges in hydraulic fracturing of tight reservoirs: A critical review. Energy Geosci. 2021, 3, 427–435. [Google Scholar] [CrossRef]
- Li, Q.; Xing, H.; Liu, J.; Liu, X. A review on hydraulic fracturing of unconventional reservoir. Petroleum 2015, 1, 8–15. [Google Scholar] [CrossRef]
- Wang, W.; Zheng, D.; Sheng, G.; Zhang, Q.; Su, Y. A review of stimulated reservoir volume characterization for multiple fractured horizontal well in unconventional reservoirs. Adv. Geo-Energy Res. 2017, 1, 54–63. [Google Scholar] [CrossRef]
- Chen, B.; Barboza, B.R.; Sun, Y.; Bai, J.; Thomas, H.R.; Dutko, M.; Cottrell, M.; Li, C. A Review of Hydraulic Fracturing Simulation. Arch. Comput. Methods Eng. 2022, 29, 1–58. [Google Scholar] [CrossRef]
- Sone, H.; Zoback, M.D. Visco-plastic properties of shale gas reservoir rocks. In Proceedings of the 45th U.S. Rock Mechanics/Geomechanics Symposium, San Francisco, CA, USA, 26–29 June 2011. [Google Scholar]
- Martin, A.N. Crack tip plasticity: A different approach to modelling fracture propagation in soft formations. In Proceedings of the 2000 SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 1–4 October 2000. [Google Scholar]
- Marsden, H.; Basu, S.; Striolo, A.; MacGregor, M. Advances of nanotechnologies for hydraulic fracturing of coal seam gas reservoirs: Potential applications and some limitations in Australia. Int. J. Coal. Sci. Technol. 2022, 9, 27. [Google Scholar] [CrossRef]
- Papanastasiou, P. The influence of plasticity in hydraulic fracturing. Int. J. Fract. 1997, 84, 61–79. [Google Scholar] [CrossRef]
- Pak, A. Numerical Modeling of Hydraulic Fracturing. Ph.D. Thesis, The University of Alberta, Edmonton, AB, Canada, 1997. [Google Scholar]
- Jin, X.; Shah, S.N.; Sheng, M. Hydraulic fracturing model based on nonlinear fracture mechanics: Theory and simulation. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 8–10 October 2012. [Google Scholar]
- Carrier, B.; Granet, S. Numerical modeling of hydraulic fracture problem in permeable medium using cohesive zone model. Eng. Fract. Mech. 2012, 79, 312–328. [Google Scholar] [CrossRef]
- Sarris, E.; Papanastasiou, P. The influence of the cohesive process zone in hydraulic fracturing modelling. Int. J. Fract. 2011, 167, 33–45. [Google Scholar] [CrossRef]
- Sarris, E.; Papanastasiou, P. Modeling of hydraulic fracturing in a poroelastic cohesive formation. Int. J. Geomech. 2012, 12, 160–167. [Google Scholar] [CrossRef]
- Yao, Y.; Liu, L.; Keer, L.M. Pore pressure cohesive zone modeling of hydraulic fracture in quasi-brittle rocks. Mech. Mater. 2015, 83, 17–29. [Google Scholar] [CrossRef]
- Wang, Y.; Fotios, K. Induced stresses near a hydraulic fracture and fracture geometry with plasticity. In Proceedings of the SPE Asia Pacific Hydraulic Fracturing Conference, Beijing, China, 24–26 August 2016. [Google Scholar]
- Cleary, M.P.; Wright, C.A.; Wright, T.B. Experimental and modeling evidence for major changes in hydraulic fracturing design and field procedures. In Proceedings of the SPE Gas Technology Symposium, Houston, TX, USA, 22 January 1991. [Google Scholar]
- Papanastasiou, P.; Thiercelin, M. Influence of inelastic rock behaviour in hydraulic fracturing. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1993, 30, 1241–1247. [Google Scholar] [CrossRef]
- Papanastasiou, P.; Atkinson, C. Representation of crack-tip plasticity in pressure sensitive geomaterials: Large scale yielding. Int. J. Fract. 2006, 139, 137–144. [Google Scholar] [CrossRef]
- Sarris, E.; Papanastasiou, P. Numerical modeling of fluid-driven fractures in cohesive poroelastoplastic continuum. Int. J. Numer. Anal. Meth. Geomech. 2013, 37, 1822–1846. [Google Scholar] [CrossRef]
- Zaki, K.S.; Wang, G.; Meng, F.; Abou-Sayed, A.S. A 3-D plastic fracture simulation to assess fracture volumes in compacting reservoir. In Proceedings of the Gulf Rocks 2004, the 6th North America Rock Mechanics Symposium (NARMS): Rock Mechanics Across Borders and Disciplines, Houston, TX, USA, 5–9 June 2004. [Google Scholar]
- Parker, M.; Petre, E.; Dreher, D.; Buller, D. Haynesville shale: Hydraulic fracture stimulation approach. In Proceedings of the International Coalbed & Shale Gas Symposium, Tuscaloosa, AL, USA, 18–22 May 2009. [Google Scholar]
- Germanovich, L.N.; Astakhov, D.K.; Shlyapobersky, J.; Mayerhofer, M.J.; Dupont, C.; Ring, L.M. Modeling multi-segmented hydraulic fracture in two extreme cases: No leak-off and dominating leak-off. Int. J. Rock Mech. Min. Sci. 1998, 35, 551–554. [Google Scholar] [CrossRef]
- Papanastasiou, P. The effective fracture toughness in hydraulic fracturing. Int. J. Fract. 1999, 96, 127–147. [Google Scholar] [CrossRef]
- Van Dam, D.B.; Papanastasiou, P.; De Pater, C.J. Impact of rock plasticity on hydraulic fracture propagation and closure. SPE Prod. Facil. 2002, 17, 149–159. [Google Scholar] [CrossRef]
- Medlin, W.L.; Fitch, J.L. Abnormal treating pressures in MHF treatments. In Proceedings of the 58th SPE Annual Technical Conference, San Francisco, CA, USA, 5 October 1983. [Google Scholar]
- Shlyapobersky, J.; Chudnovsky, A. Review of recent developments in fracture mechanics with petroleum engineering applications. In Proceedings of the SPE/ISRM Rock Mechanics in Petroleum Engineering Conference, Delft, The Netherlands, 29 August 1994. [Google Scholar]
- Shlyapobersky, J.; Issa, M.A.; Issa, M.A.; Islam, M.; Dudley, J.W.; Shulkin, Y.; Chudnovsky, A. Scale effects on fracture growth resistance in poroelastic materials. In Proceedings of the SPE Annual Technical Conference and Exhibition, Orleans, LA, USA, 27 September 1998. [Google Scholar]
- Shlyapobersky, J. Energy analysis of hydraulic fracturing. In Proceedings of the 26th US Symposium on Rock Mechanics (USRMS), Rapid City, SD, USA, 26 June 1985. [Google Scholar]
- Shlyapobersky, J.; Wong, G.; Walhaug, W. Overpressure calibrated design of hydraulic fracture stimulations. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 2 October 1988. [Google Scholar]
- Bunger, A.P. A rigorous tool for evaluating the importance of viscous dissipation in sill formation: It’s in the tip. Geol. Soc. Lond. Spec. Publ. 2008, 304, 71–81. [Google Scholar] [CrossRef]
- Rivalta, E.; Taisne, B.; Bunger, A.; Katz, R. A review of mechanical models of dike propagation: Schools of thought, results and future directions. Tectonophysics 2015, 638, 1–42. [Google Scholar] [CrossRef]
- Olson, J.E. Sublinear scaling of fracture aperture versus length: An exception or the rule? J. Geophys. Res. Solid Earth 2003, 108, 2413. [Google Scholar] [CrossRef]
- Delaney, P.T.; Pollard, D.D. Deformation of Host Rocks and Flow of Magma during Growth of Minette Dikes and Breccia-Bearing Intrusions Near Ship Rock, New Mexico; Geological Survey Professional Paper 1202; United States Government Printing Office: Washington, DC, USA, 1981.
- Jin, Z.H.; Johnson, S.E. Magma-driven multiple dike propagation and fracture toughness of crustal rocks. J. Geophys. Res. Solid Earth 2008, 113, B03206. [Google Scholar] [CrossRef]
- Rivalta, E.; Dahm, T. Acceleration of buoyancy-driven fractures and magmatic dikes beneath the free surface. Geophys. J. Int. 2006, 166, 1424–1439. [Google Scholar] [CrossRef]
- Bunger, A.; Cruden, A. Modeling the growth of laccoliths and large mafic sills: Role of magma body forces. J. Geophys. Res. 2011, 116, B02203. [Google Scholar] [CrossRef]
- Atkinson, B.K. Subcritical crack growth in geological materials. J. Geophys. Res. Solid Earth 1984, 89, 4077–4114. [Google Scholar] [CrossRef]
- Atkinson, B.K.; Meredith, P.G. Experimental fracture mechanics data for rocks and minerals. In Fracture Mechanics of Rock; Atkinson, B.K., Ed.; Academic Press: London, UK, 1987; pp. 477–525. [Google Scholar]
- Palmer, I.D.; Veatch, R.W., Jr. Abnormally high fracturing pressures in step-rate tests. SPE Prod. Eng. 1990, 5, 315–323. [Google Scholar] [CrossRef]
- Bunger, A.; Lecampion, B. Four critical issues for successful hydraulic fracturing applications. In Rock Mechanics and Engineering, Vol. 5: Surface and Underground Projects; Feng, X., Ed.; CRC Press: London, UK, 2017; pp. 551–593. [Google Scholar]
- Labuz, J.; Shah, S.; Dowding, C. Experimental analysis of crack propagation in granite. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1985, 22, 85–98. [Google Scholar] [CrossRef]
- Garagash, D.I. Roughness-dominated hydraulic fracture propagation. In Proceedings of the 2015 AGU Fall Meeting Abstracts, AGU, San Francisco, CA, USA, 17 December 2015. [Google Scholar]
- Warpinski, N.R. Measurement of width and pressure in a propagating hydraulic fracture. Soc. Petrol. Eng. J. 1985, 25, 46–54. [Google Scholar] [CrossRef]
- Bunger, A.P.; Detournay, E.; Jeffrey, R.G. Crack tip behavior in near-surface fluid-driven fracture experiments. Comptes Rendus Mécanique 2005, 333, 299–304. [Google Scholar] [CrossRef]
- Groenenboom, J.; Dam, D.V. Monitoring hydraulic fracture growth: Laboratory experiments. Geophysics 2000, 65, 603–611. [Google Scholar] [CrossRef]
- Ispas, I.; Eve, R.; Hickman, R.J.; Keck, R.G.; Willson, S.M.; Olson, K.E. Laboratory testing and numerical modelling of fracture propagation from deviated wells in poorly consolidated formations. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 8 October 2012. [Google Scholar]
- Naidu, R.N.; Rylance, M. A simple method for identifying fracture initiation pressure. In Proceedings of the SPE/IADC Drilling Conference and Exhibition, The Hague, The Netherlands, 14 March 2017. [Google Scholar]
- Van Dam, D.B. The Influence of Inelastic Rock Behaviour on Hydraulic Fracture Geometry. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 1999. [Google Scholar]
- Barenblatt, G.I. The mathematical theory of equilibrium cracks in brittle fracture. Adv. Appl. Mech. 1962, 7, 55–129. [Google Scholar]
- Bazant, Z.P.; Le, J.L. Probabilistic Mechanics of Quasibrittle Structures; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Garagash, D.I. Cohesive-zone effects in hydraulic fracture propagation. J. Mech. Phys. Solids 2019, 133, 103727. [Google Scholar] [CrossRef]
- Swanson, P.L. Tensile fracture resistance mechanisms in brittle polycrystals: An ultrasonics and in situ microscopy investigation. J. Geophys. Res. 1987, 92, 8015–8036. [Google Scholar] [CrossRef]
- Johnson, E.; Cleary, M.P. Implications of recent laboratory experimental results for hydraulic fractures. In Proceedings of the Low Permeability Reservoir Symposium, Denver, CO, USA, 15 April 1991. [Google Scholar]
- Moradian, Z.; Fathi, A.; Evans, B. Shear reactivation of natural fractures in hydraulic fracturing. In Proceedings of the 50th US Rock Mechanics/Geomechanics Symposium, Houston, TX, USA, 26–29 June 2016. [Google Scholar]
- Rahman, M.; Hossain, M.; Rahman, S. A shear-dilation-based model for evaluation of hydraulically stimulated naturally fractured reservoirs. Int. J. Numer. Anal. Methods Geomech. 2002, 26, 469–497. [Google Scholar] [CrossRef]
- Zoback, M.D.; Kohli, A.; Das, I.; Mcclure, M.W. The importance of slow slip on faults during hydraulic fracturing stimulation of shale gas reservoirs. In Proceedings of the SPE Americas Unconventional Resources Conference, Pittsburgh, PA, USA, 5 June 2012. [Google Scholar]
- Feng, R.; Sarmadivaleh, M. Shear dilation in hydraulic fracturing: Insight from Laboratory experiment. In Proceedings of the 53rd US Rock Mechanics/Geomechanics Symposium, New York, NY, USA, 23–26 June 2019. [Google Scholar]
- Abou-Sayed, A.S.; Brechtel, C.E.; Clifton, R.J. In situ stress determination by hydrofracturing: A fracture mechanics approach. J. Geophys. Res. 1978, 83, 2851. [Google Scholar] [CrossRef]
- Ito, T.; Evans, K.; Kawai, K.; Hayashi, K. Hydraulic fracture reopening pressure and the estimation of maximum horizontal stress. Int. J. Rock Mech. Min. Sci. 1999, 36, 811–826. [Google Scholar] [CrossRef]
- Lhomme, T.; Detournay, E.; Jeffrey, R.G. Effect of fluid compressibility and borehole on the initiation and propagation of a tranverse hydraulic fracture. Strength Fract. Complex. 2005, 3, 149–162. [Google Scholar]
- Lakirouhani, A.; Detournay, E.; Bunger, A. A reassessment of in situ stress determination by hydraulic fracturing. Geophys. J. Int. 2016, 205, 1859–1873. [Google Scholar] [CrossRef]
- Gao, Y.; Detournay, E. Fracture toughness interpretation from breakdown pressure. Eng. Fract. Mech. 2021, 243, 107518. [Google Scholar] [CrossRef]
- Gao, Y.; Eve, R.; Heller, R.; Ispas, I.; McLennan, J.; Detournay, E. A reinterpretation of fracture toughness from fluid injection testing. In Proceedings of the 55th US Rock Mechanics/Geomechanics Symposium, Houston, TX, USA, 21–25 June 2021. [Google Scholar]
- Mahrer, K.D. Microseismic logging: A new hydraulic fracture diagnostic method. In Proceedings of the 1991 SPE Joint Rocky Mountain Regional/Low Permeability Reservoirs Symposium, Denver, CO, USA, 15–17 April 1991. [Google Scholar]
- Mahrer, K.D.; Mauk, F.J. Seismic wave motion for a new model of hydraulic fracture with an induced low-velocity zone. J. Geophys. Res. 1987, 92, 9293–9309. [Google Scholar] [CrossRef]
- Warpinski, N.R.; Teufel, L.W. Influence of geologic discontinuities on hydraulic fracture propagation. J. Pet. Technol. 1987, 39, 209–220. [Google Scholar] [CrossRef]
- Warpinski, N.R.; Lorenz, J.C.; Branagan, P.T.; Myal, F.R.; Gall, B.L. Examination of a cored hydraulic fracture in a deep gas well. SPE Prod. Fac. 1993, 8, 150–158. [Google Scholar] [CrossRef]
- Delaney PTPollard, D.D.; Ziony, J.I.; McKee, E.H. Field relations between dikes and joints: Emplacement processes and paleostress analysis. J. Geophys. Res. Solid Earth 1986, 91, 4920–4938. [Google Scholar] [CrossRef]
- Perkins, T.K.; Krech, W.W. Effect of cleavage rate and stress level on apparent surface energies of rocks. Soc. Petrol. Eng. J. 1966, 6, 308–314. [Google Scholar] [CrossRef]
- Thiercelin, M. Fracture toughness under confining pressure using the modified ting test. In Proceedings of the 28th U.S. Symposium on Rock Mechanics (USRMS), Tucson, AZ, USA, 29 June 1987. [Google Scholar]
- Al-Shayea, N.A.; Khan, K.; Abduljauwad, S.N. Effects of confining pressure and temperature on mixed-mode (I–II) fracture toughness of a limestone rock. Int. J. Rock Mech. Min. Sci. 2000, 37, 629–643. [Google Scholar] [CrossRef]
- Guo, H.; Aziz, N.I.; Schmidt, L.C. Rock fracture-toughness determination by the Brazilian Test. Eng. Geol. 1993, 33, 177–188. [Google Scholar] [CrossRef]
- Schmidt, R.; Huddle, C. Effect of confining pressure on fracture toughness of Indiana limestone. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1977, 14, 289–293. [Google Scholar] [CrossRef]
- Gehne, S.; Forbes Inskip, N.D.; Benson, P.M.; Meredith, P.G.; Koor, N. Fluid-driven tensile fracture and fracture toughness in Nash point shale at elevated pressure. J. Geophys. Res. Solid Earth 2020, 125, 1–11. [Google Scholar] [CrossRef]
- Stanchits, S.; Burghardt, J.; Surdi, A. Hydraulic fracturing of heterogeneous rock monitored by acoustic emission. Rock Mech. Rock Eng. 2015, 48, 2513–2527. [Google Scholar] [CrossRef]
- Stoeckhert, F.; Brenne, S.; Molenda, M.; Alber, M. Mode I fracture toughness of rock under confining pressure. In Proceedings of the ISRM International Symposium—EUROCK 2016, Ürgüp, Turkey, 29 August 2016. [Google Scholar]
- Chandler, M.R.; Mecklenburgh, J.; Rutter, E.; Lee, P. Fluid injection experiments in shale at elevated confining pressures: Determination of flaw sizes from mechanical experiments. J. Geophys. Res. Solid Earth 2019, 124, 5500–5520. [Google Scholar] [CrossRef]
- Thallak, S.; Holder, J.; Gray, K. The pressure dependence of apparent hydrofracture toughness. In Proceedings of the 34th US Symposium on Rock Mechanics (USRMS), Madison, WI, USA, 28 June 1993. [Google Scholar]
- Bohloli, B.; de Pater, C.J. Experimental study on hydraulic fracturing of soft rocks: Influence of fluid rheology and confining stress. J. Pet. Sci. Eng. 2006, 53, 1–12. [Google Scholar] [CrossRef]
- Omori, Y.; Jin, S.; Ito, T.; Nagano, Y.; Sekine, K. Experimental study of hydraulic fracturing in unconsolidated sands using X-ray CT method. In Proceedings of the 47th U.S. Rock Mechanics/Geomechanics Symposium, San Francisco, CA, USA, 23 June 2013. [Google Scholar]
- De Pater, C.J.; Dong, Y.; Bohloli, B. Experimental study of hydraulic fracturing in sand as a function of stress and fluid rheology. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, College Station, TX, USA, 29 January 2007. [Google Scholar]
- Germanovich, L.N.; Hurt, R.S.; Ayoub, J.A.; Siebrits, E.; Norman, D.; Ispas, I.; Montgomery, C.T. Experimental study of hydraulic fracturing in unconsolidated materials. In Proceedings of the SPE International Symposium and Exhibition on Formation Damage Control, Lafayette, LA, USA, 15 February 2012. [Google Scholar]
- Golovin, E.; Jasarevic, H.; Chudnovsky, A.; Dudley, J.W.; Wong, G.K. Observation and Characterization of Hydraulic Fracture in Cohesionless Sand. In Proceedings of the 44th U.S. Rock Mechanics Symposium and 5th U.S.-Canada Rock Mechanics Symposium, Salt Lake City, UT, USA, 27 June 2010. [Google Scholar]
- Brooks, Z.; Ulm, F.J.; Einstein, H.H.; Abousleiman, Y. A nanomechanical investigation of the crack tip process zone. In Proceedings of the 44th US Rock Mechanics Symposium and 5th U.S.-Canada Rock Mechanics Symposium, Salt Lake City, UT, USA, 27–30 June 2010. [Google Scholar]
- Hashida, T.; Oghikubo, H.; Takahashi, H.; Shoji, T. Numerical simulation with experimental verification of the fracture behavior in granite under confining pressures based on the tension-softening model. Int. J. Fract. 1993, 59, 227–244. [Google Scholar] [CrossRef]
- Rubin, A.M. Tensile fracture of rock at high confining pressure: Implications for dike propagation. J. Geophys. Res. Solid Earth 1993, 98, 15919–15935. [Google Scholar] [CrossRef]
- Yue, K.; Lee, H.P.; Olson, J.E.; Schultz, R.A. Apparent fracture toughness for LEFM applications in hydraulic fracture modeling. Eng. Fract. Mech. 2020, 230, 106984. [Google Scholar] [CrossRef]
- Rocco, C.; Guinea, G.V.; Planas, J.; Elices, M. Size effect and boundary conditions in the Brazilian test: Experimental verification. Mater. Struct. 1999, 32, 210–217. [Google Scholar] [CrossRef]
- Ayatollahi, M.R.; Akbardoost, J. Size and geometry effects on rock fracture toughness: Mode I fracture. Rock Mech. Rock Eng. 2014, 47, 677–687. [Google Scholar] [CrossRef]
- Fakhimi, A.; Tarokh, A. Process zone and size effect in fracture testing of rock. Int. J. Rock Mech. Min. Sci. 2013, 60, 95–102. [Google Scholar] [CrossRef]
- Galouei, M.; Fakhimi, A. Size effect, material ductility and shape of fracture process zone in quasi-brittle materials. Comput. Geotech. 2015, 65, 126–135. [Google Scholar] [CrossRef]
- Fakhimi, A.; Galouei, M. Size effect on length and width of fracture process zone. In Proceedings of the 49th US Rock Mechanics/Geomechanics Symposium, San Francisco, CA, USA, 28 June–1 July 2015. [Google Scholar]
- Aliha, M.R.M.; Ayatollahi, M.R.; Smith, D.J.; Pavier, M.J. Geometry and size effects on fracture trajectory in a limestone rock under mixed mode loading. Eng. Fract. Mech. 2010, 77, 2200–2212. [Google Scholar] [CrossRef]
- Bazant, Z.P.; Gettu, R.; Kazemi, M.T. Identification of nonlinear fracture properties from size effect tests and structural analysis based on geometry-dependent R-curves. Int. J. Rock Mech. Min. Sci. 1991, 28, 43–51. [Google Scholar] [CrossRef]
- Khan, K.; Al-Shayea, N.A. Effect of specimen geometry and testing method on mixed mode I–II fracture toughness of a limestone rock from Saudi Arabia. Rock Mech. Rock Eng. 2000, 33, 179–206. [Google Scholar] [CrossRef]
- Wei, M.D.; Dai, F.; Xu, N.W.; Zhao, T.; Xia, K.W. Experimental and numerical study on the fracture process zone and fracture toughness determination for ISRM-suggested semicircular bend rock specimen. Eng. Fract. Mech. 2016, 154, 43–56. [Google Scholar] [CrossRef]
- Funatsu, T.; Shimizu, N.; Kuruppu, M.; Matsui, K. Evaluation of mode I fracture toughness assisted by the numerical determination of K-resistance. Rock Mech. Rock Eng. 2015, 48, 143–157. [Google Scholar] [CrossRef]
- Funatsu, T.; Seto, M.; Shimada, H.; Matsui, K.; Kuruppu, M. Combined effects of increasing temperature and confining pressure on the fracture toughness of clay bearing rocks. Int. J. Rock Mech. Min. Sci. 2004, 41, 927–938. [Google Scholar] [CrossRef]
- Ingraffea, A.R.; Schmidt, R.A. Experimental verification of a fracture mechanics model for tensile strength prediction of Indiana limestone. In Proceedings of the 19th U.S. Symposium on Rock Mechanics (USRMS), Reno, NV, USA, 1 May 1978. [Google Scholar]
- Schmidt, R.A.; Lutz, T.J. KIc and JIc of Westerly granite—Effects of thickness and in-plane dimensions. In Proceedings of the 11th Symposium on Fracture Mechanics, Blacksburg, VA, USA, 12 June 1978. [Google Scholar]
- Hashida, T.; Sato, K.; Takahashi, H. Significance of crack opening for determining the growth behavior monitoring of hydrofractures. In Proceedings of the Eighteenth Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 26–28 January 1993; pp. 79–84. [Google Scholar]
- Weisinger, R.; Costin, L.S.; Lutz, T.J. KIc and J-resistance-curve measurements on Nevada Tuff. Exp. Mech. 1980, 26, 68–72. [Google Scholar] [CrossRef]
- Scholz, C.H. A note on the scaling relations for opening mode fractures in rock. J. Struct. Geol. 2010, 32, 1485–1487. [Google Scholar] [CrossRef]
- Schultz, R.A.; Soliva, R.; Fossen, H.; Okubo, C.H.; Reeves, D.M. Dependence of displacement–length scaling relations for fractures and deformation bands on the volumetric changes across them. J. Struct. Geol. 2008, 30, 1405–1411. [Google Scholar] [CrossRef]
- Schultz, R.A.; Mège, D.; Diot, H. Emplacement conditions of igneous dikes in Ethiopian traps. J. Volcanol. Geotherm. Res. 2008, 178, 683–692. [Google Scholar] [CrossRef]
- Labuz, J.F.; Shah, S.P.; Dowding, C.H. The fracture process zone in granite: Evidence and effect. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1987, 24, 235–246. [Google Scholar] [CrossRef]
- Kobayashi, R.; Matsuki, K.; Otsuka, N. Size effect in the fracture toughness in Ogina Tuff. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1986, 23, 13–18. [Google Scholar] [CrossRef]
- Olson, J.E.; Schultz, R.A. Comment on “A note on the scaling relations for opening mode fractures in rock” by C.H. Scholz. J. Struct. Geol. 2011, 33, 1523–1524. [Google Scholar] [CrossRef]
- Schultz, R.A.; Klimczak, C.; Fossen, H.; Olson, J.E.; Exner, U.; Reeves, D.M.; Soliva, R. Statistical tests of scaling relationships for geologic structures. J. Struct. Geol. 2013, 48, 85–94. [Google Scholar] [CrossRef]
- Abe, H.; Mura, T.; Keer, L.M. Growth rate of a penny-shape crack in hydraulic fracturing of rocks. J. Geophys. Res. 1976, 8, 5335–5340. [Google Scholar] [CrossRef]
- Savitski, A.; Detournay, E. Propagation of a fluid-driven penny-shaped fracture in an impermeable rock: Asymptotic solutions. Int. J. Solids Struct. 2002, 39, 6311–6337. [Google Scholar] [CrossRef]
- Daneshy, A.A. Hydraulic Fracture Propagation in Layered Formations. SPE J. 1978, 18, 33–41. [Google Scholar] [CrossRef]
- Roodhart, L.P.; Fokker, P.A.; Davies, D.R.; Shlyapobersky, J.; Wong, G.K. Frac-and Pack Stimulation: Application, Design, and Field Experience. J. Pet. Technol. 1994, 46, 230–238. [Google Scholar] [CrossRef]
- Johnson, D.E.; Wright, C.A.; Stachel, A.; Schmidt, H.; Cleary, M.P. On-site real-time analysis allows optimal propped fracture stimulation of a complex gas reservoir. In Proceedings of the SPE 25414, SPE Production Operations Symposium, Oklahoma City, OK, USA, 21–23 March 1993. [Google Scholar]
- Chudnovsky, A.; Fan, F.; Shulkin, Y.; Dudley, J.W.; Nichols, W.B.; Wong, G.K. Hydraulic Fracture Containment in Layered Media, Experiment and Computer Simulation. In Proceedings of the 38th US Rock Mechanics Symposium, Washington, DC, USA, 10–12 June 2001. [Google Scholar]
- Britt, L.K.; Smith, M.B.; Cunningham, L.E.; Waters, F.; Dannish, G.A.; Lachance DMackow, H.M. Frac-packing high-permeability sands in the mahogany field, offshore Trinidad. In Proceedings of the SPE Annual Technical Conference, Dallas, TX, USA, 1–4 October 2000. [Google Scholar]
- Kizaki, A.; Ohashi, K.; Tanaka, H.; Sakaguchi, K. Effects of vertical stress on fracture propagation using super critical carbon dioxide. In Rock Mechanics for Resources, Energy and Environment; Kwasniewski, M., Lydzba, D., Eds.; Taylor & Francis Group: London, UK, 2013. [Google Scholar]
- Chudnovsky, A.; Fan, F.; Shulkin, Y.; Zhang, H.; Dudley, J.W.; Wong, G.K. Hydraulic Fracture Simulation Revisited. In Proceedings of the 42nd US Rock Mechanics Symposium and 2nd U.S.-Canada Rock Mechanics Symposium, San Francisco, CA, USA, 29 June–2 July 2008. [Google Scholar]
- Schmidt, R.A. A microcrack model and its significance to hydraulic fracturing and fracture toughness testing. In Proceedings of the 21st U.S. Symposium on Rock Mechanics (USRMS), Rolla, MO, USA, 27 May 1980. [Google Scholar]
- Haberfield, C.M.; Ian, J. Determination of fracture toughness of a saturated soft rock. Can. Geotech. J. 1990, 27, 276–284. [Google Scholar] [CrossRef]
- Lim, I.L.; Johnston, I.W.; Choi, S.K.; Boland, J.N. Fracture testing of a soft rock with semi-circular specimens under three point bending, part 1: Mode-I. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1994, 31, 185–197. [Google Scholar] [CrossRef]
- Kenner, V.H.; Advani, S.H.; Richard, T.G. A Study of Fracture Toughness for an anisotropic Shale. In Proceedings of the 23rd U.S. Symposium on Rock Mechanics(USRMS), Berkeley, CA, USA, 25 August 1982; pp. 471–479. [Google Scholar]
- Singh, R.N.; Sun, G.X. An investigation into the factors affecting the fracture toughness of coal measures sandstones. J. Mines Met. Fuels 1990, 38, 111–118. [Google Scholar]
- Rao, K.S.; Rao, G.V.; Ramamurthy, T. A comparative evaluation of rock strength measurement: Discussion of paper by K.L. Gunsallus and F.H. Kulhawy. Int. J. Rock Mech. Min. Sci. & Geomech. Abstr. 21, 233–248 (1984). Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1987, 24, 193–196. [Google Scholar]
- Yin, T.B.; Wu, Y.; Wang, C.; Zhuang, D.D.; Wu, B.Q. Mixed-mode I+II tensile fracture analysis of thermally treated granite using straight-through notch Brazilian disc specimens. Eng. Fract. Mech. 2020, 234, 107111. [Google Scholar] [CrossRef]
- Peng, K.; Lv, H.; Zou, Q.; Wen, Z.; Zhang, Y. Evolutionary characteristics of mode-I fracture toughness and fracture energy in granite from different burial depths under high-temperature effect. Eng. Fract. Mech. 2020, 239, 107306. [Google Scholar] [CrossRef]
- Zhang, Z.X.; Yu, J.; Kou, S.Q.; Lindqvist, P.-A. Effects of high temperatures on dynamic rock fracture. Int. J. Rock Mech. Min. Sci. 2001, 38, 211–225. [Google Scholar] [CrossRef]
- Su, H.; Qin, X.; Feng, Y.; Yu, L.; Sun, Z. Experimental investigation of mixed mode I-II fracture property of thermally treated granite under dynamic loading. Theor. Appl. Fract. Mech. 2022, 118, 103267. [Google Scholar] [CrossRef]
- Ali, A.; Bahador, B.; Reza, A.M.; Morteza, N. On the role of fracture process zone size in specifying fracturing mechanism under dominant mode II loading. Theor. Appl. Fract. Mech. 2022, 117, 103150. [Google Scholar]
- Rashidi Moghaddam, M.; Ayatollahi, M.R.; ·Berto, F. Rock fracture toughness under mode ii loading: A theoretical model based on local strain energy density. Rock Mech. Rock Eng. 2018, 51, 243–253. [Google Scholar] [CrossRef]
- Swanson, P.L.; Spetzler, H. Ultrasonic probing of the fracture process zone in rock using surface waves. In Proceedings of the 25th U.S. Symposium on Rock Mechanics (USRMS), Evanston, IL, USA, 25 June 1984. [Google Scholar]
- Vinegar, H.J.; Wills, P.B.; DeMartini, D.C.; Shlyapobersky, J.; Deeg, W.F.J.; Adair, R.G.; Woerpel, J.C.; Fix, J.E.; Sorrells, G.G. Active and passive seismic imaging of a hydraulic fracture in Diatomite. J. Pet. Technol. 1992, 44, 28–90. [Google Scholar] [CrossRef]
- Meadows, M.A.; Winterstein, D.F. Seismic detection of a hydraulic fracture from shear-wave VSP data at Lost Hills Field, California. Geophysics 1994, 59, 11–26. [Google Scholar] [CrossRef]
- IIderton, D.C.; Patzek, T.W.; Rector, J.W.; Vinegar, H.J. Passive imaging of hydrofractures in the south Belridge Diatomite. SPE Form. Eval. 1996, 11, 46–54. [Google Scholar] [CrossRef]
- Block, L.V.; Cheng, C.H.; Fehler, M.C.; Phillips, W.S. Seismic imaging using microearthquakes induced by hydraulic fracturing. Geophysics 1994, 59, 102–112. [Google Scholar] [CrossRef]
- Rector, J.W., III; Dong, Q.; Patzek, T.W. Passive characterization of hydrofracture properties using signals from hydraulic pumps. J. Pet. Sci. Eng. 2000, 27, 49–58. [Google Scholar] [CrossRef]
- Clarkson, C.R.; Jensen, J.L.; Chipperfield, S. Unconventional gas reservoir evaluation: What do we have to consider? J. Nat. Gas Sci. Eng. 2012, 8, 9–33. [Google Scholar] [CrossRef]
- Barree, R.D.; Cox, S.A.; Gilbert, J.V.; Dobson, M. Closing the gap: Fracture half-length from design, buildup, and production analysis. SPE Prod. Facil. 2005, 20, 274–285. [Google Scholar] [CrossRef]
- Barree, R.D.; Duenckel, R.J.; Hlidek, B.T. The Limits of Fluid Flow in Propped Fractures- the Disparity Between Effective Flowing and Created Fracture Lengths. In Proceedings of the SPE Hydraulic Fracturing Technology Conference and Exhibition, The Woodlands, TX, USA, 5–7 February 2019. [Google Scholar]
- Zang, A.; Wagner, F.C.; Stanchits, S.; Janssen, C.; Dresen, G. Fracture process zone in Granite. J. Geophys. Res. 2000, 105, 23651–23661. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, H.; Li, X.; Zhang, X.; An, D.; Yu, B. Experimental study on development characteristics and size effect of rock fracture process zone. Eng. Fract. Mech. 2021, 241, 107377. [Google Scholar] [CrossRef]
- Moazzami, M.; Ayatollahi, M.R.; Akhavan-Safar, A. Assessment of the fracture process zone in rocks using digital image correlation technique: The role of mode-mixity, size, geometry and material. Int. J. Damage Mech. 2020, 29, 646–666. [Google Scholar] [CrossRef]
- Kim, K.; Yao, C. The influence of constitutive behavior on the fracture process zone and stress field evolution during hydraulic fracturing. In Proceedings of the 1st North American Rock Mechanics Symposium, Austin, TX, USA, 1 June 1994. [Google Scholar]
- Barton, C.C. Variables in fracture energy and toughness testing of rock. In Proceedings of the 23rd U.S Symposium on Rock Mechanics (USRMS), Berkeley, CA, USA, 25 August 1982. [Google Scholar]
- Brooks, Z.; Ulm, F.J.; Einstein, H.H. Role of microstructure size in fracture process zone development of marble. In Proceedings of the 46th U.S. Rock Mechanics/Geomechanics Symposium, Chicago, IL, USA, 24-27 June 2012. [Google Scholar]
- Tarokh, A.; Fakhimi, A. Discrete element simulation of the effect of particle size on the size of fracture process zone in quasi-brittle materials. Comput. Geotech. 2014, 62, 51–60. [Google Scholar] [CrossRef]
- Bochenek, A.; Prokopski, G. The investigation of aggregate grain size effect on fracture toughness of ordinary concrete structures. Int. J. Fract. 1989, 41, 197–205. [Google Scholar] [CrossRef]
- Dempsey, J.P.; Adamson, R.M.; Mulmule, S.V. Scale effects on the in-situ tensile strength and fracture of ice. Part II: First-year sea ice at Resolute, N.W.T. Int. J. Fract. 1999, 95, 347. [Google Scholar] [CrossRef]
- Dempsey, J.P.; Defranco, S.J.; Adamson, R.M.; Mulmule, S.V. Scale effects on the in-situ tensile strength and fracture of ice. Part I: Large grained freshwater ice at Spray Lakes Reservoir, Alberta. Int. J. Fract. 1999, 95, 325. [Google Scholar] [CrossRef]
- Ouchterlony, F. Review of fracture toughness testing of rocks. SM Arch. 1982, 7, 131–211. [Google Scholar]
- Tarokh, A.; Fakhimi, A. Relationship between grain size and fracture properties of rock. In Proceedings of the 47th US Rock Mechanics/Geomechanics Symposium, San Francisco, CA, USA, 23–26 June 2013. [Google Scholar]
- Nolen-Hoeksema, R.C.; Gordon, R.B. Optical detection of crack patterns in the opening-mode fracture of Marble. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1987, 24, 135–144. [Google Scholar] [CrossRef]
- Wawersik, W.R.; Brace, W.F. Post-failure behavior of a granite and diabase. Rock Mech. 1971, 3, 61–85. [Google Scholar] [CrossRef]
- Liu, H.Z.; Lin, J.-S.; He, J.-D.; Xie, H.-Q. Size effect and fracture: A discrete modeling perspective. In Proceedings of the 51st US Rock Mechanics/Geomechanics Symposium, San Francisco, CA, USA, 25–28 June 2017. [Google Scholar]
- Bazant, Z.P.; Kazemi, M.T. Determination of fracture energy, process zone length and brittleness number from size effect, with application to rock and concrete. Int. J. Fract. 1990, 44, 111–131. [Google Scholar] [CrossRef]
- Bahrami, V.; Mortazavi, A. A numerical investigation of hydraulic fracturing process in oil reservoirs using non-linear fracture mechanics. In Proceedings of the ISRM International Symposium—5th Asian Rock Mechanics Symposium, Tehran, Iran, 24 November 2008. [Google Scholar]
- Pollard, D.D.; Segall, P. Theoretical displacements and stresses near fractures in rock: With applications to faults, joints, veins, dikes, and solution surfaces. In Fracture Mechanics of Rock; Atkinson, B.K., Ed.; Academic Press: London, UK, 1987; pp. 277–349. [Google Scholar]
- Engvik, A.K.; Bertram, A.; Kalthoff, J.F.; Stöckhert, B.; Austrheim, H.; Elvevold, S. Magma-driven hydraulic fracturing and infiltration of fluids into the damaged host rock, an example from Dronning Maud Land, Antarctica. J. Struct. Geol. 2005, 27, 839–854. [Google Scholar] [CrossRef]
- Lin, Q.; Yuan, H.N.; Biolzi, L.; Labuz, J.F. Opening and Mixed Mode Fracture Process in a Quasi-Brittle Material via Digital Imaging. Eng. Fract. Mech. 2014, 131, 176–193. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, L.; Gao, M. Experimental investigation of the size effect of the mode I static fracture toughness of limestone. Adv. Civil Eng. 2019, 2019, 1–11. [Google Scholar] [CrossRef]
- Wei, M.; Dai, F.; Xu, N.; Zhao TLiu, Y. An experimental and theoretical assessment of semi-circular bend specimens with chevron and straight-through notches for mode I fracture toughness testing of rocks. Int. J. Rock Mech. Min. Sci. 2017, 99, 28–38. [Google Scholar] [CrossRef]
- Lie, K.; Gamage, R.P.; Zhao, J.; Rathnaweera, T.; Ma, Z. Tensile behaviors of Granite: Grain scale cracking and fracture process zone. In Proceedings of the 53rd US Rock Mechanics/Geomechanics Symposium, New York, NY, USA, 23–26 June 2019. [Google Scholar]
- Chen, L.; Zhang, G.; Zou, Z.; Guo, Y.; Du, X. Experimental observation of fracture process zone in sandstone from digital imaging. In Proceedings of the 54th US Rock Mechanics/Geomechanics Symposium, Golden, CO, USA, 28 June–1 July 2020. [Google Scholar]
- Le, J.-L.; Manning, J.; Labuz, J.F. Scaling of fatigue crack growth in rock. Int. J. Rock Mech. Min. Sci. 2014, 72, 71–79. [Google Scholar] [CrossRef]
- Zietlow, W.K.; Labuz, J.F. Measurement of the intrinsic process zone in rock using acoustic emission. Int. J. Rock Mech. Min. Sci. 1998, 35, 291–299. [Google Scholar] [CrossRef]
- Tarokh, A.; Fakhim, A.; Labuz, J.F. Size of process zone in fracture testing of rock. In Proceedings of the 46th US Rock Mechanics/Geomechanics Symposium, Chicago, IL, USA, 24–27 June 2012. [Google Scholar]
- Fakhimi, A.; Wan, F. Discrete element modeling of the process zone shape in mode I fracture at peak load and in post-peak regime. Int. J. Rock Mech. Min. Sci. 2016, 85, 119–128. [Google Scholar] [CrossRef]
- Wan, F.; Fakhimi, A. Numerical three-point bending test of fracture process zone in post-peak deformation of rock. In Proceedings of the 50th US Rock Mechanics/Geomechanics Symposium, Houston, TX, USA, 26–29 June 2016. [Google Scholar]
- Tarokh, A.; Makhnenko, R.Y.; Fakhimi, A.; Labuz, J.F. Scaling of the fracture process zone in rock. Int. J. Fract. 2017, 204, 191–204. [Google Scholar] [CrossRef]
- Wong, L.N.Y.; Guo, T.Y. Microcracking behavior of two semi-circular bend specimens in mode I fracture toughness test of granite. Eng. Fract. Mech. 2019, 221, 106565. [Google Scholar] [CrossRef]
- Backers, T.; Stanchits, S.; Dresen, G. Tensile fracture propagation and acoustic emission activity in sandstone: The effect of loading rate. Int. J. Rock Mech. Min. Sci. 2005, 42, 1094–1101. [Google Scholar] [CrossRef]
- Bazant, Z.P.; Bai, S.-P.; Gettu, R. Fracture of rock: Effect of loading rate. Eng. Fract. Mech. 1993, 45, 393–398. [Google Scholar] [CrossRef]
- Xing, Y.; Huang, B.; Ning, E.; Zhao, L.; Jin, F. Quasi-static loading rate effects on fracture process zone development of mixed-mode (I-II) fractures in rock-like materials. Eng. Fract. Mech. 2020, 240, 107365. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, G.; Zou, Z.; Guo, Y.; Zheng, X. The effect of fracture growth rate on fracture process zone development in quasi-brittle rock. Eng. Fract. Mech. 2021, 258, 108086. [Google Scholar] [CrossRef]
- Ko, T.Y.; Kemeny, J. Effect of confining stress and loading rate on fracture toughness of rocks. In Proceedings of the 1st Canada–U.S. Rock Mechanics Symposium, Vancouver, BC, Canada, 27 May 2007. [Google Scholar]
- Ghamgosar, M.; Erarslan, N. Experimental and numerical studies on development of fracture process zone (FPZ) in rocks under cyclic and static loadings. Rock Mech. Rock Eng. 2016, 49, 893–908. [Google Scholar] [CrossRef]
- Nie, Y.; Zhao, Z.; Zhang, G.; Zhao, B.; Jiang, Y.; Wan, B.; Zhao, H. The influence of water-oil saturation on the length of fracture process zone. In Proceedings of the 52nd US Rock Mechanics/Geomechanics Symposium, Seattle, Washington, DC, USA, 17–20 June 2018. [Google Scholar]
- Lin, Q.; Labuz, J.F. Identifying quasi-brittle facture by AE and Digital Imaging. J. Acoust. Emiss. 2011, 29, 68–77. [Google Scholar]
- Liu, H.Z.; Lin, J.S.; He, J.-D.; Xie, H.Q. Dominant mode of planar fractures and the role of material properties. Eng. Fract. Mech. 2018, 195, 57–79. [Google Scholar] [CrossRef]
- Ji, W.W.; Pan, P.Z.; Lin, Q.; Feng, X.T.; Du, M.P. Do disk-type specimens generate a mode II fracture without confinement? Int. J. Rock Mech. Min. Sci. 2016, 87, 48–54. [Google Scholar] [CrossRef]
- Lin, Q.; Ji, W.W.; Pan, P.Z.; Wang, S.; Lu, Y. Comments on the mode II fracture from disk-type specimens for rock-type materials. Eng. Fract. Mech. 2019, 211, 303–320. [Google Scholar] [CrossRef]
- Lin, Q.; Wang, S.; Pan, P.Z.; Ji, W.W.; Lu, Y. Fracture initiation under pure shear revisited: Remarks on the mode II fracture in quasi-brittle materials. Theor. Appl. Fract. Mech. 2020, 109, 102700. [Google Scholar] [CrossRef]
- Prasoon, G.; Ahmadreza, H.; Griffiths, D.V. Investigation of fracture process zone in Barre Granite under mode II loading. In Proceedings of the 55th US Rock Mechanics/Geomechanics Symposium, Houston, TX, USA, 20–23 June 2021. [Google Scholar]
- Li, B.Q.; Einstein, H.H. Comparison of visual and acoustic emission observations in a four point bending experiment on barre granite. Rock Mech. Rock Eng. 2017, 50, 2277–2296. [Google Scholar] [CrossRef]
- Nasseri, M.H.B.; Mohanty, B.; Young, R.P. Fracture toughness measurements and acoustic emission activity in brittle rocks. Pure Appl. Geophys. 2006, 163, 917–945. [Google Scholar] [CrossRef]
- Van Dam, D.B.; de Pater, C.J. Roughness of hydraulic fractures: The importance of in-situ stress and tip processes. In Proceedings of the 1999 SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 3–6 October 1999. [Google Scholar]
- Yang, W. Macroscopic and Microscopic Fracture Mechanics; National Defense Industry Press: Beijing, China, 1995. [Google Scholar]
- Rice, J.R. Mechanics of Crack Tip Deformation and Extension by Fatigue; ASTM STP 415; American Society for Testing and Materials: West Conshohocken, PA, USA, 1967; pp. 247–311. [Google Scholar]
- Hilton, P.D.; Hutchinson, J.W. Plastic intensity factors for cracked plates. Eng. Fract. Mech. 1971, 3, 435–451. [Google Scholar] [CrossRef]
- Barenblatt, G.I. The formation of equilibrium cracks during brittle fracture: General ideas and hypothesis, axially symmetric cracks. J. Appl. Math. Mech. 1959, 23, 622–636. [Google Scholar] [CrossRef]
- Dugdale, D.S. Yielding of steel sheets containing slits. J. Mech. Phys. Solids 1960, 8, 100–104. [Google Scholar] [CrossRef]
- Mokryakov, V. Analytical solution for propagation of hydraulic fracture with Barenblatt’s cohesive tip zone. Int. J. Fract. 2011, 169, 159–168. [Google Scholar] [CrossRef]
- Lecampion, B.; Bunger, A.; Zhang, X. Numerical methods for hydraulic fracture propagation: A review of recent trends. J. Nat. Gas Sci. Eng. 2018, 49, 66–83. [Google Scholar] [CrossRef]
- Khazan, Y.M.; Fialko, Y.A. Fracture criteria at the tip of fluid-driven cracks in the earth. Geophys. Res. Lett. 1995, 22, 2541–2544. [Google Scholar] [CrossRef]
- Liu, D.; Lecampion, B.; Garagash, D.I. Propagation of a fluid-driven fracture with fracture length dependent apparent toughness. Eng. Fract. Mech. 2019, 220, 106616. [Google Scholar] [CrossRef]
- Zhang, Z.; Nakamura, T. Simulations of crack propagation in elastic-plastic graded materials. Mech. Mater. 2004, 36, 601–622. [Google Scholar]
- Chudnovsky, N. Crack Layer Theory; NASA Report 17463; Case Western University: Cleveland, OH, USA, 1984. [Google Scholar]
- Chudnovsky, N.; Fan, J.; Shulkin, Y.; Dudley, J.W.; Shlyapobersky, J.; Shraufnagel, R. A new hydraulic fracture tip mechanism in a statistically homogenous medium. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 6–9 October 1996. [Google Scholar]
- Valkó, P.; Economides, M.J. Continuum Damage Mechanics Model of Hydraulic Fracturing. J. Pet. Technol. 1993, 45, 198–205. [Google Scholar] [CrossRef]
- Kemp, L.F. Discussion of Continuum Damage Mechanics Model of Hydraulic Fracturing. J. Pet. Technol. 1993, 45, 338. [Google Scholar]
- Germanovich, L.N.; Roegiers, J.-C. Discussion of Continuum Damage Mechanics Model of Hydraulic Fracturing. J. Pet. Technol. 1993, 45, 1191–1193. [Google Scholar]
- Valko, P.; Economides, M.J. Reply to Discussion of Continuum Damage Mechanics Model of Hydraulic Fracturing. J. Pet. Technol. 1993, 45, 1191. [Google Scholar] [CrossRef]
- Valco, P.; Economides, M.J. Propagation of hydraulically induced fractures—A continuum damage mechanics approach. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1994, 31, 221–229. [Google Scholar] [CrossRef]
- Mobasher, M.E.; Waisman, H. Non-local continuum damage and transport modeling framework for hydraulic fracturing. In Proceedings of the ARMA/DGS/SEG International Geomechanics Symposium, Online, 1–4 November 2021. [Google Scholar]
- Mobasher, M.E.; Waisman, H.; Woelke, P.B. A Continuum Non-Local Damage-Transport Model for Hydraulic Fracturing. In Proceedings of the 54th US Rock Mechanics/Geomechanics Symposium, Golden, CO, USA, 28 June–1 July 2020. [Google Scholar]
- Barree, R.D. A Practical numerical simulator for three- dimensional fracture propagation in heterogeneous media. In Proceedings of the SPE Reservoir Simulation Symposium, San Francisco, CA, USA, 15–18 November 1983. [Google Scholar]
- Li, S.; He, T.; Yin, X. Rock Fracture Mechanics; Science Press: Beijing, China, 2016. [Google Scholar]
- Smith, D.J.; Ayatollahi, M.R.; Pavier, M.J. The role of T-stress in brittle fracture for linear elastic materials under mixed-mode loading. Fatigue Fract. Eng. Mater. Struct. 2001, 24, 137–150. [Google Scholar] [CrossRef]
- Mirsayar, M.M.; Razmi, A.; Aliha, M.R.M.; Berto, F. EMTSN criterion for evaluating mixed mode I/II crack propagation in rock materials. Eng. Fract. Mech. 2018, 190, 186–197. [Google Scholar] [CrossRef]
- Ayatollahi, M.R.; Rashidi Moghaddam, M.; Berto, F. A generalized strain energy density criterion for mixed mode fracture analysis in brittle and quasi-brittle materials. Theor. Appl. Fract. Mech. 2015, 79, 70–76. [Google Scholar] [CrossRef]
- Rashidi Moghaddam, M.; Ayatollahi, M.R.; Berto, F. Mixed mode fracture analysis using generalized averaged strain energy density criterion for linear elastic materials. Int. J. Solids Struct. 2017, 120, 137–145. [Google Scholar] [CrossRef]
- Hou, C.; Jin, X.; Fan, X.; Xu, R.; Wang, Z. A generalized maximum energy release rate criterion for mixed mode fracture analysis of brittle and quasi-brittle materials. Theor. Appl. Fract. Mech. 2019, 100, 78–85. [Google Scholar] [CrossRef]
- Khan, S.M.A.; Khraisheh, M.K. A new criterion for mixed mode fracture initiation bases on the crack tip plastic core region. Int. J. Plast. 2004, 20, 55–84. [Google Scholar] [CrossRef]
- Theocaris, P.S. Discussion of ‘On the use of the T-criterion in fracture mechanics’ by N. A. B. Yehia. Eng. Fract. Mech. 1986, 24, 371–382. [Google Scholar] [CrossRef]
- Theocaris, P.S.; Andrianopoulos, N.P. The Mises elastic plastic boundary as the core region in fracture criteria. Eng. Fract. Mech. 1982, 16, 425–432. [Google Scholar] [CrossRef]
- Theocaris, P.S.; Andrianopoulos, N.P. The T-criterion applied to ductile fracture. Int. J. Fract. 1982, 20, R125–R130. [Google Scholar] [CrossRef]
- Theocaris, P.S.; Kardomateas, G.A.; Andrianopoulos, N.P. Experimental study of the T- criterion in ductile fracture. Eng. Fracture Mech. 1982, 17, 439–447. [Google Scholar] [CrossRef]
- Gil, I.; Roegiers, J.-C. Coupled elasto-plastic model for hydraulic fracturing of unconsolidated formations. In Proceedings of the 10th ISRM Congress, Sandton, South Africa, 8 September 2003. [Google Scholar]
- Zeng, Q.; Yao, J.; Shao, J. Effect of plastic deformation on hydraulic fracturing with extended element method. Acta Geotech. 2019, 14, 2083–2101. [Google Scholar] [CrossRef]
- Yao, Y. Linear elastic and cohesive fracture analysis to model hydraulic fracture in brittle and ductile rocks. Rock Mech. Rock Eng. 2012, 45, 375–387. [Google Scholar] [CrossRef]
- Manchanda, R.; Bryant, E.C.; Bhardwaj, P.; Cardiff, P.; Sharma, M.M. Strategies for effective stimulation of multiple perforation clusters in horizontal wells. SPE Prod. Oper. 2017, 33, 539–556. [Google Scholar]
- Guo, J.; Luo, B.; Lu, C.; Lai, J.; Ren, J. Numerical investigation of hydraulic fracture propagation in a layered reservoir using the cohesive zone method. Eng. Fract. Mech. 2017, 186, 195–207. [Google Scholar] [CrossRef]
- Dahi Taleghani, A.; Gonzalez-Chavez, M.; Yu, H.; Asala, H. Numerical simulation of hydraulic fracture propagation in naturally fractured formations using the cohesive zone model. J. Pet. Sci. Eng. 2018, 165, 42–57. [Google Scholar] [CrossRef]
- Baykin, A.N.; Golovin, S.V. Application of the fully coupled planar 3d poroelastic hydraulic fracturing model to the analysis of the permeability contrast impact on fracture propagation. Rock Mech. Rock Eng. 2018, 51, 3205–3217. [Google Scholar] [CrossRef]
- Zhang, G.M.; Liu, H.; Zhang, J.; Wu, H.A.; Wang, X.X. Three-dimensional finite element simulation and parametric study for horizontal well hydraulic fracture. J. Pet. Sci. Eng. 2010, 72, 310–317. [Google Scholar] [CrossRef]
- Xing, Y.; Zhang, G.; Huang, B. Recent Advances in Nonlinear Fracturing Characteristics of the Hydraulic Fracture in the Deep Reservoir. IOP Conf. Ser. Earth Environ. Sci. 2020, 570, 032062. [Google Scholar] [CrossRef]
- Wang, H.; Economides, M.J. Poroelastic versus poroplastic modeling of hydraulic fracturing. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 4–6 February 2014. [Google Scholar]
- Liu, W.; Yao, J.; Zeng, Q. A numerical hybrid model for non-planar hydraulic fracture propagation in ductile formations. J. Pet. Sci. Eng. 2021, 196, 107796. [Google Scholar] [CrossRef]
- Liu, W.; Zeng, Q.; Yao, J. Numerical simulation of elasto-plastic hydraulic fracture propagation in deep reservoir coupled with temperature field. J. Petrol. Sci. Eng. 2018, 171, 115–126. [Google Scholar] [CrossRef]
- Hu, Y.; Zhao, J.; Cao, L.; Zhao, J.; Li, J.; Wu, Z.; Hou, J. Numerical simulation for fracture propagation in elastoplastic formations. Geofluids 2021, 2021, 6680023. [Google Scholar] [CrossRef]
- Lin, H.; Deng, J.G.; Liu, W.; Xie, T.; Xu, J.; Liu, H.L. Numerical simulation of hydraulic fracture propagation in weakly consolidated sandstone reservoirs. J. Cent. South Univ. 2018, 25, 2944–2952. [Google Scholar] [CrossRef]
- Wang, H.Y.; Marongiu-Porcu, M.; Economides, M.J. Poroelastic and poroplastic modeling of hydraulic fracturing in brittle and ductile formations. SPE Prod. Oper. 2016, 31, 47–59. [Google Scholar] [CrossRef]
- Wang, H.Y. Hydraulic fracture propagation in naturally fractured reservoirs: Complex fracture or fracture networks. J. Nat. Gas Sci. Eng. 2019, 68, 102911. [Google Scholar] [CrossRef]
- Li, Y.; Liu, W.; Deng, J.; Yang, Y.; Zhu, H. A 2D explicit numerical scheme–based pore pressure cohesive zone model for simulating hydraulic fracture propagation in naturally fractured formation. Energy Sci. Eng. 2019, 7, 1527–1543. [Google Scholar] [CrossRef]
- Sun, T.; Zeng, Q.; Xing, H. A quantitative model to predict hydraulic fracture propagating across cemented natural fracture. J. Pet. Sci. Eng. 2022, 208, 109595. [Google Scholar] [CrossRef]
- Mohammadnejad, T.; Khoei, A. An extended finite element method for hydraulic fracture propagation in deformable porous media with the cohesive crack model. Finite Elem. Anal. Des. 2013, 73, 77–95. [Google Scholar] [CrossRef]
- Mohammadnejad, T.; Khoei, A. Hydro-mechanical modeling of cohesive crack propagation in multiphase porous media using the extended finite element method. Int. J. Numer. Anal. Methods Geo Mech. 2013, 37, 1247–1279. [Google Scholar] [CrossRef]
- Liu, F.; Gordon, P.; Meier, H.; Valiveti, D. A stabilized extended finite element framework for hydraulic fracturing simulations. Int. J. Numer. Anal. Methods GeoMech. 2017, 41, 654–681. [Google Scholar] [CrossRef]
- Wang, H.Y. Numerical modeling of non-planar hydraulic fracture propagation in brittle and ductile rocks using XFEM with cohesive zone method. J. Pet. Sci. Eng. 2015, 135, 127–140. [Google Scholar] [CrossRef]
- Paul, B.; Faivre, M.; Massin, P.; Giot, R.; Colombo, D.; Golfier, F.; Martin, A. 3D coupled HM–XFEM modeling with cohesive zone model and applications to non planar hydraulic fracture propagation and multiple hydraulic fractures interference. Comput. Methods Appl. Mech. Eng. 2018, 342, 321–353. [Google Scholar] [CrossRef]
- Liu, F.; Gordon, P.A.; Valiveti, D.M. Modeling competing hydraulic fracture propagation with the extended finite element method. Acta Geotech. 2018, 13, 243–265. [Google Scholar] [CrossRef]
- Wang, H.Y. Numerical investigation of fracture spacing and sequencing effects on multiple hydraulic fracture interference and coalescence in brittle and ductile reservoir rocks. Eng. Fract. Mech. 2016, 157, 107–124. [Google Scholar] [CrossRef]
- Wang, H. Poro-elasto-plastic modeling of complex hydraulic fracture propagation: Simultaneous multi-fracturing and producing well interference. Acta Mech. 2016, 227, 507–525. [Google Scholar] [CrossRef]
- Liu, D.; Lecampion, B. Propagation of a plane-strain hydraulic fracture accounting for the presence of a cohesive zone and a fluid lag. In Proceedings of the 53rd US Rock Mechanics/Geomechanics Symposium, New York, NY, USA, 23–26 June 2019. [Google Scholar]
- Liu, W.; Zeng, Q.; Yao, J.; Liu, Z.; Li, T.; Yan, X. Numerical study of elasto-plastic hydraulic fracture propagation in deep reservoirs using a hybrid EDFM–XFEM method. Energies 2021, 14, 2610. [Google Scholar] [CrossRef]
- Shojaei, A.; Dahi Taleghani, A.; Li, G. A continuum damage failure model for hydraulic fracturing of porous rocks. Int. J. Plast. 2014, 59, 199–212. [Google Scholar] [CrossRef]
- Mobasher, M.E.; Waisman, H.; Berger-Vergiat, L. Thermodynamic framework for non-local transport-damage modeling of fluid driven fracture in porous media. Int. J. Rock Mech. Min. Sci. 2018, 111, 64–83. [Google Scholar] [CrossRef]
- Busetti, S.; Mish, K.; Reches, Z. Damage and plastic deformation of reservoir rocks: Part 1. Damage fracturing. AAPG Bull. 2012, 96, 1687–1709. [Google Scholar] [CrossRef]
- Busetti, S.; Mish, K.; Hennings, P.; Reches, Z. Damage and plastic deformation of reservoir rocks: Part 2. Propagation of a hydraulic fracture. AAPG Bull. 2012, 96, 1711–1732. [Google Scholar] [CrossRef]









Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, D.; Han, G.; Zou, H.; Cui, M.; Liang, C.; Yao, F. A Review of the Hydraulic Fracturing in Ductile Reservoirs: Theory, Simulation, and Experiment. Processes 2022, 10, 2022. https://doi.org/10.3390/pr10102022
Zhu D, Han G, Zou H, Cui M, Liang C, Yao F. A Review of the Hydraulic Fracturing in Ductile Reservoirs: Theory, Simulation, and Experiment. Processes. 2022; 10(10):2022. https://doi.org/10.3390/pr10102022
Chicago/Turabian StyleZhu, Dawei, Guofeng Han, Honglan Zou, Mingyue Cui, Chong Liang, and Fei Yao. 2022. "A Review of the Hydraulic Fracturing in Ductile Reservoirs: Theory, Simulation, and Experiment" Processes 10, no. 10: 2022. https://doi.org/10.3390/pr10102022
APA StyleZhu, D., Han, G., Zou, H., Cui, M., Liang, C., & Yao, F. (2022). A Review of the Hydraulic Fracturing in Ductile Reservoirs: Theory, Simulation, and Experiment. Processes, 10(10), 2022. https://doi.org/10.3390/pr10102022







