Pore Size Distribution Characterization by Joint Interpretation of MICP and NMR: A Case Study of Chang 7 Tight Sandstone in the Ordos Basin
Abstract
:1. Introduction
2. Materials and Methods
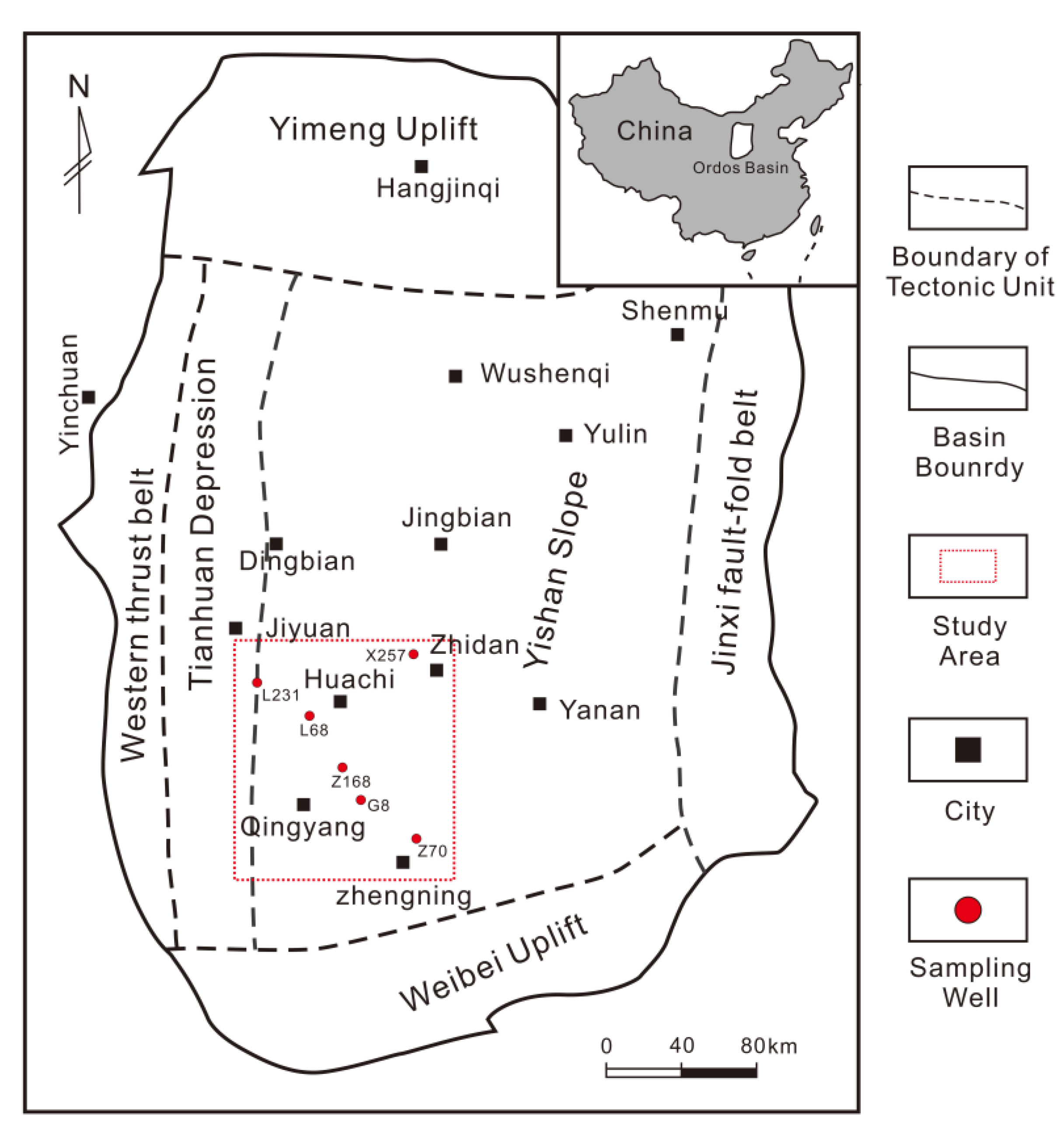
2.1. Geological Setting and Samples
2.2. MICP
2.3. NMR
3. Results
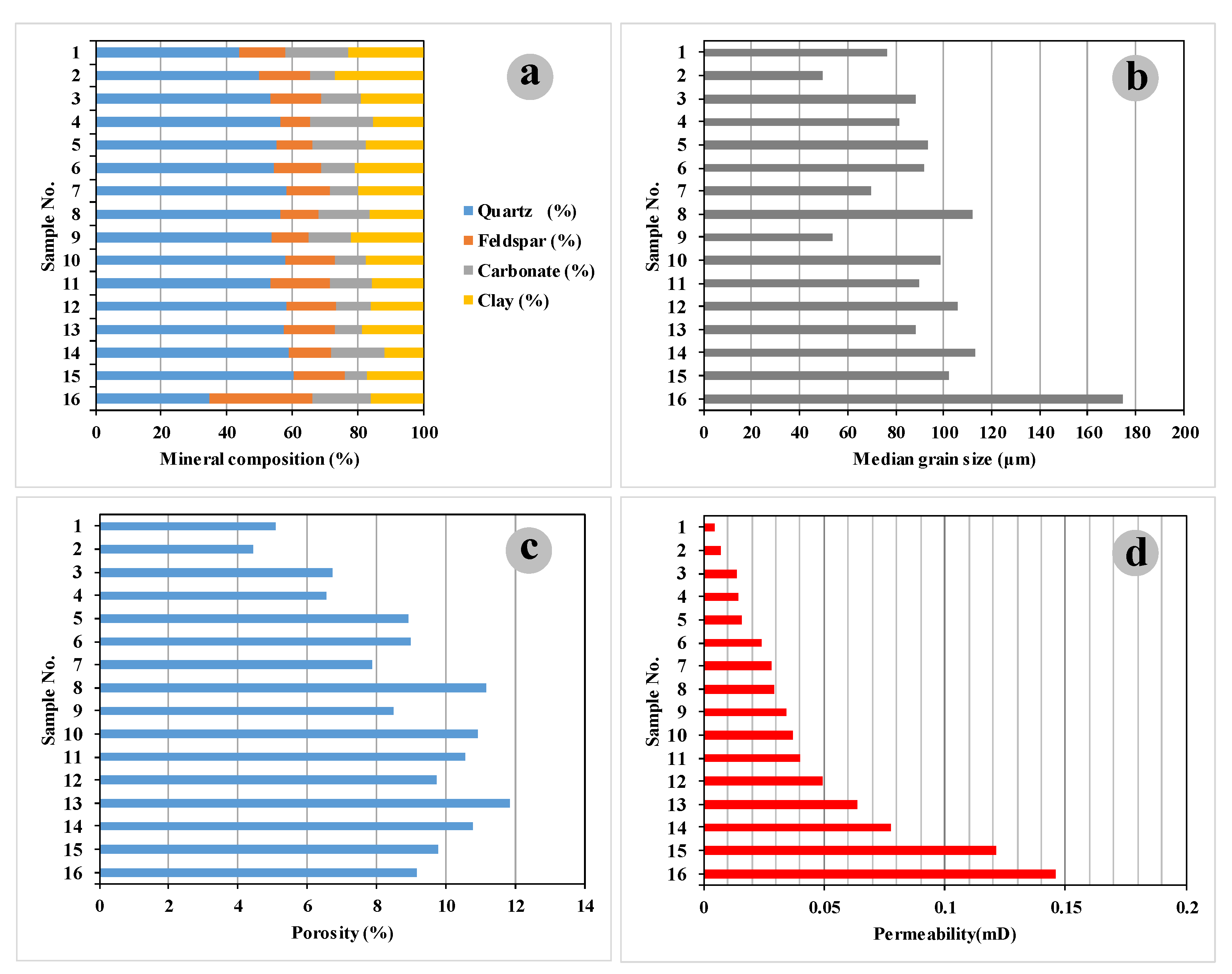
3.1. Petrology and Pore Characteristics
3.1.1. Petrology Characteristics
3.1.2. Pore Characteristics
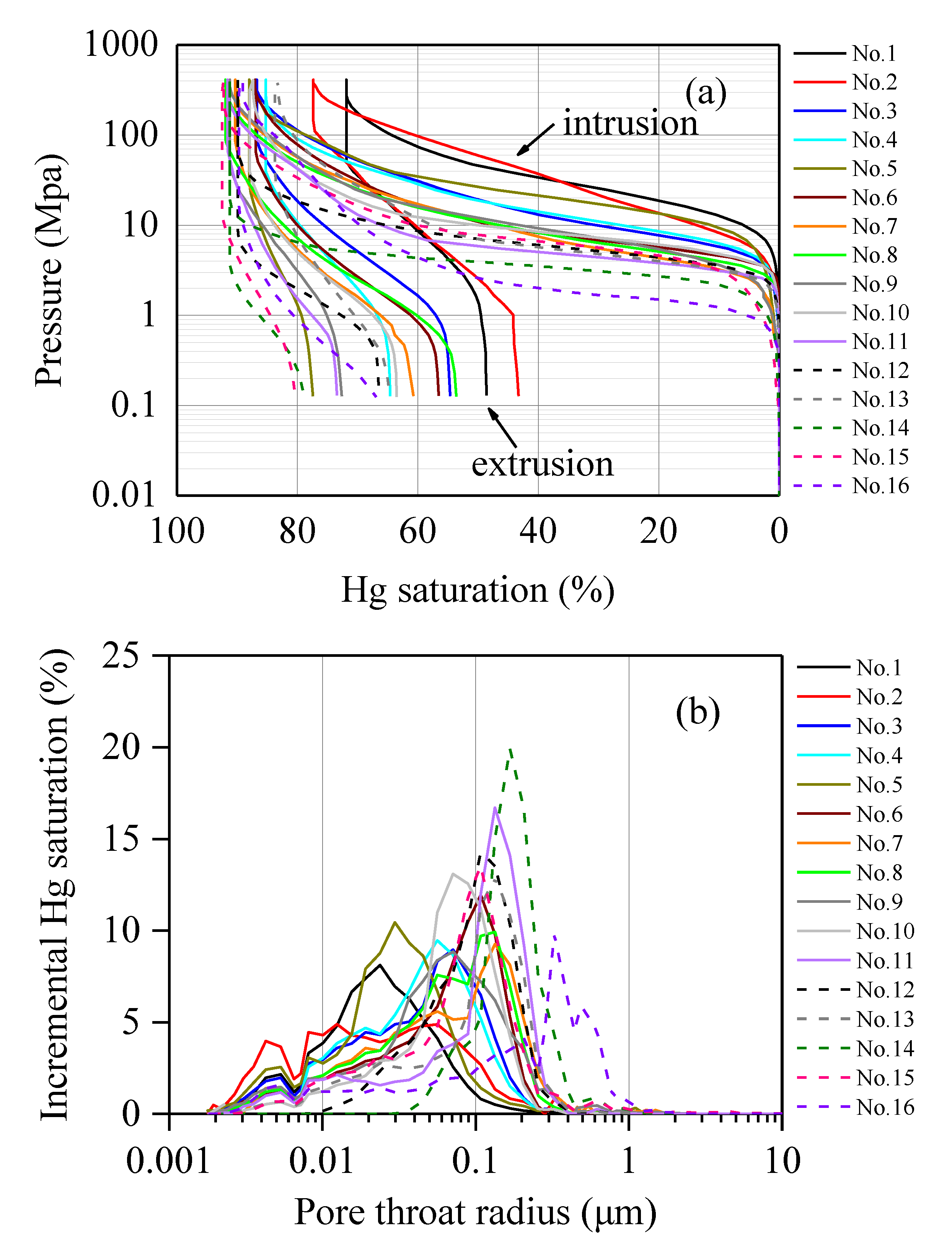
3.2. MICP Curves and Parameters
3.3. NMR T2 Spectrum
4. Discussion
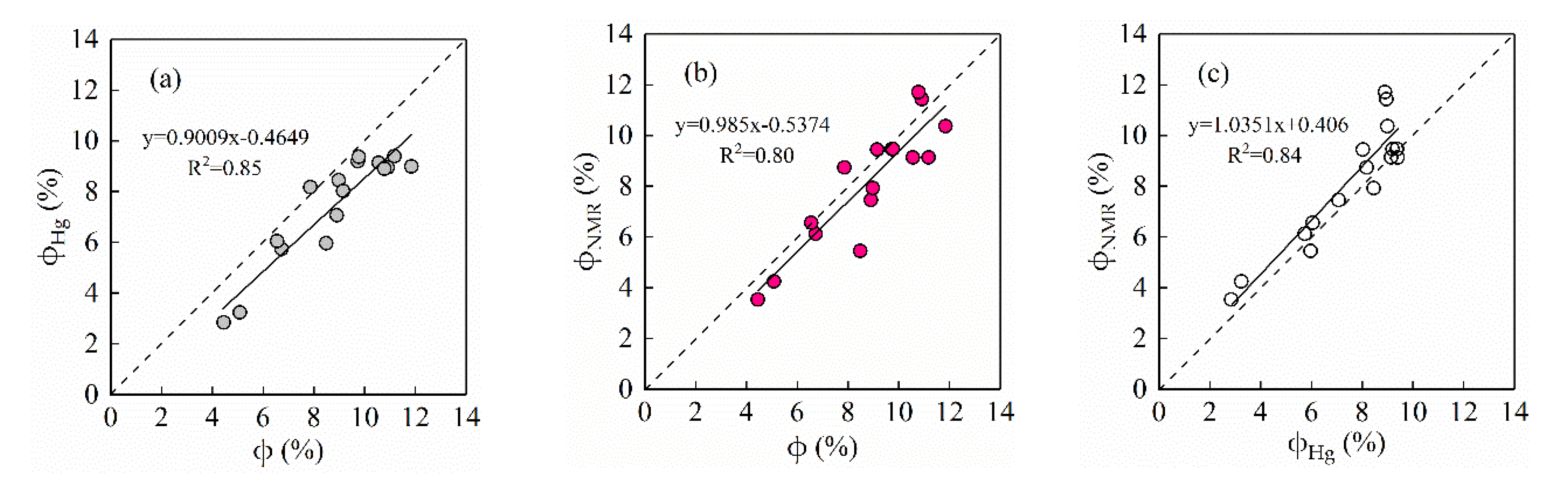
4.1. Comparison of Pore Volume and Size from MICP and NMR
4.1.1. Porosity
4.1.2. Pore and Pore Throat Size
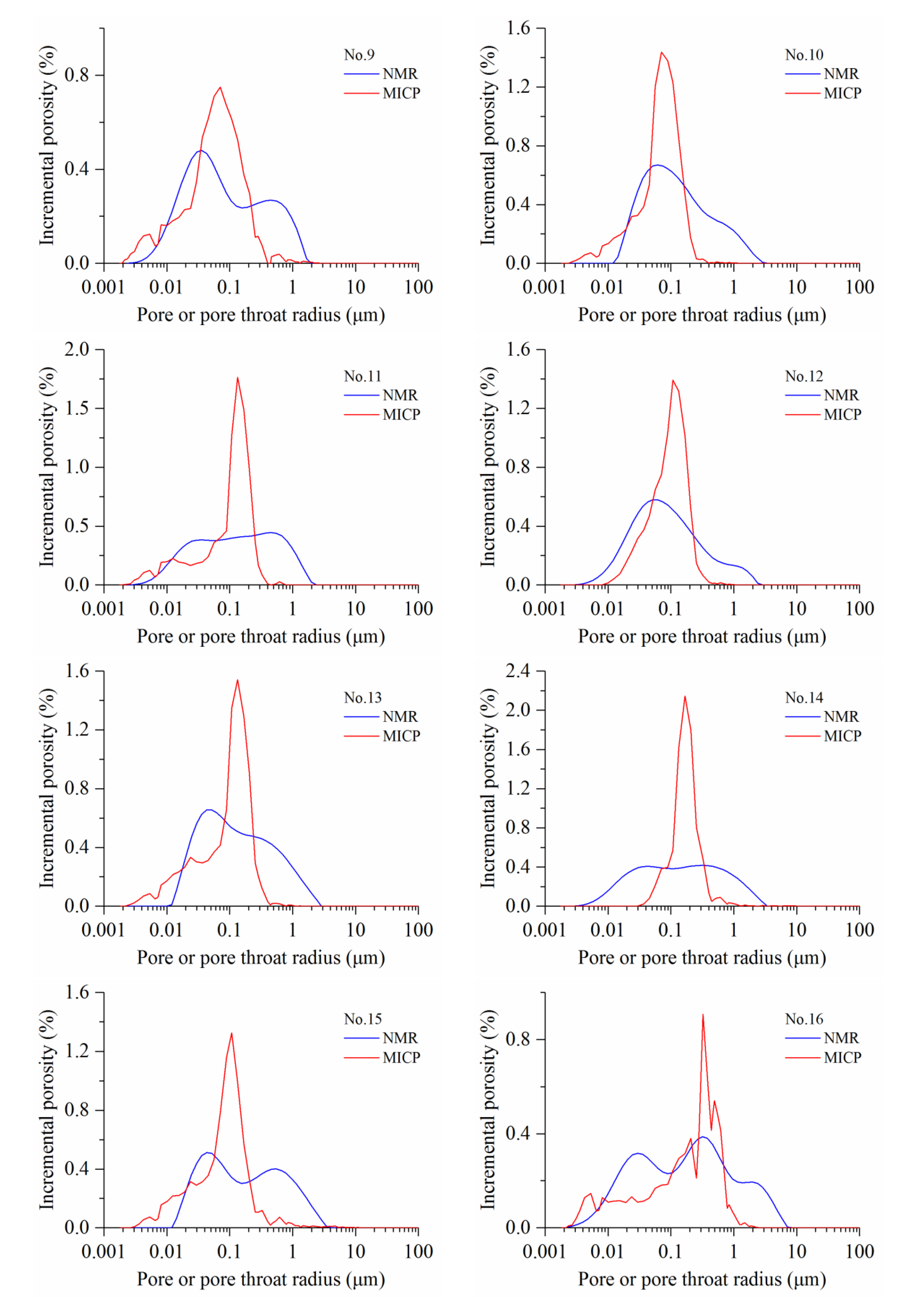
4.2. Pore Size Distribution
4.2.1. Calibration of PSD
4.2.2. The PSD and PTD
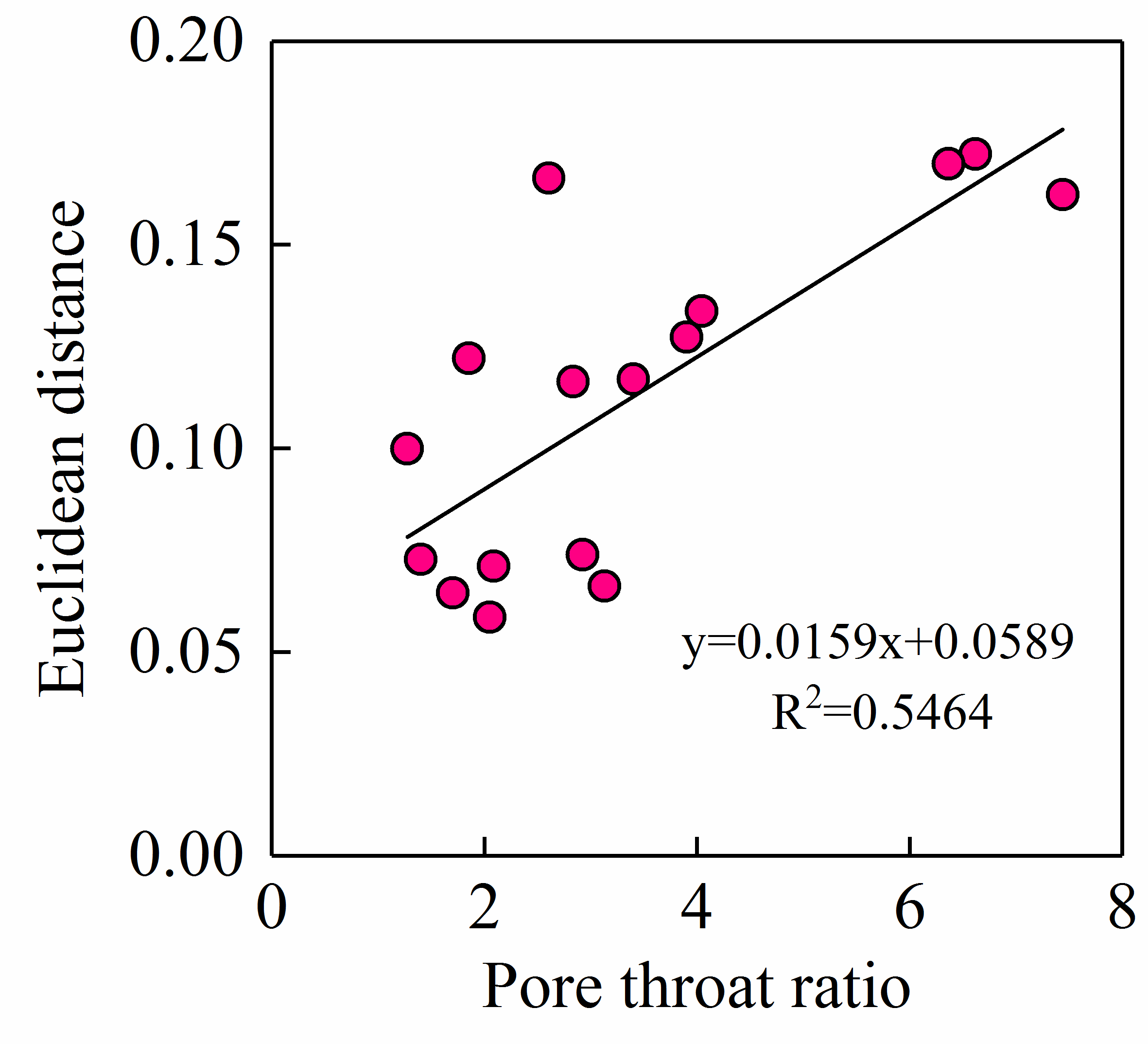
4.3. The Difference between MICP-PTD and NMR-Derived PSD
4.3.1. The Pore Network Model
4.3.2. Difference of Pores and Throats
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zou, C.; Tao, S.; Yang, Z.; Yuan, X.; Zhu, R.; Hou, L.; Jia, J.; Wang, F.; Wu, S.; Bai, B.; et al. New advance in unconventional petroleum exploration and research in China. Bull. Mineral. Petrol. Geochem. 2012, 31, 312–322. [Google Scholar]
- Zhou, Y.; Ji, Y.; Xu, L.; Che, S.; Niu, X.; Wan, L.; Zhou, Y.; Li, Z.; You, Y. Controls on reservoir heterogeneity of tight sand oil reservoirs in Upper Triassic Yanchang Formation in Longdong Area, southwest Ordos Basin, China: Implications for reservoir quality prediction and oil accumulation. Mar. Pet. Geol. 2016, 78, 110–135. [Google Scholar] [CrossRef]
- Li, C.; Liu, G.; Cao, Z.; Niu, Z.; Wang, P.; Zhang, M.; Zhang, K. The study of Chang 7 tight sandstone micro pore characteristics in Longdong area, Ordos Basin. Nat. Gas Geosci. 2016, 27, 1236–1247. [Google Scholar]
- Hu, Z.; Gaus, G.; Seemann, T.; Zhang, Q.; Littke, R.; Fink, R. Pore structure and sorption capacity investigations of Ediacaran and Lower Silurian gas shales from the Upper Yangtze platform, China. Geomech. Geophys. Geo-Energy Geo-Resour. 2021, 7, 1–26. [Google Scholar] [CrossRef]
- Nelson, P.H. Pore-throat sizes in sandstones, tight sandstones, and shales. AAPG Bull. 2009, 93, 329–340. [Google Scholar] [CrossRef]
- Rezaee, R.; Saeedi, A.; Clennell, B. Tight gas sands permeability estimation from mercury injection capillary pressure and nuclear magnetic resonance data. J. Pet. Sci. Eng. 2012, s88–s89, 92–99. [Google Scholar] [CrossRef]
- Zhao, H.; Ning, Z.; Wang, Q.; Zhang, R.; Zhao, T.; Niu, T.; Zeng, Y. Petrophysical characterization of tight oil reservoirs using pressure-controlled porosimetry combined with rate-controlled porosimetry. Fuel 2015, 154, 233–242. [Google Scholar] [CrossRef]
- Hu, Z.; Lu, S.; Klaver, J.; Dewanckele, J.; Amann-Hildenbrand, A.; Gaus, G.; Littke, R. An Integrated Imaging Study of the Pore Structure of the Cobourg Limestone—A Potential Nuclear Waste Host Rock in Canada. Minerals 2021, 11, 1042. [Google Scholar] [CrossRef]
- Comisky, J.; Santiago, M.; Mccollom, B.; Buddhala, A. Sample Size Effects on the Application of Mercury Injection Capillary Pressure for Determining the Storage Capacity of Tight Gas and Oil Shales. In Proceedings of the Canadian Unconventional Resources Conference, Society of Petroleum Engineers, Calgary, AB, Canada, 15–17 November 2011. [Google Scholar]
- Schmitt, M.; Fernandes, C.P.; Wolf, F.G.; Neto, J.A.B.D.C.; Rahner, C.P.; Santos, V.S.S.D. Characterization of Brazilian tight gas sandstones relating permeability and angstrom-to micron-scale pore structures. J. Nat. Gas Sci. Eng. 2015, 27, 785–807. [Google Scholar] [CrossRef]
- Purcell, W.R. Capillary pressures-their measurement using mercury and the calculation of permeability therefrom. J. Pet. Technol. 1949, 1, 39–48. [Google Scholar] [CrossRef]
- Cao, Z.; Liu, G.; Zhan, H.; Li, C.; Yuan, Y.; Yang, C.; Jiang, H. Pore structure characterization of chang-7 tight sandstone using MICP combined with N2GA techniques and its geological control factors. Sci. Rep. 2016, 6, 36919. [Google Scholar] [CrossRef] [PubMed]
- Bustin, R.M.; Bustin, A.M.M.; Cui, A.; Ross, D.; Pathi, V.M. Impact of shale properties on pore structure and storage characteristics. In Proceedings of the Society of Petroleum Engineers Shale Gas Production Conference, Fort Worth, TX, USA, 16–18 November 2008; p. SPE119892. [Google Scholar]
- Zhang, N.; He, M.; Zhang, B.; Qiao, F.; Sheng, H.; Hu, Q. Pore structure characteristics and permeability of deep sedimentary rocks determined by mercury intrusion porosimetry. J. Earth Sci. 2016, 27, 670–676. [Google Scholar] [CrossRef]
- Washburn, E.W. Note on the method of determining the distribution of pore sizes in a porous material. Proc. Natl. Acad. Sci. USA 1921, 7, 115–116. [Google Scholar] [CrossRef] [PubMed]
- Timur, A. Pulsed nuclear magnetic resonance studies of porosity, movable fluid, and permeability of sandstones. J. Pet. Technol. 1969, 21, 775–786. [Google Scholar] [CrossRef]
- Coates, G.; Xiao, L.; Prammer, M. NMR Logging Principles and Applications; Halliburton Energy Services: Houston, TX, USA, 1999; pp. 2–72. [Google Scholar]
- Al-Mahrooqi, S.H.; Grattoni, C.A.; Moss, A.K.; Jing, X.D. An investigation of the effect of wettability on NMR characteristics of sandstone rock and fluid systems. J. Pet. Sci. Eng. 2003, 39, 389–398. [Google Scholar] [CrossRef]
- Yao, Y.; Liu, D.; Che, Y.; Tang, D.; Tang, S.; Huang, W. Petrophysical characterization of coals by low-field nuclear magnetic resonance (NMR). Fuel 2010, 89, 1371–1380. [Google Scholar] [CrossRef]
- Xiao, L.; Xie, R.; Liao, G. NMR Logging Principles and Applications of Complex Hydrocarbon Reservoirs in China; Science Press: Beijing, China, 2012; pp. 2–6. [Google Scholar]
- Wang, F.; Tang, T.; Liu, T.; Zhang, H. Evaluation of the pore structure of reservoirs based on NMR T2 Spectrum decomposition. Appl. Magn. Reson. 2016, 47, 361–373. [Google Scholar] [CrossRef]
- Cohen, M.H.; Mendelson, K.S. Nuclear magnetic relaxation and the internal geometry of sedimentary rocks. J. Appl. Phys. 1982, 53, 1127–1135. [Google Scholar] [CrossRef]
- Hodgkins, M.A.; Howards, J.J. Application of NMR logging to reservoir characterization of low-resistivity sands in the Gulf of Mexico. AAPG Bull. 1999, 83, 114–127. [Google Scholar]
- Westphal, H.; Surholt, I.; Kiesl, C.; Thern, H.; Kruspe, T. NMR Measurements in carbonate rocks: Problems and an approach to a solution. Pure Appl. Geophys. 2005, 162, 549–570. [Google Scholar] [CrossRef]
- Xu, H.; Tang, D.; Zhao, J.; Li, S. A precise measurement method for shale porosity with low-field nuclear magnetic resonance: A case study of the Carboniferous–Permian strata in the Linxing area, eastern Ordos Basin, China. Fuel 2015, 143, 47–54. [Google Scholar] [CrossRef]
- Hinai, A.A.; Rezaee, R.; Esteban, L.; Labani, M. Comparisons of pore size distribution: A case from the western Australian gas shale formations. J. Unconv. Oil Gas Resour. 2014, 8, 1–13. [Google Scholar] [CrossRef]
- Li, C.; Liu, G.; Cao, Z.; Yuan, W.; Wang, P.; You, Y. Analysis of petrophysical characteristics and water movability of tight sandstone using low-field nuclear magnetic resonance. Nat. Resour. Res. 2020, 29, 2547–2573. [Google Scholar] [CrossRef]
- Soete, J.; Claes, S.; Claes, H.; Erthal, M.; Hamaekers, H.; De Boever, E.; Foubert, A.; Klitzsch, N.; Swennen, R. Unravelling the pore network and its behaviour: An integrated NMR, MICP, XCT and petrographical study of continental spring carbonates from the Ballık area, SW Turkey. Depos. Recor 2020, 8, 292–316. [Google Scholar] [CrossRef]
- Zhang, N.; Wang, S.; Zhao, F.; Sun, X.; He, M. Characterization of the pore structure and fluid movability of coal-measure sedimentary rocks by nuclear magnetic resonance (NMR). ACS Omega 2021, 6, 22831–22839. [Google Scholar] [CrossRef]
- Clarkson, C.R.; Solano, N.; Bustin, R.M.; Bustin, A.M.M.; Chalmers, G.R.L.; He, L.; Melnichenko, Y.B.; Radliński, A.P.; Blach, T.P. Pore structure characterization of north american shale gas reservoirs using USANS/SANS, gas adsorption, and mercury intrusion. Fuel 2013, 103, 606–616. [Google Scholar] [CrossRef]
- Yang, J. Tectonic Evolution and Oil-gas Reservoirs Distribution in Ordos Basin; Petroleum Industry Press: Beijing, China, 2002; pp. 36–37. [Google Scholar]
- Yuan, W.; Liu, G.; Xu, L.; Niu, X.; Li, C. Petrographic and geochemical characteristics of organic-rich shale and tuff of the upper triassic yanchang formation, ordos basin, China: Implications for lacustrine fertilization by volcanic ash. Can. J. Earth Sci. 2019, 56, 47–59. [Google Scholar] [CrossRef]
- Yang, H.; Dou, W.; Liu, X.; Zhang, L. Analysis on sedimentary facies of member 7 in Yanchang Formation of Triassic in Ordos Basin. Acta Sedimentol. Sin. 2010, 28, 254–263. [Google Scholar]
- Zhu, H.; Zhong, D.; Yao, J.; Sun, H.; Niu, X.; Liang, X.; You, Y.; Li, X. Alkaline diagenesis and its effects on reservoir porosity: A case study of Upper Triassic Chang 7 Member tight sandstone in Ordos Basin, NW China. Pet. Explor. Dev. 2015, 42, 56–65. [Google Scholar] [CrossRef]
- Wardlaw, N.C. Pore Geometry of carbonate rocks as revealed by pore casts and capillary pressure. AAPG Bull. 1976, 60, 245–257. [Google Scholar]
- Rootare, H.M.; Prenzlow, C.F. Surface area from mercury porosimetry measurements. J. Phys. Chem. 1967, 71, 2733–2735. [Google Scholar] [CrossRef]
- Giesche, H. Mercury porosimetry: A general (practical) overview. Part. Part. Syst. Charact. 2006, 23, 9–19. [Google Scholar] [CrossRef]
- Gan, H.; Nandi, S.P.; Walker, P.L. Nature of the porosity in American coals. Fuel 1972, 51, 272–277. [Google Scholar] [CrossRef]
- Mosher, K.; He, J.; Liu, Y.; Rupp, E.; Wilcox, J. Molecular simulation of methane adsorption in micro- and mesoporous carbons with applications to coal and gas shale systems. Int. J. Coal Geol. 2013, 109, 36–44. [Google Scholar] [CrossRef]
- Kenyon, W.E. Petrophysical principles of applications of NMR logging. Log Analyst. 1997, 38, 21–40. [Google Scholar]
- Daigle, H.; Johnson, A.; Thomas, B. Determining fractal dimension from nuclear magnetic resonance data in rocks with internal magnetic field gradients. Geophysics 2014, 79, 425–431. [Google Scholar] [CrossRef]
- Brownstein, K.R.; Tarr, C.E. Importance of classical diffusion in NMR studies of water in biological cells. Phys. Rev. A 1979, 19, 2446–2453. [Google Scholar] [CrossRef]
- Kleinberg, R.L.; Horsfield, M.A. Transverse relaxation processes in porous sedimentary rock. J. Magn. Reson. 1990, 88, 9–19. [Google Scholar] [CrossRef]
- Sigal, R.F. Pore-size distributions for organic-shale-reservoir rocks from nuclear-magnetic-resonance spectra combined with adsorption measurements. SPE J. 2015, 20, 824–830. [Google Scholar] [CrossRef]
- Yan, W.; Sun, J.; Cheng, Z.; Li, J.; Sun, Y.; Shao, W.; Shao, Y. Petrophysical characterization of tight oil formations using 1D and 2D NMR. Fuel 2017, 206, 89–98. [Google Scholar] [CrossRef]
- Folk, R.L.; Ward, W.C. Brazos River bar: A study in the significance of grain size parameters. J. Sediment. Res. 1957, 27, 3–16. [Google Scholar] [CrossRef]
- Li, C.; Liu, G.; Cao, Z.; Sun, M.; You, Y.; Liu, N. Oil charging pore throat threshold and accumulation effectiveness of tight sandstone reservoir using the physical simulation experiments combined with NMR. J. Pet. Sci. Eng. 2022, 208, 109338. [Google Scholar] [CrossRef]
- Giles, M.R.; Boer, R.B.D. Origin and significance of redistributional secondary porosity. Mar. Pet. Geol. 1990, 7, 378–397. [Google Scholar] [CrossRef]
- Mastalerz, M.; Drobniak, A.; Hower, J. Controls on reservoir properties in organic-matter-rich shales: Insights from MICP analysis. J. Pet. Sci. Eng. 2021, 196, 107775. [Google Scholar] [CrossRef]
- Zhou, Y.; You, L.; Zi, H.; Lan, Y.; Cui, Y.; Xu, J.; Fan, Q.; Wang, G. Determination of pore size distribution in tight gas sandstones based on Bayesian regularization neural network with MICP, NMR and petrophysical logs. J. Nat. Gas Sci. Eng. 2022, 100, 104468. [Google Scholar] [CrossRef]
- Kaufmann, J.; Loser, R.; Leemann, A. Analysis of cement-bonded materials by multi-cycle mercury intrusion and nitrogen sorption. J. Colloid Interface Sci. 2009, 336, 730–737. [Google Scholar] [CrossRef]
- Wardlaw, N.C.; Malcolm, M.; Li, Y. Pore and throat size distributions determined by mercury porosimetry and by direct observation. Carbonates Evaporites 1988, 3, 1–16. [Google Scholar] [CrossRef]
- Rylander, E.; Philip, M.S.; Jiang, T.; Lewis, R. NMR T2 distributions in the Eagle Ford shale: Reflections on pore size. In Proceedings of the SPE Unconventional Resources Conference, The Woodlands, TX, USA, 10–12 April 2013; p. SPE164554. [Google Scholar]
- Schowalter, T.T. Mechanics of secondary hydrocarbon migration and entrapment. AAPG Bull. 1979, 63, 723–760. [Google Scholar]
- Hognesen, E.J.; Strand, S.; Austad, T. Waterflooding of Preferential Oil-wet Carbonates: Oil Recovery Related to Reservoir Temperature and Brine Composition. In Proceedings of the SPE Europec/EAGE Annual Conference, Madrid, Spain, 13–16 June 2005; p. SPE94166. [Google Scholar]
- Meng, W.; Haroun, M.R.; Sarma, H.K.; Adeoye, J.T.; Aras, P.; Punjabi, S.; Rahman, M.M.; Al Kobaisi, M. A novel approach of using phosphate-spiked smart brines to alter wettability in mixed oil-wet carbonate reservoirs. In Proceedings of the Abu Dhabi International Petroleum Exhibition and Conference, Abu Dhabi, United Arab Emirates, 9–12 November 2015; p. SPE17755. [Google Scholar]
- Dai, C.; Cheng, R.; Sun, X.; Liu, Y.; Zhou, H.; Wu, Y.; You, Q.; Zhang, Y.; Sun, Y. Oil migration in nanometer to micrometer sized pores of tight oil sandstone during dynamic surfactant imbibition with online NMR. Fuel 2019, 245, 544–553. [Google Scholar] [CrossRef]
- Wardlaw, N.C.; Mckellar, M. Mercury porosimetry and the interpretation of pore geometry in sedimentary rocks and artificial modelsy. Powder Technol. 1981, 29, 127–143. [Google Scholar] [CrossRef]
- Lala, A.M.S.; El-Sayed, N.A.A. Effect of pore framework and radius of pore throats on permeability estimation. J. Afr. Earth Sci. 2015, 110, 64–74. [Google Scholar] [CrossRef]
- Volokitin, Y.; Looyestijn, W.J.; Slijkerman, W.F.J.; Hofman, J.P. A Practical approach to obtain primary drainage capillary pressure curves from NMR core and log Data. Petrophysics 2001, 42, 334–343. [Google Scholar]
- Liu, T.; Wang, S.; Fu, R.; Zhou, M.; Li, Y.; Luo, M. Analysis of rock pore throat structure with NMR spectra. Oil Geophys. Prospect. 2003, 18, 737–742. [Google Scholar]
- Li, H.; Zhu, J.; Guo, H. Methods for calculating pore radius distribution in rock from NMR T2 spectra. Chin. J. Magn. Reson. 2008, 25, 273–280. [Google Scholar]
- Li, H.; Guo, H.; Li, H.; Liu, W.; Jiang, B.; Hua, J. Thickness analysis of bound water film in tight reservoir. Nat. Gas Geosci. 2015, 26, 186–192. [Google Scholar]
- Yang, S.; Wei, J. Reservoir Physics; Petroleum Industry Press: Beijing, China, 2004; pp. 188–208. [Google Scholar]
- Liu, P.; Chen, X. Foam Metel; Centrol South University Press: Changsha, China, 2012; pp. 298–309. [Google Scholar]
- Mesquita, D.P.P.; Gomes, J.P.P.; Junior, A.H.S.; Nobre, J.S. Euclidean distance estimation in incomplete datasets. Neurocomputing 2017, 248, 11–18. [Google Scholar] [CrossRef]
- Wang, C.; Jiang, M.; Liu, Z. A new method to distinguish sedimentary environment based on the data of the grain size frequency distribution. Bull. Tianjing Inst. Geol. Min. Res. 1989, 23, 61–69. [Google Scholar]
- Yang, T.; Li, T.; Zhang, J.; Li, J.; Liu, H.; Wang, Y. Rapid identification of bolete mushrooms by UV spectroscopy combined with Euclidean distance and principal component analysis. Food Sci. 2014, 35, 105–109. [Google Scholar]
- Ghosh, A.; Barman, S. Application of Euclidean distance measurement and principal component analysis for gene identification. Gene 2016, 583, 112–120. [Google Scholar] [CrossRef]
- Wang, X.; Wang, W.; Zhang, K.; Bi, K. Approaching the study on the similarity analysis of HPLC fingerprints spectra for traditional Chinese medicines. J. Shenyang Pharm. Univ. 2003, 20, 360–362. [Google Scholar]







| Sample No. | So | Pc50 (MPa) | Pd (MPa) | rmax (μm) | Smax (%) | We (%) | PTR | φHg (%) | r2.5 (μm) | r25 (μm) | r75 (μm) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1.69 | 46.11 | 6.82 | 0.108 | 71.83 | 32.42 | 2.08 | 3.24 | 0.104 | 0.034 | 0.002 |
| 2 | 1.87 | 59.51 | 4.39 | 0.167 | 77.35 | 44.04 | 1.27 | 2.85 | 0.173 | 0.043 | 0.003 |
| 3 | 1.59 | 19.37 | 3.56 | 0.206 | 86.70 | 36.99 | 1.70 | 5.74 | 0.203 | 0.084 | 0.010 |
| 4 | 1.43 | 18.97 | 3.56 | 0.206 | 85.21 | 24.22 | 3.13 | 6.06 | 0.195 | 0.075 | 0.012 |
| 5 | 1.51 | 26.88 | 6.02 | 0.122 | 89.33 | 11.85 | 7.44 | 7.07 | 0.213 | 0.048 | 0.009 |
| 6 | 1.49 | 11.02 | 2.87 | 0.256 | 86.99 | 35.04 | 1.85 | 8.45 | 0.212 | 0.118 | 0.016 |
| 7 | 1.69 | 11.42 | 1.84 | 0.400 | 90.31 | 32.78 | 2.05 | 8.18 | 0.415 | 0.151 | 0.019 |
| 8 | 1.53 | 11.30 | 2.60 | 0.283 | 91.92 | 41.67 | 1.40 | 9.39 | 0.258 | 0.129 | 0.021 |
| 9 | 1.65 | 12.21 | 1.83 | 0.401 | 91.20 | 20.41 | 3.90 | 5.97 | 0.471 | 0.117 | 0.020 |
| 10 | 1.23 | 10.06 | 4.40 | 0.167 | 87.87 | 27.73 | 2.61 | 8.96 | 0.214 | 0.110 | 0.028 |
| 11 | 1.54 | 5.90 | 2.25 | 0.326 | 91.59 | 19.83 | 4.04 | 9.14 | 0.293 | 0.180 | 0.033 |
| 12 | 0.98 | 7.11 | 2.26 | 0.326 | 89.88 | 26.09 | 2.83 | 9.20 | 0.287 | 0.155 | 0.051 |
| 13 | 1.49 | 7.06 | 2.88 | 0.256 | 83.71 | 22.73 | 3.40 | 8.99 | 0.318 | 0.167 | 0.017 |
| 14 | 0.81 | 3.94 | 0.94 | 0.782 | 91.23 | 13.58 | 6.36 | 8.90 | 0.645 | 0.254 | 0.135 |
| 15 | 1.59 | 7.86 | 4.39 | 0.167 | 92.46 | 13.13 | 6.61 | 9.37 | 0.834 | 0.139 | 0.032 |
| 16 | 2.03 | 2.59 | 1.19 | 0.619 | 89.70 | 25.49 | 2.92 | 8.03 | 0.917 | 0.460 | 0.032 |
| Sample No. | Sir* (%) | Sw* (%) | C (μm/ms) | R2.5 (μm) | R25 (μm) | R50 (μm) | R75 (μm) |
|---|---|---|---|---|---|---|---|
| 1 | 67.99 | 32.01 | 0.027 | 0.151 | 0.037 | 0.022 | 0.013 |
| 2 | 58.57 | 41.43 | 0.047 | 0.068 | 0.025 | 0.016 | 0.010 |
| 3 | 56.80 | 43.20 | 0.034 | 0.153 | 0.053 | 0.029 | 0.017 |
| 4 | 56.47 | 43.53 | 0.024 | 0.491 | 0.096 | 0.040 | 0.021 |
| 5 | 63.85 | 36.15 | 0.006 | 0.826 | 0.261 | 0.090 | 0.034 |
| 6 | 53.02 | 46.98 | 0.027 | 0.525 | 0.077 | 0.038 | 0.019 |
| 7 | 58.87 | 41.13 | 0.019 | 0.954 | 0.123 | 0.046 | 0.023 |
| 8 | 58.37 | 41.63 | 0.011 | 0.630 | 0.221 | 0.084 | 0.030 |
| 9 | 40.80 | 59.20 | 0.027 | 1.019 | 0.175 | 0.066 | 0.026 |
| 10 | 42.26 | 57.74 | 0.015 | 1.318 | 0.177 | 0.064 | 0.028 |
| 11 | 52.47 | 47.53 | 0.009 | 1.184 | 0.308 | 0.092 | 0.032 |
| 12 | 55.57 | 44.43 | 0.014 | 1.224 | 0.229 | 0.085 | 0.038 |
| 13 | 39.60 | 60.40 | 0.017 | 1.347 | 0.310 | 0.083 | 0.034 |
| 14 | 44.94 | 55.06 | 0.012 | 1.680 | 0.381 | 0.122 | 0.038 |
| 15 | 26.83 | 73.17 | 0.024 | 0.954 | 0.306 | 0.069 | 0.024 |
| 16 | 15.06 | 84.94 | 0.057 | 3.414 | 0.419 | 0.128 | 0.032 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Liu, X.; You, F.; Wang, P.; Feng, X.; Hu, Z. Pore Size Distribution Characterization by Joint Interpretation of MICP and NMR: A Case Study of Chang 7 Tight Sandstone in the Ordos Basin. Processes 2022, 10, 1941. https://doi.org/10.3390/pr10101941
Li C, Liu X, You F, Wang P, Feng X, Hu Z. Pore Size Distribution Characterization by Joint Interpretation of MICP and NMR: A Case Study of Chang 7 Tight Sandstone in the Ordos Basin. Processes. 2022; 10(10):1941. https://doi.org/10.3390/pr10101941
Chicago/Turabian StyleLi, Chaozheng, Xiangbai Liu, Fuliang You, Peng Wang, Xinluo Feng, and Zhazha Hu. 2022. "Pore Size Distribution Characterization by Joint Interpretation of MICP and NMR: A Case Study of Chang 7 Tight Sandstone in the Ordos Basin" Processes 10, no. 10: 1941. https://doi.org/10.3390/pr10101941
APA StyleLi, C., Liu, X., You, F., Wang, P., Feng, X., & Hu, Z. (2022). Pore Size Distribution Characterization by Joint Interpretation of MICP and NMR: A Case Study of Chang 7 Tight Sandstone in the Ordos Basin. Processes, 10(10), 1941. https://doi.org/10.3390/pr10101941









