Data-Driven Intelligent Model for the Classification, Identification, and Determination of Data Clusters and Defect Location in a Welded Joint

Abstract

In this paper, a data-driven approach that is based on the k-mean clustering and local outlier factor (LOF) algorithm has been proposed and deployed for the management of non-destructive evaluation (NDE) in a welded joint. The k-mean clustering and LOF model algorithm, which was implemented for the classification, identification, and determination of data clusters and defect location in the welded joint datasets, were trained and validated such that three (3) different clusters and noise points were obtained. The noise points, which are regarded as the welded joint defects/flaws, allow for the determination of the cluster size, heterogeneity, and silhouette score of the welded joint data. Similarly, the LOF model algorithm was implemented for the detection, visualization, and management of flaws due to internal cracks, porosity, fusion, and penetration in the welded joint. It is believed that the management of welded joint flaws would aid the actualization of the Industry 4.0 concept in the development of lightweight products for manufacturing.

1. Introduction

The global demand for the reduction of carbon (CO₂) emissions, and thus for the design, development, and implementation of a lightweight product concept in the manufacturing industry, has resulted in the call for innovation in the management of welding techniques and procedures [1,2]. Welding technology, which is not only a critical factor to consider in this regard, could pose a major challenge to the actualization of this drive [3,4]. Although, it is believed that the introduction of innovative welding techniques and procedures could address these issues holistically and save up to about 50% of the CO₂ emissions [3,5]. However, the nature and types of welded joints produced from these welding techniques when trying to achieve the lightweight product concept are not free from their problems. It has been suggested that welding techniques are critical to the management of manufacturing energy consumption, the cost of achieving the lightweight product concept, and the quality and reliability of the welds produced [6]. Hence, it has been recommended that welded joints under the lightweight product concepts should be monitored continuously, such as to ensure balance and stability in the micro-structural and mechanical properties of the welded joints [7].

In monitoring welded joints, non-destructive evaluation (NDE) techniques, which can also be referred to as non-destructive testing (NDT) methods, are often used, where the generation, propagation, and response signals from the joints are modeled and simulated. It allows for a complete check of the welded joints for cracks/flaws and for managing the negative impact of the CO₂ emissions balance. The high cost and time required for using destructive test methods has made the NDE a sought-after technique for many industries [8,9]. Furthermore, since some parts of the Industrial Revolution 4.0 are gaining traction both in the manufacturing and the oil and gas industry lately [10,11]. It is believed, therefore, that innovation in the management and implementation of the NDE techniques, especially for welding technology, will greatly impact the concept [12]. In addition, the combination of data from welding techniques and NDT methods, historical data from the production steps of the lightweight product construction, or their manufacturing environment will greatly benefit the Industrial Revolution 4.0, as well as the actualization of reduced CO₂ emissions and the lightweight product concept [13].

Non-destructive evaluation is a group of methods/tools that have found application in several industries for determining the properties and integrity of components, parts, or structures without physically altering their shape or causing damage to them. Generally, the NDE methods/tools rely heavily on experimental methods for their measurements. These experimental methods, however, are costly and time-consuming. Hence, they have become very unpopular, lately, and so many of the industries that normally use them are now calling for an autonomous deep-computing approach for the management and implementation of the NDE techniques.

A number of deep-computing approaches has been proposed for the management and implementation of the NDE techniques. Among them include Liu et al. [14], who investigate the use of a laser sensor as a non-destructive technique for detecting welding defects in seam contours. The method incorporates image coding into the laser sensors before applying deep-learning algorithms for the classification and detection of weld defect images. Zeng et al. [15], proposed a visual sensor that is based on image features and support vector machines (SVM) for the automatic identification of weld joint type before welding. The model, which is aimed at the improvement of the weld efficiency and automation of the welding system, is applied in the field of welding robotics.

As part of the Industry 4.0 paradigm that has resulted in the introduction of modern technologies, Tripicchio & D’Avella [16] proposed the deep neural network within the context of welding defect detection by analyzing the common problems in industrial applications of such modern technologies and discussing potential solutions in the specific case of quality checks in fuel injector welding during the manufacturing stage. Similarly, weld bead identification, which is critical for providing data for automatic welding process control, has been faced with the complex characteristics of the industrial environment, such as weak texture, low contrast, and rust. Yang et al. [17], propose a deep neural network-based detection and identification method for weld beads. To begin, high-quality training samples were generated with a small number of samples, combined with image processing and a generative adversarial network (GAN). Secondly, a mechanism for updating training samples was established to ensure the deep neural network model could cover all samples, and finally, the deep neural network was used to detect and identify weld beads by avoiding the handcrafted features of traditional machine learning methods.

Provencal & Laperrière [18] applied the deep learning approach for the identification of welding defects in a weld geometry by using NDT (ultrasound scan) data. The method, which allows a more accurate automated assessment of the ultrasound data, provides a deeper insight into the management of the welding and the improvement of the quality and reliability of the weld defect analysis. Unlike traditional NDT methods that rely solely on certified analysts to assess weld quality, the proposed deep learning framework presented, here, expands the NDT industry’s understanding of ultrasonic scan analysis.

Among the prominent traditional available NDE methods, the ultrasonic inspection testing method stands out as one which uses a high-frequency sound approach to detect flaws in components, parts, or structures by visualizing the different sections (the deep and shallow parts). Studies, however, noted that it is difficult to use the ultrasonic inspection testing (UT) method on components and structures with intricate shapes and high curvatures [19]. Hence, a manual inspection approach is always recommended and used. This approach, however, is costly, time-consuming, and produces inconsistent results most of the time, mainly due to human factors. To address this issue, a data-driven approach for analyzing the inspection data has been proposed in the paper. The data-driven intelligent approach that is based on the k-mean clustering and local outlier factor (LOF) model is aimed at supporting the NDE tool for intricate shape analysis and for structures that cannot be easily accessed using the traditional UT scan method. Additionally, it is used for addressing inconsistency in the results obtained using the UT scan method and for managing the amount of time spent when a manual approach is used by providing a novel approach for internal flaw/defect location and detection in the welded joint.

The primary contributions of the data-driven intelligent approach to NDE and welding technology literature can be summed as follows:

(1)

The k-mean clustering method, which was implemented for data analysis of welded joints with intricate shapes, provides statistically relevant features from NDE data by classifying the dataset into clusters and noise points. To the best of my knowledge, this is the first study to apply the k-mean clustering method for the classification of the dataset from a welded joint with intricate shapes and structures.

(2)

The k-mean clustering method provides a visualization schema of the NDE data features of the welded joint considered, showing the clustering means, clustering coefficient, cluster heterogeneity, silhouette score, and the size and measurement in the form of clusters and noise point information.

(3)

Finally, the LOF model algorithm is implemented for the detection of flaws due to internal cracks, internal porosity, internal fusion, and internal penetration in the welded joint. To the best of my knowledge, this is the first study to apply the LOF model algorithm for the detection of flaws in welded joints, especially for welded joints with intricate shapes and structures.

The practical advantages and significance of the data-driven intelligent approach as part of the Industry 4.0 paradigm are listed as follows:

(a)

Less Waste: The use of modeling and simulation in NDE does not change or alter the structure or composition of a component or structure; therefore, their usage is not restricted and results in no samples wasted, unlike the traditional NDE where samples may be wasted.

(b)

Reduced downtime: There is no need to halt operations when using the modeling and simulation approach for the NDE of components and structures because the procedures allow testing to take place while the materials are still in use.

(c)

Prevention of accidents: Accidents can be avoided with the aid of modeling and simulation of the NDE process, which also lowers the price of maintenance, replacement, and equipment loss, as well as the need to close down a firm.

(d)

We see the NDE and process (and environmental) monitoring being applied seamlessly as Industry 4.0 envisions cyber–physical systems, where they talk with each other in terms of processes, quality, and logistical aspects.

(e)

Data collection with NDE at various stages of the value chain can be merged into a “digital twin” of a component or structure, which can be used as a reference for the condition or structural health monitoring later on. For predictive analytics to compute preventative maintenance or a remaining lifetime, machine learning algorithms must be used.

The rest of the paper is organized as follows. In the next section, the data-driven intelligent model for the welded joint is presented, followed by the implementation of the model in Section 3. In Section 4, the results from the analysis is discussed and then a concluding remark is presented in Section 5.

2. The Data-Driven Intelligent Model for Welded Joints

The clustering method, which has been adopted in this study for flaw/defect detection in welded joints, is an unsupervised learning method that takes input features and data such that it does not require proper labels to predict and evaluate them. It is a data analysis technique for identifying intriguing patterns in data, such as fault patterns and groupings. It provides a quick summary of the data that could be utilized to make inferences. Since the purpose of a clustering task is to find data structures, the clustering method must, therefore, be able to determine the number of structures/groups in the data and how the features are distributed within each group.

Clustering, for example, can be used to detect defects, faults, and anomalies in a system by using the system’s database or historical data or the locations of the faults or defects in the system. Additionally, the area where errors occur more frequently can also be determined using the clustering method. Several clustering methods can be used for this task, including k-mean clustering [20], mini-batch k-means clustering [21], spectral clustering, gaussian mixture clustering [20], birch clustering [22], density-based clustering [23,24], hierarchical clustering, and random forest clustering [25]. All of these methods can be successfully implemented to address the two objectives (flaw/defect detection and their internal damage location). In this paper, however, the study will be focused only on the k-mean clustering and the local outlier factor model algorithm.

2.1. K-Mean Clustering and the Local Outlier Factor (LOF) Model

K-means clustering is a vector quantization approach that seeks to partition n observations into k clusters, with each observation belonging to the cluster with the closest mean (cluster centers or cluster centroid), which serves as the cluster’s prototype such that the data space is divided into Voronoi cells as a result of this [26]. Within-cluster variances (squared Euclidean distances) are minimized by k-means clustering, but not the regular Euclidean distances. The mean optimizes squared errors, while only the geometric median minimizes the Euclidean distances [27]. The use of k-medians and k-medoids, for example, can lead to better Euclidean solutions.

There are three main characteristics of k-means that make it very efficient for solving engineering problems; however, these same characteristics are also frequently seen as its most significant drawbacks. These characteristics include [28]:

• The Euclidean distance is used as both the metric and variance, and for measuring the cluster scatter.
• The number of clusters k, when used as an input parameter; selecting an incorrect value for k, may result in bad results. It is important, therefore, to check the number of clusters in the data set when performing a diagnostic check with the k-mean clustering method.
• Finally, the convergence to a local minimum can have unexpected (“wrong”) results.

Although the problem is computationally challenging, effective heuristic techniques quickly converge to a local optimum. Both k-means and gaussian mixture modeling use an iterative refining method that is comparable to the expectation–maximization algorithm for mixtures of gaussian distributions. They both use cluster centers to represent the data; however, k-means clustering finds clusters with similar spatial extents, whereas the gaussian mixture model enables clusters to have diverse shapes.

Definition 1.

If a set of observations is given by $\left(x_1,x_2,x_3,\dots ,x_n\right)$ where each of the observations is a d-dimensional real vector, the k-means clustering, therefore, aims to partition the n observations into $k\left(k\le n\right)$ sets $S=\left(S_1,S_2,S_3,\dots ,S_k\right)$, such that the within-cluster sum of squares (WCSS) is minimized as much as possible (i.e., variance). The objective, therefore, is given as:

$$ar{g}_{S}min{\displaystyle \sum }_{i=1}^k{\displaystyle \sum }_{X\in S_i}\Vert x-{\mu }_i\Vert {}^2=ar{g}_{S}min{\displaystyle \sum }_{i=1}^k\left|S_i\right|Var S_i$$

(1)

where${\mu }_i$is the mean of points in$S_i$and it is the equivalent to the minimization of the pairwise squared deviations of the different points within the same clusters.

$$ar{g}_{S}min{\displaystyle \sum }_{i=1}^k\frac{1}{\left|S_i\right|}{\displaystyle \sum }_{x,y\in S_i}\Vert x-{\mu }_i\Vert {}^2$$

(2)

The overall variance is constant, and this is equivalent to maximizing the sum of squared deviations between points in various clusters, and it is equal to the between-cluster sum of squares (BCSS). The algorithm for the implementation of the k-mean clustering method that has been proposed for supporting the physics-based analysis used in the detection of flaws/defects and for the determination of the internal damage location in welded joints has been developed using the Python 3 programming language. The flowchart of the algorithm have been given in Figure 1.

The task of detecting observations that do not conform to typical, expected behavior is referred to as anomaly identification. In various application domains, these observations are sometimes referred to as anomalies, defects, outliers, flaws, novelties, exceptions, or surprises. Anomalies, flaws, and outliers are three of the most commonly used phrases in literature. The most recognized and commonly utilized local anomaly and flaws detection algorithm is the local outlier factor (LOF) model. It employs the concept of k nearest neighbors to calculate and identify anomaly or outlier scores in a dataset.

The LOF model is an unsupervised anomaly/flaw detection method that computes a particular data point’s local density deviation to its neighbors. Outliers are samples that have a significantly lower density than their neighbors. A point’s LOF is determined by the ratios of the local density of the area surrounding the point and the local densities of its neighbors. It takes into account the relative density of data points. When employing a LOF model, the following steps can be taken:

(a)

Using a distance function such as Euclidean or Manhattan, calculate the distance between P and all of the specified points.

(b)

Locate the nearest k (k-nearest neighbor) point. For example, if k = 3, find the distance to the third nearest neighbor.

(c)

Locate the k nearest points.

(d)

Using the following equation, calculate the local reachability density (lrd), $lr{d}_k=\frac{\Vert N_k\left(0\right)\Vert }{{{\displaystyle \sum }}_{0^{\prime }ϵN_k\left(0\right)}reachdis{t}_k\left(0^{\prime }\leftarrow 0\right)}$, where reachable distance can be calculated as $reachdis{t}_k\left(0^{\prime }\leftarrow 0\right)=max\left\{dis{t}_k\left(0\right),dist\left(0,0^{\prime }\right)\right\}$, $N_k\left(0\right)$ is the number of neighbors.

(e)

The final step is to compute the local outlier factor, which is as follows, $LOF=\frac{{{\displaystyle \sum }}_{0^{\prime }ϵN_k\left(0\right)}\frac{lr{d}_k\left(0^{\prime }\right)}{lr{d}_k\left(0\right)}}{\Vert N_k\left(0\right)\Vert }$.

2.2. Data Collection for the Implementation of a Data-Driven Intelligent Model

The welded joint dataset used in this paper was obtained from published studies and from the quality control unit from a leading oil and gas company around Port Harcourt, Nigeria, which unfortunately doesn’t want to be mentioned. The dataset, which comprises quality control records of welded joints, includes labels such as temperature, hardness of the welded joint (HB), base material nominal yield strength (MPa), base material nominal ultimate tensile strength (MPa), weld length (mm), porosity area and ratio, roughness, bead width and area, internal crack length, fusion data, groove angle (°) data, and spatters data. About 25 datasets were collected from published works for each of the labels presented above, while 100 were obtained from quality control units. Some of the experimental data used for the implementation of the intelligent model are given in

Table 1. Experimental data for the intelligent model.

S/N	Predictive Parameters	Data Range	Source
1	The temperature in the middle of the weld	18–20	[29] and from quality control units
2	Hardness (HB)	Max. 290	[30] and from quality control units
3	Nominal yield strength (MPa)	420–610	[30] and from quality control units
4	Nominal ultimate tensile strength (MPa)	640–790	[31] and from quality control units
5	Impact strength (J) at 20 °C	30–100	[29] and from quality control units
6	Weld length (mm)	8.53–9.0	[32] and quality control units
7	Roughness (μm)	0.24–1.35	[33] and quality control units
8	Porosity area (mm2)	2.95–7.0	[34] and quality control units
9	Bead width (mm)	4.5–5.2	[34] and quality control units
10	Bead area (mm2)	40.5–46.9	[35] and quality control units
11	Porosity ratio (%)	6.7–15.2	[35] and quality control units
12	Crack initiation from weld (mm)	6.6–14.2	[34] and quality control units
13	Groove angle (°)	45 and 60	[34] and quality control units
14	Welding speed (mm/s)	3–4	[34] and quality control units
15	Welding current (A)	80–140	[36] and quality control units

below. The datasets’ training/test ratio is set to 8:2. That is, 80% of the training data is drawn at random from the label database, while the remaining 20% serves as the test dataset. It should be noted that the samples in the training dataset are completely different from the samples in the test dataset.

3. Implementation of the Data-Driven Intelligent Model

In this section, the results of the analysis for the classification of the welded joint data collected are presented. First, they are classified into clusters and then flaws/defects in a welded joint are identified and detected, finally, the internal flaw/defect locations in the welded joint are visualized. In implementing the intelligent data-driven model for the dataset which has been collected from the application of the NDE techniques, first, the data are observed and then analyzed using the k-mean clustering method and finally, with the LOF model algorithm. The k-mean clustering method is implemented for the determination of data cluster and the computation of the cluster means which depict how organized the data are and the quality of the clusters, while the LOF model algorithm help in the identification and visualization of the internal flaws/defects and their locations in the welded joint.

3.1. The K-Mean Clustering Algorithm for Defect Classification for Welded Joint Data

In the classification and identification of potential defects and hidden patterns in the welded joint data presented above, the k-mean clustering model algorithm has been applied. The dataset used for this purpose includes temperature data, hardness of the welded joint (HB), base material nominal yield strength (MPa), base material nominal ultimate tensile strength (MPa), pin feature aggressiveness, roughness data, and the groove angle. The simulated results from the algorithm have been presented in the t-SNE cluster plot as shown in Figure 2. The t-distributed stochastic neighbor embedding (t-SNE) is a non-linear plot that maps multi-dimensional data into two or more clusters. It enjoys the advantage of being able to present data explicitly as compared to other features.

From the t-SNE cluster plot result, it is not hard to see that there are some noise points (defects) in the obtained dataset. Additionally, from the dataset, we can easily see that the trained and validated data in the k-mean clustering algorithm have been classified automatically into three (3) different clusters, which also show their size, heterogeneity, and silhouette score. The silhouette score is used to determine the quality, performance, and similarity of the features in the clusters. In

Table 2. Cluster information for the welded joint data.

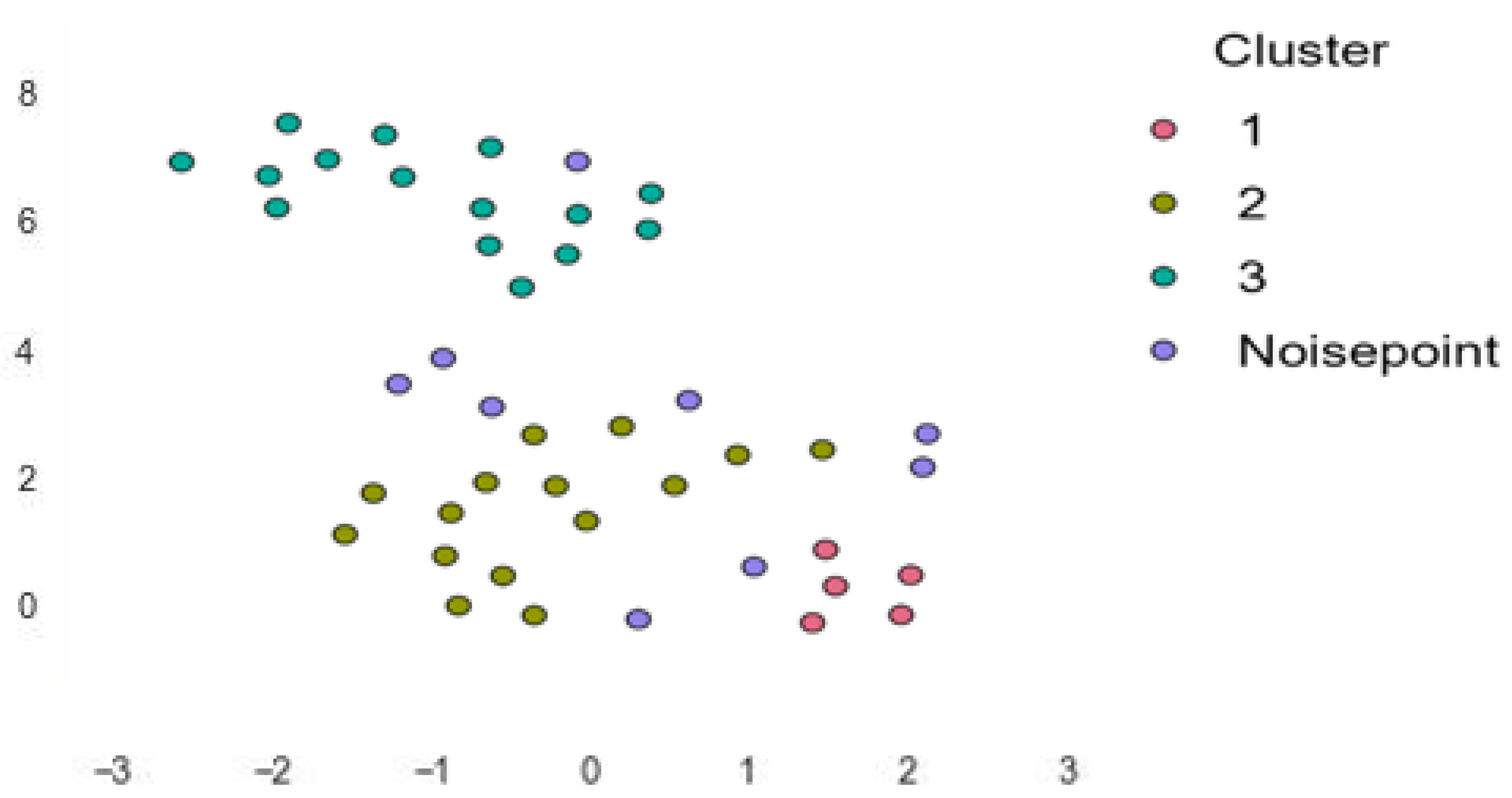
Cluster Information
Cluster	Noise Points	1	2	3
Size	9	5	15	15
Explained proportion within-cluster heterogeneity	0.000	0.073	0.506	0.421
Within the sum of squares	0.000	8.569	59.157	49.263
Silhouette score	0.000	0.455	0.194	0.390

Notes. The between sum of squares of the 3 cluster model is 142.09. The total sum of squares of the 3 cluster model is 259.08.

and

Table 3. The clustering means of the welded joint data.

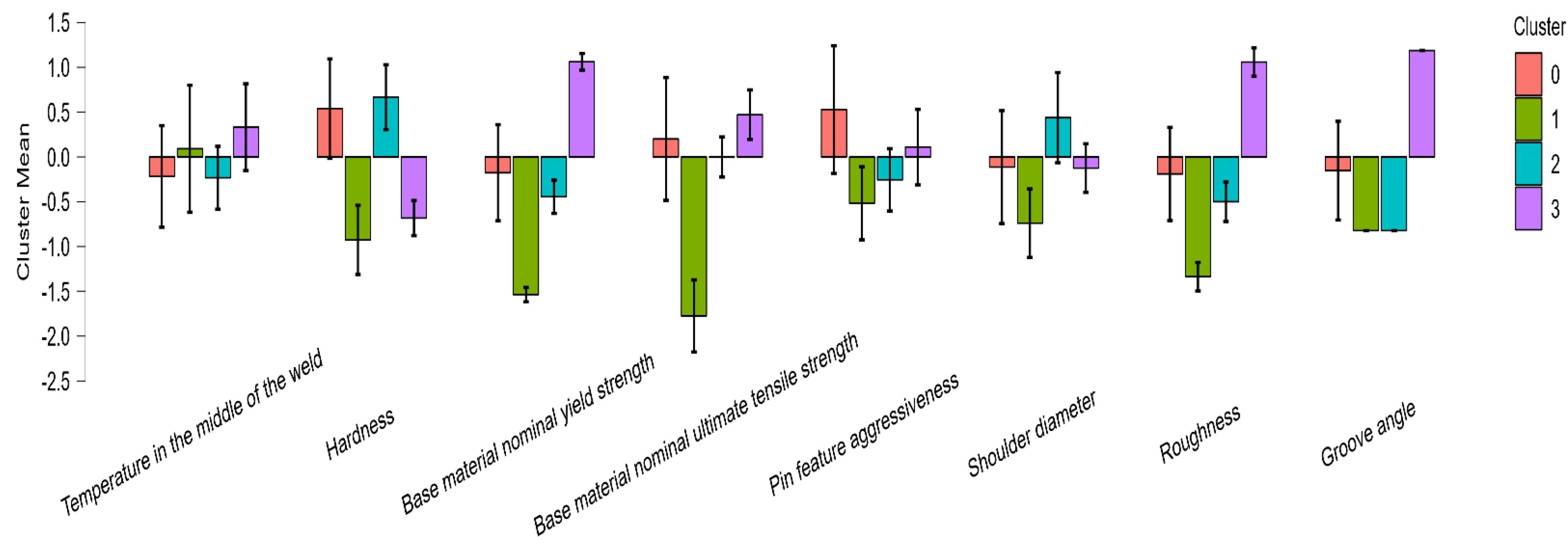
Cluster Means
	The Temperature in the Middle of the Weld	Hardness (HB)	Nominal Yield Strength (MPa)	Nominal Ultimate Tensile Strength (MPa)	Pin Feature Aggressiveness	Shoulder Diameter (mm)	Roughness (μm)	Groove Angle
Cluster 0	−0.217	0.540	−0.176	0.201	0.529	−0.113	−0.190	−0.152
Cluster 1	0.092	−0.927	−1.537	−1.775	−0.517	−0.740	−1.336	−0.823
Cluster 2	−0.232	0.667	−0.444	1.465 × 10−8	−0.256	0.439	−0.500	−0.823
Cluster 3	0.332	−0.682	1.063	0.471	0.111	−0.125	1.060	1.188

below, the cluster information for the dataset and the cluster mean values, respectively, have been presented.

Similarly, from Table 2 and Table 3 above, the k-means algorithm is applied to determine the range of the features in the cluster and their importance. The results, which have been presented in Figure 3, show the clustering coefficient of the features as well as how they influence the overall defect in the welded joint dataset. The clustering coefficient measures the degree to which the nodes in the dataset tend to cluster together as well as the noise points. It also shows the tightly knit group created from the dataset, which is characterized by a relatively high density of ties.

3.2. Application of LOF Model Algorithm for Flaw Detection in Welded Joints

The LOF model algorithm has been applied for welded joint sample data from a field in the oil and gas industry. This is mainly to address the gaps in the NDE literature, where it has been found that there are difficulties in the use of the NDE method on welded joint structures with intricate shapes and high curvatures, as well as the challenges in the interpretation of NDE data due to human factors (subjectiveness and uncertainty). The LOF model algorithm considers the density of data instances surrounding a given instance A to the density of data instances surrounding A’s neighbors, such that if the former is lower than the latter, it indicates that A is substantially isolated. This isolation (anomaly) is deemed as the flaws or defects of the welded joint.

Using the dataset in Table 1 above, flaws due to internal cracks, internal porosity of the welded joint, internal fusion, and internal penetration are identified in the welded joint, which has intricate shapes and high curvature. The following results from the analysis of the dataset using the LOF model algorithm have been presented in Figure 4.

It is not difficult to see from the results presented in Figure 4a that there are several flaws, which are represented as abnormal data behavior scattered in and around the welded joints, such that this can be interpreted as a gradual propagation of the internal crack in and around the welded joint and to other parts of the material. Hence, if not repaired immediately, the joint could become weak and collapse. In Figure 4b, there are very few flaws around the welded joints; hence, it can be concluded and interpreted that the internal porosity in the welded joint has no significant effect on the entire welded joint or the materials in general. With this result, it is recommended therefore, that the welded joint should be monitored regularly to prevent total failure. Similar to the result in Figure 4b above, Figure 4c,d shows some few anomalies and flaws, which is as a result of a very significant defect in the welded joint due to internal fusion and internal weld penetration, respectively. Hence, it has been recommended that the welded joint should be monitored regularly.

4. Discussion of the Results

Welded joint data collected and analyzed in this thesis has proven to be very critical in the understanding of welded joint defect identification, classification, location, and propagation. The study has presented two novel computational model algorithms for the management of flaws and defects in welded joints with intricate shapes and curvatures, which are very common in the oil and gas industry.

In the implementation of the model algorithms, a dataset that comprises the hardness of the welded joint (HB), base material nominal yield strength (MPa), base material nominal ultimate tensile strength (MPa), pin feature aggressiveness, roughness data, temperature, and the groove angle of the joints were analyzed to classify and identify defects in the welded joint. Similarly, a dataset that comprises the internal crack length check, internal porosity of the welded joint, internal fusion assessment, internal slag inclusion assessment, and lack of penetration assessment and spatters data of the welded joint were simulated to detect flaws and defects in the welded joint considered. From the results obtained from the analysis, the study can conclude, therefore, that the proposed model algorithms are feasible and can address and manage flaws and defects in the welded joint, which in extension has addressed the gap in the literature.

5. Conclusions

Given the diversity of NDE applications and the stringent quality control standards which have been encouraged for the actualization of Industry 4.0, researchers and practitioners are now frequently tasked to provide low-cost and time-efficient solutions to NDE-related problems. Lately, data engineering has proven to be an effective numerical tool for NDE. In this paper, a data-driven approach that is based on the k-mean clustering and LOF algorithm has been proposed and deployed as a special tool for the management of the NDE of welded joints. The k-mean clustering and LOF algorithm was implemented for the classification, identification, and determination of data clusters and defects in the welded joints dataset.

In the application of the model algorithm, flaws due to internal cracks, porosity, fusion, and penetration in the welded joint were analyzed and visualized. In the future, the proposed data-driven intelligent approach will be applied in other domains for the improvement of welding technology and the actualization of the Industry 4.0 concept for the development of lightweight products for manufacturing.