Averaging Level Control to Reduce Off-Spec Material in a Continuous Pharmaceutical Pilot Plant
Abstract
:1. Introduction
2. Approach
2.1. Process Description and Control Structure
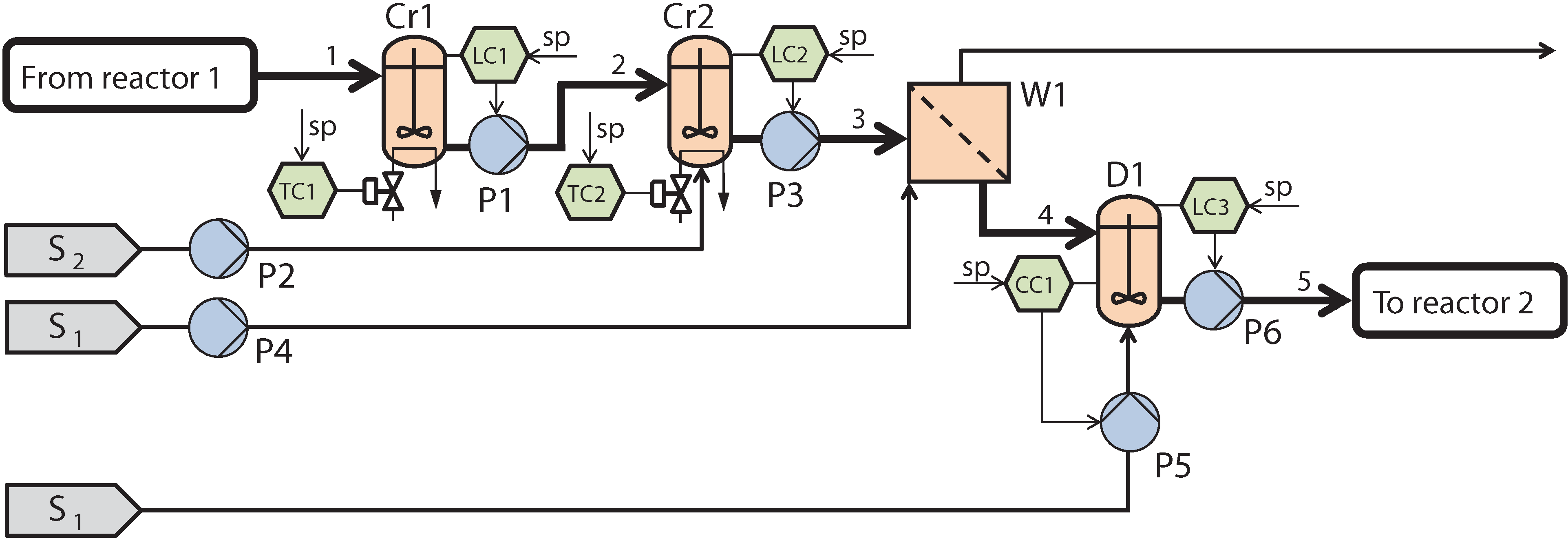
2.2. Process Modeling and Parameter Estimation
| Controller | Setpoint | Comments | |||
|---|---|---|---|---|---|
| LC1 | P | – | |||
| LC2 | P | – | |||
| PI-ALC | |||||
| OALC | |||||
| LC3 | P | – | |||
| PI-ALC | |||||
| OALC | |||||
| CC1 | P | g/g | – | ||
| Parameter | Estimated value | Initial guess | Bounds |
|---|---|---|---|
| Flow rate of stream 1 | |||
| Mass fraction of A in stream 1 | |||
| Slurry liquid fraction at outlet of W1 | |||
| Initial liquid fraction in Cr1 | |||
| Initial liquid fraction in Cr2 |
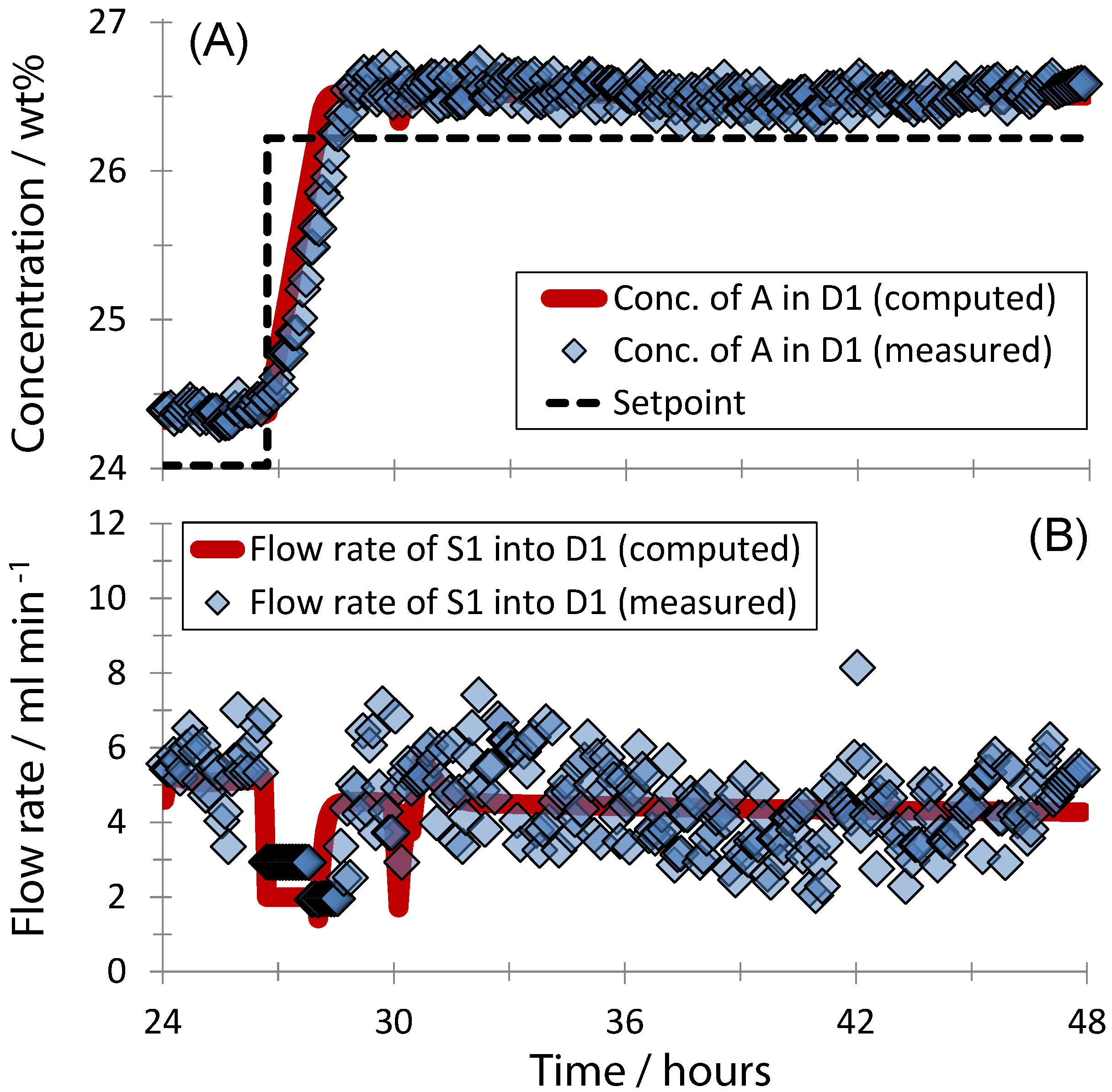
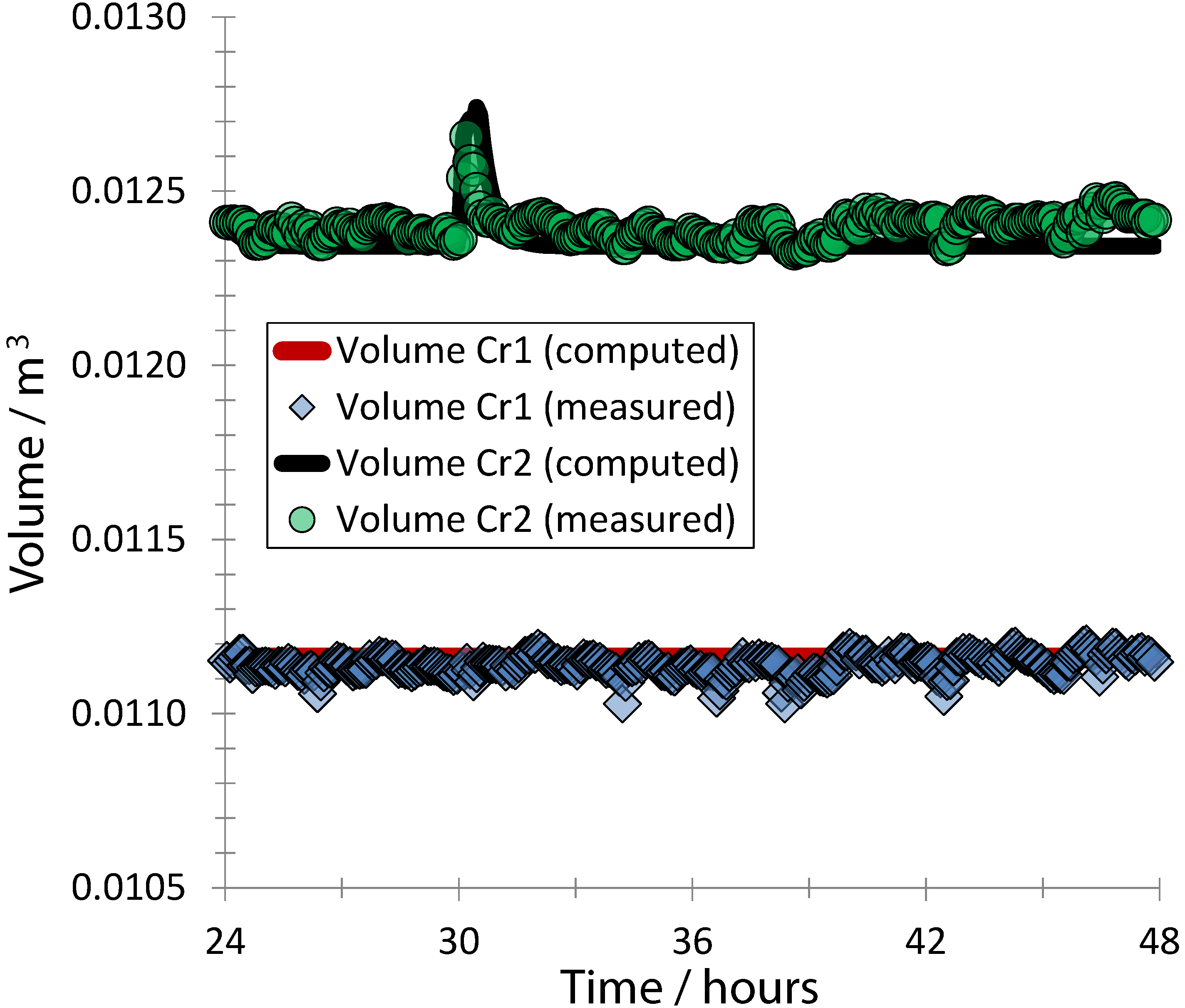
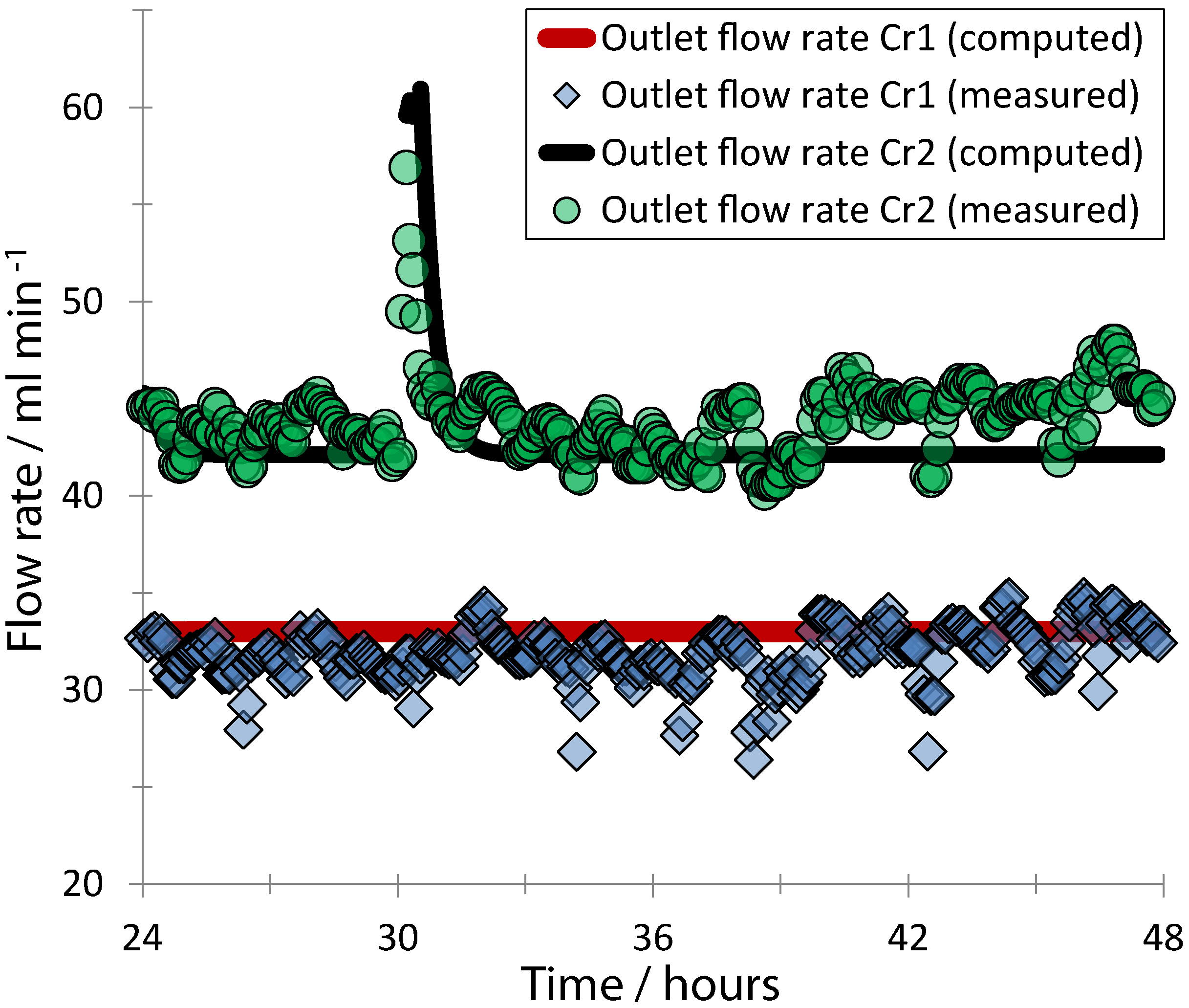
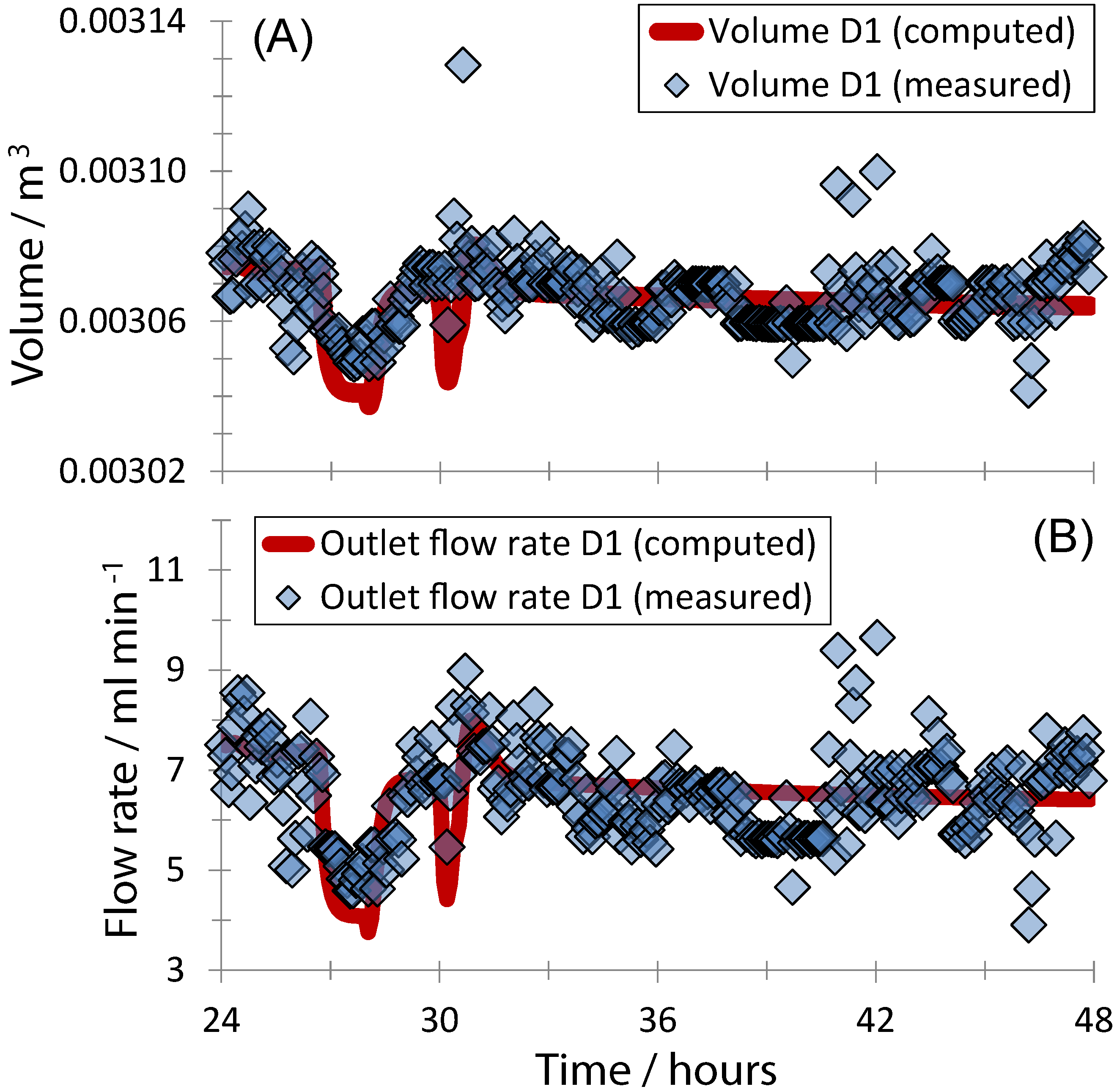
3. Results and Discussion
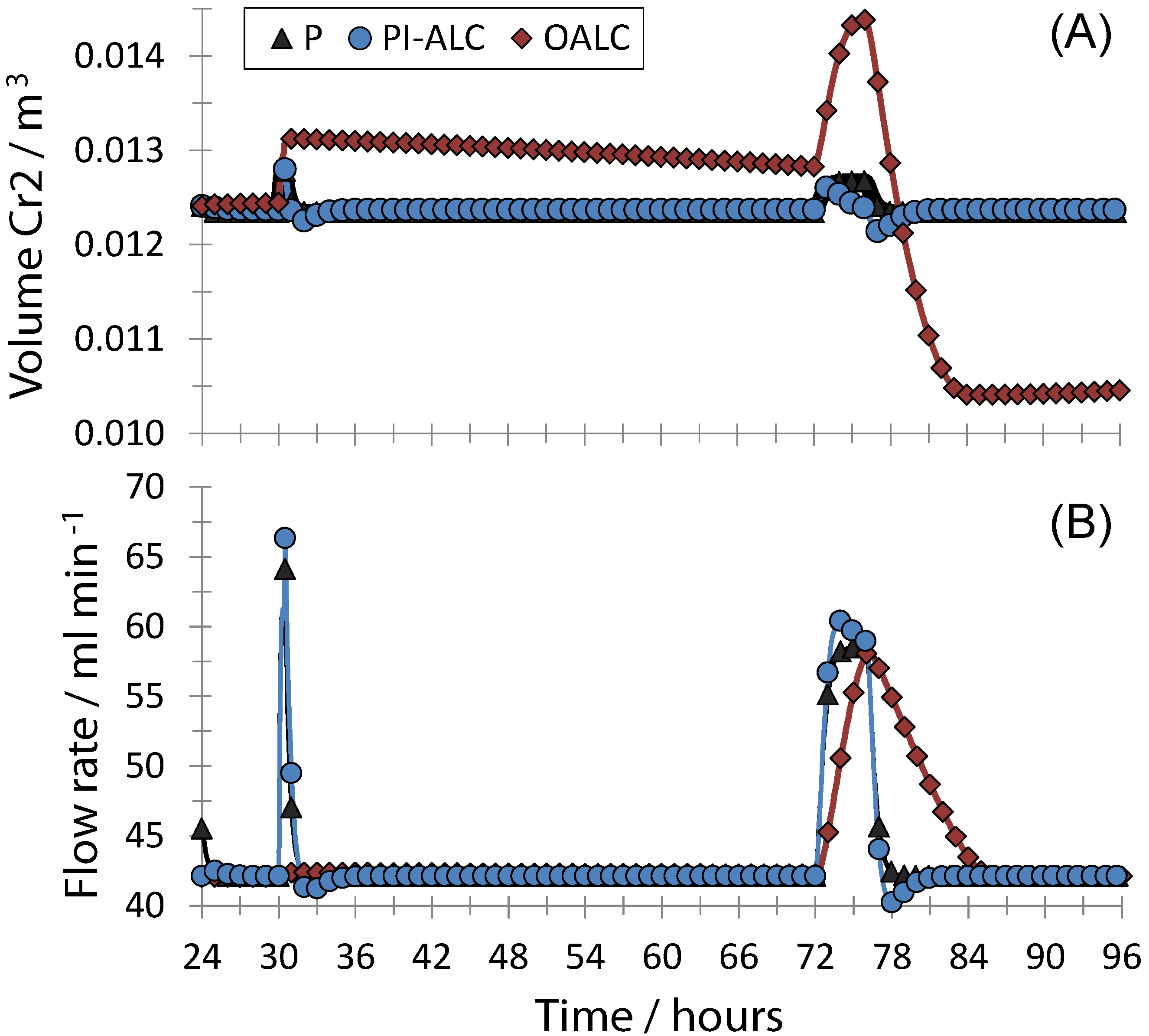
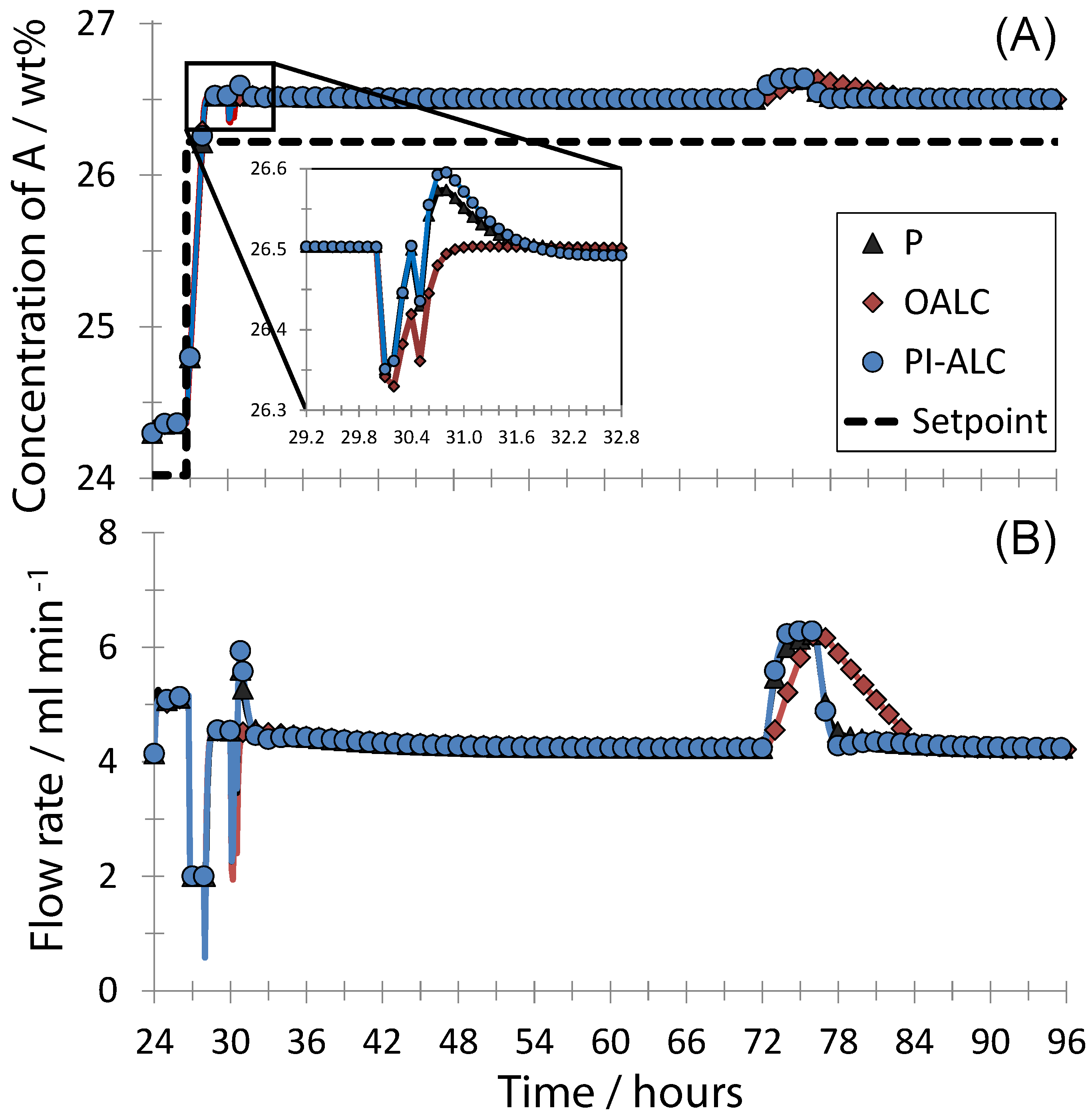
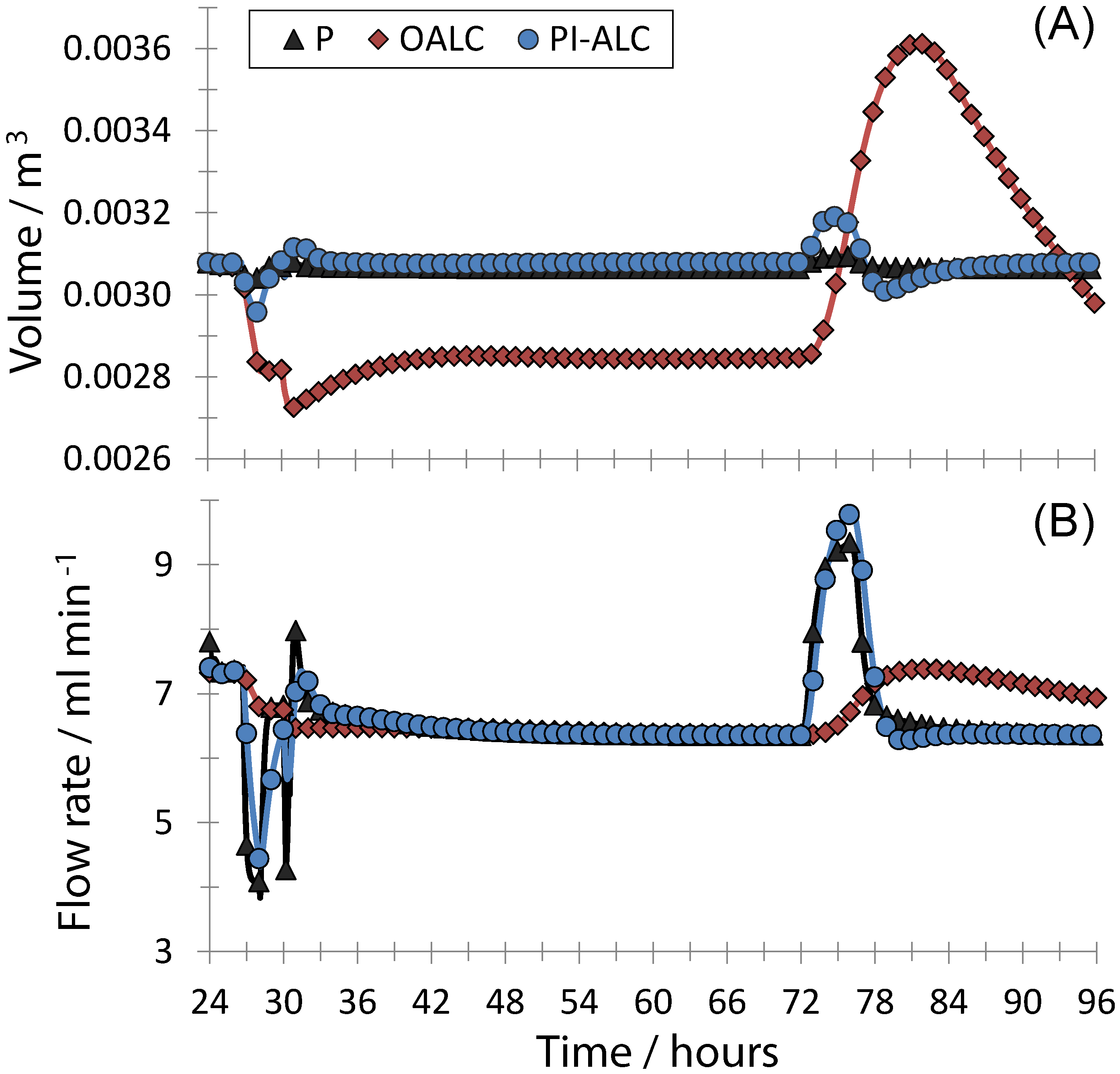
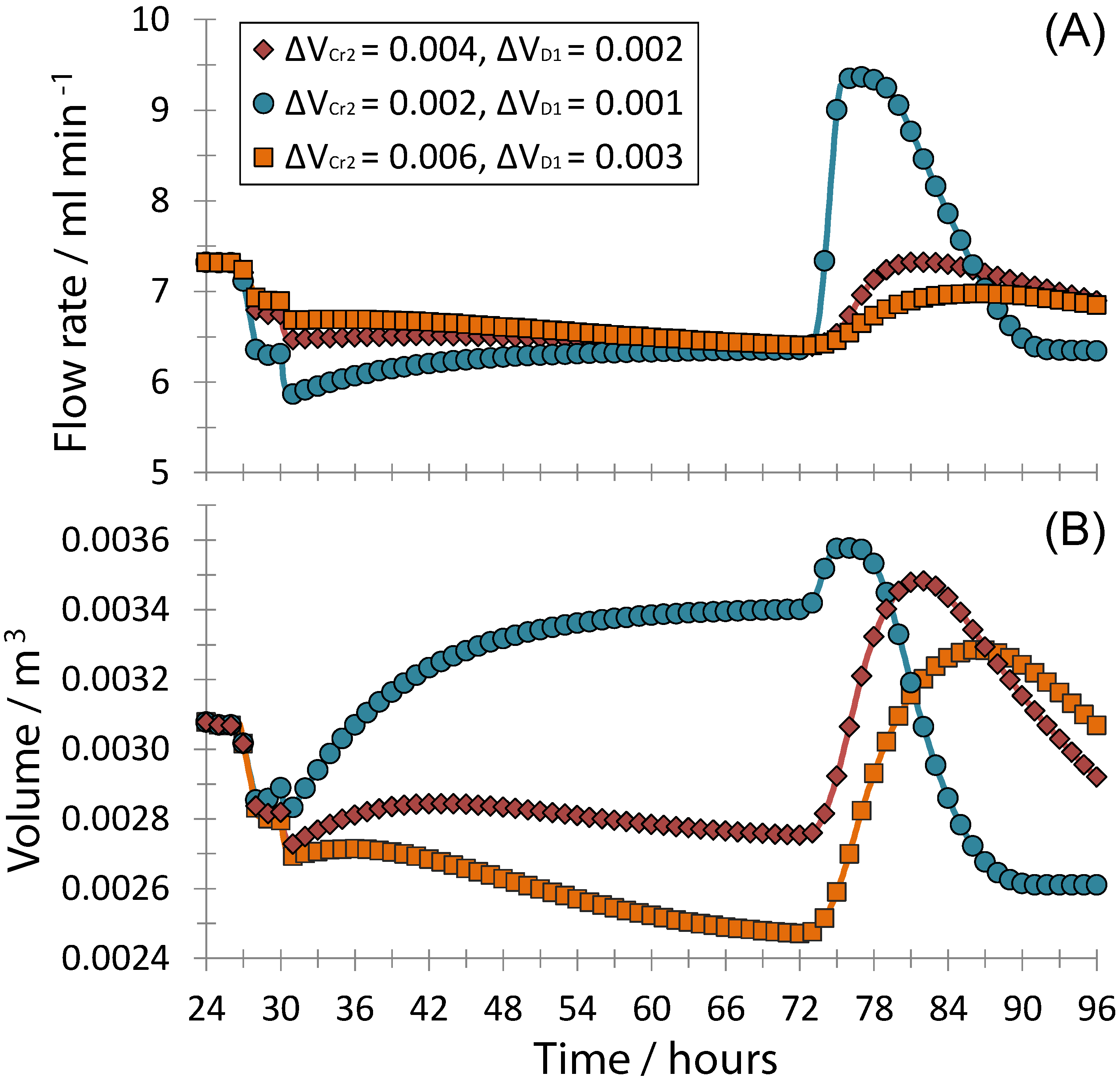
4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Schaber, S.D.; Gerogiorgis, D.I.; Ramachandran, R.; Evans, J.M.B.; Barton, P.I.; Trout, B.L. Economic analysis of integrated continuous and batch pharmaceutical manufacturing: A case study. Ind. Eng. Chem. Res. 2011, 50, 10083–10092. [Google Scholar] [CrossRef]
- Plumb, K. Continuous processing in the pharmaceutical industry: Changing the mind set. Chem. Eng. Res. Des. 2005, 83, 730–738. [Google Scholar] [CrossRef]
- Roberge, D.M.; Ducry, L.; Bieler, N.; Cretton, P.; Zimmermann, B. Microreactor technology: A revolution for the fine chemical and pharmaceutical industries? Chem. Eng. Technol. 2005, 28, 318–323. [Google Scholar] [CrossRef]
- Roberge, D.M.; Zimmermann, B.; Rainone, F.; Gottsponer, M.; Eyholzer, M.; Kockmann, N. Microreactor technology and continuous processes in the fine chemical and pharmaceutical industry: Is the revolution underway? Org. Process Res. Dev. 2008, 12, 905–910. [Google Scholar] [CrossRef]
- Jimenez-Gonzalez, C.; Poechlauer, P.; Broxterman, Q.B.; Yang, B.S.; Am Ende, D.; Baird, J.; Bertsch, C.; Hannah, R.E.; Dell’Orco, P.; Noorrnan, H.; et al. Key green engineering research areas for sustainable manufacturing: A perspective from pharmaceutical and fine chemicals manufacturers. Org. Process. Res. Dev. 2011, 15, 900–911. [Google Scholar] [CrossRef]
- LaPorte, T.L.; Wang, C. Continuous processes for the production of pharmaceutical intermediates and active pharmaceutical ingredients. Curr. Opin. Drug Discovery Dev. 2007, 10, 738–745. [Google Scholar]
- Kockmann, N.; Gottsponer, M.; Zimmermann, B.; Roberge, D.M. Enabling continuous-flow chemistry in microstructured devices for pharmaceutical and fine-chemical production. Chem. Eur. J. 2008, 14, 7470–7477. [Google Scholar] [CrossRef] [PubMed]
- Hartman, R.L.; McMullen, J.P.; Jensen, K.F. Deciding whether to go with the flow: Evaluating the merits of flow reactors for synthesis. Angew. Chem. Int. Ed. 2011, 50, 7502–7519. [Google Scholar] [CrossRef] [PubMed]
- Wegner, J.; Ceylan, S.; Kirschning, A. Ten key issues in modern flow chemistry. Chem. Commun. 2011, 47, 4583–4592. [Google Scholar] [CrossRef] [PubMed]
- Wegner, J.; Ceylan, S.; Kirschning, A. Flow chemistry— A key enabling technology for (multistep) organic synthesis. Adv. Synth. Catal. 2012, 354, 17–57. [Google Scholar] [CrossRef]
- Pollet, P.; Cope, E.D.; Kassner, M.K.; Charney, R.; Terett, S.H.; Richman, K.W.; Dubay, W.; Stringer, J.; Eckertt, C.A.; Liotta, C.L. Production of (S)-1-benzyl-3-diazo-2-oxopropylcarbamic acid tert-butyl ester, a diazoketone pharmaceutical intermediate, employing a small scale continuous reactor. Ind. Eng. Chem. Res. 2009, 48, 7032–7036. [Google Scholar] [CrossRef]
- Christensen, K.M.; Pedersen, M.J.; Dam-Johansen, K.; Holm, T.L.; Skovby, T.; Kiil, S. Design and operation of a filter reactor for continuous production of a selected pharmaceutical intermediate. Chem. Eng. Sci. 2012, 26, 111–117. [Google Scholar] [CrossRef]
- Chen, J.; Sarma, B.; Evans, J.M.B.; Myerson, A.S. Pharmaceutical crystallization. Cryst. Growth Des. 2011, 11, 887–895. [Google Scholar] [CrossRef]
- Griffin, D.W.; Mellichamp, D.A.; Doherty, M.F. Reducing the mean size of API crystals by continuous manufacturing with product classification and recycle. Chem. Eng. Sci. 2010, 65, 5770–5780. [Google Scholar] [CrossRef]
- Wong, S.Y.; Tatusko, A.P.; Trout, B.L.; Myerson, A.S. Development of continuous crystallization processes using a single-stage mixed-suspension, mixed-product removal crystallizer with recycle. Cryst. Growth Des. 2012, 12, 5701–5707. [Google Scholar] [CrossRef]
- Alvarez, A.J.; Myerson, A.S. Continuous plug flow crystallization of pharmaceutical compounds. Cryst. Growth Des. 2010, 10, 2219–2228. [Google Scholar] [CrossRef]
- Alvarez, A.J.; Singh, A.; Myerson, A.S. Crystallization of Cyclosporine in a multistage continuous MSMPR crystallizer. Cryst. Growth Des. 2011, 11, 4392–4400. [Google Scholar] [CrossRef]
- Lawton, S.; Steele, G.; Shering, P.; Zhao, L.H.; Laird, I.; Ni, X.W. Continuous crystallization of pharmaceuticals using a continuous oscillatory baffled crystallizer. Org. Process Res. Dev. 2009, 13, 1357–1363. [Google Scholar] [CrossRef]
- Eder, R.J.P.; Schmitt, E.K.; Grill, J.; Radl, S.; Gruber-Woelfler, H.; Khinast, J.G. Seed loading effects on the mean crystal size of acetylsalicylic acid in a continuous-flow crystallization device. Cryst. Res. Technol. 2011, 46, 227–237. [Google Scholar] [CrossRef]
- Eder, R.J.P.; Schrank, S.; Besenhard, M.O.; Roblegg, E.; Gruber-Woelfler, H.; Khinast, J.G. Continuous sonocrystallization of acetylsalicylic acid (ASA): Control of crystal size. Cryst. Growth Des. 2012, 12, 4733–4738. [Google Scholar] [CrossRef]
- Quon, J.; Zhang, H.; Alvarez, A.J.; Evans, J.M.B.; Myerson, A.S.; Trout, B.L. Continuous crystallization of aliskiren hemifumarate. Org. Process Res. Dev. 2012, 12, 3036–3044. [Google Scholar] [CrossRef]
- Zhang, H.; Quon, J.; Alvarez, A.J.; Evans, J.M.B.; Myerson, A.S.; Trout, B.L. Development of continuous anti-solvent/cooling crystallization process using cascaded mixed suspension, mixed product removal crystallizers. Org. Process Res. Dev. 2012, 16, 915–924. [Google Scholar] [CrossRef]
- Mortier, S.T.F.C.; De Beer, T.; Gernaey, K.V.; Vercruysse, J.; Fonteyne, M.; Remon, J.P.; Vervaet, C.; Nopens, I. Mechanistic modelling of the drying behaviour of single pharmaceutical granules. Eur. J. Pharm. Biopharm. 2012, 80, 682–689. [Google Scholar] [CrossRef] [PubMed]
- Gonnissen, Y.; Remon, J.P.; Vervaet, C. Development of directly compressible powders via co-spray drying. Eur. J. Pharm. Biopharm. 2007, 67, 220–226. [Google Scholar] [CrossRef] [PubMed]
- Gonnissen, Y.; Goncalves, S.I.V.; De Geest, B.G.; Remon, J.P.; Vervaet, C. Process design applied to optimise a directly compressible powder produced via a continuous manufacturing process. Eur. J. Pharm. Biopharm. 2008, 68, 760–770. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Rutledge, G.C.; Myerson, A.S.; Trout, B.L. Production and characterization of carbamazepine nanocrystals by electrospraying for continuous pharmaceutical manufacturing. J. Pharm. Sci. 2012, 101, 1178–1188. [Google Scholar] [CrossRef] [PubMed]
- Brettmann, B.; Bell, E.; Myerson, A.; Trout, B. Solid-state NMR characterization of high-loading solid solutions of API and excipients formed by electrospinning. J. Pharm. Sci. 2012, 101, 1538–1545. [Google Scholar] [CrossRef] [PubMed]
- Brettmann, B.K.; Cheng, K.; Myerson, A.S.; Trout, B.L. Electrospun formulations containing crystalline active pharmaceutical ingredients. Pharm. Res. 2013, 30, 238–246. [Google Scholar] [CrossRef] [PubMed]
- Dubey, A.; Vanarase, A.U.; Muzzio, F.J. Impact of process parameters on critical performance attributes of a continuous blender A DEM-based study. AIChE J. 2012, 58, 3676–3684. [Google Scholar] [CrossRef]
- Dubey, A.; Sarkar, A.; Ierapetritou, M.; Wassgren, C.R.; Muzzio, F.J. Computational approaches for studying the granular dynamics of continuous blending processes, 1-DEM based methods. Macromol. Mater. Eng. 2011, 296, 290–307. [Google Scholar] [CrossRef]
- Portillo, P.M.; Ierapetritou, M.G.; Muzzio, F.J. Effects of rotation rate, mixing angle, and cohesion in two continuous powder mixers–A statistical approach. Powder Technol. 2009, 194, 217–227. [Google Scholar] [CrossRef]
- Hamdan, I.M.; Reklaitis, G.V.; Venkatasubramanian, V. Exceptional events management applied to roller compaction of pharmaceutical powders. J. Pharm. Innov. 2010, 5, 147–160. [Google Scholar] [CrossRef]
- Singh, R.; Ierapetritou, M.; Ramachandran, R. An engineering study on the enhanced control and operation of continuous manufacturing of pharmaceutical tablets via roller compaction. Int. J. Pharm. 2012, 438, 307–326. [Google Scholar] [CrossRef] [PubMed]
- Wiles, C.; Watts, P. Continuous flow reactors: A perspective. Green Chem. 2012, 14, 38–54. [Google Scholar] [CrossRef]
- Poechlauer, P.; Manley, J.; Broxterman, R.; Gregertsen, B.; Ridemark, M. Continuous processing in the manufacture of active pharmaceutical ingredients and finished dosage forms: An industry perspective. Org. Process Res. Dev. 2012, 16, 1586–1590. [Google Scholar] [CrossRef]
- Singh, R.; Gernaey, K.V.; Gani, R. Model-based computer-aided framework for design of process monitoring and analysis systems. Comput. Chem. Eng. 2009, 33, 22–42. [Google Scholar] [CrossRef]
- Gernaey, K.V.; Cervera-Padrell, A.E.; Woodley, J.M. A perspective on PSE in pharmaceutical process development and innovation. Comput. Chem. Eng. 2012, 42, 15–29. [Google Scholar] [CrossRef]
- Cervera-Padrell, A.E.; Skovby, T.; Kiil, S.; Gani, R.; Gernaey, K.V. Active pharmaceutical ingredient (API) production involving continuous processes—A process systems engineering (PSE)-assisted design framework. Eur. J. Pharm. Biopharm. 2012, 82, 437–456. [Google Scholar] [CrossRef] [PubMed]
- Gernaey, K.V.; Gani, R. A model-based systems approach to pharmaceutical product-process design and analysis. Chem. Eng. Sci. 2010, 65, 5757–5769. [Google Scholar] [CrossRef]
- Gernaey, K.V.; Cervera-Padrell, A.E.; Woodley, J.M. Development of continuous pharmaceutical production processes supported by process systems engineering methods and tools. Future Med. Chem. 2012, 4, 1371–1374. [Google Scholar] [CrossRef] [PubMed]
- Boukouvala, F.; Niotis, V.; Ramachandran, R.; Muzzio, F.J.; Ierapetritou, M.G. An integrated approach for dynamic flowsheet modeling and sensitivity analysis of a continuous tablet manufacturing process. Comput. Chem. Eng. 2012, 42, 30–47. [Google Scholar] [CrossRef]
- Benyahia, B.; Lakerveld, R.; Barton, P.I. A plant-wide dynamic model of a continuous pharmaceutical process. Ind. Eng. Chem. Res. 2012, 51, 15393–15412. [Google Scholar] [CrossRef]
- Lakerveld, R.; Benyahia, B.; Braatz, R.D.; Barton, P.I. Model-based design of a plant-wide control strategy for a continuous pharmaceutical plant. AIChE J. 2013, 59, 3671–3685. [Google Scholar] [CrossRef]
- McDonald, K.A.; McAvoy, T.J.; Tits, A. Optimal averaging level control. AIChE J. 1986, 32, 75–86. [Google Scholar] [CrossRef]
- Mascia, S.; Heider, P.L.; Zhang, H.; Lakerveld, R.; Benyahia, B.; Barton, P.I.; Braatz, R.D.; Cooney, C.L.; Evans, J.M.B.; Jamison, T.F.; et al. End-to-end continuous manufacturing of pharmaceuticals: Integrated synthesis, purification, and final dosage formation. Angew. Chem. Int. Ed. 2013, 52, 12359–12363. [Google Scholar] [CrossRef] [PubMed]
- Seborg, D.E.; Edgar, T.F.; Mellichamp, D.A.; Doyle, F.J., III. Process Dynamics and Control, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2011; pp. 107–108. [Google Scholar]
- St. Clair, D.W. Controller Tuning and Control Loop Performance: “PID without the Math”, 2nd ed.; Straight-line Control Co. Inc.: Newark, NJ, USA, 1993. [Google Scholar]
- Campo, P.J.; Morari, M. Model predictive optimal averaging level control. AIChE J. 1989, 35, 579–591. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Lakerveld, R.; Benyahia, B.; Heider, P.L.; Zhang, H.; Braatz, R.D.; Barton, P.I. Averaging Level Control to Reduce Off-Spec Material in a Continuous Pharmaceutical Pilot Plant. Processes 2013, 1, 330-348. https://doi.org/10.3390/pr1030330
Lakerveld R, Benyahia B, Heider PL, Zhang H, Braatz RD, Barton PI. Averaging Level Control to Reduce Off-Spec Material in a Continuous Pharmaceutical Pilot Plant. Processes. 2013; 1(3):330-348. https://doi.org/10.3390/pr1030330
Chicago/Turabian StyleLakerveld, Richard, Brahim Benyahia, Patrick L. Heider, Haitao Zhang, Richard D. Braatz, and Paul I. Barton. 2013. "Averaging Level Control to Reduce Off-Spec Material in a Continuous Pharmaceutical Pilot Plant" Processes 1, no. 3: 330-348. https://doi.org/10.3390/pr1030330
APA StyleLakerveld, R., Benyahia, B., Heider, P. L., Zhang, H., Braatz, R. D., & Barton, P. I. (2013). Averaging Level Control to Reduce Off-Spec Material in a Continuous Pharmaceutical Pilot Plant. Processes, 1(3), 330-348. https://doi.org/10.3390/pr1030330







