Limits of Compartmental Models and New Opportunities for Machine Learning: A Case Study to Forecast the Second Wave of COVID-19 Hospitalizations in Lombardy, Italy
Abstract
:1. Introduction
2. Materials and Methods
2.1. Population and Data Sources
2.2. The Basic SEIR Model
2.3. The Hybrid SEIR Model
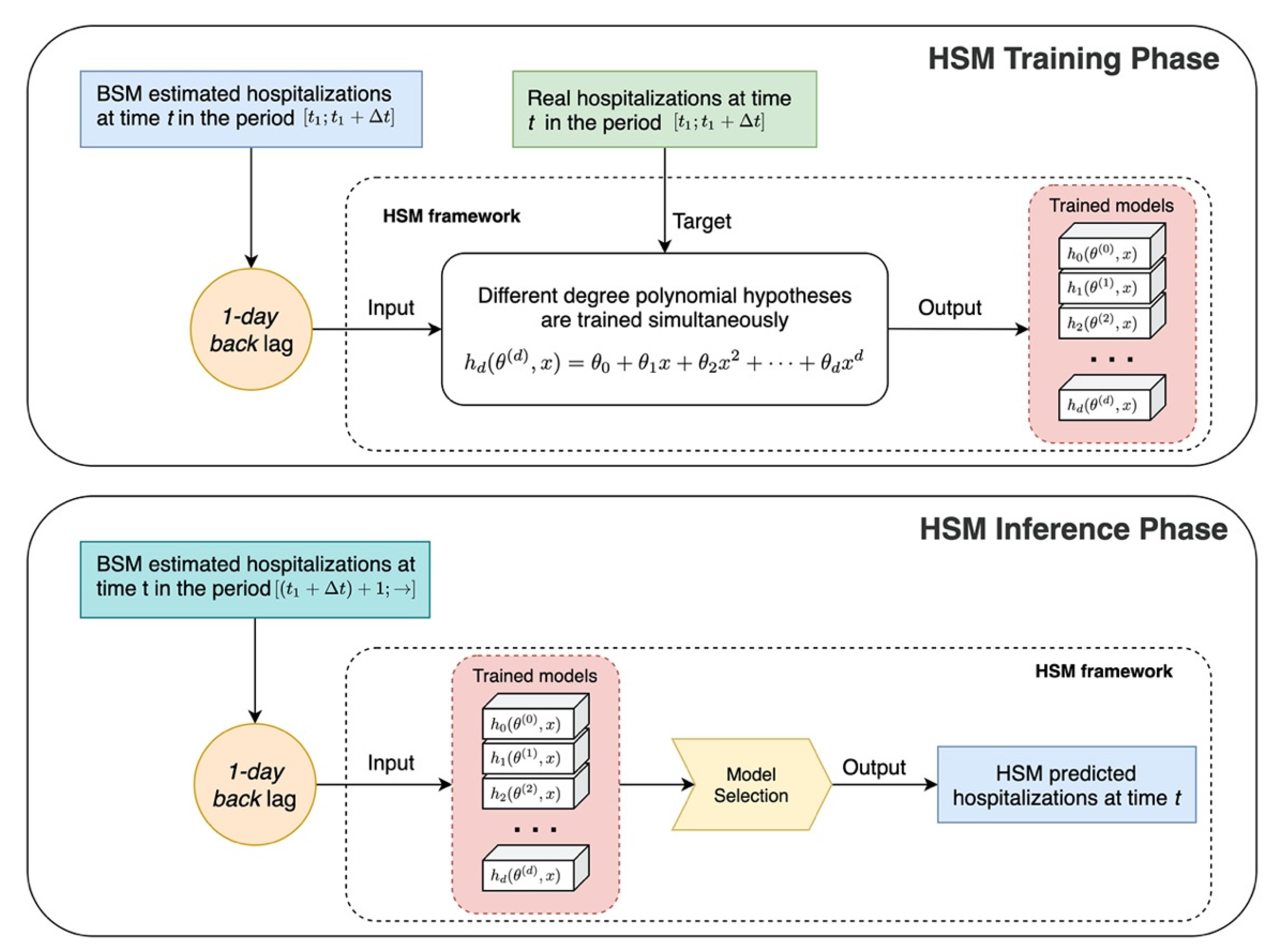
The Machine Learning Module
2.4. What-If Analysis: Scenarios during the First and the Second Lockdown
2.5. The Daily Reproduction Number Estimation
3. Results
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Definitions | Values | Sources | |
|---|---|---|---|
| Susceptible | 10,025,948 | [17] | |
| Residents as of 31 October 2019 | 10,097,171 | [41] | |
| Deaths | 333 | [33] | |
| Hospitalized | 3242 | [33] | |
| Known Infected | 4823 | [33] | |
| Undetected Infected | 48,230 | [17] | |
| Undetected asymptomatic Infected | 32,153 | [17] | |
| Undetected symptomatic Infected | 16,077 | [17] | |
| Tests | 20,135 | [33] | |
| Quarantined | 15,312 | [17] | |
| Quarantined exposed | 24 | [17] | |
| Quarantined susceptible | 15,288 | [17] | |
| Unknown exposed | 2212 | [17] | |
| Recovered | 646 | [33] |
| Definitions | Values | Sources | |
|---|---|---|---|
| Number of days of the first wave lockdown | 58 | BSM | |
| Number of days from the beginning of the first lockdown (9 March 2020) to the start of the second lockdown (6 November 2020) | 242 | BSM | |
| Number of days for the gradual decrease in contacts after the second wave lockdown | 8 | BSM | |
| Contact rate on 9 March 2020 | 10 | BSM | |
| Lowest contact rate achieved during the first wave lockdown (9 March–18 May 2020) | 3 | [42] | |
| Highest contact rate achieved after the first wave lockdown (9 March–18 May 2020) | 24 | BSM | |
| Lowest contact rate after the second wave lockdown started on 6 November 2020 | {3, 6, 10, 12} | BSM | |
| Exponential decreasing rate of the contact function | 1.3768 | [16] | |
| Exponential increasing rate of the contact function | 0.01 | BSM | |
| Sigmoid function rate of decay | 0.8 | BSM | |
| Sigmoid function rate of growth | 0.1 | BSM | |
| Probability of transmission per contact | 2.0011 × 10−8 | BSM | |
| Quarantined rate of exposed individuals | 1.887 × 10−7 | [17] | |
| Transition rate of individuals exposed to the infected class | 1/14 | [43] | |
| Rate at which the quarantined uninfected contacts were released into the wider community | 1/14 | [16] | |
| Probability of symptoms among infected individuals | 0.86834 | [16] | |
| Initial transition rate of symptomatic infected individuals to the quarantined infected class | 0.3266 | [16] | |
| The shortest period of diagnosis | 0.3654 | [16] | |
| Exponential decreasing rate of diagnose rate | 0.158 | BSM | |
| Transition rate of quarantined exposed individuals to the quarantined infected class | 0.1259 | [16] | |
| Recovery rate of symptomatic infected individuals | 0.33029 | [16] | |
| Recovery rate of asymptomatic infected individuals | 0.1 | BSM | |
| Recovery rate of hospitalized individuals | 0.0769 | BSM | |
| Disease induced death rate | 1.7826 × 10−7 | [16] | |
| Infected rate of asymptomatic/symptomatic | 0.05 | [17] | |
| Rate of home isolation for infected individuals | 0.2 | [17] | |
| Rate of home isolation for quarantined exposed individuals | 0.2 | [17] | |
| Recovery rate for isolated infected individuals | 0.13978 | [17] | |
| Hospitalization rate for isolated infected individuals | 0.2 | [17] |
Appendix B
References
- Zhu, N.; Zhang, D.; Wang, W.; Li, X.; Yang, B.; Song, J.; Zhao, X.; Huang, B.; Shi, W.; Lu, R.; et al. A Novel Coronavirus from Patients with Pneumonia in China, 2019. N. Engl. J. Med. 2020, 382, 727–733. [Google Scholar] [CrossRef] [PubMed]
- WHO. Coronavirus Disease (COVID-2019) Situation Reports. 2020. Available online: https://www.who.int/emergencies/diseases/novel-coronavirus-2019/situation-reports (accessed on 21 July 2021).
- WHO. Naming the Coronavirus Disease (COVID-19) and the Virus That Causes It. 2020. Available online: https://www.who.int/emergencies/diseases/novel-coronavirus-2019/technical-guidance/naming-the-coronavirus-disease-(covid-2019)-and-the-virus-that-causes-it (accessed on 21 July 2021).
- Guan, W.-J.; Ni, Z.-Y.; Hu, Y.; Liang, W.-H.; Ou, C.-Q.; He, J.-X.; Liu, L.; Shan, H.; Lei, C.-L.; Hui, D.S.; et al. Clinical Characteristics of Coronavirus Disease 2019 in China. N. Engl. J. Med. 2020, 382, 1708–1720. [Google Scholar] [CrossRef]
- Romagnani, P.; Gnone, G.; Guzzi, F.; Negrini, S.; Guastalla, A.; Annunziato, F.; Romagnani, S.; De Palma, R. The COVID-19 infection: Lessons from the Italian experience. J. Public Health Policy 2020, 41, 238–244. [Google Scholar] [CrossRef] [PubMed]
- Prime Minister Decree. Further Implementing Provisions of the Decree-Law 23 February 2020, No. 6, with Urgent Measures in Relation to Containment and Management of the Epidemiological Emergency from COVID-19, Applicable Throughout the Country. (20A01605) G.U. General Series, no. 64 [in Italian]. 11 March 2020. Available online: https://www.trovanorme.salute.gov.it/norme/dettaglioAtto?id=73643 (accessed on 21 July 2021).
- Italian Institute of Health (ISS). Epicentro. Web Infographic—COVID-19 Integrated Surveillance Data in Italy. 2021. Available online: https://www.epicentro.iss.it/en/coronavirus/sars-cov-2-dashboard (accessed on 21 July 2021).
- Kermack, W.O.; McKendrick, A.G. Contributions to the mathematical theory of epidemics—I. Bull. Math. Biol. 1991, 53, 33–55. [Google Scholar] [CrossRef] [PubMed]
- Boquet, G.; Stigler, B. A Discrete Study of the SIR Model. 2004. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.601.265&rep=rep1&type=pdf (accessed on 21 July 2021).
- Chen, T.-M.; Rui, J.; Wang, Q.-P.; Zhao, Z.-Y.; Cui, J.-A.; Yin, L. A mathematical model for simulating the phase-based transmissibility of a novel coronavirus. Infect. Dis. Poverty 2020, 9, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Integration of Ordinary Differential Equations. In Numerical Recipes: The Art of Scientific Computing; Cambridge University Press: Cambridge, UK, 2007; pp. 710–714.
- Prem, K.; Liu, Y.; Russell, T.W.; Kucharski, A.J.; Eggo, R.M.; Davies, N.; Jit, M.; Klepac, P.; Flasche, S.; Clifford, S.; et al. The effect of control strategies to reduce social mixing on outcomes of the COVID-19 epidemic in Wuhan, China: A modelling study. Lancet Public Health 2020, 5, e261–e270. [Google Scholar] [CrossRef] [Green Version]
- Kucharski, A.J.; Russell, T.W.; Diamond, C.; Liu, Y.; Edmunds, J.; Funk, S.; Eggo, R.M.; Sun, F.; Jit, M.; Munday, J.D.; et al. Early dynamics of transmission and control of COVID-19: A mathematical modelling study. Lancet Infect. Dis. 2020, 20, 553–558. [Google Scholar] [CrossRef] [Green Version]
- Yang, Z.; Zeng, Z.; Wang, K.; Wong, S.-S.; Liang, W.; Zanin, M.; Liu, P.; Cao, X.; Gao, Z.; Mai, Z.; et al. Modified SEIR and AI prediction of the epidemics trend of COVID-19 in China under public health interventions. J. Thorac. Dis. 2020, 12, 165–174. [Google Scholar] [CrossRef]
- Tang, B.; Wang, X.; Li, Q.; Bragazzi, N.L.; Tang, S.; Xiao, Y.; Wu, J. Estimation of the Transmission Risk of the 2019-nCoV and Its Implication for Public Health Interventions. J. Clin. Med. 2020, 9, 462. [Google Scholar] [CrossRef] [Green Version]
- Tang, B.; Bragazzi, N.; Li, Q.; Tang, S.; Xiao, Y.; Wu, J. An updated estimation of the risk of transmission of the novel coronavirus (2019-nCov). Infect. Dis. Model. 2020, 5, 248–255. [Google Scholar] [CrossRef]
- Reno, C.; Lenzi, J.; Navarra, A.; Barelli, E.; Gori, D.; Lanza, A.; Valentini, R.; Tang, B.; Fantini, M.P. Forecasting COVID-19-Associated Hospitalizations under Different Levels of Social Distancing in Lombardy and Emilia-Romagna, Northern Italy: Results from an Extended SEIR Compartmental Model. J. Clin. Med. 2020, 9, 1492. [Google Scholar] [CrossRef]
- Bollon, J.; Paganini, M.; Nava, C.R.; De Vita, N.; Vaschetto, R.; Ragazzoni, L.; Della Corte, F.; Barone-Adesi, F. Predicted Effects of Stopping COVID-19 Lockdown on Italian Hospital Demand. Disaster Med. Public Health Prep. 2020, 14, 638–642. [Google Scholar] [CrossRef] [PubMed]
- Rǎdulescu, A.; Williams, C.; Cavanagh, K. Management strategies in a SEIR-type model of COVID 19 community spread. Sci. Rep. 2020, 10, 1–16. [Google Scholar] [CrossRef]
- Giordano, G.; Blanchini, F.; Bruno, R.; Colaneri, P.; Di Filippo, A.; Di Matteo, A.; Colaneri, M. Modelling the COVID-19 epidemic and implementation of population-wide interventions in Italy. Nat. Med. 2020, 26, 855–860. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, Z.; Arif, M.; Ali, F.; Khan, I.; Nisar, K.S. A report on COVID-19 epidemic in Pakistan using SEIR fractional model. Sci. Rep. 2020, 10, 1–14. [Google Scholar] [CrossRef]
- Kuzdeuov, A.; Baimukashev, D.; Karabay, A.; Ibragimov, B.; Mirzakhmetov, A.; Nurpeiissov, M.; Lewis, M.; Varol, H.A. A Network-Based Stochastic Epidemic Simulator: Controlling COVID-19 With Region-Specific Policies. IEEE J. Biomed. Health Inform. 2020, 24, 2743–2754. [Google Scholar] [CrossRef]
- Gaglione, D.; Braca, P.; Millefiori, L.M.; Soldi, G.; Forti, N.; Marano, S.; Willett, P.K.; Pattipati, K.R. Adaptive Bayesian Learning and Forecasting of Epidemic Evolution—Data Analysis of the COVID-19 Outbreak. IEEE Access 2020, 8, 175244–175264. [Google Scholar] [CrossRef]
- Bherwani, H.; Gupta, A.; Anjum, S.; Anshul, A.; Kumar, R. Exploring dependence of COVID-19 on environmental factors and spread prediction in India. Npj Clim. Atmos. Sci. 2020, 3, 1–13. [Google Scholar] [CrossRef]
- Battineni, G.; Chintalapudi, N.; Amenta, F. SARS-CoV-2 epidemic calculation in Italy by SEIR compartmental models. Appl. Comput. Inform. 2020. [Google Scholar] [CrossRef]
- Chintalapudi, N.; Battineni, G.; Amenta, F. Second wave of COVID-19 in Italy: Preliminary estimation of reproduction number and cumulative case projections. Results Phys. 2021, 28, 104604. [Google Scholar] [CrossRef]
- Zisad, S.; Hossain, M.; Hossain, M.; Andersson, K. An Integrated Neural Network and SEIR Model to Predict COVID-19. Algorithms 2021, 14, 94. [Google Scholar] [CrossRef]
- Alanazi, S.A.; Kamruzzaman, M.M.; Alruwaili, M.; Alshammari, N.; Alqahtani, S.A.; Karime, A. Measuring and Preventing COVID-19 Using the SIR Model and Machine Learning in Smart Health Care. J. Healthc. Eng. 2020, 2020, 8857346. [Google Scholar] [CrossRef] [PubMed]
- Tovissodé, C.F.; Lokonon, B.E.; Kakaï, R.G. On the use of growth models to understand epidemic outbreaks with application to COVID-19 data. PLoS ONE 2020, 15, e0240578. [Google Scholar] [CrossRef]
- Wu, Y.; Zhang, L.; Cao, W.; Liu, X.; Feng, X. The Generalized-Growth Modeling of COVID-19. Front. Phys. 2021, 8. [Google Scholar] [CrossRef]
- Worldometers. Coronavirus Update (Live): 76,104,704 Cases and 1,683,354 Deaths from COVID-19 Virus Pandemic. 2020. Available online: https://www.worldometers.info/coronavirus/ (accessed on 21 July 2021).
- Regione Lombardia. Dashboard COVID-19. 2020. Available online: https://www.regione.lombardia.it/wps/portal/istituzionale/HP/servizi-e-informazioni/cittadini/salute-e-prevenzione/coronavirus/dashboard-covid19 (accessed on 21 July 2021).
- Italian Civil Protection Department (ICPD). GitHub Data Repository. 2020. Available online: https://github.com/pcm-dpc/COVID-19 (accessed on 21 July 2021).
- Gemmi, F.; Bachini, L.; Forni, S. I Ricoveri per Covid-19 in Toscana. Prime Analisi. ARS Agenzia Regionale di Sanità Toscana. 2020. Available online: https://www.ars.toscana.it/collana-documenti-ars/2-articoli/4355-ricoveri-covid-19-in-toscana-prime-analisi-ars-toscana.html (accessed on 21 July 2021).
- Apple Mobility. COVID-19—Mobility Trends Reports—Apple. 2020. Available online: https://covid19.apple.com/mobility (accessed on 21 July 2021).
- Gazzettaufficiale.it. Prime Minister Decree, October 13th. 2020. Available online: https://www.gazzettaufficiale.it/eli/id/2020/10/13/20A05563/sg (accessed on 21 July 2021).
- Gazzettaufficiale.it. Prime Minister Decree, November 3rd. 2020. Available online: https://www.gazzettaufficiale.it/eli/id/2020/11/04/20A06109/sg (accessed on 21 July 2021).
- GOV.UK. COVID-19 Guidance for TIER 1 areas in UK. 2020. Available online: https://www.gov.uk/guidance/tier-1-medium-alert (accessed on 21 July 2021).
- van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Gorkin, P. Numericon by Marianne Freiberger and Rachel Thomas. Math. Intell. 2015, 37, 96. [Google Scholar] [CrossRef]
- Dati.istat.it. Istat Statistics. 2020. Available online: http://dati.istat.it/?lang=en (accessed on 21 July 2021).
- CTS Report, Valutazione di Politiche di Riapertura Utilizzando Contatti Sociali e Rischio di Esposizione Professionale. April 2020. Available online: https://drive.google.com/file/d/1pe1gEp4-UAPxLW_vnqntAa4AT5D_nyR1/view (accessed on 21 July 2021).
- WHO. COVID-19 Virtual Press Conference Transcript. 7 September 2020. Available online: https://www.who.int/docs/default-source/coronaviruse/transcripts/covid-19-virtual-press-conference---7-september-corrects-name.pdf?sfvrsn=e00b8954_2#:~:text=The%2014%20days%20is%20based,the%20quarantine%20period%2014%20days (accessed on 21 July 2021).
- Treccani.it. Wuhan nell’Enciclopedia Treccani. 2020. Available online: https://www.treccani.it/enciclopedia/wuhan (accessed on 21 July 2021).
- Ministry of Health. Covid-19: Indicazioni per la Durata e il Termine Dell’isolamento e della Quarantena. Salute.gov.it. 2020. Available online: http://www.salute.gov.it/portale/nuovocoronavirus/dettaglioNotizieNuovoCoronavirus.jsp?lingua=italiano&id=5117 (accessed on 21 July 2021).
- Barratt, H.; Kirwan, M.; Shantikumar, S. Epidemic Theory (Effective & Basic Reproduction Numbers, Epidemic Thresholds) & Techniques for Analysis of Infectious Disease Data (Construction & Use of Epidemic Curves, Generation Numbers, Exceptional Reporting & Identification of Significant Clusters). Health Knowledge. 2020. Available online: https://www.healthknowledge.org.uk/public-health-textbook/research-methods/1a-epidemiology/epidemic-theory#:~:text=The%20effective%20reproductive%20number%20(R,the%20start%20of%20an%20epidemic (accessed on 21 July 2021).
- Morris, Q.A. Analysis of a Co-Epidemic Model. SIAM Undergrad. Res. Online 2011, 4, 121–133. [Google Scholar] [CrossRef]
| BSM RMSE | HSM RMSE | Improvement (%) | |
|---|---|---|---|
| 3 | 2834.34 | 151.63 | 94.65 |
| 6 | 2864.07 | 128.03 | 95.53 |
| 10 | 2905.20 | 103.96 | 96.42 |
| 12 | 2926.43 | 95.78 | 96.73 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gatto, A.; Accarino, G.; Aloisi, V.; Immorlano, F.; Donato, F.; Aloisio, G. Limits of Compartmental Models and New Opportunities for Machine Learning: A Case Study to Forecast the Second Wave of COVID-19 Hospitalizations in Lombardy, Italy. Informatics 2021, 8, 57. https://doi.org/10.3390/informatics8030057
Gatto A, Accarino G, Aloisi V, Immorlano F, Donato F, Aloisio G. Limits of Compartmental Models and New Opportunities for Machine Learning: A Case Study to Forecast the Second Wave of COVID-19 Hospitalizations in Lombardy, Italy. Informatics. 2021; 8(3):57. https://doi.org/10.3390/informatics8030057
Chicago/Turabian StyleGatto, Andrea, Gabriele Accarino, Valeria Aloisi, Francesco Immorlano, Francesco Donato, and Giovanni Aloisio. 2021. "Limits of Compartmental Models and New Opportunities for Machine Learning: A Case Study to Forecast the Second Wave of COVID-19 Hospitalizations in Lombardy, Italy" Informatics 8, no. 3: 57. https://doi.org/10.3390/informatics8030057
APA StyleGatto, A., Accarino, G., Aloisi, V., Immorlano, F., Donato, F., & Aloisio, G. (2021). Limits of Compartmental Models and New Opportunities for Machine Learning: A Case Study to Forecast the Second Wave of COVID-19 Hospitalizations in Lombardy, Italy. Informatics, 8(3), 57. https://doi.org/10.3390/informatics8030057






