Improving Smart Cities Safety Using Sound Events Detection Based on Deep Neural Network Algorithms
Abstract
1. Introduction
Related Work
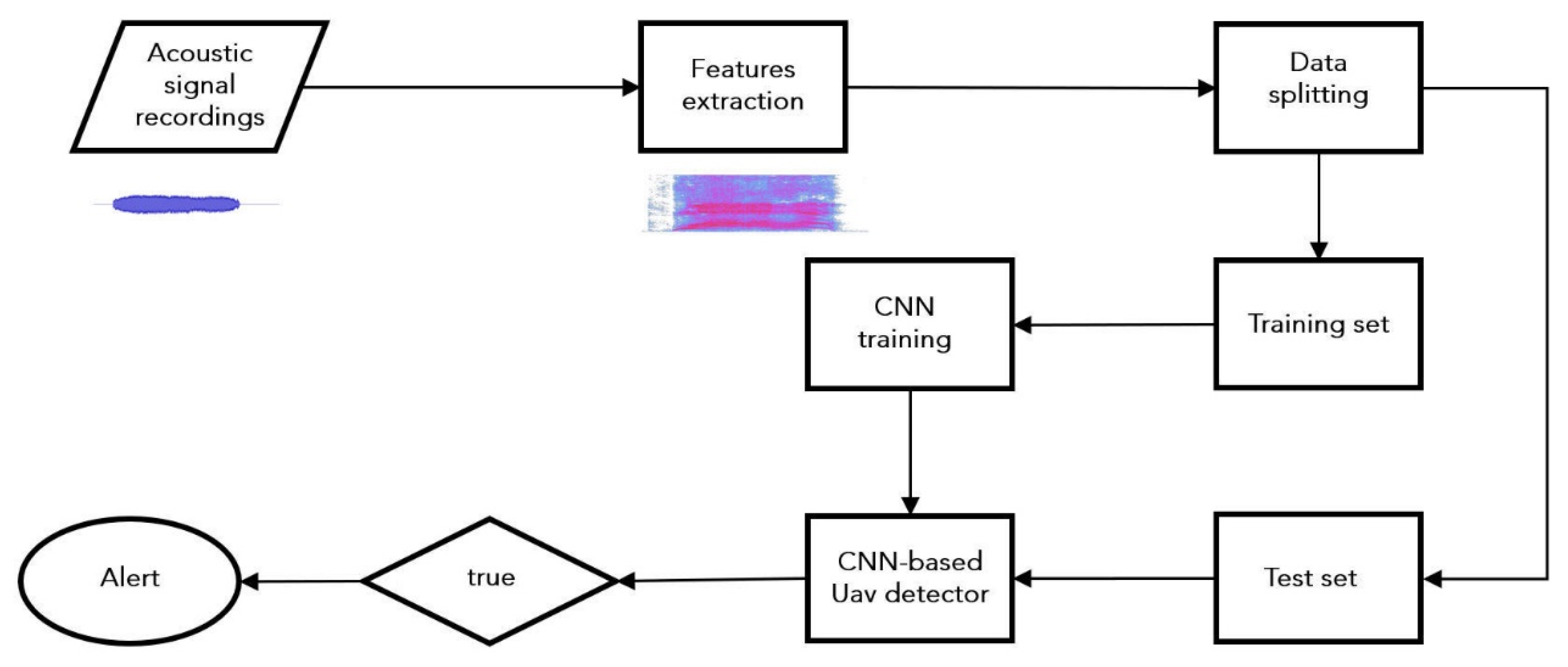
2. Materials and Methods
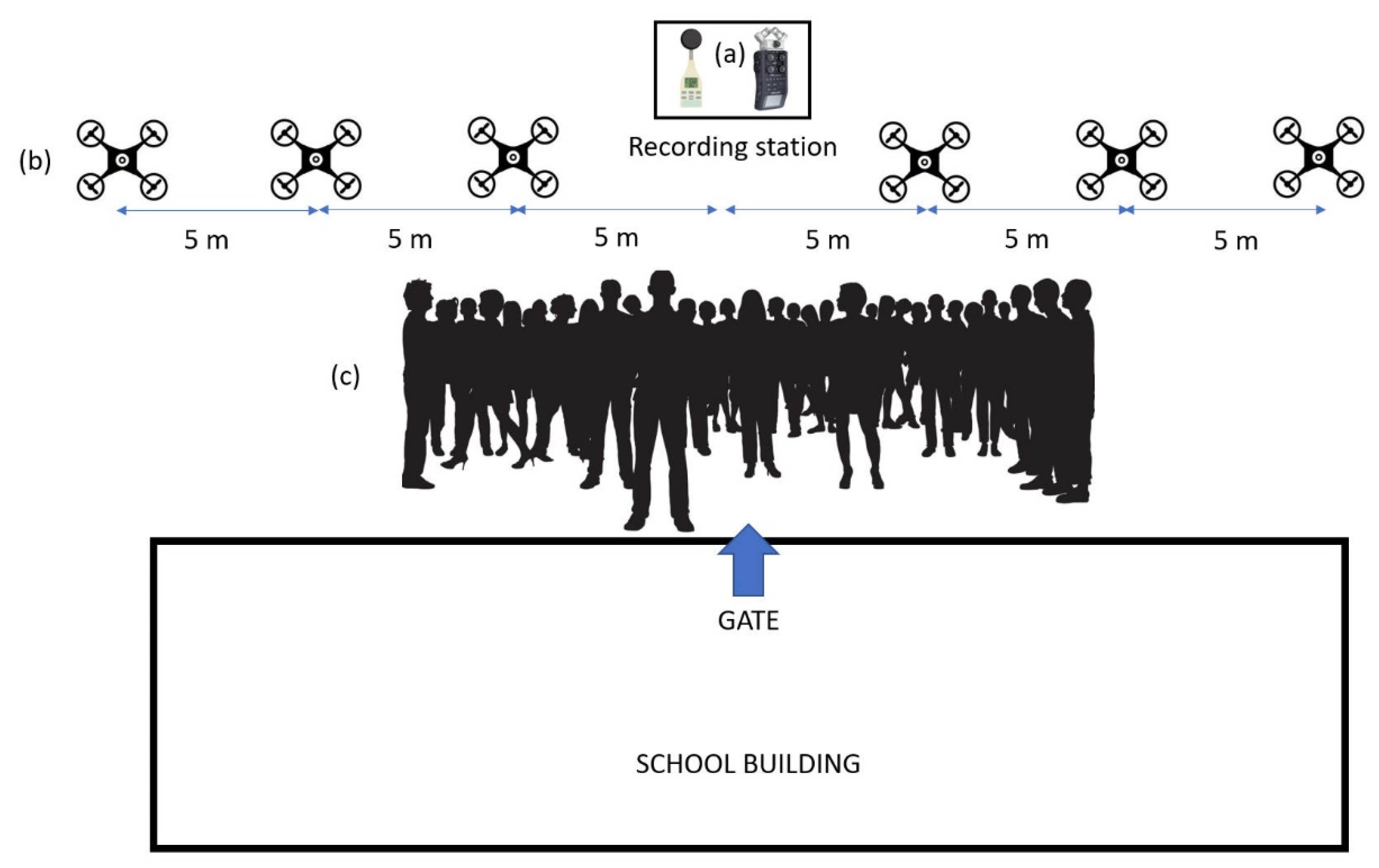
2.1. Audio Data Registrations
2.2. UAV Characterization
2.3. Features Extraction
2.4. Convolutional Neural Network-Based Model
- Convolutional layer;
- Activation layer;
- Pooling layer.
- is the kernel;
- is the input passed to the convolutional layer;
- is the bias.
- is the activation function.
2.4.1. Convolutional Layer
2.4.2. ReLU Activation Function
2.4.3. Pooling Layer
2.4.4. Fully Connected Layer
3. Results and Discussion
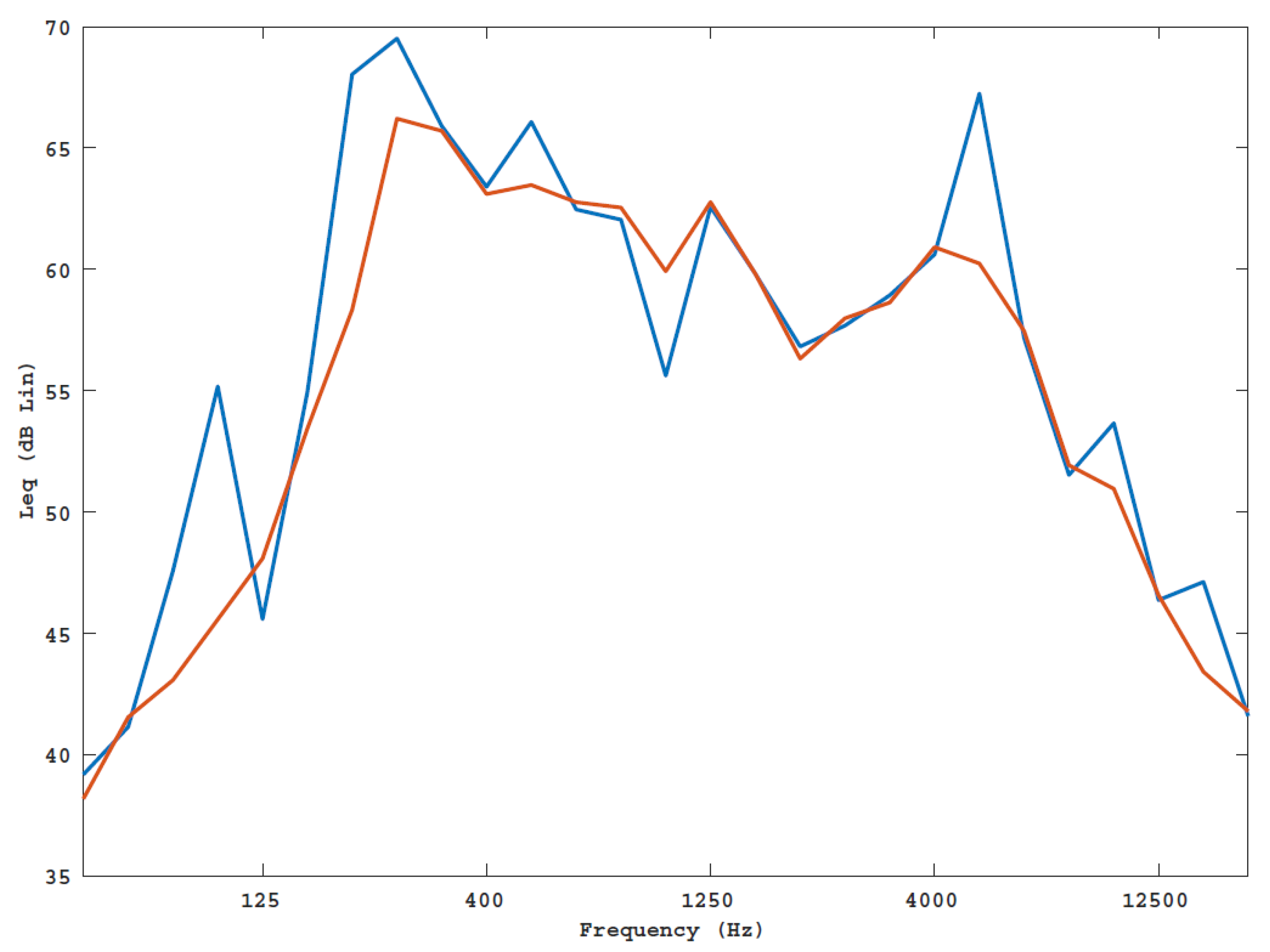
3.1. Characterization of the Acoustic Scenarios
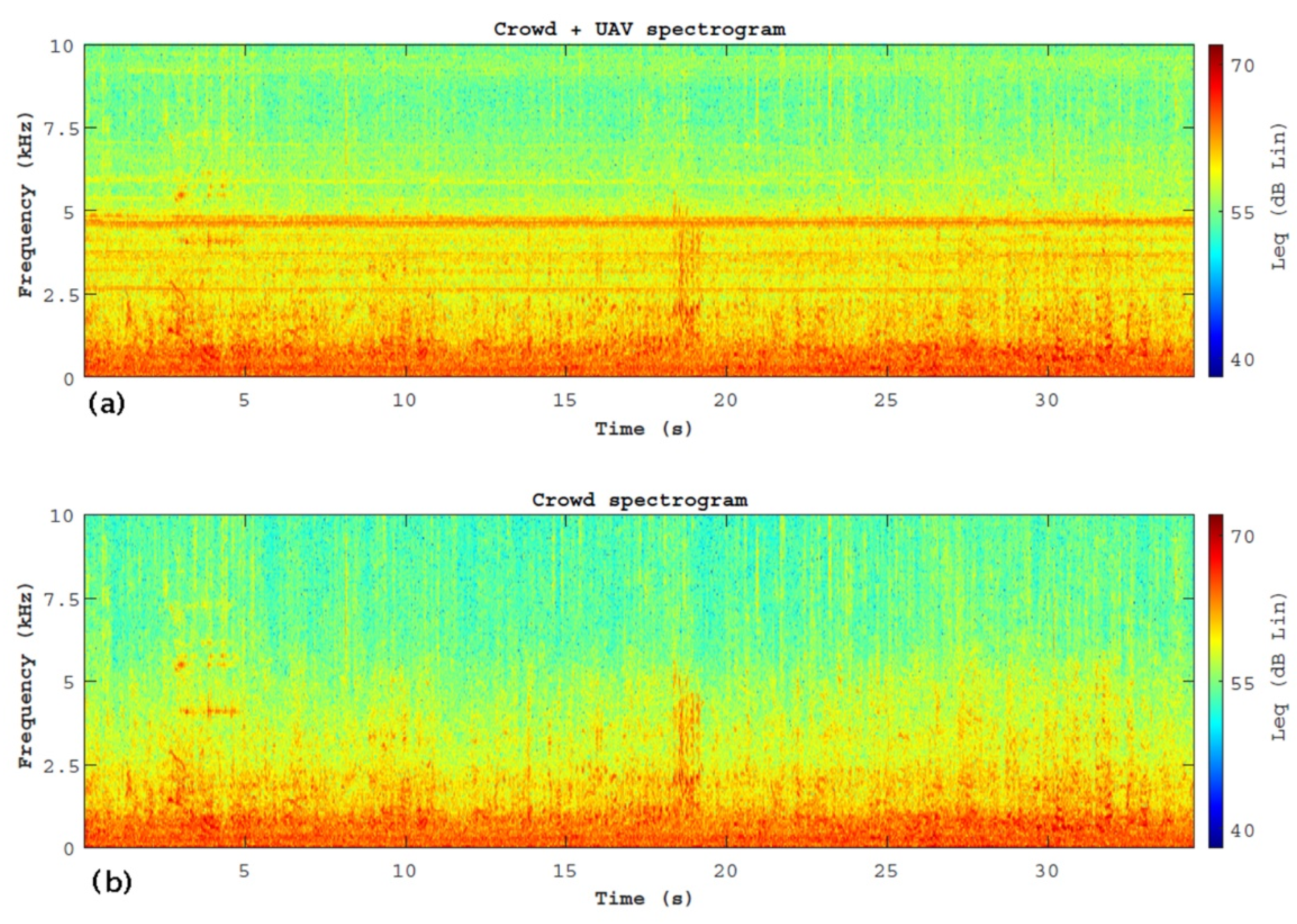
3.2. Features Extraction
3.3. UAV Detector Based on Convolutional Neural Network
4. Conclusions
- The characterization of the acoustic emission of the UAV highlighted three tonal components: two at low frequency and one at high frequency;
- From a comparison between the measures of the environmental noise emitted during the two scenarios (UAV, NoUAV) it is comparable. This confirms that the ambient noise in such scenarios is so complex that it is not possible to distinguish between the different acoustic sources, at least in the time domain;
- The comparison between the frequency spectra of the two scenarios has shown that the 5000 Hz tonal component is a descriptor capable of discriminating between the two scenarios. This result is evident in the spectrograms of the measures;
- A classification system based on CNN has proven capable of identifying the presence of UAVs with an accuracy of 0.91.
Author Contributions
Funding
Conflicts of Interest
References
- Gaur, A.; Scotney, B.; Parr, G.; McClean, S. Smart City Architecture and its Applications Based on IoT. Procedia Comput. Sci. 2015, 52, 1089–1094. [Google Scholar] [CrossRef]
- Wenge, R.; Zhang, X.; Dave, C.; Chao, L.; Hao, S. Smart city architecture: A technology guide for implementation and design challenges. China Commun. 2014, 11, 56–69. [Google Scholar] [CrossRef]
- Bianchini, D.; Ávila, I. Smart Cities and Their Smart Decisions: Ethical Considerations. IEEE Technol. Soc. Mag. 2014, 33, 34–40. [Google Scholar] [CrossRef]
- Balakrishna, C. Enabling technologies for smart city services and applications. In Proceedings of the Sixth International Conference on Next Generation Mobile Applications, Services and Technologies, Paris, France, 12–14 September 2012; Institute of Electrical and Electronics Engineers: Piscataway, NJ, USA, 2012; pp. 223–227. [Google Scholar]
- Elmaghraby, A.; Losavio, M.M. Cyber security challenges in Smart Cities: Safety, security and privacy. J. Adv. Res. 2014, 5, 491–497. [Google Scholar] [CrossRef] [PubMed]
- Jabbar, M.A.; Samreen, S.; Aluvalu, R.; Reddy, K.K. Cyber Physical Systems for Smart Cities Development. Int. J. Eng. Technol. 2018, 7, 36–38. [Google Scholar] [CrossRef]
- Hammoudeh, M.; Arioua, M. Sensors and Actuators in Smart Cities. J. Sens. Actuator Netw. 2018, 7, 8. [Google Scholar] [CrossRef]
- Batty, M. Artificial intelligence and smart cities. Environ. Plan. B Urban Anal. City Sci. 2018, 45, 3–6. [Google Scholar] [CrossRef]
- Ismagilova, E.; Hughes, D.L.; Dwivedi, Y.K.; Raman, K.R. Smart cities: Advances in research—An information systems perspective. Int. J. Inf. Manag. 2019, 47, 88–100. [Google Scholar] [CrossRef]
- Din, I.U.; Guizani, M.; Rodrigues, J.J.P.C.; Hassan, S.; Korotaev, V. Machine learning in the Internet of Things: Designed techniques for smart cities. Futur. Gener. Comput. Syst. 2019, 100, 826–843. [Google Scholar] [CrossRef]
- Gu, G.H.; Noh, J.; Kim, I.; Jung, Y. Machine learning for renewable energy materials. J. Mater. Chem. A 2019, 7, 17096–17117. [Google Scholar] [CrossRef]
- Nichols, J.A.; Chan, H.W.H.; Ab Baker, M. Machine learning: Applications of artificial intelligence to imaging and diagnosis. Biophys. Rev. 2018, 11, 111–118. [Google Scholar] [CrossRef] [PubMed]
- Iannace, G.; Ciaburro, G.; Trematerra, A. Heating, Ventilation, and Air Conditioning (HVAC) Noise Detection in Open-Plan Offices Using Recursive Partitioning. Buildings 2018, 8, 169. [Google Scholar] [CrossRef]
- McCoy, J.; Auret, L. Machine learning applications in minerals processing: A review. Miner. Eng. 2019, 132, 95–109. [Google Scholar] [CrossRef]
- Iannace, G.; Ciaburro, G.; Trematerra, A. Wind Turbine Noise Prediction Using Random Forest Regression. Machines 2019, 7, 69. [Google Scholar] [CrossRef]
- Sun, Y.; Peng, M.; Zhou, Y.; Huang, Y.; Mao, S. Application of Machine Learning in Wireless Networks: Key Techniques and Open Issues. IEEE Commun. Surv. Tutor. 2019, 21, 3072–3108. [Google Scholar] [CrossRef]
- Iannace, G.; Ciaburro, G.; Trematerra, A. Modelling sound absorption properties of broom fibers using artificial neural networks. Appl. Acoust. 2020, 163, 107239. [Google Scholar] [CrossRef]
- Rutledge, R.B.; Chekroud, A.M.; Huys, Q.J. Machine learning and big data in psychiatry: Toward clinical applications. Curr. Opin. Neurobiol. 2019, 55, 152–159. [Google Scholar] [CrossRef]
- Lostanlen, V.; Salamon, J.; Farnsworth, A.; Kelling, S.; Bello, J.P. Robust sound event detection in bioacoustic sensor networks. PLoS ONE 2019, 14, e0214168. [Google Scholar] [CrossRef]
- Lim, W.; Suh, S.; Jeong, Y. Weakly Labeled Semi Supervised Sound Event Detection Using CRNN with Inception Module. In Proceedings of the Workshop on Detection and Classification of Acoustic Scenes and Events, Surrey, UK, 19–20 November 2018; pp. 74–77. [Google Scholar]
- Kong, Q.; Xu, Y.; Sobieraj, I.; Wang, W.; Plumbley, M.D. Sound Event Detection and Time–Frequency Segmentation from Weakly Labelled Data. IEEE/ACM Trans. Audio Speech Lang. Process. 2019, 27, 777–787. [Google Scholar] [CrossRef]
- Oord, A.V.D.; Dieleman, S.; Zen, H.; Simonyan, K.; Vinyals, O.; Graves, A.; Kavukcuoglu, K. Wavenet: A generative model for raw audio. arXiv 2016, arXiv:1609.03499. [Google Scholar]
- Ozer, Z.; Findik, O.; Ozer, I. Noise robust sound event classification with convolutional neural network. Neurocomputing 2018, 272, 505–512. [Google Scholar] [CrossRef]
- Jung, M.; Chi, S. Human activity classification based on sound recognition and residual convolutional neural network. Autom. Constr. 2020, 114, 103177. [Google Scholar] [CrossRef]
- Cakır, E.; Virtanen, T. Convolutional recurrent neural networks for rare sound event detection. In Proceedings of the Workshop on Detection and Classification of Acoustic Scenes and Events, New York, NY, USA, 35–26 October 2019. [Google Scholar]
- Kille, T.; Bates, P.R.; Lee, S.Y. (Eds.) Unmanned Aerial Vehicles in Civilian Logistics and Supply Chain Management; IGI Global: Hersley, PA, USA, 2019. [Google Scholar]
- Yu, K. Research on the Improvement of Civil Unmanned Aerial Vehicles Flight Control System. In Advances in Intelligent Systems and Computing; Springer Science and Business Media LLC: Singapore, 2018; pp. 375–384. [Google Scholar]
- Oh, H. Countermeasure of Uumanned Aerial Vehicle (UAV) against terrorist’s attacks in South Korea for the public crowded places. J. Soc. Disaster Inf. 2019, 15, 49–66. [Google Scholar]
- Kartashov, V.M.; Oleynikov, V.N.; Sheyko, S.A.; Babkin, S.I.; Korytsev, I.V.; Zubkov, O.V. PECULIARITIES OF SMALL UNMANNED AERIAL VEHICLES DETECTION AND RECOGNITION. Telecommun. Radio Eng. 2019, 78. [Google Scholar] [CrossRef]
- Iannace, G.; Ciaburro, G.; Trematerra, A. Fault Diagnosis for UAV Blades Using Artificial Neural Network. Robotics 2019, 8, 59. [Google Scholar] [CrossRef]
- International Organization for Standardization (ISO) 3745: 2012. Acoustics.Determination of Sound Power Levels of Noise Sources Using Sound Pressure Precision Methods for Anechoic and Hemi-Anechoic Rooms. Available online: https://www.iso.org/standard/45362. html (accessed on 28 May 2020).
- Gröchenig, K. Foundations of Time-Frequency Analysis; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Veggeberg, K. Octave analysis explored: A tutorial. Eval. Eng. 2008, 47, 40–44. [Google Scholar]
- Fulop, S.A. Speech Spectrum Analysis; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Aghdam, H.H.; Heravi, E.J. Guide to Convolutional Neural Networks; Springer: Berlin/Heidelberg, Germany, 2017; Volume 10, p. 978. [Google Scholar]
- Aggarwal, C.C. Neural Networks and Deep Learning; Springer: Berlin/Heidelberg, Germany, 2018; Volume 10, p. 978. [Google Scholar]
- Kiranyaz, S.; Ince, T.; Abdeljaber, O.; Avci, O.; Gabbouj, M. 1-d Convolutional Neural Networks for Signal Processing Applications. In Proceedings of the International Conference on Acoustics, Speech and Signal Processing, Brighton, UK, 12–17 May 2019; Institute of Electrical and Electronics Engineers: Piscataway, NJ, USA, 2019; pp. 8360–8364. [Google Scholar]
- Tan, M.; Le, Q.V. Efficientnet: Rethinking model scaling for convolutional neural networks. arXiv 2019, arXiv:1905.11946. [Google Scholar]
- Nair, V.; Hinton, G.E. Rectified linear units improve restricted boltzmann machines. In Proceedings of the 27th International Conference on Machine Learning, Haifa, Israel, 21–24 June 2010; pp. 807–814. [Google Scholar]
- Scherer, D.; Müller, A.; Behnke, S. Evaluation of pooling operations in convolutional architectures for object recognition. In Proceedings of the International Conference on Artificial Neural Networks, Thessaloniki, Greece, 15–18 September 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 92–101. [Google Scholar]
- Kurtz, D.W.; Marte, J.E. A Review of Aerodynamic Noise from Propellers, Rotors, and Lift Fans; Jet Propulsion Laboratory, California Institute of Technology: Pasadena, CA, USA, 1970; pp. 32–1462.
- Zawodny, N.S.; Boyd, D.D. Investigation of Rotor–Airframe Interaction Noise Associated with Small-Scale Rotary-Wing Unmanned Aircraft Systems. J. Am. Helicopter Soc. 2020, 65, 1–17. [Google Scholar] [CrossRef]
- Regier, A.A.; Hubbard, H.H. Status of research on propeller noise and its reduction. J. Acoust. Soc. Am. 1953, 25, 395–404. [Google Scholar] [CrossRef]
- Hubbard, H.H. Aeroacoustics of Flight Vehicles: Theory and Practice. Volume 1: Noise Sources; No. NASA-L-16926-VOL-1; National Aeronautics and Space Admin Langley Research Center: Hampton, VA, USA, 1991.
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Hershey, S.; Chaudhuri, S.; Ellis, D.P.; Gemmeke, J.F.; Jansen, A.; Moore, R.C.; Plakal, M.; Platt, D.; Saurous, R.A.; Seybold, B.; et al. CNN architectures for large-scale audio classification. In Proceedings of the International Conference on Acoustics, Speech and Signal Processing, New Orleans, LA, USA, 5–9 March 2017; Institute of Electrical and Electronics Engineers: Piscataway, NJ, USA, 2017; pp. 131–135. [Google Scholar]
- Lee, J.; Kim, T.; Park, J.; Nam, J. Raw waveform-based audio classification using sample-level CNN architectures. arXiv 2017, arXiv:1712.00866. [Google Scholar]
- Lim, M.; Lee, D.; Park, H.; Kang, Y.; Oh, J.; Park, J.-S.; Jang, G.-J.; Kim, J.-H. Convolutional Neural Network based Audio Event Classification. KSII Trans. Internet Inf. Syst. 2018, 12. [Google Scholar] [CrossRef]

| Type | Specifications |
|---|---|
| Microphone | Sensitivity: −41 dB, 1 kHz at 1 Pa |
| Input gain: −∞ to 46.5 dB | |
| Maximum sound pressure input: 136 dB SPL | |
| Recording device | Sampling rate: 48 KHz |
| Bit depth: 24 bit |
| Layer Name | Layer Description | Output Shape |
|---|---|---|
| Input layer | Input | (64 × 64 × 3) |
| First hidden layer | 2D convolutional layer | (31 × 31 × 32) |
| Average pooling operation for spatial data | (15 × 15 × 32) | |
| Rectified linear unit activation | (15 × 15 × 32) | |
| Second hidden layer | 2D convolutional layer | (15 × 15 × 64) |
| Average pooling operation for spatial data | (7 × 7 × 64) | |
| Rectified linear unit activation | (7 × 7 × 64) | |
| Third hidden layer | 2D convolutional layer | (7 × 7 × 64) |
| Average pooling operation for spatial data | (3 × 3 × 64) | |
| Rectified linear unit activation | (3 × 3 × 64) | |
| Flatten layer | Flatten operation | (576) |
| dropout | (576) | |
| Fully connected layer | Densely connected NN layer | (64) |
| Rectified linear unit activation | (64) | |
| dropout | (64) | |
| Output layer | Densely connected NN layer | (2) |
| Softmax activation | (2) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ciaburro, G.; Iannace, G. Improving Smart Cities Safety Using Sound Events Detection Based on Deep Neural Network Algorithms. Informatics 2020, 7, 23. https://doi.org/10.3390/informatics7030023
Ciaburro G, Iannace G. Improving Smart Cities Safety Using Sound Events Detection Based on Deep Neural Network Algorithms. Informatics. 2020; 7(3):23. https://doi.org/10.3390/informatics7030023
Chicago/Turabian StyleCiaburro, Giuseppe, and Gino Iannace. 2020. "Improving Smart Cities Safety Using Sound Events Detection Based on Deep Neural Network Algorithms" Informatics 7, no. 3: 23. https://doi.org/10.3390/informatics7030023
APA StyleCiaburro, G., & Iannace, G. (2020). Improving Smart Cities Safety Using Sound Events Detection Based on Deep Neural Network Algorithms. Informatics, 7(3), 23. https://doi.org/10.3390/informatics7030023






