A New Co-Evolution Binary Particle Swarm Optimization with Multiple Inertia Weight Strategy for Feature Selection
Abstract
:1. Introduction
2. Binary Particle Swarm Optimization
3. Co-evolution Binary Particle Swarm Optimization with Multiple Inertia Weight Strategy
3.1. Multiple Inertia Weight Strategy
| Algorithm 1. Pseudocode of CBPSO-MIWS |
| Input:N, Tmax, vmax, vmin, ns, c1 and c2 |
| 1) Initialize a population of particles, Xi (i = 1, 2 …, N) |
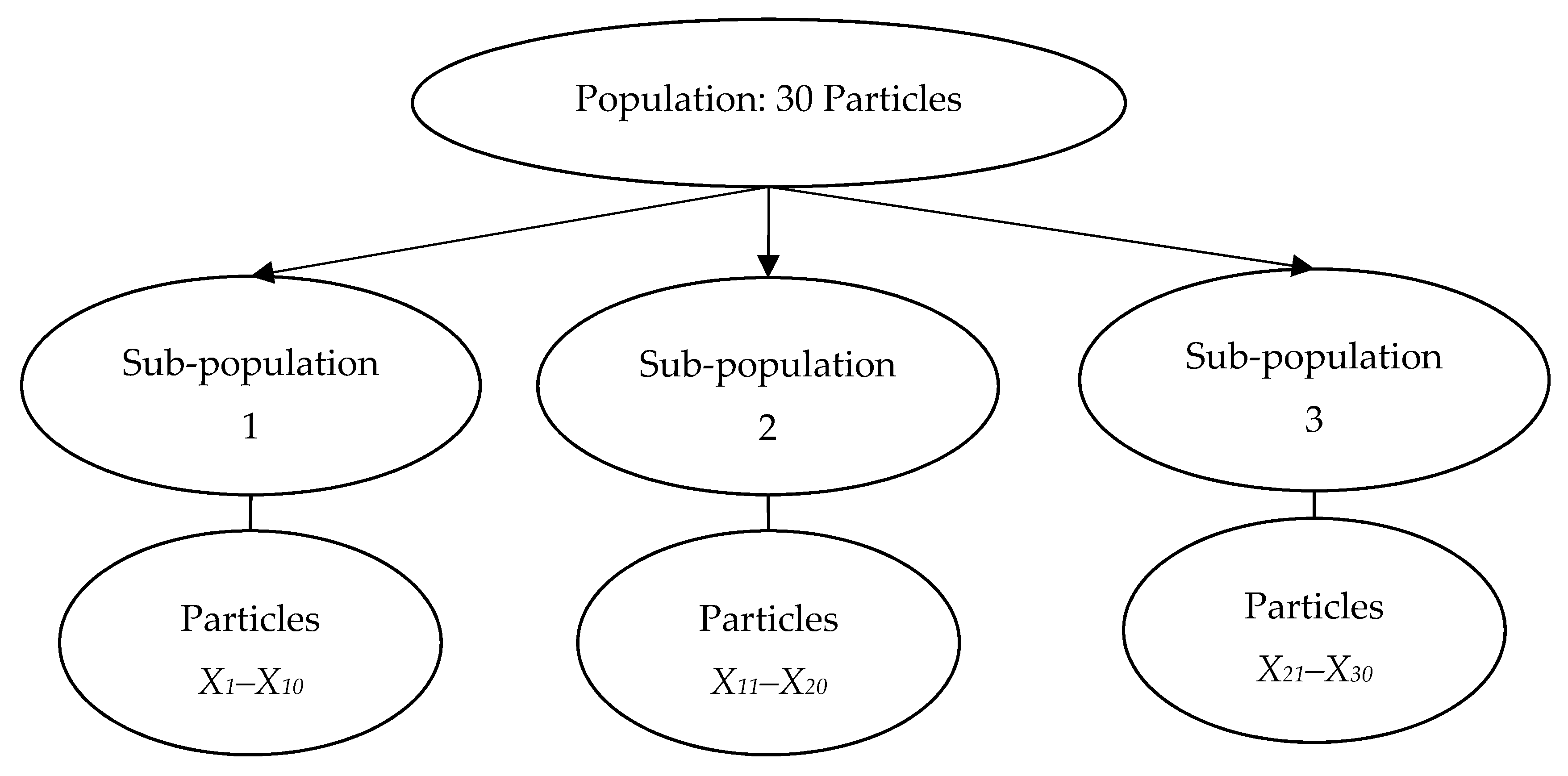
| 2) Divide the population into ns sub-populations/species, Sn (n = 1, 2 …, ns) |
| 3) Evaluate the fitness of particles for each species, F(Sn) using fitness function |
| 4) Define the global best particle of each species as gbestn (n = 1, 2 …, ns), and select the overall global best particle from gbestn and set it as Gbest |
| 5) Set the personal best particles for each species aspbestn (n = 1, 2 …, ns) |
| 6) for t = 1 to the maximum number of iteration, Tmax |
| 7) for n = 1 to the number of sub-population/species, ns |
| // Multiple Inertia Weight Strategy // |
| 8) Randomly select one IWS using Equation (10) |
| 9) Compute the inertia weight based on the selected IWS |
| 10) for i = 1 to the number of particles in each species |
| 11) for d = 1 to the number of dimension, D |
| // Velocity and Position Update // #Note that pbesti is selected from pbestn |
| 12) Update the velocity of particle as shown in Equation (1) |
| 13) Convert the velocity into probability value using Equation (2) |
| 14) Update the position of particle as shown in Equation (3) |
| 15) next d |
| 16) Evaluate the fitness of particle by applying the fitness function |
| 17) Update pbestn,i and gbestn |
| 18) next i |
| 19) next n |
| 20) Update Gbest |
| 21) next t |
| Output: Overall global best particle |
3.2. Proposed CBPSO-MIWS for Feature Selection
4. Results
4.1. Dataset and Parameter Setting
4.2. Evaluation Metrics
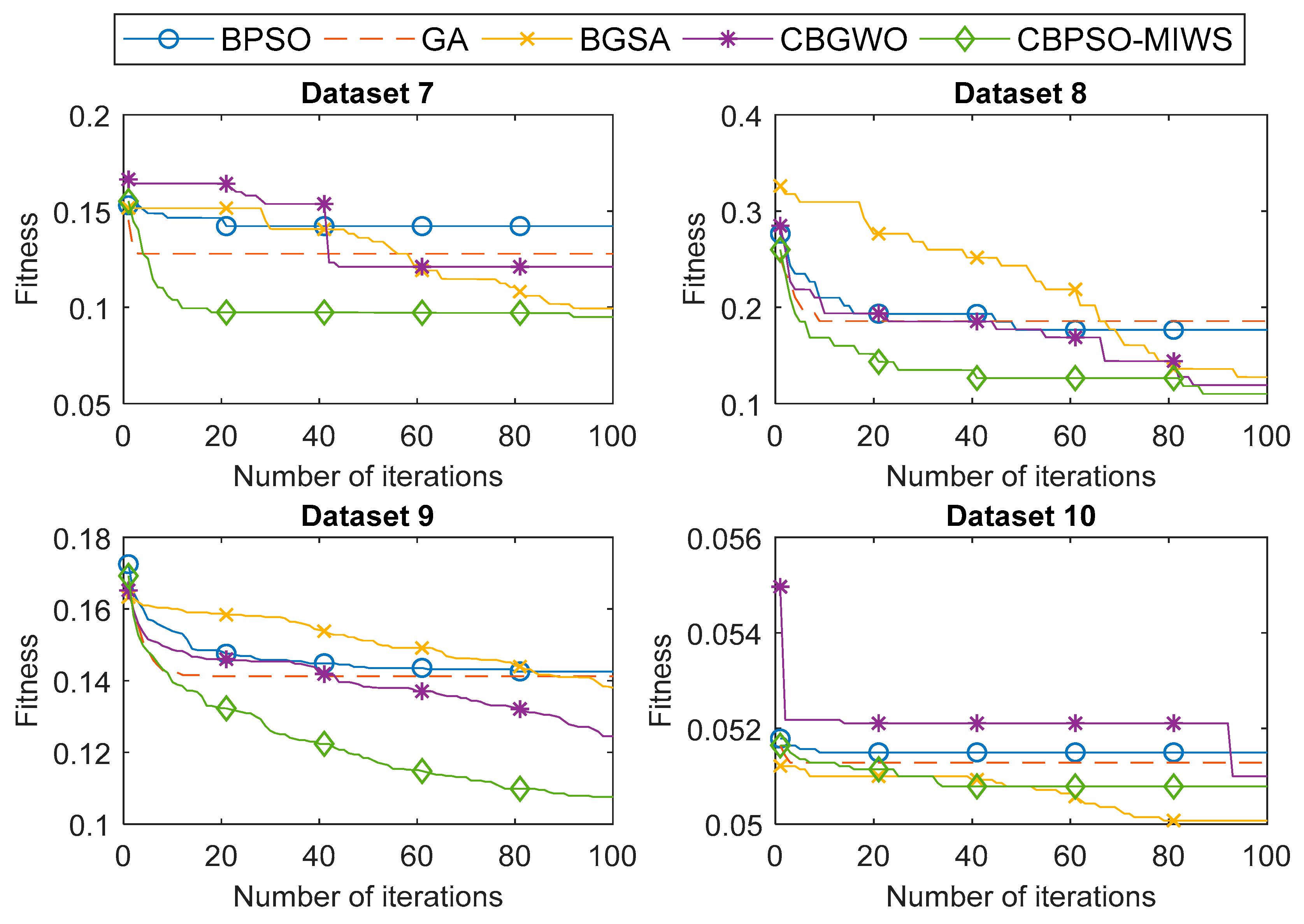
4.3. Experimental Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Xue, B.; Zhang, M.; Browne, W.N. Particle swarm optimisation for feature selection in classification: Novel initialisation and updating mechanisms. Appl. Soft Comput. 2014, 18, 261–276. [Google Scholar] [CrossRef]
- Al-Madi, N.; Faris, H.; Mirjalili, S. Binary multi-verse optimization algorithm for global optimization and discrete problems. Int. J. Mach. Learn. Cybern. 2019, 1–21. [Google Scholar] [CrossRef]
- Emary, E.; Zawbaa, H.M.; Hassanien, A.E. Binary ant lion approaches for feature selection. Neurocomputing 2016, 213, 54–65. [Google Scholar] [CrossRef]
- Faris, H.; Mafarja, M.M.; Heidari, A.A.; Aljarah, I.; Al-Zoubi, A.M.; Mirjalili, S.; Fujita, H. An efficient binary Salp Swarm Algorithm with crossover scheme for feature selection problems. Knowl-Based Syst. 2018, 154, 43–67. [Google Scholar] [CrossRef]
- Hafiz, F.; Swain, A.; Patel, N.; Naik, C. A two-dimensional (2-D) learning framework for Particle Swarm based feature selection. Pattern Recognit. 2018, 76, 416–433. [Google Scholar] [CrossRef]
- Tran, B.; Xue, B.; Zhang, M. Variable-Length Particle Swarm Optimisation for Feature Selection on High-Dimensional Classification. IEEE Trans. Evol. Comput. 2018, 1. [Google Scholar] [CrossRef]
- Huang, H.; Xie, H.B.; Guo, J.Y.; Chen, H.J. Ant colony optimization-based feature selection method for surface electromyography signals classification. Comput. Biol. Med. 2012, 42, 30–38. [Google Scholar] [CrossRef] [PubMed]
- Mesa, I.; Rubio, A.; Tubia, I.; De No, J.; Diaz, J. Channel and feature selection for a surface electromyographic pattern recognition task. Expert Syst. Appl. 2014, 41, 5190–5200. [Google Scholar] [CrossRef]
- Venugopal, G.; Navaneethakrishna, M.; Ramakrishnan, S. Extraction and analysis of multiple time window features associated with muscle fatigue conditions using sEMG signals. Expert Syst. Appl. 2014, 41, 2652–2659. [Google Scholar] [CrossRef]
- Phinyomark, A.; N Khushaba, R.; Scheme, E. Feature Extraction and Selection for Myoelectric Control Based on Wearable EMG Sensors. Sensors 2018, 18, 1615. [Google Scholar] [CrossRef]
- Purushothaman, G.; Vikas, R. Identification of a feature selection based pattern recognition scheme for finger movement recognition from multichannel EMG signals. Australas Phys. Eng. Sci. Med. 2018, 41, 549–559. [Google Scholar] [CrossRef]
- Too, J.; Abdullah, A.; Mohd Saad, N.; Mohd Ali, N.; Tee, W. A New Competitive Binary Grey Wolf Optimizer to Solve the Feature Selection Problem in EMG Signals Classification. Computers 2018, 7, 58. [Google Scholar] [CrossRef]
- Chuang, L.Y.; Chang, H.W.; Tu, C.J.; Yang, C.H. Improved binary PSO for feature selection using gene expression data. Comput. Biol. Chem. 2008, 32, 29–38. [Google Scholar] [CrossRef] [PubMed]
- Xue, B.; Zhang, M.; Browne, W.N. Particle Swarm Optimization for Feature Selection in Classification: A Multi-Objective Approach. IEEE Trans. Cybern. 2013, 43, 1656–1671. [Google Scholar] [CrossRef]
- Gou, J.; Lei, Y.X.; Guo, W.P.; Wang, C.; Cai, Y.Q.; Luo, W. A novel improved particle swarm optimization algorithm based on individual difference evolution. Appl. Soft. Comput. 2017, 57, 468–481. [Google Scholar] [CrossRef]
- Dong, W.; Zhou, M. A Supervised Learning and Control Method to Improve Particle Swarm Optimization Algorithms. IEEE Trans. Syst. Man. Cybern. Syst. 2017, 47, 1135–1148. [Google Scholar] [CrossRef]
- Jensi, R.; Jiji, G.W. An enhanced particle swarm optimization with levy flight for global optimization. Appl. Soft Comput. 2016, 43, 248–261. [Google Scholar] [CrossRef]
- Adeli, A.; Broumandnia, A. Image steganalysis using improved particle swarm optimization based feature selection. Appl. Intell. 2018, 48, 1609–1622. [Google Scholar] [CrossRef]
- Banka, H.; Dara, S. A Hamming distance based binary particle swarm optimization (HDBPSO) algorithm for high dimensional feature selection, classification and validation. Pattern Recognit. Lett. 2015, 52, 94–100. [Google Scholar] [CrossRef]
- Bharti, K.K.; Singh, P.K. Opposition chaotic fitness mutation based adaptive inertia weight BPSO for feature selection in text clustering. Appl. Soft Comput. 2016, 43, 20–34. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R.C. A discrete binary version of the particle swarm algorithm. In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics, Orlando, FL, USA, 12–15 October 1997. [Google Scholar] [CrossRef]
- Too, J.; Abdullah, A.R.; Mohd Saad, N.; Tee, W. EMG Feature Selection and Classification Using a Pbest-Guide Binary Particle Swarm Optimization. Computation 2019, 7, 12. [Google Scholar] [CrossRef]
- Unler, A.; Murat, A. A discrete particle swarm optimization method for feature selection in binary classification problems. Eur. J. Oper. Res. 2010, 206, 528–539. [Google Scholar] [CrossRef]
- Taherkhani, M.; Safabakhsh, R. A novel stability-based adaptive inertia weight for particle swarm optimization. Appl. Soft Comput. 2016, 38, 281–295. [Google Scholar] [CrossRef]
- Chatterjee, A.; Siarry, P. Nonlinear inertia weight variation for dynamic adaptation in particle swarm optimization. Comput. Oper. Res. 2006, 33, 859–871. [Google Scholar] [CrossRef]
- Shi, Y.; Eberhart, R. A modified particle swarm optimizer. In Proceedings of the IEEE International Conference on Evolutionary Computation, Anchorage, AK, USA, 4–9 May 1998. [Google Scholar] [CrossRef]
- Emary, E.; Zawbaa, H.M.; Hassanien, A.E. Binary grey wolf optimization approaches for feature selection. Neurocomputing 2016, 172, 371–381. [Google Scholar] [CrossRef]
- Huang, C.L.; Wang, C.J. A GA-based feature selection and parameters optimization for support vector machines. Expert Syst. Appl. 2006, 31, 231–240. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. BGSA: Binary gravitational search algorithm. Nat. Comput. 2010, 9, 727–745. [Google Scholar] [CrossRef]
- Zawbaa, H.M.; Emary, E.; Grosan, C. Feature Selection via Chaotic Antlion Optimization. PLoS ONE 2016, 11, e0150652. [Google Scholar] [CrossRef]
- Sayed, G.I.; Hassanien, A.E. Moth-flame swarm optimization with neutrosophic sets for automatic mitosis detection in breast cancer histology images. Appl. Intell. 2017, 47, 397–408. [Google Scholar] [CrossRef]




| No | UCI Dataset | Number of Instances | Number of Features | Number of Classes |
|---|---|---|---|---|
| 1 | Breast Cancer Wisconsin | 699 | 9 | 2 |
| 2 | Diabetic Retinopathy | 1151 | 19 | 2 |
| 3 | Glass Identification | 214 | 10 | 6 |
| 4 | Ionosphere | 351 | 34 | 2 |
| 5 | Libras Movement | 360 | 90 | 15 |
| 6 | Musk 1 | 476 | 167 | 2 |
| 7 | Breast Cancer Coimbra | 116 | 9 | 2 |
| 8 | Lung Cancer | 32 | 56 | 3 |
| 9 | Parkinson’s Disease | 756 | 754 | 2 |
| 10 | Seeds | 210 | 7 | 3 |
| Parameters | Values | ||||
|---|---|---|---|---|---|
| Proposed Method (CBPSO-MIWS) | Binary Particle Swarm Optimization (BPSO) | Genetic Algorithm (GA) | Binary Gravitational Search Algorithm (BGSA) | Competitive Binary Grey Wolf Optimizer (CBGWO) | |
| Population size, N | 10 | 10 | 10 | 10 | 10 |
| Maximum number of iterations, Tmax | 100 | 100 | 100 | 100 | 100 |
| Number of runs | 20 | 20 | 20 | 20 | 20 |
| Number of species, ns | 3 | - | - | - | - |
| wmax | 0.9 | - | - | - | - |
| wmin | 0.4 | - | - | - | - |
| w0 | 0.9 | - | - | - | - |
| c1 | 2 | 2 | - | - | - |
| c2 | 2 | 2 | - | - | - |
| vmax | 6 | 6 | - | 6 | - |
| vmin | −6 | −6 | - | - | - |
| p | 1.2 | - | - | - | - |
| CR | - | - | 0.8 | - | - |
| MR | - | - | 0.01 | - | - |
| w | - | 0.9–0.4 | - | - | - |
| G0 | - | - | - | 100 | - |
| Dataset | Feature Selection Method | Best Fitness | Worst Fitness | Mean Fitness | STD | Accuracy (%) | Feature Size |
|---|---|---|---|---|---|---|---|
| 1 | BPSO | 0.0155 | 0.0233 | 0.0156 | 0.0009 | 98.96 | 4.70 |
| GA | 0.0150 | 0.0181 | 0.0151 | 0.0004 | 99.00 | 4.60 | |
| BGSA | 0.0117 | 0.0179 | 0.0143 | 0.0026 | 99.29 | 4.15 | |
| CBGWO | 0.0161 | 0.0187 | 0.0165 | 0.0006 | 98.96 | 5.25 | |
| Proposed | 0.0131 | 0.0202 | 0.0133 | 0.0009 | 99.14 | 4.15 | |
| 2 | BPSO | 0.2973 | 0.3102 | 0.2984 | 0.0025 | 70.41 | 8.40 |
| GA | 0.2925 | 0.3056 | 0.2928 | 0.0016 | 70.89 | 8.30 | |
| BGSA | 0.2749 | 0.3062 | 0.2934 | 0.0108 | 72.70 | 8.70 | |
| CBGWO | 0.2703 | 0.3178 | 0.2876 | 0.0193 | 73.11 | 7.80 | |
| Proposed | 0.2721 | 0.3095 | 0.2740 | 0.0063 | 72.89 | 7.00 | |
| 3 | BPSO | 0.0572 | 0.0720 | 0.0576 | 0.0024 | 94.65 | 4.20 |
| GA | 0.0371 | 0.0595 | 0.0375 | 0.0027 | 96.63 | 3.75 | |
| BGSA | 0.0271 | 0.0515 | 0.0412 | 0.0083 | 97.56 | 2.90 | |
| CBGWO | 0.0458 | 0.0570 | 0.0513 | 0.0021 | 95.70 | 3.25 | |
| Proposed | 0.0189 | 0.0662 | 0.0250 | 0.0129 | 98.37 | 2.75 | |
| 4 | BPSO | 0.1229 | 0.1432 | 0.1239 | 0.0035 | 88.00 | 14.10 |
| GA | 0.1172 | 0.1402 | 0.1180 | 0.0037 | 88.57 | 13.65 | |
| BGSA | 0.1020 | 0.1374 | 0.1225 | 0.0117 | 90.07 | 12.55 | |
| CBGWO | 0.0873 | 0.1441 | 0.0978 | 0.0145 | 91.50 | 10.80 | |
| Proposed | 0.0892 | 0.1381 | 0.0951 | 0.0103 | 91.36 | 12.35 | |
| 5 | BPSO | 0.2084 | 0.2730 | 0.2147 | 0.0124 | 79.44 | 44.50 |
| GA | 0.2349 | 0.2660 | 0.2357 | 0.0042 | 76.74 | 41.65 | |
| BGSA | 0.2123 | 0.2661 | 0.2386 | 0.0150 | 79.03 | 42.30 | |
| CBGWO | 0.2008 | 0.2592 | 0.2191 | 0.0162 | 80.21 | 43.90 | |
| Proposed | 0.1825 | 0.2729 | 0.1958 | 0.0170 | 82.01 | 39.95 | |
| 6 | BPSO | 0.0849 | 0.1222 | 0.0907 | 0.0092 | 91.89 | 77.05 |
| GA | 0.0939 | 0.1133 | 0.0946 | 0.0032 | 91.00 | 80.15 | |
| BGSA | 0.0809 | 0.1170 | 0.1006 | 0.0116 | 92.32 | 80.10 | |
| CBGWO | 0.0606 | 0.1107 | 0.0753 | 0.0109 | 94.32 | 71.70 | |
| Proposed | 0.0736 | 0.1207 | 0.0782 | 0.0099 | 93.05 | 80.30 | |
| 7 | BPSO | 0.1422 | 0.1531 | 0.1434 | 0.0031 | 86.09 | 4.05 |
| GA | 0.1278 | 0.1454 | 0.1280 | 0.0018 | 87.61 | 4.65 | |
| BGSA | 0.0995 | 0.1517 | 0.1296 | 0.0227 | 90.43 | 4.30 | |
| CBGWO | 0.1211 | 0.1665 | 0.1371 | 0.0203 | 88.26 | 4.40 | |
| Proposed | 0.0950 | 0.1552 | 0.1000 | 0.0118 | 90.87 | 4.15 | |
| 8 | BPSO | 0.1768 | 0.2766 | 0.1894 | 0.0262 | 82.50 | 20.10 |
| GA | 0.1857 | 0.2519 | 0.1879 | 0.0113 | 81.67 | 23.60 | |
| BGSA | 0.1276 | 0.3261 | 0.2233 | 0.0789 | 87.50 | 21.70 | |
| CBGWO | 0.1193 | 0.2849 | 0.1693 | 0.0452 | 88.33 | 21.35 | |
| Proposed | 0.1102 | 0.2600 | 0.1359 | 0.0355 | 89.17 | 16.45 | |
| 9 | BPSO | 0.1425 | 0.1725 | 0.1460 | 0.0060 | 86.09 | 366.40 |
| GA | 0.1413 | 0.1659 | 0.1421 | 0.0038 | 86.23 | 368.10 | |
| BGSA | 0.1380 | 0.1633 | 0.1512 | 0.0079 | 86.56 | 371.65 | |
| CBGWO | 0.1245 | 0.1652 | 0.1394 | 0.0092 | 87.88 | 338.75 | |
| Proposed | 0.1075 | 0.1692 | 0.1217 | 0.0138 | 89.60 | 347.10 | |
| 10 | BPSO | 0.0515 | 0.0518 | 0.0515 | 0.0001 | 95.24 | 3.05 |
| GA | 0.0513 | 0.0516 | 0.0513 | 0.0000 | 95.24 | 2.90 | |
| BGSA | 0.0501 | 0.0512 | 0.0506 | 0.0005 | 95.24 | 2.05 | |
| CBGWO | 0.0510 | 0.0550 | 0.0521 | 0.0006 | 95.24 | 2.70 | |
| Proposed | 0.0508 | 0.0516 | 0.0509 | 0.0003 | 95.24 | 2.55 |
| Dataset | p-Value | |||
|---|---|---|---|---|
| BPSO | GA | BGSA | CBGWO | |
| 1 | 0.36414 | 0.22519 | 0.03557 ** | 0.20295 |
| 2 | 0.00061 * | 6.00 × 10−5 * | 0.54053 | 0.53562 |
| 3 | 0.00162 * | 0.02147 * | 0.28239 | 0.00183 * |
| 4 | 1.00 × 10−5 * | 0.00000 * | 0.00271 * | 0.72344 |
| 5 | 0.00016 * | 0.00000 * | 0.00000 * | 0.00176 * |
| 6 | 0.00548 * | 1.00 × 10−5 * | 0.02268 * | 0.00281 ** |
| 7 | 0.00012 * | 0.00000 * | 0.38880 | 3.00 × 10−5 * |
| 8 | 0.00197 * | 0.00963 * | 0.50274 | 0.74359 |
| 9 | 0.00000 * | 0.00000 * | 0.00000 * | 1.00 × 10−5 * |
| 10 | 1.00000 | 1.00000 | 1.00000 | 1.00000 |
| Dataset | Average Computational Time (s) | ||||
|---|---|---|---|---|---|
| BPSO | GA | BGSA | CBGWO | CBPSO-MIWS | |
| 1 | 5.603 | 8.952 | 5.613 | 4.524 | 6.861 |
| 2 | 15.321 | 24.499 | 14.646 | 12.388 | 17.731 |
| 3 | 1.687 | 2.380 | 1.693 | 1.331 | 2.091 |
| 4 | 2.465 | 3.804 | 2.435 | 1.951 | 3.208 |
| 5 | 2.884 | 4.182 | 3.082 | 2.213 | 3.663 |
| 6 | 4.043 | 6.008 | 4.390 | 3.036 | 4.931 |
| 7 | 1.233 | 1.858 | 1.629 | 1.010 | 1.496 |
| 8 | 1.177 | 1.654 | 1.439 | 0.916 | 1.492 |
| 9 | 13.496 | 19.645 | 13.851 | 9.849 | 16.273 |
| 10 | 1.528 | 2.476 | 1.611 | 1.211 | 2.057 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Too, J.; Abdullah, A.R.; Mohd Saad, N. A New Co-Evolution Binary Particle Swarm Optimization with Multiple Inertia Weight Strategy for Feature Selection. Informatics 2019, 6, 21. https://doi.org/10.3390/informatics6020021
Too J, Abdullah AR, Mohd Saad N. A New Co-Evolution Binary Particle Swarm Optimization with Multiple Inertia Weight Strategy for Feature Selection. Informatics. 2019; 6(2):21. https://doi.org/10.3390/informatics6020021
Chicago/Turabian StyleToo, Jingwei, Abdul Rahim Abdullah, and Norhashimah Mohd Saad. 2019. "A New Co-Evolution Binary Particle Swarm Optimization with Multiple Inertia Weight Strategy for Feature Selection" Informatics 6, no. 2: 21. https://doi.org/10.3390/informatics6020021
APA StyleToo, J., Abdullah, A. R., & Mohd Saad, N. (2019). A New Co-Evolution Binary Particle Swarm Optimization with Multiple Inertia Weight Strategy for Feature Selection. Informatics, 6(2), 21. https://doi.org/10.3390/informatics6020021





