Constructing Interactive Visual Classification, Clustering and Dimension Reduction Models for n-D Data
Abstract
:1. Introduction
2. Methods: Linear Dependencies for Classification with Visual Interactive Means
2.1. Base GLC-L Algorithm
- Step 1: Normalize C = (c1, c2, …, cn+1) by creating as set of normalized parameters K = (k1, k2, …, kn+1): ki = ci/cmax. The resulting normalized equation yn = k1x1 + k2x2 + … + knxn + kn+1 with normalized rule: if yn < T/cmax then x belongs to class 1, else x belongs to class 2, where yn is a normalized value, yn = F(x)/cmax. Note that for the classification task we can assume cn+1 = 0 with the same task generality. For regression, we also deal with all data normalized. If actual yact is known, then it is normalized by Cmax for comparison with yn, yact/cmax.
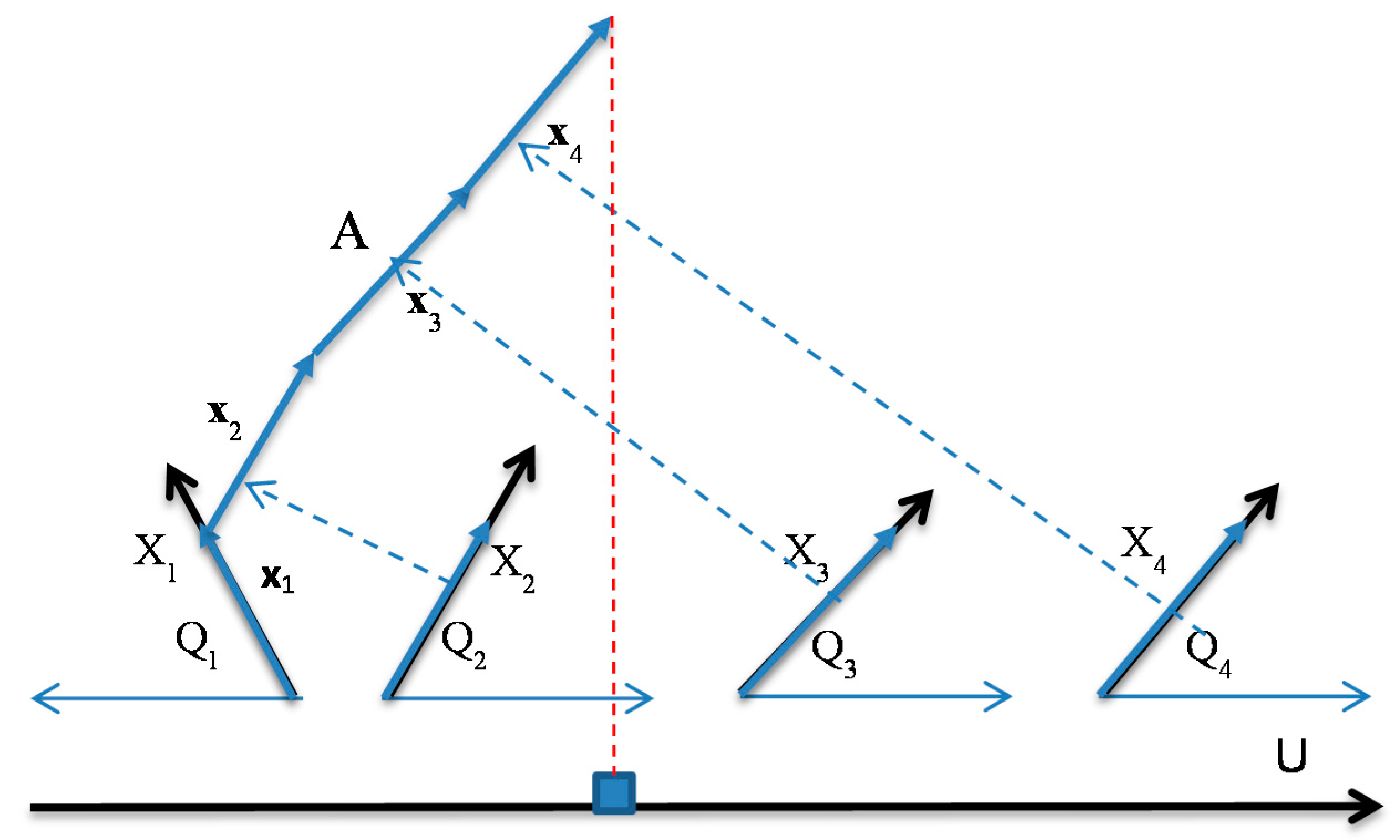
- Step 2: Compute all angles Qi = arccos(|ki|) of absolute values of ki and locate coordinates X1 – Xn in accordance with these angles as shown in Figure 1 relative to the horizontal lines. If ki < 0, then coordinate Xi is oriented to the left, otherwise Xi is oriented to the right (see Figure 1). For a given n-D point x = (x1, x2, …, xn), draw its values as vectors x1, x2, …, xn in respective coordinates X1 – Xn (see Figure 1).
- Step 3. Draw vectors x1, x2, …, xn one after another, as shown on the left side of Figure 1. Then project the last point for xn onto the horizontal axis U (see a red dotted line in Figure 1). To simplify, visualization axis U can be collocated with the horizontal lines that define the angles Qi as shown in Figure 2.
- Step 4.
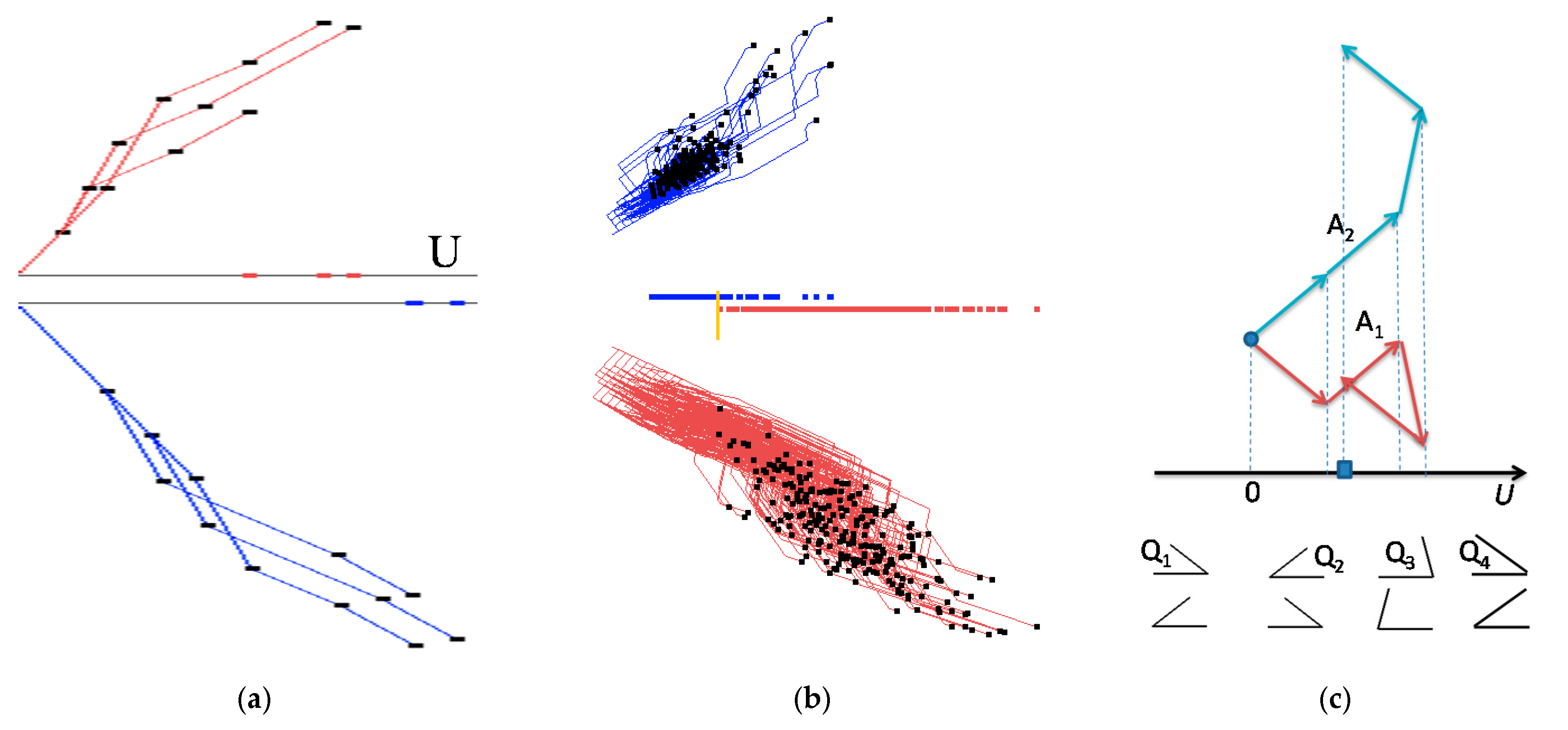
- Step 4a. For regression and linear optimization tasks, repeat step 3 for all n-D points as shown in the upper part of Figure 2a,b.
- Step 4b. For the two-class classification task, repeat step 3 for all n-D points of classes 1 and 2 drawn in different colors. Move points of class 2 by mirroring them to the bottom with axis U doubled as shown in Figure 2. For more than two classes, Figure 1 is created for each class and m parallel axis Uj are generated next to each other similar to Figure 2. Each axis Uj corresponds to a given class j, where m is the number of classes.
- Step 4c. For multi-class classification tasks, conduct step 4b for all n-D points of each pair of classes i and j drawn in different colors, or draw each class against all other classes together.
2.2. Interactive GLC-L Algorithm
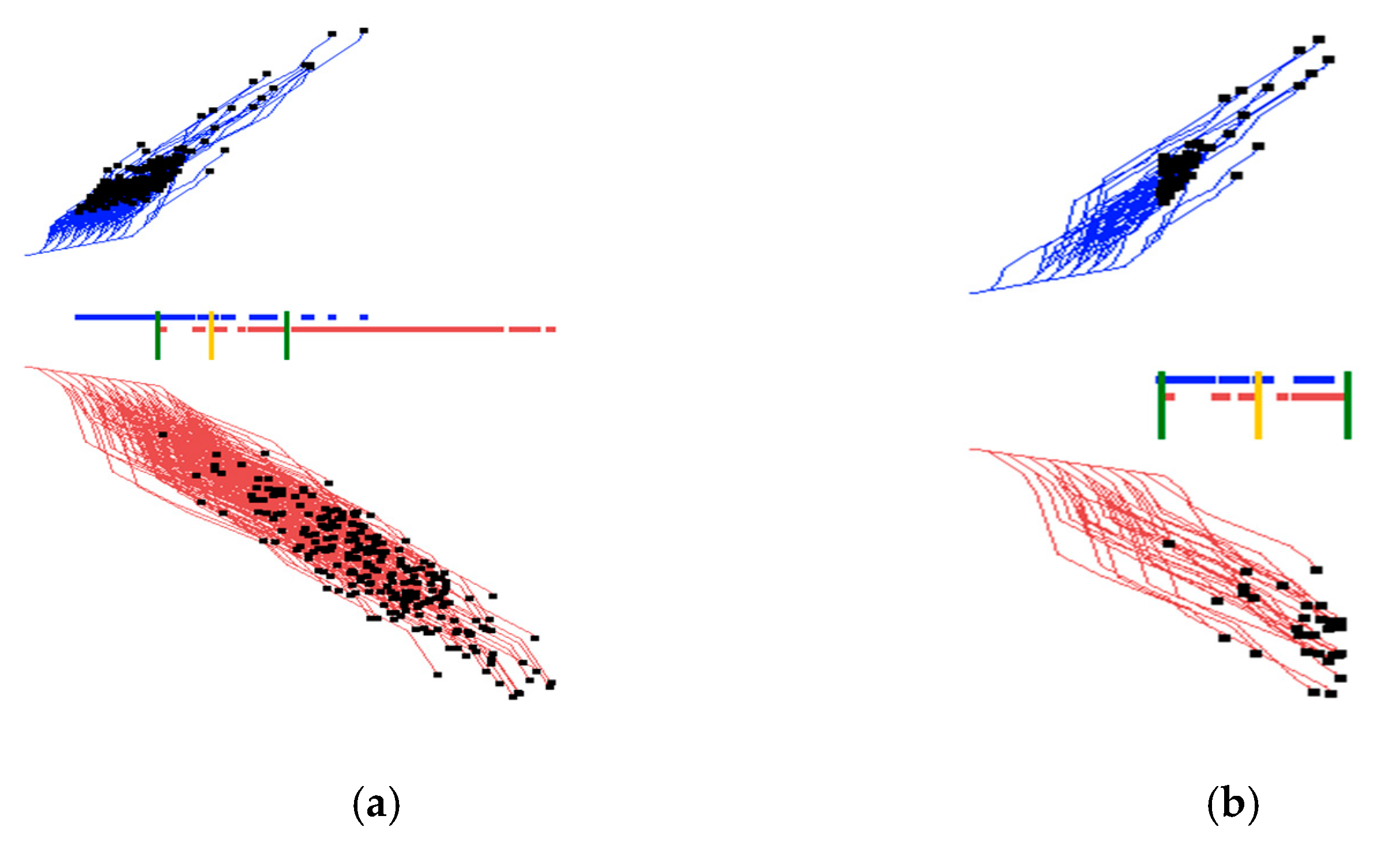
- It starts from the results of GLC-L such as shown in Figure 2b.
- Next, a user can interactively slide a yellow bar in Figure 2b to change a classification threshold. The algorithm updates the confusion matrix and the accuracy of classification, and pops it up for the user.
- An appropriate threshold found by a user can be interactively recorded. Then, a user can request an analytical form of the linear discrimination rule be produced and also be recorded.
- At this stage of the exploration the user has three options:
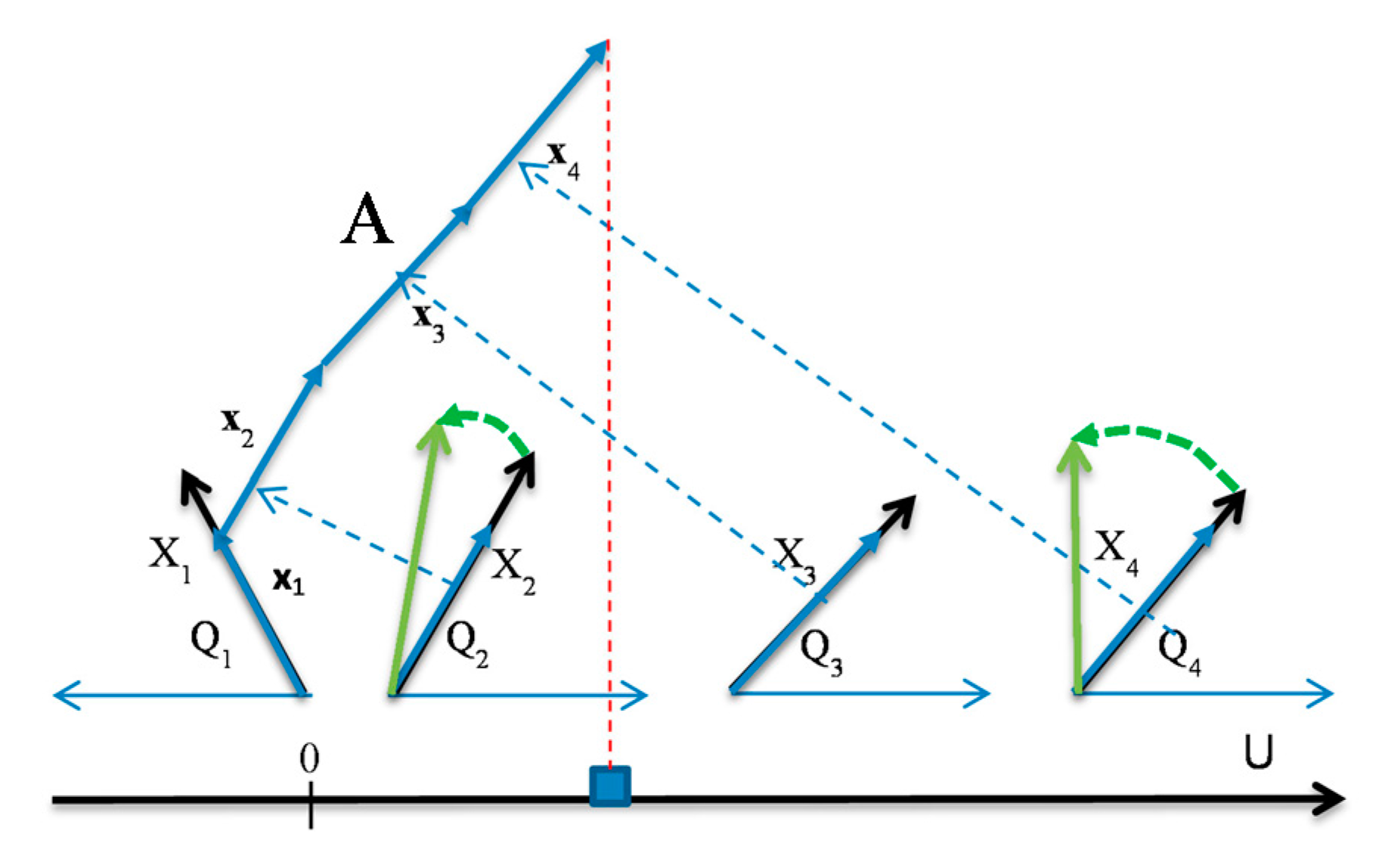
- (a)
- modify interactively the coefficients by rotating the ends of the selected arrows (see Figure 4),
- (b)
- run an automatic coefficient optimization algorithm GLC-AL described in Section 2.3,
- (c)
- apply a visual structure analysis of classes presented in the visualization described in section.
2.3. Algorithm GLC-AL for Automatic Discovery of Relation Combined with Interactions
- Step 1:
best_coefficients = [] while n > 0 coefficients <- random(−1, 1) all_lines = 0 for i data_samples: line = 0 for x data_dimensions: if coefficients[x] < 0: line = line – data_dimensions[x]*cos(acos(coefficients[x])) else: line = line + data_dimensions[x]*cos(acos(coefficients[x])) all_lines.append(line) //update best_coefficients n-- - Step 2: Projects the end points for the set of coefficients that correspond to the highest A value (in the same way as in Figure 4) and prints off the confusion matrix, i.e., for the best separation of the two classes.
- Step 3:
- Step 3a:
- 1:
- User moves around the class separation line.
- 2:
- A new confusion matrix is calculated.
- Step 3b:
- 1:
- User picks the two thresholds to project a subset of the dataset.
- 2:
- n-D points of this subset (between the two thresholds) are projected.
- 3:
- A new confusion matrix is calculated.
- 4:
- User visually discovers patterns from the projection.
- Step 4: User can repeat Step 3a or Step 3b to further zoom in on a subset of the projection or go back to Step 1.
- (1)
- indexing all m given samples from 1 to m, w = (1,2,…,m)
- (2)
- randomly permuting these indexes, and getting a new order of indexes, π(w)
- (3)
- picking up first 70% of indexes from π (w)
- (4)
- assigning samples with these indexes to be training data
- (5)
- assigning remaining 30% of samples to be validation data.
- (i)
- applying data splitting process.
- (ii)
- computing accuracy A of classification for this k.
- (iii)
- repeating (i) and (ii) t times (each times with different data split).
- (iv)
- computing average of accuracies found in all these runs.
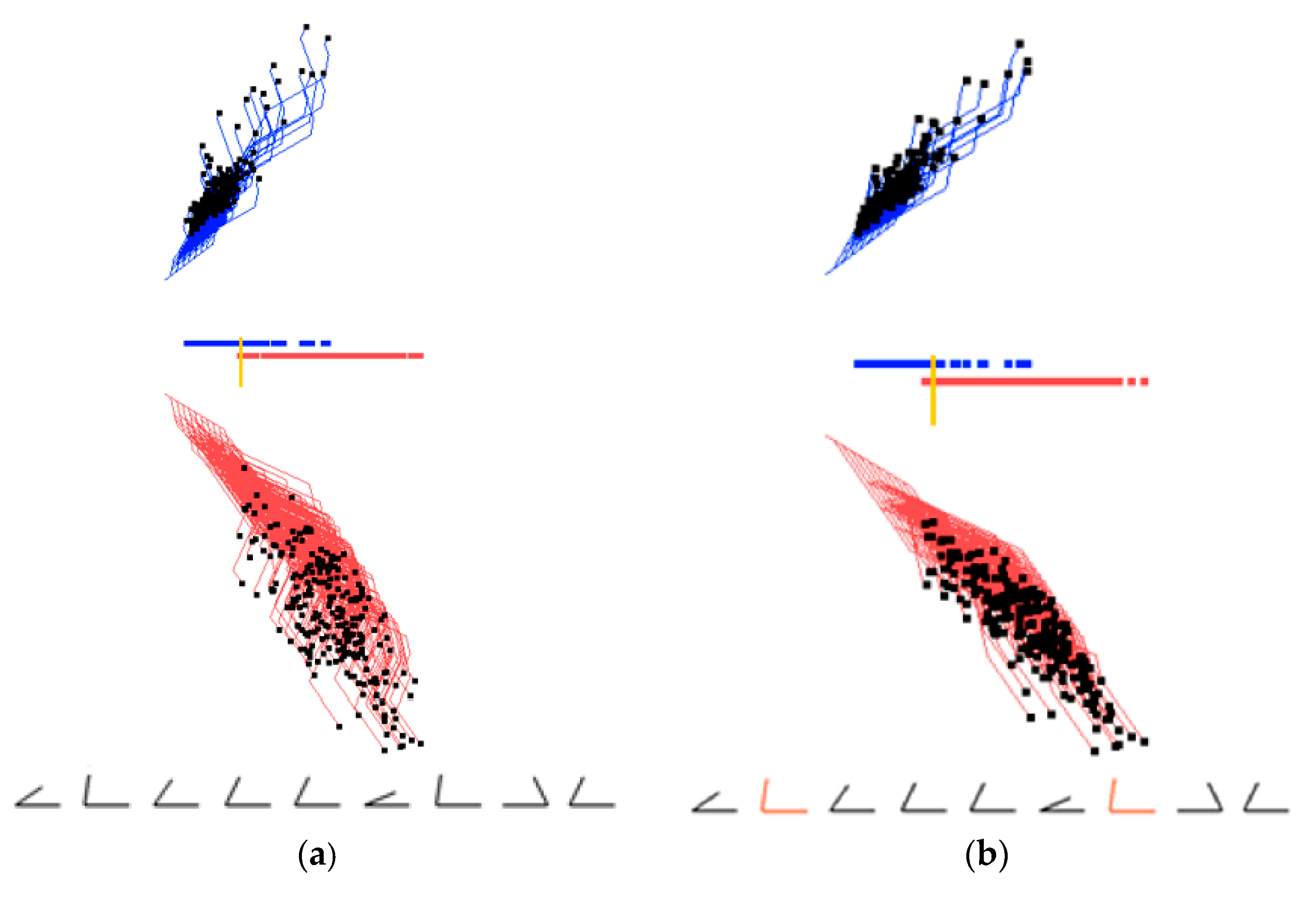
2.4. Visual Structure Analysis of Classes
- Select border points of each class, coloring them in different colors.
- Outline classes by constructing an envelope in the form of a convex or a non-convex hull.
- Select most important coordinates by coloring them differently from other coordinates.
- Selecting misclassified and overlapped cases by coloring them differently from other cases.
- Drawing the prevailing direction of the envelope and computing its location and angle.
- Contrasting envelopes of difference classes to find the separating features.
2.5. Algorithm GLC-DRL for Dimension Reduction
- Step 1: Setting up a threshold for the dimensions, which did not contribute to the line significantly in the horizontal projection.
- Step 2: Based on the threshold from Step 1, dimensions are removed from the data, and the threshold is incremented by a constant.
- Step 3: A new projection is made from the reduced data.
- Step 4: A new confusion matrix is calculated.
- Step 1: The user visually examines the angles for each dimension, and determines which one is not contributing much to the overall line.
- Step 2: The user selects and clicks on the angle from Step 1.
- Step 3: The dimension, which has been selected, is removed from the dataset and a new projection is made along with a new confusion matrix. The dimension, which has been removed, is highlighted.
- Step 4:
- Step 4a: The user goes back to Step 1 to further reduce the dimensions.
- Step 4b: The user selects to find other coefficients with the remaining dimensions for a better projection using the automatic algorithm GLC-AL described above.
2.6. Generalization of the Algorithms for Discovering Non-Linear Functions and Multiple Classes
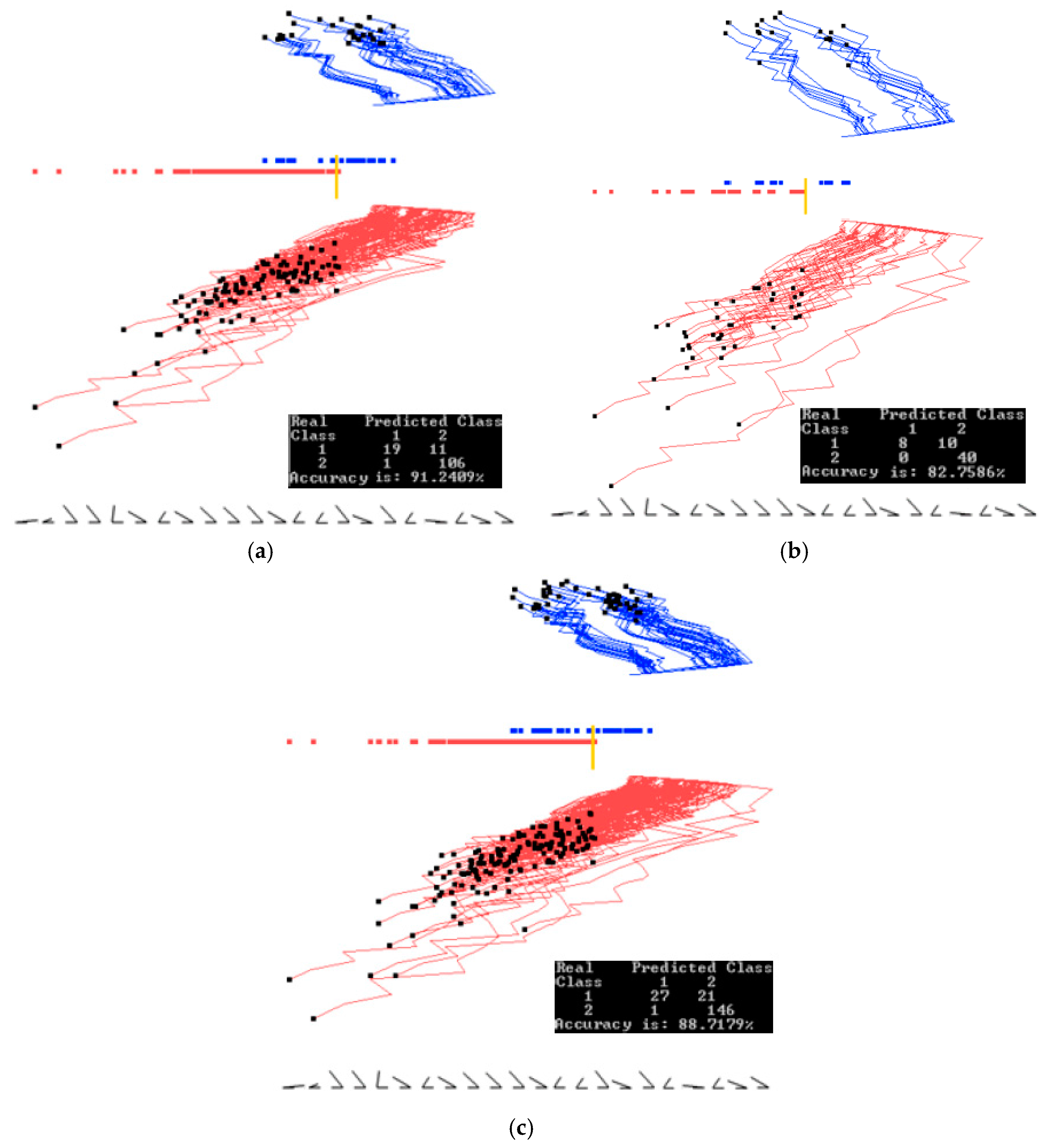
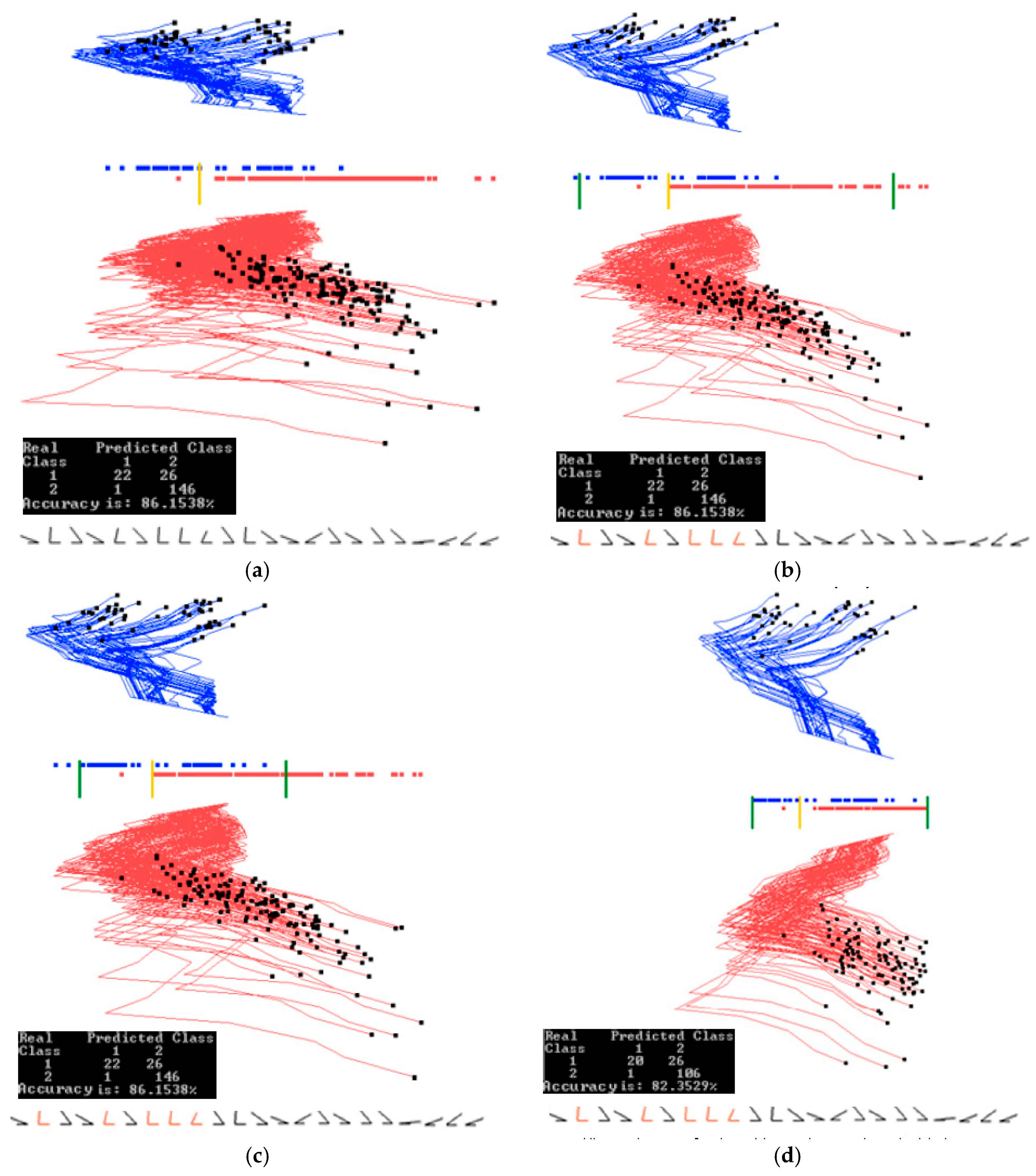
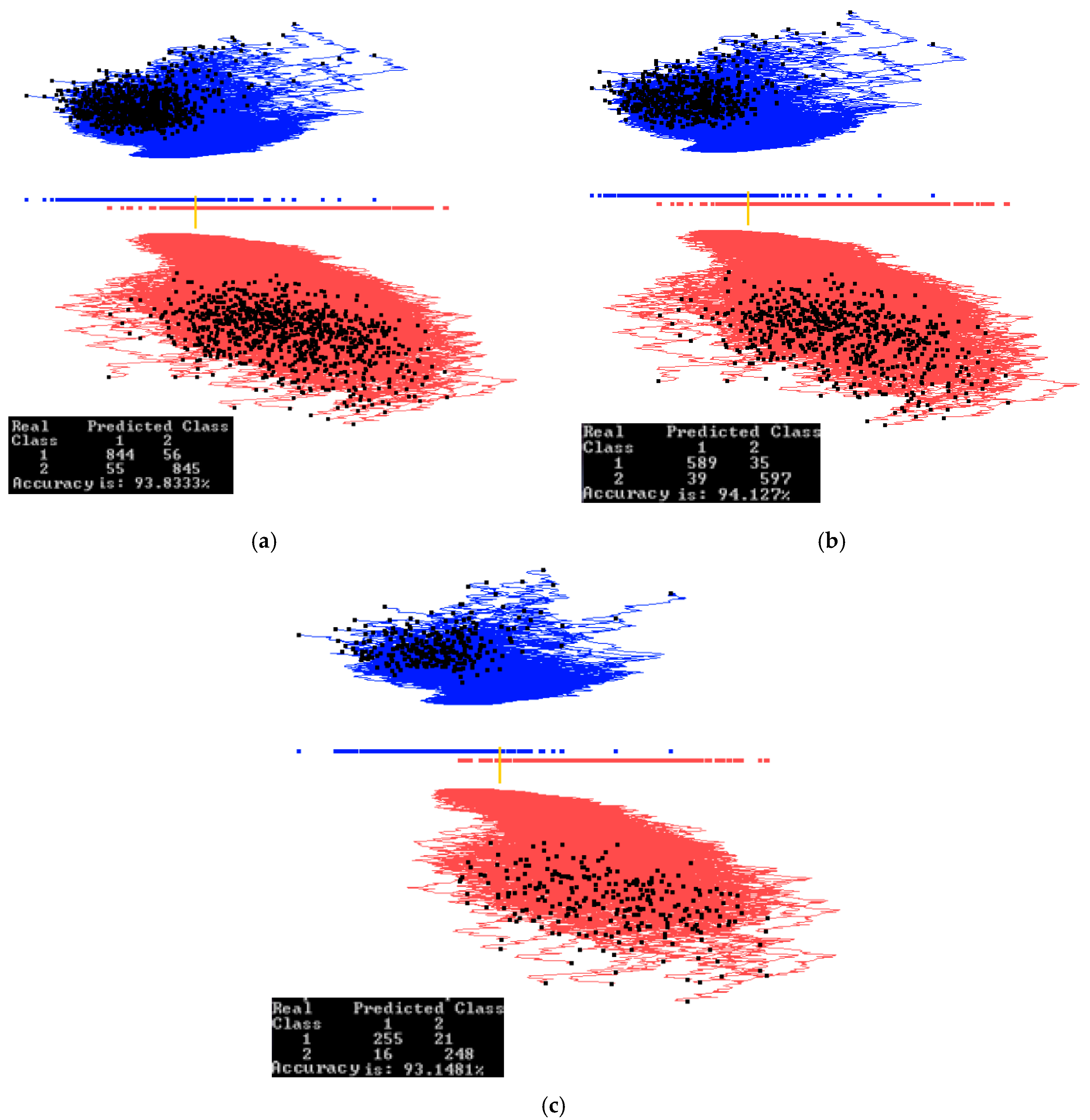
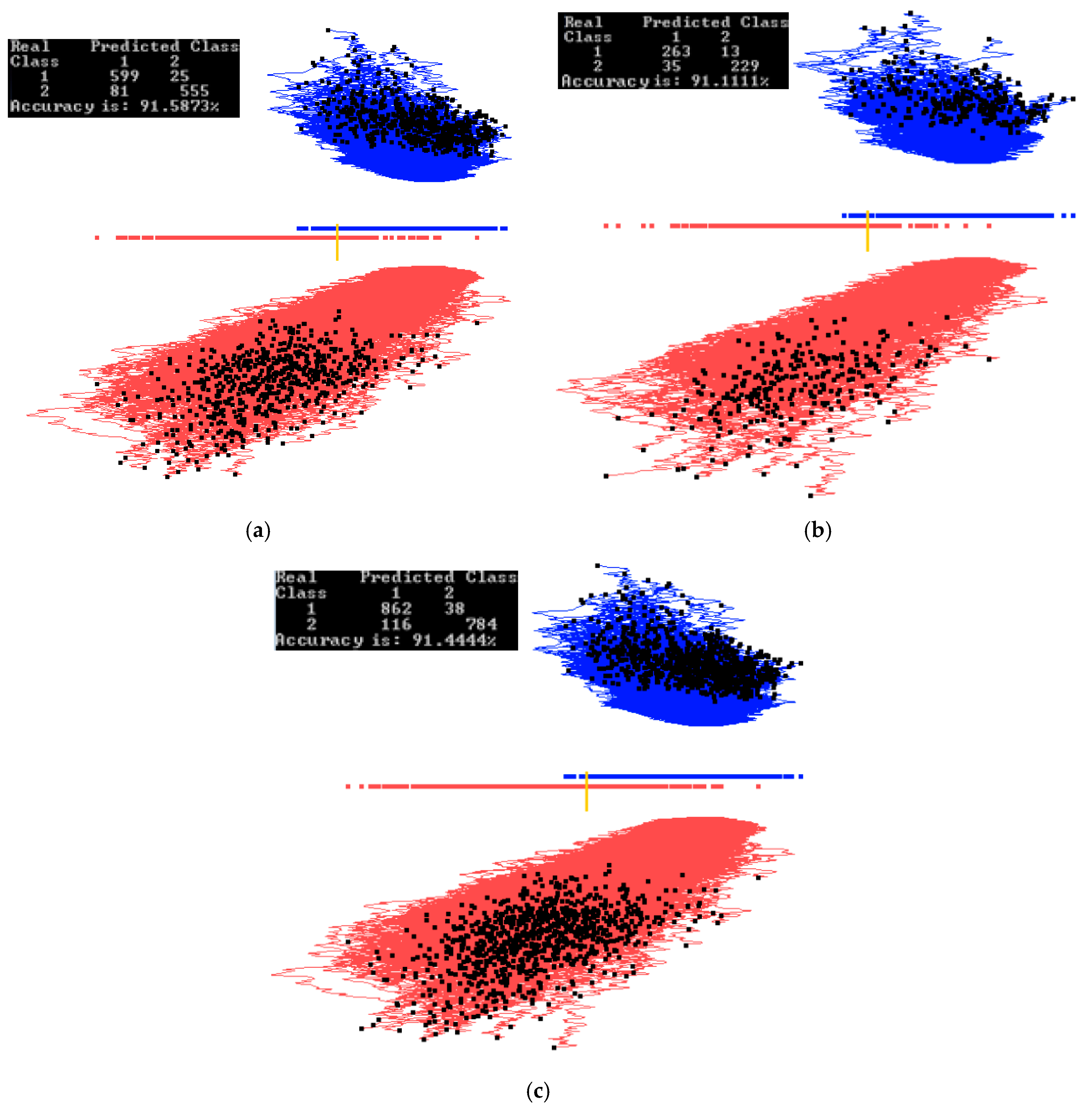
3. Results: Case Studies
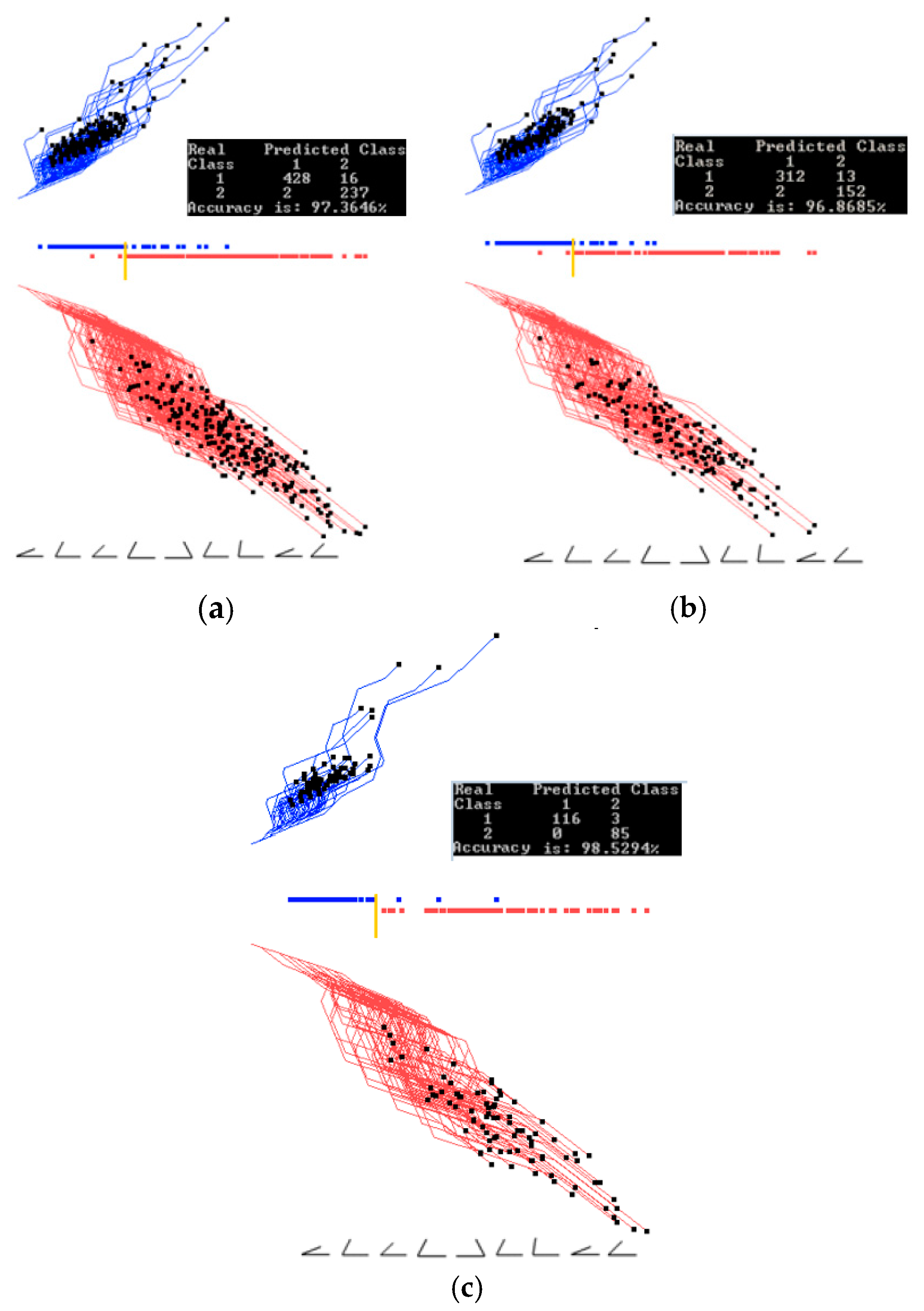
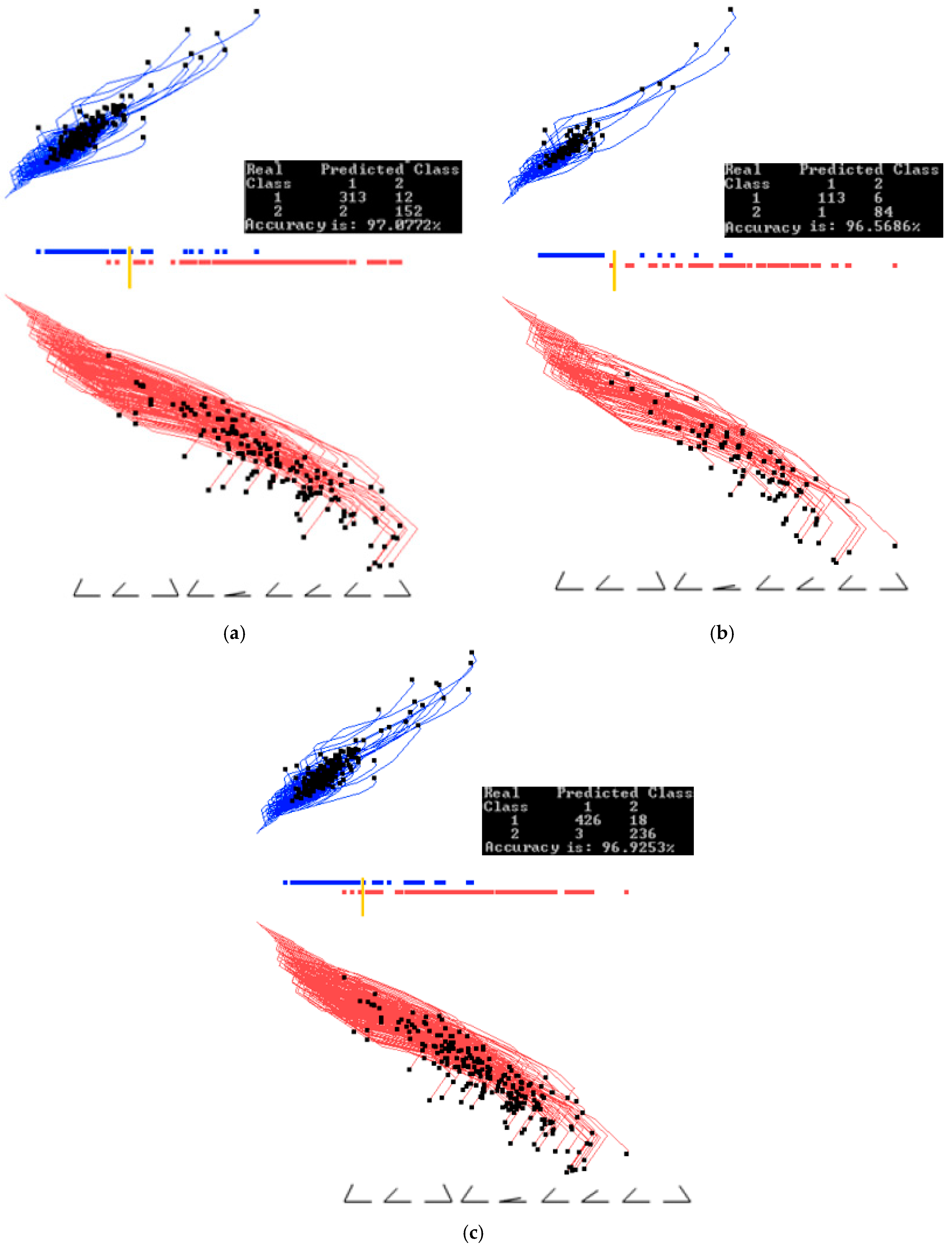
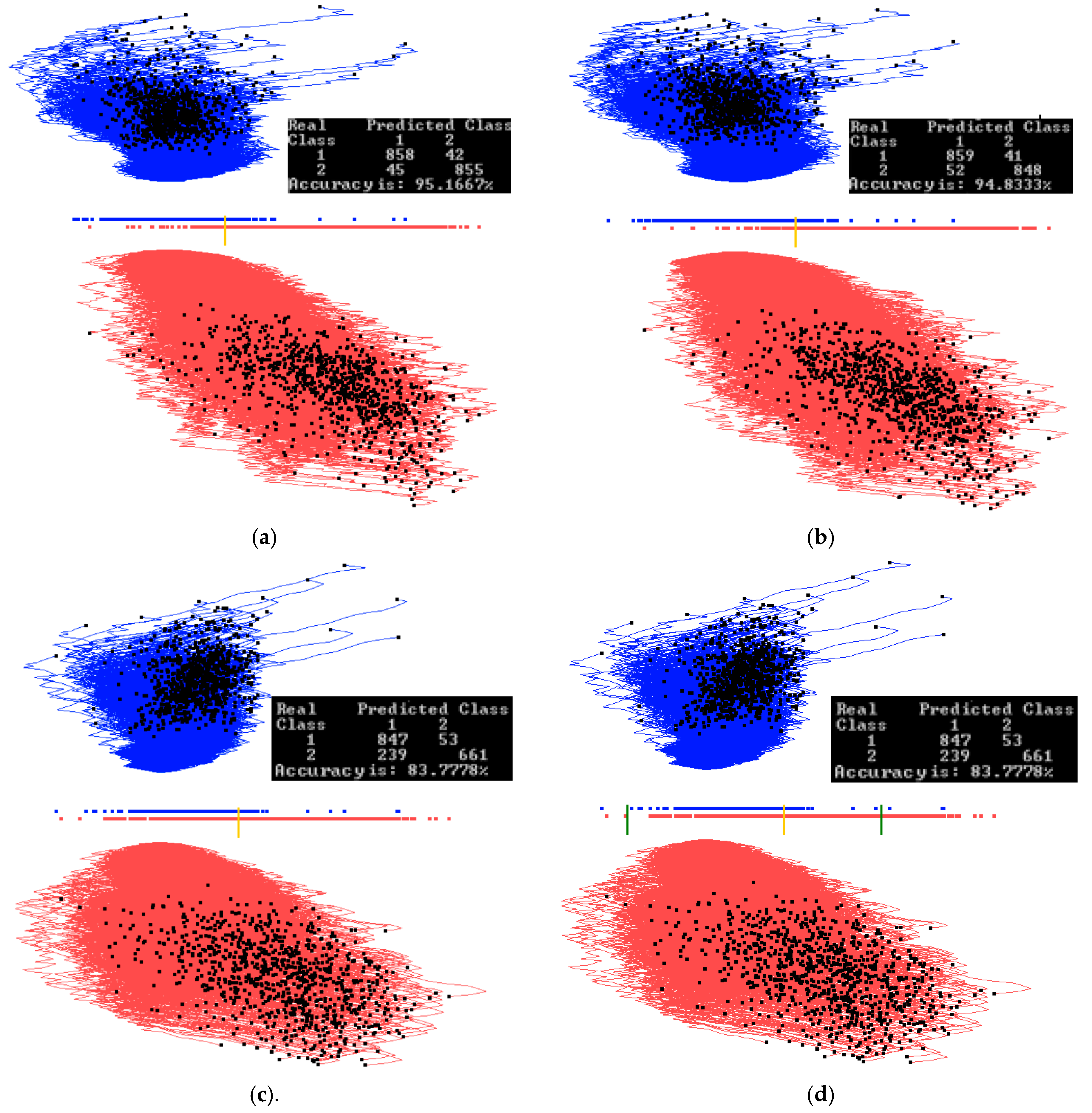
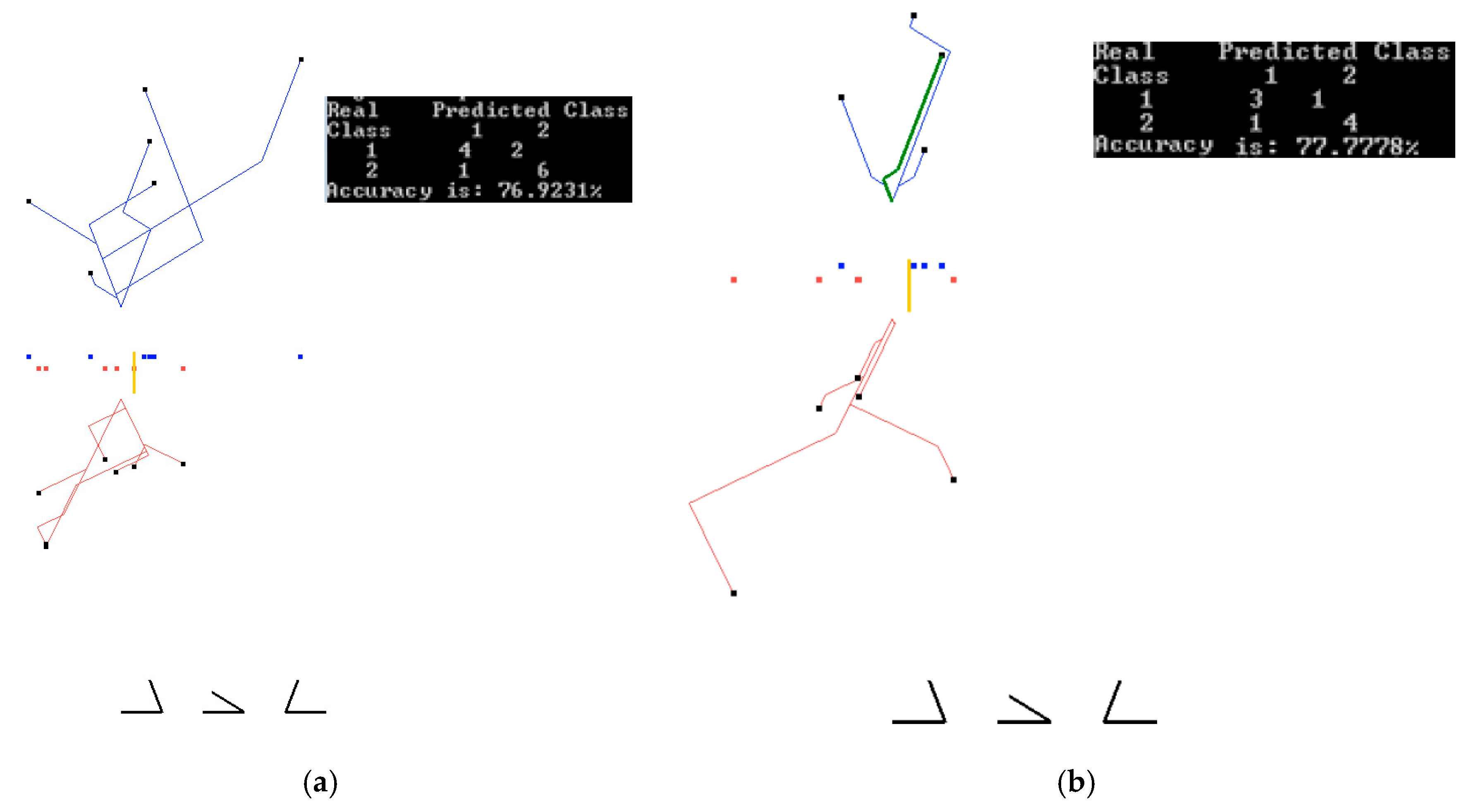
3.1. Case Study 1
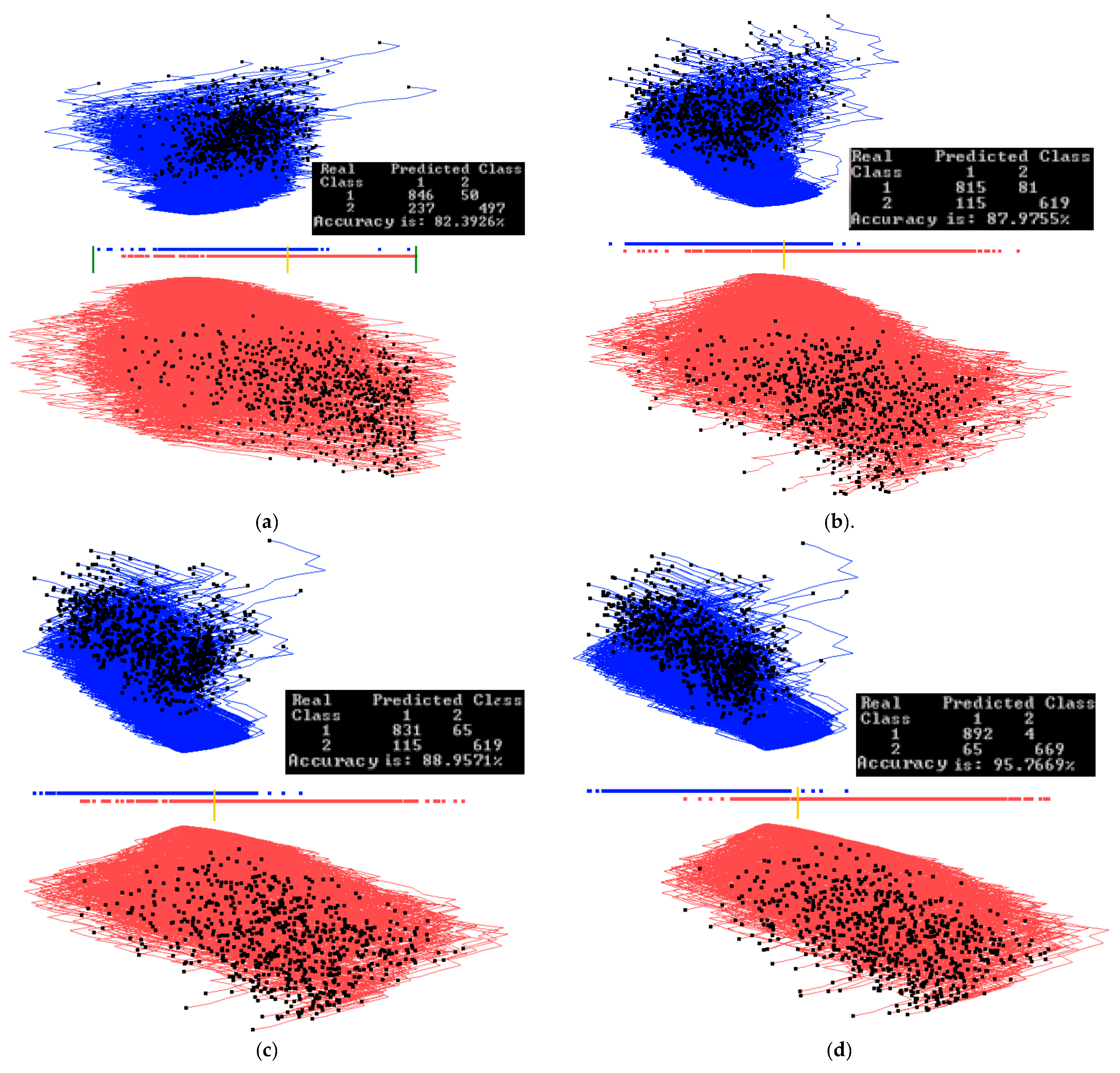
3.2. Case Study 2
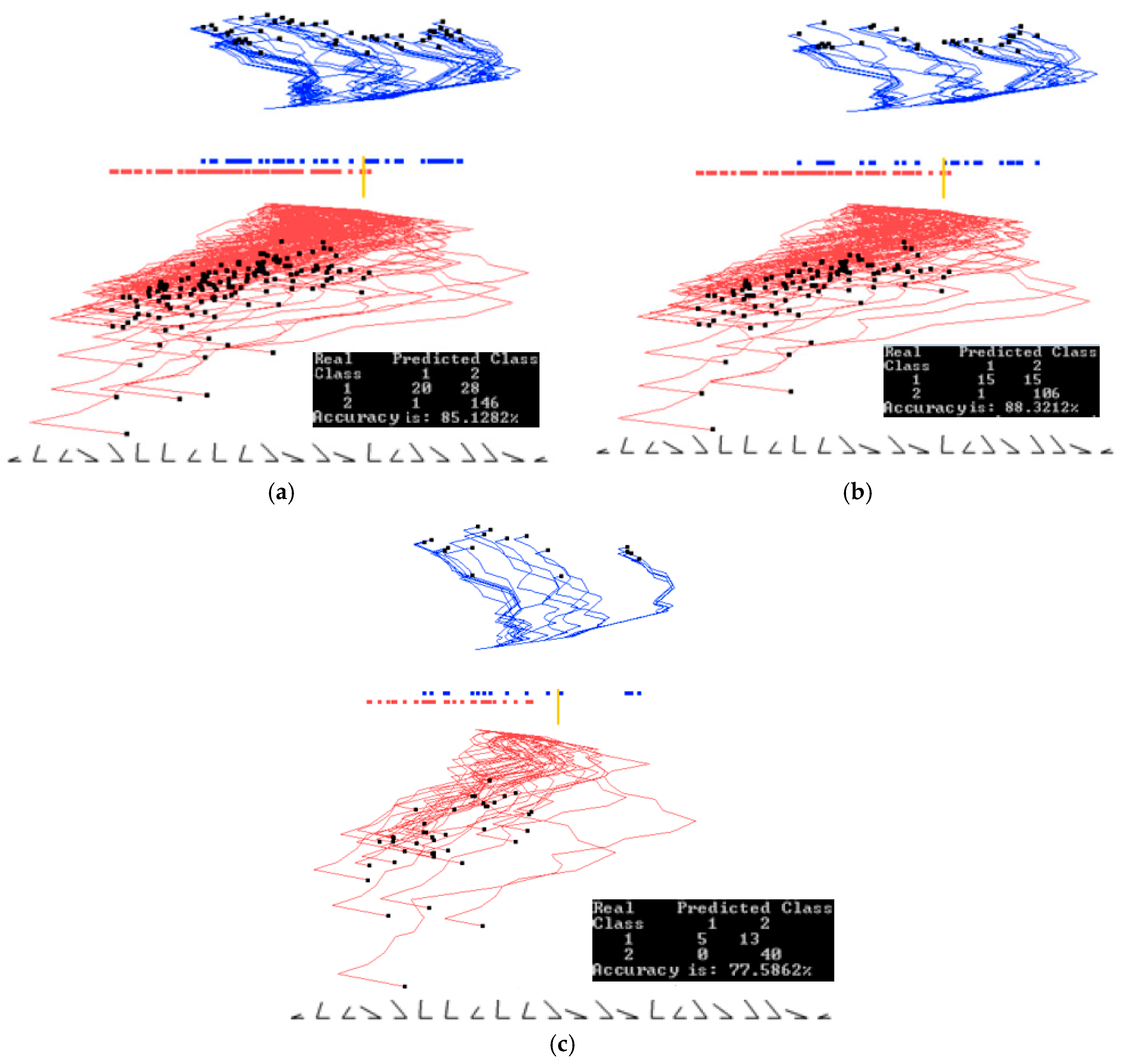
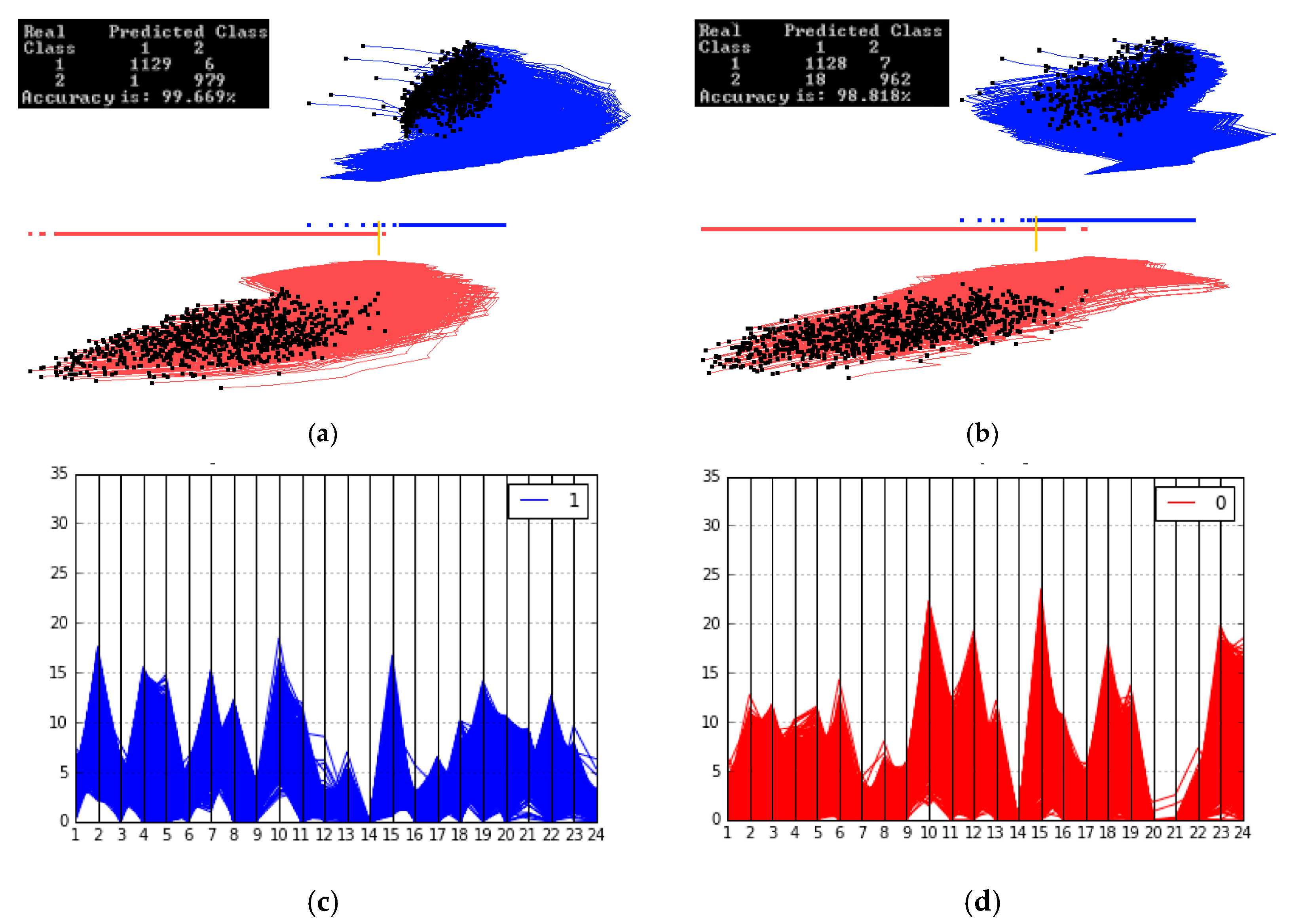
3.3. Case Study 3
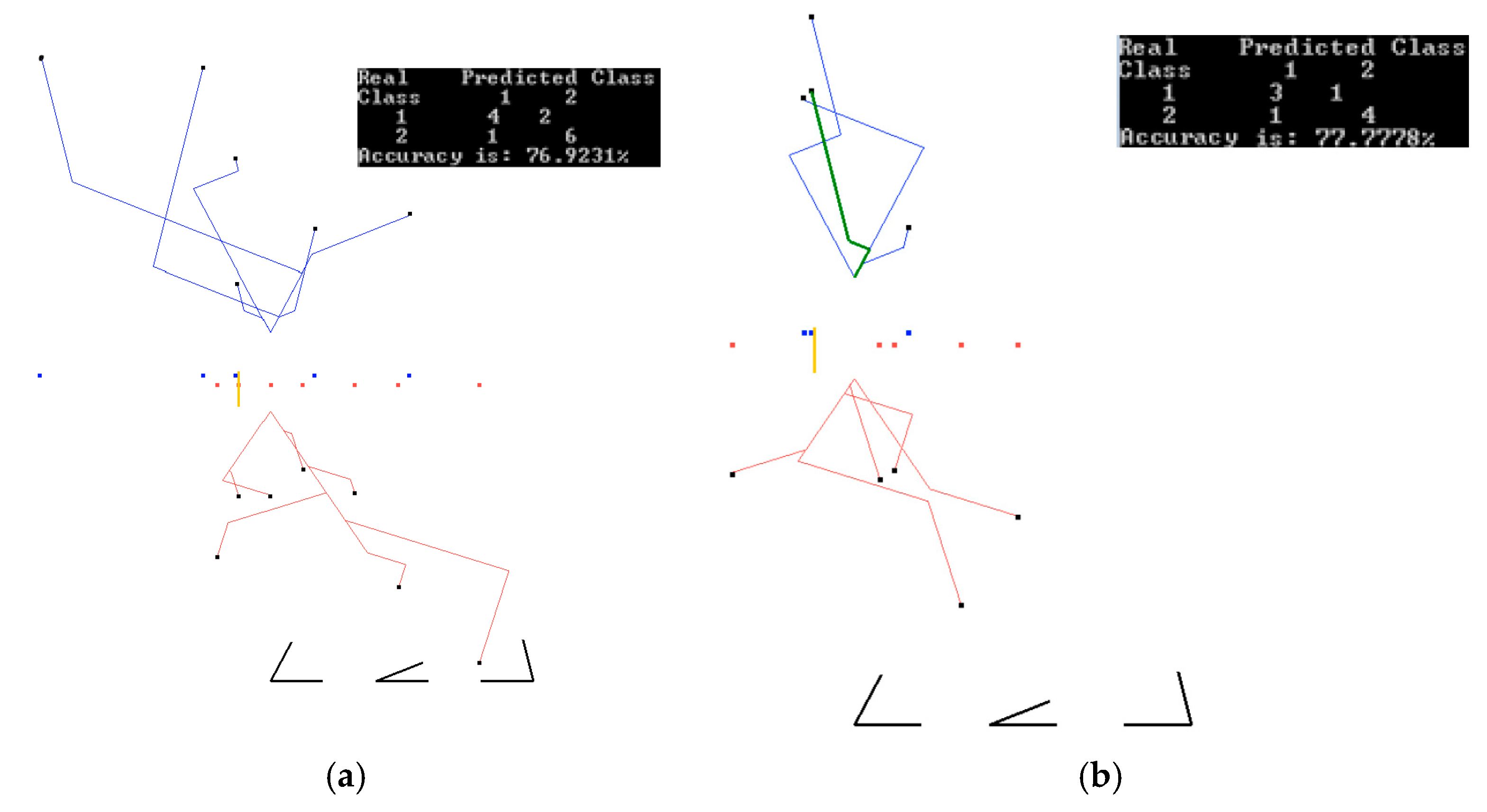
3.4. Case Study 4
3.5. Case Study 5
- S1(w), S2(w), S3(w), S4(w), and S5(w) are S&P 500 values for Monday-Friday, respectively, of week w;
- Di(w) = Si+1(w) − Si(w) are differences in S&P 500 values on adjacent days, i = 1:4;
- Class(w) = 1 (down) if D4(w) < 0, Class(w) = 2 (up) if D4(w) > 0, Class(w) = 0 (no change) if D4(w) = 0.
4. Discussion and Analysis
4.1. Software Implementation, Time and Accuracy
4.2. Comparison with Published Results
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bertini, E.; Tatu, A.; Keim, D. Quality metrics in high-dimensional data visualization: An overview and systematization. IEEE Trans. Vis. Comput. Gr. 2011, 17, 2203–2212. [Google Scholar] [CrossRef] [PubMed]
- Ward, M.; Grinstein, G.; Keim, D. Interactive Data Visualization: Foundations, Techniques, and Applications; A K Peters/CRC Press: Natick, MA, USA, 2010. [Google Scholar]
- Rübel, O.; Ahern, S.; Bethel, E.W.; Biggin, M.D.; Childs, H.; Cormier-Michel, E.; DePace, A.; Eisen, M.B.; Fowlkes, C.C.; Geddes, C.G.; et al. Coupling visualization and data analysis for knowledge discovery from multi-dimensional scientific data. Procedia Comput. Sci. 2010, 1, 1757–1764. [Google Scholar] [CrossRef] [PubMed]
- Inselberg, A. Parallel Coordinates: Visual Multidimensional Geometry and Its Applications; Springer: New York, NY, USA, 2009. [Google Scholar]
- Wong, P.; Bergeron, R. 30 years of multidimensional multivariate visualization. In Scientific Visualization—Overviews, Methodologies and Techniques; Nielson, G.M., Hagan, H., Muller, H., Eds.; IEEE Computer Society Press: Washington, DC, USA, 1997; pp. 3–33. [Google Scholar]
- Kovalerchuk, B.; Kovalerchuk, M. Toward virtual data scientist. In Proceedings of the 2017 International Joint Conference On Neural Networks, Anchorage, AK, USA, 14–19 May 2017; pp. 3073–3080. [Google Scholar]
- XmdvTool Software Package for the Interactive Visual Exploration of Multivariate Data Sets. Version 9.0 Released 31 October 2015. Available online: http://davis.wpi.edu/~xmdv/ (accessed on 24 June 2017).
- Yang, J.; Peng, W.; Ward, M.O.; Rundensteiner, E.A. Interactive hierarchical dimension ordering, spacing and filtering for exploration of high dimensional datasets. In Proceedings of the 9th Annual IEEE Conference on Information Visualization, Washington, DC, USA, 19–21 October 2003; pp. 105–112. [Google Scholar]
- Lin, X.; Mukherji, A.; Rundensteiner, E.A.; Ward, M.O. SPIRE: Supporting parameter-driven interactive rule mining and exploration. Proc. VLDB Endow. 2014, 7, 1653–1656. [Google Scholar] [CrossRef]
- Yang, D.; Zhao, K.; Hasan, M.; Lu, H.; Rundensteiner, E.; Ward, M. Mining and linking patterns across live data streams and stream archives. Proc. VLDB Endow. 2013, 6, 1346–1349. [Google Scholar] [CrossRef]
- Zhao, K.; Ward, M.; Rundensteiner, E.; Higgins, H. MaVis: Machine Learning Aided Multi-Model Framework for Time Series Visual Analytics. Electron. Imaging 2016, 1–10. [Google Scholar] [CrossRef]
- Kovalerchuk, B.; Grishin, V. Adjustable general line coordinates for visual knowledge discovery in n-D data. Inf. Vis. 2017. [Google Scholar] [CrossRef]
- Grishin, V.; Kovalerchuk, B. Multidimensional collaborative lossless visualization: Experimental study. In Proceedings of the International Conference on Cooperative Design, Visualization and Engineering (CDVE 2014), Seattle, WA, USA, 14–17 September 2014; Luo, Y., Ed.; Springer: Basel, Switzerland, 2014; pp. 27–35. [Google Scholar]
- Kovalerchuk, B. Super-intelligence challenges and lossless visual representation of high-dimensional data. In Proceedings of the 2016 International Joint Conference on Neural Networks (IJCNN), Vancouver, BC, Canada, 24–29 July 2016; pp. 1803–1810. [Google Scholar]
- Kovalerchuk, B. Visualization of multidimensional data with collocated paired coordinates and general line coordinates. Proc. SPIE 2014, 9017. [Google Scholar] [CrossRef]
- Wilinski, A.; Kovalerchuk, B. Visual knowledge discovery and machine learning for investment strategy. Cogn. Syst. Res. 2017, 44, 100–114. [Google Scholar] [CrossRef]
- UCI Machine Learning Repository. Breast Cancer Wisconsin (Original) Data Set. Available online: https://archive.ics.uci.edu/ml/datasets/breast+cancer+wisconsin+(original) (accessed on 15 June 2017).
- Freund, Y.; Schapire, R. Large margin classification using the perceptron algorithm. Mach. Learn. 1999, 37, 277–296. [Google Scholar] [CrossRef]
- Freedman, D. Statistical Models: Theory and Practice; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Maszczyk, T.; Duch, W. Support vector machines for visualization and dimensionality reduction. In International Conference on Artificial Neural Networks; Springer: Berlin/Heidelberg, Germany, 2008; pp. 346–356. [Google Scholar]
- Cristianini, N.; Shawe-Taylor, J. An Introduction to Support Vector Machines and Other Kernel-Based Learning Methods; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- UCI Machine Learning Repository. Parkinsons Data Set. Available online: https://archive.ics.uci.edu/ml/datasets/parkinsons (accessed on 15 June 2017).
- LeCun, Y.; Cortes, C.; Burges, C. MNIST Handwritten Digit Database, 2013. Available online: http://yann.lecun.com/exdb/mnist/ (accessed on 12 March 2017).
- Keras: The Python Deep Learning Library. Available online: http://keras.io (accessed on 14 June 2017).
- Chollet, F. Keras. 2015. Available online: https://github.com/fchollet/keras (accessed on 14 June 2017).
- Salama, G.I.; Abdelhalim, M.; Zeid, M.A. Breast cancer diagnosis on three different datasets using multi-classifiers. Breast Cancer (WDBC) 2012, 32, 2. [Google Scholar]
- Aruna, S.; Rajagopalan, D.S.; Nandakishore, L.V. Knowledge based analysis of various statistical tools in detecting breast cancer. Comput. Sci. Inf. Technol. 2011, 2, 37–45. [Google Scholar]
- Christobel, A.; Sivaprakasam, Y. An empirical comparison of data mining classification methods. Int. J. Comput. Inf. Syst. 2011, 3, 24–28. [Google Scholar]
- Weka 3: Data Mining Software in Java. Available online: http://www.cs.waikato.ac.nz/ml/weka/ (accessed on 14 June 2017).
- Ramani, R.G.; Sivagami, G. Parkinson disease classification using data mining algorithms. Int. J. Comput. Appl. 2011, 32, 17–22. [Google Scholar]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-Based Learning Applied to Document Recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Domingos, P. A unified bias-variance decomposition. In Proceedings of the 17th International Conference on Machine Learning, Stanford, CA, USA, 29 June–2 July 2000; Morgan Kaufmann: Burlington, MA, USA, 2000; pp. 231–238. [Google Scholar]
- Pereira, F.; Mitchell, T.; Botvinick, M. Machine learning classifiers and fMRI: A tutorial overview. NeuroImage 2009, 45 (Suppl. 1), S199–S209. [Google Scholar] [CrossRef] [PubMed]



| Case Study 1 Results. Wisconsin Breast Cancer Data | Case Study 2 Results. Parkinson’s Disease | Case Study 3 Results. MNIST-Subset | ||||||
|---|---|---|---|---|---|---|---|---|
| Run | Training Accuracy, % | Validation Accuracy, % | Run | Training Accuracy, % | Validation Accuracy, % | Run | Training Accuracy, % | Validation Accuracy, % |
| 1 | 96.86 | 96.56 | 1 | 89.05 | 74.13 | 1 | 98.17 | 98.33 |
| 2 | 96.65 | 97.05 | 2 | 85.4 | 84.48 | 2 | 94.28 | 94.62 |
| 3 | 97.91 | 96.56 | 3 | 84.67 | 94.83 | 3 | 95.07 | 94.81 |
| 4 | 96.45 | 96.56 | 4 | 84.67 | 84.48 | 4 | 97.22 | 96.67 |
| 5 | 97.07 | 96.57 | 5 | 85.4 | 77.58 | 5 | 94.52 | 93.19 |
| 6 | 97.91 | 96.07 | 6 | 84.67 | 93.1 | 6 | 92.85 | 91.48 |
| 7 | 97.07 | 96.56 | 7 | 84.67 | 86.2 | 7 | 96.03 | 95.55 |
| 8 | 97.49 | 98.04 | 8 | 87.59 | 87.93 | 8 | 94.76 | 94.62 |
| 9 | 97.28 | 98.03 | 9 | 86.13 | 82.76 | 9 | 96.11 | 95.56 |
| 10 | 96.87 | 97.55 | 10 | 83.94 | 87.93 | 10 | 95.43 | 95.17 |
| Average | 97.16 | 96.95 | Average | 85.62 | 85.34 | Average | 95.44 | 95.00 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kovalerchuk, B.; Dovhalets, D. Constructing Interactive Visual Classification, Clustering and Dimension Reduction Models for n-D Data. Informatics 2017, 4, 23. https://doi.org/10.3390/informatics4030023
Kovalerchuk B, Dovhalets D. Constructing Interactive Visual Classification, Clustering and Dimension Reduction Models for n-D Data. Informatics. 2017; 4(3):23. https://doi.org/10.3390/informatics4030023
Chicago/Turabian StyleKovalerchuk, Boris, and Dmytro Dovhalets. 2017. "Constructing Interactive Visual Classification, Clustering and Dimension Reduction Models for n-D Data" Informatics 4, no. 3: 23. https://doi.org/10.3390/informatics4030023
APA StyleKovalerchuk, B., & Dovhalets, D. (2017). Constructing Interactive Visual Classification, Clustering and Dimension Reduction Models for n-D Data. Informatics, 4(3), 23. https://doi.org/10.3390/informatics4030023




