Opening up the Black Box of Sensor Processing Algorithms through New Visualizations
Abstract
:1. Introduction: Human–Computation–Sensor Systems
2. Cognitive Task Analysis
2.1. Weaknesses of Alert/Investigate Human–Machine Architectures
2.1.1. Corroboration
2.1.2. Brittleness
2.1.3. Low Observability
2.1.4. Poor Mental Models
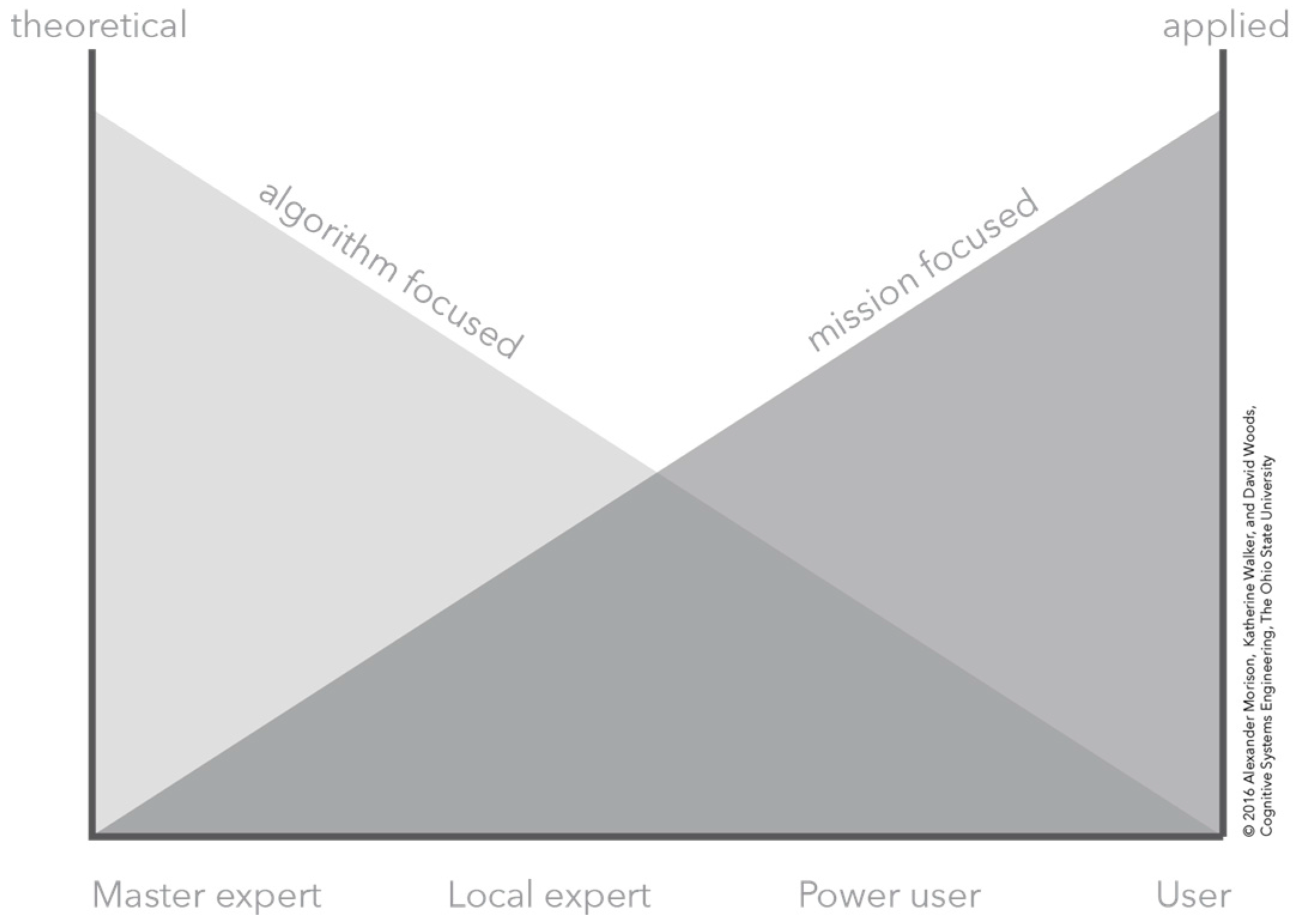
2.2. CTA of Hyperspectral Imaging as a Sample Human–Computation–Sensor System
3. Making Automation Observable
3.1. The Conceptual Problem
3.2. Similarity Matching in Hyperspectral Analysis
- weak targets—low discriminability between target and background;
- masked targets—a background material hides a target material; and
- confusor targets—a background material that is similar to a target material.
3.3. Example Similarity Computation—Cosine Similarity
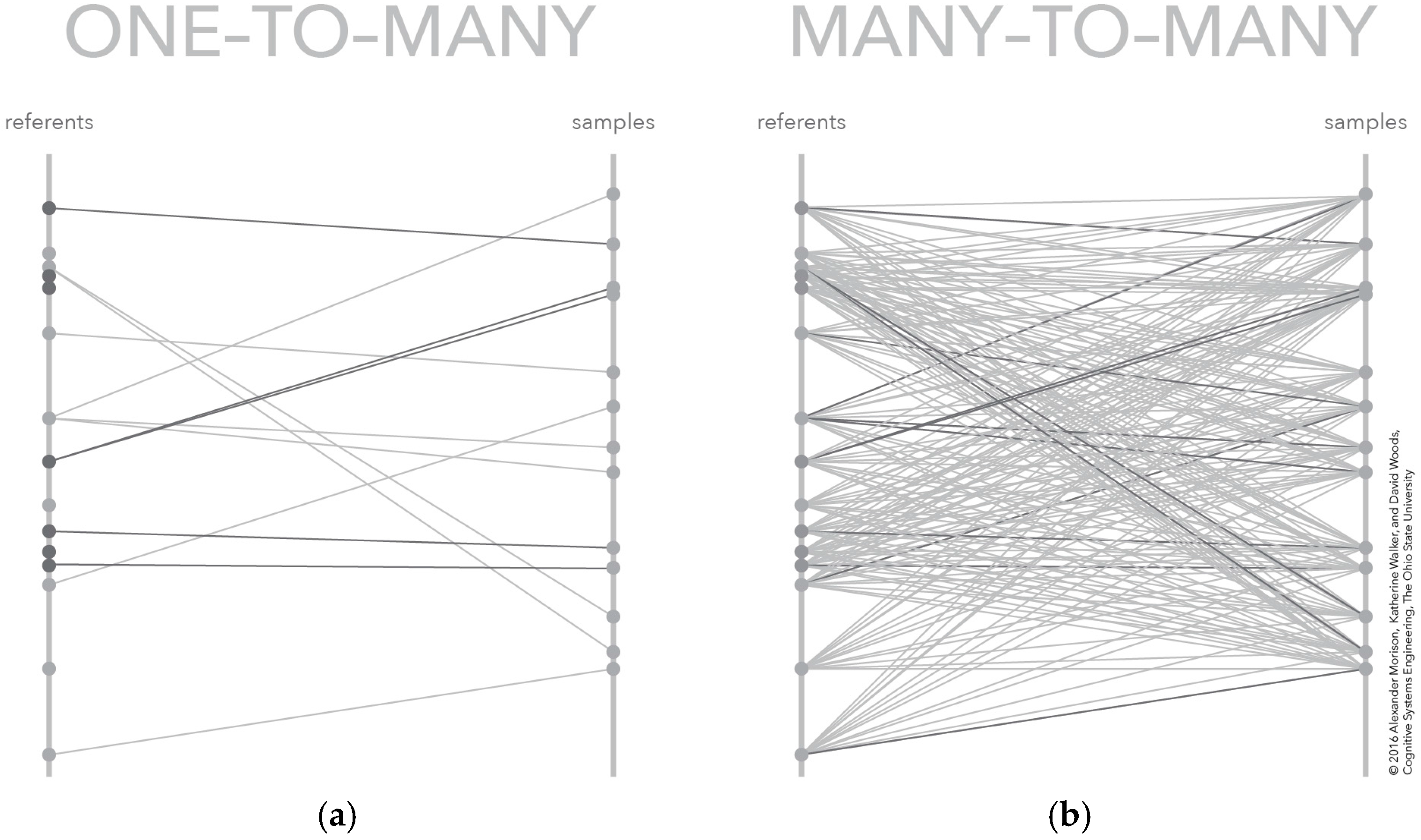
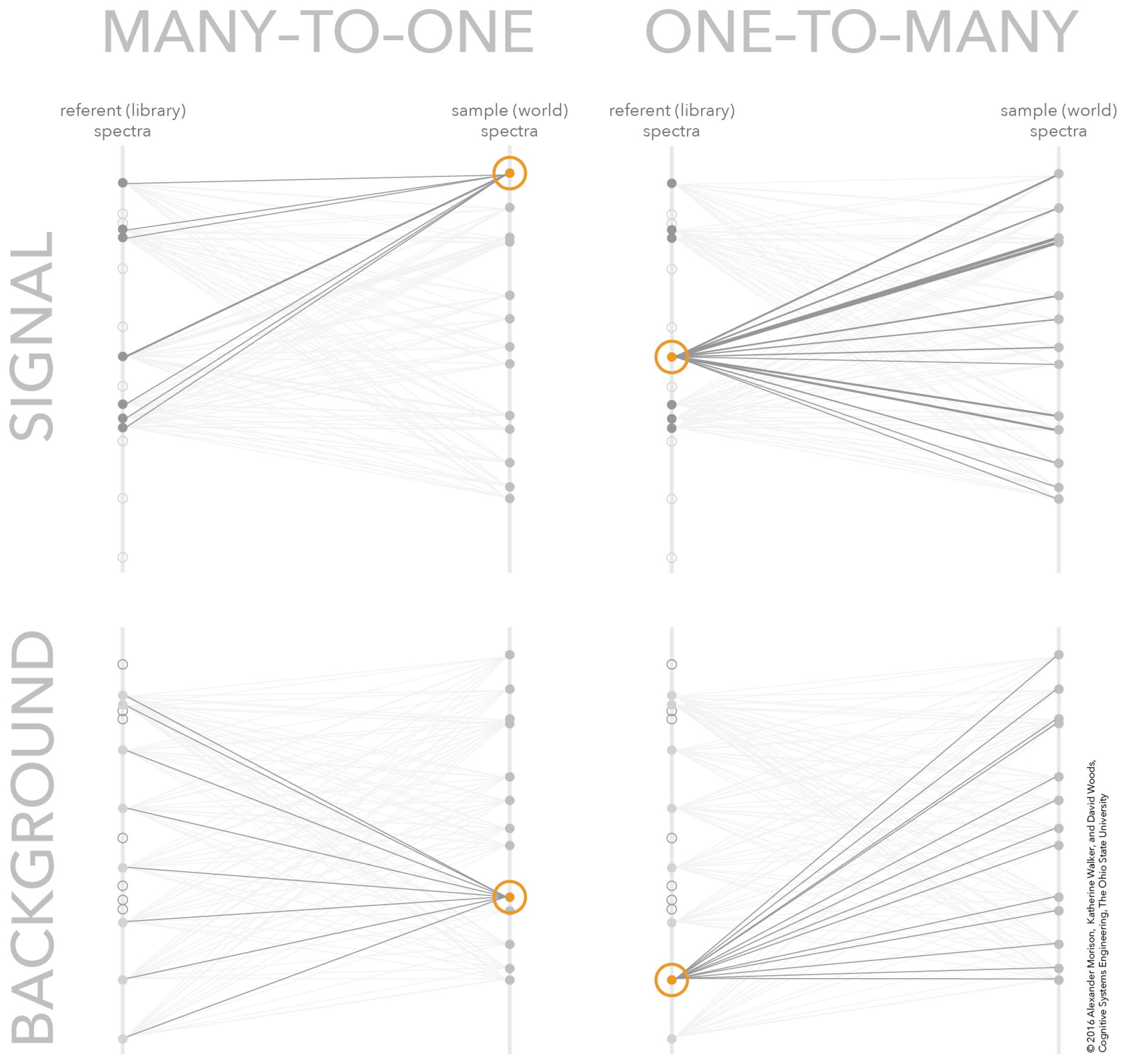
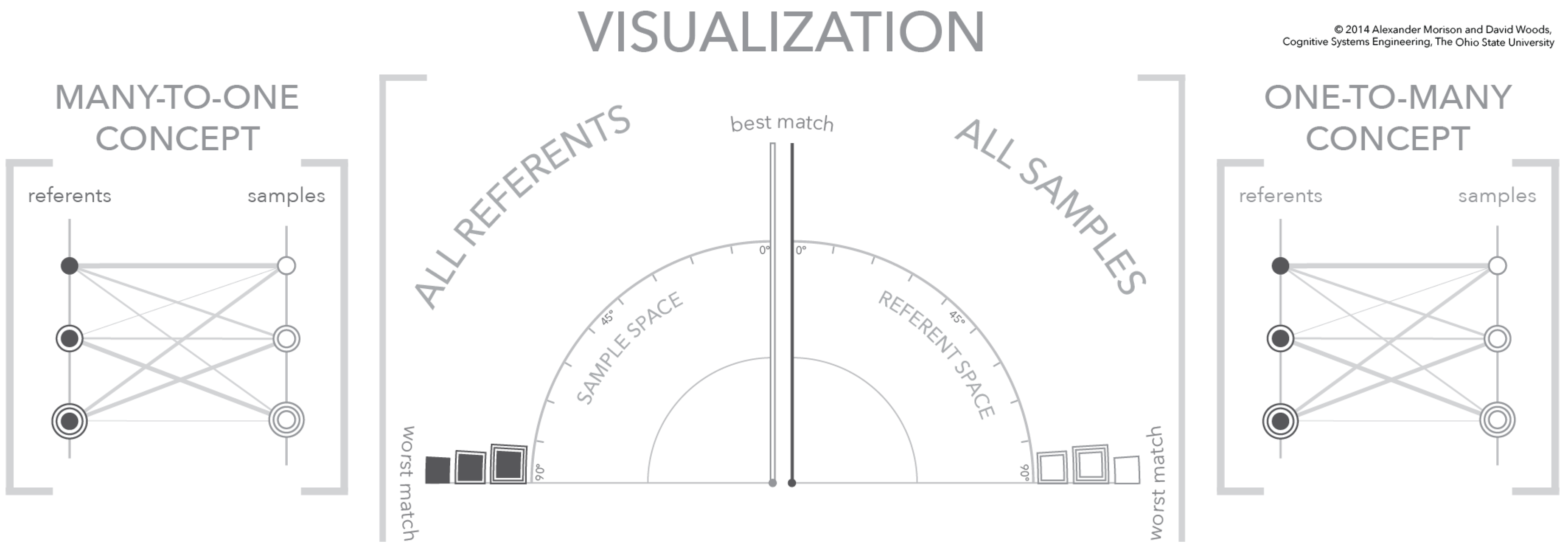
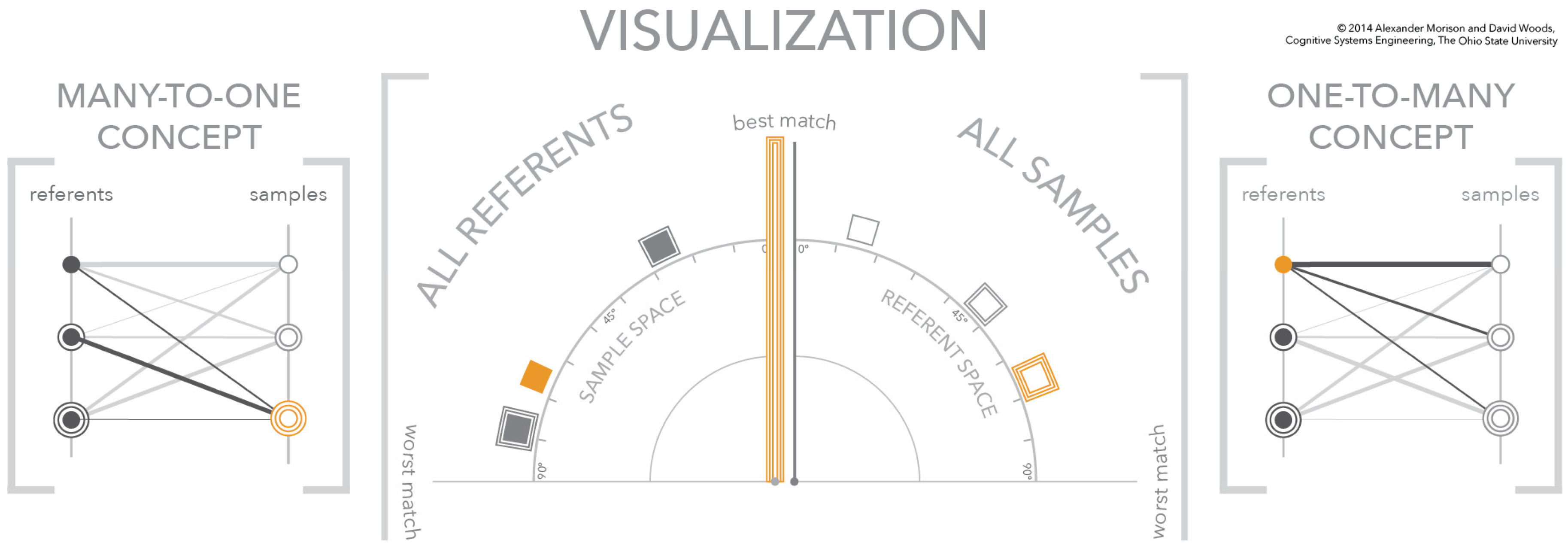
3.4. Many-to-Many Mapping
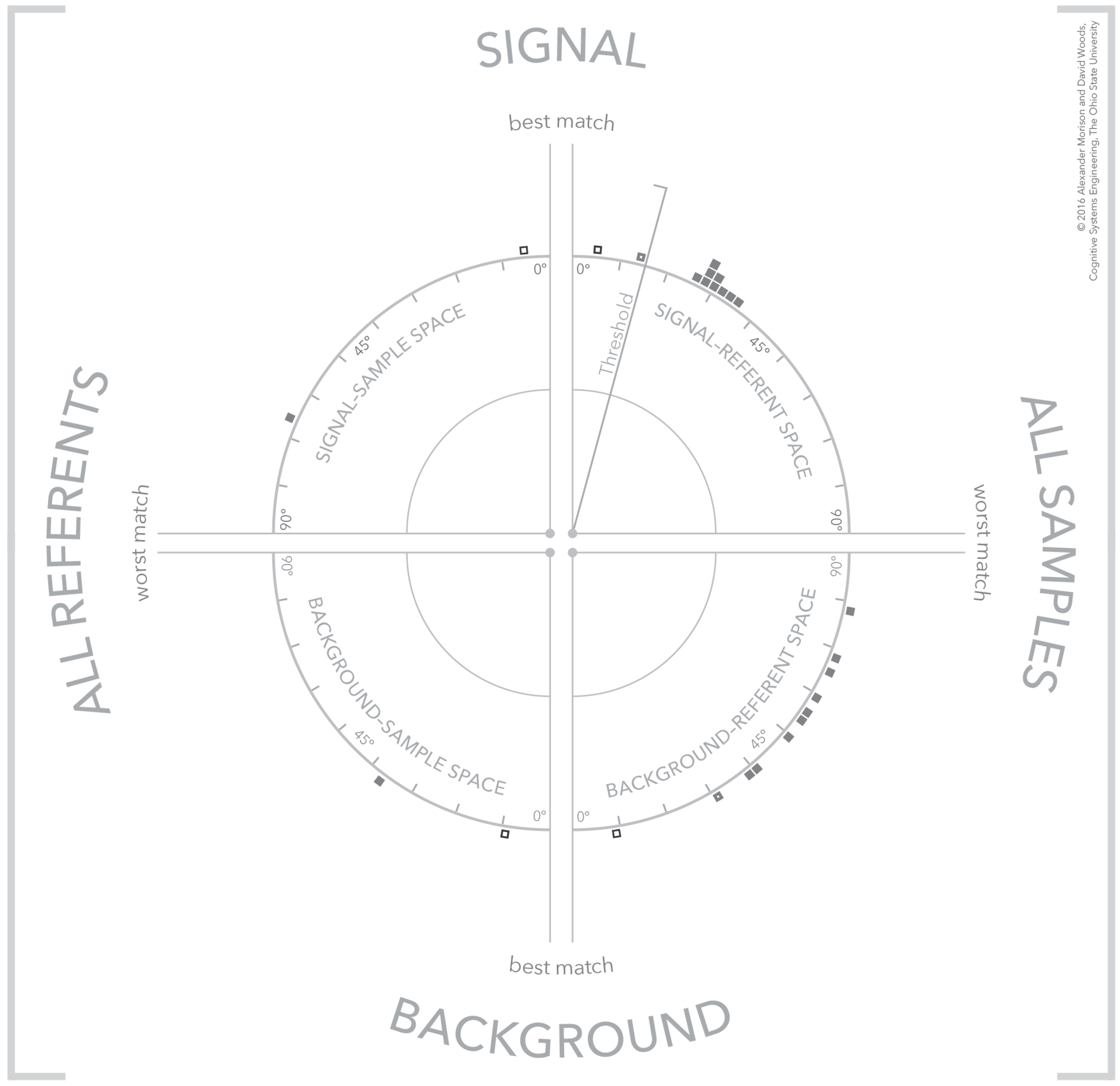
4. Interactive Visualization of Similarity Spaces
4.1. Relating Visualization to Conceptual Model
4.2. The Visualization Similarity Space
4.3. Visualization Dynamics
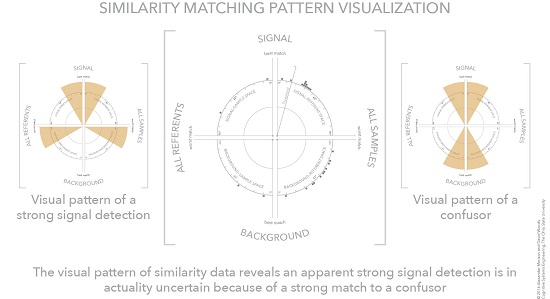
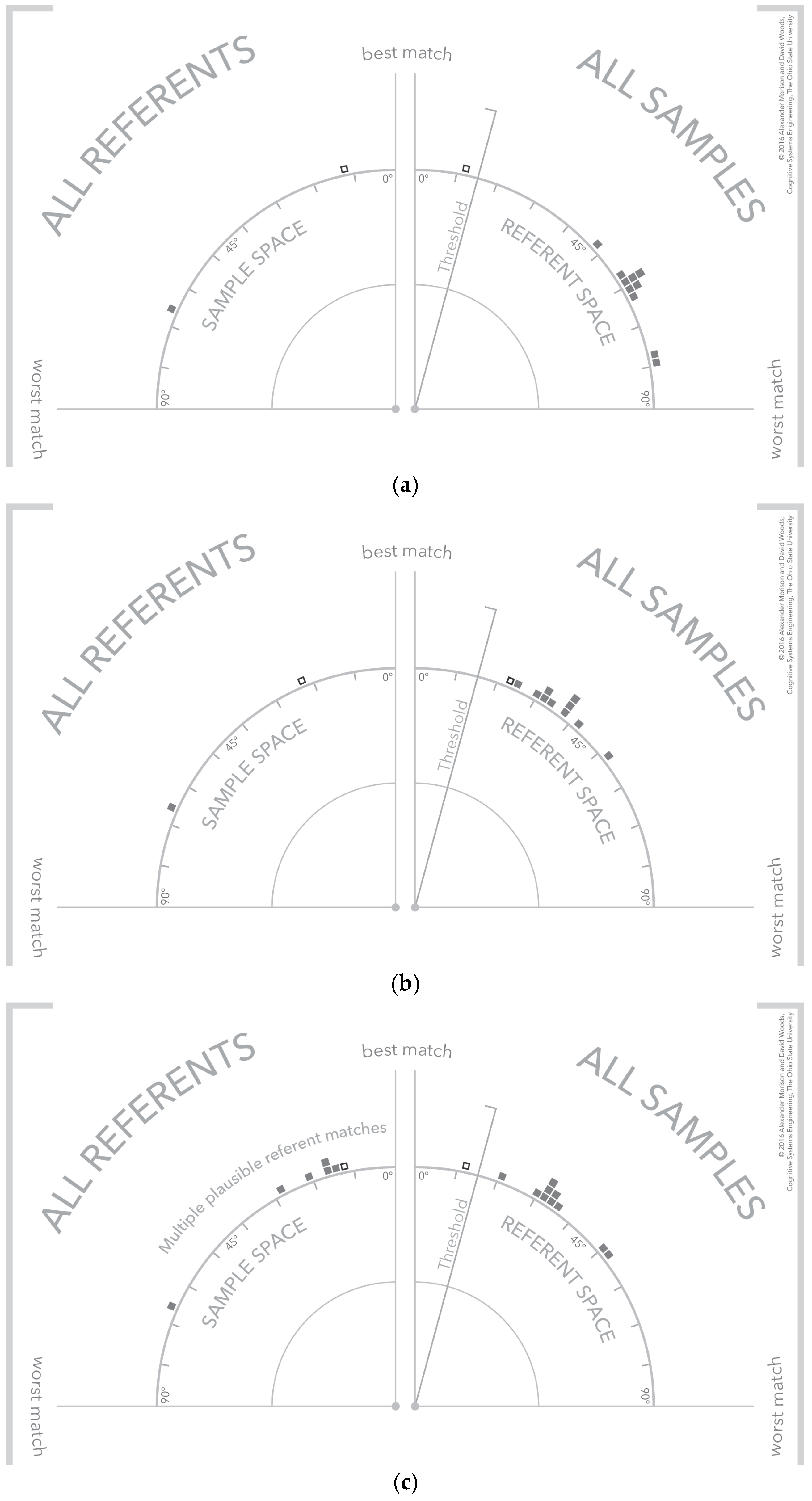
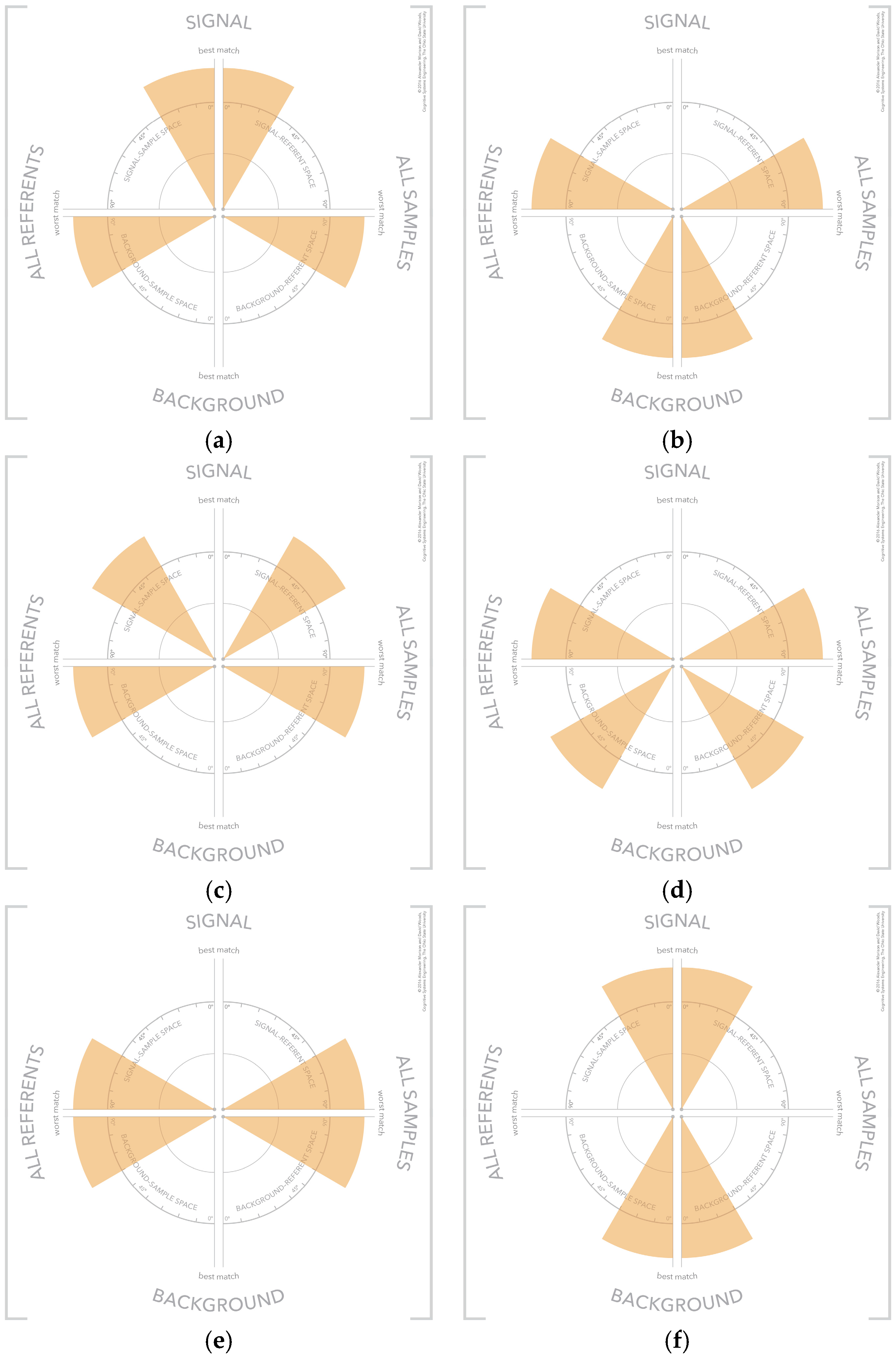
4.4. Visualization Cases—Clear Signal, No Signal, and Signal with Multiple Plausible Matches
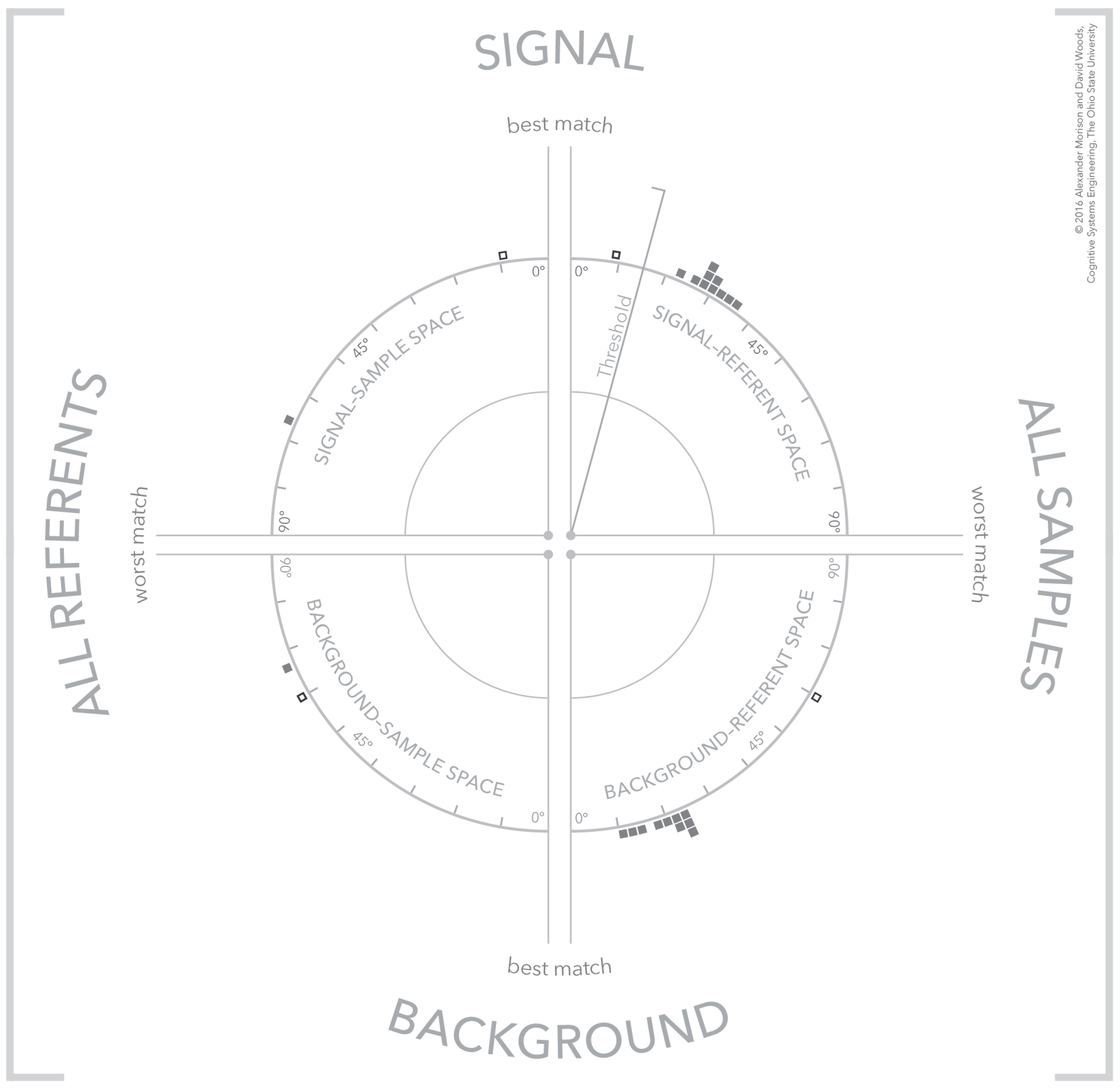
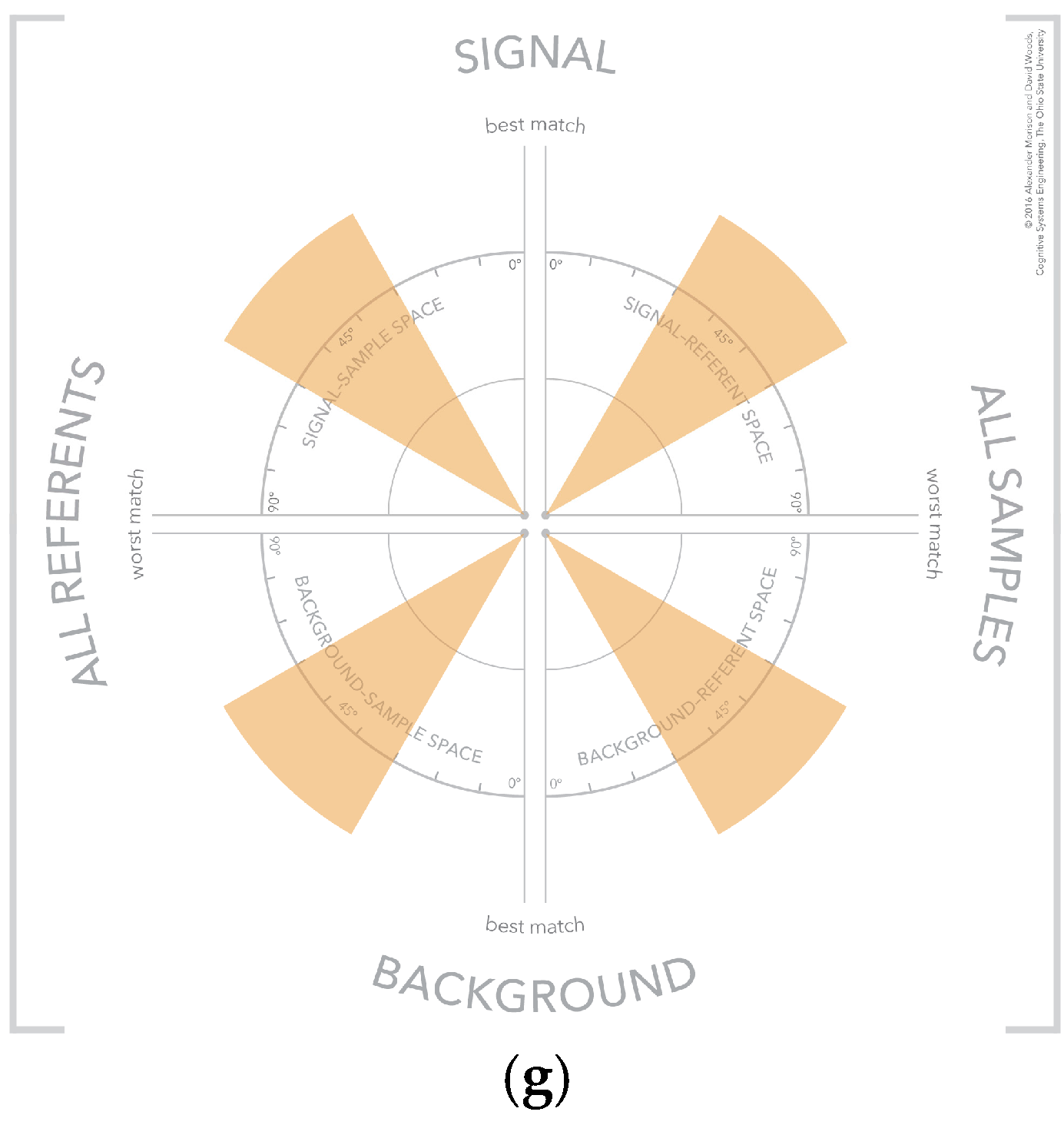
4.5. Separating Signal and Background
4.6. Visual Patterns at Scale
5. Discussion
5.1. An Analogical Representation
5.2. Analogical or Categorical Forms of Representation
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| ISR | Intelligence, Surveillance, and Reconnaissance |
| FMV | Full Motion Video |
| HSA | Hyperspectral Analysis |
| CTA | Cognitive Task Analysis |
| SAM | Spectral Angle Mapper |
References
- Morison, A.; Woods, D.; Murphy, T. Human-Robot Interaction as Extending Human Perception to New Scales. In Cambridge Handbook of Applied Perception Research; Hoffman, R., Hancock, P., Parasuraman, R., Szalma, J., Scerbo, M., Eds.; Cambridge University Press: Cambridge, UK, 2015; pp. 848–868. [Google Scholar]
- Kaisler, S.; Armour, F.; Espinosa, J.A.; Money, W. Big Data: Issues and Challenges Moving Forward. In Proceedings of the 2013 46th Hawaii International Conference on System Sciences (HICSS), Maui, HI, USA, 7–10 January 2013; pp. 995–1004.
- Woods, D.D.; Patterson, E.S.; Roth, E.M. Can We Ever Escape from Data Overload? A Cognitive Systems Diagnosis. Cogn. Technol. Work 2002, 4, 22–36. [Google Scholar] [CrossRef]
- Sonka, M.; Hlavac, V.; Boyle, R. Image Processing, Analysis, and Machine Vision; Cengage Learning: Belmont, CA, USA, 2014. [Google Scholar]
- Jensen, J.R. Introductory Digital Image Processing: A Remote Sensing Perspective; Prentice Hall, Inc.: Old Tappan, NJ, USA, 1986. [Google Scholar]
- Ekbia, H.; Mattioli, M.; Kouper, I.; Arave, G.; Ghazinejad, A.; Bowman, T.; Suri, V.R.; Tsou, A.; Weingart, S.; Sugimoto, C.R. Big Data, Bigger Dilemmas: A Critical Review. J. Assoc. Inf. Sci. Technol. 2015, 66, 1523–1545. [Google Scholar] [CrossRef]
- Chang, C.-I.; Du, Q. Estimation of Number of Spectrally Distinct Signal Sources in Hyperspectral Imagery. IEEE Trans. Geosci. Remote Sens. 2004, 42, 608–619. [Google Scholar] [CrossRef]
- Sorkin, R.D.; Woods, D.D. Systems with Human Monitors: A Signal Detection Analysis. Hum.-Comput. Interact. 1985, 1, 49–75. [Google Scholar] [CrossRef]
- Murphy, R.; Shields, J. The Role of Autonomy in DoD Systems. Available online: https://fas.org/irp/agency/dod/dsb/autonomy.pdf. (accessed on 5 February 2016).
- Smith, P.J.; McCoy, C.E.; Layton, C. Brittleness in the Design of Cooperative Problem-Solving Systems: The Effects on User Performance. IEEE Trans. Syst. Man Cybern. Part Syst. Hum. 1997, 27, 360–371. [Google Scholar] [CrossRef]
- Klein, G.; Woods, D.D.; Bradshaw, J.M.; Hoffman, R.R.; Feltovich, P.J. Ten Challenges for Making Automation a “Team Player” in Joint Human-Agent Activity. IEEE Intell. Syst. 2004, 19, 91–95. [Google Scholar] [CrossRef]
- Crandall, B.; Klein, G.A.; Hoffman, R.R. Working Minds: A Practitioner’s Guide to Cognitive Task Analysis; MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Shaw, G.; Manolakis, D. Signal Processing for Hyperspectral Image Exploitation. IEEE Signal Process. Mag. 2002, 19, 12–16. [Google Scholar] [CrossRef]
- Cook, K.A.; Thomas, J.J. Illuminating the Path: The Research and Development Agenda for Visual Analytics; Pacific Northwest National Laboratory (PNNL): Richland, WA, USA, 2005.
- Keim, D.; Andrienko, G.; Fekete, J.-D.; Görg, C.; Kohlhammer, J.; Melançon, G. Visual analytics: Definition, process, and challenges. In Information Visualization; Springer: Heidelberg, Germany, 2008; pp. 154–175. [Google Scholar]
- Hutchins, E. Cognition in the Wild; The MIT Press: Cambridge, MA, USA, 1995. [Google Scholar]
- De Keyser, V. Why Field Studies. In Design for Manufacturability: A Systems Approach to Concurrent Engineering in Ergonomics; Taylor & Francis: London, UK, 1992; pp. 305–316. [Google Scholar]
- Flanagan, J.C. The Critical Incident Technique. Psychol. Bull. 1954, 51, 327–358. [Google Scholar] [CrossRef] [PubMed]
- Hoffman, R.; Shadbolt, N.; Burton, A.; Klein, G.A. Eliciting Knowledge from Experts: A Methodological Analysis. Organ. Behav. Hum. Decis. Process. 1995, 62, 129–158. [Google Scholar] [CrossRef]
- Trent, S.A.; Patterson, E.S.; Woods, D.D. Challenges for Cognition in Intelligence Analysis. J. Cogn. Eng. Decis. Mak. 2007, 1, 75–97. [Google Scholar] [CrossRef]
- Handel, M.I. Intelligence and the Problem of Strategic Surprise. J. Strateg. Stud. 1984, 7, 229–281. [Google Scholar] [CrossRef]
- Johnson-Laird, P.N. Mental Models and Deduction. Trends Cogn. Sci. 2001, 5, 434–442. [Google Scholar] [CrossRef]
- Norman, D.A. Some Observations on Mental Models. Ment. Models 1983, 7, 7–14. [Google Scholar]
- Cook, R.I.; Potter, S.S.; Woods, D.D.; McDonald, J.S. Evaluating the Human Engineering of Microprocessor-Controlled Operating Room Devices. J. Clin. Monit. 1991, 7, 217–226. [Google Scholar] [CrossRef] [PubMed]
- Woods, D.D. Visual Momentum: A Concept to Improve the Cognitive Coupling of Person and Computer. Int. J. Man-Mach. Stud. 1984, 21, 229–244. [Google Scholar] [CrossRef]
- Yuhas, R.H.; Goetz, A.F.; Boardman, J.W. Discrimination among Semi-Arid Landscape Endmembers Using the Spectral Angle Mapper (SAM) Algorithm. In Proceedings of Summaries 3rd Annual JPL Airborne Geoscience Workshop, Pasadena, CA, USA, 1–5 June 1992; pp. 147–149.
- Clark, R.N.; Swayze, G.; Boardman, J.; Kruse, F. Comparison of Three Methods for Materials Identification and Mapping with Imaging Spectroscopy, 1993. Available online: http://ntrs.nasa.gov/search.jsp?R=19950017433 (accessed on 6 May 2016).
- Harsanyi, J.C.; Chang, C.-I. Hyperspectral Image Classification and Dimensionality Reduction: An Orthogonal Subspace Projection Approach. IEEE Trans. Geosci. Remote Sens. 1994, 32, 779–785. [Google Scholar] [CrossRef]
- Van der Meer, F. The Effectiveness of Spectral Similarity Measures for the Analysis of Hyperspectral Imagery. Int. J. Appl. Earth Obs. Geoinformation 2006, 8, 3–17. [Google Scholar] [CrossRef]
- Card, S.K.; Mackinlay, J.D.; Shneiderman, B. Readings in Information Visualization: Using Vision to Think; Morgan Kaufmann: San Fransisco, CA, USA, 1999. [Google Scholar]
- Inselberg, A.; Dimsdale, B. Parallel coordinates. In Human-Machine Interactive Systems; Plenum Press: New York, NY, USA, 1991; pp. 199–233. [Google Scholar]
- Heinrich, J.; Weiskopf, D. State of the Art of Parallel Coordinates. STAR Proc. Eurograph. 2013, 2013, 95–116. [Google Scholar]
- Ware, C. Information Visualization: Perception for Design, 3rd ed.; Morgan Kaufmann: Waltham, MA, USA, 2012. [Google Scholar]
- Bennett, K.; Toms, M.; Woods, D. Emergent Features and Graphical Elements—Designing More Effective Configural Displays. Hum. Factors 1993, 35, 71–97. [Google Scholar]
- Bennett, K.B.; Flach, J.M. Graphical Displays: Implications for Divided Attention, Focused Attention, and Problem Solving. Hum. Factors 1992, 34, 513–533. [Google Scholar] [PubMed]
- Dunbar, K. Concept Discovery in a Scientific Domain. Cogn. Sci. 1993, 17, 397–434. [Google Scholar] [CrossRef]


© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morison, A.M.; Woods, D.D. Opening up the Black Box of Sensor Processing Algorithms through New Visualizations. Informatics 2016, 3, 16. https://doi.org/10.3390/informatics3030016
Morison AM, Woods DD. Opening up the Black Box of Sensor Processing Algorithms through New Visualizations. Informatics. 2016; 3(3):16. https://doi.org/10.3390/informatics3030016
Chicago/Turabian StyleMorison, Alexander M., and David D. Woods. 2016. "Opening up the Black Box of Sensor Processing Algorithms through New Visualizations" Informatics 3, no. 3: 16. https://doi.org/10.3390/informatics3030016
APA StyleMorison, A. M., & Woods, D. D. (2016). Opening up the Black Box of Sensor Processing Algorithms through New Visualizations. Informatics, 3(3), 16. https://doi.org/10.3390/informatics3030016