Tagging Users’ Social Circles via Multiple Linear Regression
Abstract
:1. Introduction
2. Related Work
2.1. Social Circle
2.2. Tag Detection
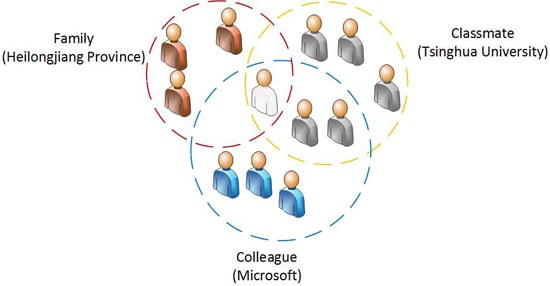
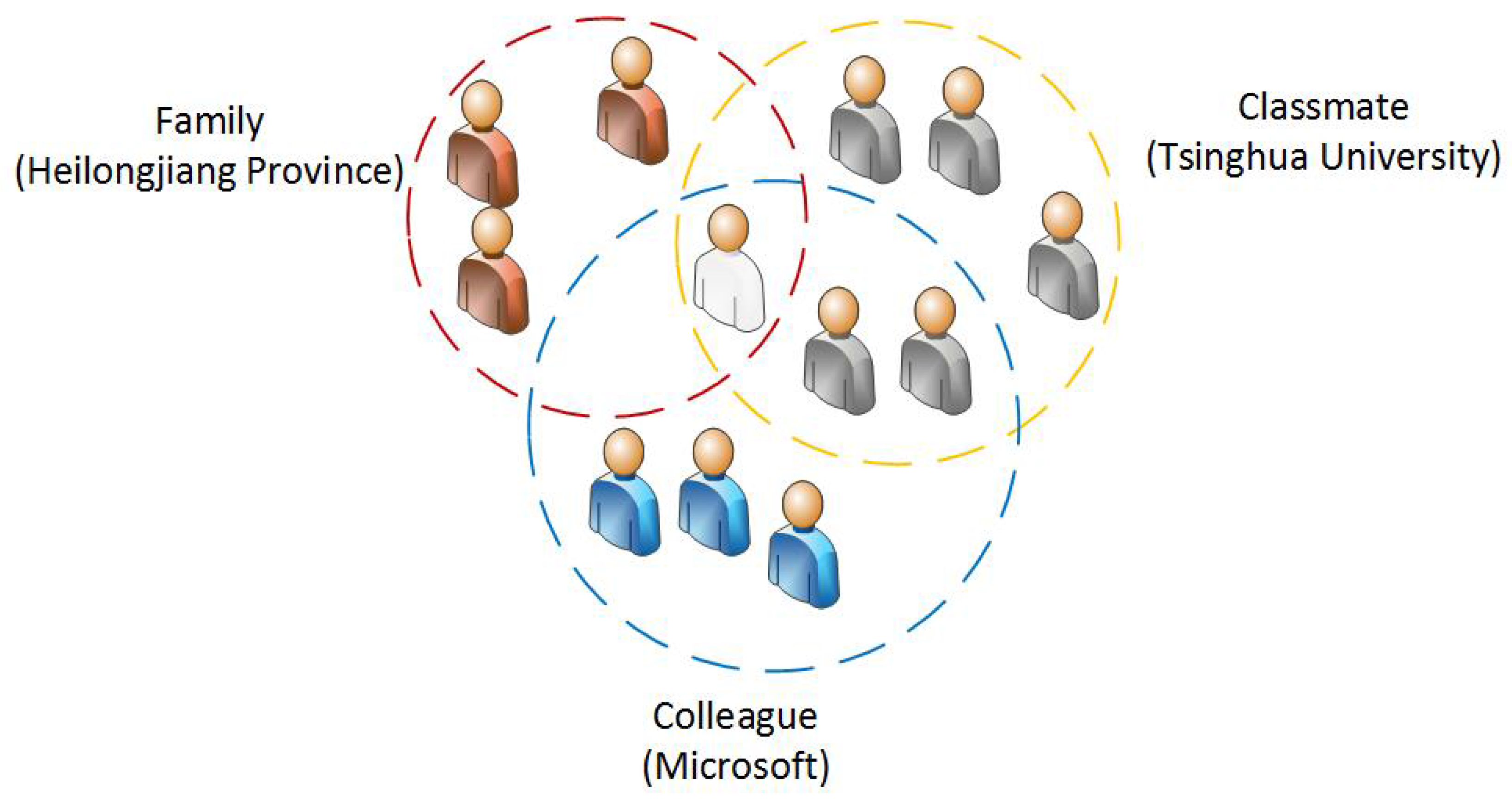
3. Tag Detection of Social Circles
3.1. Overview
3.2. Features
- (1)
- Percentage of members who own the tagt is a tag and is the amount of members who own this tag.
- (2)
- The members’ average centrality who own the tagu is a circle member who owns the tag, is the number of this user’s friends in the circle.
- (3)
- The tag’s TF (Term Frequency) value in a circleIn our work, we regard the set of all members’ tags in a social circle as a document, and every tag in the set as a word of this document. For example, a user has two tags user:id:27 and school:id:10. The two items are words and all members’ words constitute the tag document of this social circle. Count(tag) is the amount of a tag item in the circle.
- (4)
- The tag’s IDF (Inverse Document Frequency) value in a circle
- (5)
- The tag’s TF-IDF value
- (6)
- If only one user owns the tagIf only one user owns this tag, is 1, otherwise, this is 0.
- (7)
- If only one social circle owns the tagIf only one social circle owns this tag, is 1, otherwise, is 0.
- (8)
- Prefix of the tagSome tags cannot be tags of social circles since they can only belong to a single user, such as user:id. We filter types of all tags and if a tag might be a social circle’s tag, is 1, otherwise, is 0.
3.3. Multiple Linear Regression
4. Experiment
4.1. Dataset
4.2. Baseline
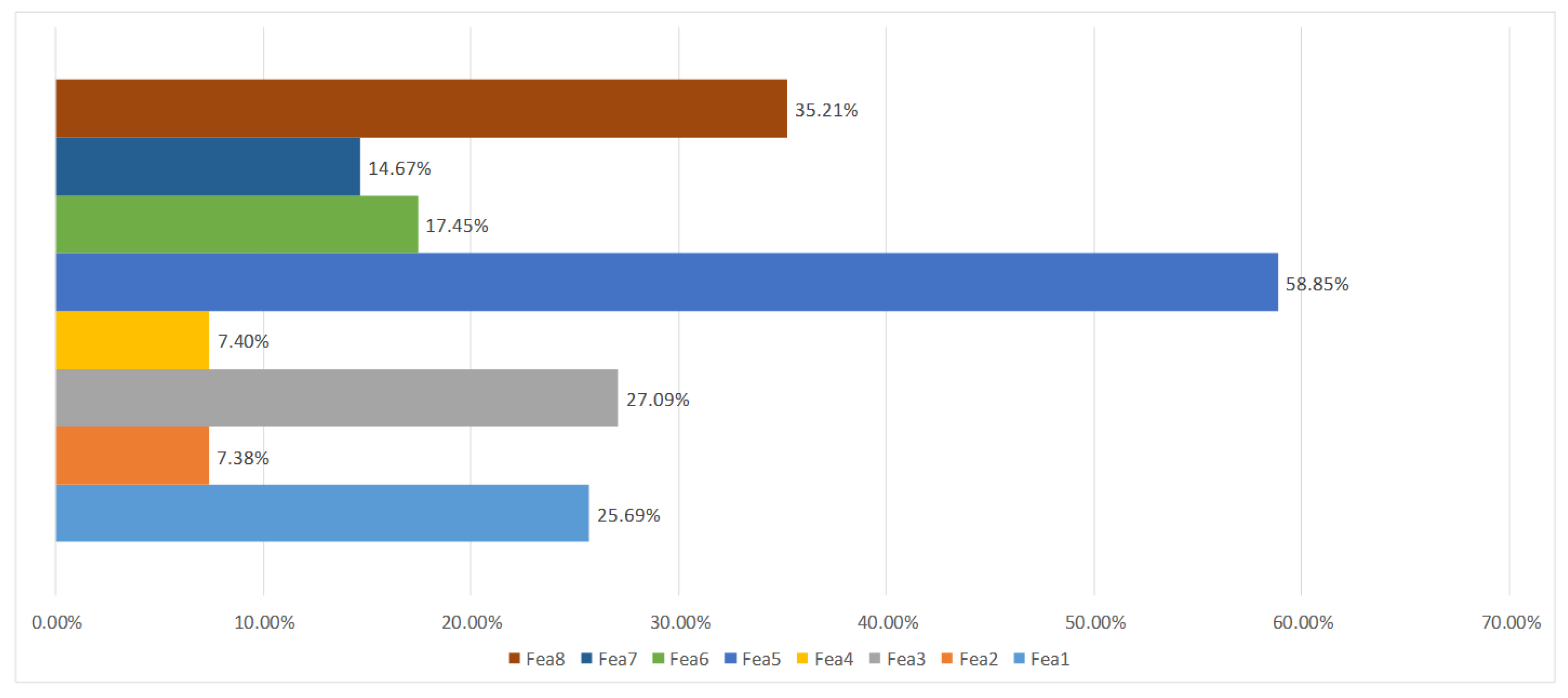
4.3. Result Analysis
5. Conclusion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ajzen, I.; Fishbein, M. Understanding Attitudes and Predicting Social Behaviour; Pearson: London, UK, 1980. [Google Scholar]
- Roserberg, M. Society and the Adolescent Self-Image, revised edition; Wesleyan University Press: Middletown, CT, USA, 1989. [Google Scholar]
- Yen, I.H.; Syme, S.L. The social environment and health: A discussion of the epidemiologic literature. Ann. Rev. Public Health 1999, 20, 287–308. [Google Scholar] [CrossRef] [PubMed]
- Ståhl, T.; Rütten, A.; Nutbeam, D.; Bauman, A.; Kannas, L.; Abel, T.; Lüschen, G.; Rodriquez, D.J.; Vinck, J.; van der Zee, J. The importance of the social environment for physically active lifestyle—Results from an international study. Soc. Sci. Med. 2001, 52, 1–10. [Google Scholar] [CrossRef]
- Wei, C. Formation of Norms in a Blog Community; University of Minnesota: Saint Paul, MN, USA, 2004. [Google Scholar]
- Goldberg, M.; Kelley, S.; Magdon-Ismail, M.; Mertsalov, K.; Wallace, A. Finding overlapping communities in social networks. In Proceedings of the 2010 IEEE Second International Conference on Social Computing (SocialCom), Minneapolis, MN, USA, 20–22 August 2010; pp. 104–113.
- De Klepper, M.; Sleebos, E.; van de Bunt, G.; Agneessens, F. Similarity in friendship networks: Selection or influence? The effect of constraining contexts and non-visible individual attributes. Soc. Netw. 2010, 32, 82–90. [Google Scholar] [CrossRef]
- Girvan, M.; Newman, M.E. Community structure in social and biological networks. Proc. Natl. Acad. Sci. USA 2002, 99, 7821–7826. [Google Scholar] [CrossRef] [PubMed]
- Granovetter, M.S. The strength of weak ties. Am. J. Soc. 1973, 78, 1360–1380. [Google Scholar] [CrossRef]
- Ferrara, E.; de Meo, P.; Fiumara, G.; Provetti, A. The role of strong and weak ties in Facebook: A community structure perspective. Commun. ACM 2012. [Google Scholar] [CrossRef]
- Petróczi, A.; Nepusz, T.; Bazsó, F. Measuring tie-strength in virtual social networks. Connections 2007, 27, 39–52. [Google Scholar]
- Gilbert, E.; Karahalios, K. Predicting tie strength with social media. In Proceedings of the SIGCHI Conference on Human Factors in Computing Systems, ACM, Boston, MA, USA, 4–9 April 2009; pp. 211–220.
- Burton, S.H.; Giraud-Carrier, C.G. Discovering social circles in directed graphs. ACM Trans. Knowl. Discov. Data 2014, 8, 21. [Google Scholar] [CrossRef]
- Leskovec, J.; Mcauley, J.J. Learning to discover social circles in ego networks. In Proceedings of the Twenty-Sixth Annual Conference on Neural Information Processing Systems (NIPS), Lake Tahoe, CA, USA, 3–8 December 2012; pp. 539–547.
- Qin, H.; Liu, T.; Ma, Y. Mining User’s Real Social Circle in Microblog. In Proceedings of the 2012 International Conference on Advances in Social Networks Analysis and Mining (ASONAM 2012), Istanbul, Turkey, 26–29 August 2012; pp. 348–352.
- Liu, T.; Qin, H. Detecting and tagging users’ social circles in social media. Multimed. Sys. 2014, 22. [Google Scholar] [CrossRef]
- Wang, M.; Morrison, D.; Hayes, C. Information fusion methods for the automatic creation of Twitter lists. Int. J. Soc. Netw. Min. 2015, 2, 19–43. [Google Scholar] [CrossRef]
- Gusfield, J.R. Community: A Critical Response; Harper & Row: New York, NY, USA, 1975. [Google Scholar]
- Sharma, A.; Gemici, M.; Cosley, D. Friends, strangers, and the value of ego networks for recommendation. In Proceedings of the 7th International AAAI Conference on Weblogs and Social Media, Boston, MA, USA, 8–10 July 2013.
- Liu, T.; Zhang, W.N.; Zhang, Y. SocialRobot: A big data-driven humanoid intelligent system in social media services. Multimed. Syst. 2014, 22. [Google Scholar] [CrossRef]
- Liu, T.; Zhang, W.N.; Cao, L.; Zhang, Y. Question Popularity Analysis and Prediction in Community Question Answering Services. PloS ONE 2014, 9, e85236. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Zhang, F.; Song, X.; Song, Y.I.; Lin, C.Y.; Hon, H.W. What’s in a name? An unsupervised approach to link users across communities. In Proceedings of the Sixth ACM International Conference on Web Search and Data Mining, Rome, Italy, 4–8 February 2013; pp. 495–504.
- Huberman, B.A.; Romero, D.M.; Wu, F. Social networks that matter: Twitter under the microscope. First Monday 2009, 14, 1–5. [Google Scholar]
- Kairam, S.R.; Wang, D.J.; Leskovec, J. The life and death of online groups: Predicting group growth and longevity. In Proceedings of the Fifth ACM International Conference on Web Search and Data Mining, Washington, DC, USA, 8–12 February 2012; pp. 673–682.
- Qu, Z.; Liu, Y. Interactive group suggesting for Twitter. In HLT-Short ’08 Proceedings of the 49th Annual Meeting of the Association for Computational Linguistics on Human Language Technologies: Short Papers; Association for Computational Linguistics: Stroudsburg, PA, USA, 2011; Volume 2, pp. 519–523. [Google Scholar]
- Kairam, S.; Brzozowski, M.; Huffaker, D.; Chi, E. Talking in circles: Selective sharing in Google+. In Proceedings of the SIGCHI Conference on Human Factors in Computing Systems; ACM: New York, NY, USA, 2012; pp. 1065–1074. [Google Scholar]
- Savage, S.; Forbes, A.; Toxtli, C.; McKenzie, G.; Desai, S.; Höllerer, T. Visualizing targeted audiences. In Proceedings of the 11th International Conference on the Design of Cooperative Systems (COOP 2014), Nice, France, 27–30 May 2014; pp. 17–34.
- Huang, J.; Thornton, K.M.; Efthimiadis, E.N. Conversational tagging in Twitter. In Proceedings of the 21st ACM Conference on Hypertext and Hypermedia; ACM: New York, NY, USA, 2010; pp. 173–178. [Google Scholar]
- Salton, G.; Buckley, C. Term-weighting approaches in automatic text retrieval. Inf. Process. Manag. 1988, 24, 513–523. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, X.; Sun, M. Mining the interests of Chinese microbloggers via keyword extraction. Front. Comput. Sci. 2012, 6, 76–87. [Google Scholar]
- Wang, X.; Zhai, C.; Roth, D. Understanding Evolution of Research Themes: A Probabilistic Generative Model for Citations. In Proceedings of the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining; ACM: New York, NY, USA, 2013; pp. 1115–1123. [Google Scholar]
- He, Q.; Chen, B.; Pei, J.; Qiu, B.; Mitra, P.; Giles, L. Detecting topic evolution in scientific literature: How can citations help? In Proceedings of the 18th ACM Conference on Information and Knowledge Management; ACM: New York, NY, USA, 2009; pp. 957–966. [Google Scholar]
- Lu, Z.; Mamoulis, N.; Cheung, D.W. A Collective Topic Model for Milestone Paper Discovery. In Proceedings of the 37th International ACM SIGIR Conference on Research & Development in Information Retrieval; ACM: New York, NY, USA, 2014; pp. 1019–1022. [Google Scholar]
- Chang, J.; Blei, D.M. Relational topic models for document networks. In Proceedings of the Twelfth International Conference on Artificial Intelligence and Statistics, Clearwater, FL, USA, 16–19 April 2009; pp. 81–88.
- Nallapati, R.M.; Ahmed, A.; Xing, E.P.; Cohen, W.W. Joint latent topic models for text and citations. In Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining; ACM: New York, NY, USA, 2008; pp. 542–550. [Google Scholar]
- Guo, Z.; Zhang, Z.; Zhu, S.; Chi, Y.; Gong, Y. A Two-Level Topic Model Towards Knowledge Discovery from Citation Networks. IEEE Trans. Knowl. Data Eng. 2014, 26, 780–794. [Google Scholar]
- Bolelli, L.; Ertekin, S.; Giles, C.L. Clustering scientific literature using sparse citation graph analysis. In Knowledge Discovery in Databases: PKDD 2006; Springer: Berlin Heidelberg, Germany, 2006; pp. 30–41. [Google Scholar]
- Learning Social Circles in Networks. Available online: https://www.kaggle.com/c/learning-social-circles/data (accessed on 15 December 2015).
- Microsoft Academic Search. Available online: http://libra.msra.cn/ (accessed on 15 December 2015).
| last_name, first_name, birthday, name, gender |
| locale, hometown-name, hometown-id, education-school-name, education-school-id |
| education-type, education-year-name, education-year-id, education-concentration-name |
| education-concentration-id, id, location-name, location-id, education-classes-from-name |
| education-classes-from-id, education-classes-with-name, education-classes-with-id |
| education-classes-name education-classes-id, work-position-name work-position-id |
| work-start_date, work-end_date work-employer-name, work-employer-id |
| work-location-name, work-location-id, languages-name, languages-id |
| middle_name, work-projects-name, work-projects-id, education-with-name |
| education-with-id, work-projects-with-name, work-projects-with-id, work-description |
| education-degree-name, education-degree-id, work-projects-start_date, work-with-name |
| work-with-id, work-projects-from-name, work-projects-from-id |
| education-classes-description, work-from-name, work-from-id, political, religion |
| work-projects-end_date, work-projects-description, location |
| Microsoft Academic Search | |||
| Popular | P@10 | 28.29% | N/A |
| FKE | P@10 | 12.01% | 15.08% |
| TF-IDF | P@10 | 60.02% | 17.10% |
| Multiple Linear Regression | P@10 | 71.54% | 40.63% |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, H.; Liu, J.; Lin, C.-Y.; Liu, T. Tagging Users’ Social Circles via Multiple Linear Regression. Informatics 2016, 3, 10. https://doi.org/10.3390/informatics3030010
Qin H, Liu J, Lin C-Y, Liu T. Tagging Users’ Social Circles via Multiple Linear Regression. Informatics. 2016; 3(3):10. https://doi.org/10.3390/informatics3030010
Chicago/Turabian StyleQin, Hailong, Jing Liu, Chin-Yew Lin, and Ting Liu. 2016. "Tagging Users’ Social Circles via Multiple Linear Regression" Informatics 3, no. 3: 10. https://doi.org/10.3390/informatics3030010
APA StyleQin, H., Liu, J., Lin, C.-Y., & Liu, T. (2016). Tagging Users’ Social Circles via Multiple Linear Regression. Informatics, 3(3), 10. https://doi.org/10.3390/informatics3030010