Deep Learning-Based Forecasting of Boarding Patient Counts to Address Emergency Department Overcrowding

Abstract

Emergency department (ED) overcrowding remains a major challenge for hospitals, resulting in worse outcomes, longer waits, elevated hospital operating costs, and greater strain on staff. Boarding count, the number of patients who have been admitted to an inpatient unit but are still in the ED waiting for transfer, is a key patient flow metric that affects overall ED operations. This study presents a deep learning-based approach to forecasting ED boarding counts using only operational and contextual features—derived from hourly ED tracking, inpatient census, weather, holiday, and local event data—without patient-level clinical information. Different deep learning algorithms were tested, including convolutional and transformer-based time-series models, and the best-performing model, Time Series Transformer Plus (TSTPlus), achieved strong performance at the 6-h prediction horizon, with a mean absolute error of 4.30 and an R² score of 0.79. After identifying TSTPlus as the best-performing model, its performance was further evaluated at additional horizons of 8, 10, and 12 h. The model was also evaluated under extreme operational conditions, demonstrating robust and accurate forecasts. These findings highlight the potential of the proposed forecasting approach to support proactive operational planning and reduce ED overcrowding.

1. Introduction

Emergency Department (ED) overcrowding continues to be a significant challenge in hospital operations, negatively impacting patient outcomes, extending wait times, increasing healthcare costs, and even increasing violence against healthcare staff [1,2]. A commonly used strategy for improving patient movement throughout hospitals is the Full Capacity Protocol (FCP), which has received recognition from the American College of Emergency Physicians (ACEP) as an effective framework for addressing operational challenges in emergency departments [3]. FCP serves as a hospital-wide communication and escalation framework between the ED and inpatient units and includes a tiered set of interventions aligned with varying levels of crowding severity. These intervention levels are triggered by specific Patient Flow Measure (PFM) metrics, also referred to in the literature as Key Performance Indicators (KPIs) [4], which reflect the operational pressure within the ED. Key PFMs influencing ED overcrowding cover the entire patient journey—from initial registration to the end of the boarding period—and encompass factors both within the ED and in the broader hospital environment. Mehrolhassani et al. [4] conducted a comprehensive scoping review of 125 studies, and identified 109 unique PFMs used to evaluate ED operations. The identified measures included key flow-related indicators such as treatment time, waiting time, boarding time, boarding count, triage time, registration time, diagnostic turnaround times (e.g., x-rays and lab results), etc. These represent just a subset of the many metrics used to monitor and improve ED performance. This study focuses specifically on the boarding process, which occurs when patients are admitted to the hospital but remain in the ED while awaiting an inpatient bed. This phase is widely recognized as one of the major causes of ED congestion, as boarded patients occupy treatment spaces and consume critical resources that could otherwise be used for incoming cases [5,6,7].

Boarding count refers to the number of patients who have received an admission decision—typically marked by an Admit Bed Request in the ED—but remain physically present in the ED while waiting for transfer to an inpatient unit [8]. Studies have investigated the impact of boarding on both patient outcomes and hospital operations. Su et al. [9] employed an instrumental variable approach to quantify the causal effects of boarding, reporting that each additional hour was associated with a 0.8% increase in hospital length of stay, a 16.7% increase in the odds of requiring escalated care, and a 1.3% increase in total hospital charges. Salehi et al. [10] conducted a retrospective analysis at a high-volume Canadian hospital and found that patients admitted to the medicine service had a mean ED length of stay of 25.6 h and a mean time to bed of 15.9 h. Older age, comorbidities, and isolation or telemetry requirements were significantly associated with longer boarding times, which in turn led to approximately a 0.9-day increase in inpatient length of stay after adjustment for confounders. Joseph et al. [11] found that longer ED boarding durations were independently associated with an increased risk of developing delirium or severe agitation during hospitalization, especially among older adults and those with dementia. Yiadom et al. [12] note that keeping admitted patients in the ED due to a lack of available inpatient beds puts considerable pressure on ED operations and is a leading cause of crowding and bottlenecks in patient movement. Boulain et al. [13] also reported that, in their matched cohort analysis, patients who experienced ED boarding times greater than 4 h had a significantly higher risk of hospital mortality. Loke et al. [14] reported that extended ED boarding is associated with high rates of verbal abuse toward staff—experienced by 87% of nurses and 41% of providers—and contributes to clinician burnout and dissatisfaction. All the mentioned studies show that inadequate management of the boarding process causes a longer length of stay, negatively affects patient health, could increase mortality, contributes to overcrowding, and leads to burnout and verbal abuse of ED employees.

Several studies have addressed ED overcrowding by modeling or predicting boarding by using both statistical and machine learning approaches. For example, Cheng et al. [15] developed a linear regression model to estimate the staffed bed deficit—defined as the difference between the number of ED boarders and available staffed inpatient beds—using real-time data on boarding count, bed availability, pending consults, and discharge orders. Their model predicts the number of beds needed 4 h in advance of each shift change. However, the model uses limited features, cannot capture nonlinear patterns due to its linear regression design, and is constrained by a short 4-h prediction window. Hoot et al. [16] introduced a discrete-event simulation model to forecast several ED crowding metrics, including boarding count, boarding time, waiting count, and occupancy level, at 2, 4, 6, and 8-h intervals. The model, which used 6 patient-level features, achieved a Pearson correlation of 0.84 when forecasting boarding count 6 h into the future. However, this approach does not employ machine learning; it is based on simulation techniques rather than data-driven predictive modeling. More recent studies have leveraged machine learning to enable earlier predictions. Suley [17] developed predictive models to forecast boarding counts 1–6 h ahead, using multiple machine learning approaches, with Random Forest regression achieving the best performance. They demonstrated that when boarding levels exceed 60% of ED capacity, average length of stay increases from 195 to 224 min (min). However, these findings were based on agent-based simulation modeling rather than real hospital data, which may not reflect actual ED operations. Additionally, the study lacks key descriptives (e.g., mean, standard deviation of hourly boarding counts), limiting full performance evaluation. Kim et al. [18] used data collected within the first 20 min of ED patient arrival—including vital signs, demographics, triage level, and chief complaints—to predict ED hospitalization, employing five models: logistic regression, XGBoost, NGBoost, support vector machines (SVMs), and decision trees. At 95% specificity, their approach reduced ED length of stay by an average of 12.3 min per patient, totaling over 340,000 min annually. Unlike our study, which leverages aggregate operational data along with contextual features, their approach relies on early patient-level clinical information and employs traditional machine learning methods. Similarly, Lee et al. [19] modeled early disposition prediction as a hierarchical multiclass classification task using patient-level ED data, including lab results and clinical features available approximately 2.5 h prior to disposition. This model aims to reduce boarding delays, but relies on patient-level clinical data, which is labor-intensive to collect, subject to privacy constraints, and often inconsistent across hospitals—limiting its scalability and real-time applicability. The short and variable prediction window, triggered only after lab results, may limit its effectiveness for enabling proactive resource allocation and operational decision-making.

Most existing models rely on a narrow set of input features, often limited to internal ED data. In contrast, this study integrates a wider range of features, combining operational indicators with contextual variables such as weather conditions and significant events (e.g., holidays and football games), which originate outside of the hospital system. Many prior models also depend on patient-level clinical data, including vital signs, chief complaints, demographics, diagnoses, ED laboratory results, and past medical history, which require extensive data sharing and raise privacy and regulatory concerns. Our approach is fundamentally different: it does not use patient-level clinical data but instead relies solely on aggregate operational data—structured, time-stamped numerical indicators that reflect system-level dynamics. The proposed design simplifies data integration and enhances model generalizability across settings. Additionally, to our knowledge, there is no existing model that performs hourly boarding count prediction using real-world data from US EDs with deep learning models, and there remains a clear research gap in this area. It is hypothesized that a deep learning-based framework leveraging aggregate operational features can accurately forecast ED boarding counts across multiple prediction horizons, providing actionable insights that enable proactive management of ED resources and mitigation of overcrowding. The results are intended to proactively inform FCP activation and serve as inputs to a clinical decision support system, enabling more timely and informed operational responses.

We developed a predictive model to estimate boarding count at multiple future horizons (6, 8, 10, and 12 h) using real-world data from a partner hospital located in Alabama, United States of America, relying solely on ED operational flow and external features, without incorporating patient-level clinical data. During this study, we worked closely with an advisory board consisting of representatives from various emergency department teams at our collaborating hospital. Based on recommendations from our advisory board and prior research identifying a 6-h window as a critical threshold for boarding interventions [17], we evaluated four prediction horizons (6, 8, 10, and 12 h) to balance early-warning capability with operational feasibility. As part of our contribution, we perform extensive feature engineering to derive key flow-based variables—such as waiting count, waiting time, treatment count, treatment time, boarding count, boarding time, and hospital census—that are not directly observable in the raw data. We also construct and evaluate multiple datasets with different combinations of these features, to identify the most effective input configuration for prediction. Then we implement deep learning models with automated hyperparameter optimization, enabling dynamic definition of search spaces and efficient trial pruning. To enhance model interpretability, we applied three complementary approaches: (1) Input Weight Norm analysis [20] to estimate feature importance, based on the magnitude of learned embedding weights, (2) attention analysis of the transformer-based deep learning model [21] to visualize temporal focus patterns learned during prediction, and (3) Gradient Shapley Additive Explanations (Gradient SHAP) [22] to quantify each input feature’s contribution through sensitivity-based attribution scores. Moreover, because our method does not use sensitive patient-level information, the approach is easier to implement and more adaptable to different hospital systems, though models must still be trained on each institution’s data. Overall, the proposed framework offers three key innovations. First, it leverages only aggregate operational and contextual data, enhanced through extensive feature engineering to derive critical PFMs that were not directly available from the raw inputs. Second, it performs multi-horizon forecasting using real-world hospital data to enable proactive, real-time ED resource management before critical thresholds are reached. Third, it promotes interpretability through feature design and attention-based analysis, demonstrates generalizability by avoiding patient-level data, and assesses extreme-case performance across different crowding scenarios.

2. Materials and Methods

The methodological workflow of this study comprises several key stages designed to develop a reliable model for predicting boarding count. The process begins with the collection of multi-source data that captures both internal ED operations and external contextual factors. Next, feature engineering is applied separately to each data source, with a focus on creating patient flow metrics to derive informative variables. Following preprocessing steps such as cleaning, categorization, and normalization, all data sources are merged into a unified dataset at an hourly resolution.

Table 1. Data Description Table.

Feature	Date Range, Average ± Standard Deviation (Range) for Numerical Features, % for Categorical Features, and Event Counts
Date Range
Year	5 years
Month	12 Months
Day of Month	Days 1–31
Day of Week	7 Days
Hour	24 h
Boarding Count (Target Variable)	28.7± 11.2 (0–73)
Boarding Count by ESI Levels
ESI levels 1and 2        ESI level 3	17.2 ± 7.5 (0–52) 11.4 ± 5.5 (0–37)
ESI levels 4 and 5	0.1 ± 0.4 (0–5)
Average Boarding Time	621 ± 295.8 (0–2446) (minutes)
Waiting Count	18 ± 10 (0–65)
Waiting Count by ESI Levels
ESI levels 1and 2	4.7 ± 3.9 (0–24)
ESI level 3	10.6 ± 6.7 (0–46)
ESI levels 4 and 5	2.5 ± 2.2 (0–18)
Average Waiting Time	86.7 ± 62.9 (0–425) (minutes)
Treatment Count	53.9 ± 11.7 (5–98)
Average Treatment Time	502.8 ± 196 (71–1643) (minutes)
Extreme-Case Indicator	6361 rows
Hospital Census	788 ± 75 (421–1017)
Temperature	62.84 ± 15.55 (8.3–100) °F
Weather Status
Clouds	60.1%
Clear	22.9%
Rain	15.45%
Thunderstorm	1.22%
Others	0.4%
Football Game 1	54 Games
Football Game 2	49 Games
Federal Holidays	46 Days

shows all the features of the unified hourly dataset together with their descriptive statistics. Using this unified dataset, five distinct datasets are created based on different feature combinations, as shown in

Table 2. Summary Statistics of Hourly Features Used in Model Training and Testing.

Data Sources	Features	Lags and Rolling Mean	DS1	DS2	DS3	DS4	DS5
ED Tracking	Boarding Count (Target)	Lags (W = 12)	X	X	X	X
		Lags (W = 24)					X
		Rolling Mean (W = 4)				X	X
	Average Boarding Time	No Lags		X	X	X
		Lags (W = 12)					X
	Treatment Count	No Lags		X	X	X
		Lags (W = 12)					X
	Waiting Count	No Lags		X	X	X
		Lags (W = 12)					X
	Boarding Count by ESI Levels					X	X
	Waiting Count by ESI Levels					X	X
	Average Treatment Time			X	X	X	X
	Average Waiting Time			X	X	X	X
	Extreme-Case Indicator			X	X	X	X
	Year, Month, Day of the Month, Day of the Week, Hour		X	X	X	X	X
Inpatient	Hospital Census	No Lags		X	X	X
		Lags (W = 12)					X
Weather	Weather Status (five Categories)			X	X	X	X
	Temperature				X	X	X
Holiday	Federal Holiday				X	X	X
Events	Football Game 1				X	X	X
	Football Game 2				X	X	X

. In the subsequent stage, model training is carried out using three deep learning models: Time Series Transformer Plus (TSTPlus) [23], Time Series Vision Transformer Plus (TSiTPlus) [24], and Residual Networks Plus (ResNetPlus) [25].

Following training, model evaluation is performed to assess predictive performance across the constructed datasets, using standard regression metrics. The primary objective is to predict the boarding count 6 h in advance, supporting proactive decision-making to mitigate ED overcrowding. We first identified the best-performing deep learning model using the 6-h prediction horizon, and then evaluated its performance at the 8-, 10-, and 12-h horizons. Additionally, performance under high-volume boarding conditions was examined through extreme case analysis to assess the model’s reliability during periods of elevated crowding. For interpretability, we applied three approaches: Input Weight Norm analysis to estimate the relative importance of each feature; attention analysis to identify the time steps most emphasized during prediction; and Gradient SHAP to quantify feature contributions and produce a ranked importance list.

2.1. Data Source

To accurately predict boarding counts, five distinct data sources were utilized to construct a comprehensive dataset capturing internal ED operations and external contextual factors relevant to ED dynamics. These sources include (1) ED tracking, (2) inpatient records, (3) weather, (4) federal holiday, and (5) event schedules. The same data sources were also used in our previous study [26], which focused on predicting another PFM—waiting count. All data were processed and aligned to an hourly frequency, resulting in a unified dataset with one row per hour. The dataset spans from January 2019 to July 2023, providing over four years of continuous hourly records to support model development and evaluation.

The ED tracking data source captures patient movement throughout the ED, starting from arrival in the waiting room to transfer to an inpatient unit or discharge from the ED. Each patient visit is linked to a unique Visit ID, with 308,196 distinct visits included in the data source. The data provides timestamps for location arrivals and departures, enabling reconstruction of patient flow over time. It also includes room-level information that indicates whether the patient is in the waiting area or the treatment area during their stay. The Emergency Severity Index (ESI) is recorded using standardized levels from 1 to 5, along with a separate category for obstetrics-related cases. Clinical event labels indicate the type of care activity at each step (e.g., triage, admission, examination, inpatient-bed request), while clinician interaction types identify the provider involved (e.g., nurse or physician).

The inpatient dataset contains hospital-wide records of patients admitted to inpatient units, independent of their ED status. Each record includes timestamps for both arrival and discharge, allowing accurate calculation of hourly inpatient census across the entire hospital. By aligning these timestamps with the study period, the number of admitted patients present in the hospital at any given hour can be determined. A total of 293,716 unique Visit IDs are included in this data source, forming the basis for constructing a continuous hospital census variable used in the prediction models.

The weather dataset was obtained from the OpenWeather History Bulk [27] and includes hourly observations collected from the meteorological station nearest to the hospital. This external data source provides environmental context not captured by internal hospital systems. It includes both categorical weather conditions—such as Clouds, Clear, Rain, Mist, Thunderstorm, Drizzle, Fog, Haze, Snow, and Smoke—and one continuous variable: temperature. These features were used to enrich the dataset with relevant temporal environmental information.

The holiday data source captures official federal holidays observed in the United States, obtained from the U.S. government’s official calendar [28]. Each holiday was mapped into the dataset at an hourly resolution by marking all 24 h of the holiday with a binary indicator variable. This representation allows the model to incorporate the presence of holidays consistently across the entire study period.

The event data source includes football game schedules for two major NCAA Division I teams located in nearby cities close to our partner hospital. Game dates were collected from the teams’ official athletic websites [29,30] and added to the dataset by marking all 24 h of each game day with a binary indicator. This information was incorporated to provide additional temporal context associated with scheduled local events.

Table 1 presents a summary of all data sources and the descriptive analysis of the features derived from these sources. The table reflects the structure and content of the dataset after completing all preprocessing and feature-engineering steps.

2.2. Feature Engineering and Preprocessing

Feature engineering and preprocessing were applied to combine and refine data from multiple sources, creating structured, time-aligned features for model training. Aggregated flow metrics were then calculated to represent hourly inpatient and ED activity, ensuring the models used well-defined and temporally consistent inputs.

Feature engineering was primarily applied to the ED tracking and inpatient datasets, from which operational metrics were calculated to describe patient flow across different areas of the hospital. From the ED tracking data, nine aggregated PFMs were engineered to represent hourly patient activity within the department: (1) boarding count: the number of patients in the boarding phase, which is the period after an inpatient bed request is submitted and before the patient leaves the ED for the inpatient unit. This interval begins when the inpatient bed request is entered into the system and ends at the ED discharge timestamp marking the patient’s transfer. For instance, if a patient receives an admit-bed request at 4:20 PM and is checked out of the ED at 6:35 PM, that patient would be included in the boarding count for the hours 4–5 PM, 5–6 PM, and 6–7 PM. (2) Boarding count by ESI level: boarding counts grouped into three Emergency Severity Index (ESI) categories (1 and 2, 3, and 4 and 5) to assess boarding distribution by acuity. (3) Average boarding time: the mean duration, in minutes, that patients spend in the boarding phase during each hour. To calculate this metric, we determine how many minutes of each patient’s boarding interval fall within a given hourly window, sum these minutes across all patients, and then divide by the number of patients boarding during that hour. For example, during the hour 01:00–02:00, three patients (IDs 1, 2, and 3) were boarding, and their combined boarding time totaled 135 min (30 + 60 + 45), resulting in an average boarding time of 45 min (135 ÷ 3). (4) Waiting count: the number of patients in the waiting room during each hour, calculated using the same logic as boarding count. The waiting period begins at the timestamp when the patient arrives at the waiting room location and ends at the timestamp when the patient leaves the waiting room location. This calculation is cumulative across hours. For example, if a patient arrives at the ED waiting room at 10:20 AM and departs at 12:50 PM, they would be counted in the waiting count for the hours 10–11 AM, 11 AM–12 PM, and 12–1 PM. (5) Waiting count by ESI level: the total waiting count broken into the same three ESI categories to reflect differences in waiting room congestion by acuity. (6) Average waiting time: the mean duration, in minutes, that patients spend in the waiting room during each hour. It is calculated using the same logic as average boarding time, but the timestamps used are the waiting room location arrival and departure times. For each hour, the total waiting minutes of all patients are summed and then divided by the number of patients waiting during that hour, ensuring that patients spanning multiple hours are only counted for the portion of time they were waiting in each hour. (7) Treatment count: the number of patients in treatment rooms during each hour, calculated using the same logic as boarding count. The treatment period is defined as the time between the timestamp when a patient arrives at a treatment room location and the timestamp when they leave that location. Patients whose treatment period spans multiple hours are counted in each applicable hourly interval. (8) Average treatment time: the mean duration, in minutes, that patients spend in treatment rooms during each hour, calculated using the same logic as average boarding time, but with treatment room timestamps. (9) Extreme-case indicator: a binary variable flagging hours in which a selected flow metric exceeded its historical mean plus one standard deviation. From the inpatient data, a single feature—hospital census—was engineered to capture the number of admitted patients present in the hospital at each hour. The feature list used in this study includes more than nine features, as detailed in Table 1. However, feature engineering was specifically applied to these nine features because they are not directly available in the raw dataset and must be created through additional calculations.

To prepare the data for modeling, several preprocessing steps were applied, including the following:

• Categorical weather conditions were grouped into five broader categories—Clear, Clouds, Rain, Thunderstorm, and Others—based on their semantic similarity, to simplify downstream modeling. Specifically, ‘Clouds’ and ‘Mist’ were grouped under Clouds; ‘Rain’ and ‘Drizzle’ under Rain; ‘Thunderstorm’ remained as Thunderstorm; and ‘Fog,’ ‘Haze,’ ‘Snow,’ and ‘Smoke’ were combined under Others.
• To improve data quality and ensure consistency, specific steps were taken to address missing values and remove unrealistic records. For missing values in the Emergency Severity Index (ESI) field—approximately 2% of the dataset—a value of 3 was assigned, as ESI level 3 accounted for nearly 60% of all recorded entries. Visits with waiting times exceeding 9 h were excluded, representing 2.1% of the data, since 90% of these cases were extreme outliers with durations spanning several months. Additionally, 51 visits were removed where patients remained in the treatment room for more than seven months with identical treatment-leaving timestamps, indicating likely system logging errors. Finally, 74 visits with recorded boarding times longer than 300 h were excluded, 70 of which had identical checkout timestamps and were also likely caused by data entry or logging issues.
• Lagged and rolling features were computed using a custom function that systematically transformed each selected variable by generating lagged versions and rolling averages. For each variable, lag features were created by shifting the original values backward by 1 to N hours, producing a series of lagged inputs corresponding to different historical time steps. This enables the model to learn from recent historical values. To capture local trends and smooth out noise, rolling mean features were calculated using a centered moving average over a specified window size. To prevent data leakage, lagged and rolling features were generated, based strictly on historical values prior to each prediction timestamp, ensuring that no future information was included in the input features during training, validation, or testing.
• All non-binary features and the target variable were standardized using the StandardScaler from scikit-learn [31], with the scaling parameters computed on the training set and applied to the validation and test sets, to avoid data leakage.
• Given the unusual operational conditions during the early stages of the COVID-19 pandemic, data from April 2020 to July 2020 were excluded, as boarding patterns during this period did not reflect routine processes. As shown in Figure A1, the monthly average boarding counts and times were notably lower than in other years, likely due to the uncertainty and disruption experienced by individuals and healthcare institutions at that time.

After completing the feature engineering and preprocessing steps, all data sources were merged into a unified dataset with an hourly resolution. An hourly timeline was created from 1 January 2019 09:00:00 to 1 July 2023 20:00:00, totaling 37,236 time points. This timeline served as the basis for aligning and merging the five data sources, with each row representing one hour. Table 1 presents the descriptive analysis of the final dataset, summarizing the distribution of both engineered features and raw variables across the full study period. This includes statistical details for numerical variables (mean, standard deviation, and range), percentages for categorical features, and event counts for binary indicators. The resulting dataset provides a structured and comprehensive foundation for predictive modeling of boarding count and other ED-related dynamics.

2.3. Dataset Construction

Following the completion of feature engineering and preprocessing, five distinct datasets were constructed, each representing a different combination of features. These variations were intentionally designed to assess the impact of specific feature groups—such as flow metrics, weather conditions, hospital census, and temporal indicators—on model performance. The primary objective of this approach was to systematically evaluate which combination of features yields the most accurate and reliable predictions for boarding count, and to identify which configurations perform best in detecting extreme-case scenarios—defined using statistical thresholds and explained in detail in the Extreme-Case Analysis section. Each dataset was independently used to train and test the selected deep learning models, allowing for a comprehensive comparison of model outcomes across different data configurations.

2.4. Model Architecture and Training

Three time-series deep learning models—TSTPlus, TSiTPlus, and ResNetPlus—were used to forecast ED boarding count. These models were implemented using the tsai library [32], a PyTorch 2.0 [33] and fastai-based framework [34] tailored for time-series tasks such as forecasting, classification, and regression. The models were selected based on their strong performance in our previous study [26], which focused on predicting ED waiting count.

TSTPlus is inspired by the Time Series Transformer (TST) architecture [35], and utilizes multi-head self-attention mechanisms to capture temporal dependencies across input sequences. The model is composed of stacked encoder layers, each containing a self-attention module followed by a position-wise feedforward network. These components are equipped with residual connections and normalization steps, to enhance training stability and performance. Model explainability is based on attention scores, highlighting which time steps and features most influence predictions.

TSiTPlus is a time-series model inspired by the Vision Transformer (ViT) architecture [36], designed to improve the modeling of long-range dependencies in sequential data. It transforms multivariate time series into a sequence of patch-like tokens, enabling the model to process the input in a way similar to how ViT handles image patches. The architecture incorporates a stack of transformer encoder blocks, each composed of multi-head self-attention layers and position-wise feed-forward networks, with optional features such as locality self-attention, residual connections, and stochastic depth.

ResNetPlus is a convolutional neural network (CNN) designed for time-series forecasting, utilizing residual blocks to capture hierarchical temporal features across multiple scales. Each block applies three convolutional layers with progressively smaller kernel sizes (e.g., 7, 5, 3), combined with batch normalization and residual connections to promote stable training and effective deep feature learning. This architecture enables efficient extraction of both short- and long-term patterns from sequential data.

The dataset was partitioned into training (70%), validation (15%), and testing (15%) subsets for all three deep learning models. The datasets follow the format (n_samples, n_features, sequence_length), where n_samples is the number of hourly observations (e.g., 26,051 for training), n_features is the total number of predictors, including both original and lagged features (e.g., Dataset 3 has 34), and sequence_length is the number of time steps. Here, sequence_length = 1 because each row represents a single hourly time point, with lags incorporated as separate features rather than additional time steps. Hyperparameter optimization was conducted using Optuna [37] for the TSTPlus, TSiTPlus, and ResNetPlus models. Optuna enables dynamic construction of the hyperparameter search space through a define-by-run programming approach. The framework primarily uses the Tree-structured Parzen Estimator (TPE) [38] for sampling, but also supports other algorithms such as random search and CMA-ES [39]. To improve search efficiency, Optuna implements asynchronous pruning strategies that terminate unpromising trials, based on intermediate evaluation results. The number of optimization trials is defined by the user to control the overall search budget. For each of these models, 50 trials were conducted to explore hyperparameters including learning rate, dropout, weight decay, optimizer (Adam [40], SGD [41], Lamb [42], RAdam [43]), activation function (relu, gelu), batch size, number of fusion layers, and training epochs.

2.5. Model Evaluation

Model performance was evaluated on the test set, using the following metrics:

• Mean Absolute Error (MAE): measures the average size of the errors.
• Mean Squared Error (MSE): gives more weight to larger errors.
• Root Mean Squared Error (RMSE): the square root of MSE, in the same unit as the target.
• Coefficient of Determination (R²) Score: shows how well the predictions match the actual values.

The model was also evaluated in extreme cases. An hour was classified as “Extreme” if the boarding count was 40 or higher (mean plus one standard deviation), “Very Extreme” if it was 51 or higher (mean plus two standard deviations), and “Highly Extreme” if it was 62 or higher (mean plus three standard deviations). The distribution of the boarding count and the classification thresholds are provided in Figure A2.

3. Results

Following model training and evaluation, performance metrics were computed for each model–dataset combination using four standard measures: MAE, MSE, RMSE, and R² score. As illustrated in Figure 1, these metrics summarize model performance for the 6 h prediction window across all datasets. After identifying TSTPlus as the best-performing model, based on the 6 h prediction results, we further evaluated its performance on the 8, 10, and 12 h prediction windows, as shown in Figure 2. We then conducted an extreme-case and bootstrap analysis, as described in Section 3.1. The extreme-case analysis, summarized in

Table 3. Performance of the TSTPlus model, reported as MAE and RMSE, under different extreme-case scenarios for each dataset.

Dataset	Mean + 1σ Extreme (≥40)	Mean + 2σ Very Extreme (≥51)	Mean + 3σ Highly Extreme (≥62)
	MAE/RMSE	MAE/RMSE	MAERMSE
Dataset 1	4.85/6.01	6.92/7.95	11.70/12.40
Dataset 2	4.34/5.45	5.79/6.89	10.03/10.95
Dataset 3	4.25/5.35	5.31/6.44	8.88/9.95
Dataset 4	4.45/5.58	5.89/6.99	10.38/11.27
Dataset 5	4.10/5.17 *	4.57/5.65 *	7.17/8.56 *

* Bolded values indicate the best results.

, evaluated the model’s ability to detect periods of severe overcrowding in the boarding process. The bootstrap analysis [44] assessed the robustness and variability of the model’s predictive performance on the test set, with the results presented in

Table 4. Performance of the TSTPlus model, reported as MAE, MSE and R², under different extreme-case scenarios for each dataset.

Model	Datasets	MAE (Median/IQR)	MSE (Median/IQR)	R2 (Median/IQR)
TSTPlus	Dataset 1	4.77/4.70–4.83	35.05/34.17–35.99	0.75/0.74–0.76
	Dataset 2	4.50/4.44–4.57	32.43/31.50–33.30	0.77/0.76–0.78
	Dataset 3	4.30/4.24–4.37 *	29.47/28.86–30.56 *	0.79/0.78–0.80 *
	Dataset 4	4.44/4.38–4.50	31.19/30.2–32.1	0.78/0.77–0.79
	Dataset 5	4.37/4.31–4.44	30.78/29.76–31.71	0.78/0.77–0.79

* Bolded values indicate the best results.

. Finally, we applied Input Weight Norm analysis to estimate feature importance based on the magnitude of learned embedding weights (Figure 3), attention analysis to highlight the time steps most emphasized during prediction (Figure 4), and Gradient SHAP to quantify each feature’s contribution through sensitivity-based attribution scores (Figure A3). These methods are described in detail in Section 3.2.

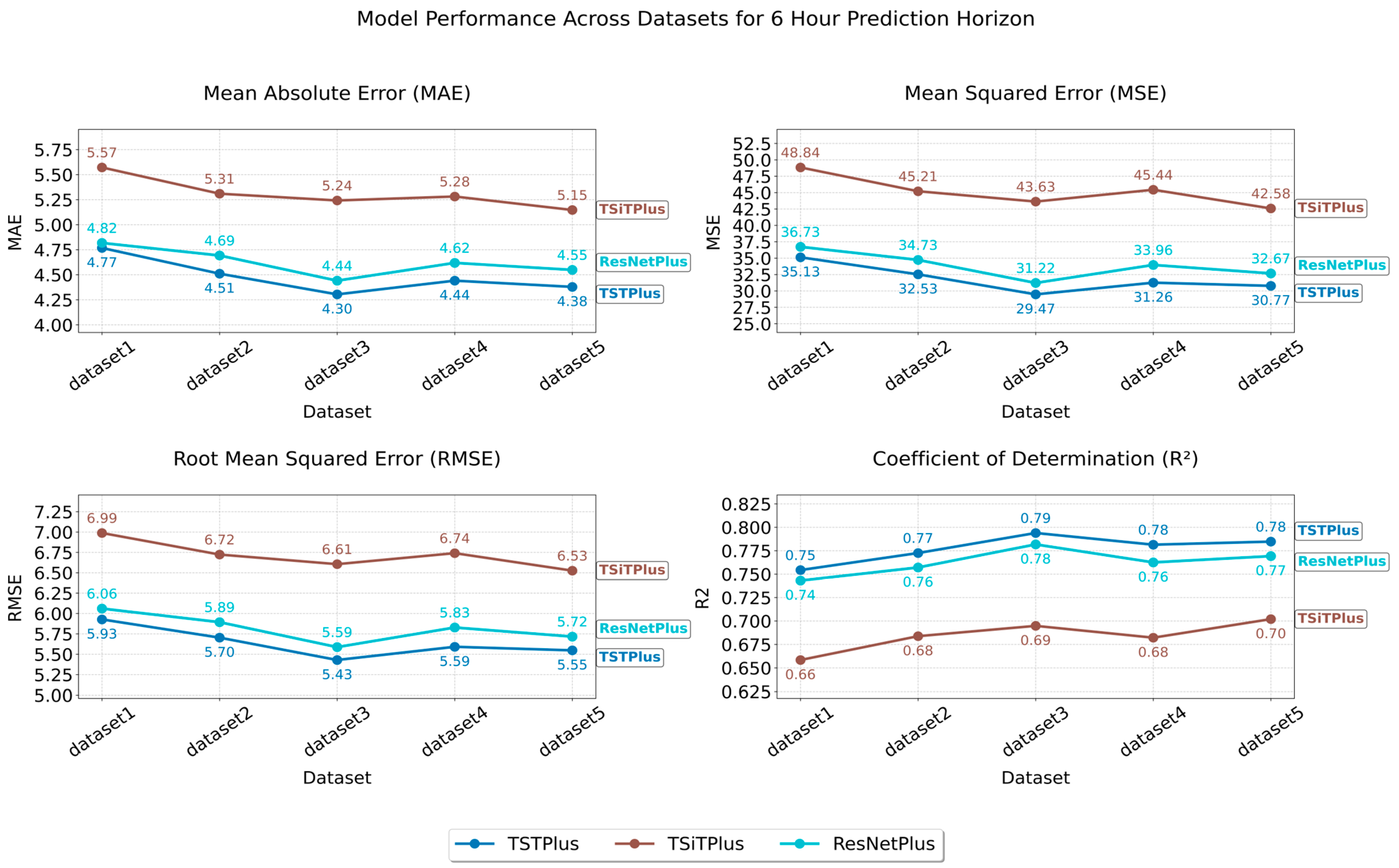
The best result was achieved by the TSTPlus model trained on Dataset 3 for the 6 h prediction window, yielding an MAE of 4.30, MSE of 29.66, RMSE of 5.44, and R² of 0.79 on the test set. This configuration was selected through automated hyperparameter search using Optuna, which systematically explores the parameter space and can identify sensitive, non-integer values—such as a learning rate of 0.0246, dropout rate of 0.1335, and weight decay of 0.0542—that yield optimal model performance. The most effective combination also included 200 epochs, the Lamb optimizer, and the relu activation function. The TSTPlus model architecture consists of a stack of three transformer encoder layers, each incorporating multi-head self-attention, residual connections, normalization, and position-wise feed-forward networks. After feature extraction, the output is passed through a dense fusion layer with 128 neurons and relu activation to aggregate temporal features before the final prediction. Dropout is applied to the fusion layer to reduce overfitting, and weight decay further helps to regularize the model by penalizing large weights. The model is trained using MSE loss.

Figure 1 shows that the performance of the three models varied across datasets, depending on which feature set was used. As shown in Table 2, Dataset 1 serves as our baseline, including only the target variable’s lagged values, along with standard temporal features such as year, month, day, and hour. As a result, all models performed worst on Dataset 1, likely due to limited features, with MAE/MSE values of 4.77/35.13 (TSTPlus), 4.82/36.73 (ResNetPlus), and 5.57/48.84 (TSiTPlus). For Dataset 2, adding features such as average boarding time, treatment count, waiting count, average treatment time, average waiting time, extreme-case indicator, hospital census, and weather status improved performance, reducing MAE to 4.51 (TSTPlus), 4.69 (ResNetPlus), and 5.31 (TSiTPlus). In Dataset 3, in addition to the features in Dataset 2, temperature, federal holiday, and two separate football game indicators were added as additional contextual features. This further improved model performance, with MAE decreasing to 4.30 for TSTPlus, 4.44 for ResNetPlus, and 5.24 for TSiTPlus. In Dataset 4, additional features were added for both boarding count and waiting count, each broken down by three ESI categories: ESI 1 and 2, ESI 3, and ESI 4 and 5. However, these additions did not improve model performance, and error rates increased for all models, with MAE values of 4.44 for TSTPlus, 4.62 for ResNetPlus, and 5.28 for TSiTPlus. Finally, in Dataset 5, different lag windows were applied to various features, resulting in MAE values of 4.38 for TSTPlus, 4.55 for ResNetPlus, and 5.15 for TSiTPlus. TSiTPlus showed a decrease in error rate, achieving its best results on Dataset 5, while TSTPlus and ResNetPlus obtained their second-best results on the same dataset.

Figure 2 presents the performance of the TSTPlus model across five datasets for 6, 8, 10, and 12 h prediction horizons. As expected, shorter prediction intervals produced more accurate and reliable forecasts, consistent with the general principle that predictive accuracy decreases as the prediction horizon lengthens and uncertainty increases. The best results for different prediction horizons were obtained from two datasets: Dataset 3 achieved the highest accuracy for the 6 and 12 h horizons, while Dataset 5 performed best for the 8 and 10 h horizons. Figure 2 shows that different feature sets can be more effective for different forecasting horizons. As a result, the best MAE values achieved by the TSTPlus algorithm were 4.30 for the 6 h horizon, 4.72 for 8 h, 5.14 for 10 h, and 5.39 for 12 h.

3.1. Extreme-Case and Bootstrap Analysis

Extreme-case analysis aims to identify periods when hourly boarding counts significantly exceed typical levels, indicating unusual strain on hospital resources. To define these cases, the data were categorized using the hourly mean (µ) (28.7) and standard deviation (σ) (11.2) values in Table 1. Based on this, and as illustrated in Figure A2, hourly boarding counts were classified into four groups: Normal (<40), Extreme (≥40), Very Extreme (≥51), and Highly Extreme (≥62). Thresholds were determined using one, two, and three standard deviations above the mean boarding count, denoted as 1σ, 2σ, and 3σ, respectively, providing a structured approach to detect and quantify extreme overcrowding events.

Table 3 shows the prediction performance of TSTPlus across all datasets under extreme-case scenarios. TSTPlus was selected for this analysis because it achieved the best overall results among the models. This evaluation is important for understanding how well the model performs during periods of severe ED crowding and for identifying which dataset provides the most reliable predictions in extreme situations. As shown in the table, Dataset 5 consistently produced the lowest MAE and RMSE values across all extreme thresholds, highlighting its strong predictive performance during periods of high boarding counts. These results suggest that the features included in Dataset 5 are especially effective for forecasting ED overcrowding under challenging conditions. Notably, for Dataset 5, the MAE for the entire test dataset was 4.38, while the MAE for the “Extreme” scenario (boarding count ≥ 40) was lower, at 4.10. This demonstrates that the model improves its prediction accuracy during periods of high crowding, reinforcing its robustness in critical situations. In the Very Extreme case (boarding count ≥ 51 patients per hour), the model achieved an MAE of 4.57, while in the Highly Extreme case (boarding count > 61 patients per hour), the MAE was 7.17. The model can provide valuable forecasts to help proactively manage ED operations, even in severe crowding.

Bootstrap analysis is a resampling-based technique used to assess the stability and variability of model performance metrics. We employed a block bootstrap approach, sampling consecutive 12 h segments for Datasets 1–4 and 24 h segments for Dataset 5, to maintain the temporal structure of the test data. Across 500 bootstrap iterations, the model was evaluated on each resampled set, and performance metrics—MAE, MSE, and R²—were calculated. The interquartile range (IQR), reported as the 25th to 75th percentile values for each metric, reflects the spread of the middle 50% of bootstrap results, providing a robust evaluation of performance variability. These median and IQR values are summarized in Table 4. As shown in Figure 1, TSTPlus on Dataset 3 achieved a median MAE of 4.30. The narrow IQR range of 4.24–4.37 indicates high stability and low variability across bootstrap samples, underscoring the robustness of the results.

3.2. Model Explainability

To enhance interpretability, we applied three complementary explainability techniques to our best-performing TSTPlus model: Input Weight Norm analysis, inspired by the principle that larger post-training weight magnitudes reflect greater variable influence [20], here adapted to compute the L₂ norm of each feature’s learned embedding vector to assess relative importance (Figure 3); attention analysis to identify which past time steps received the most focus during prediction (Figure 4); and Gradient SHAP to quantify each feature’s contribution to individual predictions through sensitivity analysis (Figure A3). For the attention analysis, we reshaped the dataset from a single time step (sequence length = 1) to 12 time steps, allowing lagged values to be represented as a sequence, rather than as separate features. For example, Dataset 3 changed from (26,051, 34, 1) to (26,051, 22, 12), where each variable spans 12 consecutive hourly lags.

The Weight Norm method measures feature importance by calculating the L2 norm of each input feature’s weight vector in the model’s first learnable layer, with higher norms indicating greater initial influence. These norms are normalized to sum to 1, providing comparable importance scores without requiring additional data. Figure 3 shows the ranked importance scores from this analysis, with Boarding Count having the highest importance (0.1772), followed by Day of Week (0.0880), Hospital Census (0.0697), Hour (0.0673), and Treatment Count (0.0626), indicating these features are most heavily weighted by TSTPlus at the model’s input stage. The three lowest-importance features were Year (0.0104), Weather: Rain (0.0174), and Football Game 2 (0.0195).

In transformer models, the attention mechanism learns how much each time step should focus on others when making predictions. During training, we saved the model’s attention weights from a selected layer for later analysis. To calculate temporal importance, these weights were averaged across all heads and batches, summed for each time step to capture its total received attention, and normalized with a softmax function. 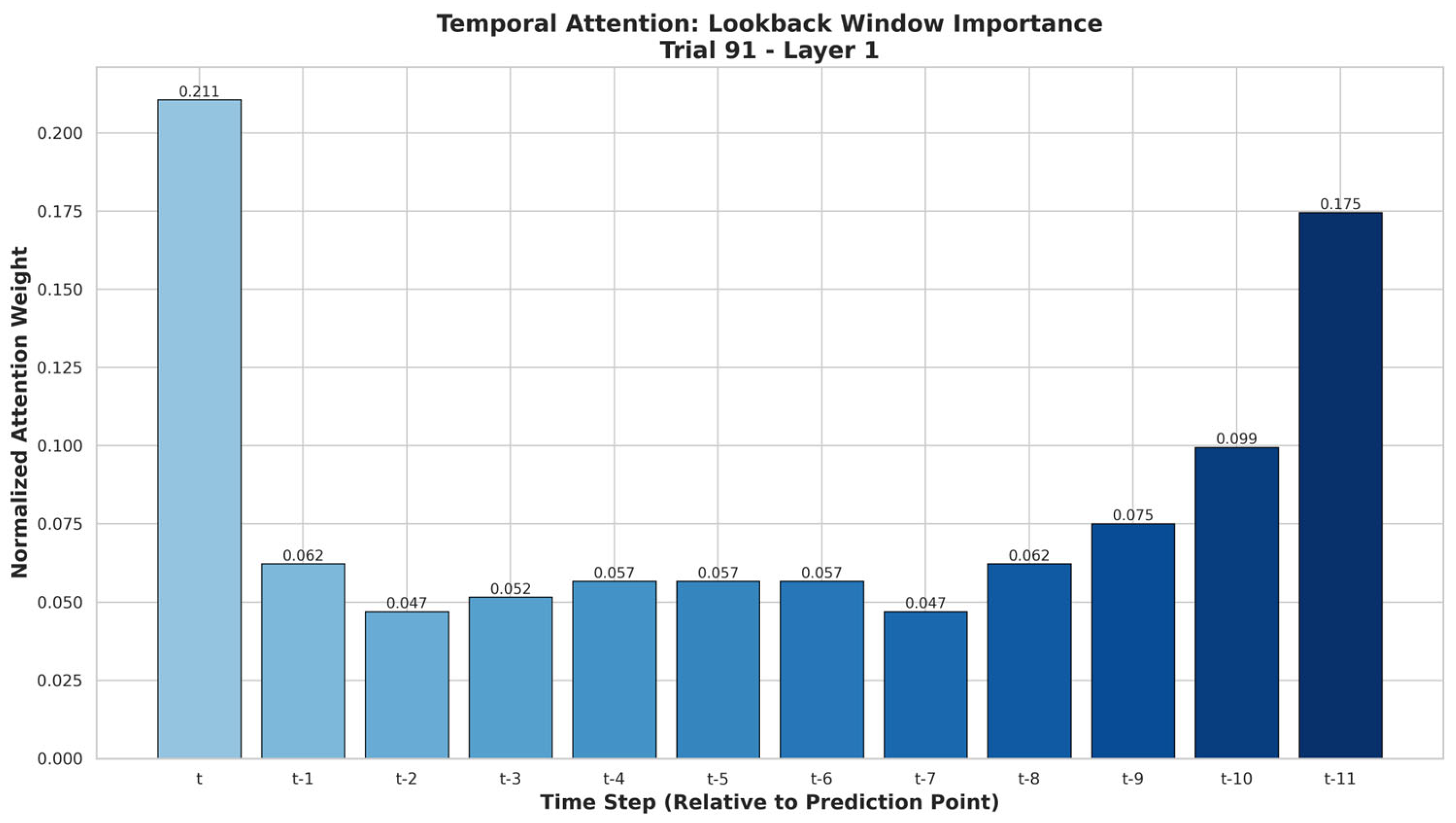Figure 4 shows that the current time step t (0.211) received the highest attention, followed by t-11 (0.175) and t-10 (0.099), while t-2 and t-7 (both 0.047) had the lowest influence on the model’s predictions.

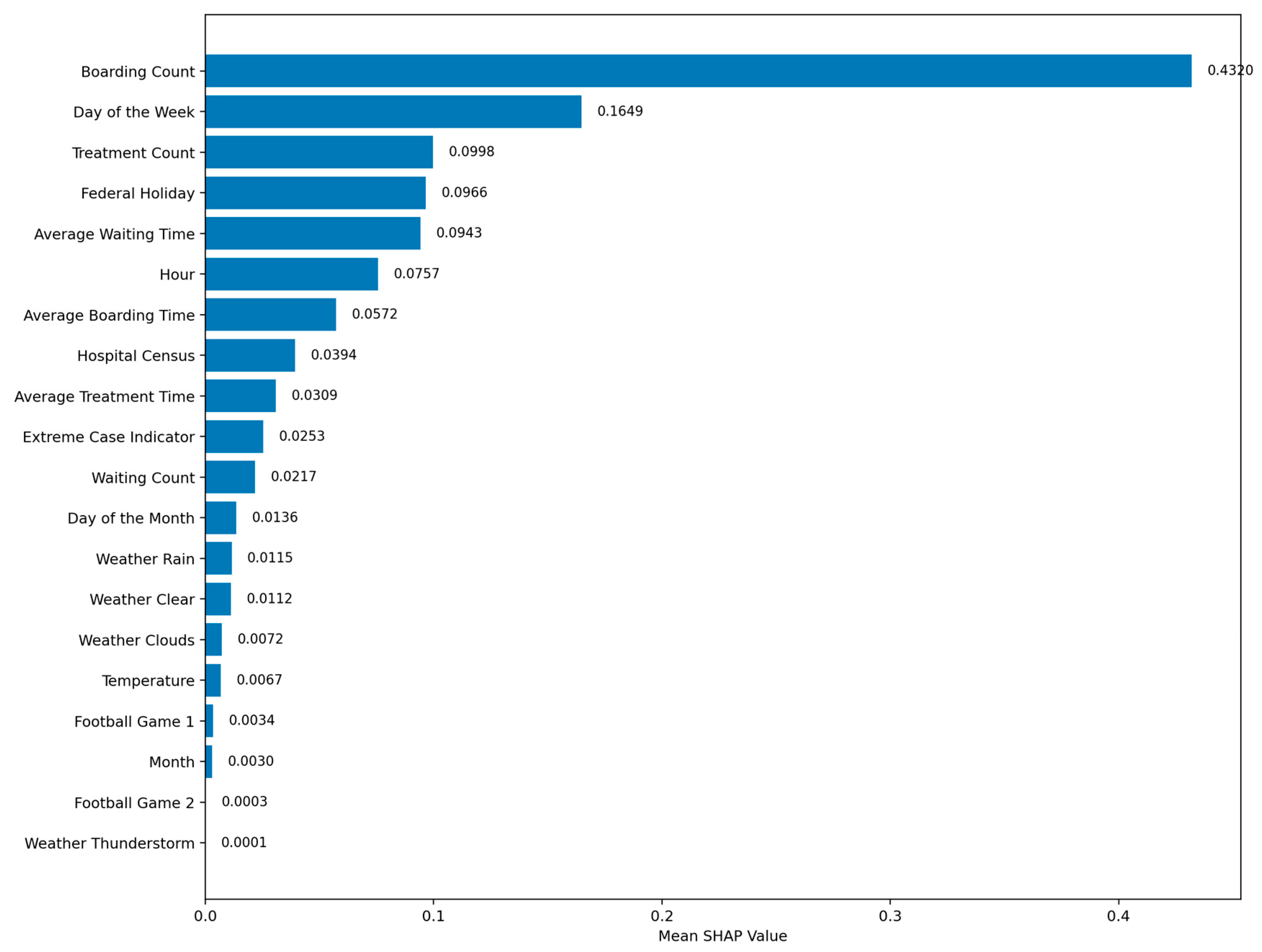
Gradient SHAP estimates each feature’s contribution to the model’s predictions by combining integrated gradients with Shapley values. Using a background dataset and evaluation samples, we computed SHAP values for the trained TSTPlus model and averaged their absolute magnitudes across all samples, to obtain comparable importance scores. Figure A3 shows that Boarding Count had the highest mean absolute SHAP value (0.4318), followed by Day of the Week (0.1650), Treatment Count (0.1004), Federal Holiday (0.0964), and Average Waiting Time (0.0944), indicating these features had the greatest influence on the model’s outputs. The lowest-ranked features were Football Game 2 (0.0003), Weather Thunderstorm (0.0001), and Month (0.0030). Unlike weight-based metrics or attention patterns, Gradient SHAP attributes importance by directly measuring each feature’s marginal effect on the model’s output, making it more robust to the effects of feature scaling, correlated variables, and hidden-layer transformations.

Feature-importance patterns from the Weight Norm method (Figure 3) and Gradient SHAP (Figure A3) showed strong agreement in identifying the most influential predictors. Both analyses ranked Boarding Count as the top feature (Weight Norm: 0.1772; SHAP: 0.4318), followed by high importance for Day of Week and Treatment Count. Weight Norm additionally emphasized Hospital Census and Hour, while SHAP highlighted Federal Holiday and Average Waiting Time. Lower-ranked features in both methods included weather variables and external event indicators, such as Football Game 2, indicating minimal impact on predictions. This convergence across two complementary methods strengthens confidence in the robustness of the identified top predictors.

4. Discussion

This study demonstrates that deep learning-based time-series models can reliably forecast ED boarding counts across multiple prediction horizons (6, 8, 10, and 12 h) using only aggregate operational and contextual features, without patient-level clinical inputs. The best-performing configuration—TSTPlus trained on Dataset 3—achieved an MAE of 4.30, MSE of 29.47, RMSE of 5.43, and R² of 0.79, which is substantially lower than the natural variability of the target (mean = 28.7, standard deviation = 11.2), with narrow bootstrap IQR ranges indicating high stability. Forecasts at all horizons provided meaningful lead times for operational planning, enabling timely FCP activation and supporting proactive measures such as bed allocation adjustments, staff redeployment, and coordination with inpatient units to mitigate overcrowding before critical thresholds are reached.

Performance patterns indicated that both model architecture and feature composition substantially influenced forecasting accuracy. TSTPlus generally achieved the best results, with richer feature sets outperforming more limited configurations. The fact that different datasets performed best at different horizons suggests that the most effective feature combination depends on the prediction window, highlighting trade-offs between representing current operational conditions and capturing longer-term temporal trends. Even simpler datasets retained reasonable accuracy, reflecting the persistence of boarding patterns over time, but consistently lagged behind feature-rich configurations. Notably, while the difference between Dataset 1 (MAE = 4.77) and Dataset 3 (MAE = 4.30) in TSTPlus may appear modest, this 0.47 reduction in hourly error equates to roughly 5.64 fewer misestimated boarders per day and over 2000 per year, representing a meaningful operational improvement for staffing, bed allocation, and surge planning.

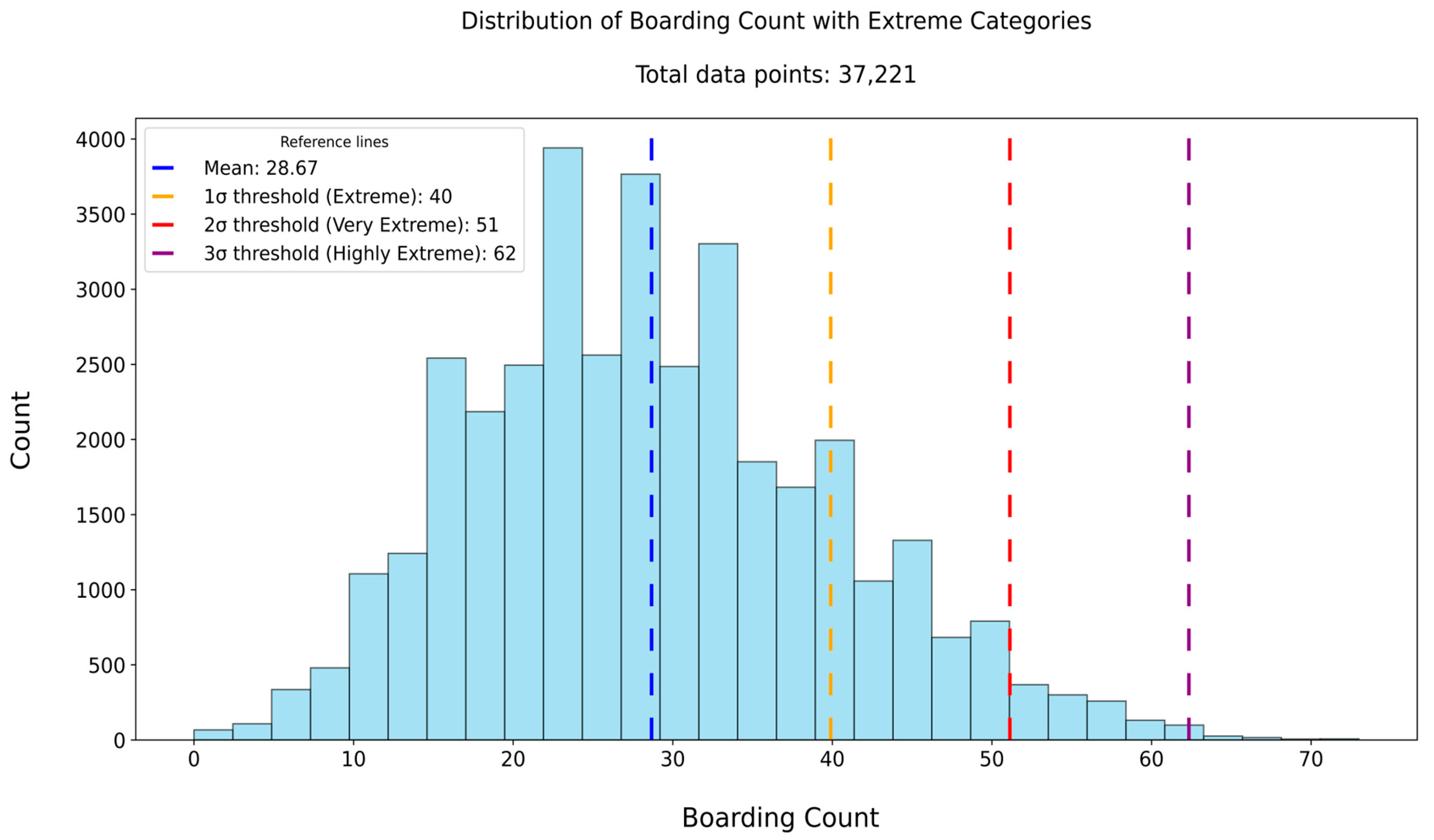
Model performance under extreme operational conditions further reinforced the robustness of our approach. In Dataset 5, the MAE during extreme crowding periods (boarding count ≥ 40) was 4.10—lower than the overall MAE—indicating improved accuracy when demand was highest. This trend persisted in “Very Extreme” (≥51) and “Highly Extreme” (≥62) scenarios, although error magnitude increased with severity, as expected. Such stability under peak load is operationally significant, as forecasting precision during these periods is critical for initiating timely interventions. Bootstrap analysis supported these findings, showing consistently narrow interquartile ranges for MAE, MSE, and R², further demonstrating the model’s reliability across resampled test sets.

Explainability analysis provided complementary perspectives on the TSTPlus model’s decision-making, improving interpretability and supporting operational trust. Weight Norm analysis highlighted Boarding Count as the most influential feature, followed by Day of Week, Hospital Census, Hour, and Treatment Count, with minimal contributions from weather variables and external events such as football games. Attention analysis revealed that the model assigned the greatest weight to the current time step (t), as well as distant lags t-11 and t-10, indicating that both immediate conditions and patterns from the same time on the previous day play key roles in forecasting. Intermediate lags (e.g., t-2, t-7) had lower attention, suggesting less relevance for short-term fluctuations. Gradient SHAP results reinforced these findings, ranking Boarding Count, Day of Week, and Treatment Count as top drivers, with Federal Holiday and Average Waiting Time also contributing meaningfully. Across methods, weather variables and football game indicators consistently showed the least importance, indicating limited short-term predictive value.

From an implementation standpoint, using only aggregate operational and contextual features offers distinct advantages for scalability and adoption. This design avoids reliance on patient-level clinical data, reducing privacy concerns and simplifying integration with existing hospital information systems. Multi-horizon forecasting allows administrators to choose a lead time that balances predictive accuracy with operational readiness, making the approach adaptable to varying resource constraints and situational demands. By combining robust performance, interpretability, and ease of deployment, the proposed framework provides a practical tool for supporting proactive ED management and mitigating the impact of overcrowding.

5. Limitations and Future Work

This study presents a predictive framework for ED operations, yet, like any data-driven approach, it is subject to certain limitations, and offers several avenues for future enhancement. While the model demonstrates strong performance using aggregate operational data, further developments are necessary to optimize its applicability across diverse healthcare settings.

One primary limitation is that this study did not evaluate how the predictions would perform in a real-world operational or simulation-based setting. Although the model provides accurate forecasts at 6, 8, 10, and 12 h intervals, its practical value—particularly whether these windows allow sufficient lead time for effective intervention—remains untested. Beyond operational considerations, the study also faces some technical limitations related to model design and training. Despite an extensive hyperparameter search, alternative or more comprehensive strategies could yield better-performing combinations. Likewise, exploring different feature set configurations within the datasets could further enhance predictive performance. While explainability approaches (e.g., Gradient SHAP, attention-weight visualization) provide insights into feature importance, these methods cannot guarantee full transparency of the model’s decision-making, especially in cases involving complex nonlinear relationships between inputs and outputs. From a deployment perspective, our approach offers broad generalizability and potential adoption in diverse ED settings, because it relies on aggregate operational data rather than patient-level records. It assumes clearly defined waiting and treatment areas with accurate timestamp tracking; without these, the necessary feature engineering for PFMs would not be possible. The model must also be retrained for each site to ensure optimal performance, as healthcare policies, workflows, and patient flow patterns vary considerably between institutions, especially outside the United States. For example, some hospitals use fast-track systems for low-acuity patients, while others manage all patients through a unified treatment stream. Another example is that pediatric EDs follow different operational models than adult EDs.

In future work, we plan to evaluate the model in simulation-based or real-world ED settings, to assess its operational effectiveness. We will also extend the framework to predict additional PFMs used in this study, and integrate these models into a unified prediction platform. This system will generate real-time forecasts for multiple critical PFMs, offering a comprehensive view of anticipated ED operational status and supporting proactive resource management. The deployment will include standardized data preparation, feature engineering, and preprocessing routines, along with automated model retraining, performance monitoring, and anomaly detection, to maintain accuracy and robustness in the presence of data drift. Multiple predictive modules—each targeting a specific PFM—will run concurrently, coordinated by a central orchestration layer, to ensure data consistency and manage dependencies. To further enhance reliability, we will establish infrastructure for real-time data ingestion and implement fallback strategies for external data sources (e.g., weather APIs). For instance, if the primary source becomes unavailable or returns anomalous data, the system will automatically switch to a secondary provider and validate consistency. Additionally, user-facing dashboards will be developed to integrate seamlessly with existing ED workflows and support actionable, data-driven decision-making as part of the full deployment process.

6. Conclusions

Boarding count is a critical patient flow measure and a major driver of emergency department (ED) overcrowding, which can negatively impact patient care, increase wait times, and strain hospital resources. This study addresses the need for timely forecasting of boarding counts by developing deep learning models trained on real-world emergency department data from a partner hospital. In our dataset, the boarding count had a mean of 28.7 and a standard deviation of 11.2 per hour, providing context for evaluating model performance. Leveraging comprehensive feature engineering, multiple dataset configurations, and automated hyperparameter optimization, the TSTPlus model achieved the best results, with a mean absolute error of 4.30 and an R² of 0.79 on the test set. Short-term, within-day predictions across 6, 8, 10 and 12 h horizons enable hospital administrators to anticipate and manage crowding before critical thresholds are reached, supporting proactive Full Capacity Protocol activation, effective staff and bed management, and inpatient surge planning. The proposed framework does not rely on patient-level clinical data, thereby facilitating generalizability, protecting privacy, and making it applicable to diverse hospital environments. Future work will evaluate the real-world impact of these forecasts through simulation or operational studies and integrate these models into clinical decision support systems, to enhance ED crowding management.