Abstract
H-score is a semi-quantitative method used to assess the presence and distribution of proteins in tissue samples by combining the intensity of staining and the percentage of stained nuclei. It is widely used but time-consuming and can be limited in terms of accuracy and precision. Computer-aided methods may help overcome these limitations and improve the efficiency of pathologists’ workflows. In this work, we developed a model EndoNet for automatic H-score calculation on histological slides. Our proposed method uses neural networks and consists of two main parts. The first is a detection model which predicts the keypoints of centers of nuclei. The second is an H-score module that calculates the value of the H-score using mean pixel values of predicted keypoints. Our model was trained and validated on 1780 annotated tiles with a shape of 100 × 100 µm and we achieved 0.77 mAP on a test dataset. We obtained our best results in H-score calculation; these results proved superior to QuPath predictions. Moreover, the model can be adjusted to a specific specialist or whole laboratory to reproduce the manner of calculating the H-score. Thus, EndoNet is effective and robust in the analysis of histology slides, which can improve and significantly accelerate the work of pathologists.
1. Introduction
Immunohistochemical analysis constitutes a classic technology used to assess the expression and spatial distribution of a particular protein biomarker in tissue samples. This method is widely used in clinical practice, especially in diagnostics in oncology, such as in the identification and classification of a tumor, as well as its localization and mutation-specific status. A qualitative and semi-quantitative evaluation of slides is carried out by a pathologist, something which has a number of limitations including, for example, the subjectivity of the specialist’s evaluation, the limited range of grades of staining (scale from 0 to 3+), the time-consuming nature of the assessment, and the complexity of scaling the process for large projects. An increasing number of works indicate that computer-aided analysis can replace or at least facilitate and standardize the work of pathologists [1,2,3]. H-score, a method of assessing the extent of nuclear immunoreactivity, something that is applicable to steroid receptors, is used in the semi-quantitative assessment of the degree of slide staining, first mentioned in research in the 1980s [4,5]. Since then, H-score has been successfully applied in immunohistochemical analysis [6,7,8] and has recently even been reborn into a digital image analysis-based approach, called the pixelwise H-score [9]. Automated H-score proves to be a successful and efficient alternative to visual H-score.
With the invention of the first whole-slide scanners in the 1990s [10], it became possible to make whole-slide images of various tissues with a level of resolution whereby nuclei become distinct. With the advent of the first digital slides, the first algorithms for their analysis appeared, which included trainable and non-trainable algorithms [11,12,13,14]. Whole-slide image analysis has many challenging aspects, such as in the cases where the slide is large in terms of pixels while the region of interest may be less than 10 pixels. Also, a slide could contain a large number of such regions in different places, the information about which needs to be aggregated and analyzed. Therefore, whole-slide images are often divided into smaller square images, or tiles, and processed separately, with subsequent aggregation of the information received from each tile.
Digital pathology tools, such as neural networks, can significantly facilitate the work of pathologists in that they provide results with a level of accuracy and precision that conventional methods cannot provide. Whole-slide images contain a large amount of information that is not always visible to the human eye, especially when it is necessary to process myriads of similar slides in a row. Therefore, pathologists can process only a small part of the entire image, the so-called “region of interest”, which can bias the final score of the whole slide. These factors contributed to the growth of interest in the use of neural networks for the analysis of whole-slide images, particularly histology images. Neural networks rose to prominence with the invention of AlexNet [15] and, later, when neural networks outperformed humans in the classification of images [16], which further increased interest in the development of deep learning methods. Convolutional neural networks proved to be effective in image analysis and processing. At present, CNNs are quite popular in the analysis of histology images such as in detection, tissue classification, annotation, and quantification. Their strong performance means that they do not require a large amount of training data. This contrasts with visual transformers [17], which are only gaining in popularity. Therefore, in this paper, a convolutional architecture was chosen for our model.
The main concept in the detection is how to represent the position of an object. This can be represented as a Bounding Box (a vector of a length of 4, which contains the coordinates of the upper-left and lower-right). There are many methods and models that use this approach with Bounding Boxes. For instance, in [18], the authors used convolutional neural networks, where ResNet [19] and ResNeXt [20] were used as the backbone. The main feature of this work is the presence of additional layers with embeddings that improve the detection and classification of nuclei, unlike standard models of this type, such as those in reference [21].
CNN architectures come in a broad range, including VGG, ResNet, Unet, and others. The Unet architecture was created specifically for medical imaging, and it has become very successful in this area. It looks like an HourGlass that compresses and decompresses the supplied image to create a heatmap. In order to compute the H-score, we must know the number of nuclei with varying staining levels on the slide. For the determination of the H-score, neural networks can function as detectors that locate and categorize the cells on the slide. Here, utilizing all of these methods, we provide EndoNet, the model for automatic H-score calculation on histological slides.
2. Methods
2.1. Data
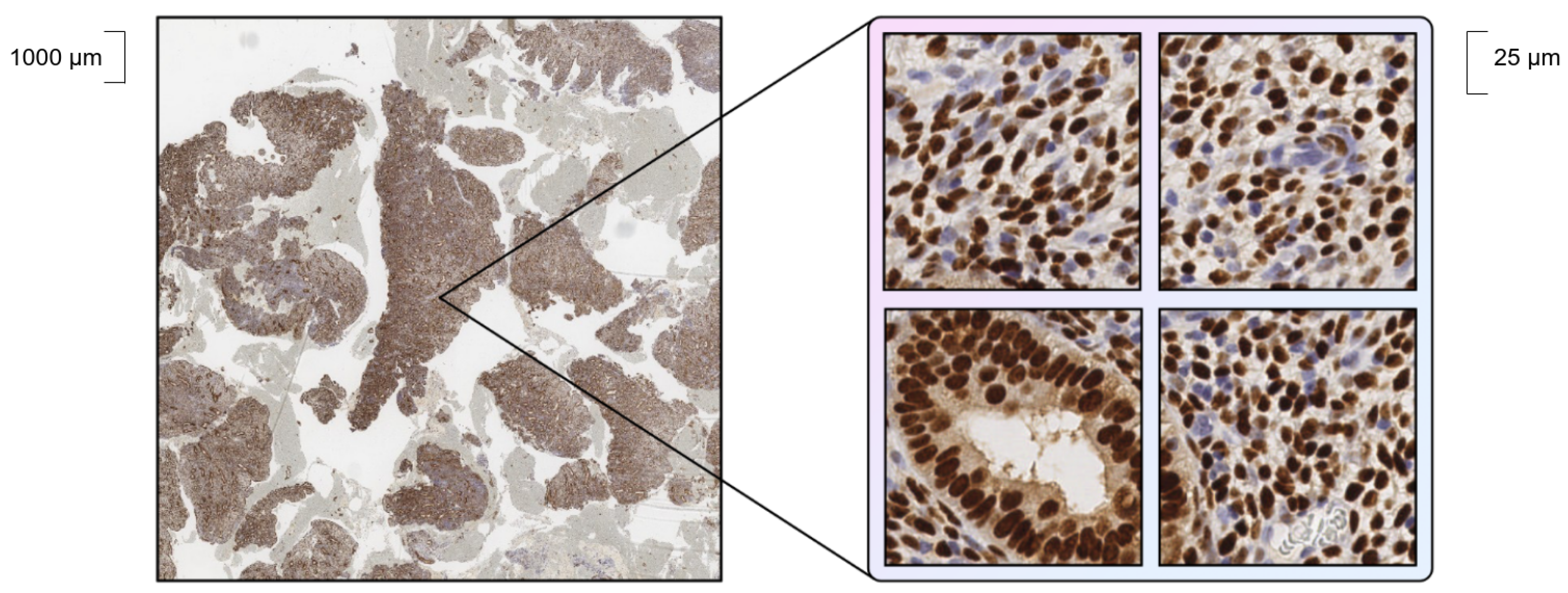
Our dataset consists of slides of endometrium obtained from immunohistochemical (IHC) analysis of progesterone and estrogen receptors. The slides were taken from two different sources: the EndoNuke [22] open histology dataset (the “bulk” part) and a pathology laboratory dataset (hereinafter called PathLab dataset). There are some differences in the slides, such as in terms of methods of staining, equipment, reagents for staining, types of tissue, etc., which make the detection a challenging task. Within the manual annotation of the dataset, nuclei stained with antibodies to the progesterone (1E2, VENTANA) or estrogen (SP1, VENTANA) receptor in Ventana BenchMark XT stainer (Ventana Medical-Systems, Oro Valley, AZ, USA) were labeled with the definition of one of two localizations: “stroma” or “epithelium” classes. Due to their gigapixel size, whole slides were cut into small tiles, examples of which are shown in Figure 1.
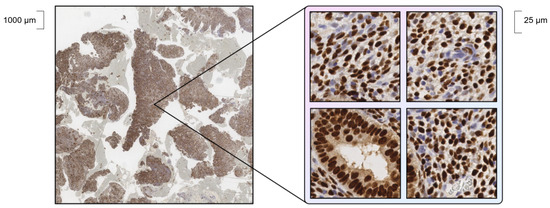
Figure 1.
Example of a part of whole slide (left) and cut tiles (right).
The EndoNuke dataset consists of 1740 manually annotated tiles. The annotation comprises a set of keypoints for each nucleus within a tile. These keypoints encompass the x and y coordinates of the nucleus center, and class (stroma or epithelium). To clarify, if there are 100 cells within a tile, the annotation takes the form of an array with a size of (100, 3). Tiles in EndoNuke are images of various sizes in pixels (mainly 200 × 200 and 400 × 400 pixels), because slides have different µm/pixel values, but they all capture a field of view of 100 × 100 µm. All tiles were resized (by bilinear interpolation) into 512 × 512 pixels before being fed as inputs into the model.
The PathLab dataset consists of 40 tiles. Initially, slides from PathLab were received without annotation; thus, they were cut into tiles and annotated. Each cell was classified not only by stroma and epithelium, but also by color (blue cell, weak brown, medium brown, and strongly brown). Therefore, these tiles were used both for the detection task and for the H-score estimation task. The protocol for the annotation of tiles from the laboratory matches the EndoNuke [22] annotation protocol; two experts annotated, independently from each other, a set of 20 tiles, some overlapping, to measure the agreement between the tiles. Since such an annotation is a time-consuming task, a total of 7 slides were used, with 1 slide being mutual for both annotators. Five tiles were cut from each slide from different areas without overlapping. First, to calculate the agreement, we established matches between keypoints for pairs of experts using a Keypoint Similarity measure [23]:
where
- = point locations;
- s = scale parameter, which equals the mean square nuclei radius.
These similarities formed a matrix, treated as an adjacency matrix for a bipartite graph, and we employed the Hungarian algorithm [24] to find the best keypoint matches based on maximum similarity. After matching, we computed Kohen’s kappa statistics [25] to measure the agreement. Since 1 slide was mutual for measuring consent, 40 annotated tiles appeared in the PathLab dataset (both annotations of the mutual slide are used for future analysis). Tiles from PathLab are primarily 395 × 395 pixels, but they also capture the field of view of 100 × 100 µm. They have also been resized (via bilinear interpolation) into 512 × 512 pixels so that the size of all tiles is the same.
All datasets were merged and split into training, validation, and test parts in a proportion of 3:1:1 (1068 in training, 356 in validation, and 356 in the test part). The training part was used to train the model, the validation part was used to select the best epoch during the training, and the test part was used to evaluate the model.
2.2. General Architecture
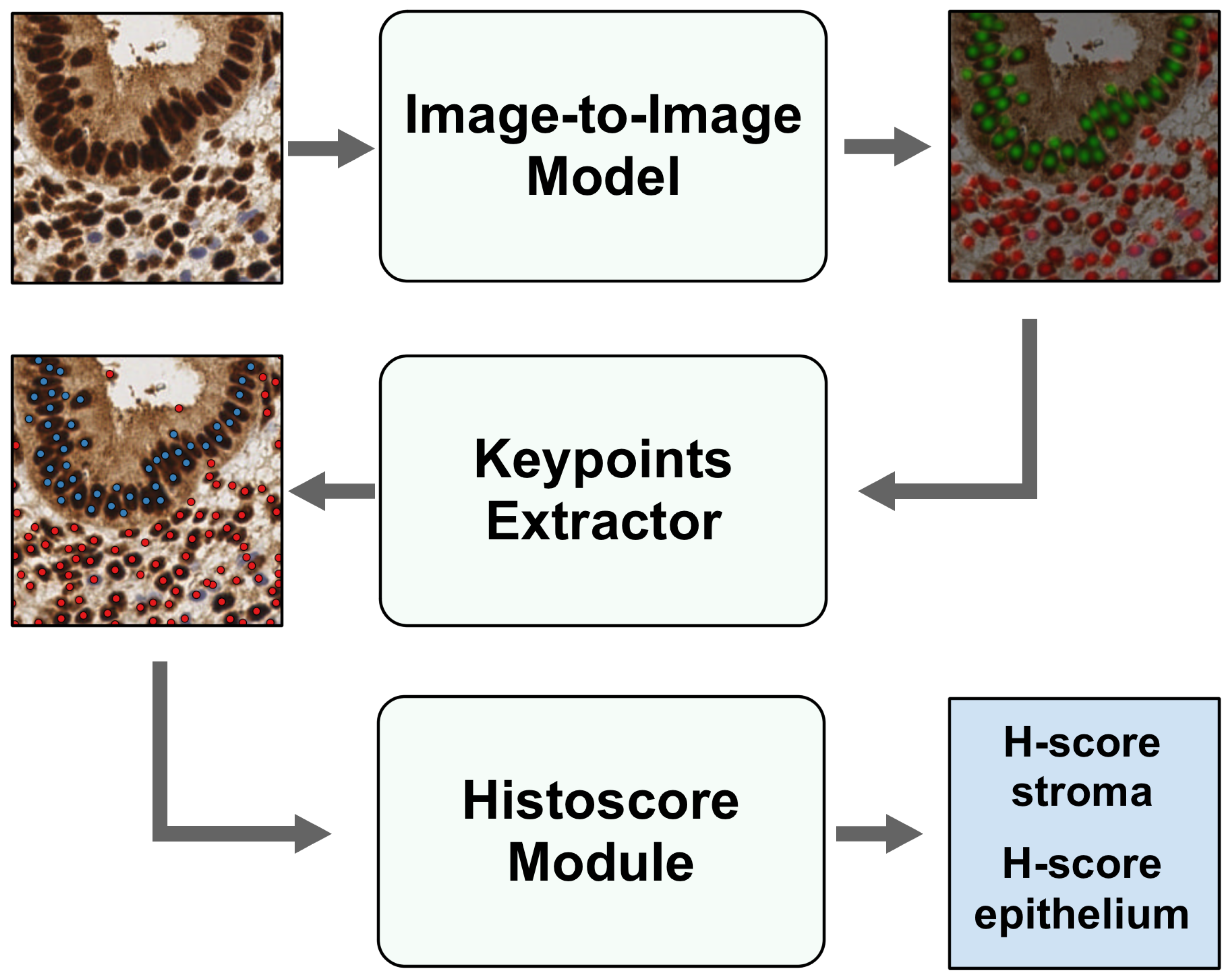
EndoNet is a deep learning-based model for predicting H-score in stroma and epithelium on endometrium slides. The model consists of two important parts. The first part is a detection model that detects nuclei and predicts their keypoints using input tiles. In the context of deep learning and object detection tasks, keypoints refer to localized points or landmarks on a specific object that are used to identify and track key features or attributes of the object. A keypoint is a vector of length 3, which contains the coordinates of the center of the object x and y and the class of the object. The second part is a module for calculating the H-score based on the predicted keypoints. The general architecture of the EndoNet model is presented in Figure 2.
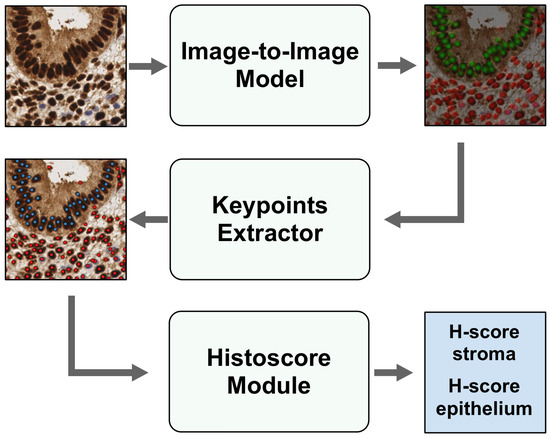
Figure 2.
Architecture of EndoNet model. Tiles go through an Image-to-Image model to be converted into heatmaps, while Keypoint Extractor obtains the coordinates and classes of the centers of nuclei and passes them to the H-score Module to calculate H-score in stroma and epithelium.
The detection model consists of an Image-to-Image model and a Keypoint Extractor. The Image-to-Image model is an HourGlass model because it has an encoder, narrowing an image into a smaller array, and a decoder, expanding this array to the size of the input image. Input tiles go through the Image-to-Image model to be converted into a heatmap, which shows the location of the cores in the input image. Following this, the heatmaps are processed via the Keypoint Extractor, and keypoints are obtained. The keypoints include the coordinates of the nuclei centers and their corresponding class (stroma or epithelium). At the output of the Keypoint Extractor, an array of keypoints and their associated probabilities is generated for each image.
The input image, along with the derived keypoints, undergoes processing in the Histoscore Module. This module performs the following steps: it extracts a small area around each keypoint from the input image, translates this pixel set into the HSV color space, then compares the pixel’s hue and value with predefined thresholds. Subsequently, it assigns a color label (ranging from non-stained to weak, medium, or strong-stained) to each keypoint. After this color-labeling process, the H-score is computed separately for stroma and epithelium as a weighted sum of the cell percentages for each color category.
2.3. Detection Model Architecture
To detect the object’s position, we used a modified version of the usual Bounding Box, which captures the coordinates of the object’s center (a vector of length 2). Since we only need the 2 coordinates of the nuclei centers instead of the 4 for Bounding Boxes, we reduce the number of predicted values by half. Instead of directly predicting the coordinates of objects, it is possible to predict a probability map, called a heatmap. A heatmap is a field of probabilities of the object being at each point: the higher the value in the pixel, the greater the probability of finding the object. Accordingly, the maximum of the probability peak corresponds to the center of the cell nucleus. The coordinates of the peaks on the heatmap, which can be found with the max-pooling procedure, are the coordinates of the center of the expected object. The Image-to-Image model generates two heatmaps, one for each class (stroma and epithelium). Each heatmap displays the probabilities of exclusively locating nuclei of a single class.
As an Image-to-Image model, we used such architectures such as UNet, UNet++, LinkNet, and FPNet (Supplementary Materials Figures S3–S5). These models consist of an encoder, which compresses and extracts essential information from the image, and a decoder, which expands the image after the encoder. The architecture of the decoder is mirrored to the architecture of the encoder.
Predicting keypoints using heatmaps is an Image-to-Image task, and convolutional neural networks perform well in this regard. After obtaining heatmaps as logits of neural networks, we need to extract keypoints from them. We first aggregate all heatmaps. This aggregated heatmap is then subjected to a pooling operation with a parameterized kernel size (this depends on the size of input image; we used a kernel size equal to 13) and a stride of 1; the points in this heatmap that match the pooled results indicate local maxima. Each detected local maximum translates into a keypoint; the x and y coordinates on the heatmap determine its position, the value from the aggregated heatmap at that location defines the confidence, and the channel from the original heatmap denotes the class. The class of a keypoint is determined using the heatmap from which it originates. In other words, each heatmap yields keypoints belonging to only one class. Following that, the keypoints can be post-processed, which includes thresholding by confidence level and a weighted boxes fusion procedure [26].
2.4. Training of Detection Model
To find the optimal architecture for the detection model, a grid search of parameters was performed. We were in a situation where we had to trade off between the desire to conduct a grid search encompassing all conceivable parameters and the time needed for calculations. As a result, we opted to confine ourselves to a curated list of what we deemed to be the most crucial model parameters. The set of optimized parameters included the following: the backbone architecture, the parameters of the Keypoint Extractor (the threshold, the minimum distance between keypoints, and the value of pooling). The optimized value was the mean Average Precision (mAP), which we also used as a quality metric. Traditionally, predictions of object detection models are presented as BBoxes, whereas our model predictions are presented as Keypoints. To determine TP, FP, and FN, we used the Minkowski distance with degree two (which is the Euclidean distance). As a threshold distance, we used the value of the average radius of the nuclei (15.26 pixels for a 512 × 512 image size) obtained in EndoNuke [22]. The optimization step consists of training the model over 100 epochs with the current set parameters described above, choosing the best epoch based on the quality metric on a validation dataset and saving the results. A total of 100 epochs were chosen because our models were mainly trained to plateau in 40–50 epochs, but a surplus was allowed for architectures that needed more epochs.
After performing a grid search and choosing the optimal architecture of the detection model, such parameters as schedulers, optimizers, and augmentations were selected separately from each other.
From the list of loss functions—Huber loss, MSE, and Gaussian Focal loss (similar to a common Focal loss [27] function but for a continuous distribution)—we chose the Huber loss function because it performed effectively in our previous tasks:
where
- y = true label;
- = predicted label;
- = the threshold where the Huber loss function transitions from quadratic to linear.
2.5. Pre-Training
To improve the generalization ability of our CNN model, we employed self-supervised learning techniques. Pre-training refers to the process of training a model on a larger dataset before fine-tuning it on a more specific dataset. A schematic representation of the pre-training pipeline is depicted in Figure S1 in the Supplementary Materials. We utilized unlabeled tiles and employed the SimCLR method [28] to enhance the model’s generalization ability without the need for additional labeled tiles.
SimCLR works by maximizing the level of agreement between differently augmented versions of the same image using a contrastive loss function. The augmentations include random cropping, resizing, color distortion, and Gaussian blur. Figure 3 provides a detailed description of the model’s training process using SimCLR.
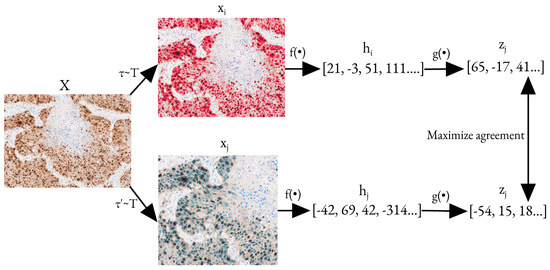
Figure 3.
Pre-training process with SimCLR [28]. Here, and are two augmentations taken from the same family of augmentations. is a base encoding network and is a projection head that maps a hidden representation to another space, where contrastive loss is applied. X is the initial image, and are the augmented images, and are the hidden representations of corresponding augmented images, and and are the outputs of the decoding network. The optimization task here is to maximize the agreement between and .
The unlabeled part of the PathLab dataset slides was filtered to exclude empty tiles by comparing the mean and standard deviation of choosing tiles with the corresponding threshold values. Cutting slides into tiles works the same way as in the labeled part. The resulting dataset contains 877,286 unlabeled tiles. We decided to test a model with an architecture that performed best in a grid search. A ResNet50 encoder with random initialized weights was pre-trained on an unlabeled dataset with the SimCLR method for 80 epochs.
To derive more conclusive insights, the predictions of the baseline model were subtracted from those of the pre-trained model. We employed bootstrapping, a statistical resampling method involving random sampling with replacement, to resample the resulting distribution. A total of 10,000 resamples were taken, and confidence intervals were calculated at a 95% confidence level. The bootstrapping procedure was repeated 10,000 times to obtain objective results.
2.6. H-Score Module
To calculate the H-score, we should add up the weighted counts of no, weak, moderate, and strong stained nuclei in the stroma and epithelium:
The EndoNet determines the degree of staining of each nucleus predicted by the detection model. It takes some area around the predicted keypoint (a square slightly smaller than the average radius of the core calculated in EndoNuke) averaged over each of the three channels. As a result, a vector of length 3 was obtained for each keypoint.
There are two types of nuclei on the tiles: unstained and stained. Unstained cells are blue cells that should not be counted. Stained cells are brown and have three degrees of staining: weak, moderate, and strong. The task of determining the degree of staining was divided into two subtasks: the separation of unstained from stained nuclei and the further classification of stained nuclei.
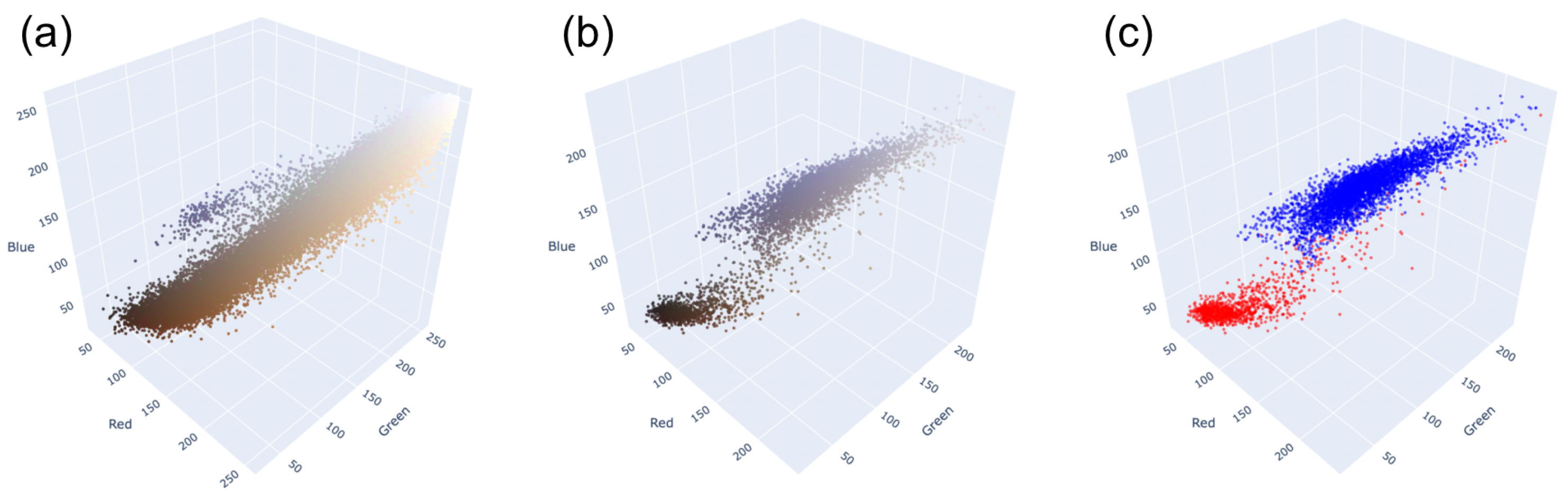
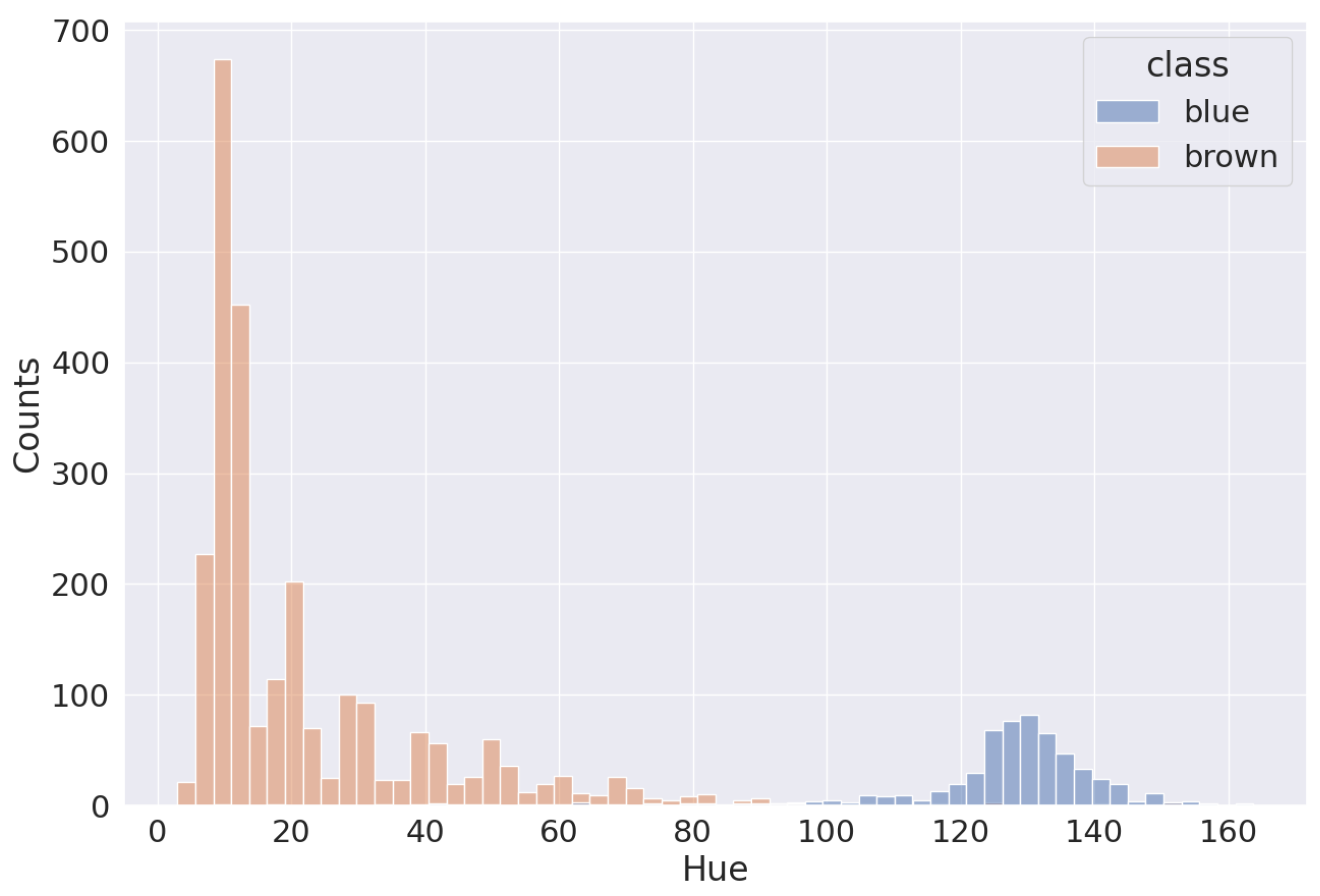
The first task is to separate the blue and brown nuclei on slides. As we can see in Figure 4, blue and brown nuclei are pretty well separated, even in the RGB-space. The distribution shown in the picture is based on the annotation by pathologists. The HSV-space is more useful in this case because the blue and brown colors are far from each other on Hue axis, as shown in Figure 5. Thus, it is easy to separate most of them (except nuclei with very weak staining). Because the two distributions are distinctly separated, there are multiple approaches to determining the threshold value. One common method involves calculating it as the average between the two peaks of the distributions. This is achieved by first smoothing out the distributions, which can be carried out through techniques like kernel density estimation or others, and then identifying the maximum point. Alternatively, one can employ an iterative approach, exploring various threshold values within a specific range to pinpoint the most appropriate one for the dataset. This is the method we used to establish the threshold in our analysis.
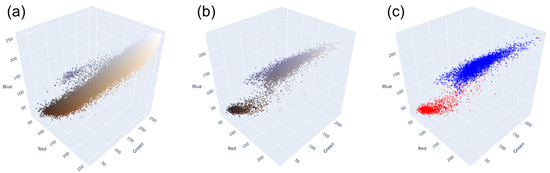
Figure 4.
Distributions of pixels of (a) the whole tile; (b) blue and brown nuclei, stained in their colors; (c) blue and brown nuclei, where red are brown nuclei and blue are blue nuclei.
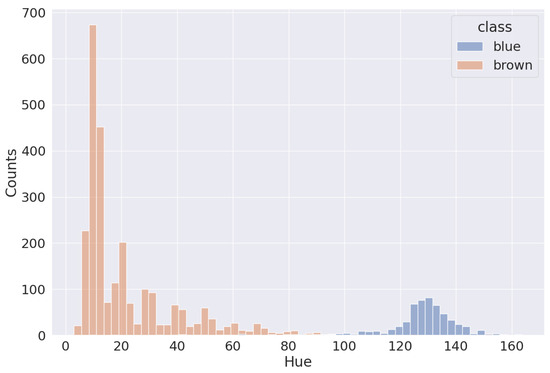
Figure 5.
Distribution of blue and brown nuclei in Hue channel.
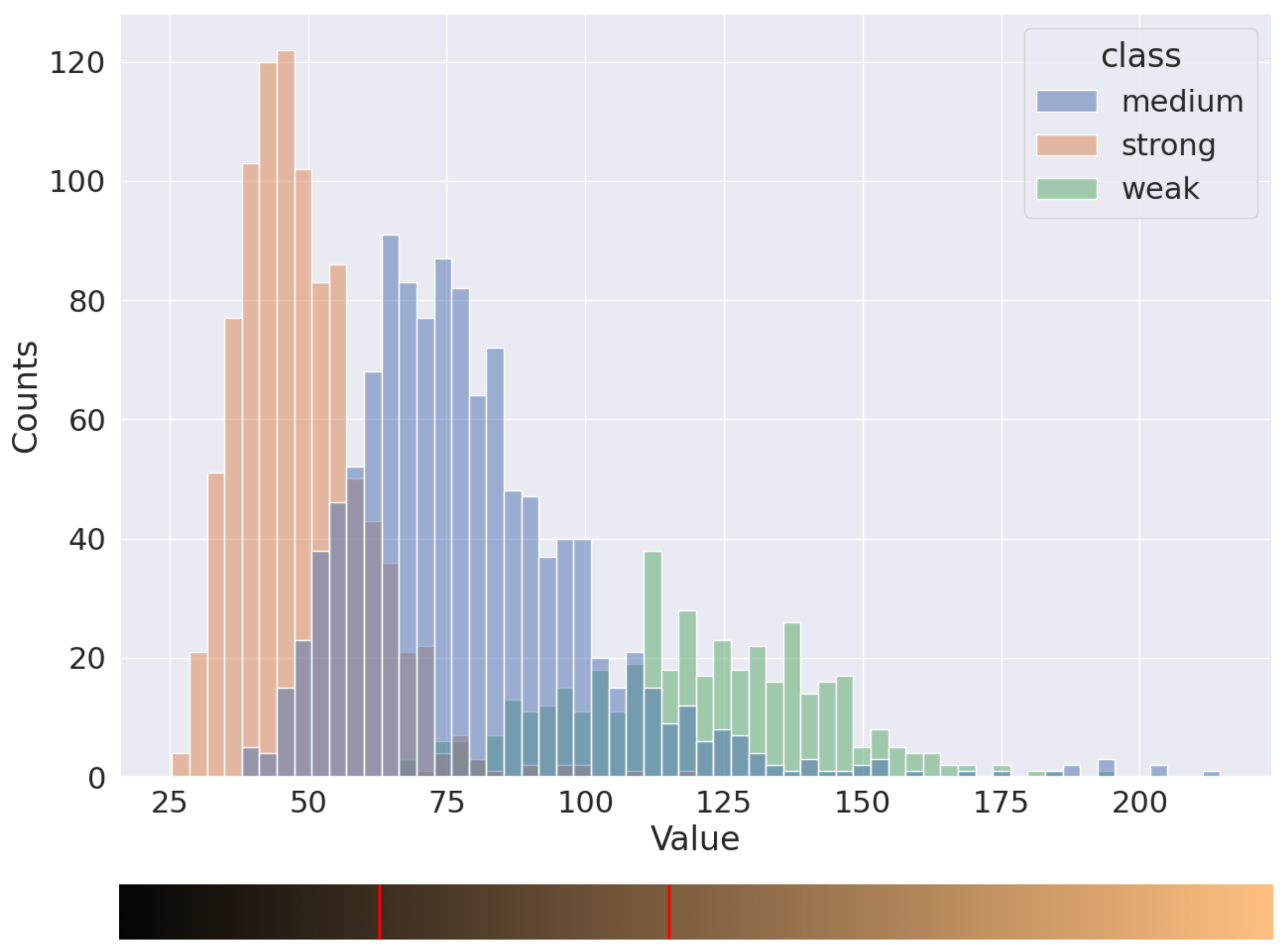
The second task is to classify stained brown nuclei into three classes: weak, moderate, and strong. However, there are no solid thresholds for these classes, and classification is a very subjective process. Thus, we annotated 40 tiles by 2 pathologists for 8 classes: no, weak, moderate, and strong stained nuclei for the stroma and epithelium. The pathologists annotated tiles independently from each other.
The distribution of pixels into three classes, marked by histopathologists, is presented in Figure 6. The distributions of weak and strong nuclei are easily distinguishable, but the moderate ones intersect a lot with others. With this distribution, it is possible to separate nuclei into three classes by using two thresholds. To determine the value of these thresholds, we iterated over a set of possible parameters and calculated the deviation between two H-scores: the H-score based on annotations made by pathologists and the H-score based on model predictions and the current set of thresholds. For instance, we obtained values 60 and 105 for the thresholds for the distribution in Figure 6.
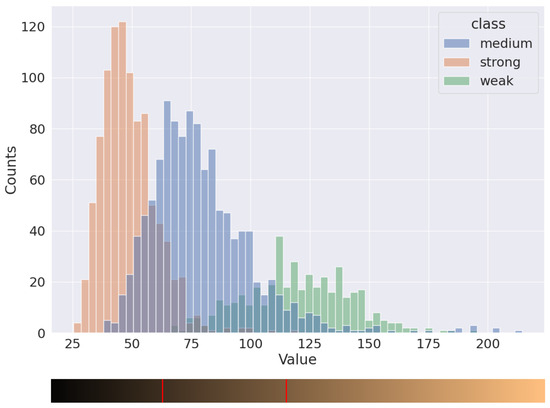
Figure 6.
Distribution of brown nuclei in Value channel.
Using an algorithm for selecting parameters, one can create a profile with thresholds for each pathologist. For this, one first needs to calibrate the model. For this purpose, several different regions of interest are selected and annotated. The model selects thresholds for annotated regions of interest. The thresholds received are saved for each doctor and can be used again.
2.7. Statistical Testing
Statistical testing was performed for the analysis of the obtained H-score values. To do this, the Holm–Sidak test was used for multiple comparisons. We considered a significance level of 0.05. Calculations for our statistical analysis were carried out in the Prism 7.0 software (GraphPad, Boston, MA, USA) program.
3. Results
3.1. Pre-Training Results
A model with the SimCLR pre-trained weights and a model with ImageNet pre-trained weights were compared against each other on a test dataset using the mAP metric. The metric was calculated for each batch in order to obtain a set of results instead of one number. The results are shown in Table 1. Table 1 also presents the confidence intervals for the mean difference in metrics between the pre-trained and baseline models. These intervals were calculated to estimate the range in which the true mean difference in metrics (Stroma AP, Epithelium AP, and mAP) would fall with a 95% confidence level. The potential for performance improvement is indicated by the upper bounds of the confidence intervals, especially for the Epithelium AP and mAP metrics. This suggests that the pre-training approach has merit and may offer advantages in specific scenarios.

Table 1.
Resulting metrics for the SimCLR pre-trained model and the ImageNET-based model, computed on the test dataset and with confidence interval bounds for mean differences in models.
3.2. Training
After finishing a grid search, we obtained “the best” model using a UnetPlusPlus with a ResNet50 backbone because it achieved the highest score. Moreover, during all iterations, we used image augmentations such as rotations, flips, Gaussian noise, HSV shift, and others. The training was conducted on a combined dataset and the results are presented in Table 2. The results for other trained models are presented in Supplementary Materials in Table S1. The performance metrics for the EndoNuke dataset and the Combined dataset exhibit minor variations only at the third decimal place. Nevertheless, it is crucial to underscore that the PathLab dataset, while an indispensable constituent of the combined test dataset, represents a relatively small fraction. Due to this proportionality, its influence on the final overall results remains limited, underscoring the assertion that its contribution to the conclusive outcomes is notably small.

Table 2.
Results computed on test samples.
3.3. H-Score
We annotated seven whole-slide images (Progesterone and Estrogen tiles) with five tiles per slide. The fourth slide was mutual for both pathologists to measure the level of agreement between them. Then, we calculated the thresholds for dividing colors of nuclei in the following way: we used three slides as a training dataset to find the optimal thresholds for the fourth, and we did so for each slide. For instance, to calculate thresholds for the third slide, we used the first, second, and fourth slides in the training process. The results are presented in Table 3.

Table 3.
Calculated thresholds of “Value” dimension in HSV space for each slide for both annotators. “Left” means threshold which divides strong and moderate staining and “Right” means threshold which divides moderate and weak staining, as in Figure 6. The fourth slide is mutual for calculating the agreement level.
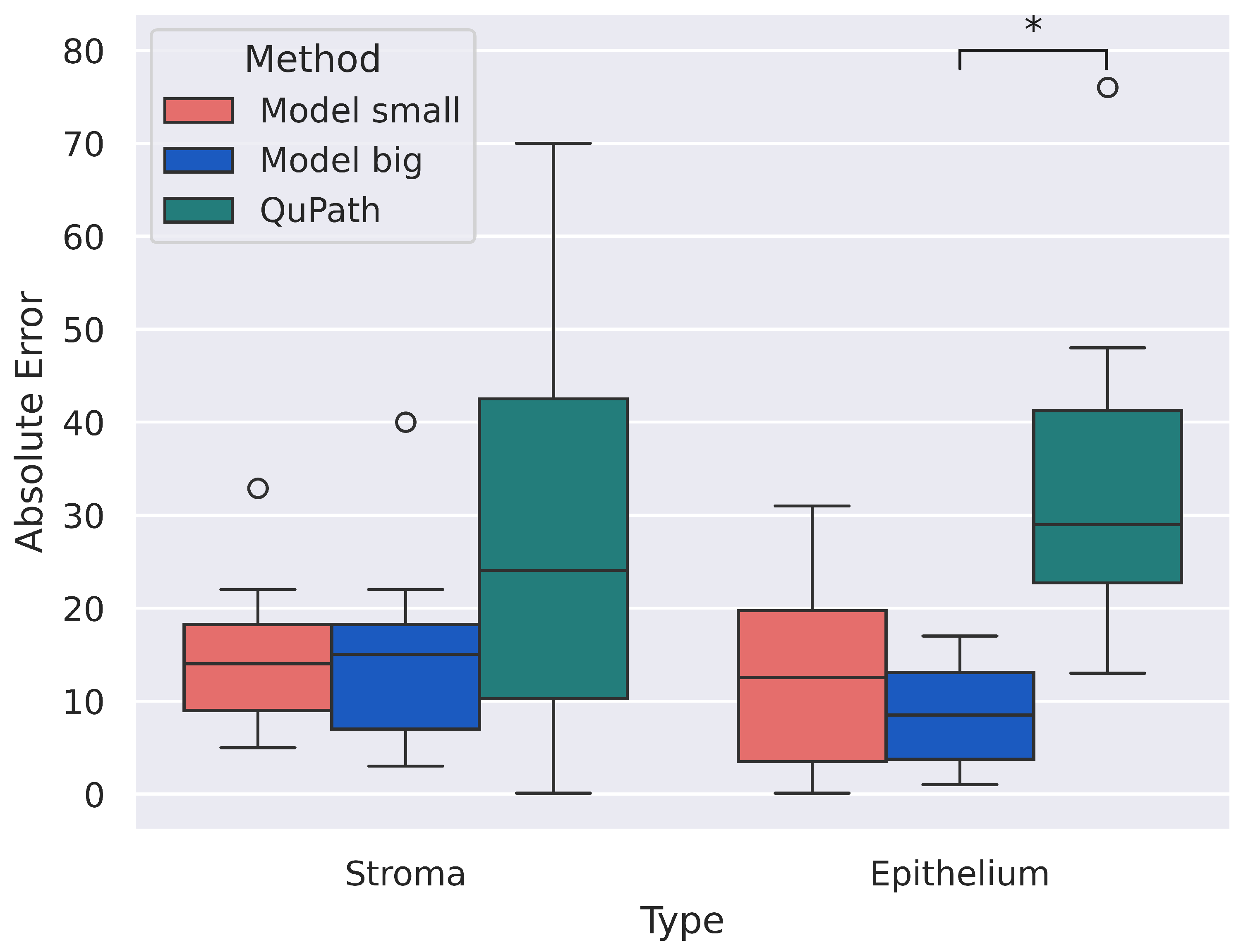
After calculating the thresholds, we measured the H-score for each slide using these thresholds. Our neural network provides keypoint annotations, i.e., the coordinates of centers and classes (stroma or epithelium) of nuclei. To classify stained nuclei into three classes—strong, moderate, and weak—we transformed the RGB image into HSV, took pixels in a small area around keypoints (with the mean radius of a nucleus being 2.98 µm [22]), calculated the mean value of the “Value” channel, and compared it with the thresholds. Moreover, we compared our model with the QuPath. The results presented in Table 4 are for stroma and epithelium. No significant differences were found during statistical analysis at a significance level of 0.05. Also, a calculation for the absolute error for the predicted H-score values was conducted. The absolute error was calculated as the modulus of the difference between the predicted H-score value and the “Manual” value. The results are shown in Figure 7. Significant differences were found between the values of “Model big” and “QuPath” for the epithelium at a significance level of 0.05. We can explain this significant difference found by the fact that “Model big” on the epithelium shows good and solid results and slightly deviates from the manual annotation, and “QuPath”, on the contrary, shows poor results.

Table 4.
Calculated H-score in stroma and epithelium for each slide for both annotators. The model scores for each slide are calculated based on thresholds from Table 3. The “Man.” H-score is based on the keypoint annotations of pathologists, the “Model small” H-score is based on annotations provided by our model on the same tiles, the “Model big” H-score is based on annotations provided by our model (but on the large amount of tiles from the same slides), and the “QP” H-score is calculated in the QuPath program (0.4.4 version).
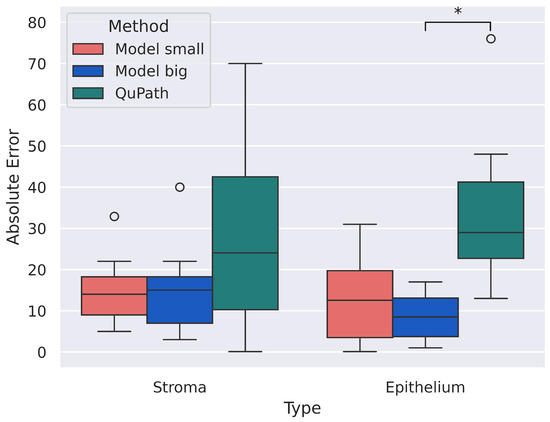
Figure 7.
Absolute error for “Model small”, “Model big”, and “QuPath”. Significant differences were found between “Model big” and “QuPath” for epithelium. Circles are outliers in the distributions, and ∗ indicates significant statistical difference among the distributions.
Despite the presence of discrepancies in the calculation of the H-score between experts and the model, such discrepancies do not lead to discrepancies in the interpretation of the expression class (weak, moderate, or strong). The results of the QuPath’s work are close to the results of our model; however, the “Model big” shows better results. Moreover, QuPath cannot separate cells into stromal and epithelial; this had to be performed manually. It also required considerable effort to select thresholds, find cells, and so on. Our model addresses all these shortcomings.
Many laboratories could differ from each other by even greater values. To compute the H-score, one can use the model without pre-calculating the thresholds by doctors. Instead, one can utilize the standard values calculated using the PathLab dataset. However, given the potential significant variations in slides, due to factors like diverse reagents, distinct equipment, varied staining techniques, and numerous other variables, it is advisable to establish specific thresholds for each novel laboratory.
Furthermore, an additional comparison was conducted to assess the H-score results by pathologists and the model. The H-score assessment by pathologists was performed in a “working conditions” setting, wherein cells were not marked in selected regions of interest and Formula (3) for counting was not used. Instead, pathologists relied on their internal intuition and approximate estimation of H-score. The results are illustrated in Figure S2 in the Supplementary Materials. The model utilized the average threshold values provided in Table 3 to evaluate the H-score.
4. Discussion
Immunohistochemical (IHC) analysis plays a crucial role in assessing protein biomarker expression in tissue samples, especially in oncology diagnostics. By visualizing the presence and distribution of specific proteins in tissues, IHC analysis provides valuable insights into disease diagnosis, prognosis, and treatment selection. However, traditional IHC analysis has limitations that can impact its reliability and reproducibility. These limitations include subjectivity in interpretation, a limited grading scale for scoring, and time-consuming manual evaluation, which can lead to inter-observer variability and inconsistency in results.
To overcome these challenges, computer-aided analysis, including automated H-score, has emerged as a promising alternative to standardize and streamline the IHC analysis process. The utilization of computer-aided analysis has the potential to greatly enhance the efficiency and accuracy of IHC analysis in clinical practice, leading to more reliable and reproducible results in many fields of diagnostics.
In this paper, we propose EndoNet, a CNN-based model designed to automatically calculate H-scores on histological slides. EndoNet can accurately and objectively analyze IHC-stained slides, reducing subjectivity and significantly speeding up the evaluation process. It achieved high results, such as a 0.77 Mean Average Precision on a test dataset. Furthermore, the model can be customized to suit the preferences of a specific specialist or an entire laboratory, enabling the replication of their preferred style of calculating the H-score. Moreover, we provide weights and code for models in the paper’s repository [29].
In recent years, the application of neural networks in the analysis of histological images has emerged as a promising approach for automated and efficient image analysis in various medical and scientific domains. Currently, several other models used for analyzing IHC slides are being developed. Hao Sun et el. [30] developed a CAD approach based on a CNN and attention mechanisms. They used 10-fold cross-validation on 3300 hematoxylin and eosin (H&E) image patches from 500 endometrial specimens, outperforming 3 human experts and 5 CNN-based classifiers in terms of overall classification performance. Amal Lahiani et al. [31] presented a deep learning method to automatically segment digitized slide images with multiple stainings into compartments of tumor, healthy tissue, necrosis, and background. Their method utilizes a full CNN that incorporates a color deconvolution segment that is trained end-to-end. This color deconvolution segment aids in accelerating the network’s convergence and enables it to effectively handle staining variability within the dataset. Also, they used 77 whole-slide images of colorectal carcinoma metastases in liver tissue from biopsy slides stained with H&E (blue, pink) and 8 additional IHC slides. Harshita Sharma et al. [32] analyzed H&E whole-slide images of gastric carcinoma with the help of deep learning methods in digital histopathology. Their proposed convolutional neural network architecture reports a classification accuracy of 0.6990 for cancer classification and 0.8144 for necrosis detection. A technique for automatic immune cell counting on digitally scanned images of IHC-stained slides was presented by Ting Chen et al. [33]. The method employs a sparse color unmixing approach to segregate the IHC image into distinct color channels that correspond to different cell structures. The algorithm’s performance was evaluated on a clinical dataset that comprised a substantial number of IHC slides.
Despite the studies being most closely aligned with our task, they are trained on data from a distinct domain, encompassing different tissue types and coloring methods. Furthermore, these studies lack a crucial H-score evaluation module that is of significance to our research. In addition, our model is unique in its task of assessing endometrium receptivity. Furthermore, our model offers the flexibility of individual customization for pathologists or the entire laboratory, rendering it a versatile tool in addressing specific requirements.
The H-score method for assessing the presence and distribution of proteins in tissue samples has some limitations, as it is time-consuming and lacks accuracy and precision. We propose a solution to these issues by developing a computer-aided method called EndoNet, which uses neural networks to automatically calculate the H-score on histological slides.
EndoNet consists of two main parts: a detection model that predicts the keypoints of the centers of nuclei, and an H-score module that calculates the value of the H-score using mean pixel values of predicted keypoints. The model was trained and validated on a set of annotated tiles and achieved high scores on a test dataset. Additionally, the model can be customized for specific specialists or laboratories to reproduce the manner of calculating the H-score.
The development of EndoNet can have significant benefits for pathologists, as it could improve the accuracy and efficiency of H-score calculations, which are important for the diagnosis and treatment of many diseases. However, EndoNet has some limitations.
The first is that the detection model proves to be less accurate on tiles from other labs. To mitigate this constraint and increase the generalizing ability of the model, several techniques can be explored, such as expanding the training dataset with slides from other labs or using special augmentation.
In addition, there are some works in this field that provide methods for nuclei with different staining on histology slides [1,34] (usually blue nuclei from brown). Many of them use specific transformations on the RBG space of input images. The most common transformation is a transformation into HSV space, where Red, Blue, and Green channels transform into Hue, Saturation, and Value. We also use this transformation. We carried out some experiments involving “HSV shift” augmentation aimed at increasing the metric value of a model trained on tiles from one lab and tested on tiles from another lab. Notably, these experiments yielded a significant improvement in the quality of the results. We maintain that further research on augmentations that are even more effective could lead to further enhancements in the quality of the model.
The second limitation pertains to the disparity between the real data and the data present in the dataset. To evaluate the H-score, a specialist is required to manually annotate and assess the color of each nucleus in the selected areas of interest. This is a time-consuming and monotonous task, particularly when evaluating numerous slides. Consequently, pathologists infrequently utilize this method to evaluate H-score. Instead of counting the number of weak, moderate, and strong nuclei, pathologists estimate the ratio of stained nuclei. This H-score assessment method is commonly employed in practice because of the large volume of samples that need to be processed each day. As a result, such results often vary from those obtained with an accurate assessment of stained nuclei. As depicted in Figure S2, the results differ significantly, and pathologists using this method often overestimate the H-score value. However, pathologists and the model reproduce similar H-score line shapes.
It is our belief that, upon addressing all the limitations, the model will be capable of demonstrating even more impressive outcomes. Nonetheless, EndoNet has already exhibited promising results and is endowed with significant potential. As a possible future direction for EndoNet, we envision its integration into the QuPath program and its deployment in laboratory testing.
5. Conclusions
Currently, endometrium evaluation in patients experiencing miscarriages, infertility, and unsuccessful IVF attempts is a dramatically important issue in reproduction. The endometrial receptivity assessment with immunohistochemistry (estrogen and progesterone receptor expression and their proportion) is one of the best available tools for this purpose. At the same time, the manual method of ER and PgR expression evaluation with H-score calculation is inconvenient and time-consuming because the endometrium is a heterogeneous multicomponent tissue that requires many fields of assessment to obtain a standardized and representative result. The development of an automated system for the evaluation of endometrial receptivity with H-score calculation not only speeds up the determination of this parameter but also compensates for errors resulting from different approaches to immunostaining (different antibody clones, staining protocols, dilution, and manual staining), as well as to reduce the scatter of data resulting from different pathologists’ calculation biases. EndoNet is a universally applicable and suitable algorithm for implementation in any pathology department.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/informatics10040090/s1, Figure S1: General pipeline of pre-training process; Table S1: Results computed on test sample for all trained models; Figure S2: H-scores by pathologists and EndoNet model for 6 slides in (a) stroma and (b) epithelium; Figure S3: Schematic view of (a) U-Net and (b) UNet++ architecture; Figure S4: Schematic view of LinkNET architecture; Figure S5: Schematic view of FPNet architecture.
Author Contributions
E.U., A.N. and V.F. contributed to the conception and design of the study. A.A., A.B. and A.T. organized the dataset. P.V. wrote sections of the manuscript. E.K., G.S. and T.F. contributed to revising the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Ministry of Science and Higher Education of the Russian Federation, agreement No. 075-15-2022-294, dated 15 April 2022. The section concerning the collecting and processing of samples was supported by the Ministry of Health of the Russian Federation within the framework of State Assignment №121032500100-3. The work of Vishnyakova P. was supported by the Russian Science Foundation [grant number 22-75-00048].
Institutional Review Board Statement
Slides that were not included in the dataset from [22] were provided by the pathology department of the National Medical Research Center for Obstetrics, Gynecology, and Perinatology, named after academician V.I. Kulakov of the Ministry of Healthcare of the Russian Federation. The Commission of Biomedical Ethics at the National Medical Research Center for Obstetrics, Gynecology, and Perinatology, and the Ministry of Healthcare of the Russian Federation, approved that the study was performed according to Good Clinical Practice guidelines and according to the Declaration of Helsinki (Ethics committee approval Protocol No. 5, 27 May 2021).
Informed Consent Statement
Each participant provided informed consent for the purposes of the study. Written consent for publication was obtained from the patients or their relatives.
Data Availability Statement
The PathLab dataset will be made available on request. Weights and code for models are provided in this study’s repository [29].
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Rizzardi, A.E.; Johnson, A.T.; Vogel, R.I.; Pambuccian, S.E.; Henriksen, J.; Skubitz, A.P.; Metzger, G.J.; Schmechel, S.C. Quantitative comparison of immunohistochemical staining measured by digital image analysis versus pathologist visual scoring. Diagn. Pathol. 2012, 7, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Srinidhi, C.L.; Ciga, O.; Martel, A.L. Deep neural network models for computational histopathology: A survey. Med Image Anal. 2021, 67, 101813. [Google Scholar] [CrossRef] [PubMed]
- Iizuka, O.; Kanavati, F.; Kato, K.; Rambeau, M.; Arihiro, K.; Tsuneki, M. Deep Learning Models for Histopathological Classification of Gastric and Colonic Epithelial Tumours. Sci. Rep. 2020, 10, 1504. [Google Scholar] [CrossRef] [PubMed]
- Budwit-Novotny, D.A.; McCarty, K.S.; Cox, E.B.; Soper, J.T.; Mutch, D.G.; Creasman, W.T.; Flowers, J.L.; McCarty, K.S., Jr. Immunohistochemical analyses of estrogen receptor in endometrial adenocarcinoma using a monoclonal antibody. Cancer Res. 1986, 46, 5419–5425. [Google Scholar] [PubMed]
- van Netten, J.P.; Thornton, I.G.; Carlyle, S.J.; Brigden, M.L.; Coy, P.; Goodchild, N.L.; Gallagher, S.; George, E.J. Multiple microsample analysis of intratumor estrogen receptor distribution in breast cancers by a combined biochemical/immunohistochemical method. Eur. J. Cancer Clin. Oncol. 1987, 23, 1337–1342. [Google Scholar] [CrossRef] [PubMed]
- Babu, R.; Balaji, D.; Reddy, G.; Paramaswamy, B.; Ramasundaram, M.; Agarwal, P.; Joseph, L.; D’Cruze, L.; Sundaram, S. Androgen receptor expression in hypospadias. J. Indian Assoc. Pediatr. Surg. 2020, 25, 6. [Google Scholar] [CrossRef]
- Pierceall, W.E.; Wolfe, M.; Suschak, J.; Chang, H.; Chen, Y.; Sprott, K.M.; Kutok, J.L.; Quan, S.; Weaver, D.T.; Ward, B.E. Strategies for H-score Normalization of Preanalytical Technical Variables with Potential Utility to Immunohistochemical-Based Biomarker Quantitation in Therapeutic Reponse Diagnostics. Anal. Cell. Pathol. 2011, 34, 159–168. [Google Scholar] [CrossRef]
- Sharada, P.; Swaminathan, U.; Nagamalini, B.; Vinod Kumar, K.; Ashwini, B. Histoscore and Discontinuity Score - A Novel Scoring System to Evaluate Immunohistochemical Expression of COX-2 and Type IV Collagen in Oral Potentially Malignant Disorders and Oral Squamous Cell Carcinoma. J. Orofac. Sci. 2021, 13, 96–104. [Google Scholar] [CrossRef]
- Ram, S.; Vizcarra, P.; Whalen, P.; Deng, S.; Painter, C.L.; Jackson-Fisher, A.; Pirie-Shepherd, S.; Xia, X.; Powell, E.L. Pixelwise H-score: A novel digital image analysis-based metric to quantify membrane biomarker expression from immunohistochemistry images. PLoS ONE 2021, 16, e0245638. [Google Scholar] [CrossRef]
- Pantanowitz, L.; Sharma, A.; Carter, A.B.; Kurc, T.; Sussman, A.; Saltz, J. Twenty Years of Digital Pathology: An Overview of the Road Travelled, What is on the Horizon, and the Emergence of Vendor-Neutral Archives. J. Pathol. Inform. 2018, 9, 40. [Google Scholar] [CrossRef]
- Gurcan, M.; Boucheron, L.; Can, A.; Madabhushi, A.; Rajpoot, N.; Yener, B. Histopathological Image Analysis: A Review. IEEE Rev. Biomed. Eng. 2009, 2, 147–171. [Google Scholar] [CrossRef]
- Madabhushi, A.; Lee, G. Image analysis and machine learning in digital pathology: Challenges and opportunities. Med Image Anal. 2016, 33, 170–175. [Google Scholar] [CrossRef] [PubMed]
- Veta, M.; Pluim, J.P.W.; van Diest, P.J.; Viergever, M.A. Breast Cancer Histopathology Image Analysis: A Review. IEEE Trans. Biomed. Eng. 2014, 61, 1400–1411. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Chen, H.; Li, X.; Xu, N.; Hu, Z.; Xue, D.; Qi, S.; Ma, H.; Zhang, L.; Sun, H. A review for cervical histopathology image analysis using machine vision approaches. Artif. Intell. Rev. 2020, 53, 4821–4862. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. In Advances in Neural Information Processing Systems; Pereira, F., Burges, C., Bottou, L., Weinberger, K., Eds.; Curran Associates, Inc.: San Diego, CA, USA, 2012; Volume 25. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 11–18 December 2015. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Sun, Y.; Huang, X.; Zhou, H.; Zhang, Q. SRPN: Similarity-based region proposal networks for nuclei and cells detection in histology images. Med Image Anal. 2021, 72, 102142. [Google Scholar] [CrossRef] [PubMed]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. arXiv 2015, arXiv:1512.03385. [Google Scholar]
- Avranas, A.; Kountouris, M. Coded ResNeXt: A network for designing disentangled information paths. arXiv 2022, arXiv:2202.05343. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. arXiv 2015, arXiv:1506.01497. [Google Scholar] [CrossRef]
- Naumov, A.; Ushakov, E.; Ivanov, A.; Midiber, K.; Khovanskaya, T.; Konyukova, A.; Vishnyakova, P.; Nora, S.; Mikhaleva, L.; Fatkhudinov, T.; et al. EndoNuke: Nuclei Detection Dataset for Estrogen and Progesterone Stained IHC Endometrium Scans. Data 2022, 7, 75. [Google Scholar] [CrossRef]
- Ronchi, M.R.; Perona, P. Benchmarking and Error Diagnosis in Multi-instance Pose Estimation. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017. [Google Scholar] [CrossRef]
- Kuhn, H.W. The Hungarian method for the assignment problem. Nav. Res. Logist. Q. 1955, 2, 83–97. [Google Scholar] [CrossRef]
- Cohen, J. A Coefficient of Agreement for Nominal Scales. Educ. Psychol. Meas. 1960, 20, 37–46. [Google Scholar] [CrossRef]
- Solovyev, R.; Wang, W.; Gabruseva, T. Weighted boxes fusion: Ensembling boxes from different object detection models. Image Vis. Comput. 2021, 107, 104117. [Google Scholar] [CrossRef]
- Lin, T.Y.; Goyal, P.; Girshick, R.; He, K.; Dollár, P. Focal Loss for Dense Object Detection. arXiv 2017, arXiv:1708.02002. [Google Scholar]
- Chen, T.; Kornblith, S.; Norouzi, M.; Hinton, G. A Simple Framework for Contrastive Learning of Visual Representations. arXiv 2020, arXiv:2002.05709. [Google Scholar]
- Ushakov, E.; Naumov, A.; Fomberg, V. EndoNet: Code and Weights. Available online: https://github.com/ispras/endonet (accessed on 26 November 2023).
- Sun, H.; Zeng, X.; Xu, T.; Peng, G.; Ma, Y. Computer-Aided Diagnosis in Histopathological Images of the Endometrium Using a Convolutional Neural Network and Attention Mechanisms. IEEE J. Biomed. Health Inform. 2020, 24, 1664–1676. [Google Scholar] [CrossRef]
- Lahiani, A.; Gildenblat, J.; Klaman, I.; Navab, N.; Klaiman, E. Generalising multistain immunohistochemistry tissue segmentation using end-to-end colour deconvolution deep neural networks. IET Image Process. 2019, 13, 1066–1073. [Google Scholar] [CrossRef]
- Sharma, H.; Zerbe, N.; Klempert, I.; Hellwich, O.; Hufnagl, P. Deep convolutional neural networks for automatic classification of gastric carcinoma using whole slide images in digital histopathology. Comput. Med Imaging Graph. 2017, 61, 2–13. [Google Scholar] [CrossRef]
- Chen, T.; Chefd’hotel, C. Deep Learning Based Automatic Immune Cell Detection for Immunohistochemistry Images. In Machine Learning in Medical Imaging; Springer International Publishing: Berlin/Heidelberg, Germany, 2014; pp. 17–24. [Google Scholar] [CrossRef]
- Krajewska, M.; Smith, L.H.; Rong, J.; Huang, X.; Hyer, M.L.; Zeps, N.; Iacopetta, B.; Linke, S.P.; Olson, A.H.; Reed, J.C.; et al. Image Analysis Algorithms for Immunohistochemical Assessment of Cell Death Events and Fibrosis in Tissue Sections. J. Histochem. Cytochem. 2009, 57, 649–663. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).