Analyzing Indo-European Language Similarities Using Document Vectors
Abstract
1. Introduction
1.1. Related Work
1.2. Research Aim
2. Materials and Methods
2.1. Dataset
2.1.1. Text Corpus
2.1.2. Preprocessing
2.1.3. Document Vectors
2.2. Determining Language Families and Structure
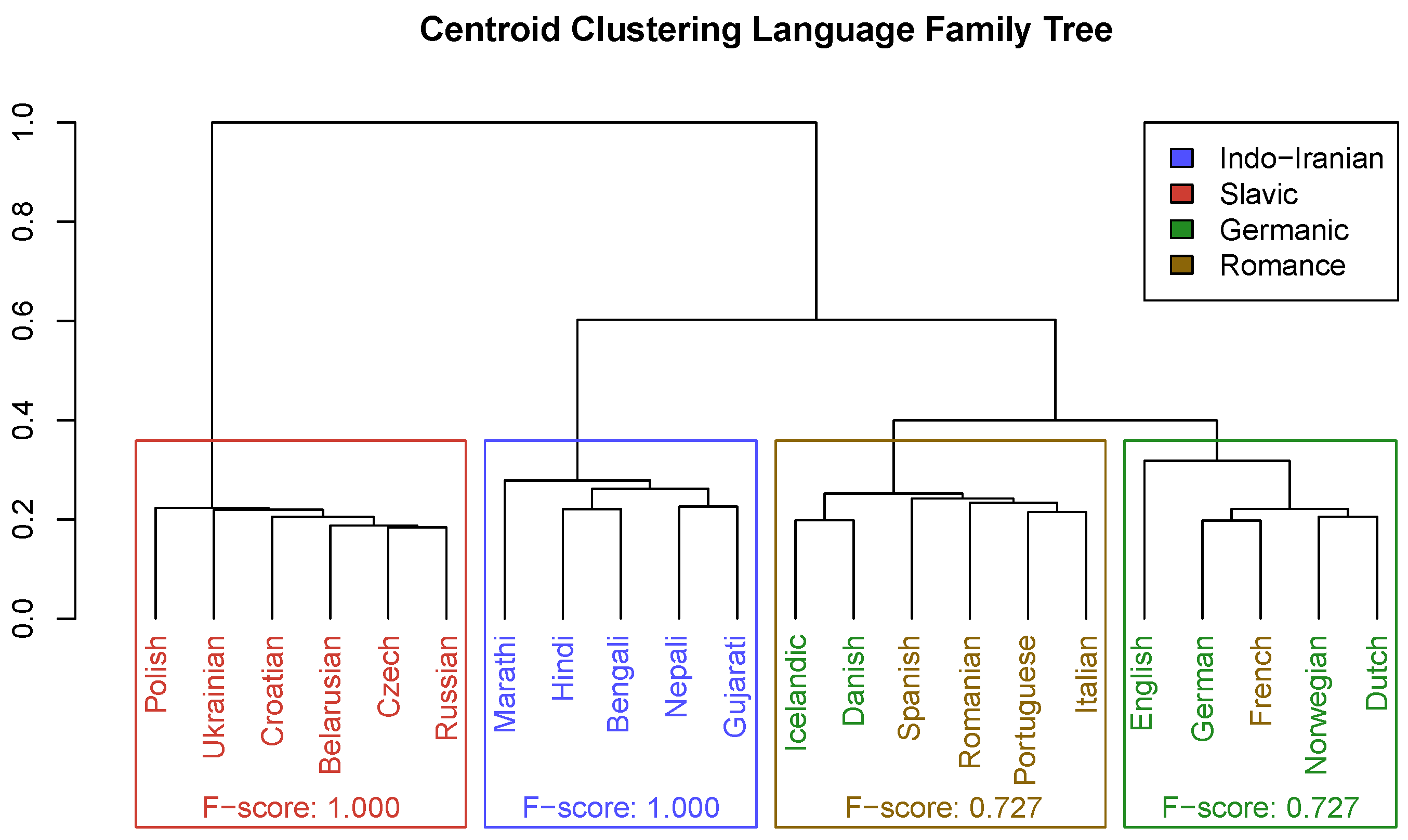
2.2.1. Method A: Hierarchical Clustering of Language Centroids
2.2.2. Method B: Network Partitioning and NMI
2.2.3. Method C: Deep Embedded Clustering
2.3. Performance Evaluation
Significance Testing
3. Results
3.1. Ground Truth
3.2. Evaluation of Centroid Clustering Method
3.3. Evaluation of Network Partitioning Method
Family-to-Family Similarity
3.4. Tree Distance Metrics
3.5. Evaluation of DEC Method
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DEC | Deep Embedded Clustering |
| POS | Part-of-Speech |
| LSTM | Long Short-Term Memory |
| NLP | Natural Language Processing |
| kNNs | K-Nearest Neighbors |
| NMI | Normalized Mutual Information |
| DM | Distributed Memory |
| DBOW | Distributed Bag of Words |
| PCA | Principal Component Analysis |
| KNC | Known Node-Correspondence |
| KL Divergence | Kullback–Leibler Divergence |
| SGD | Stochastic Gradient Descent |
| CDF | Cumulative Distribution Function |
References
- Jasonoff, J.H.; Cowgill, W. Indo-European Languages|Definition, Map, Characteristics, & Facts|Britannica. Available online: https://www.britannica.com/topic/Indo-European-languages/ (accessed on 24 July 2023).
- Gray, R.D.; Atkinson, Q.D. Language-tree divergence times support the Anatolian theory of Indo-European origin. Nature 2003, 426, 435–439. [Google Scholar] [CrossRef]
- Nagata, R.; Whittaker, E. Reconstructing an Indo-European family tree from non-native English texts. In Proceedings of the 51st Annual Meeting of the Association for Computational Linguistics, Sofia, Bulgaria, 4–9 August 2013; Volume 1: Long Papers, pp. 1137–1147. [Google Scholar]
- Rabinovich, E.; Ordan, N.; Wintner, S. Found in Translation: Reconstructing Phylogenetic Language Trees from Translations. In Proceedings of the 55th Annual Meeting of the Association for Computational Linguistics, Vancouver, BC, Canada, 30 July–4 August 2017; Volume 1: Long Papers, pp. 530–540. [Google Scholar] [CrossRef]
- Serva, M.; Petroni, F. Indo-European languages tree by Levenshtein distance. EPL 2008, 81, 68005. [Google Scholar] [CrossRef]
- Crawford, D. Language Family Analysis and Geocomputation. Bachelor’s Thesis, University of Pittsburgh, Pittsburgh, PA, USA, 2020. [Google Scholar]
- Zhao, Y.; Sun, W.; Wan, X. Constructing a Family Tree of Ten Indo-European Languages with Delexicalized Cross-linguistic Transfer Patterns. arXiv 2020, arXiv:2007.09076. [Google Scholar]
- Petroni, F.; Serva, M. Language distance and tree reconstruction. J. Stat. Mech. Theory Exp. 2008, 2008, P08012. [Google Scholar] [CrossRef]
- Wu, P.; Zhong, Y.; Black, A.W. Automatically Identifying Language Family from Acoustic Examples in Low Resource Scenarios. arXiv 2020, arXiv:2012.00876. [Google Scholar]
- Johnson, M.P. eBible: Bible Translations|Bible List. Available online: https://ebible.org/download.php (accessed on 13 June 2023).
- WordProject. WordProject Bibles Index—Choose the Bible in Your Own Language. Available online: https://www.wordproject.org/bibles/index.htm (accessed on 21 February 2023).
- Bader, B.W.; Kegelmeyer, W.P.; Chew, P.A. Multilingual Sentiment Analysis Using Latent Semantic Indexing and Machine Learning. In Proceedings of the 2011 IEEE 11th International Conference on Data Mining Workshops, Vancouver, BC, Canada, 11 December 2011; pp. 45–52. [Google Scholar] [CrossRef]
- Östling, R.; Tiedemann, J. Continuous multilinguality with language vectors. In Proceedings of the 15th Conference of the European Chapter of the Association for Computational Linguistics, Valencia, Spain, 3–7 April 2017; Volume 2, Short Papers, pp. 644–649. [Google Scholar] [CrossRef]
- Malaviya, C.; Neubig, G.; Littell, P. Learning Language Representations for Typology Prediction. In Proceedings of the 2017 Conference on Empirical Methods in Natural Language Processing, Copenhagen, Denmark, 7–11 September 2017; pp. 2529–2535. [Google Scholar] [CrossRef]
- Koehn, P. Europarl: A Parallel Corpus for Statistical Machine Translation. In Proceedings of the Machine Translation Summit X: Papers, Phuket, Thailand, 13–15 September 2005; pp. 79–86. [Google Scholar]
- Granger, S.; Dagneaux, E.; Meunier, F.; Paquot, M. International Corpus of Learner English v2; Presses universitaires de Louvain: Louvain-la-Neuve, Belgium, 2009. [Google Scholar]
- Wycliffe Global Alliance. 2022 Global Scripture Access. 2022. Available online: https://www.wycliffe.net/resources/statistics/ (accessed on 24 July 2023).
- Rabinovich, E.; Wintner, S.; Lewinsohn, O.L. A parallel corpus of translationese. In Proceedings of the Computational Linguistics and Intelligent Text Processing: 17th International Conference, CICLing 2016, Konya, Turkey, 3–9 April 2016; Revised Selected Papers, Part II. pp. 140–155. [Google Scholar]
- Le, Q.; Mikolov, T. Distributed Representations of Sentences and Documents. In Proceedings of the 31st International Conference on Machine Learning, Bejing, China, 22–24 June 2014; Xing, E.P., Jebara, T., Eds.; Proceedings of Machine Learning Research. JMLR: Cambridge, MA, USA, 2014; Volume 32, pp. 1188–1196. [Google Scholar]
- Dai, A.M.; Olah, C.; Le, Q.V. Document Embedding with Paragraph Vectors. arXiv 2015, arXiv:1507.07998. [Google Scholar]
- Mikolov, T.; Sutskever, I.; Chen, K.; Corrado, G.S.; Dean, J. Distributed representations of words and phrases and their compositionality. Adv. Neural Inf. Process. 2013, 26, 3111–3119. [Google Scholar]
- Rehurek, R.; Sojka, P. Gensim–Python Framework for Vector Space Modelling; NLP Centre, Faculty of Informatics, Masaryk University: Brno, Czech Republic, 2011; Volume 3, p. 2. [Google Scholar]
- Rossiello, G.; Basile, P.; Semeraro, G. Centroid-based text summarization through compositionality of word embeddings. In Proceedings of the MultiLing 2017 Workshop on Summarization and Summary Evaluation across Source Types and Genres, Valencia, Spain, 3 April 2017; pp. 12–21. [Google Scholar] [CrossRef]
- Radev, D.R.; Jing, H.; Styś, M.; Tam, D. Centroid-based summarization of multiple documents. Inf. Process. Manag. 2004, 40, 919–938. [Google Scholar] [CrossRef]
- Ward, J.H., Jr. Hierarchical Grouping to Optimize an Objective Function. J. Am. Stat. Assoc. 1963, 58, 236–244. [Google Scholar] [CrossRef]
- Tantardini, M.; Ieva, F.; Tajoli, L.; Piccardi, C. Comparing methods for comparing networks. Sci. Rep. 2019, 9, 17557. [Google Scholar] [CrossRef]
- Newman, M.E.J.; Girvan, M. Finding and evaluating community structure in networks. Phys. Rev. E 2004, 69, 026113. [Google Scholar] [CrossRef]
- Blondel, V.D.; Guillaume, J.L.; Lambiotte, R.; Lefebvre, E. Fast unfolding of communities in large networks. J. Stat. Mech. Theory Exp. 2008, 2008, P10008. [Google Scholar] [CrossRef]
- RAPIDS Development Team. RAPIDS: Libraries for End to End GPU Data Science. 2023. Available online: https://rapids.ai (accessed on 24 July 2023).
- Strehl, A.; Ghosh, J. Cluster ensembles—A knowledge reuse framework for combining multiple partitions. J. Mach. Learn. Res. 2002, 3, 583–617. [Google Scholar] [CrossRef][Green Version]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory (Wiley Series in Telecommunications and Signal Processing); Wiley-Interscience: Hoboken, NJ, USA, 2006. [Google Scholar]
- Xie, J.; Girshick, R.; Farhadi, A. Unsupervised deep embedding for clustering analysis. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; pp. 478–487. [Google Scholar]
- Guo, X. Keras Implementation for Deep Embedding Clustering (DEC). Available online: https://github.com/XifengGuo/DEC-keras/commit/2438070110b17b4fb9bc408c11d776fc1bd1bd56 (accessed on 18 April 2023).
- Robinson, D.F.; Foulds, L.R. Comparison of phylogenetic trees. Math. Biosci. 1981, 53, 131–147. [Google Scholar] [CrossRef]
- Kuhner, M.K.; Felsenstein, J. A simulation comparison of phylogeny algorithms under equal and unequal evolutionary rates. Mol. Biol. Evol. 1994, 11, 459–468. [Google Scholar] [CrossRef]
- Steel, M.A.; Penny, D. Distributions of Tree Comparison Metrics—Some New Results. Syst. Biol. 1993, 42, 126–141. [Google Scholar] [CrossRef]
- Schliep, K. Phangorn: Phylogenetic analysis in R. Bioinformatics 2011, 27, 592–593. [Google Scholar] [CrossRef] [PubMed]
- Kuhn, H.W. The Hungarian method for the assignment problem. Nav. Res. Logist. Q. 1955, 2, 83–97. [Google Scholar] [CrossRef]
- Gultepe, E.; Makrehchi, M. Improving clustering performance using independent component analysis and unsupervised feature learning. Hum. Cent. Comput. Inf. Sci. 2018, 8, 25. [Google Scholar] [CrossRef]
- Gultepe, E.; Conturo, T.E.; Makrehchi, M. Predicting and grouping digitized paintings by style using unsupervised feature learning. J. Cult. Herit 2018, 31, 13–23. [Google Scholar] [CrossRef]
- Beinborn, L.; Choenni, R. Semantic Drift in Multilingual Representations. Comput. Linguist. Assoc. Comput. Linguist. 2020, 46, 571–603. [Google Scholar] [CrossRef]
- Dutta Chowdhury, K.; España-Bonet, C.; van Genabith, J. Tracing Source Language Interference in Translation with Graph-Isomorphism Measures. In Proceedings of the International Conference on Recent Advances in Natural Language Processing (RANLP 2021), Online, 1–3 September 2021; pp. 375–385. [Google Scholar] [CrossRef]










| Family | Languages |
|---|---|
| Indo-Iranian | Bengali, Gujarati, Hindi, Marathi, Nepali |
| Slavic | Belarusian, Croatian, Czech, Polish, Russian, Ukrainian |
| Germanic | Danish, Dutch, English, German, Icelandic, Norwegian |
| Romance | French, Italian, Portuguese, Romanian, Spanish |
| Predicted Family | Actual Family | |||
|---|---|---|---|---|
| Indo-Iranian | Slavic | Germanic | Romance | |
| Indo-Iranian | 5 | 0 | 0 | 0 |
| Slavic | 0 | 6 | 0 | 0 |
| Germanic | 0 | 0 | 4 | 1 |
| Romance | 0 | 0 | 2 | 4 |
| Method | Family | Precision | Recall | F-Score |
|---|---|---|---|---|
| Centroid clustering | Indo-Iranian | 1.000 | 1.000 | 1.000 |
| Slavic | 1.000 | 1.000 | 1.000 | |
| Germanic | 0.800 | 0.667 | 0.727 | |
| Romance | 0.667 | 0.800 | 0.727 | |
| Network partitioning | Indo-Iranian | 1.000 | 1.000 | 1.000 |
| Slavic | 1.000 | 1.000 | 1.000 | |
| Germanic | 0.857 | 1.000 | 0.923 | |
| Romance | 1.000 | 0.800 | 0.889 | |
| Deep Embedded Clustering (DEC) | Indo-Iranian | 0.984 | 0.906 | 0.944 |
| Slavic | 0.864 | 0.999 | 0.927 | |
| Germanic | 0.643 | 0.834 | 0.726 | |
| Romance | 0.648 | 0.348 | 0.453 |
| Predicted Family | Actual Family | |||
|---|---|---|---|---|
| Indo-Iranian | Slavic | Germanic | Romance | |
| Indo-Iranian | 5 | 0 | 0 | 0 |
| Slavic | 0 | 6 | 0 | 0 |
| Germanic | 0 | 0 | 6 | 1 |
| Romance | 0 | 0 | 0 | 4 |
| Method | Symmetric Distance | Branch Score Difference | Path Difference | Quadratic Path Difference |
|---|---|---|---|---|
| Network tree | 24.000 | 0.972 | 32.311 | 2.747 |
| Centroid tree | 30.000 | 0.526 | 32.078 | 4.114 |
| Random tree (mean) | 37.498 | 1.181 | 50.102 | 5.712 |
| Random tree (stdev) | 0.947 | 0.077 | 2.337 | 0.218 |
| Predicted Family | Actual Family | |||
|---|---|---|---|---|
| Indo-Iranian | Slavic | Germanic | Romance | |
| Indo-Iranian | 109,557 | 119 | 1001 | 639 |
| Slavic | 11,367 | 144,997 | 284 | 11,106 |
| Germanic | 5 | 0 | 121,026 | 67,149 |
| Romance | 1 | 0 | 22,805 | 42,036 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schrader, S.R.; Gultepe, E. Analyzing Indo-European Language Similarities Using Document Vectors. Informatics 2023, 10, 76. https://doi.org/10.3390/informatics10040076
Schrader SR, Gultepe E. Analyzing Indo-European Language Similarities Using Document Vectors. Informatics. 2023; 10(4):76. https://doi.org/10.3390/informatics10040076
Chicago/Turabian StyleSchrader, Samuel R., and Eren Gultepe. 2023. "Analyzing Indo-European Language Similarities Using Document Vectors" Informatics 10, no. 4: 76. https://doi.org/10.3390/informatics10040076
APA StyleSchrader, S. R., & Gultepe, E. (2023). Analyzing Indo-European Language Similarities Using Document Vectors. Informatics, 10(4), 76. https://doi.org/10.3390/informatics10040076




