Motif-Based Graph Representation Learning with Application to Chemical Molecules
Abstract
1. Introduction
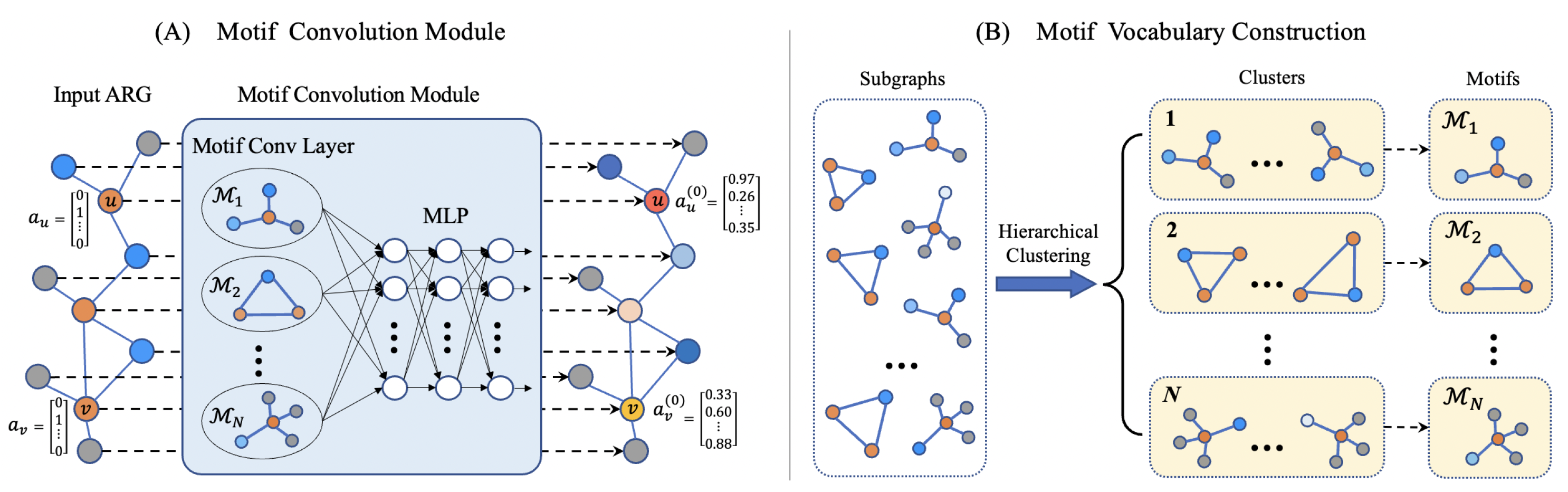
2. Motif-Based Graph Representation Learning
2.1. Motif Vocabulary Construction
2.2. ARG Similarity Measurement
2.3. Motif Convolution
2.4. Coupling Motif Convolution with GNNs
3. Experiments and Results
3.1. Classification on the Synthetic Dataset
3.2. Classification on Molecular Benchmarks
3.3. Molecule Property Prediction on QM9
3.4. Explainability of Motif Convolution
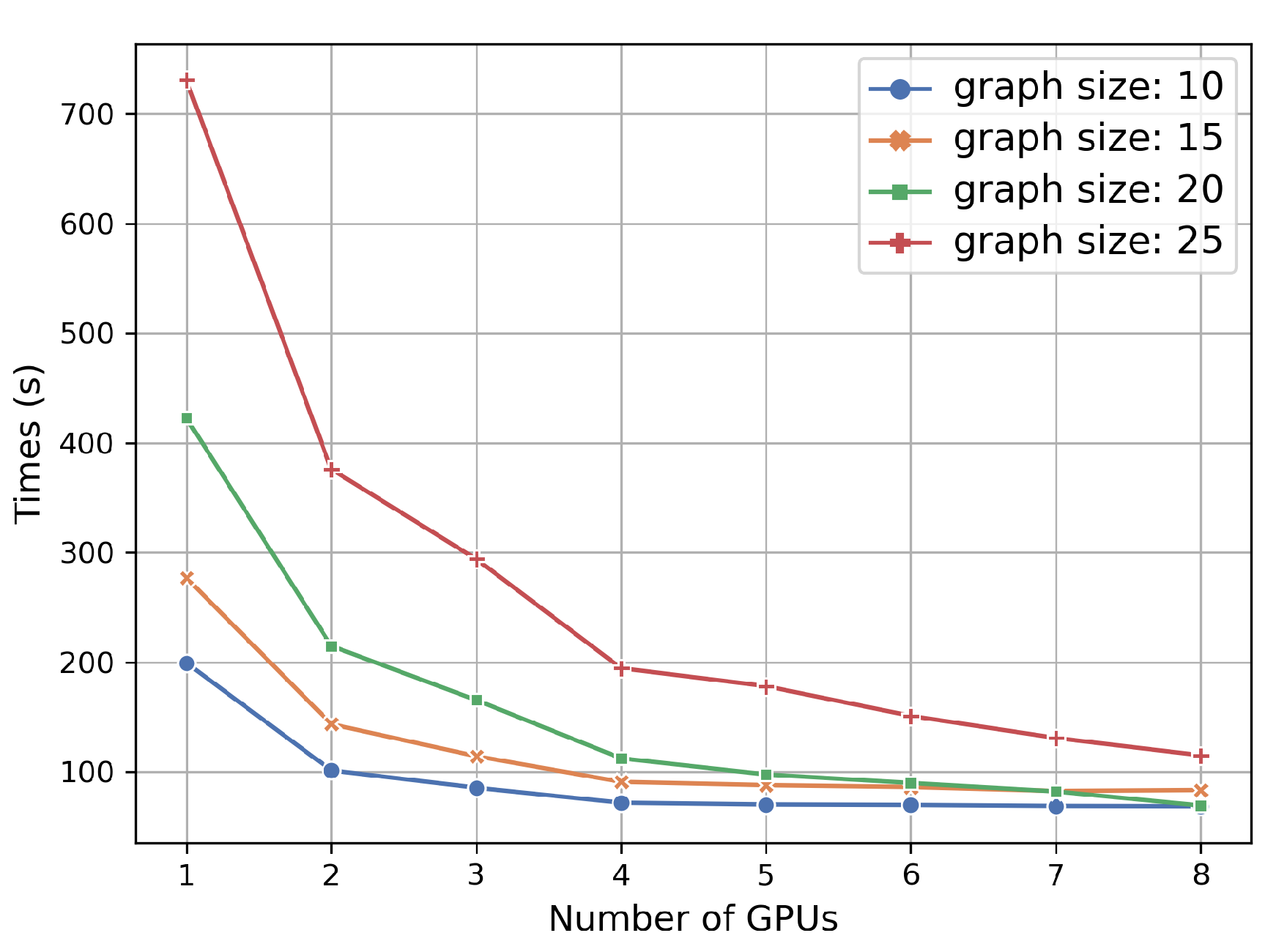
3.5. Efficiency of GPU Accelerated Motif Convolution
4. Related Works
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ARG | Attributed relational graph. |
| GNN | Graph neural network. |
| MLP | Multiple layer perceptron. |
| MCL | Motif convolution layer. |
| MCM | Motif convolution module. |
Appendix A. Proof of Theorem 1
Appendix B. GPU-Enabled ARG Matching
Appendix B.1. ARG Matching Used in MCM
Appendix B.2. ARG Matching
Appendix B.3. Simplified Graduated Assignment Algorithm for ARG Matching
| Algorithm A1 Simplified graduated assignment for ARG matching. |
|
Appendix B.4. GPU Accelerated ARG Matching
Appendix B.5. Complexity Analysis
Appendix C. Implementation Details and Additional Results
Appendix C.1. Settings of ARG Matching
Appendix C.2. Training Settings Used in the Synthetic Data Experiment
Appendix C.3. Additional Results in the Synthetic Data Experiment
| Class 1 | Class 2 | Class 3 | Class 4 | Class 5 | |
|---|---|---|---|---|---|
| GAT | |||||
| GCN | |||||
| GIN | |||||
| MCL-LR |
Appendix C.4. Experimental Settings of Molecular Benchmarks
| Dataset | # Graphs | # Graphs after Cleaning | # Tasks |
|---|---|---|---|
| bace | 1513 | 1513 | 1 |
| bbbp | 2039 | 1953 | 1 |
| clintox | 1478 | 1469 | 2 |
| sider | 1427 | 1295 | 27 |
| tox21 | 7831 | 7774 | 12 |
| toxcast | 8578 | 7245 | 617 |
| hiv | 41,127 | 41,125 | 1 |
Appendix C.5. Training Settings of MCM+MXMNet on QM9
| Model | # Params |
|---|---|
| DimeNet | 2,100,064 |
| MXMNet | 3,674,758 |
| MXMNet+MCM, vocab_size = 100 | 3,703,302 |
| MXMNet+MCM, vocab_size = 600 | 3,767,302 |
Appendix C.6. Efficiency of Executing MCM on QM9
Appendix C.7. Additional Results Demonstrating MCM’s Interpretability
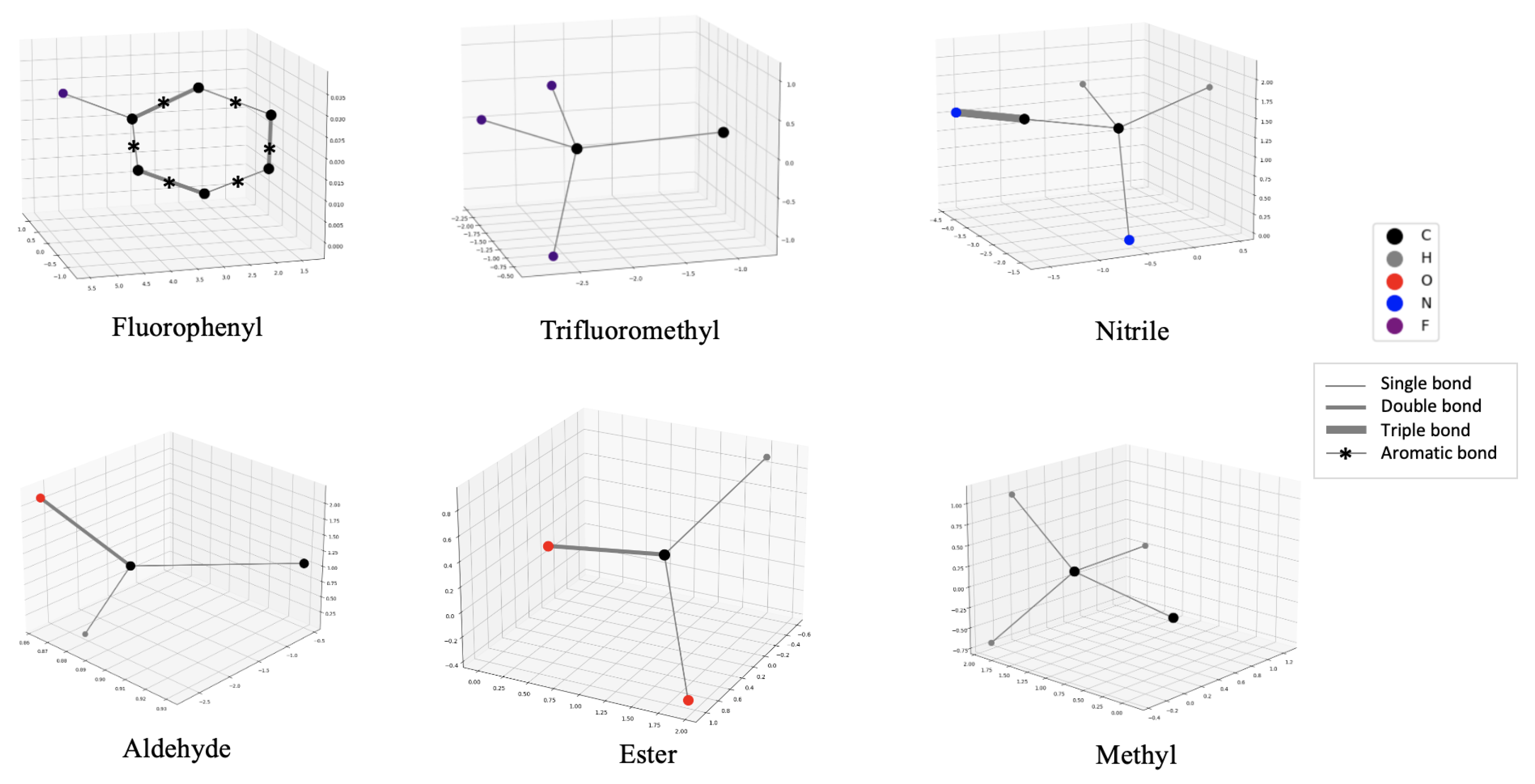
| Abbr | Name | Structural Formula |
|---|---|---|
| RPhF | Fluorophenyl |  |
| RCF | Trifluoromethyl |  |
| RCHOH | Alcohol |  |
| RCHO | Aldehyde |  |
| RCOOR’ | Ester |  |
| RCOR’ | Ketone |  |
| RCN | Nitrile |  |
| RCHR’ | Methylene | 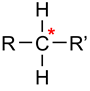 |
| RCH | Methyl | 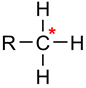 |
References
- Barrow, H.; Popplestone, R. Relational descriptions in picture processing. Mach. Intell. 1971, 6, 377–396. [Google Scholar]
- Tsai, W.H.; Fu, K.S. Error-correcting isomorphisms of attributed relational graphs for pattern analysis. IEEE Trans. Syst. Man Cybern. 1979, 9, 757–768. [Google Scholar] [CrossRef]
- Baskin, I.I.; Palyulin, V.A.; Zefirov, N.S. A neural device for searching direct correlations between structures and properties of chemical compounds. J. Chem. Inf. Comput. Sci. 1997, 37, 715–721. [Google Scholar] [CrossRef]
- Sperduti, A.; Starita, A. Supervised neural networks for the classification of structures. IEEE Trans. Neural Netw. 1997, 8, 714–735. [Google Scholar] [CrossRef] [PubMed]
- Gori, M.; Monfardini, G.; Scarselli, F. A new model for learning in graph domains. In Proceedings of the IEEE International Joint Conference on Neural Networks, Montreal, QC, Canada, 31 July–4 August 2005; pp. 729–734. [Google Scholar]
- Scarselli, F.; Yong, S.L.; Gori, M.; Hagenbuchner, M.; Tsoi, A.C.; Maggini, M. Graph neural networks for ranking web pages. In Proceedings of the 2005 IEEE/WIC/ACM International Conference on Web Intelligence, Washington, DC, USA, 19–22 September 2005; pp. 666–672. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Bruna, J.; Zaremba, W.; Szlam, A.; LeCun, Y. Spectral networks and locally connected networks on graphs. In Proceedings of the International Conference on Learning Representations, Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Henaff, M.; Bruna, J.; LeCun, Y. Deep Convolutional Networks on Graph-Structured Data. arXiv 2015, arXiv:1506.05163. [Google Scholar]
- Duvenaud, D.K.; Maclaurin, D.; Iparraguirre, J.; Bombarell, R.; Hirzel, T.; Aspuru-Guzik, A.; Adams, R.P. Convolutional networks on graphs for learning molecular fingerprints. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; pp. 2224–2232. [Google Scholar]
- Defferrard, M.; Bresson, X.; Vandergheynst, P. Convolutional neural networks on graphs with fast localized spectral filtering. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 3844–3852. [Google Scholar]
- Li, Y.; Tarlow, D.; Brockschmidt, M.; Zemel, R. Gated graph sequence neural networks. In Proceedings of the International Conference on Learning Representations, San Juan, Puerto Rico, 2–4 May 2016. [Google Scholar]
- Monti, F.; Boscaini, D.; Masci, J.; Rodola, E.; Svoboda, J.; Bronstein, M.M. Geometric deep learning on graphs and manifolds using mixture model cnns. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Chang, M.B.; Ullman, T.; Torralba, A.; Tenenbaum, J.B. A Compositional Object-Based Approach to Learning Physical Dynamics. In Proceedings of the International Conference on Learning Representations, Toulon, France, 24–26 April 2017. [Google Scholar]
- Gilmer, J.; Schoenholz, S.; Riley, P.F.; Vinyals, O.; Dahl, G. Neural Message Passing for Quantum Chemistry. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017. [Google Scholar]
- Chang, J.; Gu, J.; Wang, L.; Meng, G.; Xiang, S.; Pan, C. Structure-aware convolutional neural networks. In Proceedings of the Neural Information Processing Systems, Montréal, QC, Canada, 3–8 December 2018. [Google Scholar]
- Velickovic, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention networks. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Xu, K.; Li, C.; Tian, Y.; Sonobe, T.; Kawarabayashi, K.; Jegelka, S. Representation learning on graphs with jumping knowledge networks. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018. [Google Scholar]
- Ramakrishnan, R.; Dral, P.O.; Rupp, M.; Von Lilienfeld, O.A. Quantum chemistry structures and properties of 134 kilo molecules. Sci. Data 2014, 1, 1–7. [Google Scholar] [CrossRef]
- Schütt, K.; Kindermans, P.J.; Sauceda Felix, H.E.; Chmiela, S.; Tkatchenko, A.; Müller, K.R. Schnet: A continuous-filter convolutional neural network for modeling quantum interactions. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Lu, C.; Liu, Q.; Wang, C.; Huang, Z.; Lin, P.; He, L. Molecular property prediction: A multilevel quantum interactions modeling perspective. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 1052–1060. [Google Scholar]
- Klicpera, J.; Groß, J.; Günnemann, S. Directional message passing for molecular graphs. In Proceedings of the International Conference on Learning Representations, Addis Ababa, Ethiopia, 26–30 April 2020. [Google Scholar]
- Klicpera, J.; Giri, S.; Margraf, J.T.; Günnemann, S. Fast and uncertainty-aware directional message passing for non-equilibrium molecules. In Proceedings of the Machine Learning for Molecules Workshop, Neural Information Processing Systems, Online, 12 December 2020. [Google Scholar]
- Zhang, S.; Liu, Y.; Xie, L. Molecular Mechanics-Driven Graph Neural Network with Multiplex Graph for Molecular Structures. In Proceedings of the Machine Learning for Structural Biology Workshop at the 34th Conference on Neural Information Processing Systems, Online, 6–12 December 2020. [Google Scholar]
- Johnson, S.C. Hierarchical clustering schemes. Psychometrika 1967, 32, 241–254. [Google Scholar] [CrossRef]
- Demšar, J.; Curk, T.; Erjavec, A.; Črt Gorup; Hočevar, T.; Milutinovič, M.; Možina, M.; Polajnar, M.; Toplak, M.; Starič, A.; et al. Orange: Data Mining Toolbox in Python. J. Mach. Learn. Res. 2013, 14, 2349–2353. [Google Scholar]
- Gold, S.; Rangarajan, A. A graduated assignment algorithm for graph matching. IEEE Trans. Pattern Anal. Mach. Intell. 1996, 18, 377–388. [Google Scholar] [CrossRef]
- Menke, J.; Yang, A.Y. Graduated Assignment Graph Matching for Realtime Matching of Image Wireframes. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 25–29 October 2020; pp. 5909–5916. [Google Scholar]
- Wang, M.; Zheng, D.; Ye, Z.; Gan, Q.; Li, M.; Song, X.; Zhou, J.; Ma, C.; Yu, L.; Gai, Y.; et al. Deep Graph Library: A Graph-Centric, Highly-Performant Package for Graph Neural Networks. arXiv 2019, arXiv:1909.0131. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-Supervised Classification with Graph Convolutional Networks. arXiv 2017, arXiv:1609.02907. [Google Scholar]
- Xu, K.; Hu, W.; Leskovec, J.; Jegelka, S. How Powerful are Graph Neural Networks? In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018.
- Wu, Z.; Ramsundar, B.; Feinberg, E.N.; Gomes, J.; Geniesse, C.; Pappu, A.S.; Leswing, K.; Pande, V. MoleculeNet: A benchmark for molecular machine learning. Chem. Sci. 2018, 9, 513–530. [Google Scholar] [CrossRef]
- Subramonian, A. MOTIF-Driven Contrastive Learning of Graph Representations. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtually, 2–9 February 2021; Volume 35, pp. 15980–15981. [Google Scholar]
- Zhang, Z.; Liu, Q.; Wang, H.; Lu, C.; Lee, C.K. Motif-based Graph Self-Supervised Learning for Molecular Property Prediction. In Proceedings of the 35th Conference on Advances in Neural Information Processing Systems, Online, 6–14 December 2021; Volume 34. [Google Scholar]
- Landrum, G. Rdkit documentation. Release 2013, 1, 4. [Google Scholar]
- Hu, W.; Liu, B.; Gomes, J.; Zitnik, M.; Liang, P.; Pande, V.; Leskovec, J. Strategies for Pre-training Graph Neural Networks. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Ramsundar, B.; Eastman, P.; Walters, P.; Pande, V. Deep Learning for the Life Sciences: Applying Deep Learning to Genomics, Microscopy, Drug Discovery, and More; O’Reilly Media: Sebastopol, CA, USA, 2019. [Google Scholar]
- Faber, F.A.; Hutchison, L.; Huang, B.; Gilmer, J.; Schoenholz, S.S.; Dahl, G.E.; Vinyals, O.; Kearnes, S.; Riley, P.F.; Von Lilienfeld, O.A. Prediction errors of molecular machine learning models lower than hybrid DFT error. J. Chem. Theory Comput. 2017, 13, 5255–5264. [Google Scholar] [CrossRef] [PubMed]
- Van der Maaten, L.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Peters, D. Problem of the Lengths and Strengths of Carbon—Fluorine Bonds. J. Chem. Phys. 1963, 38, 561–563. [Google Scholar] [CrossRef]
- Perozzi, B.; Al-Rfou, R.; Skiena, S. Deepwalk: Online learning of social representations. In Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 24–27 August 2014; pp. 701–710. [Google Scholar]
- Tang, J.; Qu, M.; Wang, M.; Zhang, M.; Yan, J.; Mei, Q. Line: Large-scale information network embedding. In Proceedings of the 24th International Conference on World Wide Web, Florence, Italy, 18–22 May 2015; pp. 1067–1077. [Google Scholar]
- Grover, A.; Leskovec, J. node2vec: Scalable Feature Learning for Networks. In Proceedings of the KDD: Proceedings. International Conference on Knowledge Discovery & Data Mining, San Francisco, CA, USA, 13–17 August 2016; Volume 2016, pp. 855–864. [Google Scholar]
- Sun, F.Y.; Hoffman, J.; Verma, V.; Tang, J. InfoGraph: Unsupervised and Semi-supervised Graph-Level Representation Learning via Mutual Information Maximization. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Velickovic, P.; Fedus, W.; Hamilton, W.L.; Liò, P.; Bengio, Y.; Hjelm, R.D. Deep Graph Infomax. ICLR (Poster) 2019, 2, 4. [Google Scholar]
- Peng, Z.; Huang, W.; Luo, M.; Zheng, Q.; Rong, Y.; Xu, T.; Huang, J. Graph representation learning via graphical mutual information maximization. In Proceedings of the Web Conference 2020, Taipei, Taiwan, 20–24 April 2020; pp. 259–270. [Google Scholar]
- Henderson, K.; Gallagher, B.; Eliassi-Rad, T.; Tong, H.; Basu, S.; Akoglu, L.; Koutra, D.; Faloutsos, C.; Li, L. Rolx: Structural role extraction & mining in large graphs. In Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Beijing, China, 12–16 August 2012; pp. 1231–1239. [Google Scholar]
- Narayanan, A.; Chandramohan, M.; Chen, L.; Liu, Y.; Saminathan, S. subgraph2vec: Learning distributed representations of rooted sub-graphs from large graphs. arXiv 2016, arXiv:1606.08928. [Google Scholar]
- Ribeiro, L.F.; Saverese, P.H.; Figueiredo, D.R. struc2vec: Learning node representations from structural identity. In Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Halifax, NS, Canada, 13–17 August 2017; pp. 385–394. [Google Scholar]
- Hu, Z.; Dong, Y.; Wang, K.; Chang, K.W.; Sun, Y. Gpt-gnn: Generative pre-training of graph neural networks. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Virtual Event, 6–10 July 2020; pp. 1857–1867. [Google Scholar]
- You, Y.; Chen, T.; Wang, Z.; Shen, Y. When does self-supervision help graph convolutional networks? In Proceedings of the International Conference on Machine Learning, Online, 13–18 July 2020; pp. 10871–10880. [Google Scholar]
- Rong, Y.; Bian, Y.; Xu, T.; Xie, W.; Wei, Y.; Huang, W.; Huang, J. Self-Supervised Graph Transformer on Large-Scale Molecular Data. In Proceedings of the NeurIPS, Online, 6–12 December 2020. [Google Scholar]
- Sun, K.; Lin, Z.; Zhu, Z. Multi-stage self-supervised learning for graph convolutional networks on graphs with few labeled nodes. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 5892–5899. [Google Scholar]
- Qiu, J.; Chen, Q.; Dong, Y.; Zhang, J.; Yang, H.; Ding, M.; Wang, K.; Tang, J. Gcc: Graph contrastive coding for graph neural network pre-training. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Virtual Event, 6–10 July 2020; pp. 1150–1160. [Google Scholar]
- Hafidi, H.; Ghogho, M.; Ciblat, P.; Swami, A. Graphcl: Contrastive self-supervised learning of graph representations. arXiv 2020, arXiv:2007.08025. [Google Scholar]
- Hassani, K.; Khasahmadi, A.H. Contrastive multi-view representation learning on graphs. In Proceedings of the International Conference on Machine Learning, Virtual, 13–18 July 2020; pp. 4116–4126. [Google Scholar]
- You, Y.; Chen, T.; Sui, Y.; Chen, T.; Wang, Z.; Shen, Y. Graph contrastive learning with augmentations. Adv. Neural Inf. Process. Syst. 2020, 33, 5812–5823. [Google Scholar]
- Xu, M.; Wang, H.; Ni, B.; Guo, H.; Tang, J. Self-Supervised Graph-Level Representation Learning with Local and Global Structure. In Proceedings of the 38th International Conference on Machine Learning, PMLR, Virtual, 18–24 July 2021; pp. 11548–11558. [Google Scholar]
- Zhao, C.; Liu, S.; Huang, F.; Liu, S.; Zhang, W. CSGNN: Contrastive self-supervised graph neural network for molecular interaction prediction. In Proceedings of the Thirtieth International Joint Conference on Artificial Intelligence, Online, 19–26 August 2021; pp. 19–27. [Google Scholar]
- Lawler, E.L. The quadratic assignment problem. Manag. Sci. 1963, 9, 586–599. [Google Scholar] [CrossRef]
- Sinkhorn, R. A relationship between arbitrary positive matrices and doubly stochastic matrices. Ann. Math. Stat. 1964, 35, 876–879. [Google Scholar] [CrossRef]
- Harris, M. Optimizing Cuda. Supercomputing 2007 Tutorial, Reno, NV, USA. November 2007. Available online: https://www.enseignement.polytechnique.fr/profs/informatique/Eric.Goubault/Cours09/CUDA/SC07_CUDA_5_Optimization_Harris.pdf (accessed on 4 January 2023).
- Chen, J.; Zheng, S.; Song, Y.; Rao, J.; Yang, Y. Learning Attributed Graph Representation with Communicative Message Passing Transformer. In Proceedings of the Thirtieth International Joint Conference on Artificial Intelligence (IJCAI), Virtual Event, 19–27 August 2021; pp. 2242–2248. [Google Scholar]
- Lim, S.; Lee, Y.O. Predicting chemical properties using self-attention multi-task learning based on SMILES representation. In Proceedings of the 2020 25th International Conference on Pattern Recognition (ICPR), Milan, Italy, 10–15 January 2021; pp. 3146–3153. [Google Scholar]
- Sterling, T.; Irwin, J.J. ZINC 15–ligand discovery for everyone. J. Chem. Inf. Model. 2015, 55, 2324–2337. [Google Scholar] [CrossRef] [PubMed]
- Walsh, A. The dependence of the properties of carbonyl compounds upon polarity. Trans. Faraday Soc. 1947, 43, 158–163. [Google Scholar] [CrossRef]


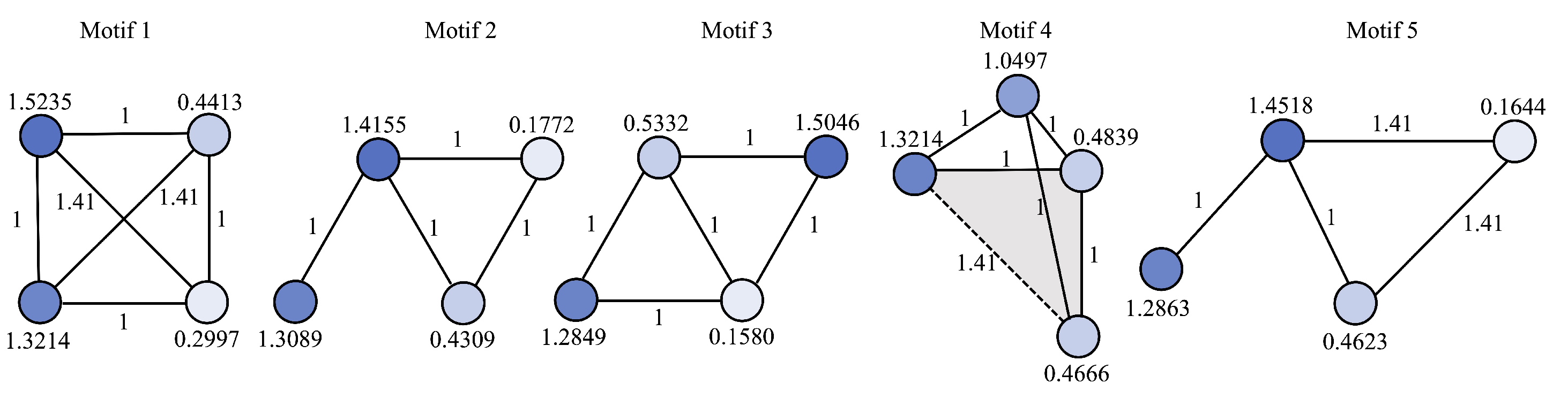


| Dataset Size | GAT | GCN | GIN | MCL-LR |
|---|---|---|---|---|
| 500 | ||||
| 10000 |
| Dataset | bace | bbbp | clintox | sider | tox21 | toxcast | hiv |
|---|---|---|---|---|---|---|---|
| GCN | 0.811 ± 0.030 | 0.881 ± 0.036 | 0.615 ± 0.102 | 0.615 ± 0.025 | 0.784 ± 0.017 | 0.633 ± 0.007 | 0.754 ± 0.067 |
| GIN | 0.797 ± 0.049 | 0.873 ± 0.036 | 0.530 ± 0.065 | 0.616 ± 0.025 | 0.783 ± 0.024 | 0.634 ± 0.009 | 0.762 ± 0.058 |
| MICRO-Graph | 0.819 ± 0.004 | 0.870 ± 0.008 | 0.540 ± 0.024 | 0.617 ± 0.018 | 0.774 ± 0.006 | 0.635 ± 0.006 | 0.780 ± 0.026 |
| MGSSL (DFS) | 0.797 ± 0.008 | 0.705 ± 0.011 | 0.797 ± 0.022 | 0.605 ± 0.007 | 0.764 ± 0.004 | 0.638 ± 0.030 | 0.795 ± 0.011 |
| MGSSL (BFS) | 0.791 ± 0.009 | 0.697 ± 0.001 | 0.807 ± 0.021 | 0.618 ± 0.008 | 0.765 ± 0.003 | 0.641 ± 0.070 | 0.788 ± 0.012 |
| MCM + GCN | 0.806 ± 0.026 | 0.917 ± 0.031 | 0.612 ± 0.145 | 0.624 ± 0.024 | 0.794 ± 0.015 | 0.650 ± 0.012 | 0.792 ± 0.046 |
| MCM + GIN | 0.820 ± 0.055 | 0.900 ± 0.031 | 0.655 ± 0.139 | 0.627 ± 0.028 | 0.802 ± 0.015 | 0.651 ± 0.010 | 0.800 ± 0.043 |
| Task | SchNet | DimeNet | DimeNet++ | MXMNet Å | MXMNet Å | MCM+MXMNet Å | MCM+MXMNet Å |
|---|---|---|---|---|---|---|---|
| (D) | 0.033 | 0.0286 | 0.0297 | 0.0382 | 0.0255 | 0.0375 | 0.0251 |
| 0.235 | 0.0469 | 0.0435 | 0.0482 | 0.0465 | 0.0477 | 0.0456 | |
| (meV) | 41 | 27.8 | 24.6 | 23.0 | 22.8 | 21.9 | 22.6 |
| (meV) | 34 | 19.7 | 19.5 | 19.5 | 18.9 | 18.5 | 18.6 |
| (meV) | 63 | 34.8 | 32.6 | 31.2 | 30.6 | 32.1 | 31.9 |
| 0.073 | 0.331 | 0.331 | 0.506 | 0.088 | 0.489 | 0.124 | |
| ZPVE (meV) | 1.7 | 1.29 | 1.21 | 1.16 | 1.19 | 1.14 | 1.18 |
| (meV) | 14 | 8.02 | 6.32 | 6.10 | 6.59 | 5.97 | 6.49 |
| U (meV) | 19 | 7.89 | 6.28 | 6.09 | 6.64 | 6.02 | 6.51 |
| H (meV) | 14 | 8.11 | 6.53 | 6.21 | 6.67 | 6.01 | 6.50 |
| G (meV) | 14 | 8.98 | 7.56 | 7.30 | 7.81 | 7.13 | 7.54 |
| () | 0.033 | 0.0249 | 0.0230 | 0.0228 | 0.0233 | 0.0230 | 0.0234 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Chen, S.; Chen, G.; Shurberg, E.; Liu, H.; Hong, P. Motif-Based Graph Representation Learning with Application to Chemical Molecules. Informatics 2023, 10, 8. https://doi.org/10.3390/informatics10010008
Wang Y, Chen S, Chen G, Shurberg E, Liu H, Hong P. Motif-Based Graph Representation Learning with Application to Chemical Molecules. Informatics. 2023; 10(1):8. https://doi.org/10.3390/informatics10010008
Chicago/Turabian StyleWang, Yifei, Shiyang Chen, Guobin Chen, Ethan Shurberg, Hang Liu, and Pengyu Hong. 2023. "Motif-Based Graph Representation Learning with Application to Chemical Molecules" Informatics 10, no. 1: 8. https://doi.org/10.3390/informatics10010008
APA StyleWang, Y., Chen, S., Chen, G., Shurberg, E., Liu, H., & Hong, P. (2023). Motif-Based Graph Representation Learning with Application to Chemical Molecules. Informatics, 10(1), 8. https://doi.org/10.3390/informatics10010008


_Bryant.png)




