Abstract
Disease phenotypes are generally caused by the failure of gene modules which often have similar biological roles. Through the study of biological networks, it is possible to identify the intrinsic structure of molecular interactions in order to identify the so-called “disease modules”. Community detection is an interesting and valuable approach to discovering the structure of the community in a complex network, revealing the internal organization of the nodes, and has become a leading research topic in the analysis of complex networks. This work investigates the link between biological modules and network communities in test-case biological networks that are commonly used as a reference point and which include Protein–Protein Interaction Networks, Metabolic Networks and Transcriptional Regulation Networks. In order to identify small and structurally well-defined communities in the biological context, a hybrid immune metaheuristic algorithm Hybrid-IA is proposed and compared with several metaheuristics, hyper-heuristics, and the well-known greedy algorithm Louvain, with respect to modularity maximization. Considering the limitation of modularity optimization, which can fail to identify smaller communities, the reliability of Hybrid-IA was also analyzed with respect to three well-known sensitivity analysis measures (NMI, ARI and NVI) that assess how similar the detected communities are to real ones. By inspecting all outcomes and the performed comparisons, we will see that on one hand Hybrid-IA finds slightly lower modularity values than Louvain, but outperforms all other metaheuristics, while on the other hand, it can detect communities more similar to the real ones when compared to those detected by Louvain.
1. Introduction
In the last few years, significant advances in biological technology and the rapid adoption of high-throughput approaches [1] have made it possible the measurement of tens of thousands of “omic” data points across multiple levels (DNA, RNA, protein, metabolite, etc.) from a biological sample. The availability of a large amount of data has led to the development of new methods based on the integration analysis of molecular data with mathematical models, and the consequent consolidation of Systems Biology, an interdisciplinary research area that uses a holistic approach to biological research by using mathematical methods to derive global models of cellular processes in physiology and disease. The challenge from the systems biology point of view is to convert the data into information and knowledge so improve personalized therapies for patients. It becomes therefore necessary to carry out a high-level analysis of the representation of a biological system.
Networks are probably the most suitable tool for this type of investigation. They allow a good representation of the binary relationships between biological entities and are, for this reason, the most used tool in systems biology [2,3]. In particular, they also provide a mathematical representation of biological systems, where nodes may represent either proteins, as in the case of protein–protein interaction networks, or genes and transcription factors, as in the case of gene co-expression networks, or metabolites, in the case of metabolic networks. These interactions determine the molecular and cellular mechanisms responsible for healthy or unhealthy states in organisms and can be physical or functional. In this second case, the network nodes are associated with each other in modules, where a tightly connected group of nodes share a common function to perform a specific task. The modules detected by biological networks are generally responsible for a common phenotype and are useful in providing insights related to biological functionality. Disease phenotypes are generally caused by the failure of groups of genes that are referred to as the disease form. Since the genes responsible for a phenotype often have common functions, there is a strong association between pathological and functional modules [3,4,5].
The detection of modules within biological networks, generally responsible for a common phenotype, is useful and crucial in providing insights into the biological function of these genes. The techniques that allow the identification of modules, known as community detection techniques, are methods that play a key role in obtaining the functional modules which appear to be closely related to pathological forms, whose recognition would be useful for the molecular understanding and the etiology of the disease. From such an understanding would arise the development of specific drugs whose targets would be the genes belonging to these modules.
In this research work, we propose a hybrid immune algorithm for community detection denoted Hybrid-IA. The algorithm is inspired by the immune system dynamics, and it carries out an effective exploration of large search spaces, by combining a random search process with a deterministic one, and by efficient exploitation of the gained knowledge. Although the algorithm has been successfully applied in several research areas, including community detection [6,7], the main goal of this work is to consolidate the robustness and reliability of the proposed algorithm in detecting community structures in large biological networks. Furthermore, to reach our goal, we studied the similarity of the detected communities to the real ones. Therefore, even though the presented algorithm is essentially the same, this research paper properly extends the work in [7] by carrying out a more detailed and complete sensitivity analysis in order to assess the real robustness of Hybrid-IA in detecting communities in complex and large networks, specifically larger and purely biological networks, which needed for the algorithm to be improved in terms of storage optimization and execution time.
The rest of the paper is organized as follows. Section 2 introduces and describes the community detection problem and its relevance in the biological context. Modularity optimization, which is the basis of the detection process, is described, and formally defined in Section 2. The proposed and developed Hybrid-IA algorithm is explained in detail in Section 3. In Section 4, we present a summary of the biological networks used as a data set, whilst outcomes and comparisons are displayed and discussed in Section 5. In particular, Section 5.1 shows the performed convergence and learning analysis, while Section 5.2 examines in detail all the obtained results and performed comparisons. In Section 5.3, we present the investigation we performed on Hybrid-IA with respect to the NMI evaluation metric. Furthermore, two other functional sensitivity metrics, namely ARI and NVI, were considered and tested, the results are presented in this section as well. Conclusions and final comments are presented in Section 6.
2. Community Detection
Community detection and clustering in networks are commonly used interchangeably. The goal of community detection is to find hidden relations among the nodes in the network and use such relations to identify clusters or communities of nodes. Generally speaking, we can define a community in a network or graph as a subset of the sets of nodes that identifies a highly dense connected subgraph with sparse connections with vertices outside the subgraph.
Community detection allows us to understand the dynamics of a complex network at different scales [8,9,10], such as connections and interactions between underlying entities, and, consequently, to uncover important information that becomes useful and crucial in many application areas such as biology; medicine; economic; social sciences; and many others. It is, however, a very difficult process due to the type of information modeled by the network. One important example is represented by social relationships among people. In such cases, the study of community structures in a network is a central issue in better understanding social dynamics, and, for this, it has inspired intense research activities also in closely related fields, such as patterns of people movements [11,12,13,14,15]. In biological sciences, the ability to detect highly linked communities and their interactions might be very beneficial in understanding how genes interact and affect each other.
Modularity (Q) is a valuation measure commonly used for assessing the quality of node partitions, i.e., communities, detected in a network [16]. Given such a valuation measure, the community detection problem can easily be summarized as the problem of finding clusters that maximize The problem is computationally hard and, specifically, -complete for its decisional version [17].
Several search algorithms for clustering problems have been developed and proven to be fast and reliable in finding as good communities as possible, even when dealing with large networks, solely based on specific topological properties of complex networks [18,19]. Some other algorithms make use of both topological and attribute information for the clustering analysis of complex networks. For example, in [20] the authors have proposed a fast fuzzy clustering algorithm, called FCAN, which integrates both types of information into a single fuzzy clustering framework [21] with a generalized momentum method to accelerate the convergence. Other algorithms, instead, are based on probabilistic models in which the problem of graph clustering is translated into a probabilistic inference problem, that is, a Bayesian model for attributed graph clustering [22,23].
In the context of biological networks, the authors in [24] propose a clustering framework that uses a variety of network motifs to identify functional modules based on the higher-order structure information included in a biological network, while in [25] they propose a fuzzy clustering algorithm which, after the semantic similarity between the attribute information of proteins is calculated, is used to identify protein complexes in a protein–protein interaction network.
Metaheuristics approaches have the ability to effectively tackle problems in complex, large and uncertain environments [26], thus they are more suitable for the optimization problems we are describing than exact methods. In this research paper we propose a Hybrid Immunological Algorithm, called Hybrid-IA, for the community detection problem, i.e., we apply a deterministic local search method within an evolutionary computation algorithm based on the workings of the immune system [27]. Briefly, the local search tries to improve the solutions found by the evolutionary mechanism. Using biological networks as a main case study, our goal is to prove the efficiency and robustness of Hybrid-IA in community detection.
Modularity Optimization in Networks
We do not expect a community structure in a graph to be randomly generated. Thus, communities in a graph can be detected by the difference of densities between the vertices of a given graph and the vertices of a random graph with the same size and same degree distribution.
We will use the following notations for the rest of the paper. Given an undirected graph , with vertices and edges, its adjacency matrix and given a partition of the set of vertices V, that is the set of communities,
- for each vertex will denote the degree of i, i.e., the total number of edges in E that have i as one of the endpoints;
- for each community will denote the sum of the degrees of the vertices belonging to community , i.e.,
- for each community will denote the number of edges or links inside the community
- for each vertex and each community will denote the number of edges or links from i to vertices in
Given a partition let now be a binary function that for every pair of vertices has value if i and j belong to the same community and otherwise. The modularity value of such a partitioning C is defined as:
where is the value at row i and column j of
An equivalent way to compute the modularity value is given by the following equation
We will use the latter equation when describing the workings of the local search operator. We note that in case of one single cluster, i.e., and therefore for all pairs of nodes i and Equation (1) gives us the value since
As proven in [17], the modularity value for any unweighted and undirected graphs G and any set of communities C verifies and it represents a quality measure for a partition of a network into communities. A bad partitioning will result in a low value for Q implying the absence of real communities. High values of Q imply good partitions and, as a consequence, highly cohesive communities. As a consequence, community detection can be seen as the problem of maximizing Q, i.e., finding a clustering that will produce the highest value for Q as defined by Equation (1). As observed in [28], modularity optimization might not be able to identify communities that are small when compared with the network size and, in turn, produce large communities. Thus, the modules obtained through the process of modularity optimization must be checked and, possibly, rearranged.
3. Hybrid-IA: The Hybrid Immune Algorithm
Immune algorithms (IA) represent a set of computational systems, population-based metaheuristics inspired by the biological immune system and the way it acts to protect living organisms. They have been successfully applied in many search and optimization [29,30] and anomaly detection tasks [31]. The immune system has the ability to self-nonself discrimination and therefore detect, learn, and remember all the discovered foreign entities.
The hybrid immune algorithm Hybrid-IA, presented in [7], uses a local search procedure that deterministically tries to improve the found solutions. It is a well tested instance of a Clonal Selection Algorithm (CSA) [32,33], a particular class of immune algorithms, and so it is based on the two main concepts of antigen (), which represents the problem to solve or optimize, and B cell, or antibody (), which represents a candidate solution, i.e., a specific point in the solution space. For our specific community detection problem, given a graph a solution is a partition of the vertices, which will identify the clusters, i.e., communities. In particular, a B cell is a sequence of integers, in the interval , with the understanding that means that vertex i belongs to the cluster
At each time step t, the algorithm maintains a population of d candidate solutions. Every element of the population at time is created by randomly assigning each vertex i to a group h, with . Equation (1) gives the fitness function of each element . The values is computed using the procedure . Hybrid-IA ends its evolution and terminates when it reaches the maximum number of generations (). Algorithm 1 shows the pseudocode of Hybrid-IA.
| Algorithm 1 Pseudo-code of Hybrid-IA. |
|
The algorithm uses three immune operators, cloning, hypermutation and aging, which are described in what follows. The input parameters d (the number of elements in the population), (the number of duplications, i.e., clones, which are produced for each element), (mutation rate), (maximum age allowed for each element), (maximum number of iterations) are user defined.
Let us now describe in detail the workings of the operators.
3.1. The Cloning Operator
Cloning is the first immune operator to be called. Each B cell is copied times and so an intermediate population of size is produced. We underline the fact that, to avoid premature convergence, the number of clones for each B cell is the same, i.e., it does not depend on its fitness value. To clarify, a number of close proportional to the fitness value of a B cell, could lead in a short amount of time to a population of B cells very similar to each other. This would in turn imply that the algorithm would not be able to perform a proper exploration of the search space, thus getting trapped in a local optimum.
Once a clone is created, Hybrid-IA assigns an age value to it. From such an assigned age until it reaches the maximum age allowed the clone would be able to remain in the population [34,35]. In more detail, a random age chosen in the range is assigned to each clone. As a consequence, each clone will stay in the population for at least generations. The age assignment and the aging operator are able to keep the right amount of diversity among the solutions, helping the algorithm in avoiding premature convergences [36].
3.2. The Hypermutation Operator
The aim of the hypermutation operator is to efficiently and carefully explore the search space by acting on each clone in In our case, if is a cloned B cell, a mutation corresponds to the action of moving one node from a community to another.
The mutation rate, i.e., the number of mutations (changes) of each clone is inversely proportional to its fitness value. In other words, similarly to what happens with the natural immune system, the higher the fitness value of a clone, the smaller the number of mutations it will have. In more detail, if is a cloned B cell, the mutation rate is the probability to move a node from one community to another and it is given by where is the fitness value of normalized in the range and is a user-defined parameter that determines the shape of the mutation rate.
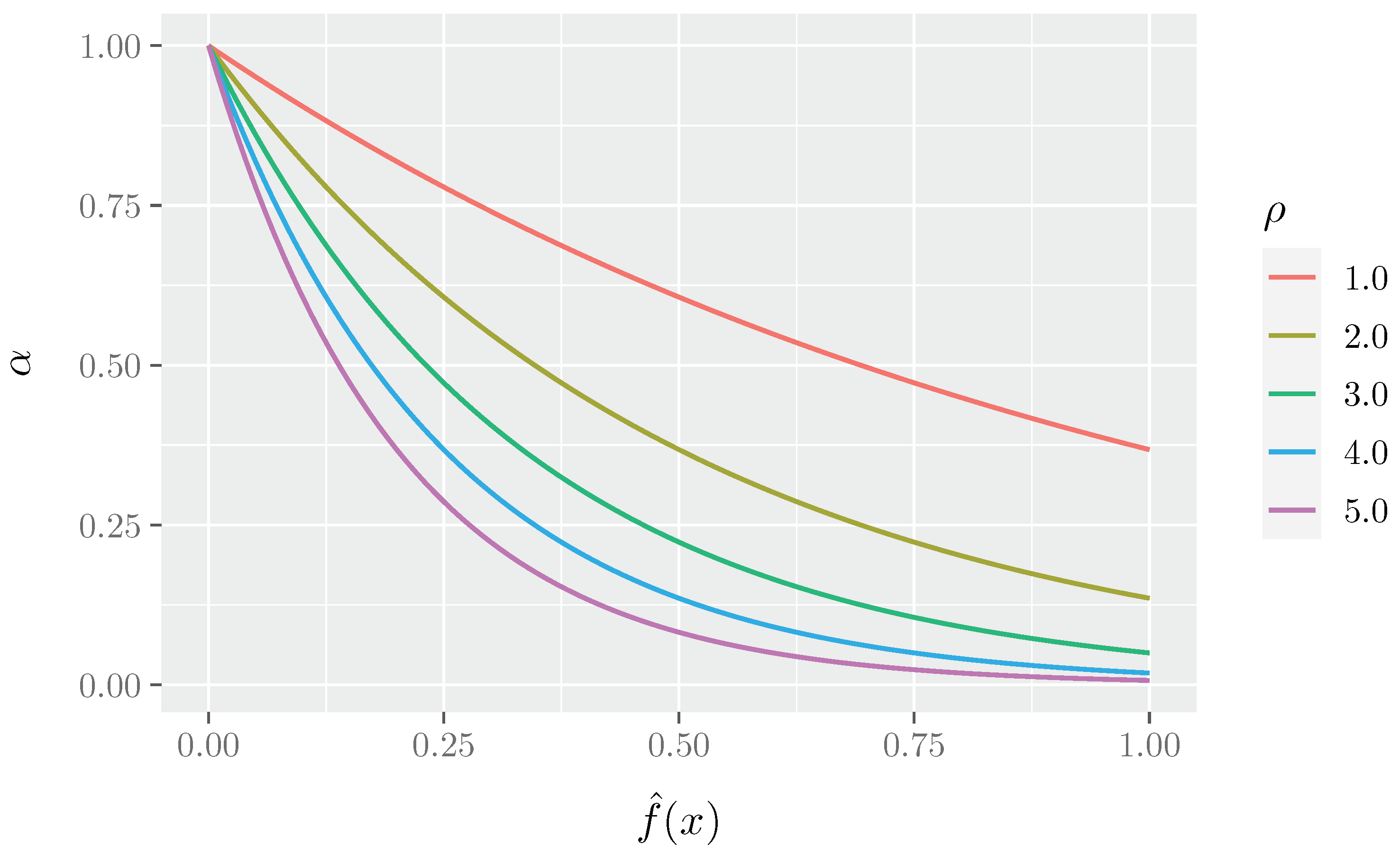
Figure 1 shows the different curves of the mutation rate behavior at the varying of the parameter. One can see how the parameter affects the probability , at different fitness function values. It is possible to observe how low fitness values (which represent not good solutions) correspond to high values, which means that a high number of nodes will be moved from one community to another; vice versa, at high fitness values (i.e., the best solutions), correspond low values, and that is only a low number of nodes will be moved. Moreover, as expected, with lower values of the values of decrease more rapidly towards 0 when increasing normalized fitness values.
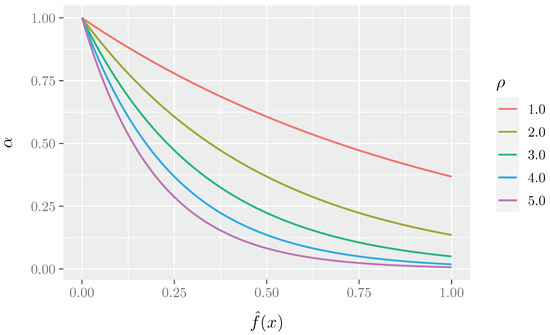
Figure 1.
The mutation curves at different values of .
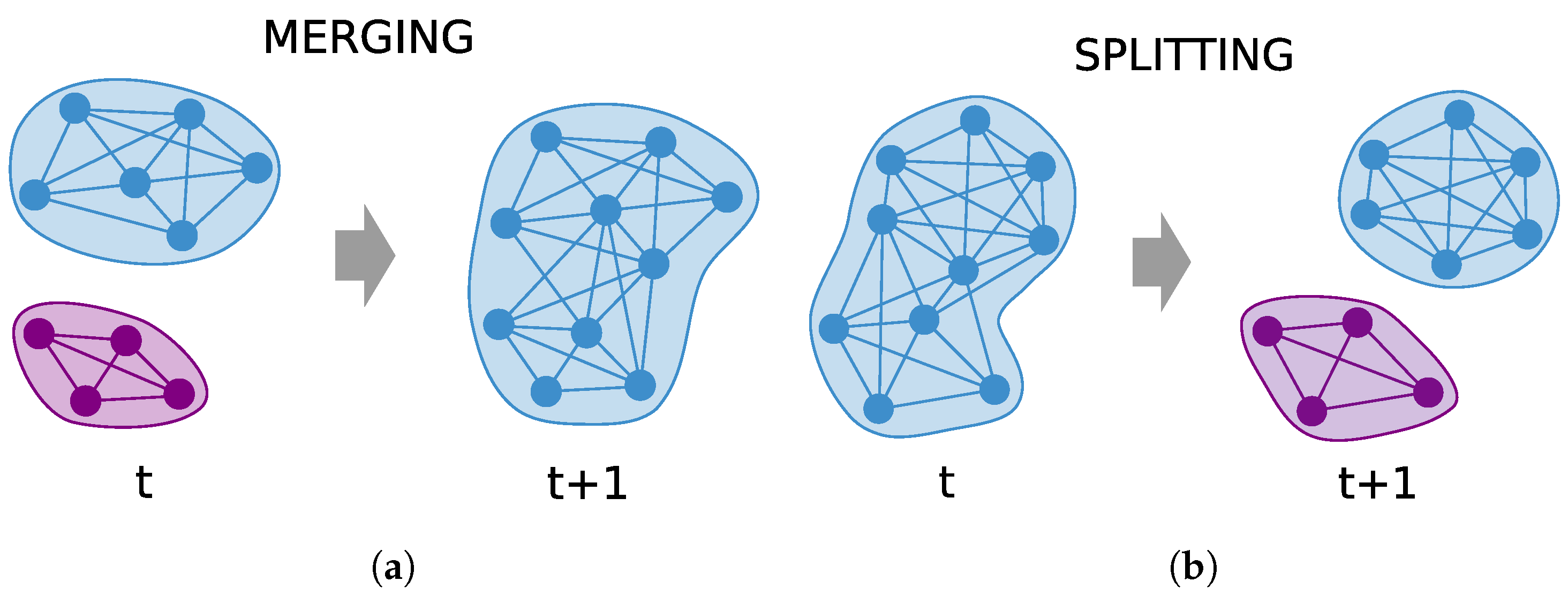
Formally, the hypermutation operator performs the following work. For each B cell, two different integers h and are randomly chosen in the range They represent two different communities, namely and The first one is chosen in particular among the existing community indices, whilst the latter is randomly chosen in the range . Then, each of the vertices in is moved into with a probability given by . In case does not match any currently existing community, a new community will be created and added to the existing ones. Thus, depending on the value of , i.e., whether or not it is the index of an existing community, two different mutations can occur: merging and splitting. In the first case, a subset of the vertices of community will be merged with the vertices of the community In the second case, instead, the community will be split into two communities: itself, and a new community . In Figure 2, we show for clarity a simple example of how these two cases work (merging in Figure 2a and splitting in Figure 2b).
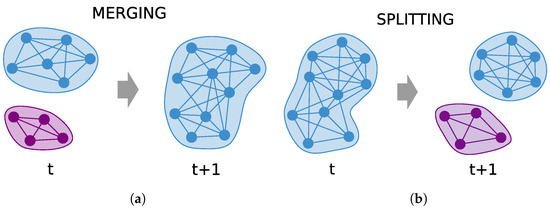
Figure 2.
Hypermutation operator. (a) A subset of nodes from community will be merged to an existing community . (b) A subset of nodes from community will be split to create a new community .
The goal of the hypermutation operator is to discover new communities by selecting a variable percentage of nodes and moving them from their communities into others. The overall goal is to balance the effect of local search (described below) and, in turn, help the algorithm to avoid premature convergence.
3.3. The Static Aging Operator
The static aging operator is the one that plays a central role in the efficiency and robustness of Hybrid-IA, particularly when it is applied to complex and large problems. Its purpose is to assure a good turnover among the B cells and, as a consequence, to have high diversity in the population. It simply acts on each mutated B cell and decides, based on its age, whether to remove it or not from both and independently from its fitness value. Therefore, when the age of a B cell reaches the value it will be removed from the population. The only exception, using the variant called elitist aging operator, could be made for the best current solution which could be kept in the population even if its age is higher than .
3.4. The Selection Operator
Among the B cells in both populations and that survived the aging phase, the -Selection operator with and selects the best d elements. The elements of this population, , will be the starting point to perform the local search. Since it selects the best d elements, the operator guarantees monotonicity of the population fitness evolution.
3.5. Local Search
Given a set of communities if we move a vertex i from the community to the community , we obtain a new set of communities which differs from C just on the placement of vertex The modularity of may differ from the modularity of C and such a variation, i.e., is called move gain.
Using Equation (2) we have
If , then moving node i from the community to the community increases the modularity value. The Move Vertex (MV) (see [37]) methodology has the goal of finding a node i to move from its community to an adjacent community so to maximize :
where and is the adjacency list of node i.
The designed local search (LS) operator drives the algorithm towards more promising regions and, consequently, it properly speeds up its convergence. It explores the neighbourhood of each solution by using Move Vertex. In more detail, for each solution in , we can compute for each community of the solution the value
i.e., the ratio between the total number of links inside the community and the sum of the degrees of its vertices.
Within each community we can compute for each of its vertices i the ratio
i.e., the ratio between the links with other vertices of the community and its degree. High values of identify dense, well-formed communities while low values poorly formed communities. Similarly, high values of identify those vertices which are strongly connected within their own community.
LS starts its work by sorting the communities in increasing order with respect to the ratio and then, within each community , it sorts the nodes in increasing order with respect to the values Then, it applies MV on each community of the solution, starting from nodes that have at least an outgoing link, i.e., nodes that lie on the border of the community.
From a computational complexity point of view, we underline the fact that the values of Equation (3) can be efficiently computed because M and are constants, using appropriate data structures the values of and can be quickly updated, while the terms can be computed during when exploring all vertices adjacent to i. It follows that the moving vertex is linear on the dimension of the neighborhood of node i.
4. Biological Networks Data Set
In this section, we briefly describe the eight different biological networks we used during the tests and for which the communities were identified. They are grouped into the three types described below and refer to biological interactions and main molecular networks.
4.1. Protein–Protein Interaction (PPI) Networks
The physical interaction between proteins has always been an important consideration for gene functions. Proteins are the main participants in a variety of biological processes inside the cells, including signal transduction, homeostasis control, maintenance of internal balance and developmental processes [38]. They rarely function independently but form protein complexes [39]. The mathematical representation of the physical contacts between proteins inside the cell can be obtained through an undirected physical PPI network [40], in which nodes represent proteins and edges connect pairs of interacting proteins. By considering the spatial and temporal aspects of interactions, networks can help in understanding the general organization of protein–protein connections and in discovering the principles of their organization within the cell. PPI has a fundamental role in all biological processes and all organisms [1]. Therefore a complete knowledge of PPIs and their protein interconnections would allow the understanding of cell physiology both in pathogenic and normal states. In turn, this would have a great impact on disease diagnosis, since disease genes often interact with other disease genes [4], as well as for drug discovery and disease treatment [41,42,43]. In this work, two small Cattle PPI and Helicobacter pylori PPI Protein–Protein interactions [44,45,46] and two large networks (with a number of vertices greater than 2000), related to Yeast PPI instances [47,48] were considered. All networks in question are related to interactions between proteins in the three different organisms mentioned before (cattle, helicobacter pylori and yeast) where each node represents a protein and proteins are linked if they interact physically within the cell.
4.2. Metabolic Networks
Technological advancements and the possibility of sequencing whole genomes have made it possible not only to reconstruct the protein–protein interaction networks described above, but also to obtain the networks of biochemical reactions in many organisms. Metabolic networks are powerful tools for representing and studying a complete set of relationships between metabolites, small chemical compounds, and proteins/enzymes. They describe the set of processes and reactions that determine the biochemical and physiological properties of a cell, including the chemical reactions of metabolism, the metabolic pathways and regulatory interactions that drive these reactions. Metabolic networks make it possible to detect diseases given an enzymatic defect in a reaction that can affect flows in subsequent reactions. These defects often cause cascading effects responsible for associated metabolic diseases [49]. Therefore, this type of network can be used to understand if metabolic disorders are linked to their related reactions [50]. In order to investigate this functional information, it is necessary to identify the functional modules in it [51]. Identifying the communities in the metabolic networks will help in understanding the pathways and cycles in metabolic networks [52]. In the two real networks, we considered the metabolic networks of Caenorhabditis elegans and E. coli bacteria [53,54], each vertex represents a metabolite, and each direct link represents a reaction between them that binds the metabolite with the reaction product.
4.3. Transcriptional Regulatory Networks
Understanding the mechanisms underlying the regulation of gene expression is the main goal of contemporary biology. Important cellular processes, such as cell differentiation, cell cycle and metabolism are controlled by the complex biological mechanism of gene regulation. However, the relationship between structure and regulatory function is not easy to observe experimentally. Therefore, a System Biology-based approach is needed. In this regard, network theory is useful for understanding the activity behind these complex transcriptional regulatory mechanisms [55]. The transcriptional network can be represented as a directed graph, composed of transcription factors (TFs) and target genes (TGs) which are regulated in a tightly coordinated way.
Within the network, each node represents a gene and the edges represent direct transcriptional regulation. In case of prokaryotic organisms, each node represents an operon, i.e., a cluster of genes that are transcribed together to give a single messenger RNA (mRNA) molecule. Each edge is directed from a gene (or operon) that encodes a transcription factor to a gene (or operon) that is regulated by that transcription factor.
Transcription factors are modular proteins that regulate the gene expression of other proteins by binding to specific sites in the DNA (promoter sites) and allowing (or preventing) the synthesis of mRNA. The relationships between TFs and their targets (TGs) determine a given phenotype [56]. Moreover, in transcription regulatory networks, modules (or communities) correspond to sets of co-regulated genes [57,58,59,60]. For this reason, the problem of community detection plays a relevant role [61]. Escherichia coli and Saccharomyces cerevisiae are two well-known organisms often used as a model for studying gene regulation. In this work, we considered two transcriptional regulatory networks, E. coli TRN and Yeast TRN [62,63], they were built using transcription factors and target genes, and each edge in the network is directed from an operon that encodes a TF to an operon that it directly regulates.
4.4. Synthetic Networks
In addition to real biological networks, artificial instances were also taken into account in the experimental phase. Synthetic networks can be generated with different characteristics and with a known community structure. Using this kind of network, we can test algorithms on different scenarios and have the possibility to evaluate how good the detected communities are. The algorithm used to generate these synthetic networks is the LFR benchmarks, proposed in [64,65].
Mathematically, both the degree distributions and community size are power laws, with exponents and , respectively. The mixing parameter , models and quantifies the relationship between the external and internal degree of each vertex. In more detail, each vertex of the networks shares a fraction of its edges with the other vertices of its own community and the remaining fraction with vertices outside of its community. Furthermore, the LFR benchmarks can be used to generate directed and weighted synthetic networks with overlapping communities.
5. Experimental Results
In order to evaluate the efficiency and reliability of Hybrid-IA, we performed many experiments on all the biological networks above described. In each experiment Hybrid-IA maintains a population of B cells; it uses a duplication parameter ; it keeps a solution for at most generations within the population, and it uses as mutation shape. Such a parameter setting is a consequence of some preliminary experimental results and of some specific knowledge previously acquired.
5.1. Convergence and Learning Analysis
In the initial part of the experimental phase, to better understand the efficiency of Hybrid-IA we focused our analysis on the convergence behavior and the learning rate. We chose artificial networks as benchmark instances. Such networks were generated using the LFR algorithm [64,65] and are described in Section 4.4.
In particular, networks with 1000 nodes and average degree 15 and 20, and networks with and average degree 20 and 25 were generated. For each of these generated networks, the maximum degree was set to 50, while the exponents of the power laws, which control the degree and community sizes distribution ( and ), were set to 2 and 1, respectively. A minimum of 10 nodes to a maximum of 50 was set as sizes of the communities. The mixing parameter was fixed to . Finally, for these experiments, the maximum number of generations was set to and 5 random instances were generated for each network parameters configuration.
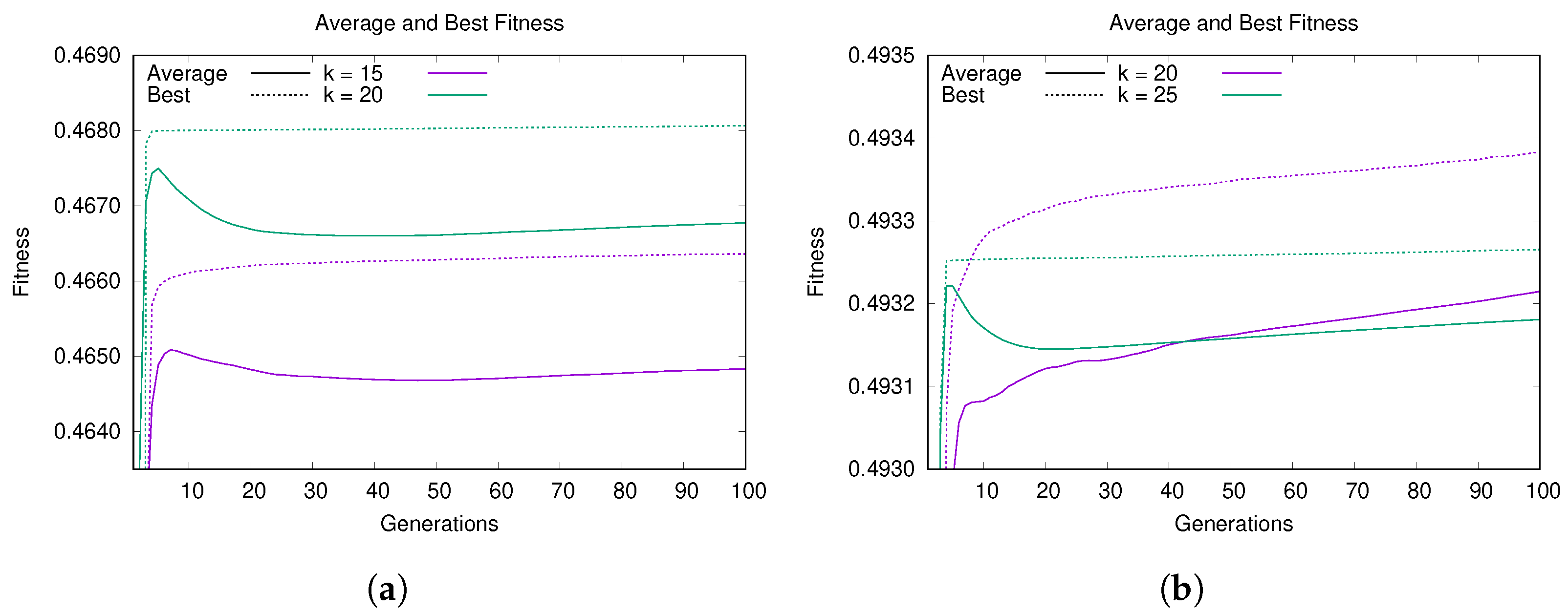
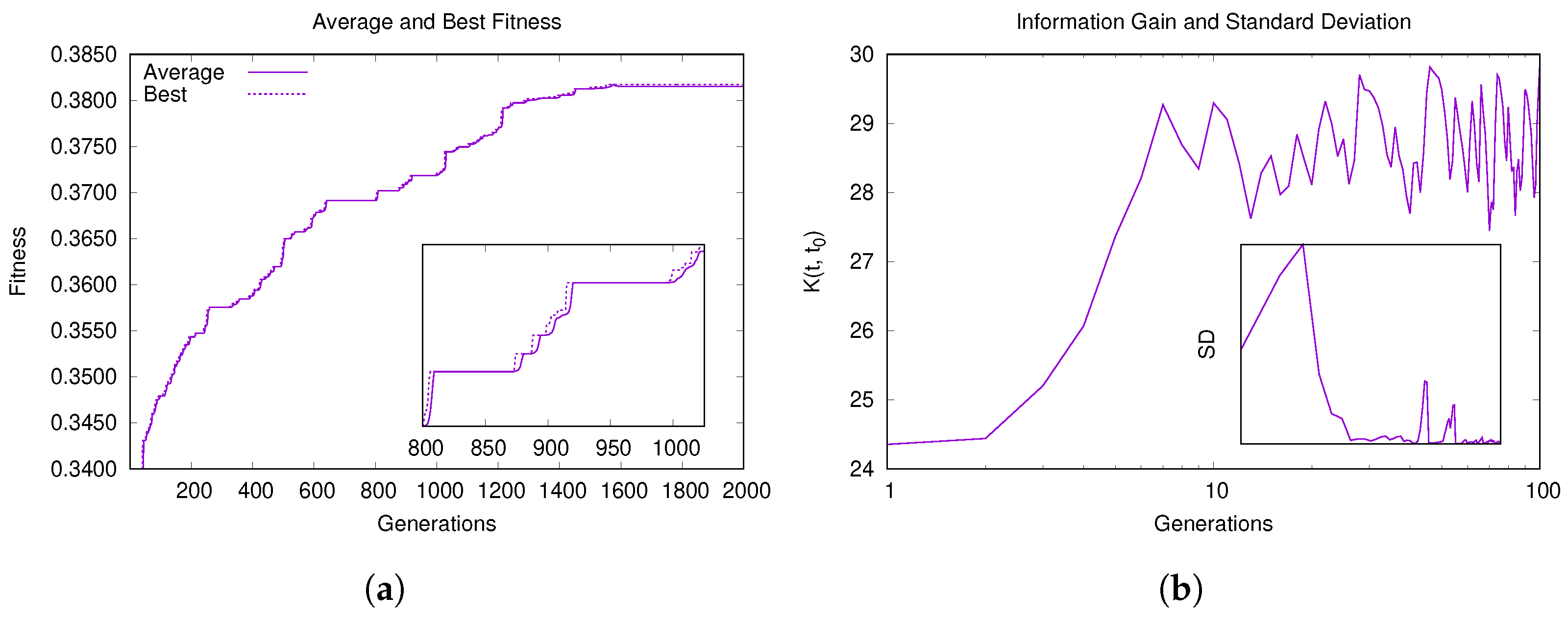
Figure 3a shows the convergence plot on LFR instances with 1000 nodes and average degrees k of 15 (purple) and 20 (green). The two curves represent the best (dotted line) and average (continuous line) fitness of the population and both are averaged over 100 independent runs. From this plot we can observe how the two curves of the best fitness have the same trend for both values of k: they reach a high value of modularity in the early generations and then improve slowly. The improvement for compared to the first generations is minimal, while for the increase in modularity is slightly more significant. Instead, the average fitness curves have a similar trend in the first generations, but subsequently decrease and then gradually increase. From these two curves it can be seen how the population maintains a good degree of diversity, thus favoring a better exploration of the search space.
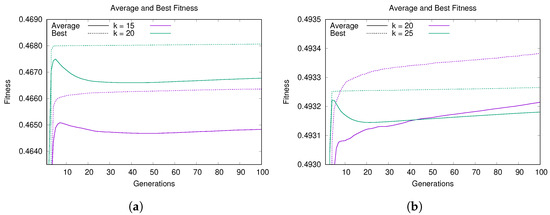
Figure 3.
Convergence behavior of Hybrid-IA: dotted lines are for best values, continuous lines for average values. Average and best fitness value versus generations on (a) LFR(1000,15,0.5) and LFR(1000,20,0.5), and on (b) LFR(5000,20,0.5) and LFR(5000,25,0.5).
A similar situation can be also observed on the LFR instances with 5000 nodes. The plots in Figure 3b show the best and average fitness of the population for (now purple) and (green). For , Hybrid-IA obtains a high value of modularity within a few generations, and after that it stays in a steady state for the rest of the execution, reaching a high-modularity plateau [66]. On the other hand, for the algorithm has a growth much more constant and linear, both in terms of the best solution and the average of the population. Furthermore, in this case, the two curves of best and average fitness are well separated, indicating that the algorithm maintains a good diversity of solutions within the population.
After the convergence behavior, we investigated the learning ability of Hybrid-IA. In order to do so, we used the quantity of information the algorithm gains during the evolutionary process [67,68], that is the learned amount of information compared to the randomly generated initial population. At each generation t, let be the number of the B cells whose fitness function value is equal to The distribution function of the candidate solutions can therefore be defined as the ratio between and the total number of candidate solutions:
It follows that the information gain can be calculated as:
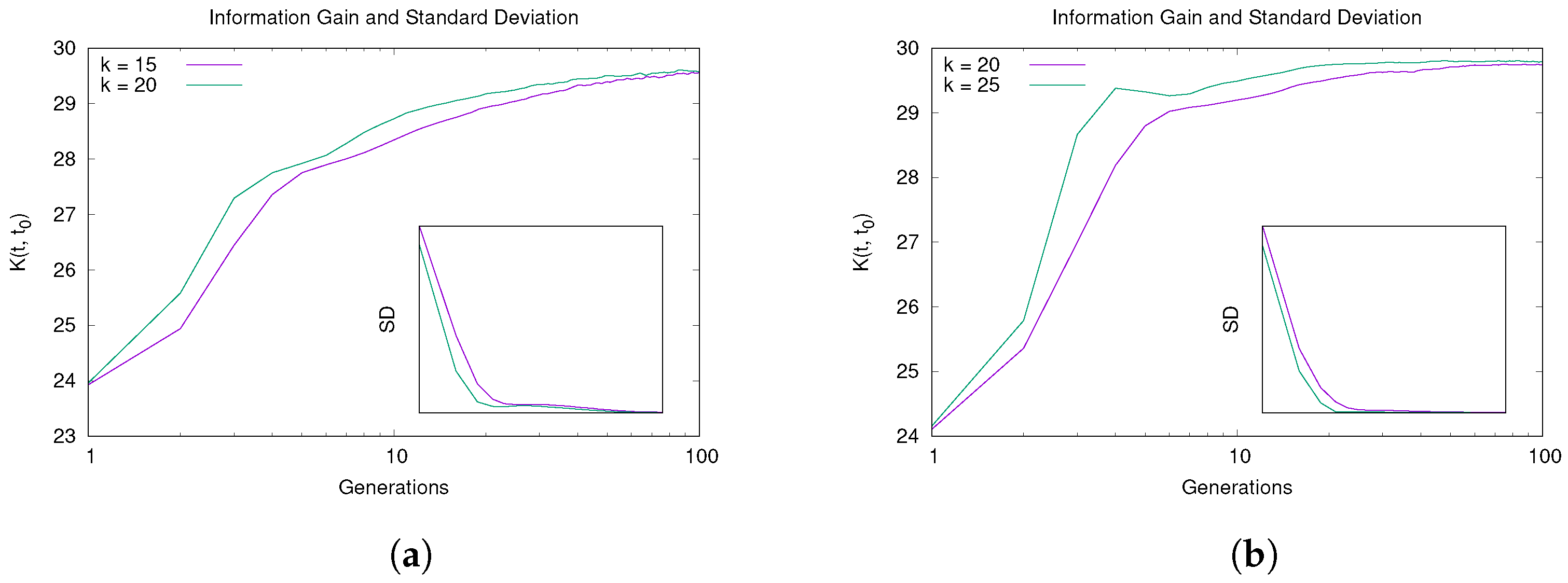
The plots in Figure 4 show the information gain obtained by the algorithm during its running in different scenarios. For both values of , Hybrid-IA is able to learn information step by step, showing thus an increasing curve until it reaches a steady state, which is exactly when the modularity of all solutions begins to become similar. The monotonically increasing of the information gain curve until reaching a steady state is consistent with the maximum information-gain principle: . Overall, the convergence behavior and learning process analyzed (Figure 3 and Figure 4), suggest that Hybrid-IA finds very quickly good solutions in networks with medium/high density (i.e., for 1000 nodes and for 5000), as the community structure is well-defined. On the other hand, on sparse networks, with an unclear community structure, the algorithm converges more slowly.
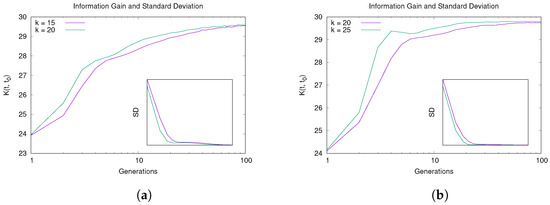
Figure 4.
Learning ability of Hybrid-IA: information gain and standard deviation versus generations on (a) LFR(1000,15,0.5) and LFR(1000,20,0.5), and on (b) LFR(5000,20,0.5) and LFR(5000,25,0.5).
In addition, we carried out a convergence analysis on the network E. coli MRN [54], which presents a very low density (see Table 1). Figure 5 shows the plots relative to the run in which Hybrid-IA has reached its best solution. Again, after the initial climb, the algorithm begins its exploration around the solutions found, improving gradually. In some places (inset plot of Figure 5a) the algorithm seems to stagnate in some local optima but, thanks to the aging operator, it manages to escape, and find better solutions. During these phases, the population tends to reduce its diversity, being almost entirely composed of solutions of equal quality.

Table 1.
The biological networks used in the experiments.
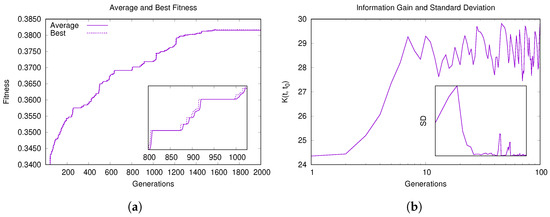
Figure 5.
Convergence behavior of Hybrid-IA on E. coli MRN network. (a) Average and best fitness value of the population versus generations. (b) Information gain and standard deviation versus generations.
5.2. The Biological Networks
Metaheuristics and hyper-heuristics have been successfully applied to several complex network problems, and, specifically, in computational biology area [69,70,71,72,73,74]. Thus, we compare the results obtained by Hybrid-IA on the above-described biological networks with other well-known metaheuristics, all based on a modularity optimization approach [75]. In particular, we compare it with an effective Hyper-Heuristics Differential Search Algorithm (HDSA) [76] based on the random-walk movement used by an organism to migrate, in our case artificial superorganisms; an improved Bat Algorithm based on Differential Evolution algorithm (BADE) [77]; a Scatter Search algorithm based, an evolutionary method that has been successfully applied to hard optimization problems (SSGA) [78,79]; a modified Big Bang–Big Crunch algorithm (BB-BC) [80] an optimization method that relies on both the Big Bang and Big Crunch Theory and, consequently, energy dissipation increasing randomness and disorder, followed a random regrouping of particles; the original Bat Algorithm based on echolocation behavior of bats adapted for community detection (BA) [81]; a variation of the original Gravitational Search Algorithm, modified for solving the community detection problem (GSA) [82]; and the Louvain algorithm [83], a greedy optimization method.
The characteristics of the biological networks are summarised in Table 1. In particular is the percentage of density of the corresponding graph, i.e.,
The parameter configuration used by Hybrid-IA is the same as described above, but the set number of generations () depends on the size of the biological network: for instance, for networks with less than 1000 nodes, was set to 1000, while for networks with more than 1000 nodes, was set to 2000. It is important to highlight that the results of all the other algorithms were taken from [75].
Table 2 displays the detailed results of Hybrid-IA compared with the other algorithms. It shows for each algorithm, the best values of the Q modularity (Best) found, the average of the values (Mean), the worst modularity (Worst), the standard deviation (StD) and the number of community structures (k) in the best solution. We stress the fact that unfortunately not all algorithms were tested on the same networks, as reported in the published results. Thus, some results are missing in the table. The results obtained by Hybrid-IA show its efficiency. Noticeably, the proposed Hybrid-IA algorithm outperforms all metaheuristics (i.e., excluding Louvain) both in terms of the obtained values of modularity and mean, except for HDSA in the E. coli TRN biological network, although its best result is very close to that obtained by HDSA. Moreover, the average values obtained on Cattle PPI, E. coli TRN, C. elegans MRN and Helicobacter pylori PPI networks are better than the best modularity values obtained by the other algorithms, with the exception of the Hyper-heuristic Differential Search Algorithm (HDSA) and the best value obtained by BADE in E. coli TRN.

Table 2.
Comparing the results obtained by Hybrid-IA on biological networks with the results obtained by other algorithms. The results are calculated over 100 independent runs for Hybrid-IA and Louvain, while over 30 runs for the rest.
Let us now compare the results obtained by Hybrid-IA with the results obtained by Louvain, the only greedy algorithm included in the comparison. It is clear how Hybrid-IA performs well equating the modularity value in the Cattle PPI dataset, and exceeding it in the C. elegans MRN and E. coli MRN networks. For these datasets, Figure 6and Figure 7a,b show the detected community structures by Hybrid-IA. Figure 6b shows the communities generated for E. coli TRN network. For the other instances, although Louvain performs generally better, the modularity reached by Hybrid-IA is however closer to the optimal one. Finally, as it will be explained in more detail in the next section, although Louvain manages to achieve a better modularity value than Hybrid-IA, the latter reveals a higher number of communities. This is due to the different nature of the two algorithms since Louvain tends to aggregate communities.

Figure 6.
Community structure identified by Hybrid-IA on (a) Cattle PPI and (b) E. coli TRN networks.
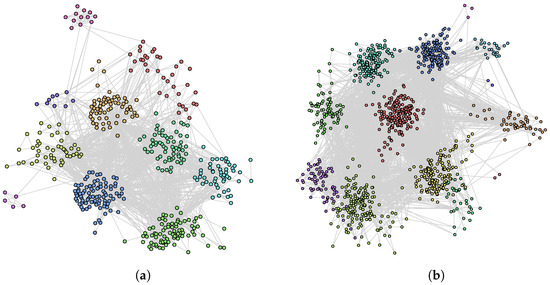
Figure 7.
Community structure identified by Hybrid-IA on (a) C. elegans MRN and (b) E. coli MRN networks.
5.3. Functional Sensitivity of Community Detection
Modularity allows measuring how cohesive the detected communities are, but not to assess how similar they are to the real ones. Synthetic networks allow us to use another evaluation metric, namely the Normalized Mutual Information (NMI) [84], which is widely used to compare community detection methods since it is able to disclose the similarity between the genuine community (target) and the detected community structures. Since for the biological networks reported in Table 1 the real community structure is unknown, a new dataset of networks was used for this analysis. In particular, a new set of instances was generated using the LFR algorithm (see Section 4.4), with the mixing parameter that ranges from to .
In Table 3, we can see the results of Hybrid-IA on these new synthetic datasets and we can compare them with the ones obtained by Louvain. The features of the LFR networks tested are shown in the first column; for each of these lists of parameters, 5 random instances were generated. The values of modularity Q and NMI were computed over 100 independent runs for both algorithms.

Table 3.
Comparing Hybrid-IA and Louvain on synthetic networks with 1000 and 5000 vertices, with respect to modularity (Q) and NMI evaluation metrics. In boldface are reported the best obtained values.
Analyzing the comparison, it is possible to see how Louvain outperforms Hybrid-IA in almost all networks with 1000 vertices with respect to the Q modularity metric, and in all instances with 5000 vertices. On the other hand, though, Hybrid-IA outperforms Louvain with respect to the NMI index, in all networks except just for one ().
What are the reasons behind such significant differences in the performances of the two algorithms? The combination of random search and local search that, along with the diversity in the population, introduced by the immune operators, require for Hybrid-IA a longer convergence time than Louvain. Louvain is a fast, multilevel algorithm that obtains good modularity values, but it aggregates communities too much, not reflecting the real community structures of the networks. These results prove, therefore, that Hybrid-IA is better able to detect communities that are closer to the true ones when compared with the greedy optimization algorithm. If on one hand modularity assesses the cohesion of the detected communities, on the other hand simply maximizing Q might not correspond to detecting true communities. Indeed, as it is also asserted in [28], when maximizing modularity it is possible to fail to identify smaller communities due to the degree of interconnection of the communities.
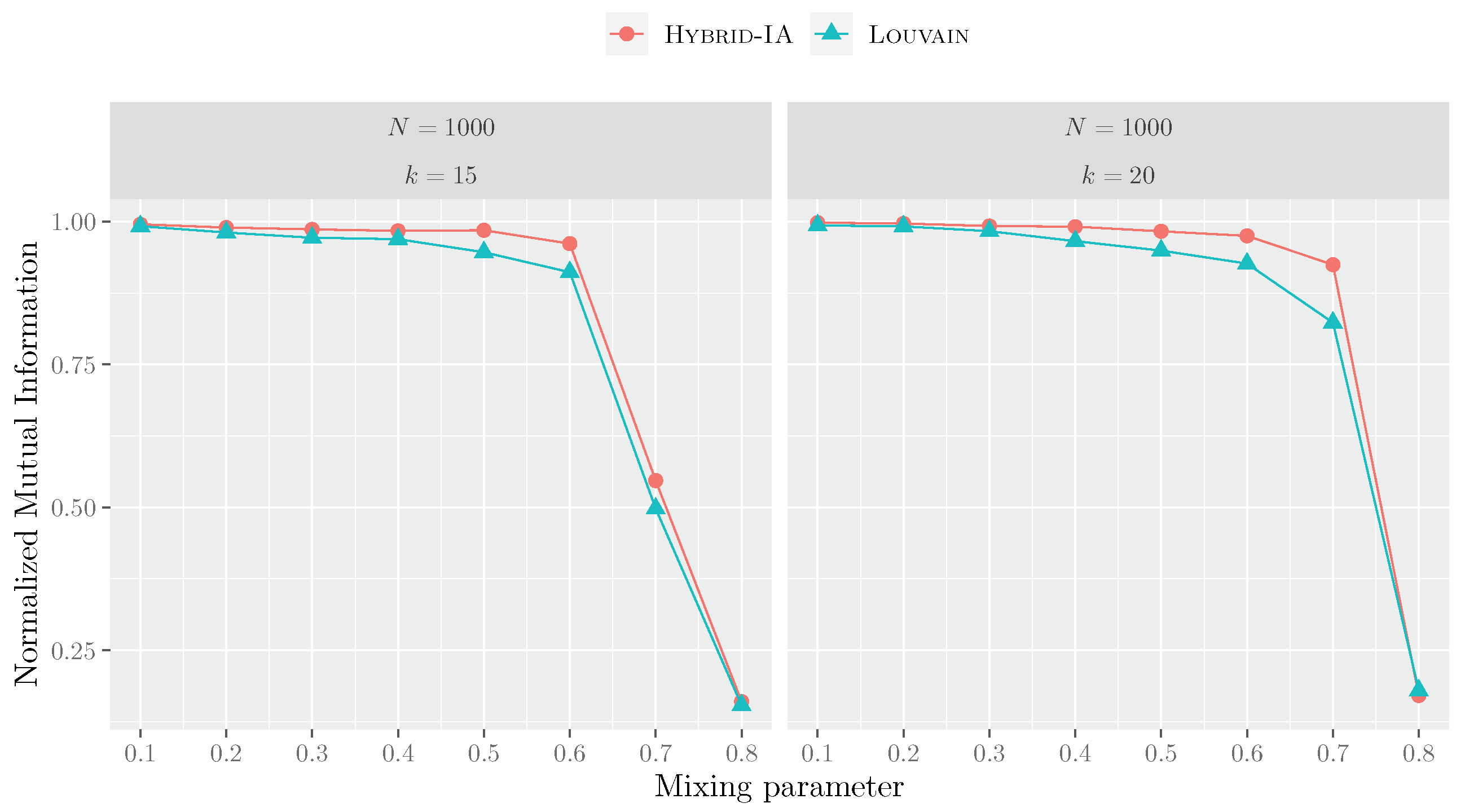
Figure 8 shows the curves of the NMI index for all LFR benchmarks with 1000 vertices. It can be observed that the two curves have the same trend: for low values of (≤0.3), both algorithms obtain similar results, as the parameter increases, the gap between Hybrid-IA and Louvain begins to be more consistent. However, when the mixing parameter assumes higher values, the generated LFR networks have community structures that are not well-defined, resulting, then, in low NMI values for both algorithms.
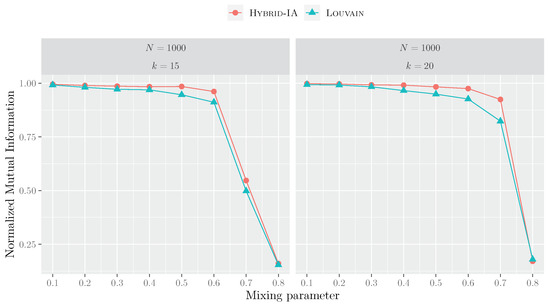
Figure 8.
Performances of Hybrid-IA and Louvain on the LFR instances with 1000 nodes and average degrees 15 and 20. The plots show the normalized mutual information as a function of the mixing parameter. Each point corresponds to an average over 5 produced graphs and 100 runs.
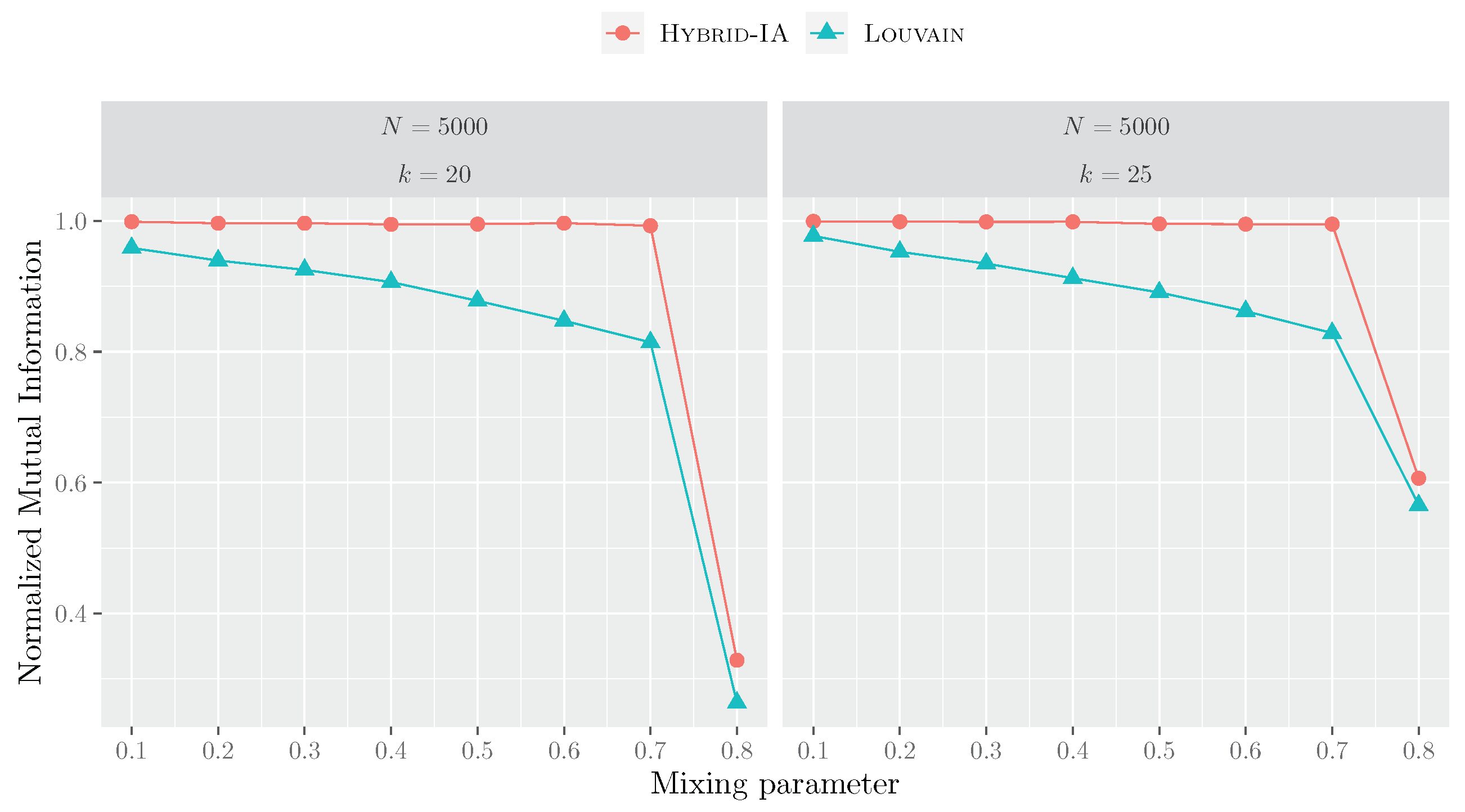
Figure 9, instead, shows the NMI curves for the LFR networks with 5000 nodes. For these instances, the difference between Louvain and Hybrid-IA is much more substantial, and it is quite evident even at low values of .
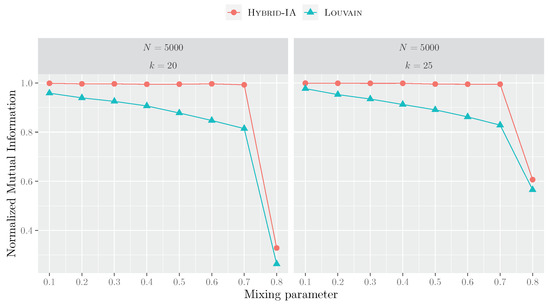
Figure 9.
Performances of Hybrid-IA and Louvain on the LFR instances with 5000 nodes and average degrees 20 and 25. The plots show the normalized mutual information as a function of the mixing parameter. Each point corresponds to an average over 5 produced graphs and 100 runs.
Following this modularity limitation, we conducted a more in-depth functional sensitivity analysis based on two other community structure similarity metrics: Adjusted Rand Index (ARI) [85], for measuring the similarity of partitions, and Normalized Variation of Information (NVI) [86], which is based on the Shannon entropy and measures the lost and the gained information in changing from one clustering to another one. It is worth recalling that while NMI and ARI values close to 1 denote strong similarity between the detected community and the real one ( identical communities), the NVI values, on the other hand, tend to 0 as the similarity between the compared communities increases ( identical communities).
Thus, following the same experimental protocol, the three measures of functional sensitivity were computed on the synthetic networks considered above, with the addition of a larger one of 10,000 vertices. The outcomes are reported in Table 4. By analyzing this table it is possible to assert that Hybrid-IA achieves better metric values than Louvain in all three sensitivity measures. It follows therefore that, albeit Louvain achieves slightly better modularity values in almost all networks considered (mainly on the larger ones), Hybrid-IA instead is able to detect communities strongly similar to the real ones outperforming Louvain in all three sensitivity metrics. It is worth pointing out how Hybrid-IA obtains NMI and ARI values close to 1 in almost all tested networks, with particular reference to the largest one ().

Table 4.
Hybrid-IA functional sensitivity analysis on synthetic networks at different sizes: from 1000 to 10,000 vertices. NMI, ARI and NVI were considered as community structure similarity metrics. In boldface are reported the best obtained values.
6. Conclusions
A Hybrid Immune Algorithm, called Hybrid-IA, was designed for the community detection problem and was tested on several large biological networks. The strength of Hybrid-IA is given not only by the immune operators (cloning, hypermutation and aging) but also by a specially designed Local Search, which aims to speed up the convergence of Hybrid-IA towards promising regions. Basically, it attempts deterministically to move a node from the belonging community to another within its neighbors with the purpose to refine and improve the solutions discovered.
In order to assess the robustness of Hybrid-IA, we performed several comparisons with other metaheuristics, hyper-heuristics and the well-known greedy algorithm Louvain. We conducted a first comparison based on the modularity function maximization. However, due to the limitation of modularity optimization in detecting communities that are comparatively small, we performed other comparisons based on Normalized Mutual Information (NMI), Adjusted Rand Index (ARI) and Normalized Variation of Information (NVI), which are evaluation metrics commonly used in community detection that simply assess how similar the communities discovered are with respect to the real ones. All in all, after inspecting all the obtained outcomes and performing all the necessary comparisons, it clearly emerges how Hybrid-IA outperforms all metaheuristics and hyper-heuristics with which it was compared, in terms of best and mean modularity values. Focusing only on the comparison with Louvain, it is possible to assert that although Hybrid-IA finds slightly lower modularity values, it is still able to detect communities more similar to the real ones than those discovered by Louvain.
Some improvements, as future works, are currently in progress. We are addressing, in particular, the problem of improving the execution time and the searchability of Hybrid-IA especially on very large networks, through an adaptive multi-level approach. In addition, since the algorithm is based on several fixed and user-defined parameters, we believe that a further significant improvement of its searchability could be obtained by dynamically adapting such parameters through Machine Learning and/or Hyper-Heuristics techniques.
Author Contributions
All authors contributed equally to the methodology, investigation, validation and fomarl analysis, as well as to the writing—original draft preparation of the manuscript. V.C. and M.P. contributed to the writing, review and editing of the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Acknowledgments
The authors would like to express their gratitude to the anonymous reviewers for their helpful feedback that measurably improved the manuscript. M. Pavone would like to thank the Advanced New Technologies Research Laboratory (ANTs lab.), Catania, Italy, for its kind support.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Von Mering, C.; Krause, R.; Snel, B.; Cornell, M.; Oliver, S.G.; Fields, S.; Bork, P. Comparative assessment of large-scale data sets of protein–protein interactions. Nature 2002, 417, 399–403. [Google Scholar] [CrossRef] [PubMed]
- Barabási, A.L.; Oltvai, Z.N. Network biology: Understanding the cell’s functional organization. Nat. Rev. Genet. 2004, 5, 101–113. [Google Scholar] [CrossRef] [PubMed]
- Barabási, A.L.; Gulbahce, N.; Loscalzo, J. Network medicine: A network-based approach to human disease. Nat. Rev. Genet. 2011, 12, 56–68. [Google Scholar] [CrossRef] [PubMed]
- Goh, K.I.; Cusick, M.E.; Valle, D.; Childs, B.; Vidal, M.; Barabási, A.L. The human disease network. Proc. Natl. Acad. Sci. USA 2007, 104, 8685–8690. [Google Scholar] [CrossRef] [PubMed]
- Aureli, M.; Masilamani, A.P.; Illuzzi, G.; Loberto, N.; Scandroglio, F.; Prinetti, A.; Chigorno, V.; Sonnino, S. Activity of plasma membrane β-galactosidase and β-glucosidase. FEBS Lett. 2009, 583, 2469–2473. [Google Scholar] [CrossRef]
- Spampinato, A.G.; Scollo, R.A.; Cavallaro, S.; Pavone, M.; Cutello, V. An Immunological Algorithm for Graph Modularity Optimization. In Advances in Intelligent Systems and Computing, Proceedings of the Advances in Computational Intelligence Systems (UKCI 2019), Portsmouth, UK, 4–6 September 2019; Ju, Z., Yang, L., Yang, C., Gegov, A., Zhou, D., Eds.; Springer: Cham, Switzerland, 2020; Volume 1043, pp. 235–247. [Google Scholar] [CrossRef]
- Cutello, V.; Fargetta, G.; Pavone, M.; Scollo, R.A. Optimization Algorithms for Detection of Social Interactions. Algorithms 2020, 13, 139. [Google Scholar] [CrossRef]
- Girvan, M.; Newman, M.E.J. Community structure in social and biological networks. Proc. Natl. Acad. Sci. USA 2002, 99, 7821–7826. [Google Scholar] [CrossRef]
- Gulbahce, N.; Lehmann, S. The art of community detection. BioEssays 2008, 30, 934–938. [Google Scholar] [CrossRef]
- Didimo, W.; Montecchiani, F. Fast layout computation of clustered networks: Algorithmic advances and experimental analysis. Inf. Sci. 2014, 260, 185–199. [Google Scholar] [CrossRef]
- Buchin, K.; Buchin, M.; Gudmundsson, J.; Löffler, M.; Luo, J. Detecting commuting patterns by clustering subtrajectories. Int. J. Comput. Geom. Appl. 2011, 21, 253–282. [Google Scholar] [CrossRef]
- Cavallaro, C.; Vizzari, G. A Novel Spatial–Temporal Analysis Approach to Pedestrian Groups Detection. Procedia Comput. Sci. 2022, 207, 2364–2373. [Google Scholar] [CrossRef]
- Cavallaro, C.; Vitrià, J. Corridor Detection from Large GPS Trajectories Datasets. Appl. Sci. 2020, 10, 5003. [Google Scholar] [CrossRef]
- Cavallaro, C.; Verga, G.; Tramontana, E.; Muscato, O. Multi-agent architecture for point of interest detection and recommendation. In Proceedings of the CEUR Workshop, Parma, Italy, 26–28 June 2019; Volume 2404, pp. 98–104. [Google Scholar]
- Cavallaro, C.; Verga, G.; Tramontana, E.; Muscato, O. Eliciting cities points of interest from people movements and suggesting effective itineraries. Intell. Artif. 2020, 14, 49–61. [Google Scholar] [CrossRef]
- Newman, M.E.J.; Girvan, M. Finding and evaluating community structure in networks. Phys. Rev. E 2004, 69, 026113. [Google Scholar] [CrossRef] [PubMed]
- Brandes, U.; Delling, D.; Gaertler, M.; Görke, R.; Hoefer, M.; Nikoloski, Z.; Wagner, D. On Modularity Clustering. IEEE Trans. Knowl. Data Eng. 2008, 20, 172–188. [Google Scholar] [CrossRef]
- Newman, M.E.J. Fast algorithm for detecting community structure in networks. Phys. Rev. E 2004, 69, 066133. [Google Scholar] [CrossRef]
- Newman, M.E.J. Finding community structure in networks using the eigenvectors of matrices. Phys. Rev. E 2006, 74, 036104. [Google Scholar] [CrossRef] [PubMed]
- Hu, L.; Pan, X.; Tang, Z.; Luo, X. A Fast Fuzzy Clustering Algorithm for Complex Networks via a Generalized Momentum Method. IEEE Trans. Fuzzy Syst. 2022, 30, 3473–3485. [Google Scholar] [CrossRef]
- Hu, L.; Chan, K.C.C. Fuzzy Clustering in a Complex Network Based on Content Relevance and Link Structures. IEEE Trans. Fuzzy Syst. 2016, 24, 456–470. [Google Scholar] [CrossRef]
- Xu, Z.; Ke, Y.; Wang, Y.; Cheng, H.; Cheng, J. GBAGC: A General Bayesian Framework for Attributed Graph Clustering. ACM Trans. Knowl. Discov. Data 2014, 9, 1–43. [Google Scholar] [CrossRef]
- Hu, L.; Zhang, J.; Pan, X.; Yan, H.; You, Z.H. HiSCF: Leveraging higher-order structures for clustering analysis in biological networks. Bioinformatics 2020, 37, 542–550. [Google Scholar] [CrossRef]
- Hu, L.; Chan, K.C.C.; Yuan, X.; Xiong, S. A Variational Bayesian Framework for Cluster Analysis in a Complex Network. IEEE Trans. Knowl. Data Eng. 2020, 32, 2115–2128. [Google Scholar] [CrossRef]
- Pan, X.; Hu, L.; Hu, P.; You, Z.H. Identifying Protein Complexes From Protein–Protein Interaction Networks Based on Fuzzy Clustering and GO Semantic Information. IEEE/ACM Trans. Comput. Biol. Bioinform. 2022, 19, 2882–2893. [Google Scholar] [CrossRef] [PubMed]
- Talbi, E.G. Metaheuristics: From Design to Implementation; Wiley Publishing: Hoboken, NJ, USA, 2009. [Google Scholar]
- Scollo, R.A.; Cutello, V.; Pavone, M. Where the Local Search Affects Best in an Immune Algorithm. In Lecture Notes in Artificial Intelligence, Proceedings of the AIxIA 2020—Advances in Artificial Intelligence (AIxIA 2020), Virtual, 25–27 November 2020; Baldoni, M., Bandini, S., Eds.; Springer: Cham, Swizterland, 2021; Volume 12414, pp. 99–114. [Google Scholar] [CrossRef]
- Fortunato, S.; Barthélemy, M. Resolution limit in community detection. Proc. Natl. Acad. Sci. USA 2007, 104, 36–41. [Google Scholar] [CrossRef] [PubMed]
- Costanza, J.; Cutello, V.; Pavone, M. A Memetic Immunological Algorithm for Resource Allocation Problem. In Lecture Notes in Computer Science, Proceedings of the 10th International Conference on Artificial Immune Systems (ICARIS 2011), Cambridge, UK, 18–21 July 2011; Liò, P., Nicosia, G., Stibor, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6825, pp. 308–320. [Google Scholar] [CrossRef]
- Stracquadanio, G.; Greco, O.; Conca, P.; Cutello, V.; Pavone, M.; Nicosia, G. Packing equal disks in a unit square: An immunological optimization approach. In Proceedings of the International Workshop on Artificial Immune Systems (AIS), Taormina-Sicily, Italy, 17–18 July 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Fouladvand, S.; Osareh, A.; Shadgar, B.; Pavone, M.; Sharafi, S. DENSA: An effective negative selection algorithm with flexible boundaries for self-space and dynamic number of detectors. Eng. Appl. Artif. Intell. 2017, 62, 359–372. [Google Scholar] [CrossRef]
- Pavone, M.; Narzisi, G.; Nicosia, G. Clonal selection: An immunological algorithm for global optimization over continuous spaces. J. Glob. Optim. 2012, 53, 769–808. [Google Scholar] [CrossRef]
- Cutello, V.; Oliva, M.; Pavone, M.; Scollo, R.A. An Immune Metaheuristics for Large Instances of the Weighted Feedback Vertex Set Problem. In Proceedings of the IEEE Symposium Series on Computational Intelligence (SSCI 2019), Xiamen, China, 6–9 December 2019; pp. 1928–1936. [Google Scholar] [CrossRef]
- Di Stefano, A.; Vitale, A.; Cutello, V.; Pavone, M. How long should offspring lifespan be in order to obtain a proper exploration? In Proceedings of the IEEE Symposium Series on Computational Intelligence (SSCI 2016), Athens, Greece, 6–9 December 2016; pp. 1–8. [Google Scholar] [CrossRef]
- Vitale, A.; Di Stefano, A.; Cutello, V.; Pavone, M. The Influence of Age Assignments on the Performance of Immune Algorithms. In Advances in Computational Intelligence Systems, Proceedings of the 18th UK Workshop on Computational Intelligence, Nottingham, UK, 5–7 September 2018; Lotfi, A., Bouchachia, H., Gegov, A., Langensiepen, C., McGinnity, M., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 16–28. [Google Scholar]
- Cutello, V.; Nicosia, G.; Pavone, M.; Stracquadanio, G. An Information-Theoretic Approach for Clonal Selection Algorithms. In Lecture Notes in Computer Science, Proceedings of the 9th International Conference on Artificial Immune Systems (ICARIS 2010), Edinburgh, UK, 26–29 July 2010; Hart, E., McEwan, C., Timmis, J., Hone, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; Volume 6209, pp. 144–157. [Google Scholar] [CrossRef]
- Kernighan, B.W.; Lin, S. An efficient heuristic procedure for partitioning graphs. Bell Syst. Tech. J. 1970, 49, 291–307. [Google Scholar] [CrossRef]
- Zhang, Y.; Gao, P.; Yuan, J.S. Plant Protein–Protein Interaction Network and Interactome. Curr. Genom. 2010, 11, 40–46. [Google Scholar] [CrossRef]
- Gu, H.; Zhu, P.; Jiao, Y.; Meng, Y.; Chen, M. PRIN: A predicted rice interactome network. BMC Bioinform. 2011, 12, 161. [Google Scholar] [CrossRef]
- Lim, Y.H.; Charette, J.M.; Baserga, S.J. Assembling a Protein–Protein Interaction Map of the SSU Processome from Existing Datasets. PLoS ONE 2011, 6, e17701. [Google Scholar] [CrossRef]
- Mullard, A. Protein–protein interaction inhibitors get into the groove. Nat. Rev. Drug Discov. 2012, 11, 173–175. [Google Scholar] [CrossRef] [PubMed]
- Taylor, I.W.; Linding, R.; Warde-Farley, D.; Liu, Y.; Pesquita, C.; Faria, D.; Bull, S.; Pawson, T.; Morris, Q.; Wrana, J.L. Dynamic modularity in protein interaction networks predicts breast cancer outcome. Nat. Biotechnol. 2009, 27, 199–204. [Google Scholar] [CrossRef] [PubMed]
- Diss, G.; Filteau, M.; Freschi, L.; Leducq, J.B.; Rochette, S.; Torres-Quiroz, F.; Landry, C.R. Integrative avenues for exploring the dynamics and evolution of protein interaction networks. Curr. Opin. Biotechnol. 2013, 24, 775–783. [Google Scholar] [CrossRef] [PubMed]
- Cattle Protein–Protein Interactions. 2009. Available online: https://biit.cs.ut.ee/graphweb/welcome.cgi?t=examples (accessed on 30 October 2022).
- Xenarios, I.; Rice, D.W.; Salwinski, L.; Baron, M.K.; Marcotte, E.M.; Eisenberg, D. DIP: The Database of Interacting Proteins. Nucleic Acids Res. 2000, 28, 289–291. [Google Scholar] [CrossRef]
- Rain, J.C.; Selig, L.; De Reuse, H.; Battaglia, V.; Reverdy, C.; Simon, S.; Lenzen, G.; Petel, F.; Wojcik, J.; Schächter, V.; et al. The protein—Protein interaction map of Helicobacter pylori. Nature 2001, 409, 211–215. [Google Scholar] [CrossRef] [PubMed]
- Yu, H.; Braun, P.; Yildirim, M.A.; Lemmens, I.; Venkatesan, K.; Sahalie, J.; Hirozane-Kishikawa, T.; Gebreab, F.; Li, N.; Simonis, N.; et al. High-Quality Binary Protein Interaction Map of the Yeast Interactome Network. Science 2008, 322, 104–110. [Google Scholar] [CrossRef] [PubMed]
- Bu, D.; Zhao, Y.; Cai, L.; Xue, H.; Zhu, X.; Lu, H.; Zhang, J.; Sun, S.; Ling, L.; Zhang, N.; et al. Topological structure analysis of the protein–protein interaction network in budding yeast. Nucleic Acids Res. 2003, 31, 2443–2450. [Google Scholar] [CrossRef]
- Lee, D.S.; Park, J.; Kay, K.A.; Christakis, N.A.; Oltvai, Z.N.; Barabási, A.L. The implications of human metabolic network topology for disease comorbidity. Proc. Natl. Acad. Sci. USA 2008, 105, 9880–9885. [Google Scholar] [CrossRef]
- Ross, R.; Dagnone, D.; Jones, P.J.H.; Smith, H.; Paddags, A.; Hudson, R.; Janssen, I. Reduction in Obesity and Related Comorbid Conditions after Diet-Induced Weight Loss or Exercise-Induced Weight Loss in Men. Ann. Intern. Med. 2000, 133, 92–103. [Google Scholar] [CrossRef]
- Yanrui, D.; Zhen, Z.; Wenchao, W.; Yujie, C. Identifying the Communities in the Metabolic Network Using ’Component’ Definition and Girvan-Newman Algorithm. In Proceedings of the 14th International Symposium on Distributed Computing and Applications for Business Engineering and Science (DCABES 2015), Guiyang, China, 18–24 August 2015; pp. 42–45. [Google Scholar] [CrossRef]
- Fortunato, S. Community detection in graphs. Phys. Rep. 2010, 486, 75–174. [Google Scholar] [CrossRef]
- Duch, J.; Arenas, A. Community detection in complex networks using extremal optimization. Phys. Rev. E 2005, 72, 027104. [Google Scholar] [CrossRef] [PubMed]
- Schellenberger, J.; Park, J.O.; Conrad, T.M.; Palsson, B.Ø. BiGG: A Biochemical Genetic and Genomic knowledgebase of large scale metabolic reconstructions. BMC Bioinform. 2010, 11, 213. [Google Scholar] [CrossRef] [PubMed]
- Barabási, A.L.; Albert, R.; Jeong, H. Scale-free characteristics of random networks: The topology of the world-wide web. Phys. A Stat. Mech. Appl. 2000, 281, 69–77. [Google Scholar] [CrossRef]
- Ravasi, T.; Suzuki, H.; Cannistraci, C.V.; Katayama, S.; Bajic, V.B.; Tan, K.; Akalin, A.; Schmeier, S.; Kanamori-Katayama, M.; Bertin, N.; et al. An Atlas of Combinatorial Transcriptional Regulation in Mouse and Man. Cell 2010, 140, 744–752. [Google Scholar] [CrossRef]
- Cantini, L.; Medico, E.; Fortunato, S.; Caselle, M. Detection of gene communities in multi-networks reveals cancer drivers. Sci. Rep. 2015, 5, 17386. [Google Scholar] [CrossRef] [PubMed]
- Marbach, D.; Costello, J.C.; Küffner, R.; Vega, N.M.; Prill, R.J.; Camacho, D.M.; Allison, K.R.; Kellis, M.; Collins, J.J.; Stolovitzky, G. Wisdom of crowds for robust gene network inference. Nat. Methods 2012, 9, 796–804. [Google Scholar] [CrossRef] [PubMed]
- Wilkinson, D.M.; Huberman, B.A. A method for finding communities of related genes. Proc. Natl. Acad. Sci. USA 2004, 101, 5241–5248. [Google Scholar] [CrossRef]
- Zhu, J.; Zhang, B.; Smith, E.N.; Drees, B.; Brem, R.B.; Kruglyak, L.; Bumgarner, R.E.; Schadt, E.E. Integrating large-scale functional genomic data to dissect the complexity of yeast regulatory networks. Nat. Genet. 2008, 40, 854–861. [Google Scholar] [CrossRef]
- Tang, B.; Hsu, H.K.; Hsu, P.Y.; Bonneville, R.; Chen, S.S.; Huang, T.H.M.; Jin, V.X. Hierarchical Modularity in ERα Transcriptional Network Is Associated with Distinct Functions and Implicates Clinical Outcomes. Sci. Rep. 2012, 2, 875. [Google Scholar] [CrossRef]
- Shen-Orr, S.S.; Milo, R.; Mangan, S.; Alon, U. Network motifs in the transcriptional regulation network of Escherichia coli. Nat. Genet. 2002, 31, 64–68. [Google Scholar] [CrossRef]
- Milo, R.; Shen-Orr, S.; Itzkovitz, S.; Kashtan, N.; Chklovskii, D.; Alon, U. Network Motifs: Simple Building Blocks of Complex Networks. Science 2002, 298, 824–827. [Google Scholar] [CrossRef] [PubMed]
- Lancichinetti, A.; Fortunato, S.; Radicchi, F. Benchmark graphs for testing community detection algorithms. Phys. Rev. E 2008, 78, 046110. [Google Scholar] [CrossRef] [PubMed]
- Lancichinetti, A.; Fortunato, S. Benchmarks for testing community detection algorithms on directed and weighted graphs with overlapping communities. Phys. Rev. E 2009, 80, 016118. [Google Scholar] [CrossRef] [PubMed]
- Good, B.H.; De Montjoye, Y.A.; Clauset, A. Performance of modularity maximization in practical contexts. Phys. Rev. E 2010, 81, 046106. [Google Scholar] [CrossRef]
- Kullback, S. Information Theory and Statistics; Wiley: Hoboken, NJ, USA, 1959. [Google Scholar]
- Cutello, V.; Nicosia, G.; Pavone, M.; Stracquadanio, G. Entropic divergence for population based optimization algorithms. In Proceedings of the IEEE Congress on Evolutionary Computation, Barcelona, Spain, 18–23 July 2010; pp. 1–8. [Google Scholar] [CrossRef]
- Zito, F.; Cutello, V.; Pavone, M. Optimizing Multi-Variable Time Series Forecasting using Metaheuristics. In Lecture Notes in Computer Science, Proceedings of the 14th Metaheuristics International Conference (MIC 2022), Ortigia-Syracuse, Italy, 11–14 July 2022; Di Gaspero, L., Festa, P., Nakib, A., Pavone, M., Eds.; Springer: Cham, Swizterland, 2023; Volume 13838. [Google Scholar]
- Altuntas, V.; Gök, M.; Kahveci, T. Stability Analysis of Biological Networks’ Diffusion State. IEEE/ACM Trans. Comput. Biol. Bioinform. 2020, 17, 1406–1418. [Google Scholar] [CrossRef]
- Penas, D.R.; González, P.; Egea, J.A.; Doallo, R.; Banga, J.R. Parameter estimation in large-scale systems biology models: A parallel and self-adaptive cooperative strategy. BMC Bioinform. 2017, 18, 52. [Google Scholar] [CrossRef]
- Barros, R.C.; Winck, A.T.; Machado, K.S.; Basgalupp, M.P.; de Carvalho, A.C.; Ruiz, D.D.; de Souza, O.N. Automatic design of decision-tree induction algorithms tailored to flexible-receptor docking data. BMC Bioinform. 2012, 13, 310. [Google Scholar] [CrossRef]
- Cutillas-Lozano, J.M.; Giménez, D.; Almeida, F. Hyperheuristics Based on Parametrized Metaheuristic Schemes. In Proceedings of the Annual Conference on Genetic and Evolutionary Computation (GECCO ’15), Madrid, Spain, 11–15 July 2015; Association for Computing Machinery: New York, NY, USA, 2015; pp. 361–368. [Google Scholar] [CrossRef]
- Bonidia, R.P.; Avila Santos, A.P.; de Almeida, B.L.S.; Stadler, P.F.; da Rocha, U.N.; Sanches, D.S.; de Carvalho, A.C.P.L.F. BioAutoML: Automated feature engineering and metalearning to predict noncoding RNAs in bacteria. Briefings Bioinform. 2022, 23, 1–13. [Google Scholar] [CrossRef]
- Atay, Y.; Koc, I.; Babaoglu, I.; Kodaz, H. Community detection from biological and social networks: A comparative analysis of metaheuristic algorithms. Appl. Soft Comput. 2017, 50, 194–211. [Google Scholar] [CrossRef]
- Civicioglu, P. Transforming geocentric cartesian coordinates to geodetic coordinates by using differential search algorithm. Comput. Geosci. 2012, 46, 229–247. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential Evolution – A Simple and Efficient Heuristic for global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Glover, F. Heuristics for integer programming using surrogate constraints. Decis. Sci. 1977, 8, 156–166. [Google Scholar] [CrossRef]
- Martí, R.; Laguna, M.; Glover, F. Principles of scatter search. Eur. J. Oper. Res. 2006, 169, 359–372. [Google Scholar] [CrossRef]
- Erol, O.K.; Eksin, I. A new optimization method: Big Bang–Big Crunch. Adv. Eng. Softw. 2006, 37, 106–111. [Google Scholar] [CrossRef]
- Yang, X.S. A New Metaheuristic Bat-Inspired Algorithm. In Studies in Computational Intelligence, Proceedings of the Nature Inspired Cooperative Strategies for Optimization (NICSO 2010), Granada, Spain, 12–14 May 2010; González, J.R., Pelta, D.A., Cruz, C., Terrazas, G., Krasnogor, N., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 65–74. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-pour, H.; Saryazdi, S. GSA: A Gravitational Search Algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Blondel, V.D.; Guillaume, J.L.; Lambiotte, R.; Lefebvre, E. Fast unfolding of communities in large networks. J. Stat. Mech. Theory Exp. 2008, 2008, P10008. [Google Scholar] [CrossRef]
- Danon, L.; Díaz-Guilera, A.; Duch, J.; Arenas, A. Comparing community structure identification. J. Stat. Mech. Theory Exp. 2005, 2005, P09008. [Google Scholar] [CrossRef]
- Hubert, L.; Arabic, P. Comparing Partitions. J. Classif. 1985, 2, 193–218. [Google Scholar] [CrossRef]
- Meilă, M. Comparing clusterings–an information based distance. J. Multivar. Anal. 2007, 98, 873–895. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).