Automatic Indexation of the Pension Age to Life Expectancy: When Policy Design Matters †
Abstract
1. Introduction
2. Materials and Methods
2.1. Life Expectancy Measures
2.2. Retirement Age Policies in Selected Countries
2.2.1. The Netherlands
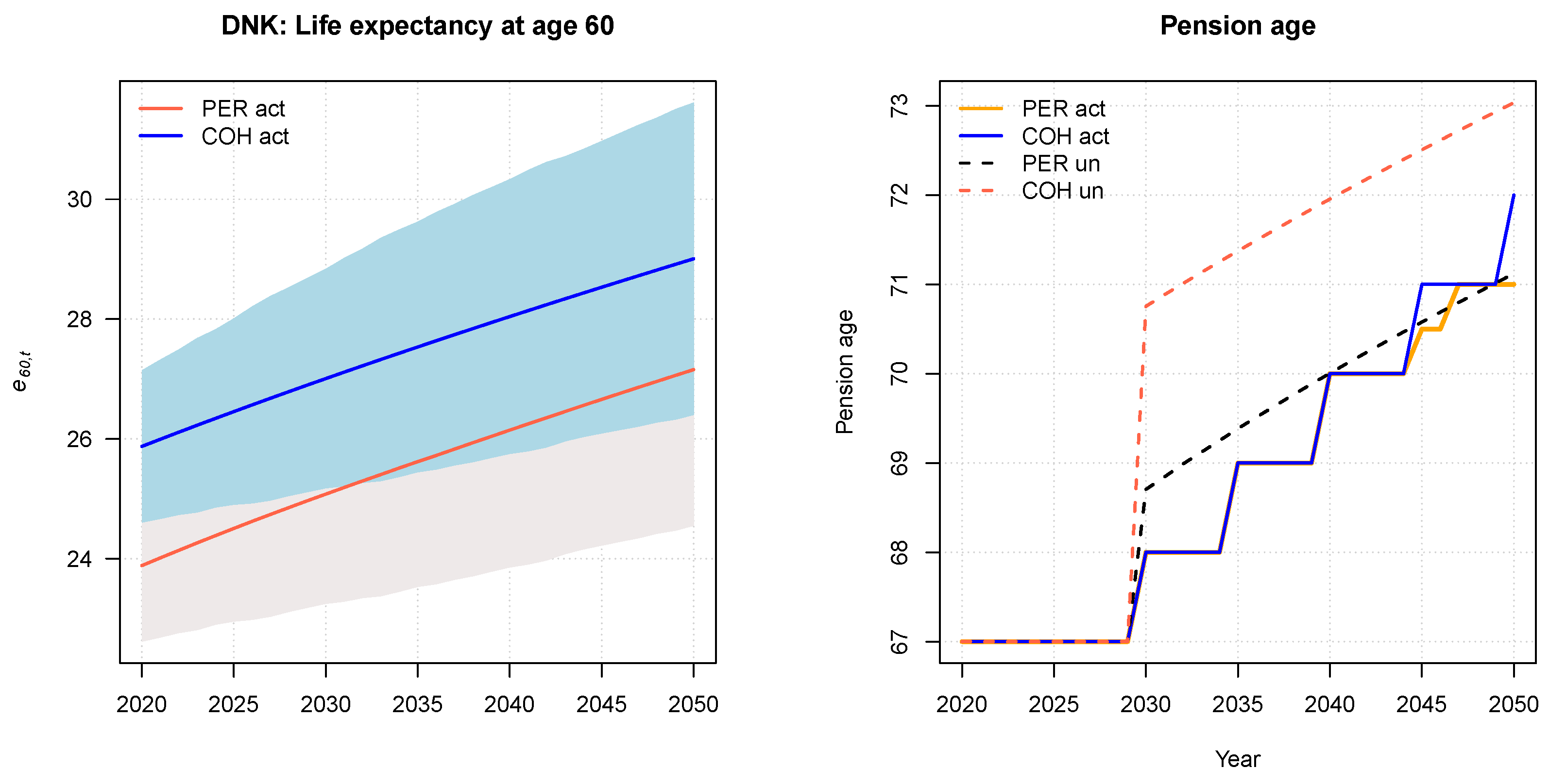
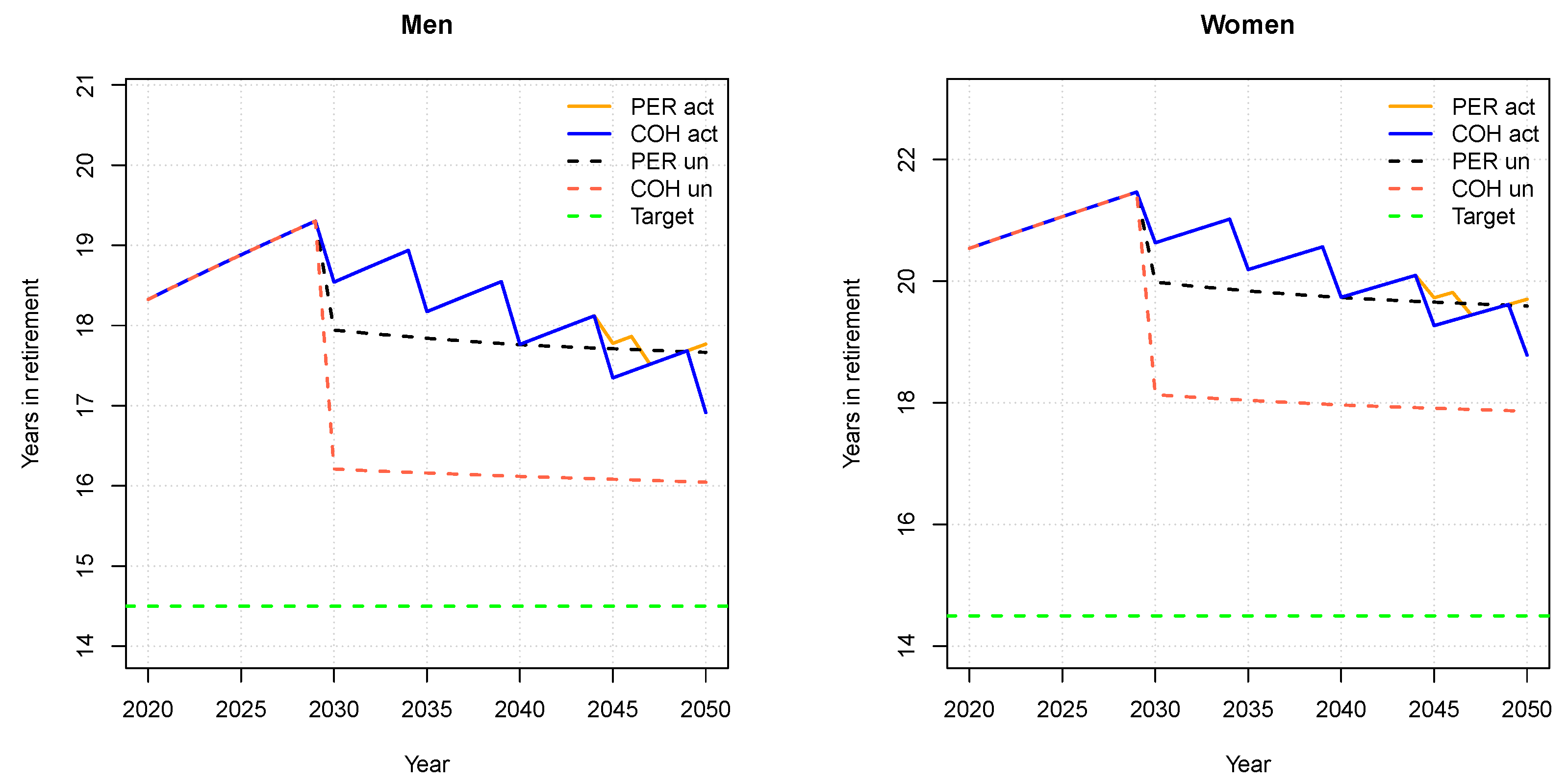
2.2.2. Denmark
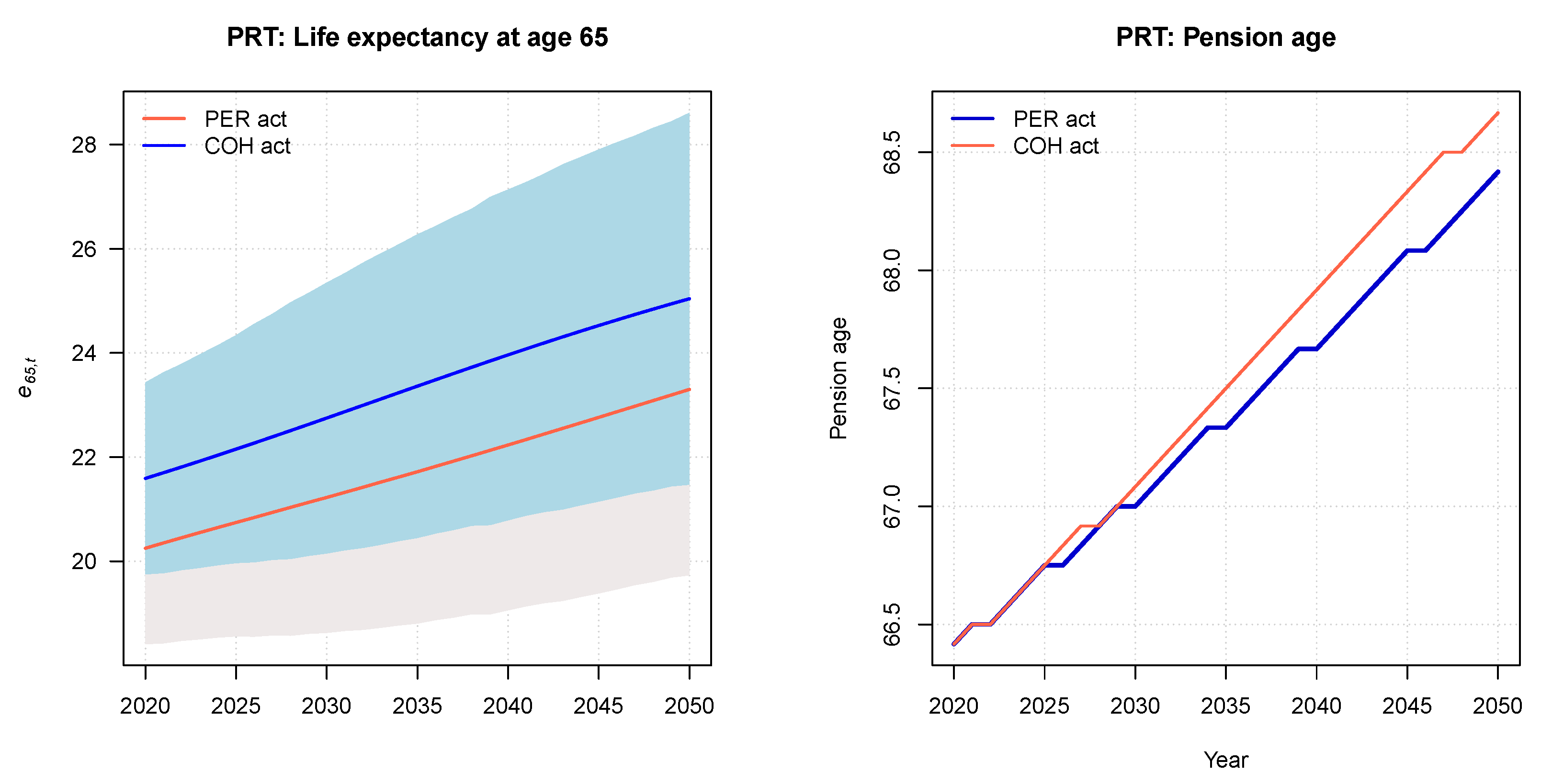
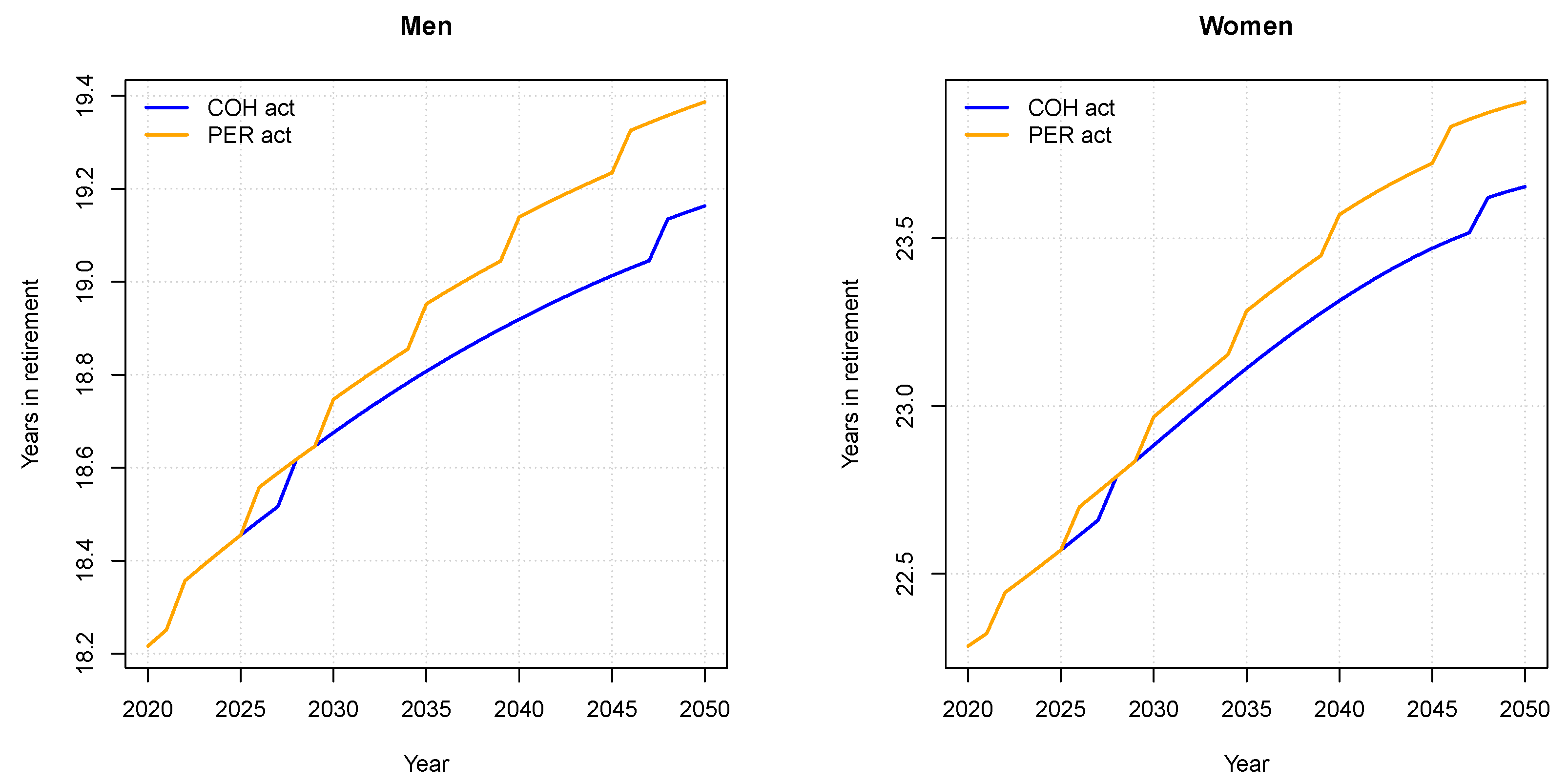
2.2.3. Portugal
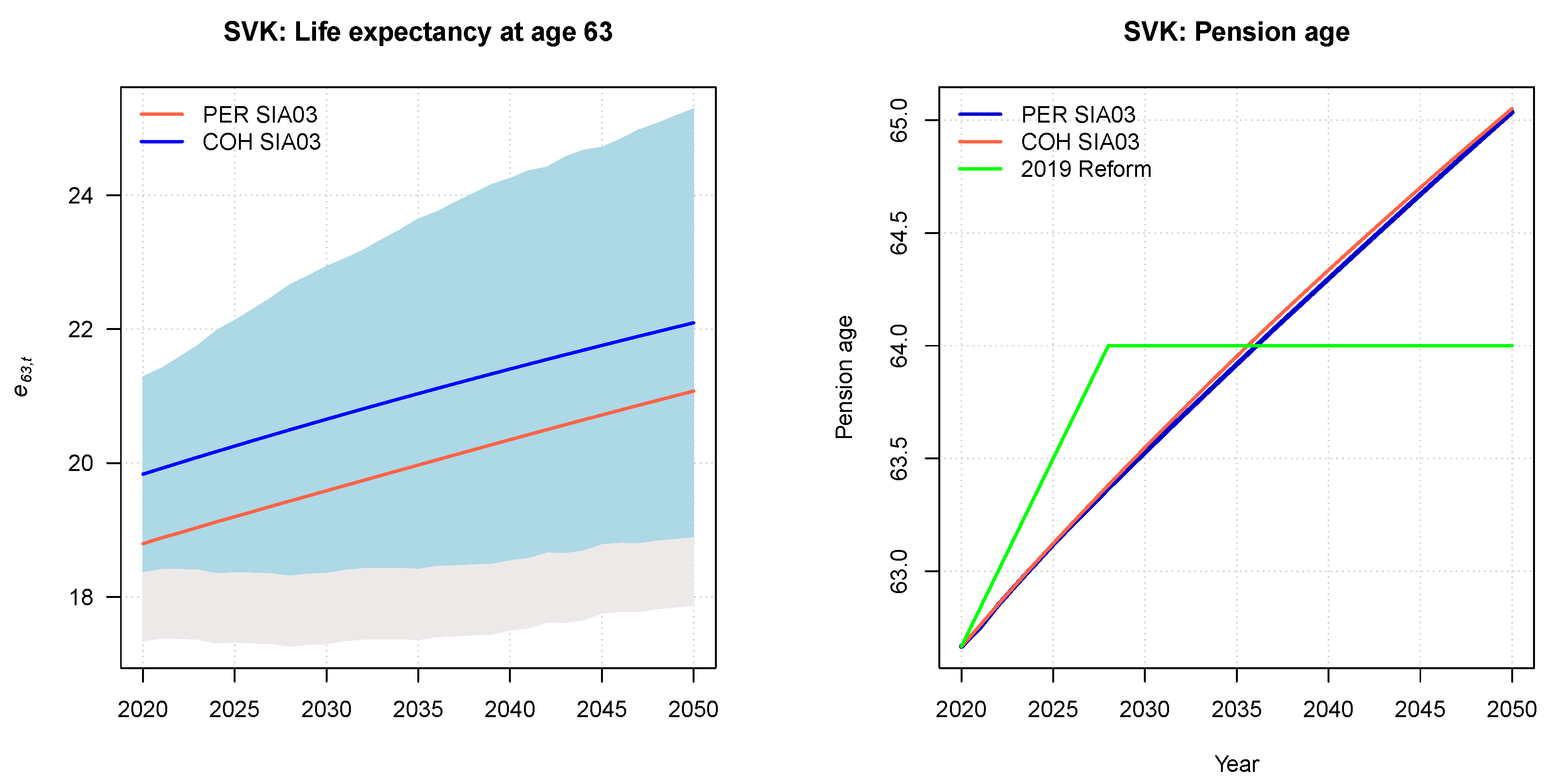
2.2.4. Slovakia
2.3. Forecasting Mortality
2.3.1. Bayesian Model Ensemble
2.3.2. Individual Stochastic Mortality Models
2.3.3. Data
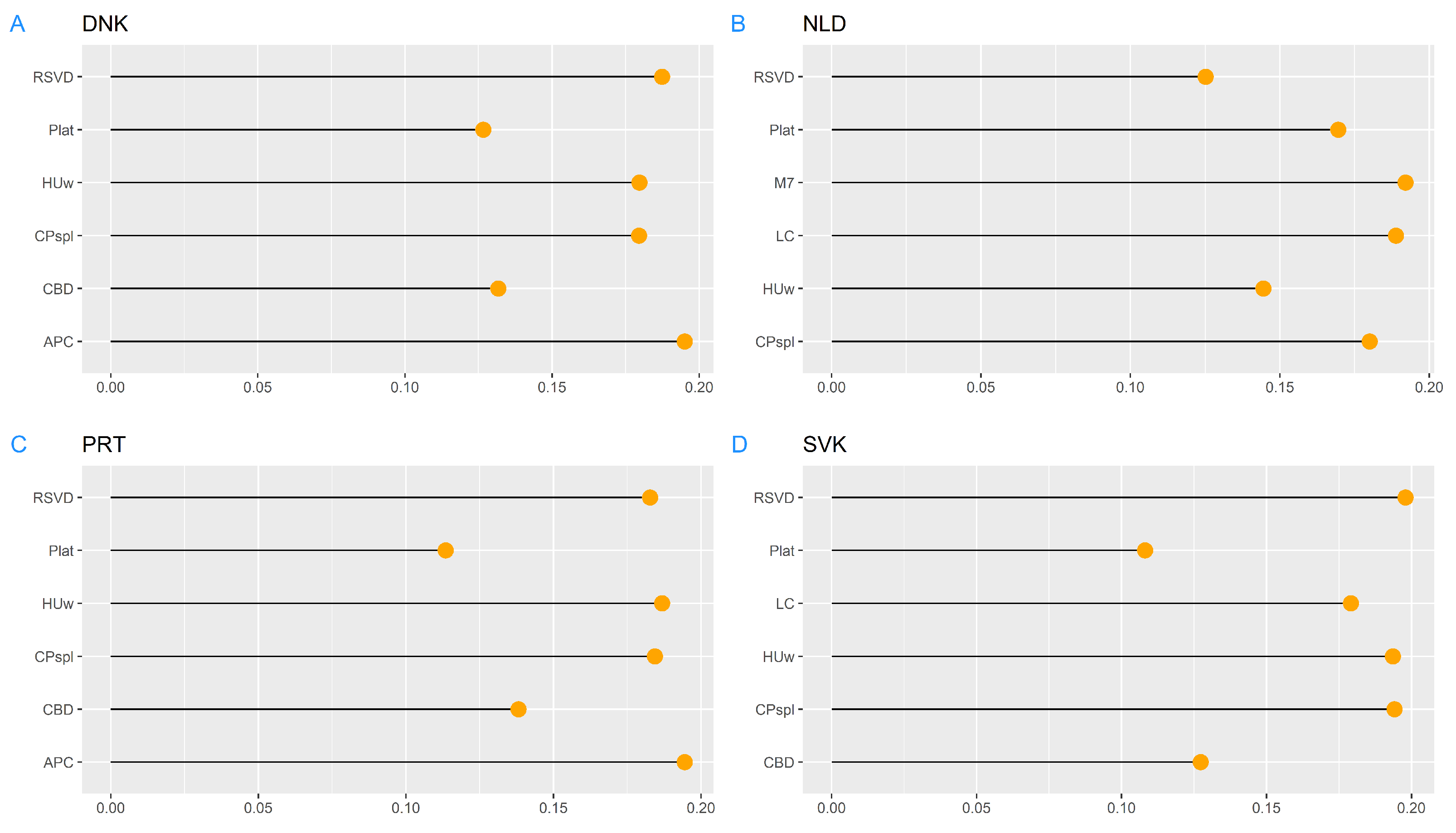
3. Results
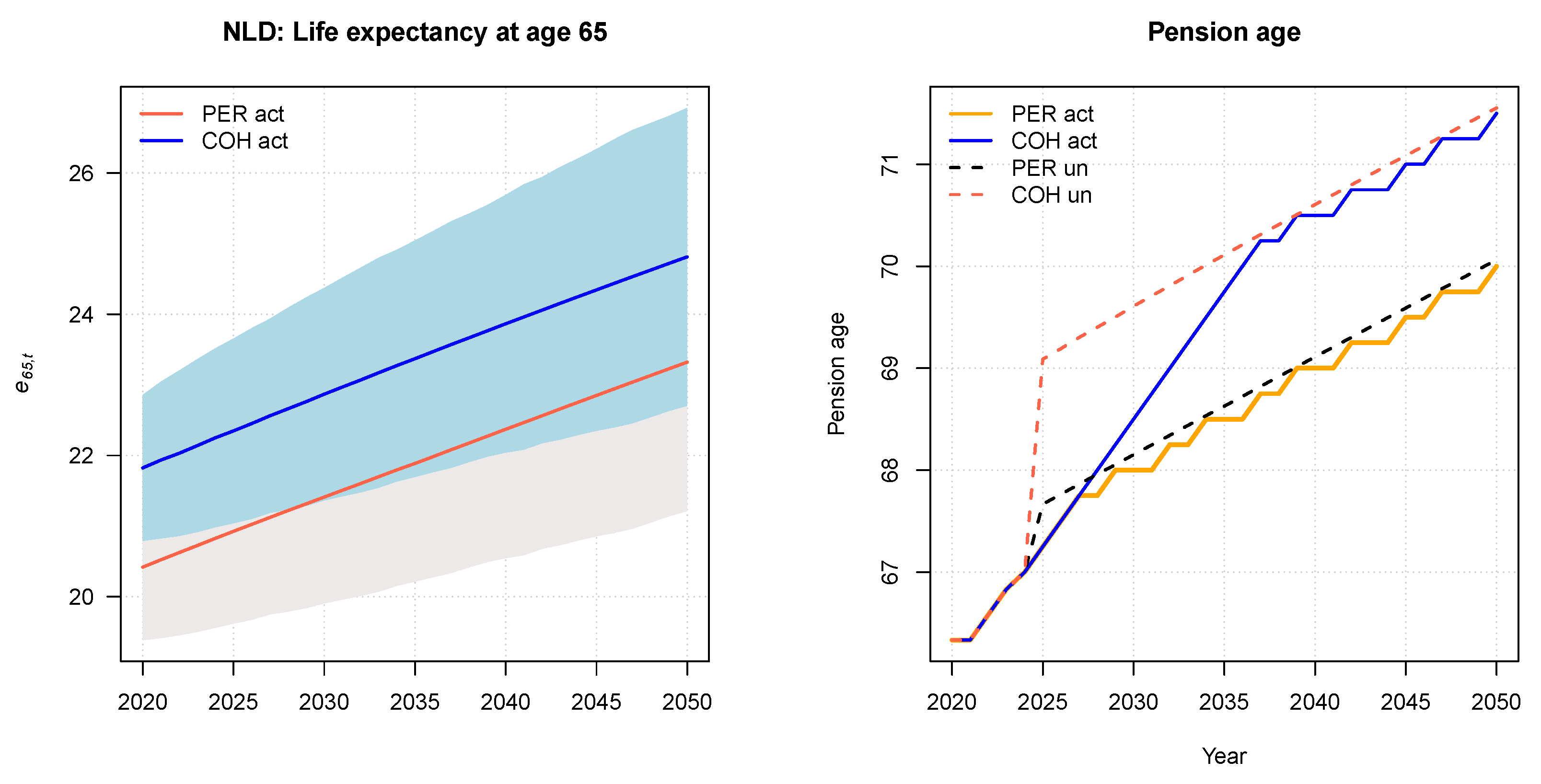
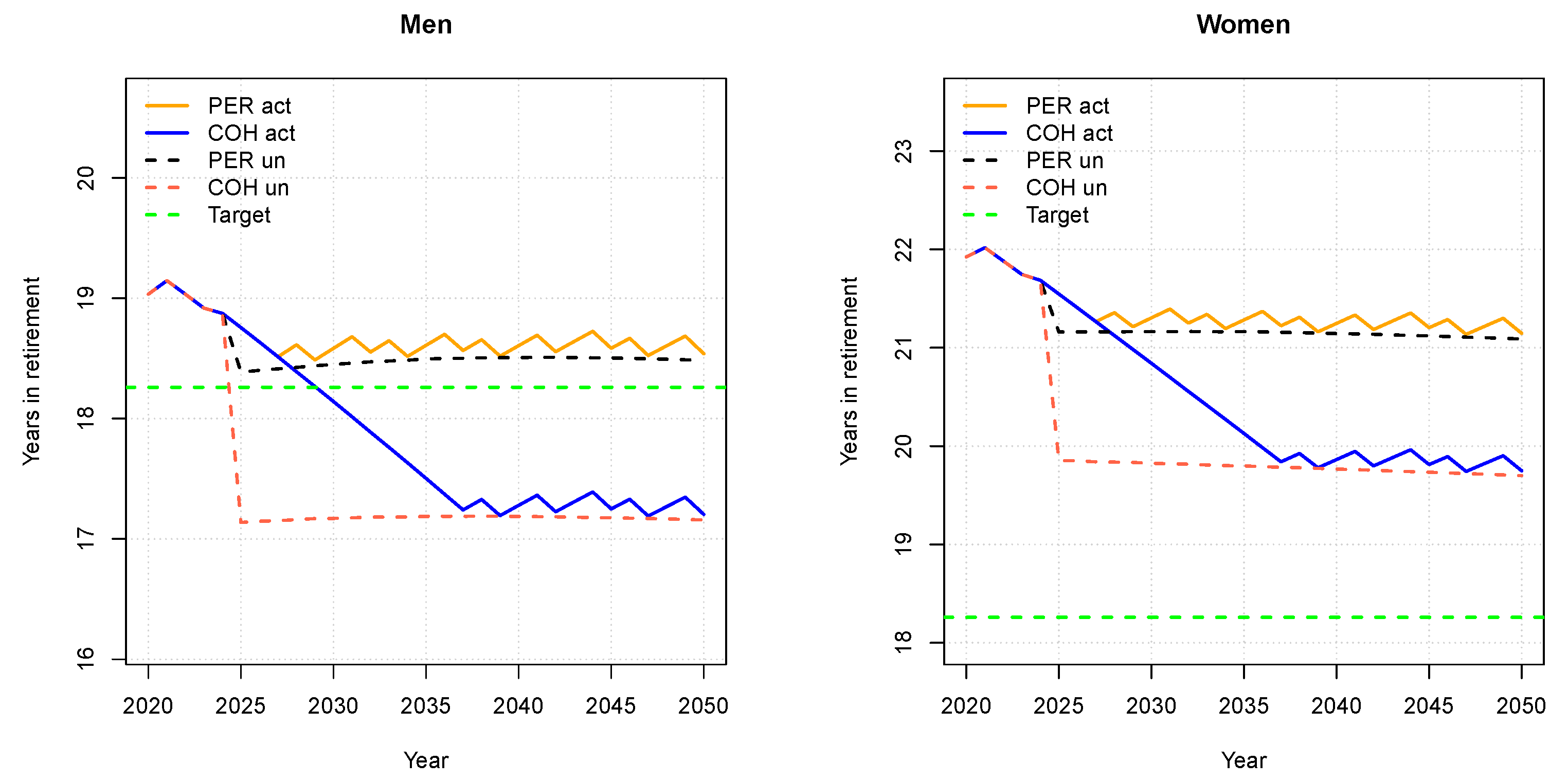
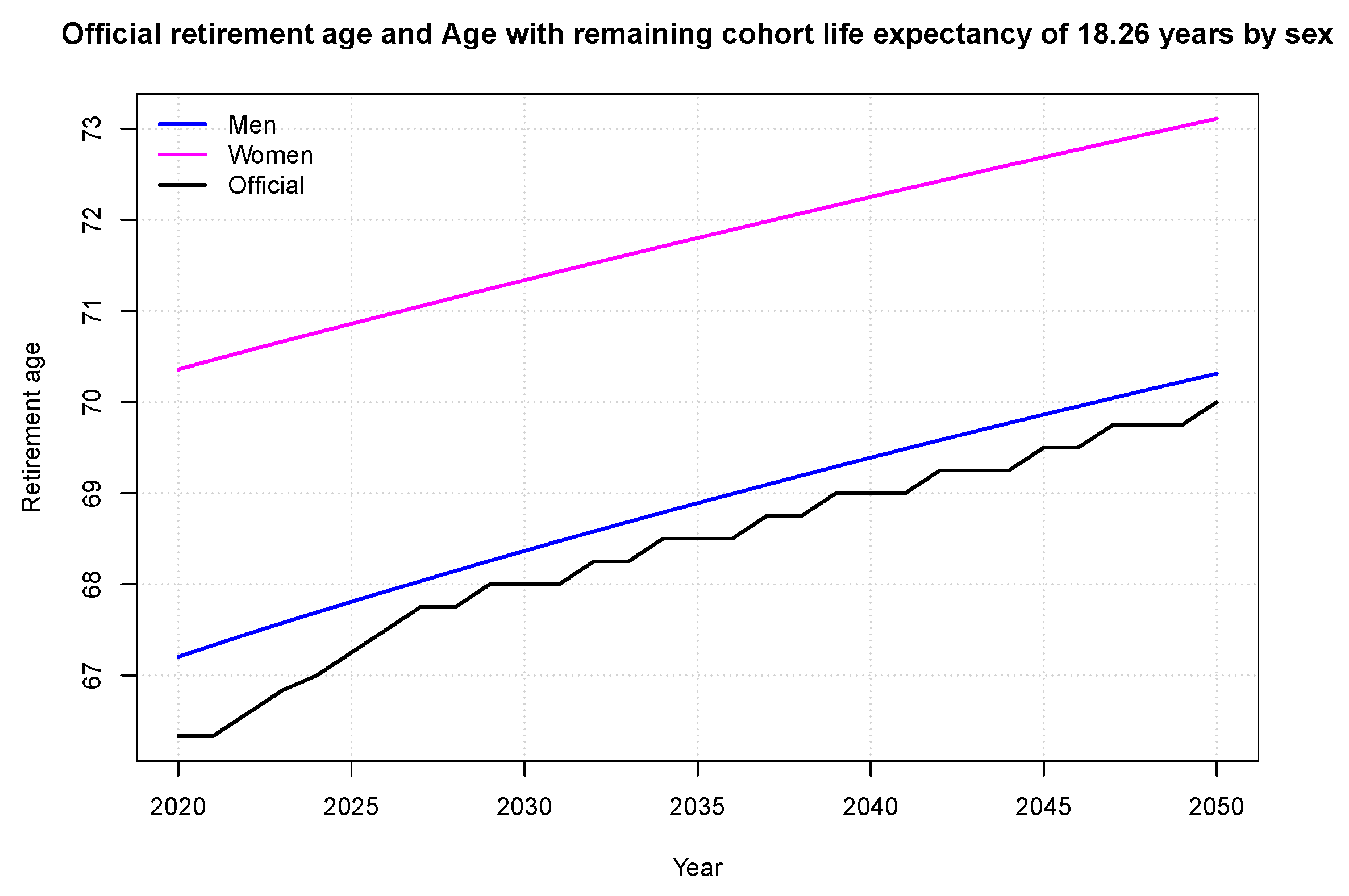
3.1. The Netherlands
3.2. Denmark
3.3. Portugal
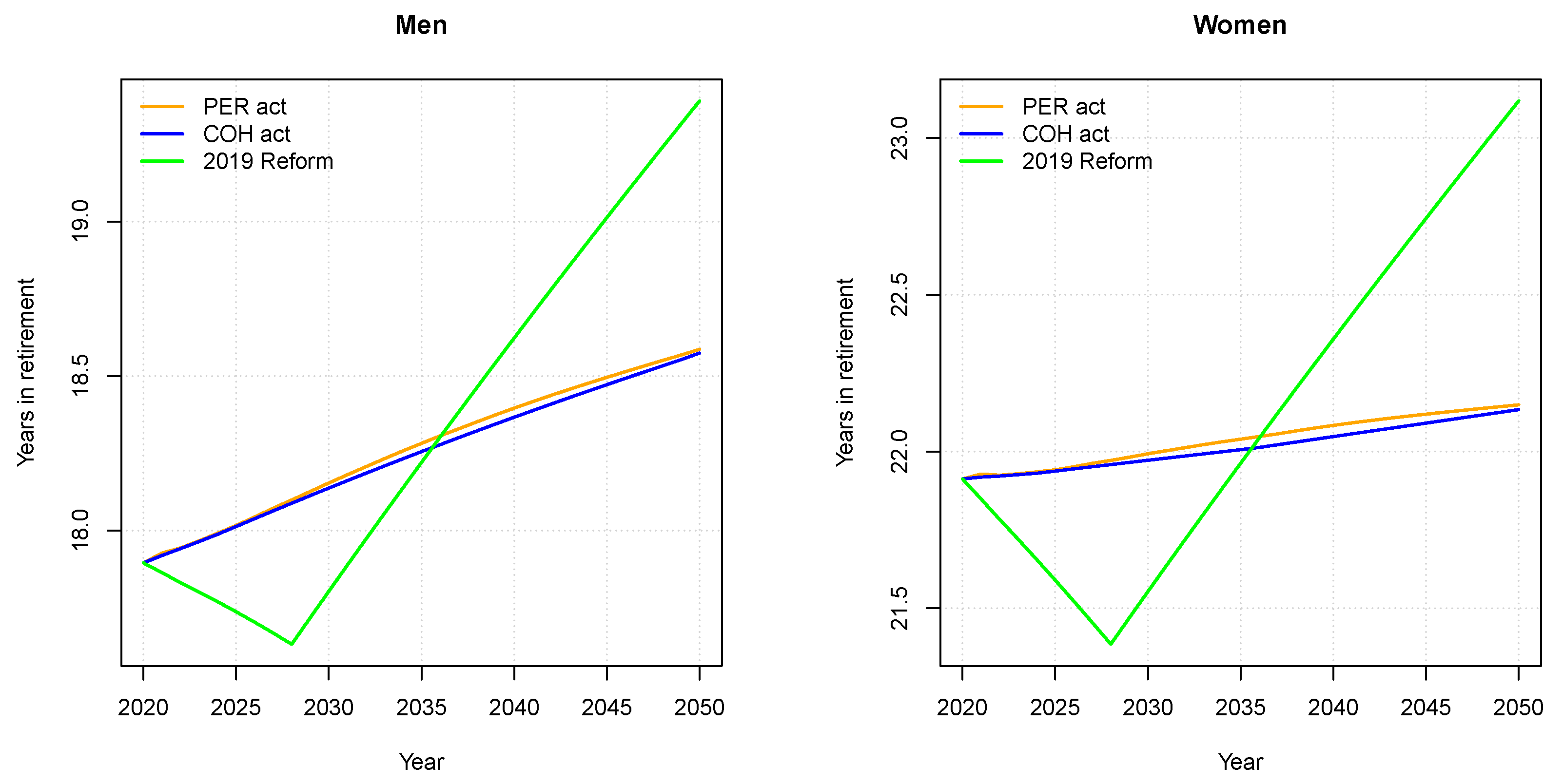
3.4. Slovakia
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Stochastic Mortality Models: Technical Description
Appendix A.1. GAPC Stochastic Mortality Models
Appendix A.2. Weighted Hyndman–Ullah Method
Appendix A.3. CP-Splines Model
Appendix A.4. Regularized SVD Model
Appendix B. Life Expectancy Gap and Implied Tax/Subsidies
| 1 | For a detailed discussion of pensions taxation, see, e.g., Holzmann and Piggott (2018) and Bravo (2016). |
| 2 | In private individual or employer-sponsored pension plans, diverse insurance and non-insurance longevity risk-sharing mechanisms (e.g., Group-Self Annuitization schemes, longevity-linked life annuities, tontine annuities) have also been proposed and some successfully implemented (Piggott et al. 2005; Valdez et al. 2006; Stamos 2008; Milevsky and Salisbury 2015; Bravo and El Mekkaoui de Freitas 2018; Bravo 2019, 2020, 2021). |
| 3 | Spain suspended the adjustment of pension benefits with the life expectancy sustainability factor in 2019 at least until 2023. |
| 4 | The standard, normal or also full retirement age is defined here as the age at which individuals can first withdraw their full pension benefits, i.e., without actuarial decrements (reductions) or increments (bonus) for early (late) retirement. In most countries, standard pension ages are clearly defined in legislation. In many countries, different standards apply to different components of the overall retirement-income package. In addition, many countries have specific provisions allowing individuals to retire earlier than the standard age with full benefits given that certain contribution requirements are met. We note that some countries have opted not to have a “standard” retirement age, defining instead an age window at which pension benefits may first be drawn. |
| 5 | In the last two decades, nearly all European countries have augmented the standard and early retirement ages (the only exception being Luxembourg), with particularly large increases legislated in some cases (e.g., Greece, Sweden, France and Finland). Some countries have limited or slowed down the increase in the retirement age following reforms adopted in the past (Italy, The Netherlands, and the Slovak Republic). |
| 6 | For instance, in the United States, only those reaching age 65 are entitled to Medicare. Those who retire earlier receive less than full social security pension benefits and will have no employer and no Medicare health coverage during the years from retirement prior to age 65. This discourages workers from retiring at a younger age to avoid an extra pension decrement. |
| 7 | Turkey has already announced it will phase out the sex difference for those entering the labour market in 2028. |
| 8 | There are some notable exceptions to this pattern, namely, South Korea and Turkey, where the effective labour market exit age is considerably higher than the standard retirement age for both men and women. In recent years, we have seen some reform reversals in this area, with some countries (e.g., Italy and Portugal) easing early-retirement conditions. For instance, in 2019, Italy suspended until 2026 the automatic indexation of both the statutory retirement age and the career-length eligibility conditions for early retirement to life expectancy and expanded early retirement options by introducing the so-called “Quota 100” (which enables retirement at age 62 with 38 years of contributions until 2021 and allows combining work and pensions before the statutory retirement age, but subject to a labour-income ceiling) and the ”women’s option” which allows women to retire at age 58 with 35 years of contributions if they fully switch to the NDC benefit calculation. |
| 9 | See, e.g., Lee and Carter (1992); Brouhns et al. (2002); Renshaw and Haberman (2003, 2006); Currie (2006); Cairns et al. (2006, 2009); Hyndman and Ullah (2007); Plat (2009); Blackburn and Sherris (2013); D’Amato et al. (2014); Villegas et al. (2017); Bravo and Ayuso (2020, 2021); Hunt and Blake (2021); Bravo and Nunes (2021) and references therein. |
| 10 | The plan was to raise the eligibility age by one month per year between 2013–2015, three months per year between 2016–2018, and four months per year in 2019–2021, reaching the age of 67.2 by 2021 (European Commission 2019). |
| 11 | Decree-law 167-D/2013 from December 31. |
| 12 | The retirement age is kept at 65 years for beneficiaries legally prevented from working beyond that age (e.g., pilots, drivers of heavy vehicles). In addition, when the scheme participants reach the age of 65, the standard pensionable age is reduced by four months for each calendar year (with registered earnings) worked in excess of the contributions ceiling of 40 years, with a 60-year threshold. There are specific early retirement provisions for those with very long contribution careers, in long-term involuntary unemployment or working in certain arduous jobs (e.g., miners). |
| 13 | The SMAPE for model k and population g is defined by
|
| 14 | For instance, model LC is nested within model RH, with for all x, and for all being a special case of APC with for all x and no cohort effects. Model APC is a special case of RH with for all x. The CBD model is a restricted version of M7 with for all t and for all c. |
| 15 |
References
- Alho, Juha, Jorge M. Bravo, and Edward Palmer. 2013. Annuities and life expectancy in NDC. In Nonfinancial Defined Contribution Pension Schemes in a Changing Pension World, Volume 2, Gender, Politics, and Financial Stability. Edited by Robert Holzmann, Edward Palmer and David Robalino. Washington, DC: World Bank, pp. 395–436. [Google Scholar]
- Arnold, Séverine, and Anca Jijiie. 2020. Retirement Ages by Socio-Economic Class. Risks 10: 102. [Google Scholar] [CrossRef]
- Auerbach, Alan J., Kerwin K. Charles, Courtney C. Coile, William Gale, Dana Goldman, Ronald Lee, and Charles M. Lucas. 2017. How the Growing Gap in Life Expectancy May Affect Retirement Benefits and Reforms. NBER Working Papers 23329. Cambridge: National Bureau of Economic Research, Inc. [Google Scholar]
- Ayuso, Mercedes, Jorge M. Bravo, and Robert Holzmann. 2017a. On the heterogeneity in longevity among socioeconomic groups: Scope, trends, and implications for Earnings-Related Pension Schemes. Global Journal of Human Social Sciences-Economics 17: 31–57. [Google Scholar]
- Ayuso, Mercedes, Jorge M. Bravo, and Robert Holzmann. 2017b. Addressing longevity heterogeneity in pension scheme design. Journal of Finance and Economics 6: 1–21. [Google Scholar] [CrossRef]
- Ayuso, Mercedes, Jorge M. Bravo, and Robert Holzmann. 2021. Getting Life Expectancy Estimates Right for Pension Policy: Period versus Cohort Approach. Journal of Pension Economics and Finance 20: 212–31. [Google Scholar] [CrossRef]
- Blackburn, Craig, and Michael Sherris. 2013. Consistent dynamic affine mortality models for longevity risk applications. Insurance: Mathematics and Economics 53: 64–73. [Google Scholar] [CrossRef]
- Bravo, Jorge M. 2016. Taxation of Pensions in Portugal: A Semi-Dual Income Tax System. CESifo DICE Report 14: 14–23. [Google Scholar]
- Bravo, Jorge M. 2019. Funding for longer lives: Retirement wallet and risk-sharing annuities. Ekonomiaz 96: 268–91. [Google Scholar]
- Bravo, Jorge M. 2020. Longevity-Linked Life Annuities: A Bayesian Model Ensemble Pricing Approach. In Proceedings of the Atas da 20a Conferência da Associação Portuguesa de Sistemas de Informação 2020. CAPSI 2020 Proceedings. Available online: https://aisel.aisnet.org/capsi2020/29 (accessed on 30 January 2021).
- Bravo, Jorge M. 2021. Pricing participating longevity-linked life annuities: A Bayesian Model Ensemble approach. European Actuarial Journal. [Google Scholar] [CrossRef]
- Bravo, Jorge M., and Najat El Mekkaoui de Freitas. 2018. Valuation of longevity-linked life annuities. Insurance: Mathematics and Economics 78: 212–29. [Google Scholar] [CrossRef]
- Bravo, Jorge M., and Jose A. Herce. 2020. Career breaks, Broken pensions? Long-run effects of early and late-career unemployment spells on pension entitlements. Journal of Pension Economics and Finance, 1–27. [Google Scholar] [CrossRef]
- Bravo, Jorge M., and João Pedro Vidal Nunes. 2021. Pricing Longevity Derivatives via Fourier Transforms. Insurance: Mathematics and Economics 96: 81–97. [Google Scholar] [CrossRef]
- Bravo, Jorge M., and Mercedes Ayuso. 2020. Previsões de mortalidade e de esperança de vida mediante combinação Bayesiana de modelos: Uma aplicação à população portuguesa. RISTI-Revista Iberica de Sistemas e Tecnologias de Informacao E40: 128–44. [Google Scholar]
- Bravo, Jorge M., and Mercedes Ayuso. 2021. Forecasting the retirement age: A Bayesian Model Ensemble Approach. In Trends and Applications in Information Systems and Technologies, WorldCIST 2021. Advances in Intelligent Systems and Computing. Edited by Á. Rocha, H. Adeli, G. Dzemyda, F. Moreira and A.M. Ramalho Correia. Cham: Springer, vol. 1365, pp. 123–35. [Google Scholar] [CrossRef]
- Bravo, Jorge M., Mercedes Ayuso, Robert Holzmann, and Edward Palmer. 2021a. Addressing the life expectancy gap in pension policy. Insurance: Mathematics and Economics 99: 200–21. [Google Scholar] [CrossRef]
- Bravo, Jorge M., Mercedes Ayuso, Robert Holzmann, and Edward Palmer. 2021b. Intergenerational actuarial fairness when longevity increases: Amending the retirement age. Scandinavian Actuarial Journal. Preprint to submit. [Google Scholar]
- Brouhns, Natacha, Michel Denuit, and Ingrid Van Keilegom. 2005. Bootstrapping the Poisson Log-Bilinear Model for Mortality Forecasting. Scandinavian Actuarial Journal 3: 212–24. [Google Scholar] [CrossRef]
- Brouhns, Natacha, Michel Denuit, and Jeroen K. Vermunt. 2002. A Poisson Log-Bilinear Regression approach to the construction of projected life tables. Insurance: Mathematics and Economics 31: 373–93. [Google Scholar]
- Cairns, Andrew J. G., David Blake, and Kevin Dowd. 2006. A two-factor model for stochastic mortality with parameter uncertainty: Theory and calibration. Journal of Risk and Insurance 73: 687–718. [Google Scholar] [CrossRef]
- Cairns, Andrew J. G., David Blake, Kevin Dowd, Guy D. Coughlan, David Epstein, Alen Ong, and Igor Balevich. 2009. A quantitative comparison of stochastic mortality models using data from England and Wales and the United States. North American Actuarial Journal 13: 1–35. [Google Scholar] [CrossRef]
- Camarda, Carlo Giovanni. 2019. Smooth constrained mortality forecasting. Demographic Research 41: 1091–130. [Google Scholar] [CrossRef]
- Chetty, Raj, Michael Stepner, Sarah Abraham, Shelby Lin, Benjamin Scuderi, Nicholas Turner, Augustin Bergeron, and David Cutler. 2016. The association between income and life expectancy in the United States, 2001–2014. The Journal of the American Medical Association 315: 1750–66. [Google Scholar] [CrossRef]
- Coppola, Mariarosaria, Maria Russolillo, and Rosaria Simone. 2019. An Indexation Mechanism for Retirement Age: Analysis of the Gender Gap. Risks 7: 21. [Google Scholar] [CrossRef]
- Currie, Ian. 2006. Smoothing and Forecasting Mortality Rates with P-Splines. Edinburgh: DP Heriot Watt University. [Google Scholar]
- D’Amato, Valeria, Steven Haberman, Gabriella Piscopo, Maria Russolillo, and Lorenzo Trapani. 2014. Detecting Common Longevity Trends by a Multiple Population Approach. North American Actuarial Journal 18: 139–49. [Google Scholar] [CrossRef]
- Denuit, Michel, and Anne-Cécile Goderniaux. 2005. Closing and projecting life tables using log-linear models. Bulletin of the Swiss Association of Actuaries 1: 29–48. [Google Scholar]
- European Commission. 2019. Joint Paper on Pensions 2019. Economic Policy Committee (EPC) & Social Protection Committee (SPC). Brussels: European Commission. [Google Scholar]
- Haberman, Steven, and Arthur Renshaw. 2011. A Comparative Study of Parametric Mortality Projection Models. Insurance: Mathematics and Economics 48: 35–55. [Google Scholar] [CrossRef]
- Hansen, Peter R., Asger Lunde, and James M. Nason. 2011. The model confidence set. Econometrica 79: 453–97. [Google Scholar] [CrossRef]
- Holzmann, Robert, and John Piggott. 2018. The Taxation of Pensions. Cambridge: MIT Press. [Google Scholar]
- Holzmann, Robert, Jennifer Alonso-García, Heloise Labit-Hardy, and Andrés M. Villegas. 2020. NDC schemes and heterogeneity in longevity: Proposals for redesign. In Progress and challenges of Nonfinancial Defined Contribution Pension (NDC) Schemes, Volume 1: Addressing Marginalization, Polarization, and the Labor Market. Edited by R. Holzmann, E. Palmer, R. Palacios and S. Sacchi. Washington, DC: World Bank, pp. 307–32. [Google Scholar]
- Holzmann, Robert, Mercedes Ayuso, and Jorge M. Bravo. 2019. Reframing lifecycle saving and dissaving by low-, middle-, and high-income groups: Initial hypotheses, literature review, and ideas for empirical testing. In IZA Discussion Paper No. 12655. Bonn: IZA Institute of Labor Economics. [Google Scholar]
- Huang, Jianhua Z., Haipeng Shen, and Andreas Buja. 2009. The analysis of two-way functional data using two-way regularized singular value decompositions. Journal of the American Statistical Association 104: 1609–20. [Google Scholar] [CrossRef]
- Human Mortality Database. 2019. University of California, Berkeley (USA), and Max Planck Institute for Demographic Research (Germany). Available online: www.mortality.org (accessed on 15 August 2019).
- Hunt, Andrew, and David Blake. 2021. On the structure and classification of mortality models. North American Actuarial Journal 25: S215–S234. [Google Scholar] [CrossRef]
- Hunt, Andrew, and Andrés M. Villegas. 2015. Robustness and convergence in the Lee–Carter model with cohort effects. Insurance: Mathematics and Economics 64: 186–202. [Google Scholar] [CrossRef]
- Hyndman, Rob J., and Md Shahid Ullah. 2007. Robust forecasting of mortality and fertility rates: A functional data approach. Computational Statistics & Data Analysis 51: 4942–56. [Google Scholar]
- Koissi, Marie-Claire, Arnold F. Shapiro, and Göran Högnäs. 2006. Evaluating and extending the Lee–Carter model for mortality forecasting: Bootstrap confidence interval. Insurance: Mathematics and Economics 38: 1–20. [Google Scholar] [CrossRef]
- Lee, Ronald D., and Lawrence R. Carter. 1992. Modeling and forecasting U.S. mortality. Journal of the American Statistical Association 87: 659–71. [Google Scholar] [CrossRef]
- Makridakis, Spyros, Evangelos Spiliotis, and Vassilios Assimakopoulos. 2018. Statistical and Machine Learning forecasting methods: Concerns and ways forward. PLoS ONE 13: e0194889. [Google Scholar] [CrossRef] [PubMed]
- Milevsky, Moshe A., and Thomas S. Salisbury. 2015. Optimal retirement income tontines. Insurance: Mathematics and Economics 64: 91–105. [Google Scholar] [CrossRef]
- NASEM (National Academy of Sciences, Engineering and Medicine). 2015. The growing gap in life expectancy by income: Implications for federal programs and policy responses. In Committee on the Long-Run Macroeconomic Effects of the Aging U.S. Population. Washington, DC: National Academies Press. [Google Scholar]
- OECD. 2019. Pensions at a Glance 2019: OECD and G20 Indicators. Paris: OECD Publishing. [Google Scholar]
- Palmer, Edward, and Yuwei Zhao de Gosson de Varennes. 2020. Annuities in (N)DC Pension Schemes: Design, heterogeneity, and estimation issues. In Progress and challenges of Nonfinancial Defined Contribution Pension Schemes, Vol. 1, Addressing Marginalization, Polarization, and the Labor Market. Edited by Holzmann Robert, Palmer Edward, Palacios Robert and Sacchi Stefano. Washington, DC: World Bank, pp. 281–306. [Google Scholar]
- Piggott, John, Emiliano A. Valdez, and Bettina Detzel. 2005. The simple analytics of pooled annuity funds. The Journal of Risk and Insurance 72: 497–520. [Google Scholar] [CrossRef]
- Plat, Richard. 2009. On stochastic mortality modeling. Insurance: Mathematics and Economics 45: 393–404. [Google Scholar]
- Raftery, Adrian E., Tilmann Gneiting, Fadoua Balabdaoui, and Michael Polakowski. 2005. Using Bayesian Model Averaging to calibrate forecast ensembles. Journal of American Meteorological Society 133: 1155–74. [Google Scholar] [CrossRef]
- Renshaw, Arthur E., and Steven Haberman. 2003. Lee–Carter mortality forecasting with age-specific enhancement. Insurance: Mathematics and Economics 33: 255–72. [Google Scholar] [CrossRef]
- Renshaw, Arthur E., and Steven Haberman. 2006. A cohort-based extension to the Lee–Carter Model for mortality reduction factors. Insurance: Mathematics and Economics 38: 556–70. [Google Scholar] [CrossRef]
- Samuels, Jon D., and Rodrigo M. Sekkel. 2017. Model confidence sets and forecast combination. International Journal of Forecasting 33: 48–60. [Google Scholar] [CrossRef]
- Shang, Han Lin, Heather Booth, and Rob J. Hyndman. 2011. Point and interval forecasts of mortality rates and life expectancy: A comparison of ten principal component methods. Demographic Research 25: 173–214. [Google Scholar] [CrossRef]
- Stamos, Michael. 2008. Optimal consumption and portfolio choice for pooled annuity funds. Insurance: Mathematics and Economics 43: 56–68. [Google Scholar] [CrossRef]
- Staudinger, Ursula M., Ruth Finkelstein, Esteban Calvo, and Kavita Sivaramakrishnan. 2016. A Global View on the Effects of Work on Health in Later Life. The Gerontologist 56: S281–S292. [Google Scholar] [CrossRef] [PubMed]
- Turek, Daniel, and David Fletcher. 2012. Model-Averaged Wald Confidence Intervals. Computational Statistics and Data Analysis 56: 2809–15. [Google Scholar] [CrossRef]
- Valdez, Emiliano A., John Piggott, and Liang Wang. 2006. Demand and Adverse Selection in a Pooled Annuity Fund. Insurance: Mathematics and Economics 39: 251–66. [Google Scholar] [CrossRef]
- Villegas, Andrés M., Steven Haberman, Vladimir K. Kaishev, and Pietro Millossovich. 2017. A comparative study of two-population models for the assessment of basis risk in longevity hedges. ASTIN Bulletin 47: 631–79. [Google Scholar] [CrossRef]
- Zaninotto, Paola, George David Batty, Sari Stenholm, Ichiro Kawachi, Martin Hyde, Marcel Goldberg, Hugo Westerlund, Jussi Vahtera, and Jenny Head. 2020. Socioeconomic Inequalities in Disability-free Life Expectancy in Older People from England and the United States: A Cross-national Population-Based Study. The Journals of Gerontology: Series A 75: 906–13. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Lingsong, Haipeng Shen, and Jianhua Z. Huang. 2013. Robust regularized singular value decomposition with application to mortality data. The Annals of Applied Statistics 7: 1540–61. [Google Scholar] [CrossRef]

| Model | Model Structure |
|---|---|
| LC | |
| APC | |
| RH | |
| CBD | |
| M7 | |
| Plat | |
| HUw | |
| CPspl | |
| RSVD |
| Year | |||||
|---|---|---|---|---|---|
| Longevity Marker/Pension Age | 2020 | 2025(a) | 2030 | 2040 | 2050 |
| 20.42 | 20.93 | 21.41 | 22.37 | 23.32 | |
| 21.82 | 22.35 | 22.87 | 23.87 | 24.81 | |
| 1.40 | 1.42 | 1.46 | 1.49 | 1.49 | |
| (b) | 66.33 | 67.25 | 68 | 69 | 70 |
| (c) | 66.33 | 67.25 | 68.5 | 70.5 | 71.5 |
| (d) | 66.33 | 67.67 | 68.15 | 69.11 | 70.06 |
| (e) | 66.33 | 69.09 | 69.61 | 70.61 | 71.55 |
| 67.20 | 67.81 | 68.37 | 69.39 | 70.31 | |
| 70.36 | 70.86 | 71.34 | 72.25 | 73.11 | |
| Expected years in retirement | |||||
| - Men (b) | 19.03 | 18.76 | 18.58 | 18.61 | 18.54 |
| - Women (b) | 21.92 | 21.54 | 21.30 | 21.25 | 21.15 |
| - Men (c) | 19.03 | 18.76 | 18.14 | 17.28 | 17.20 |
| - Women (c) | 21.92 | 21.54 | 20.84 | 19.86 | 19.75 |
| Year | ||||
|---|---|---|---|---|
| Longevity Marker/Pension Age | 2020 | 2030 | 2040 | 2050 |
| 23.88 | 25.08 | 26.15 | 27.16 | |
| 25.87 | 27.01 | 28.04 | 29.01 | |
| 1.99 | 1.93 | 1.90 | 1.85 | |
| (a) | 67 | 68 | 70 | 71 |
| (b) | 67 | 68 | 70 | 72 |
| (c) | 67 | 68.70 | 70.00 | 71.12 |
| (d) | 67 | 70.75 | 71.96 | 73.03 |
| 71.64 | 72.88 | 73.96 | 74.92 | |
| 73.95 | 75.03 | 76.04 | 77.00 | |
| Expected years in retirement | ||||
| - Men (a) | 18.33 | 18.54 | 17.76 | 17.77 |
| - Women (a) | 20.54 | 20.63 | 19.73 | 19.70 |
| - Men (b) | 18.33 | 18.54 | 17.76 | 16.91 |
| - Women (b) | 20.54 | 20.63 | 19.73 | 18.78 |
| Year | ||||
|---|---|---|---|---|
| Longevity Marker/Pension Age | 2020 | 2030 | 2040 | 2050 |
| 20.25 | 21.22 | 22.23 | 23.30 | |
| 21.59 | 22.75 | 23.96 | 25.04 | |
| 1.34 | 1.53 | 1.73 | 1.74 | |
| (a) | 66.42 | 67 | 67.67 | 68.42 |
| (b) | 66.42 | 67.08 | 67.92 | 68.67 |
| Expected years in retirement | ||||
| - Men (a) | 18.22 | 18.75 | 19.14 | 19.39 |
| - Women (a) | 22.28 | 22.97 | 23.57 | 23.91 |
| - Men (b) | 18.22 | 18.68 | 18.92 | 19.16 |
| - Women (b) | 22.28 | 22.88 | 23.31 | 23.65 |
| Year | ||||
|---|---|---|---|---|
| Longevity Marker/Pension Age | 2020 | 2030 | 2040 | 2050 |
| 18.80 | 19.59 | 20.35 | 21.07 | |
| 19.83 | 20.65 | 21.40 | 22.09 | |
| 1.04 | 1.07 | 1.06 | 1.02 | |
| (a) | 62.67 | 63.53 | 64.30 | 65.04 |
| (b) | 62.67 | 63.55 | 64.34 | 65.05 |
| 2019 Reform | 62.67 | 64.00 | 64.00 | 64.00 |
| Expected years in retirement | ||||
| - Men (a) | 17.90 | 18.15 | 18.40 | 18.59 |
| - Women (a) | 21.91 | 21.99 | 22.08 | 22.15 |
| - Men (b) | 17.90 | 18.14 | 18.37 | 18.57 |
| - Women (b) | 21.91 | 21.97 | 22.05 | 22.13 |
| - Men: 2019 Reform | 17.90 | 17.80 | 18.62 | 19.39 |
| - Women: 2019 Reform | 21.91 | 21.55 | 22.36 | 23.12 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ayuso, M.; Bravo, J.M.; Holzmann, R.; Palmer, E. Automatic Indexation of the Pension Age to Life Expectancy: When Policy Design Matters. Risks 2021, 9, 96. https://doi.org/10.3390/risks9050096
Ayuso M, Bravo JM, Holzmann R, Palmer E. Automatic Indexation of the Pension Age to Life Expectancy: When Policy Design Matters. Risks. 2021; 9(5):96. https://doi.org/10.3390/risks9050096
Chicago/Turabian StyleAyuso, Mercedes, Jorge M. Bravo, Robert Holzmann, and Edward Palmer. 2021. "Automatic Indexation of the Pension Age to Life Expectancy: When Policy Design Matters" Risks 9, no. 5: 96. https://doi.org/10.3390/risks9050096
APA StyleAyuso, M., Bravo, J. M., Holzmann, R., & Palmer, E. (2021). Automatic Indexation of the Pension Age to Life Expectancy: When Policy Design Matters. Risks, 9(5), 96. https://doi.org/10.3390/risks9050096









