Abstract
The main aim of this article is to examine the inter-relationships among the top cryptocurrencies on the crypto stock market in the presence and absence of the COVID-19 pandemic. The nine chosen cryptocurrencies are Bitcoin, Ethereum, Ripple, Litecoin, Eos, BitcoinCash, Binance, Stellar, and Tron and their daily closing price data are captured from coinmarketcap over the period from 13 September 2017 to 21 September 2020. All of the cryptocurrencies are integrated of order 1 i.e., I(1). There is strong evidence of a long-run relationship between Bitcoin and altcoins irrespective of whether it is pre-pandemic or pandemic period. It has also been found that these cryptocurrencies’ prices and their inter-relationship are resilient to the pandemic. It is recommended that when the investors create investment plans and strategies they may highly consider Bitcoin and altcoins jointly as they give sustainability and resilience in the long run against the geopolitical risks and even in the tough time of the COVID-19 pandemic.
JEL codes:
C30; E58; G28; O35
1. Introduction
Bitcoin is known to be the first distributed cryptocurrency in the foremost technology of blockchain system, which was instigated by Satoshi Nakamoto in 2008. Because of this invention, more than two thousand cryptocurrencies adhere to Bitcoin. These currencies are known as altcoins, which are traded non-stop, 24/7 in the crypto stock markets (CoinMarketCap 2019). Each of them has its own story which includes its mission, vision, and values. For instance, Ethereum is a global, open-source platform from which investors can run their smart contracts for decentralized applications, (Ethereum White Paper 2019). As another example, even though Ripple’s system is based on a central structure, Ripple aims to create a network among the international financial institutions to decrease their transaction costs and to facilitate faster global payments. Unlike many other alt currencies, Ripple is working with governments and central financial institutions (Ripple White Paper 2019). On the contrary, Binance was initiated to be an altcoin to create an independent ecosystem by freeing users from central organizations and government regulations. In addition, on the infrastructure of Tron (TRX)’s system, investors or users can freely create, publish, and store their data sets. By using this feature of blockchain infrastructure, Tron strives to create a global entertainment platform for content creators and consumers in the blockchain-based decentralized platform, (Tron White Paper 2019). After Bitcoin, these attempts of altcoins have brought about a sudden rise in the market size of cryptocurrencies. Whilst many altcoins emerged after Nakamoto’s initiative. Bitcoin, Ethereum, Ripple, Litecoin, Eos, BitcoinCash, Binance, Stellar, and Tron have been ranked among the top 20 cryptocurrencies over time by market capitalization and considered mainstream coins (CoinMarketCap 2019).
Especially after a sudden price increase of Bitcoin in 2017, people showed a great interest which has led to the rapid growth of cryptocurrencies. These attempts triggered scholars, crowdfunding managers, investors, and crypto portfolio managers to assess the long and short-term relationship among cryptocurrencies in the crypto stock market. A lot of studies were carried out to investigate about the price bubbles in cryptocurrencies in general especially Bitcoin, trading strategies and opportunities, financial bubbles being created by the crypto market, the spillovers between different crypto markets, and many more. Some of these studies are (Giudici and Pagnottoni 2019; Agosto and Cafferata 2020; Resta et al. 2020; J McNeil 2021) and many more. In addition, highly volatile cryptocurrencies have high correlations. Therefore, the number of research papers has increased to figure out long-term co-movements of prices of different cryptocurrencies and mean-reverting strategies which analyze whether prices revert to the average or mean price, (Leung and Nguyen 2019). To construct meaningful and stable models, researchers use various variables and prediction techniques. (Chuen et al. 2017), for example, examined the possibility of diversification of cryptocurrency portfolio for investors as a new investment opportunity based upon historical price and trading volume of a cryptocurrency. Accordingly, they found out that there is a low corrselation between cryptocurrencies and traditional investments. Another result showed that most cryptocurrencies have higher daily returns than traditional assets.
Another strand of literature is about the possibility of cointegrating relationships among cryptocurrencies, which makes scholars keen to search for cointegration studies. Leung and Nguyen (2019) focused on the process of constructing cointegrated portfolios of cryptocurrencies by employing Johansen and Engle–Granger cointegration tests. In addition to that Bação et al. (2018) observed that a robust relationship exists between information transmission and Bitcoin, Litecoin, Ripple, Ethereum, and Bitcoin Cash prices by using the Vector Auto-Regression (VAR) modeling approach from 1 May 2013 to 14 March 2018. Their results suggest that Bitcoin has the power to dominate others regarding information transmission due to its paramount capacity of trading volume, market capitalization, and exchange trading volume. On the other hand, they found some counterarguments against their hypothesis. Some delayed information takes place, especially from Litecoin to Bitcoin. Furthermore, the main aim of Ciaian and Rajcaniova ’s (2018) empirical investigation was to assess the virtual relationships between Bitcoin and altcoins in the short and long run. Their empirical results conclude that Bitcoin and altcoin markets are interdependent based on daily data from 2013 to 2016. Their findings confirm that in the long run, macroeconomic indicators have an impact on price creation to a certain degree. Therefore, exogenous factors might be recognized as determinants to a certain extent for the crypto market. Furthermore, the ARDL technique was used by Sovbetov (2018), to reveal that the attractiveness of cryptocurrencies plays an important role in price formation solely in the long run. On the other hand, market beta, trading volume, and volatility (crypto market-related factors) matter for both long- and short-term price determination based on evidence from Bitcoin, Ethereum, Dash, Litecoin, and Monero over 2010–2018, using weekly data. Anciaux et al. (2019) examined the co-movements in market quality of cryptocurrencies by using intraday data of the transactions and order book of the cryptocurrencies which have the highest market capitalization from August 2017 to July 2018. Finally, Göttfert (2019) organized his analysis according to Engle-Granger two-step approach, Johansen Cointegration test, and Vector Error Correction Model (VECM) to demonstrate cointegration between Bitcoin and other altcoins; Ethereum, Ripple, Bitcoin Cash, EOS, and Litecoin based upon daily prices in five different periods that due is 9 April 2019. Findings prove that Bitcoin has cointegration with Ripple, Litecoin, Bitcoin Cash, and Ethereum, albeit not with EOS. Hence, he concluded that Bitcoin is statistically crucial for the price formation of Ripple, Litecoin, Bitcoin Cash, and Ethereum, but not EOS.
Overall, this paper highlights the need for new analysis to examine price dependency and long and short-term cointegration among all cryptocurrencies regarding different periods, as this crypto market continues to develop with its new coins, along with its new applications, regulations, and attractive narratives. More specifically the long-run relationship among Bitcoin and altcoins has not been assessed in presence of the current pandemic (COVID-19). Our paper contributes to this gap. Furthermore, the resilience of this long run relationship has not been tested in the literature. This paper is aimed to address these two issues.
Our results reveals that some cryptocurrencies have a closer relationship concerning their price dependencies as time goes by in the COVID-19 pandemic. It offers investors to allocate their portfolios to balance their risks in the pandemic. Furthermore, even though each cryptocurrency has different narratives, aims, and functions, there is no one winner on the stock market or our result does not demonstrate the zero-sum game. Our research also provides objectively and reasonably adaptable analysis, especially for beginner crypto enthusiasts and investors.
Our results also shows that when investors design their portfolio, they can make diversification among these top cryptocurrencies. The paper offers investors a more diversified and balanced portfolio for the long term. Overall, this article would be beneficial for investors who would like to diversify their portfolios for the long term. Preparing a long-term portfolio would be more strategic because of the ‘‘novel features of the market’’ as Shams (2019) defined in his paper. More broadly, far from being static and narrow-minded, the market is ever-changing dynamically; it permits investors, portfolio managers, and policymakers to design or manage their portfolios. Finally, when investors create investment strategies, focusing on altcoins together with Bitcoin can provide sustainability and resilience for the long term against the geopolitical risks due to the tendency of the long-term relationship between Bitcoin and other altcoins even in the tough periods of the COVID-19 pandemic. Since every investor’s optimization relies on different parameter it is difficult to give exact calculations how their portfolio will be optimized by focusing on altcoins. Moreover, at least our results shows that there is scope for such an improvement. Portfolio optimization with altcoins could be a follow up work of this paper. However, we confidently assert that our conclusion matches partially with the conclusions of (Huang et al. 2021; Umar et al. 2021; Zhang and Wang 2021; Mariana et al. 2021).
2. Data Collection and Methodology
We use daily prices of cryptocurrencies and our data sets were obtained from the coinsmarket.cap (2020) from 13 September 2017 to 21 September 2020. The abbreviations used in this study with their complete description are listed in Table 1.

Table 1.
Abbreviations Used In The Study.
Before we employ unit root tests and the Johansen cointegration technique, we make general observations of descriptive statistics. In Table 2, there is a summary of descriptive statistics for the chosen 9 cryptocurrency prices.

Table 2.
Descriptive Statistics.
The co-movements of the 9 cryptocurrencies along the time from 13 September 2017 to 21 September 2020 are depicted in Figure 1. On the y-axis are the of the cryptocurrencies, while on the x-axis is the time. There is a vertical line on 11 March 2020, showing the declaration of COVID-19 as Pandemic by the World Health Organization (WHO). It is apparent from Figure 1 that there was a decrease in of each of the cryptocurrencies just after the declaration. However, afterward, the cryptocurrencies recovered and were back on the track.
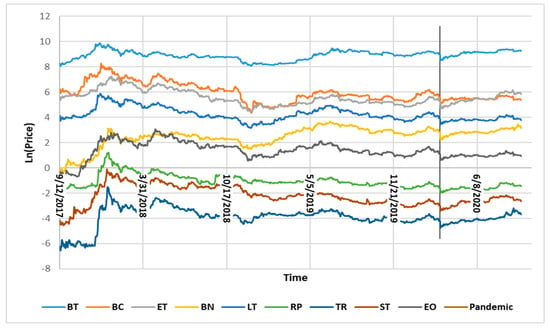
Figure 1.
Co-movements of cryptocurrencies.
2.1. Unit Root Tests
We carried out the Augmented Dickey–Fuller (ADF) test (Dickey and Fuller 1979) Test, Phillips Perron (PP) unit root test (Phillips and Perron 1988), and Kwiatkowski, Phillips, Schmidt, and Shin (KPSS) test (Kwiatkowski et al. 1992b) with the trend and without trend (constant) to decide the order of integration of each time series. We used two different models for each of the three unit root tests to make sure that our results are valid and not specific to a model and a test. If a time series has a constant mean, variance, and covariance over time (independent of time), it is defined to be a stationary time series. Therefore, an external shock to a stationary time series vanishes with the progress of time. However, on the contrary, if a series is not stationary, a shock in the time series will be permanent. In other words, non-stationary or unit root (a random walk) means that when there is a shock in time series, this shock is not going to die away in t + 1, t + 2, t + 3 +.....t + k progressively (Brooks 2014). One of the most critical issues in time series analysis is spurious regression. In this situation, the F and t-statistics are significant, showing that the time series under consideration are related to each other and in reality, there is no sense of the relationship between the time series (Granger and Newbold 1974). To deal with nonsense regression (Spurious) and to have meaningful results, before starting a time series analysis, it is required to test for possible unit roots (Harris and Sollis 2003). For this reason, we evaluated each time series for possible unit root. We employed three different unit root tests; ADF (Dickey and Fuller 1979), PP (Phillips and Perron 1988), and KPSS (Kwiatkowski et al. 1992b) with and without linear time trend (constant only). These three tests have been employed to validate the results as the two tests (ADF and PP) have the null hypothesis of the unit root while the third test, i.e., KPSS has the null hypothesis of stationarity.
2.2. Johansen Cointegration Test
After deciding about the order of integration, we choose the appropriate lag length based on the VAR model. Finally, we conduct the Johansen cointegration test (Johansen and Juselius 1990) to assess the long-run relationship among the 9 cryptocurrencies. Johansen cointegration test is used because it is based on the system estimation of multivariate time series. Another advantage of the Johansen test is that it considers all the time series as endogenous, whereas the other available techniques in the literature consider one time series as endogenous and the rest exogenous. This means that the researcher must decide a prior about the nature of time series (endogenous or exogenous), which is not realistic in our case of 9 different cryptocurrencies. Furthermore, the Johansen tests evaluate the presence of more than one cointegrating relationship among the considered time series. In our case, a maximum of eight cointegrating relationships is possible.
The Johansen cointegration test (Johansen and Juselius 1990) is based on the number of independent linear combinations. Johansen’s model hinges on Vector Auto-Regression (VAR). This model takes its first step in VAR of order k given by
where μt is the white noise disturbance term and βk denotes the coefficient matrices for each lag. If we use the Johansen Cointegration model, the above equation must be converted into Vector Error Correction Model (VECM) of the form by adding error correction components:
where represents differencing equation and k is the number of lags, and that contains two matrices. Albeit represents long-run coefficient matrix, includes short-run dynamics. “g” denotes the number of variables, which may be two or more. Johansen’s technique concentrates on the long-run coefficient matrix . Two different test statistics exist i.e.,
where r represents the number of cointegrating vectors under the null hypothesis. Besides this denotes forecasted ith ordered eigenvalue from and it can have a maximum g − 1 rank. Therefore, if there are 2 time series under investigation, then there would be a maximum of one cointegrated relationship among them. Rather, if there are four-time series then there would be a maximum of rank 3 indicating a maximum of three cointegrating relationships is possible.
where r is symbolized as the number of cointegrating vectors under the null hypothesis. Accordingly, if the null hypothesis is rejected such as , and cannot be rejected then we can conclude that there is one cointegrating vector. On the other hand, if is not rejected, it concludes that there are no cointegrating vectors in the time series. Hence, the value of is enhanced till the null hypothesis is no longer rejected. Five alternative specifications of the deterministic component have been considered by Johansen and Juselius (1990). These specifications are
H0: r = 0 versus H1: <r ≤ g
H0: r = 1 versus H1: 1 < r ≤ g
H0: r = 2 versus H1: 2 < r ≤ g and so on to
H0: r = g − 1 versus H1: r = g
Model 1: No Intercept or Trend in Cointegrating Equation (vector) and Test VAR
Model 2: Intercept (No Trend) in Cointegrating equation and No intercept or trend in test VAR
Model 3: Intercept (no Trend) in Cointegrating equation and test VAR
Model 4: Intercept and trend in Cointegrating equation and intercept or trend in test VAR
Model 5: Intercept and Trend in Cointegrating Equation and only intercept in test VAR.
3. Empirical Results
Before pursuing the assessment of a long-run relationship, first, all the series are tested for possible unit root using three tests.
3.1. Unit Root Test Results
According to the Augmented Dickey–Fuller (ADF) Test (Dickey and Fuller 1979) and Phillips Perron (PP) Test (Phillips and Perron 1988), the null hypothesis is that the time series has a unit root and the alternative hypothesis is that the time series is stationary. While, the KPSS (Kwiatkowski et al. 1992a) test evaluates the null hypothesis of stationarity against the alternative of non-stationarity. When we look at the results of unit root tests depicted in Table 3 for the ADF test, they show that for all cryptocurrencies except two (Binance and Tron), we cannot reject the null hypothesis at level; therefore, we can conclude that at the level they have unit roots with only constant and with the trend. For the two exceptions at level, Binance is stationary at a 5% level of significance when only constant is considered. However, when the trend is considered then again, Binance has a unit root at the level. The other exception Tron is stationary at the level at 5% level of significance when only constant is considered and it is stationary at 10% level of significance when the trend is considered. All the 9 cryptocurrencies are stationary at the first difference at a 1% level of significance. Hence these all cryptocurrencies’ closing prices are concluded as integrated of order 1, i.e., time series. The results of the other unit root test like the Philips Perron test conclude the same and they are identical to the ADF test with one exception of Tron having a unit root at the level when the trend is considered.

Table 3.
Unit Root Tests Results.
Coming to the results of the KPSS test having null hypothesis of stationarity, Table 3 clearly shows that at level, the null hypothesis is rejected at 1% level of significance when either constant is considered, or trend is considered, for all cryptocurrencies with only one exception and that is of Tron for only the case when constant is considered. At first difference, the null hypothesis cannot be rejected (for both cases of constant and trend) for all cryptocurrencies except one exception and, i.e., of EOS at the trend. All the cryptocurrencies’ closing price time series is concluded as integrated of order 1 according to the KPSS test.
3.2. Johansen Cointegration Test Results
To find that whether a long-run relationship exists among the nine cryptocurrencies or not, the Johansen Cointegration test was carried out with two different deterministic part combinations (Model 3 and Model 4). However, the results are not so much different. Hence, we stick with the most theoretically plausible model of Model 3 which considers constant both in the cointegrating relation and in testing VAR. Furthermore, the existence of long-run relation is evaluated considering the two scenarios: with DP as Exogenous and without it.
The Johansen test estimates the order of integration as shown in Table 4, where r is symbolized as the number of cointegrating vectors under the null hypothesis. Accordingly, if the null hypothesis is not rejected then we can conclude that there are no cointegrating vectors. However, if null hypothesis is rejected and the null hypothesis cannot be rejected then the results indicate that there is one cointegrating vector. Hence, we infer that when DP is not considered exogenous then the cryptocurrencies are cointegrated with three cointegrating vectors (long-run relationships). However, when the DP is considered as exogenous then the cryptocurrencies are cointegrated with four cointegrating vectors at a 5% level of significance and with three cointegrating vectors at a 1% level of significance.

Table 4.
Johansen Co-integration Test Results.
3.3. Vector Error Correction Model (VECM) Results
In our analysis, the long-run relationships among the cryptocurrencies are demonstrated by the Cointegrating Vectors (CV). The long-run coefficients after imposing the Johansen normalization restrictions (Johansen 1995) are tabulated in Table 5. According to Table 5, in the long run, the closing prices of Ripple, Eos, Litecoin, and Stellar are statistically crucial for the closing price of Bitcoin when the COVID-19 pandemic is not taken into account. However, when the COVID-19 pandemic is taken into account then only the closing prices of Litecoin and Tron are statistically crucial for the closing price of Bitcoin. For the closing price of Bitcoin Cash, the closing prices of Ethereum and Stellar are statistically crucial. However, when the Pandemic is considered then the closing price of Ethereum remains statistically crucial but now instead of Stellar, the closing prices of Eos and Tron are statistically crucial. Four crypto currencies’ (Ripple, Ethereum, Litecoin, and Stellar) closing prices are significantly affecting the closing price of Binance in the long run. Though when the COVID-19 pandemic is considered in the long run, only two crypto currencies’ closing prices have a statistically significant effect on the closing price of Binance. Similarly, four crypto currencies’ (Eos, Litecoin, Stellar, and Tron) closing prices have a statistically significant impact on the closing price of Ripple when the COVID-19 pandemic is considered as exogenous.

Table 5.
Johansen Normalization Restriction Imposed.
In general, Ripple’s closing price has a significant impact on the closing prices of Bitcoin and Binance when the pandemic is not considered in the model. However, the closing price of Ripple has no impact on Bitcoin’s and Binance’s closing prices when the pandemic is considered in the model. Similarly, in the long run, the closing price of Tron has no impact on any of the cryptocurrencies’ closing price when the pandemic is not considered in the model. However, it has a highly significant impact on the closing prices of Bitcoin, Binance, and Ripple when the pandemic is considered in the model.
The impact of the COVID-19 pandemic on the closing prices of nine cryptocurrencies in the short run is shown in Table 6. It is evident that the pandemic has a positive and direct highly significant (at 1% level of significance) impact on the closing prices of Binance, Ethereum, Stellar, and Tron and it has a mild (at 10% level of significance) impact on the closing price of Ripple. The rest of the cryptocurrencies’ closing prices are not affected by the COVID-19 pandemic.

Table 6.
Impact of Pandemic (DP) in the Short Run.
To investigate the interrelationships among the cryptocurrencies in presence of the COVID-19 pandemic, the variance decomposition of all the cryptocurrencies is depicted in Figure 2. It is evident that the variation (almost 100%) in Bitcoin is due to itself and not due to other cryptocurrencies. Furthermore, Bitcoin has a significant amount of portion of the variation in all other cryptocurrencies like BitcoinCash, Binance and Eos (almost 40%), Ripple, Stellar, and Tron (around 20%). However, for these six cryptocurrencies, the proportion of variation of Bitcoin is lesser than the cryptocurrency itself. Interestingly, for Litecoin and Ethereum the proportion of Bitcoin (almost 50%) is greater than the proportion of variation of cryptocurrency itself. All these results suggest that the variations in Bitcoin are the sole stronger driver of the variations in all other eight cryptocurrencies. The results of the variance decomposition when the COVID-19 pandemic is not considered are the same, indicating again that in the long run, there is no significant impact of the COVID-19 pandemic on cryptocurrencies and hence they are resilient.
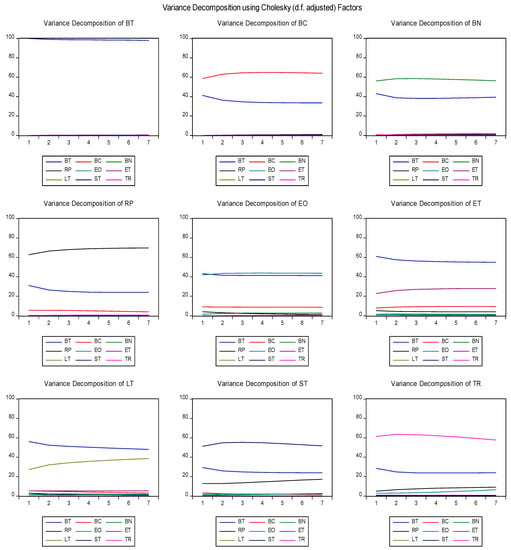
Figure 2.
Variance decomposition in presence of pandemic.
4. Conclusions
Due to the volatile structure of cryptocurrencies in the crypto stock-market, investors and portfolio managers periodically demand shocks that can alter in degree across the cryptocurrencies hinging on the co-movement of their price returns. Discoveries about what causes volatility and directions of co-movements on the market by explicit factors can be difficult to measure from time to time owing to the precarious cyclic circumstances in the entire system. In that point, our article analyzes the cointegration of top cryptocurrencies based on daily prices on the crypto stock market by using the Johansen Cointegration technique. The chosen cryptocurrencies are Bitcoin, Ethereum, Ripple, Litecoin, Eos, BitcoinCash, Binance, Stellar, and Tron. Data sets are taken from coinmarketcap (2020) over a period from 13 September 2017 to 21 September 2020. The result of this test demonstrates that there is cointegration among the Bitcoin and other chosen altcoins in the market.
Before conducting the Johansen test, we applied three different unit root tests to determine the stationarity of the ten crypto currencies’ prices. Then, before going for the Johansen cointegration test to test the existence of a long-run relationship among the ten crypto price series, we checked for the appropriate lag length order. After choosing the optimal lag order, finally, the Johansen cointegration test was carried out. In addition to that, a vector error correction model (VECM) was estimated to investigate the long-run cointegrating relationship as well as short-run relationships among the variables. The results indicate that when the COVID-19 pandemic effect is not taken into account, Bitcoin and Binance prices are not affected by the Ripple price. However, it is just the opposite when the effect of the COVID-19 pandemic is considered. This implies that the pandemic has a very grave impact on the inter-relationship of three crypto prices i.e., Bitcoin, Binance, and Ripple. Similarly, when the pandemic is not accounted into the model then Tron prices are not affecting any of the cryptocurrency prices. However, when the pandemic is considered, then Tron affects the prices of Bitcoin, Binance, and Ripple.
Specifically, the magnitude of results reveals that some cryptocurrencies have a closer relationship concerning their price dependencies as time goes by in the COVID-19 pandemic. It offers investors to allocate their portfolios to balance their risks in the pandemic. Furthermore, even though each cryptocurrency has different narratives, aims, and functions, there is no one winner on the stock market or our result does not demonstrate the zero-sum game. There is a win-win situation among cryptocurrencies. Hence, policymakers and regulators can take into account cryptocurrencies as potential alternative digital assets to reduce the risks of their national assets for the crisis term and especially in crises like the COVID-19 pandemic.
Our research provides objectively and reasonably adaptable analysis, especially for beginner crypto enthusiasts and investors, who might take many needles risks or abide by an over-cautious approach when they discover the crypto world from the scratch, to minimize their risk and maximize their returns for the long-term. Since these top cryptocurrencies in the stock market that we chose are safer and more stable due to their long-established timeline in the pandemic. Hence, these top cryptocurrencies can be accepted as the new asset opportunities because they have already proved their maturity as compared to other assets.
Our results also touch upon that these top cryptocurrencies can be divided into subcategories. Accordingly, when investors design their portfolio, they can make diversification among these top cryptocurrencies to raise their money for the long-term. For instance, Bitcoin, Ethereum, Ripple, and Litecoin are the cryptocurrencies that have the longest history as compared to their counterparts. If we divide these four cryptocurrencies, making an investment of those cryptocurrencies by matching with other altcoins among the top list that we chose, it will offer investors a more diversified and balanced portfolio for the long term. Furthermore, our analysis gives universal formula with a more global approach for each investor from all over the world without regard to their nationality which means that everyone holds the same risking portfolio. Cryptocurrencies, which are not controlled by governments and national authorities, are not affected by government regulations, rather they are affected by cyclical risks and volatility in the global financial system. To avoid these risks, our results provide a narrowing analysis for the top cryptocurrencies from the unlimited set of choices in crypto-asset allocation.
Overall, this article would be beneficial for investors who would like to diversify their portfolios for the long term. Preparing a long-term portfolio would be more strategic because of the ‘‘novel features of the market’’ as Shams (2019) defined in his paper. More broadly, far from being static and narrow-minded, the market is ever-changing dynamically; it permits investors, portfolio managers, and policymakers to design or manage their portfolios by looking at them from different angles. The more they discover the operation of business, politics, finance, and society as a whole, the more they have the capacity of knowing what factors they should take into account to manage their wealth wisely. Finally, when investors create investment strategies, focusing on altcoins together with Bitcoin can provide sustainability and resilience for the long term against the geopolitical risks due to the tendency of the long-term relationship between Bitcoin and other altcoins even in the tough periods of the COVID-19 pandemic.
Future studies can focus on other hourly, daily, and monthly prices of altcoins to investigate the long and short-term relationships among each other. For instance, researchers can choose two different types of cryptocurrencies which each group has its strategy. Then, they categorize them according to their purposes values, and narratives are given their white papers. First, the cointegration relationship between each sub-group can be evaluated within their group, and then researchers can compare the relationship of these two different groups. Furthermore, the causality relationship of each cryptocurrency can be investigated regardless of their group. Overall, results on the cointegration and causality relationship of these different cryptocurrencies will shed light on the process of the cointegrated portfolio for the investors in the financial market. Furthermore, it can also be investigated that whether the COVID-19 pandemic has affected the main stock indices. A comparative analysis of effect of COVID-19 on crypto market and the traditional stock market can be carried out. In addition to this trading strategies likewise as proposed in (Brzeszczyński and Ibrahim 2019) and (Batten et al. 2019) can be simulated about the interrelationship among cryptocurrencies in presence of the COVID-19 pandemic.
Author Contributions
Conceptualization, A.F.A. and H.T.; methodology, A.U.I.K. and H.T.; software, A.U.I.K. and H.T.; validation, A.F.A., A.U.I.K. and H.T.; formal analysis, A.U.I.K.; investigation, A.F.A. and A.U.I.K.; resources, A.F.A. and A.U.I.K.; data curation, H.T.; writing—original draft preparation, A.U.I.K. and H.T.; writing—review and editing, A.F.A. and A.U.I.K.; visualization, A.F.A. and A.U.I.K.; supervision, A.F.A. and A.U.I.K.; project administration, A.F.A.; funding acquisition, A.F.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data was obtained from https://coinmarketcap.com/ (accessed on 3 November 2019). It is freely available.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Agosto, Arianna, and Alessia Cafferata. 2020. Financial Bubbles: A Study of Co-Explosivity in the Cryptocurrency Market. Risks 8: 34. [Google Scholar] [CrossRef]
- Nicaise, Nicolas, Hubert Anciaux, and Mikael Petitjean. 2019. Co-Movements in Market Quality of cryptocurrencies. Louvain: Louvain School of Management. [Google Scholar]
- Bação, Pedro, António Portugal Duarte, Helder Sebastião, and Srdjan Redzepagic. 2018. Information Transmission Between Cryptocurrencies: Does Bitcoin Rule the Cryptocurrency World? Scientific Annals of Economics and Busines 65: 97–117. [Google Scholar] [CrossRef]
- Batten, Jonathan A., Janusz Brzeszczynski, Cetin Ciner, Marco CK Lau, Brian Lucey, and Larisa Yarovaya. 2019. Price and volatility spillovers across the international steam coal market. Energy Economics 77: 119–38. [Google Scholar] [CrossRef]
- Brooks, Chris. 2014. Introductory Econometrics for Finance, 3rd ed. Cambridge: Cambridge University Press. [Google Scholar]
- Brzeszczyński, Janusz, and Boulis Maher Ibrahim. 2019. A stock market trading system based on foreign and domestic information. Expert Systems with Applications 118: 381–99. [Google Scholar] [CrossRef]
- Chuen, David LEE Kuo, Li Guo, and Yu Wang. 2017. Cryptocurrency: A new investment opportunity? The Journal of Alternative Investments 20: 16–40. [Google Scholar] [CrossRef]
- Ciaian, Pavel, and Miroslava Rajcaniova. 2018. Virtual relationships: Short- and long-run evidence from BitCoin and altcoin markets. Journal of International Financial Markets, Institutions, and Money 52: 173–95. [Google Scholar] [CrossRef]
- CoinMarketCap. 2019. Available online: https://coinmarketcap.com (accessed on September 23, 2020).
- Dickey, David A., and Wayne A. Fuller. 1979. Distribution of the estimators for autoregressive time series with a unit root. Journal of the American Statistical Association 74: 427–31. [Google Scholar]
- Ethereum White Paper. 2019. Available online: https://ethereum.org (accessed on 3 November 2019).
- Giudici, Paolo, and Paolo Pagnottoni. 2019. High Frequency Price Change Spillovers in Bitcoin Markets. Risks 7: 111. [Google Scholar] [CrossRef]
- Joline, Göttfert. 2019. Cointegration among Cryptocurrencies: A Cointegration Analysis of Bitcoin, Bitcoin Cash, EOS, Ethereum, Litecoin, and Ripple. Master’s Thesis, MA in Economics, University in Umeå, Umeå, Sweden. [Google Scholar]
- Granger, Clive W. J., and Paul Newbold. 1974. Spurious regressions in econometrics. Journal of Econometrics 2: 111–20. [Google Scholar] [CrossRef]
- Harris, Richard, and Robert Sollis. 2003. Applied Time Series Modelling and Forecasting. New York: Wiley. [Google Scholar]
- Huang, Yingying, Kun Duan, and Tapas Mishra. 2021. Is Bitcoin really more than a diversifier? A pre- and post-COVID-19 analysis. Finance Research Letters 2021: 102016. [Google Scholar] [CrossRef]
- J McNeil, Alexander. 2021. Modelling Volatile Time Series with V-Transforms and Copulas. Risks 9: 14. [Google Scholar] [CrossRef]
- Johansen, Søren. 1995. Likelihood-Based Inference in Cointegrated Vector Autoregressive Models. Oxford: Oxford University Press on Demand. [Google Scholar]
- Johansen, Soren, and Katarina Juselius. 1990. Maximum likelihood estimation and inference on cointegration—With applications to the demand for money. Oxford Bulletin of Economics and Statistics 52: 169–210. [Google Scholar] [CrossRef]
- Kwiatkowski, Denis, Peter CB Phillips, Peter Schmidt, and Yongcheol Shin. 1992a. Testing the null hypothesis of stationarity against the alternative of a unit root: How sure are we that economic time series have a unit root? Journal of Econometrics 54: 159–78. [Google Scholar] [CrossRef]
- Kwiatkowski, Denis, Peter CB Phillips, Peter Schmidt, and Yongcheol Shin. 1992b. Testing the null hypothesis of stationarity against the alternative of a unit root. Journal of Econometrics 54: 159–78. [Google Scholar] [CrossRef]
- Leung, Tim, and Hung Nguyen. 2019. Constructing cointegrated cryptocurrency portfolios for statistical arbitrage. Studies in Economics and Finance 36: 581–59. [Google Scholar] [CrossRef]
- Mariana, Christy Dwita, Irwan Adi Ekaputra, and Zaäfri Ananto Husodo. 2021. Are Bitcoin and Ethereum safe-havens for stocks during the COVID-19 pandemic? Finance Research Letters 38: 101798. [Google Scholar] [CrossRef]
- Phillips, Peter CB, and Pierre Perron. 1988. Testing for a unit root in time series regression. Biometrika 75: 335–46. [Google Scholar] [CrossRef]
- Resta, Marina, Paolo Pagnottoni, and Maria Elena De Giuli. 2020. Technical Analysis on the Bitcoin Market: Trading Opportunities or Investors’ Pitfall? Risks 8: 44. [Google Scholar] [CrossRef]
- Ripple White Paper. 2019. Available online: https://ripple.com (accessed on 3 November 2019).
- Shams, Amin. 2019. What Drives the Covariation of Cryptocurrencies Returns? Paper presented at the Association of Financial Economists & American Economic Association Beyond Bitcoin Paper Session Conference, Atlanta, GA, USA, January 4–6. [Google Scholar]
- Sovbetov, Yhlas. 2018. Factors Influencing Cryptocurrency Prices: Evidence from Bitcoin, Ethereum, Dash, Litcoin, and Monero. Journal of Economics and Financial Analysis 2: 1–27. [Google Scholar]
- Tron White Paper. 2019. Available online: https://tron.network (accessed on 3 November 2019).
- Umar, Muhammad, Chi-Wei Su, Syed Kumail Abbas Rizvi, and Xue-Feng Shao. 2021. Bitcoin: A safe haven asset and a winner amid political and economic uncertainties in the US? Technological Forecasting and Social Change 167: 120680. [Google Scholar] [CrossRef]
- Zhang, Hongwei, and Peijin Wang. 2021. Does Bitcoin or gold react to financial stress alike? Evidence from the US and China. International Review of Economics & Finance 71: 629–48. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).