Mortality Forecasting with an Age-Coherent Sparse VAR Model
Abstract
1. Introduction
2. The Factor-Based Model
3. The Vector-Autogression-Based Models
3.1. The Sparse VAR Model
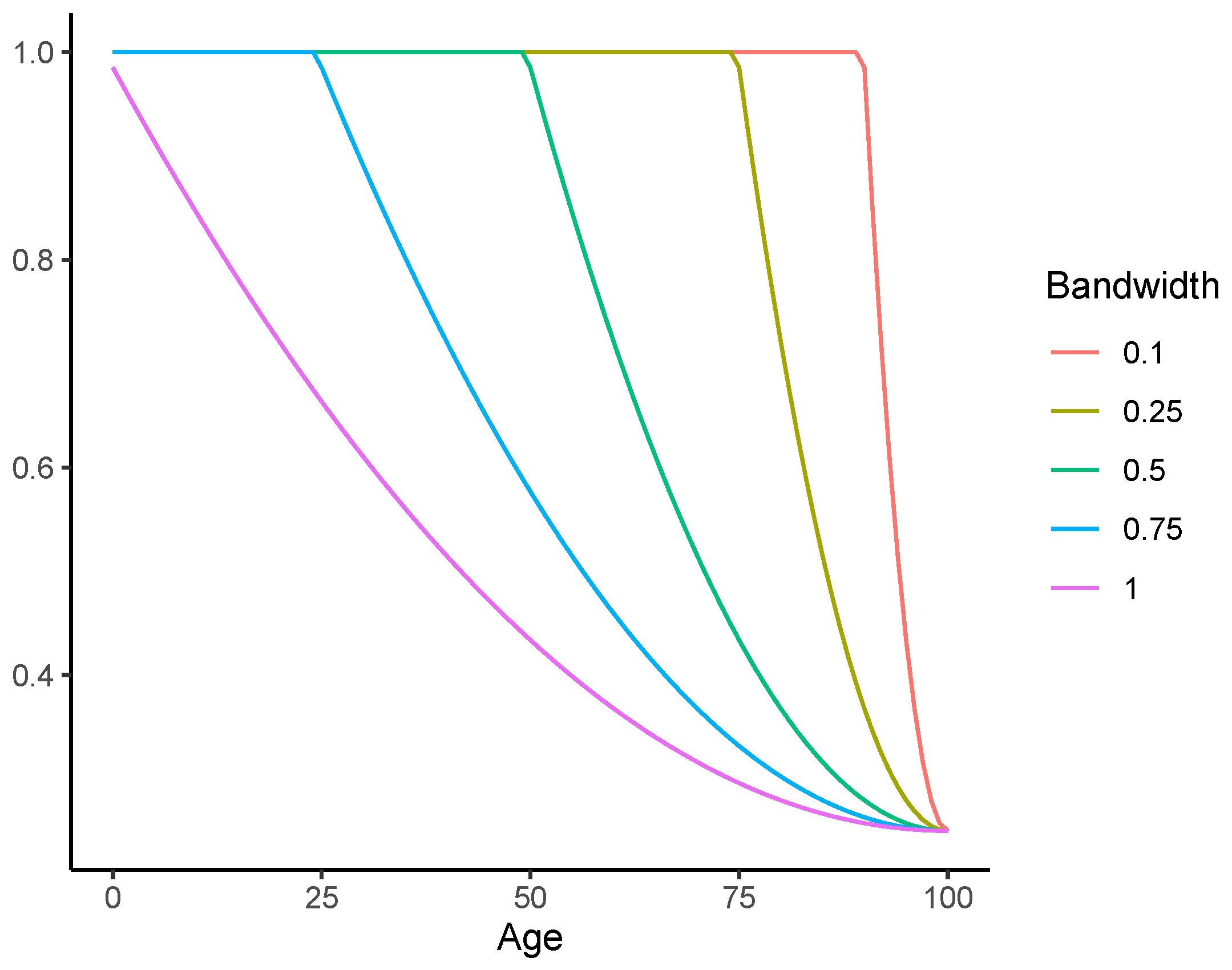
3.2. The Coherent Sparse VAR Model
The Multi-Population Extension
4. Empirical Analysis
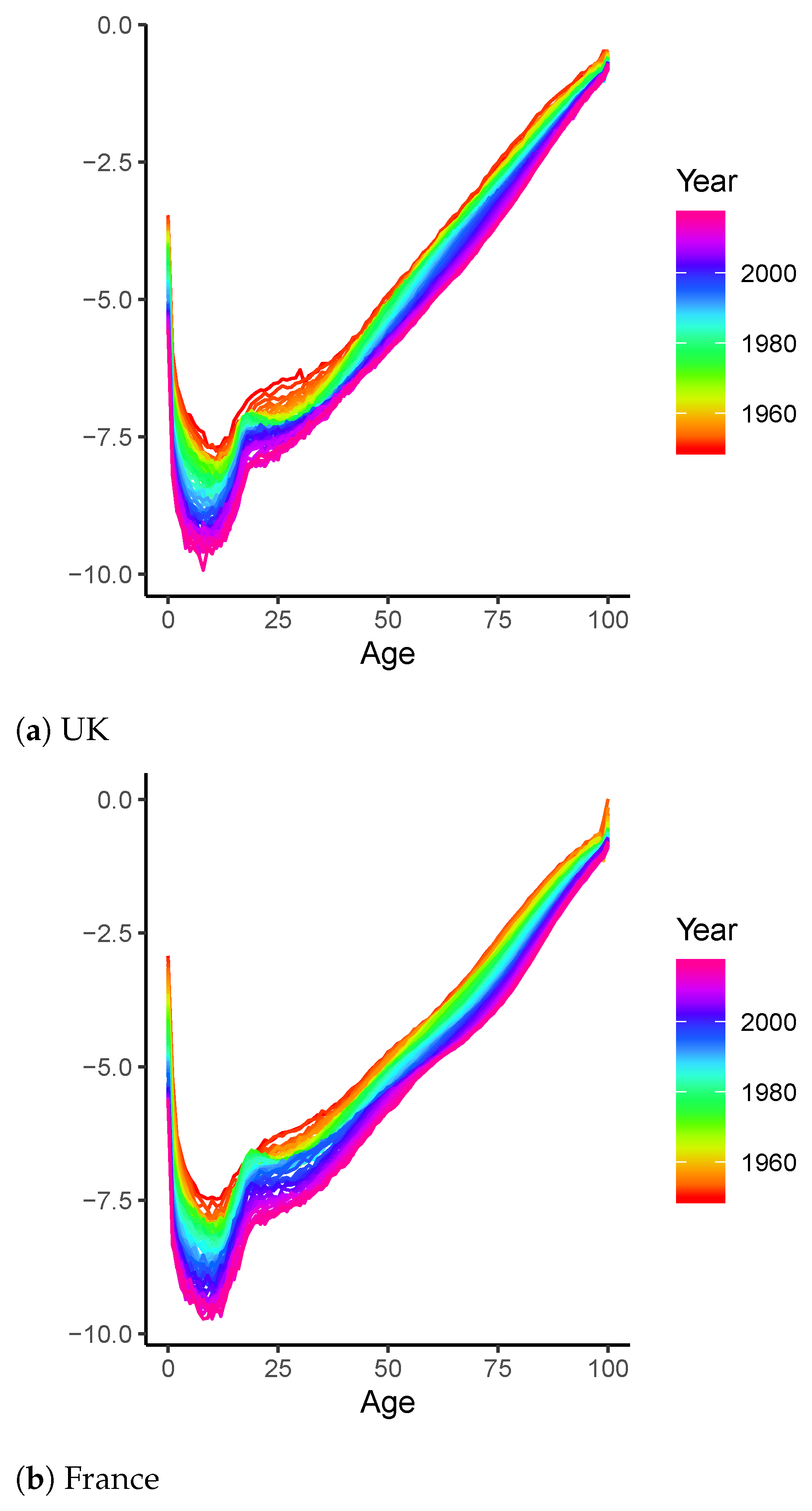
4.1. Long-Term Analysis
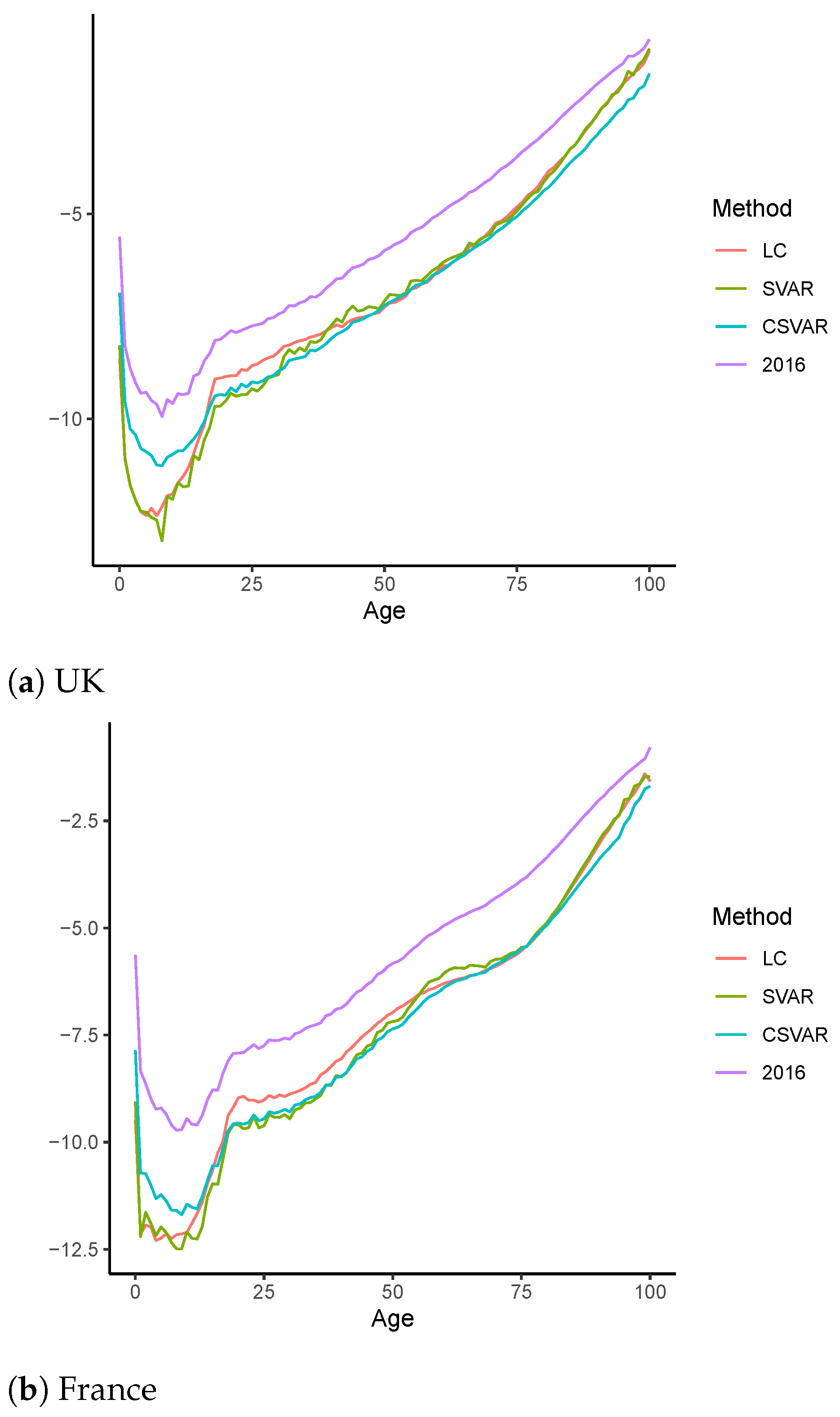
4.2. Out-of-Sample Forecast
4.2.1. Robustness Analysis
4.2.2. The Two-Population Extension
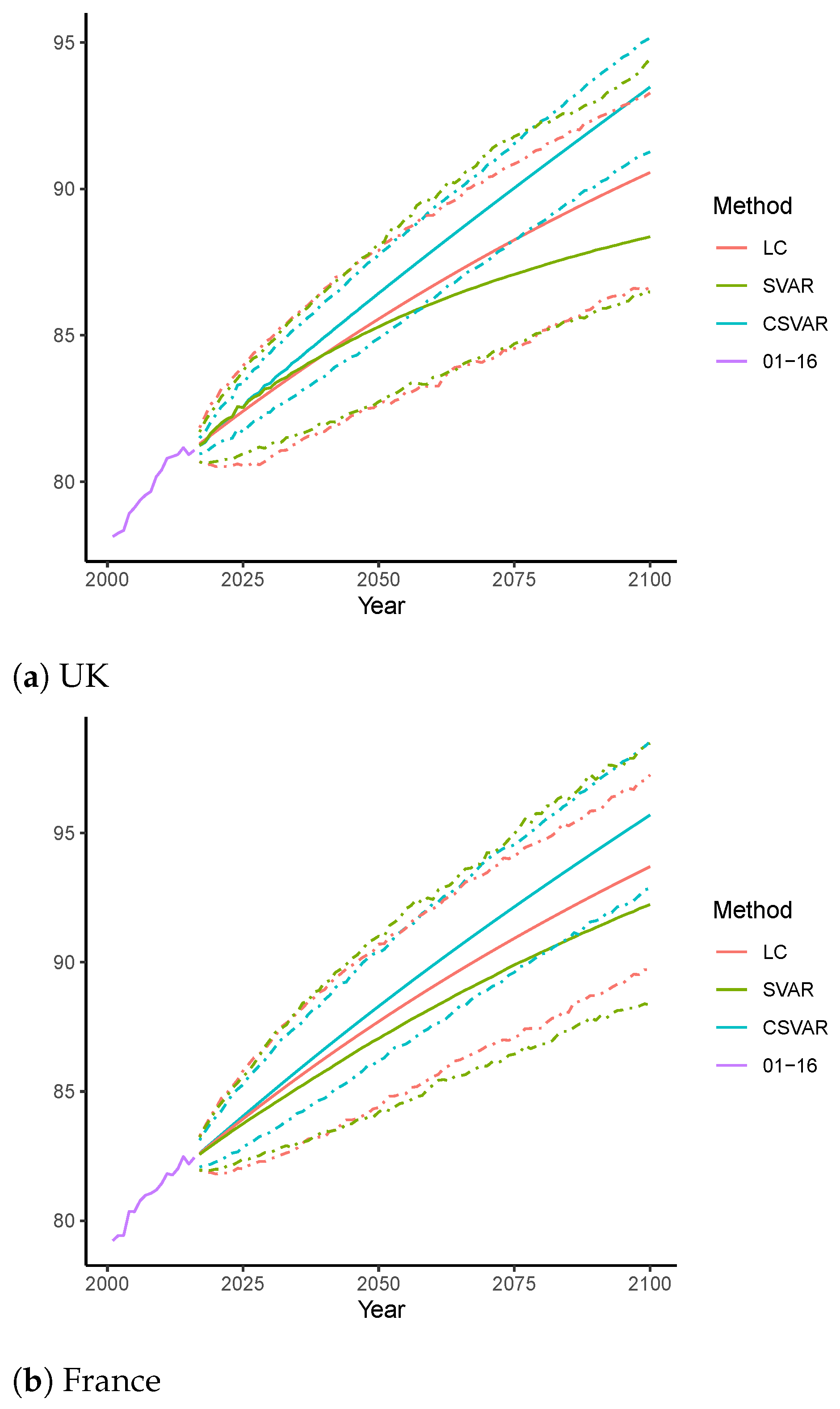
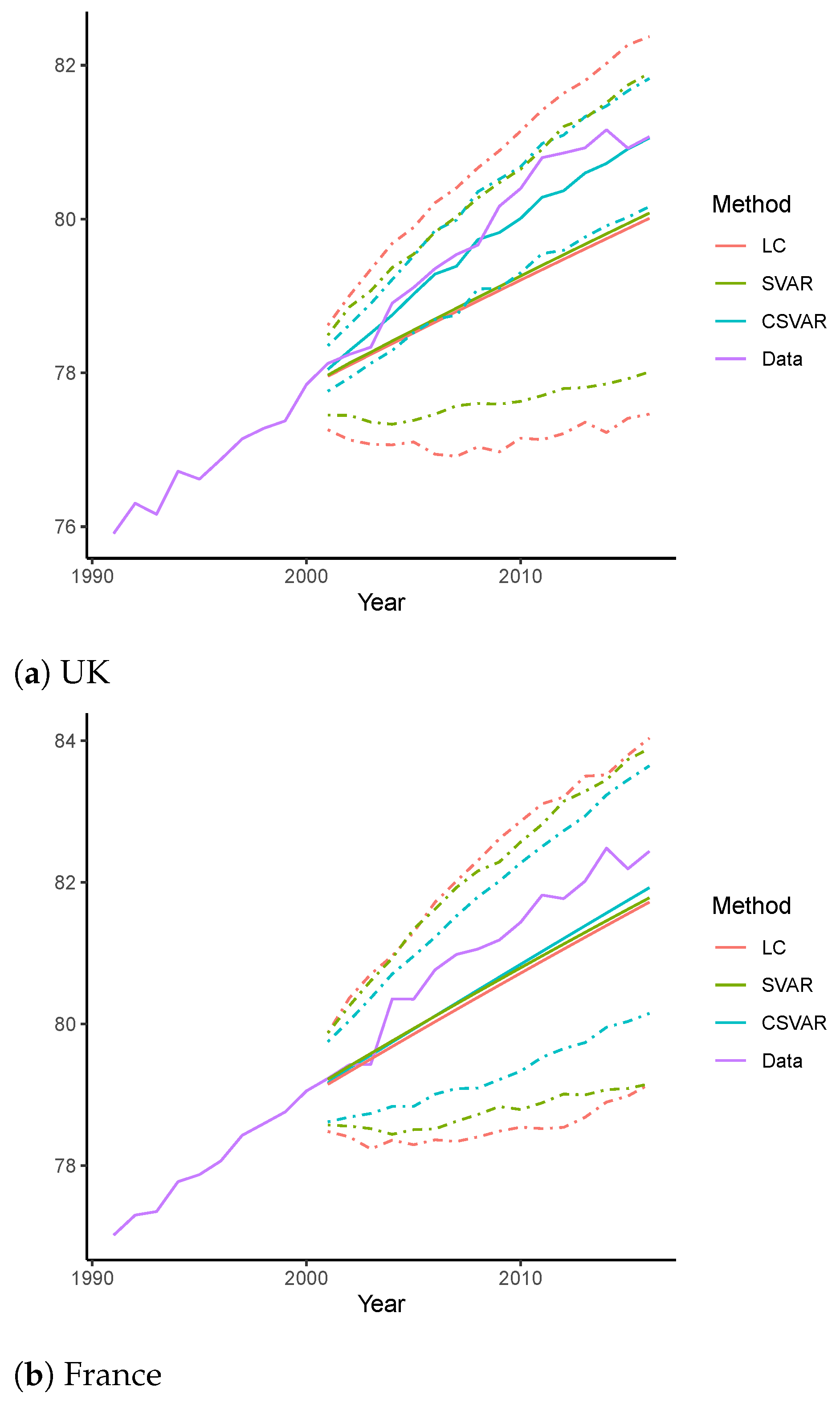
4.2.3. Forecasting of Life Expectancy of Age 0
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| LC | Lee–Carter model |
| VAR | Vector Autoregression model |
| CBD | Cairns–Blake–Dowd model |
| LL | Li–Lee model |
| STAR | Spatial-temporal Autoregression model |
| SVAR | Sparse VAR model |
| CSVAR | Coherent Sparse VAR model |
| LASSO | Least Absolute Shrinkage and Selection Operator |
| ENET | Elastic-net |
| RMSFE | Root of Mean Squared Forecasting Error |
| Variables of single population models: | |
| Log central mortality rate at age x in year t | |
| The average mortality level at each age x | |
| The mortality index at time t | |
| The age-specific sensitivity of to changes in | |
| The normal error term | |
| The vector of differenced log central mortality rate | |
| Intercept vector of the VAR-type models | |
| Coefficients of in the VAR-type models | |
| Forecast intercept term in the CSVAR model for age x at step h | |
| The hyperbolic parameter associated with | |
| The ENET penalty | |
| Additional variables of joint population models: | |
| Age effect of the common factor | |
| Period effect of the common factor | |
Appendix A. Additional Tables
| Single Models | SVAR | CSVAR | ||||||
| b | ||||||||
| UK | −11.66 | −9.26 | 0.2974 | 0.2184 | ||||
| FR | −11.30 | −6.89 | 0.7426 | 0.0621 | ||||
| Join Models | SVAR | CSVAR | CSVAR | |||||
| UK | −11.98 | −9.26 | 0.4458 | 0.1663 | −10.75 | 0.2638 | 0.2599 | |
| FR | −11.98 | −9.26 | 0.7426 | 0.4789 | −11.16 | 0.3468 | 0.5311 | |
References
- Boonen, Tim J., and Hong Li. 2017. Modeling and forecasting mortality with economic growth: A multipopulation approach. Demography 54: 1921–46. [Google Scholar] [CrossRef]
- Booth, Heather, Rob J. Hyndman, Leonie Tickle, and Piet De Jong. 2006. Lee–Carter mortality forecasting: A multi-country comparison of variants and extensions. Demographic Research 15: 289–310. [Google Scholar] [CrossRef]
- Cairns, A. J. G., David Blake, and Kevin Dowd. 2006. A two-factor model for stochastic mortality with parameter uncertainty: Theory and calibration. Journal of Risk and Insurance 73: 687–718. [Google Scholar] [CrossRef]
- Chang, Le, and Yanlin Shi. 2020a. Dynamic modelling and coherent forecasting of mortality rates: A time-varying coefficient spatial-temporal autoregressive approach. Scandinavian Actuarial Journal 9: 843–863. [Google Scholar] [CrossRef]
- Chang, Le, and Yanlin Shi. 2020b. Mortality forecasting with a spatially penalized smoothed var model. ASTIN Bulletin: The Journal of the IAA 51: 161–189. [Google Scholar] [CrossRef]
- Chen, An, Hong Li, and Mark Schultze. 2020. Tail Index-Linked Annuity: A Longevity Risk Sharing Retirement Plan. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3664433 (accessed on 1 November 2020).
- Dowd, Kevin, Andrew J. G. Cairns, David Blake, Guy D. Coughlan, and Marwa Khalaf-Allah. 2011. A gravity model of mortality rates for two related populations. North American Actuarial Journal 15: 334–56. [Google Scholar] [CrossRef]
- Eilers, Paul H. C., and Brian D. Marx. 1996. Flexible smoothing with B-splines and penalties. Statistical Science 11: 89–102. [Google Scholar] [CrossRef]
- Feng, Lingbing, and Yanlin Shi. 2017. Fractionally integrated garch model with tempered stable distribution: A simulation study. Journal of Applied Statistics 44: 2837–57. [Google Scholar] [CrossRef]
- Feng, Lingbing, and Yanlin Shi. 2018. Forecasting mortality rates: Multivariate or univariate models? Journal of Population Research 35: 289–318. [Google Scholar] [CrossRef]
- Feng, Lingbing, Yanlin Shi, and Le Chang. 2020. Forecasting mortality with a hyperbolic spatial temporal VAR model. International Journal of Forecasting 37: 255–273. [Google Scholar] [CrossRef]
- Friedman, Jerome, Trevor Hastie, and Rob Tibshirani. 2010. Regularization paths for generalized linear models via coordinate descent. Journal of Statistical Software 33: 1. [Google Scholar] [CrossRef] [PubMed]
- Gao, Guangyuan, Kin-Yip Ho, and Yanlin Shi. 2020. Long memory or regime switching in volatility? evidence from high-frequency returns on the us stock indices. Pacific-Basin Finance Journal 61: 101059. [Google Scholar] [CrossRef]
- Guibert, Quentin, Olivier Lopez, and Pierrick Piette. 2019. Forecasting mortality rate improvements with a high-dimensional VAR. Insurance: Mathematics and Economics 88: 255–72. [Google Scholar] [CrossRef]
- Ho, Kin-Yip, and Yanlin Shi. 2020. Discussions on the spurious hyperbolic memory in the conditional variance and a new model. Journal of Empirical Finance 55: 83–103. [Google Scholar] [CrossRef]
- Hosking, J. R. M. 1981. Fractional differencing. Biometrica 68: 165–76. [Google Scholar] [CrossRef]
- Human Mortality Database. 2020. University of California, Berkeley (USA), and Max Planck Institute for Demographic Research (Germany). Available online: https://www.mortality.org/ (accessed on 1 November 2020).
- Hunt, Andrew, and David Blake. 2018. Identifiability, cointegration and the gravity model. Insurance: Mathematics and Economics 78: 360–68. [Google Scholar] [CrossRef]
- Hyndman, Rob J., and George Athanasopoulos. 2018. Forecasting: Principles and Practice. Melbourne: OTexts. [Google Scholar]
- Hyndman, Rob J., Heather Booth, and Farah Yasmeen. 2013. Coherent mortality forecasting: The product-ratio method with functional time series models. Demography 50: 261–83. [Google Scholar] [CrossRef]
- Hyndman, Rob J., and Md Shahid Ullah. 2007. Robust forecasting of mortality and fertility rates: A functional data approach. Computational Statistics & Data Analysis 51: 4942–56. [Google Scholar]
- Lee, Ronald, and Lawrence Carter. 1992. Modeling and Forecasting US Mortality. Journal of the American Statistical Association 87: 659–71. [Google Scholar]
- Li, Hong. 2018. Dynamic hedging of longevity risk: The effect of trading frequency. ASTIN Bulletin: The Journal of the IAA 48: 197–232. [Google Scholar] [CrossRef]
- Li, Hong, Anja De Waegenaere, and Bertrand Melenberg. 2015. The choice of sample size for mortality forecasting: A bayesian learning approach. Insurance: Mathematics and Economics 63: 153–68. [Google Scholar] [CrossRef]
- Li, Hong, Anja De Waegenaere, and Bertrand Melenberg. 2017. Robust mean–variance hedging of longevity risk. Journal of Risk and Insurance 84: 459–75. [Google Scholar] [CrossRef]
- Li, Han, Hong Li, Yang Lu, and Anastasios Panagiotelis. 2019. A forecast reconciliation approach to cause-of-death mortality modeling. Insurance: Mathematics and Economics 86: 122–33. [Google Scholar] [CrossRef]
- Li, Hong, and Johnny Siu-Hang Li. 2017. Optimizing the lee-carter approach in the presence of structural changes in time and age patterns of mortality improvements. Demography 54: 1073–95. [Google Scholar] [CrossRef] [PubMed]
- Li, Hong, and Yang Lu. 2017. Coherent forecasting of mortality rates: A sparse vector-autoregression approach. ASTIN Bulletin: The Journal of the IAA 47: 563–600. [Google Scholar] [CrossRef]
- Li, Hong, and Yang Lu. 2018. A bayesian non-parametric model for small population mortality. Scandinavian Actuarial Journal 2018: 605–28. [Google Scholar] [CrossRef]
- Li, Hong, and Yang Lu. 2019. Modeling cause-of-death mortality using hierarchical archimedean copula. Scandinavian Actuarial Journal 2019: 247–72. [Google Scholar] [CrossRef]
- Li, Hong, Yang Lu, and Pintao Lyu. 2018. Coherent Mortality Forecasting for Less Developed Countries. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3209392 (accessed on 1 November 2020).
- Li, Hong, and Yanlin Shi. 2020. Forecasting mortality with international linkages: A global vector-autoregression approach. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3700586 (accessed on 1 November 2020).
- Li, Hong, Ken Seng Tan, Shripad Tuljapurkar, and Wenjun Zhu. 2019. Gompertz law revisited: Forecasting mortality with a multi-factor exponential model. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3495369 (accessed on 1 November 2020).
- Li, Jackie. 2014. A quantitative comparison of simulation strategies for mortality projection. Annals of Actuarial Science 8: 281. [Google Scholar] [CrossRef]
- Li, Nan, and Ronald Lee. 2005. Coherent mortality forecasts for a group of populations: An extension of the Lee–Carter method. Demography 42: 575–94. [Google Scholar] [CrossRef] [PubMed]
- Li, Nan, Ronald Lee, and Patrick Gerland. 2013. Extending the lee-carter method to model the rotation of age patterns of mortality decline for long-term projections. Demography 50: 2037–51. [Google Scholar] [CrossRef]
- Renshaw, Arthur E., and Steven Haberman. 2003. Lee–carter mortality forecasting with age-specific enhancement. Insurance: Mathematics and Economics 33: 255–72. [Google Scholar] [CrossRef]
- Renshaw, Arthur E., and Steven Haberman. 2006. A cohort-based extension to the Lee–Carter model for mortality reduction factors. Insurance: Mathematics and Economics 38: 556–70. [Google Scholar] [CrossRef]
- Shi, Yanlin. 2020. Forecasting mortality rates with the adaptive spatial temporal autoregressive model. Journal of Forecasting. [Google Scholar] [CrossRef]
| 1. | A maximum likelihood method may also be employed to calibrate the parameters (Renshaw and Haberman 2003). |
| 2. | Note that the choice of the length of test sample (one fifth) is common among existing studies. Adopting other popular alternatives such as the last third, fourth and tenth sample will lead to robust results. |
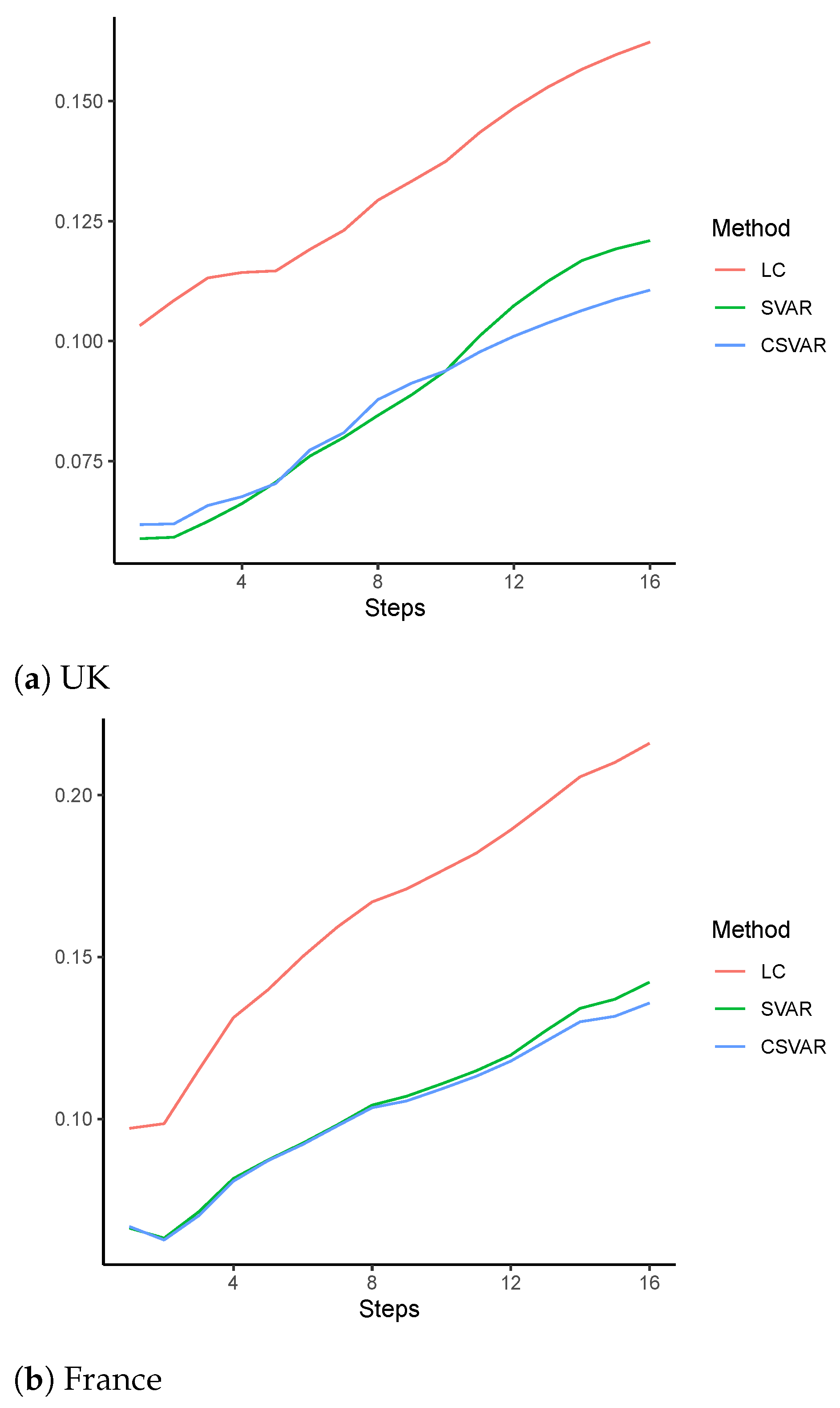
| Mean | Std. Dev. | ||||
|---|---|---|---|---|---|
| Panel A: UK | |||||
| LC | 0.1623 | 0.1454 | 0.0726 | 0.0912 | 0.1935 |
| SVAR | 0.1209 | 0.1056 | 0.0592 | 0.0536 | 0.1571 |
| CSVAR | 0.1106 | 0.1006 | 0.0463 | 0.0647 | 0.1321 |
| Panel B: France | |||||
| LC | 0.2159 | 0.1661 | 0.1387 | 0.0548 | 0.2601 |
| SVAR | 0.1422 | 0.1210 | 0.0750 | 0.0670 | 0.1594 |
| CSVAR | 0.1358 | 0.1143 | 0.0736 | 0.0584 | 0.1530 |
| UK | France | |||||
|---|---|---|---|---|---|---|
| LC | SVAR | CSVAR | LC | SVAR | CSVAR | |
| Five-year groups | 0.1674 | 0.1229 | 0.1150 | 0.2240 | 0.1429 | 0.1199 |
| 1970–2016 | 0.1507 | 0.1360 | 0.1163 | 0.1916 | 0.1428 | 0.1324 |
| Smoothed rates | 0.1562 | 0.1069 | 0.0987 | 0.2102 | 0.1285 | 0.1140 |
| Mean | Std. Dev. | ||||
|---|---|---|---|---|---|
| Panel A: UK | |||||
| LL | 0.1241 | 0.1053 | 0.0660 | 0.0530 | 0.1435 |
| SVAR | 0.1207 | 0.1052 | 0.0594 | 0.0512 | 0.1569 |
| CSVAR | 0.1159 | 0.1019 | 0.0555 | 0.0536 | 0.1354 |
| CSVAR | 0.1110 | 0.1012 | 0.0459 | 0.0666 | 0.1348 |
| Panel B: France | |||||
| LL | 0.1559 | 0.1303 | 0.0860 | 0.0630 | 0.1770 |
| SVAR | 0.1442 | 0.1220 | 0.0773 | 0.0664 | 0.1600 |
| CSVAR | 0.1396 | 0.1178 | 0.0754 | 0.0631 | 0.1469 |
| CSVAR | 0.1046 | 0.0906 | 0.0526 | 0.0521 | 0.1172 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Shi, Y. Mortality Forecasting with an Age-Coherent Sparse VAR Model. Risks 2021, 9, 35. https://doi.org/10.3390/risks9020035
Li H, Shi Y. Mortality Forecasting with an Age-Coherent Sparse VAR Model. Risks. 2021; 9(2):35. https://doi.org/10.3390/risks9020035
Chicago/Turabian StyleLi, Hong, and Yanlin Shi. 2021. "Mortality Forecasting with an Age-Coherent Sparse VAR Model" Risks 9, no. 2: 35. https://doi.org/10.3390/risks9020035
APA StyleLi, H., & Shi, Y. (2021). Mortality Forecasting with an Age-Coherent Sparse VAR Model. Risks, 9(2), 35. https://doi.org/10.3390/risks9020035







